
文档内容
1. 利用Excel进行一元线性回归分析
2. 利用Excel进行多元线性回归分析
1. 利用Excel进行一元线性回归分析
第一步,录入数据
以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。录入结果见下图(图1)。
图1
第二步,作散点图
如图2所示,选中数据(包括自变量和因变量),点击“图表向导”图标;或者在“插
入”菜单中打开“图表(H)”。图表向导的图标为。选中数据后,数据变为蓝色(图2)。
图2
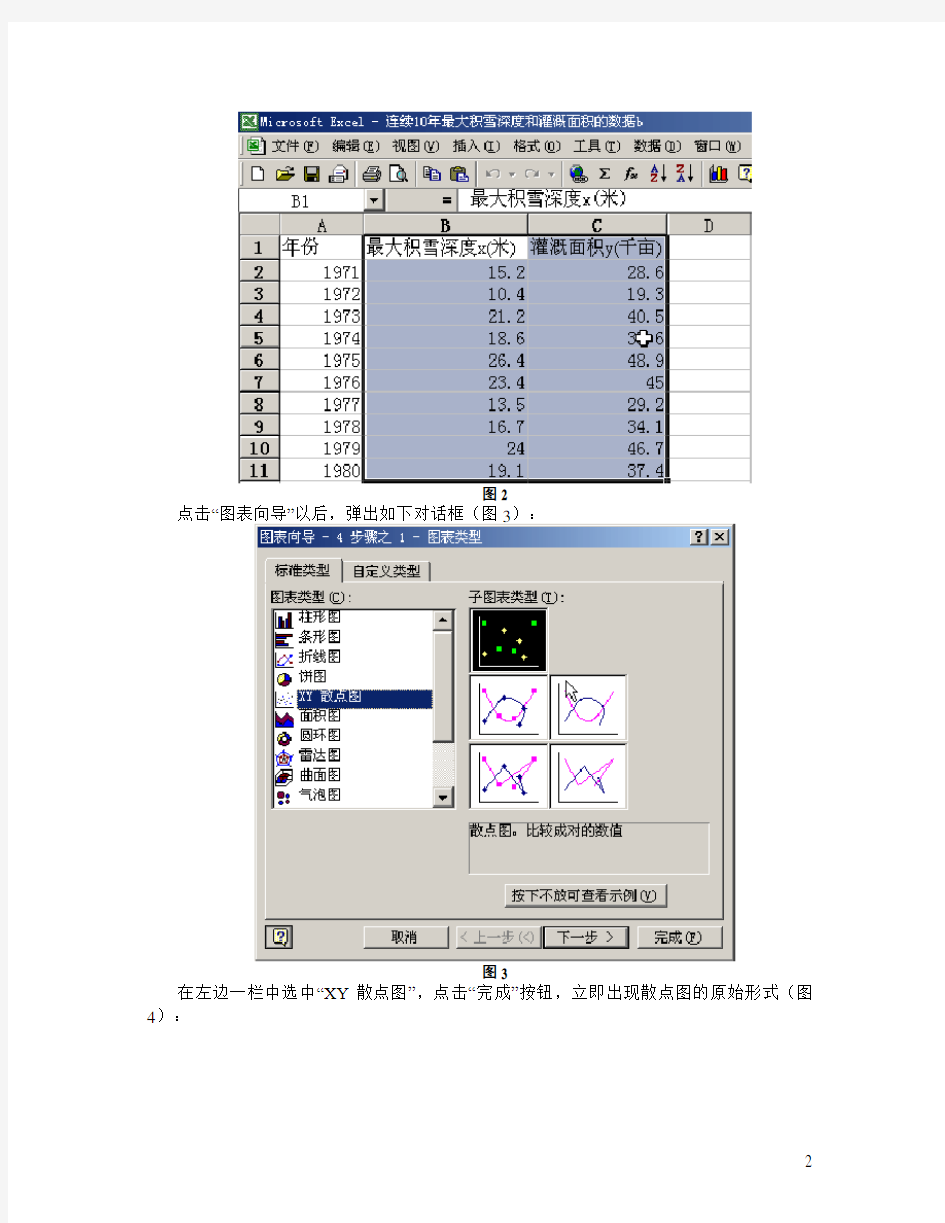
点击“图表向导”以后,弹出如下对话框(图3):
图3
在左边一栏中选中“XY散点图”,点击“完成”按钮,立即出现散点图的原始形式(图4):
灌溉面积y(千亩)
01020304050600
10
20
30
灌溉面积y(千亩)
图4
第三步,回归
观察散点图,判断点列分布是否具有线性趋势。只有当数据具有线性分布特征时,才能采用线性回归分析方法。从图中可以看出,本例数据具有线性分布趋势,可以进行线性回归。
回归的步骤如下:
1. 首先,打开“工具”下拉菜单,可见数据分析选项(见图5):
图5
用鼠标双击“数据分析”选项,弹出“数据分析”对话框(图6):
图6
2.然后,选择“回归”,确定,弹出如下选项表(图7):
图7
进行如下选择:X、Y值的输入区域(B1:B11,C1:C11),标志,置信度(95%),新工作表组,残差,线性拟合图(图8-1)。
或者:X、Y值的输入区域(B2:B11,C2:C11),置信度(95%),新工作表组,残差,线性拟合图(图8-2)。
注意:选中数据“标志”和不选“标志”,X、Y值的输入区域是不一样的:前者包括数据标志:
最大积雪深度x(米) 灌溉面积y(千亩)
后者不包括。这一点务请注意(图8)。
图8-1包括数据“标志”
图8-2不包括数据“标志”
3.再后,确定,取得回归结果(图9)。
图9线性回归结果
4. 最后,读取回归结果如下:
截距:356.2=a ;斜率:813.1=b ;相关系数:989.0=R ;测定系数:979.02=R ;F 值:945.371=F ;t 值:286.19=t ;标准离差(标准误差):419.1=s ;回归平方和:854.748SSr =;剩余平方和:107.16SSe =;y 的误差平方和即总平方和:961.764SSt =。
5. 建立回归模型,并对结果进行检验
模型为:x y
813.1356.2?+= 至于检验,R 、R 2、F 值、t 值等均可以直接从回归结果中读出。实际上,8,05.0632.0989416.0R R =>=,检验通过。有了R 值,F 值和t 值均可计算出来。
F 值的计算公式和结果为:
8,05.022
22
32.5945.371)
989416.01(1
1101
989416
.0)
1(1
1
F R k n R F =>=---=
---=
显然与表中的结果一样。
T 值的计算公式和结果为:
8,05.02
306.2286.191
110979416.01979416.01
1t k n R R t =>=---=
---=
回归结果中给出了残差(图10),据此可以计算标准离差。首先求残差的平方
2
2)?(i i i y
y -=ε,然后求残差平方和107.16174.0724.1101
2
=++==∑==Λn i i
S ε
,于是标准
离差为
419.1
8
107.161
)?(1112
===---=
∑=S v y y k n s n
i i
i 于是
15.0~1.0%15~100388.053
.36419.1=<==y s
图10y 的预测值及其相应的残差等
进而,可以计算DW 值(参见图11),计算公式及结果为
751.0417.0)911.1()313.1()833.0417.0()313.1911.1()(DW 2
222
21
22
2
1=++-+--+++-=-=
∑∑==-ΛΛn
i i n
i i i εεε
取05.0=α,1=k ,10=n (显然81110=--=v ),查表得94.0=l d ,29.1=u d 。显然,DW=0.751<94.0=l d ,可见有序列正相关,预测的结果令人怀疑。
图11利用残差计算DW 值
利用Excel快速估计模型的方法:
2.用鼠标指向图4中的数据点列,单击右键,出现如下选择菜单(图12):
图12
2. 点击“添加趋势线?”,弹出如下选择框(图13):
图13
3. 在“分析类型”中选择“线性(L)”,然后打开选项单(图14):
图14
4. 在选择框中选中“显示公式(E )”和“显示R 平方值?”(如图14),确定,立即得到回归结果如下(图15):
图表标题
y = 1.8129x + 2.3564
R 2 = 0.9789
01020304050600
10
20
30
灌溉面积y(千亩)线性 (灌溉面积y(千亩))
图15
在图15中,给出了回归模型和相应的测定系数即拟合优度。
顺便说明残差分析:如果在图8中选中“残差图(D)”,则可以自动生成残差图(图12)。
图16
回归分析原则上要求残差分布是无趋势的,如果在图中添加趋势线,则趋势线应该是与x 轴平行的,且测定系数很小。事实上,添加趋势线的结果如下(图17):
图17
可见残差分布图基本满足回归分析的要求。
预测分析
虽然DW检验似乎不能通过,但这里采用的变量相关分析,与纯粹的时间序列分析不同(时间序列分析应该以时间为自变量)。从残差图看来,模型的序列似乎并非具有较强的自相关性,因为残差分布相当随机。因此,仍有可能进行预测分析。现在假定:有人在1981年测得最大积雪深度为27.5米,他怎样预测当年的灌溉面积?
下面给出Excel 2000的操作步骤:
2.在图9所示的回归结果中,复制回归参数(包括截距和斜率),然后粘帖到图1
所示的原始数据附近;并将1981年观测的最大积雪深度27.5写在1980年之后
(图18)。
图18
2. 将光标至于图18所示的D2单元格中,按等于号“=”,点击F2单元格(对应于截距a=2.356…),按F4键,按加号“+”,点击F3单元格(对应于斜率b=1.812…),按F4键,按乘号“*”,点击B2单元格(对应于自变量x 1),于是得到表达式“=$F$2+$F$3*B2”
(图19),相当于表达式11*?x b a y
+=,回车,立即得到9128.29?1=y ,即1971年灌溉面积的计算值。
图19
3. 将十字光标标至于D2单元格的右下角,当粗十字变成细十字以后,按住鼠标左键,往下一拉,各年份的灌溉面积的计算值立即出现,其中1981年对应的D12单元格的
52.212
即我们所需要的预测数据,即有212.52?11=y
千亩(图20)。
图20
4. 进一步地,如果可以测得1982年及其以后各年份的数据,输入单元格B13及其下面的单元格中,在D13及其以下的单元格中,立即出现预测数值。例如,假定1982年的最
大积雪深度为7.2312=x 米,可以算得323.45?12=y
千亩;1983年的最大积雪深度为7.1513=x ,容易得到819.31?13=y
千亩(图21)。
图21预测结果(1981-1983)
最后大家思考一下为什么DW 检验对本例中的问题未必有效?
2. 利用Excel进行多元线性回归分析
【例】某省工业产值、农业产值、固定资产投资对运输业产值的影响分析。
Excel 2000的操作方法与一元线性回归分析大同小异:
第一步,录入数据(图1)。
图1 录入的原始数据
第二步,数据分析
1. 沿着主菜单的“工具(T)”→“数据分析(D)…” 路径打开“数据分析”对话框,选择“回归”,然后“确定”,弹出“回归”分析对话框,对话框的各选项与一元线性回归基本相同(图2)。下面只说明x值的设置方法:
首先,将光标置于“X值输入区域(X)”中(图2);
然后,从图1所示的C1单元格起,至E19止,选中用作自变量全部数据连同标志,这时“X值输入区域(X)”的空白栏中立即出现“$C$1:$E$19”——当然,也可以通过直接在“X值输入区域(X)”的空白栏中输入“$C$1:$E$19”的办法实现这一步骤。注意:与一元线性回归的设置一样,这里数据范围包括数据标志:
工业产值x1 农业产值
x2
固定资产投资
x3
运输业产
值y
故对话框中一定选中标志项(图3)。如果不设“标志”项,则“X值输入区域(X)”的空白栏中应为“$C$2:$E$19”,“Y值输入区域(Y)”的空白栏中则是“$F$2:$F$19”。否则,计算结果不会准确。
图2 x值以外的各项设置
图3 设置完毕后的对话框(包括数据标志)
2. 完成上述设置以后,确定,立即给出回归结果。由于这里的“输出选项”选中了“新工作表组(P)”(图3),输出结果在出现在新建的工作表上(图4)。
从图4的“输出摘要(SUMMARY OUTPUT)”中可以读出:
0044.1-=a ,053326.01=b ,00402.02-=b ,090694.03=b ,994296.0=R ,
988625.02=R ,335426.0=s ,5799.405=F ,940648.21=b t ,28629.02-=b t ,489706.33=b t 。
根据残差数据,不难计算DW 值,方法与一元线性回归完全一样。 根据回归系数可以建立如下多元线性模型:
321090694.000402.055326.00044.1?x x x y
+-+-= 由于① x 2的回归系数b 2的符号与事理不符,② b 2的t 检验值为负,③ b 2的绝对值很小,可以判定,自变量之间可能存在多重共线性问题。
图4 第一次回归结果
3. 剔除异常变量x 2(农业产值),用剩余的自变量x 1、x 3与y 回归(图5),回归步骤无非是重复上述过程(参见图6,注意这里没设数据“标志”),最后给出的回归结果(图7)。
图5 剔除异常变量“农业产值(x2)”
图6 回归对话框的设置(不包括数据标志)
从图7中容易读出回归结果:
89889.0-=a ,051328.01=b ,091229.03=b ,994263.0=R ,988558.02=R ,324999.0=s ,973.647=F ,200968.41=b t ,632285.33=b t 。
显然,相对于第一次回归结果,回归系数的符号正常,检验参数F 值提高了,标准误差s 值降低了,t 值检验均可通过。相关系数R 有所降低,这也比较正常——一般来说,增加变量数目通常提供复相关系数,减少变量则降低复相关系数。回归结果可以接受,建立二元回归模型如下:
89889.0091229.0051328.031-+=x x y
或者
89889.0*091229.0*051328.0固定资产投资-工业产值+运输业产值=
图7 剔除“农业产值”后的回归结果