2021闵行初三数学一模

2021年上海市16区中考数学一模汇编专题15 几何综合（解答题25题压轴题）1．（2021·上海徐汇区·九年级一模）如图，在Rt ABC 中，90ACB ∠=︒，12AC =，5BC =，点D 是边AC 上的动点，以CD 为边在ABC 外作正方形CDEF ，分别联结AE 、BE ，BE 与AC 交于点G ． （1）当AE BE ⊥时，求正方形CDEF 的面积；（2）延长ED 交AB 于点H ，如果BEH △和ABG 相似，求sin ABE ∠的值；（3）当AG AE =时，求CD 的长．2．（2021·上海长宁区·九年级一模）己知，在矩形ABCD中，点M是边AB上的一个点（与点A、B不重合），联结CM，作∠CMF＝90°，且MF分别交边AD于点E、交边CD的延长线于点F．点G为线段MF的中点，联结DG．（1）如图1，如果AD＝AM＝4，当点E与点G重合时，求∠MFC的面积；（2）如图2，如果AM＝2，BM＝4．当点G在矩形ABCD内部时，设AD＝x，DG2＝y，求y关于x的函数解析式，并写出定义域；（3）如果AM＝6，CD＝8，∠F＝∠EDG，求线段AD的长．（直接写出计算结果）3．（2021·上海宝山区·九年级一模）如图，已知ABC 中，90ACB ∠=︒，AC BC =，点D 、E 在边AB 上，45DCE ∠=︒，过点A 作AB 的垂线交CE 的延长线于点M ，联结MD ．（1）求证：2CE BE DE =⋅；（2）当3AC =，2AD BD =时，求DE 的长；（3）过点M 作射线CD 的垂线，垂足为点F ，设BD x BC=，tan FMD y ∠=，求y 关于x 的函数关系式，并写出定义域．4．（2021·上海浦东新区·九年级一模）四边形ABCD 是菱形，∠B≤90°，点E 为边BC 上一点，联结AE ，过点E 作EF∠AE ，EF 与边CD 交于点F ，且EC=3CF ．（1）如图1，当∠B=90°时，求ABE S 与ECF S 的比值；（2）如图2，当点E 是边BC 的中点时，求cos B 的值；（3）如图3，联结AF ，当∠AFE=∠B 且CF=2时，求菱形的边长．5．（2021·上海杨浦区·九年级一模）如图，已知在Rt ABC 中，90ACB ∠=︒，4AC BC ==，点D 为边BC 上一动点（与点B 、C 不重合），点E 为边AB 上一点，EDB ADC ∠=∠，过点E 作EF AD ⊥，垂足为点G ，交射线AC 于点F ．（1）如果点D 为边BC 的中点，求DAB ∠的正切值；（2）当点F 在边AC 上时，设CD x =，CF y =，求y 关于x 的函数解析式及定义域；（3）联结DF 如果CDF 与AGE 相似，求线段CD 的长．6．（2021·上海青浦区·九年级一模）在ABC 中，90C ∠=︒，2AC =，BC =D 为边AC 的中点（如图），点P 、Q 分别是射线BC 、BA 上的动点，且BQ =，联结PQ 、QD 、DP ．（1）求证：PQ AB ⊥；（2）如果点P 在线段BC 上，当PQD △是直角三角形时，求BP 的长；（3）将PQD △沿直线QP 翻折，点D 的对应点为点'D ，如果点'D 位于ABC 内，请直接写出BP 的取值范围．7. （2021黄浦一模）如图，四边形ABCD 中，4AB AD ==，3CB CD ==，90ABC ADC ∠=∠=︒，点M 、N 是边AB 、AD 上的动点，且12MCN BCD ∠=∠，CM 、CN 与对角线BD 分别交于点P 、Q ．（1）求sin MCN ∠的值：（2）当DN DC =时，求CNM ∠的度数；（3）试问：在点M 、N 的运动过程中，线段比PQ MN的值是否发生变化？如不变，请求出这个值；如变化，请至少给出两个可能的值，并说明点N 相度的位置．8．（2021·上海静安区·九年级一模）已知∠MAN是锐角，点B、C在边AM上，点D在边AN上，∠EBD=∠MAN，且CE∠BD，sin∠MAN=35，AB=5，AC=9．（1）如图1，当CE与边AN相交于点F时，求证：DF·CE=BC·BE；（2）当点E在边AN上时，求AD的长；（3）当点E在∠MAN外部时，设AD=x，∠BCE的面积为y，求y与x之间的函数解析式，并写出定义域．9．（2021·上海崇明区·九年级一模）如图，Rt ABC 中，90ACB ∠=︒，6AC =，8BC =，点D 为斜边AB 的中点，ED AB ⊥，交边BC 于点E ，点P 为射线AC 上的动点，点Q 为边BC 上的动点，且运动过程中始终保持PD QD ⊥．（1）求证：ADP EDQ △△；（2）设AP x =，BQ y =，求y 关于x 的函数解析式，并写出该函数的定义域；（3）连接PQ ，交线段ED 于点F ，当PDF 为等腰三角形时，求线段AP 的长．10．（2021·上海闵行区·九年级一模）如图，在矩形ABCD 中，2AB =，1AD =，点E 在边AB 上（点E 与端点A 、B 不重合），联结DE ，过点D 作DF DE ⊥，交BC 的延长线于点F ，连接EF ，与对角线AC 、边CD 分别交于点G 、H ．设AE x =，DH y =．（1）求证：ADE CDF ∽△△，并求EFD 的正切值；（2）求y 关于x 的函数解析式，并写出该函数的定义域；（3）连接BG ，当BGE △与DEH △相似时，求x 的值．11．（2021·上海奉贤区·九年级一模）已知圆O 的直径4AB =，点P 为弧AB 上一点，联结PA PO 、，点C 为劣弧AP 上一点(点C 不与点A 、P 重合），联结BC 交PA PO 、于点D E 、()1如图，当78cos CBO ∠=时，求BC 的长；()2当点C 为劣弧AP 的中点，且EDP ∆与AOP ∆相似时，求ABC ∠的度数；()3当2AD DP =，且BEO ∆为直角三角形时．求四边形AOED 的面积．12．（2021·上海普陀区·九年级一模）如图，矩形ABCD 中，1AB =，3BC =，点E 是边BC 上一个动点（不与点B 、C 重合），AE 的垂线AF 交CD 的延长线于点F ．点G 在线段EF 上，满足:1:2FG GE =．设BE x =．（1）求证：AD DF AB BE=； （2）当点G 在ADF 的内部时，用x 的代数式表示ADG ∠的余切；（3）当FGD AFE ∠=∠时，求线段BE 的长．13. （2021虹口一模）如图，在ABC 中，90ABC ∠=︒，3AB =，4BC =，过点A 作射线//AM BC ，点D 、E 是射线AM 上的两点（点D 不与点A 重合，点E 在点D 右侧），连接BD 、BE 分别交边AC 于点F 、G ，DBE C ∠=∠．（1）当1AD =时，求FB 的长（2）设AD x =，FG y =，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结DG 并延长交边BC 于点H ，如果DBH △是等腰三角形，请直接写出AD 的长．14.（2021宝山一模） 如图，已知ABC 中，90ACB ∠=︒，AC BC =，点D 、E 在边AB 上，45DCE ∠=︒，过点A 作AB 的垂线交CE 的延长线于点M ，联结MD ．（1）求证：2CE BE DE =⋅；（2）当3AC =，2AD BD =时，求DE 的长；（3）过点M 作射线CD 的垂线，垂足为点F ，设BD x BC=，tan FMD y ∠=，求y 关于x 的函数关系式，并写出定义域．15. （2021松江一模）如图，已知在等腰ABC 中，AB AC ==，tan 2ABC ∠=，BF AC ⊥，垂足为F ，点D 是边AB 上一点（不与A ，B 重合）（1）求边BC 的长；（2）如图2，延长DF 交BC 的延长线于点G ，如果CG 4=，求线段AD 的长；（3）过点D 作DE BC ⊥，垂足为E ，DE 交BF 于点Q ，连接DF ，如果DQF △和ABC 相似，求线段BD 的长．16.（2021嘉定一模）在矩形ABCD 中，6AB =，8AD =，点E 在CD 边上，1tan 2DAE ∠=.点F 是线段AE 上一点，联结BF ，CF .（1）如图11，如果3tan 4CBF ∠=，求线段AF 的长； （2）如图12，如果12CF BC =， ①求证：∠CFE =∠DAE ；②求线段EF 的长.2021年上海市16区中考数学一模汇编专题15 几何综合（解答题25题压轴题）1．（2021·上海徐汇区·九年级一模）如图，在Rt ABC 中，90ACB ∠=︒，12AC =，5BC =，点D 是边AC 上的动点，以CD 为边在ABC 外作正方形CDEF ，分别联结AE 、BE ，BE 与AC 交于点G ．（1）当AE BE ⊥时，求正方形CDEF 的面积；（2）延长ED 交AB 于点H ，如果BEH △和ABG 相似，求sin ABE ∠的值； （3）当AG AE =时，求CD 的长．【答案】（1）494；（2）119169；（3． 【分析】（1）利用勾股定理求出AB 的长，设CD=x ，则AD=12-x ，利用勾股定理得出13²=x²+(12-x)²+(5+x)²+x²，求出x 的值，再利用正方形的面积公式求解即可；（2）先证∠BAC=∠EBF ，设边长为x ，利用三角函数求出x 的值，再求∠ABE 的正弦值即可；（3）设边长为x ，利用∠BCG∠∠EDG ，得出5DE DG x BC GC ==，然后联立512125x AG GC x AE ⎧=-=-⎪+⎨⎪=⎩，根据AG=AE ，求解即可．【详解】解：（1）Rt∠ABC 中，∠ACB=90°，AC=12，BC=5，13= ，设CD=x ，则AD=12-x ，在∠ADE 中，AE²=DE²+AD²=x²+(12-x)²，在∠BFE 中，BE²=BF²+EF²=(5+x)²+x²，在∠ABE 中，AE∠BE ，∠AB²=AE²+BE²，即13²=x²+(12-x)²+(5+x)²+x²，解得x=72，∠正方形CDEF 的面积=CD²=72×72=494； （2）如图：延长ED 交AB 于H ，∠∠BEH∠∠ABG ，且∠ABG=∠EBH ，∠∠BEH=∠BAG ， ∠DE∠EF ，∠∠BEH=∠EBF ，∠∠BAC=∠EBF ，设边长为x ， 则tan∠EBF=5x x +，tan∠BAC=512，令5x x +=512，则x=257, ∠25125971284HDAH ADBCAB AC-====，∠59767138484AH =⋅=， ∠BH=13-AH=32584，HD=5929558484⋅=， ∠HE=HD+x=59584， 过H 作HM ，与BE 相交于M ，5sin sin 13B M AG HE ∠=∠=,595sin 84s 951419165in 81332HM HE HEM ABE BH BH ⨯⋅∠∠====；（3）∠DE//BC,∠∠BCG∠∠EDG ，设边长为x ，∠5DE DG xBC GC ==， ∠DG+GC=x ，∠DG=25x x +，GC=55x x +，则512125x AG GC x AE ⎧=-=-⎪+⎨⎪=⎩，令AG=AE ， 则或（舍去）．【点睛】本题考查了勾股定理、相似三角形的性质与判定及利用三角函数求解，解题的关键是熟练掌握相关性质，正确构造辅助线，表示相关线段的长度．2．（2021·上海长宁区·九年级一模）己知，在矩形ABCD 中，点M 是边AB 上的一个点（与点A 、B 不重合），联结CM ，作∠CMF ＝90°，且MF 分别交边AD 于点E 、交边CD 的延长线于点F ．点G 为线段MF 的中点，联结DG ．（1）如图1，如果AD ＝AM ＝4，当点E 与点G 重合时，求∠MFC 的面积；（2）如图2，如果AM ＝2，BM ＝4．当点G 在矩形ABCD 内部时，设AD ＝x ，DG 2＝y ，求y 关于x 的函数解析式，并写出定义域；（3）如果AM ＝6，CD ＝8，∠F ＝∠EDG ，求线段AD 的长．（直接写出计算结果）【答案】（1）20；（2）()4244644x x y x =-+<；（3）AD =或【分析】（1）运用ASA 证明∠AME DFE ≅∆求出FD 的长再运用三角形面积公式即可得到答案；（2）证明FHM MHC △∽△，根据相似三角形的性质列出比例式，代入相关数值即可求出函数关系式；（3）分点G 在矩形内部和外部两种情况求解即可． 【详解】解（1）过M 作MH∠DC ，垂足为H ，如图1易得四边形ADHM 是正方形，∠AE ED =又∠FED=∠MEA∠∠()AME DFE ASA ≅∆ ∠.4AM FD DH ===∠MH FC ⊥∠∠FHM=∠CHM=90°，∠HCM+∠HMC=90° ∠90FMC ∠=︒，∠∠FMH+∠HMC=90°∠∠FMH=∠HCM∠∠FMH∠∠MCH ∠12MH HC FH MH ==∠2CH =，CF 10=∠1202MFC S CF MH =⋅=△ （2）过M 作MH∠DC ，过G 点作GP∠DC ，垂足分别为H ，P ，如图2，∠FG GM =，//GP MH ∠111222GP MH AD x ===，12FP PH FH == ∠MH∠DC ，∠∠MHF=∠MHC=90°，∠HMC+∠ HCM=90° ∠∠FMC=90°，∠∠FMH+∠HMC=90° ∠∠FMH=∠HCM ，∠FHM MHC △∽△∠FH MH MH HC =，即4FH x x =，∠24x FH =∠28x PH =，228x DP =-，12GP x =∠222DG DP GP =+∠424644x x y =-+由00FH DP >⎧⎨>⎩ 可得4x <<∠定义域为4x <<（3）点G 在矩形内部时,延长DG 交AB 于J ，连接AG ，AF ，如图∠EDG EFD MCB ∠=∠=∠∠AD BC =∠ADJ BCM ≌△△， 2AJ BM == ∠1GJ GMDG GF==，∠AG DG =∠∠12=∠∠∠1390+∠=︒∠∠3490+∠=︒ ∠∠90AGE =︒∠AG 垂直平分FM ∠6AF AM ==∠4DF MJ ==∠AD ===点G 在矩形外部时，延长DG 交BA 延长线于L ，连接DM ，如图∠EDG EFD MCB ∠=∠=∠，AD BC =∠ADL BCM ≌△△， ∠2AL BM ==∠∠L CMD =∠，∠FMC 为直角，∠90DGE ∠=︒，DG 垂直平分FM ∠8DM DF ==，6AM =，∠AD =AD =或【点睛】收费题主要考查了三角形全等的判定与性质、垂直平分线的判定与性质，相似三角形的判定与性质，熟练掌握相关定理和性质是解答此题的关键．3．（2021·上海宝山区·九年级一模）如图，已知ABC 中，90ACB ∠=︒，AC BC =，点D 、E 在边AB 上，45DCE ∠=︒，过点A 作AB 的垂线交CE 的延长线于点M ，联结MD ．（1）求证：2CE BE DE =⋅；（2）当3AC =，2AD BD =时，求DE 的长； （3）过点M 作射线CD 的垂线，垂足为点F ，设BDx BC=，tan FMD y ∠=，求y 关于x 的函数关系式，并写出定义域．【答案】（1）见解析；（2）DE=6-；（3）)．【分析】（1）先证∠B=∠DCE ，再由∠DEC=∠CEB ，得出∠DEC∠∠CEB ，进而得出结论；（2）由∠DEC∠∠CEB 得BC=BE ，再由∠DEC∠∠DCA ，得AD=AC ，最后利用勾股定理求解即可；（3）连接EF ，先证∠BDC∠∠EDF ，得出FD DE CD BD =，进而得出FDMF=y ，然后结合已知条件得出结果． 【详解】解：（1）∠∠ACB=90°，∠∠B=45°，∠∠DCE=45°，∠∠B=∠DCE ，∠∠DEC=∠CEB ，∠∠DEC∠∠CEB ，∠EC DE BE CE=，故CE²=BE·DE ； （2）由题意得∠DCE 是等腰三角形，DC=CE ，由∠DEC∠∠CEB 得BC=BE ， 同理可得∠DEC∠∠DCA ，AD=AC ，∠BC=AC ，∠BE=AD=BC=AC ，∠AC=3，∠在Rt∠ABC中，AB²=BC²+AC²=9+9=18，，∠AD=2BD，∠BD=AB-AD=AB-3，-6，-3，∠DE=AB-BD--3)=6-．（3）连接EF，由三角形相似可得∠FED=∠DBC，∠EF∠BC，∠∠EFD=∠BCD，∠∠EDF=∠BDC，∠∠BDC∠∠EDF，∠FD DECD BD=，∠tan∠FMD=y，∠FDMF=y，在Rt∠MFC中，∠MCF=45°，∠MF=CF，∠FD FDCF MF==y，∠BDxBC=，BE=BC，∠BD BDxBE BC==，∠,FD BDy xCF BE==，∠DE=1xBDx-，CD=1yFDx-，∠FD DECD BD=，11y xy x=--，则y(1-y)=x(1-y)，y-xy=x-xy，．．【点睛】本题考查了相似三角形的性质与判定及勾股定理的应用，解题的关键是灵活运用相似三角形的性质与判定．4．（2021·上海浦东新区·九年级一模）四边形ABCD 是菱形，∠B≤90°，点E 为边BC 上一点，联结AE ，过点E 作EF∠AE ，EF 与边CD 交于点F ，且EC=3CF ． （1）如图1，当∠B=90°时，求ABE S与ECFS的比值；（2）如图2，当点E 是边BC 的中点时，求cos B 的值； （3）如图3，联结AF ，当∠AFE=∠B 且CF=2时，求菱形的边长．【答案】（1）94；（2）15；（3）17. 【分析】（1）先证明：,BEA CFE ∽可得：BE ABCF CE=，结合：3,EC CF =可得：3,AB BE =再设,,CF a BE b == 可得3,AB BC b a ==+而3AB b =，建立方程：33,b a b +=可得：3,2b a = 再利用相似三角形的性质可得答案．（2）延长,AE DC 相交于G ，过F 作FHAD ⊥于,H 连接AF ，先证明：,ABE GCE ≌可得：,,AB CG AE GE == 证明：AF FG =， 设,CF a = 再设DH x =， 利用22222,AF AH FH DF DH -==-求解x ，可得cos ,D 从而可得答案；（3）如图，过E 作EG DC ⊥交DC 的延长线于G ，延长CG 至H ,使,CG HG = 证明：6EH EC ==， 设,DF x = ,HG GC y == 证明：,AFE B D ECH H ∠=∠=∠=∠=∠可得：cos ,6EF ycoc AFE H AF ∠==∠=再证明：,FEH AFD ∽利用相似三角形的性质列方程组，解方程组可得答案．【详解】解：（1）四边形ABCD 是菱形，90B ∠=︒， ∴ 四边形ABCD 是正方形，90B C ∴∠=∠=︒，90BAE BEA ∴∠+∠=︒， ,EF AE ⊥ 90BEA CEF ∴∠+∠=︒， ,BAE CEF ∴∠=∠ ,BEA CFE ∴∽ BE AB CF CE ∴=，,BE CFAB CE∴= 3,EC CF =3,AB BE ∴= 设,,CF a BE b == 3,CE a ∴= 3,AB BC b a ∴==+ 而33,AB BE b ==33,b a b ∴+= 3,2b a ∴= 9,2AB a ∴= 22992.34ABE CEFaSAB SCE a ⎛⎫ ⎪⎛⎫∴===⎪ ⎪⎝⎭ ⎪⎝⎭（2）延长,AE DC 相交于G ，过F 作FH AD ⊥于,H 连接AF ，菱形ABCD ，//,AB CD ∴ ,BAE G ∴∠=∠ E 为BC 的中点，,BE CE ∴=,AEB CEG ∠=∠ ()ABE GCE AAS ∴≌,,,AB CG AE GE ∴==,AE EF ⊥ ,AF FG ∴=设,CF a = 则3,CE BE a == 6AB BC DC CG AD a =====，75,FG AF a DF a ∴===， 设,DH x = 22222,AF AH FH DF DH ∴-==-()()()2222765,a a x a x ∴--=- ,x a ∴= ,DH a ∴= 1cos ,55DH a DDF a ∴=== 由菱形ABCD 可得：,B D ∠=∠ 1cos .5B ∴=（3）如图，过E 作EG DC ⊥交DC 的延长线于G ，延长CG 至H ,使,CG HG =,,EC EH H ECH ∴=∠=∠ 23,CF CE CF ==， 6CE EH ∴==，设,DF x = ,HG GC y == 则2,DC AD x ==+ ,6HG y coc H EH ∴∠== 菱形ABCD ， ,//,B D AB CD ∴∠=∠ ,B ECH ∴∠=∠ ,AFE B ∠=∠,AFE B D ECH H ∴∠=∠=∠=∠=∠ cos ,6EF y coc AFE H AF ∴∠==∠= ,AFH AFE EFH D DAF ∠=∠+∠=∠+∠ ,EFH DAF ∴∠=∠,FEH AFD ∴∽ ,EH HF EF DF AD AF ∴== 622,26y y x x +∴==+ 361012xy xy y =⎧∴⎨=+⎩，解得：15,2.4x y =⎧⎨=⎩经检验：152.4x y =⎧⎨=⎩是原方程组的解，217,CD x ∴=+= 即菱形ABCD 的边长为：17. 【点睛】本题考查的是三角形全等的判定与性质，线段垂直平分线的性质，勾股定理的应用，菱形，正方形的性质，相似三角形的判定与性质，解直角三角形，解分式方程组，掌握以上知识是解题的关键． 5．（2021·上海杨浦区·九年级一模）如图，已知在Rt ABC 中，90ACB ∠=︒，4AC BC ==，点D 为边BC 上一动点（与点B 、C 不重合），点E 为边AB 上一点，EDB ADC ∠=∠，过点E 作EF AD ⊥，垂足为点G ，交射线AC 于点F ．（1）如果点D 为边BC 的中点，求DAB ∠的正切值；（2）当点F 在边AC 上时，设CD x =，CF y =，求y 关于x 的函数解析式及定义域；（3）联结DF 如果CDF 与AGE 相似，求线段CD 的长．【答案】（1）1tan 3DAB ∠=；（2）()2402y x x =-+<≤；（3）-4、8-． 【分析】（1））过点D 作DH AB ⊥于H ，在Rt ACB 中，利用勾股定理解得AD 、AB 的长，再结合等积法，解得DH 、AH 的长即可解题；（2）根据相似三角形对应边成比例的性质，表示()444x EH x -=+， 再证明AFE BDE 由AF AE DB BE =即)4444x y x x --=-+得到与x 的关系； （3）根据相似三角形对应边成比例的性质，结合（2）中y 关于x 的函数解析式联立方程组，继而解得x 、y 的值即可解题．【详解】（1）过点D 作DH AB ⊥于H ，在Rt ACB 中，AD =AB ==142ADB S DB AC ∴=⋅=12ADB S AB DH =⋅DH ∴=AH == 1tan 3DH DAB AH ∴∠==； （2）过E 作EH∠CB 于H∠EDB ADC ∠=∠，90C EHD ∠=∠=︒∠ACD EHD ．∠AC EH CD DH = 即44EH x x EH=--．∠()444x EH x -=+ ．∠EH∠CB ，90ACB ∠=︒，4AC BC ==∠)44x EB x -==+ ，AB =∠)44x AE x -=+∠EF AD ⊥，90C ∠=︒∠AFG ADC ∠=∠ ．∠EDB ADC ∠=∠ ∠AFG EDB ∠=∠．∠45FAE B ∠=∠=︒∠AFE BDE ．∠AF AE DB BE =即)4444x y x x --=-+()2402y x x =-+<≤； （3）在Rt∠MDB 中，DB=4-x,所以MD=MB=(4).2x - 在Rt∠ADM 中，AM=AB 一MB=)(4).22x x -=+所以tan∠DAB=44DM x AM x -=⋅+ 按照点F 的位置，分两种情况讨论∠CDF 与∠AGE 相似:①点F 在线段AC 上，此时y=4-2x.如图，如果∠FDC=∠DAB ，由tan∠FDC=tan∠DAB,得44y x x x-=⋅+结合y=4-2x ，整理，得x2+8x+16=0. 解得-4 或--4 （舍去）,如果∠CFD=∠DAB ，由tan∠CFD=tan∠DAB ，得4.4x x y x-=+ 结合y=4- -2x,整理，得x 2-16x+16=0.解得8x =-8+②点F 在线段AC 的延长线上，此时y=2x-4如图如果∠FDC=∠DAB,由44y x x x -=+结合y=2x -4，整理，得23160.x -=解得或3-（舍去） 如果∠CFD=∠DAB, 44x x y x-=+与y=2x -4整理，得238160.x x -+=此方程无解.综上，CD 的值为-4、8- 【点睛】本题考查勾股定理、相似三角形的性质，涉及解二元一次方程组等知识，解题关键是根据题意利用相似三角形性质构造方程．6．（2021·上海青浦区·九年级一模）在ABC 中，90C ∠=︒，2AC =，BC =D 为边AC 的中点（如图），点P 、Q 分别是射线BC 、BA 上的动点，且2BQ BP =，联结PQ 、QD 、DP ．（1）求证：PQ AB ⊥；（2）如果点P 在线段BC 上，当PQD △是直角三角形时，求BP 的长；（3）将PQD △沿直线QP 翻折，点D 的对应点为点'D ，如果点'D 位于ABC 内，请直接写出BP 的取值范围．【答案】（1）见解析；（2或6；（3）33BP << 【分析】（1）证明∠BPQ∠∠BAC 即可；（2）由∠PQD<90︒，只需要讨论两类情况，当90DPQ ∠=︒时，利用tan3AC B BC ===，求出∠B=30，30DPC ∠=︒，计算tan 30CD CP ︒===，根据BP=BC -CP 求值；当90PDQ ∠=︒时，过Q 作QE∠AC 交AC 于E ，则∠QED=∠PDQ=90C ∠=︒，证明∠EQD∠∠CDP ，得到QE ED CD CP=，设BP t =，过点Q 作QF∠BC 于F ，则四边形CEQF 是矩形，求出1344t QE F t t C +===，1CD =，CP t =，14DE CE CD =-=-，代入比例式求出t 的值； （3）只需考虑BP 的极限情况：①当'D 正好在BC 上时，如图3，设BP=m ，由'30DD C B ∠=∠=︒求出'CD =，'DP D P =，列得()'2CP D P CP DP m m +=+=+=计算求值即可；②另外一个极限情况时，如图4，当PQ 经过点D 时，求出PC=tan 602CD =︒，即可得到3BP =【详解】解：（1）在ABC 中，90C ∠=︒，2AC =，BC =∠4AB ==，∠BC AB ==，∠BQ BP =，∠BQ BP =∠BQ BC BP AB =，∠QBP CBA ∠=∠， BPQBAC ∴，∠90BQP BCA ∠=∠=︒，PQ AB ∴⊥；（2）90PQD ∠<︒，所以只需要讨论两类情况，当90DPQ ∠=︒时，如图1，在Rt∠ABC中，tan 3AC B BC ===，∠∠B=30， ∠9060QPB B ∠=︒-∠=︒，30DPC ∴∠=︒， ∠2AC =，点D 为边AC 的中点，∠CD=1，∠tan 30CD CP ︒===，BP BC CP ∴=-= 当90PDQ ∠=︒时，如图2，过Q 作QE∠AC 交AC 于E ，则∠QED=∠PDQ=90C ∠=︒，∠∠EQD+∠EDQ=∠EDQ+∠CDP=90︒，EQD CDP ∴，QE ED CD CP∴=， 设BP t =，过点Q 作QF∠BC 于F ，则四边形CEQF 是矩形，∠∠B=30，∠BQP=90︒， ∠PQ=12t ，∠60QPB ∠=︒，∠cos 6014PF PQ t =⋅︒=，sin 60QF PQ =⋅︒=，∠1344t QE F t t C +===，1CD =，CP t =，14DE CE CD t =-=-，134t -∴=t ∴=或t =（舍去）， 综上，BP或6；（3）只需考虑BP 的极限情况：①当'D 正好在BC 上时，如图3，设BP=m ，'DD PQ ⊥，'30DD C B ∴∠=∠=︒，'CD ∴=30CDP ∠=︒，又'DP D P =，()'2CP D P CP DP m m ∴+=+=+=3m ∴=； ②另外一个极限情况时，如图4，当PQ 经过点D 时，∠60P ∠=︒，90DCP ∠=︒，CD=1， ∠PC=tan 603CD =︒，∠3BP =BP <<． ．【点睛】此题考查相似三角形的判定及性质，锐角三角函数，直角三角形30度角所对的直角边等于斜边的性质，矩形的判定及性质，熟记各定理是解题的关键．7. （2021黄浦一模）如图，四边形ABCD 中，4AB AD ==，3CB CD ==，90ABC ADC ∠=∠=︒，点M 、N 是边AB 、AD 上的动点，且12MCN BCD ∠=∠，CM 、CN 与对角线BD 分别交于点P 、Q ．（1）求sin MCN ∠的值：（2）当DN DC =时，求CNM ∠的度数；（3）试问：在点M 、N 的运动过程中，线段比PQ MN的值是否发生变化？如不变，请求出这个值；如变化，请至少给出两个可能的值，并说明点N 相度的位置．【答案】（1）45；（2）45°；（3）不会发生变化，35． 【分析】（1）连接AC,利用垂直平分线性质，构造Rt △ABC ，由正弦三角函数即可求得；（2）证明 △BCG ≌△DCN ，得到角相等，再由角相等，得△GMC ≌△NMC ，由DN DC =解答即可； （3）由D 、C 、N 、P 四点共圆，得到∠CPD=∠CND=∠MNC ，再得△CPQ ∽△CNM ，由此解答即可．【详解】解：（1）连接AC ∵4AB AD ==，3CB CD ==∴AC 垂直平分BD∴∠ACB=∠ACD=12∠BCD=∠MCN 在Rt △ABC 中，AB=4，AC=3∴5== ∴sin MCN ∠=sin ∠ACB=45AB AC = （2）延长AB 至G 点，使BG=DN ，连接CG ，∵CB=CD ∠CBG=∠CBN=90°∴△BCG ≌△DCN ∴∠G=∠CND ，CN=CG ，∠BCG=∠DCN∴∠MCN=12∠BCD ∴∠MCB+∠NCD=12∠BCD ∴∠GCM=∠GCB+∠GCM=12∠BCD=∠MCN ∵CM=CM ， ∠G=∠CND,∴△GMC ≌△NMC ∴∠G=∠MNC=∠DNC当DN=NC时∠DNC=∠DCN=45°∴∠DNC=∠CNM=45°（3）连接NP, ∵∠ADC=∠ADO+∠CDO=90°∠ADO+∠CDO=90°∴∠ADO=∠COD=12∠BCD=∠MCN∴∠NDP=∠NCP∴D、C、N、P四点共圆，∴∠NPC+∠NDC=180°∵∠NDC=90°∴∠NPC=90°∴∠CPD=∠CND=∠MNC∴△CPQ∽△CNM∴PQ CP MN CN=在Rt△CPN中，CPCN=cos∠MCN=cos∠ACB=35∴不会发生变化35PQMN=【点睛】本题考查了线段垂直平分线的性质，三角形全等性质与判断，三角形相似等知识点，解题的关键是掌握性质与判定．8．（2021·上海静安区·九年级一模）已知∠MAN是锐角，点B、C在边AM上，点D在边AN上，∠EBD=∠MAN，且CE∠BD，sin∠MAN=35，AB=5，AC=9．（1）如图1，当CE与边AN相交于点F时，求证：DF·CE=BC·BE；（2）当点E在边AN上时，求AD的长；（3）当点E在∠MAN外部时，设AD=x，∠BCE的面积为y，求y与x之间的函数解析式，并写出定义域．【答案】（1）证明见解析；（2）AD=4±（3）224825x y x x =-+．定义域为：44x <<+． 【分析】（1）根据CE∠BD ，得出∠CEB=∠DBE ，∠DBA=∠BCE 结合题干证明出∠ABD∠∠ECB ，进而得到AD EBAB EC＝，再等量代换即可得到DF·CE=BC·BE ．（2）过点B 作BH∠AN ，垂足为H ．根据条件先证明出∠CEB∠∠CAE ，得到2CE =CB CA ⋅，代入求出CE ，再根据BD ABCE AC=求出BD ，利用三角函数求出BH ，根据勾股定理即可求出AD ． （3）过点B 作BH∠AN ，垂足为H ．BH=4，AH=3，DH=4x -根据∠ECB∠∠ABD 得到22EBC ADB S BC S BD △△＝，代入化简为224825xy x x =-+即可求解．【详解】解：（1）∠CE∠BD ，∠∠CEB=∠DBE ，∠DBA=∠BCE ．∠∠A=∠DBE ，∠∠A=∠BEC ．∠∠ABD∠∠ECB ，∠AD EB AB EC ＝．∠AD DF AB BC=，∠EB DFEC BC =，∠DF·CE=BC·BE ．（2）过点B 作BH∠AN ，垂足为H ．∠CE∠BD，∠∠CEB=∠EBD=∠A，又∠∠BCE=∠ECA，∠∠CEB∠∠CAE，∠CE CACB CE=，∠2CE=CB CA⋅．∠AB=5，AC=9，∠BC=4，∠24936CE==⨯，∠CE=6．∠BD ABCE AC=，∠561093AB CEBD==AC⋅⨯=．在Rt∠ABH中，3sin535BH AB A=⋅=⨯=，∠AH=224AB BH-=．==．AD=4±（3）过点B作BH∠AN，垂足为H．BH=4，AH=3，DH=4x-．2222224)3825BD=DH+BH x x x=-+=-+（．∠∠ECB∠∠ABD，∠22EBCADBS BCS BD△△＝．∠1322ABDS AD BH x=⋅△＝，∠21638252yx xx=-+，∠224825xyx x=-+．定义域为44x<．【点睛】此题属于平面几何的综合应用，主要利用三角形相似，找到相似比，根据相似比求值，计算量较大，有一定难度．9．（2021·上海崇明区·九年级一模）如图，Rt ABC中，90ACB∠=︒，6AC=，8BC=，点D为斜边AB 的中点，ED AB⊥，交边BC于点E，点P为射线AC上的动点，点Q为边BC上的动点，且运动过程中始终保持PD QD⊥．（1）求证：ADP EDQ △△；（2）设AP x =，BQ y =，求y 关于x 的函数解析式，并写出该函数的定义域； （3）连接PQ ，交线段ED 于点F ，当PDF 为等腰三角形时，求线段AP 的长．【答案】（1）证明见解析；（2）253250443y x x ⎛⎫=-≤≤ ⎪⎝⎭；（3）256或53 【分析】（1）根据ED AB ⊥，PD QD ⊥得A DEQ ∠=∠，ADP EDQ ∠=∠，即可得ADP EDQ △△．（2）先根据相似三角形的性质、中点性质以及锐角三角函数的概念得出tan EQ ED EDB AP AD BD===，求出34EQ x =，再根据BQ BE EQ =-，列出函数关系式，化简即可． （3）先证PDFBDQ △△，再分3种情况讨论，分别求出AP 的长．【详解】解：（1）PD QD ⊥，ED AB ⊥∠A DEQ ∠=∠，ADP EDQ ∠=∠，∠ADP EDQ △△．（2）ADP EDQ △△，∠EQ EDAP AD= 又点D 为斜边AB 的中点，∠AD BD = ， EQ ED EDAP AD BD==又ED AB ⊥在Rt BDE 中tan =ED ED EQB BD AD AP==，又6tan =8AC BC DE B BD ==，由勾股定理得：BC =10D 为AB 中点， ∠BD =5， DE =154，由勾股定理得：BE =254AP x =，可得34EQ x =，BQ BE EQ =-， 253250443y x x ⎛⎫=-≤≤ ⎪⎝⎭． （3）tan tan DQ ED EDFPD B DP AD BD∠====，∠FPD B ∠=∠，又∠PDF BDQ ∠=∠， ∠PDFBDQ △△，∠PDF 为等腰三角形时，BDQ △亦为等腰三角形．若DQ BQ =，12cos BD B BQ=，542253544x =-，解得256x ．若BD BQ =， 253544x -=，解得53x =． ③若DQ BD =，2180B DQB BDQ B BDQ ︒∠+∠+∠=∠+∠<，此种情况舍去．【点睛】本题主要考查了相似三角形的判定和性质，等腰三角形的性质和判定，三角函数，正确和熟练应用相似三角形的性质得到各线段之间的数量关系是解决本题的关键．10．（2021·上海闵行区·九年级一模）如图，在矩形ABCD 中，2AB =，1AD =，点E在边AB 上（点E与端点A 、B 不重合），联结DE ，过点D 作DF DE ⊥，交BC 的延长线于点F ，连接EF ，与对角线AC 、边CD 分别交于点G 、H ．设AE x =，DH y =．（1）求证：ADE CDF ∽△△，并求EFD ∠的正切值； （2）求y 关于x 的函数解析式，并写出该函数的定义域； （3）连接BG ，当BGE △与DEH △相似时，求x 的值．【答案】（1）证明见解析；12；（2）222(02)21x y x x +=<<+；（3）45x =或45x =【分析】（1）根据垂直关系得到ADE CDF ∠=∠，根据AA 即可证明ADE CDF ∽△△，得到12DE AD DF CD ==，再根据正切的定义即可求解tan EFD ∠； （2）先证明FCH FBE △∽△，得到FC CH FB BE =，代入得到22212x yx x-=+-，故可求解； （3）根据题意分BEG DHE △∽△和EGB HDE △∽△，分别列出比例式求出x 的值即可求解． 【详解】解：（1）∠90ADE CDE ︒∠+∠=，90CDF CDE ︒∠+∠=∠ADE CDF ∠=∠在Rt EAD 和Rt FCD 中90ADE CDFEAD FCD ∠=∠⎧⎨∠=∠=︒⎩90EAD FCD ︒∠=∠=∠FAD FCD △∽△∠2AB DC ==，1AD =，∠12DE AD DF CD == ∠1tan 2DE EFD DF ∠== （2）由（1）可知ADE CDF ∽△△∠12EA DE AD FC DF CD ===∠22FC EA x ==∠AB //CD∠FCH FBE △∽△，∠FC CH FB BE =∠22212x y x x -=+-∠222(02)21x y x x +=<<+， （3）∠AE x =，DH y =，过点E 作EM∠CD 于M 点，∠四边形AEMD 为矩形∠MH=DH -DM=DH -AE=y -x ，∠2BE x =-，DE =EH =∠AB //CD∠AEG CHG △∽△∠EG AE HG CH =∠EG AE EH AE CH =+∠AEEG EH AE CH=⋅+∠BEG DHE ∠=∠， 若BEG DHE △∽△， ∠BE EG DH HE =∠BE AEDH AE CH =+即22x x y x y -=+- 化简得2240x y +-=∠22221x y x +=+∠222212240x x x +⨯-++=化简得22508x x +=-解得x =45x =若EGB HDE △∽△∠BE EG EH HD = ∠2AE BE HD HE AE CH⋅=⋅+即2(2)1()2x x y y x x y ⎡⎤-=⋅+-⎣⎦+- ∠22221x y x +=+代入化简得22637200x x ++=∠=372-4×26×20=-711＜0，∠方程无解综上，45x =和x =BGE △与DEH △相似．【点睛】本题考查了矩形的性质、函数关系式、正切的定义、相似三角形的判定和性质等知识点，解题的关键是灵活运用所学知识解决问题，用分类讨论的思想思考问题，属于中考压轴题．11．（2021·上海奉贤区·九年级一模）已知圆O 的直径4AB =，点P 为弧AB 上一点，联结PA PO 、，点C 为劣弧AP 上一点(点C 不与点A 、P 重合），联结BC 交PA PO 、于点D E 、()1如图，当78cos CBO ∠=时，求BC 的长；()2当点C 为劣弧AP 的中点，且EDP ∆与AOP ∆相似时，求ABC ∠的度数； ()3当2AD DP =，且BEO ∆为直角三角形时．求四边形AOED 的面积．【答案】（1）72；（2）18°；（3）53【分析】（1）方法一：作OG BC ⊥，利用垂径定理和余弦即可求得；方法二：连接AC ，根据直径所对的圆周角等于90°可得∠ACB=90°，利用余弦解直角三角形即可；（2）先根据已知条件确定两个相似三角形的对应角，得出P PED PAO OEB ∠=∠=∠=∠，设ABC α∠=，利用等腰三角形等边对等角和弧与圆心角的关系，圆周角定理分别表示∠AOP 和∠OEB ，利用三角形外角的性质即可求得α即ABC ∠；（3）分当90EOB ∠=和当90OEB ∠=时两种情况讨论，画出对应图形，利用相似三角形和解直角三角形的知识求解即可．【详解】解析：方法一： 作OG BC ⊥，∠BC=2BG,7cos 4BG BO CBO =⋅∠=，722BC BG ∴==；方法二： 连接AC ，∠AB 为直径，90ACB ∴∠=7cos 2BC AB CBO ∴=⋅∠=； （2）∠AO=OP ，∠∠PAO=∠P ，∠P P ∠=∠，EDP ∆与AOP ∆相似，,DPEOPA ∴∆∆P PED PAO OEB ∴∠=∠=∠=∠，C 是AP 中点，CO ∴平分AOP ∠， CO BO =，设,ABC α∠=2,4AOC AOP αα∴∠=∠=，18049022PAO OEB αα-∴∠==-=∠，AOP OEB ABC ∴∠=∠+∠， 即4902a a a =-+，18a ABC ∴=∠=；()3 I ．当90EOB ∠=时，作DH AB ⊥∠DH//OP ，∠∠ADH∠∠APO ，∠23AH DH AD AD AO OP AP AD DP ====+， 23AH AO ∴=，∠AB=4，∠OA=OB=2，428,,333AH HO BH ∴===， 2,AO OP ==43AH DH ∴==，∠DH//OP ，∠∠BOE∠∠BHD ， 28433EO OB EODH HB ∴===，1EO ∴=， AHD AOED HOEDS S S ∆∴=+四边形梯形21414251232333⎛⎫⎛⎫=⨯+⨯+⨯= ⎪ ⎪⎝⎭⎝⎭； II ．当90OEB ∠=时连接,AC由()1得//AC DP ，∠∠ACD∠∠PED ，∠ACB∠∠OEB ，2AD DP =，∠2CD AC ADDE PE DP===，2AC EP ∴=，又,AO BO =∠=2CB AC ABBE OE BO==，2,AC EO ∴=2,30AC OP ABC ∴==∠=，60,EOB CAO ∴∠=∠=∠AO=OP ，∠∠PAO=∠APO ，∠PAO+∠APO=∠EOB=60°，∠30CAD AP O O PA ∠=∠==∠，ABC OEB ACD AOED S S S S ∆∆∆∴=--四边形111222AC BC OE BE CD AC =⋅-⋅-⋅4,AB =2,AC BC BE ∴===1OE =，CD =111212222AOED S ∴=⨯⨯⨯=四边形综上所述，四边形AOED 的面积为53 【点睛】本题考查圆周角定理、垂径定理、相似三角形的性质和判定，解直角三角形，等腰三角形的性质等．（1）中能借助定理构造直角三角形是解题关键；（2）能借助相似三角形以及圆周角定理表示相关角是解题关键；（3）中注意分类讨论和正确构造图形．12．（2021·上海普陀区·九年级一模）如图，矩形ABCD 中，1AB =，3BC =，点E 是边BC 上一个动点（不与点B 、C 重合），AE 的垂线AF 交CD 的延长线于点F ．点G 在线段EF 上，满足:1:2FG GE =．设BE x =．（1）求证：AD DFAB BE=； （2）当点G 在ADF 的内部时，用x 的代数式表示ADG ∠的余切； （3）当FGD AFE ∠=∠时，求线段BE 的长．。

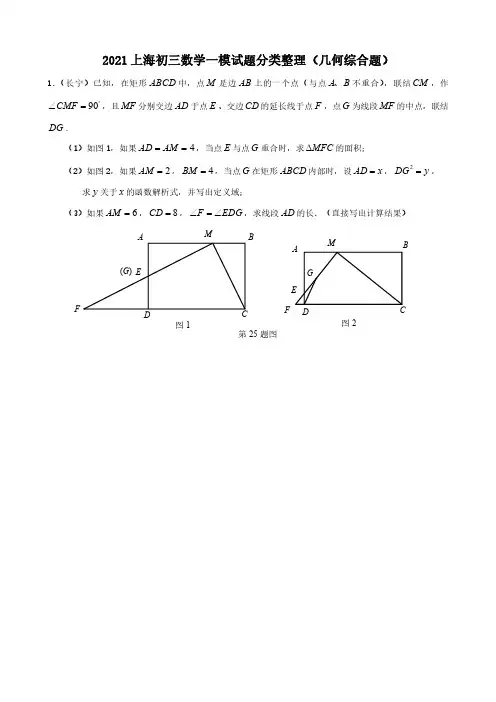
2021上海初三数学一模试题分类整理（几何综合题）1．（长宁）已知，在矩形ABCD 中，点M 是边AB 上的一个点（与点A B 、不重合），联结CM ，作90CMF ︒∠=，且MF 分别交边AD 于点E 、交边CD 的延长线于点F ，点G 为线段MF 的中点，联结DG .（1）如图1，如果4AD AM ==，当点E 与点G 重合时，求MFC ∆的面积；（2）如图2，如果2AM =，4BM =，当点G 在矩形ABCD 内部时，设AD x =，2DG y =，求y 关于x 的函数解析式，并写出定义域；（3）如果6AM =，8CD =，F EDG ∠=∠，求线段AD 的长．（直接写出计算结果）ABCDEF(G )M图1ABCDEFGM图2第25题图2．（杨浦）如图，已知在Rt△ABC 中，∠ACB =90°，AC =BC =4，点D 为边BC 上一动点（与点B 、C 不重合），点E 为边AB 上一点，∠EDB =∠ADC ，过点E 作EF ⊥AD ，垂足为点G ，交射线AC 于点F .（1）如果点D 为边BC 的中点，求∠DAB 的正切值；（2）当点F 在边AC 上时，设CD =x ，CF =y ，求y 关于x 的函数解析式及定义域；（3）联结DF ，如果△CDF 与△AGE 相似，求线段CD 的长.备用图ABC第25题图ABCEDG F3．（徐汇）如图，在ABC Rt ∆中，︒=∠90ACB ，12=AC ，5=BC ，点D 是边AC 上的动点，以CD 为边在ABC ∆外作正方形CDEF ，分别联结AE 、BE ，BE 与AC 交于点G ．（1）当BE AE ⊥时，求正方形CDEF 的面积；（2）延长ED 交AB 于点H ，如果BEH ∆和ABG ∆相似，求ABE ∠sin 的值；（3）当AE AG =时，求CD 的长．（备用图）BAC（第25题图）GFED BAC4．（松江）如图，已知在等腰△ABC中，AB=AC=，tan∠ABC=2，BF⊥AC，垂足为F，点D是边AB上一点（不与A，B重合）.（1）求边BC的长；（2）如图2，延长DF交BC的延长线于点G，如果CG=4，求线段AD的长；（3）过点D作DE⊥BC，垂足为E，DE交BF于点Q，联结DF，如果△DQF和△ABC相似，求线段BD的长.D·B AFC（图1）DBAFC（图2）G BAFC（备用图）5．（普陀）如图，矩形ABCD 中，1AB =，3BC =，点E 是边BC 上一个动点（不与点B 、C 重合），AE 的垂线AF 交CD 的延长线于点F ．点G 在线段EF 上，满足:1:2FG GE =．设BE x =．（1）求证：AD DFAB BE=；（2）当点G 在△ADF 的内部时，用x 的代数式表示ADG ∠的余切；（3）当∠FGD =∠AFE 时，求线段BE 的长．F图14CB A DE G备用图CBAD6．（浦东）四边形ABCD 是菱形，∠B ≤90°，点E 为边BC 上一点，联结AE ，过点E 作EF ⊥AE ，EF 与边CD 交于点F ，且EC =3CF ．（1）如图1，当∠B =90°时，求ABE S △与ECF S △的比值；（2）如图2，当点E 是边BC 的中点时，求cos B 的值；（3）如图3，联结AF ，当∠AFE =∠B 且CF =2时，求菱形的边长．（第25题图3）（第25题图2）（第25题图1）7．（闵行）如图，在矩形ABCD 中，2AB =，1AD =，点E 在边AB 上（点E 与端点A 、B 不重合），联结DE ，过点D 作DF ⊥DE ，交BC 的延长线于点F ，联结EF ，与对角线AC 、边CD 分别交于点G 、H ．设AE x =，DH y =．（1）求证：△ADE ∽△CDF ，并求EFD ∠的正切值；（2）求y 关于x 的函数解析式，并写出该函数的定义域；（3）联结BG ．当△BGE 与△DEH 相似时，求x 的值．（第25题图）B A CF ED GH（备用图）B A CFEDGH8．（静安）已知∠MAN 是锐角，点B 、C 在边AM 上，点D 在边AN 上，∠EBD =∠MAN ，且CE //BD ，sin∠MAN=35，AB =5，AC =9．（1）如图1，当CE 与边AN 相交于点F 时，求证：DF ·CE=BC ·BE ；（2）当点E 在边AN 上时，求AD 的长；（3）当点E 在∠MAN 外部时，设AD =x ，△BCE 的面积为y ，求y 与x 之间的函数解析式，写出定义域．（第25题图）（备用图）（图1）FAB DCE NM9.（嘉定）在矩形ABCD 中，6AB =，8AD =，点E 在CD 边上，1tan 2DAE ∠=.点F 是线段AE 上一点，联结BF ，CF.（1）如图11，如果3tan 4CBF ∠=，求线段AF 的长；（2）如图12，如果12CF BC =，①求证：∠CFE =∠DAE ；②求线段EF 的长.图11图12备用图10．（黄浦）如图10，四边形ABCD 中，AB =AD =4，CB =CD =3，∠ABC =∠ADC =90°，点M 、N 是边AB 、AD 上的动点，且∠MCN =12∠BCD ，CM 、CN 与对角线BD 分别交于点P 、Q .（1）求sin∠MCN 的值；（2）当DN =DC 时，求∠CNM 的度数；（3）试问：在点M 、N 的运动过程中，线段比PQMN的值是否发生变化？如不变，请求出这个值；如变化，请至少给出两个可能的值，并说明点N 相应的位置.P NM DC BAQ（图10）11．（虹口）如图12，在△ABC 中，∠ABC =90°，AB =3，BC =4，过点A 作射线AM //BC ，点D、E 是射线AM 上的两点（点D 不与点A 重合，点E 在点D 右侧），联结BD 、BE 分别交边AC 于点F 、G ，∠DBE =∠C ．（1）当AD =1时，求FB 的长；（2）设AD =x ，FG =y ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结DG 并延长交边BC 于点H ，如果△DBH 是等腰三角形，请直接写出AD 的长．C FGE D A B 图12C A B 备用图MM12.（奉贤）已知⊙O 的直径AB =4，点P 为弧AB 上一点，联结PA 、PO ，点C 为劣弧AP 上一点（点C 不与点A 、P 重合），联结BC 交PA 、PO 于点D 、E .（1）如图10，当cos∠CBO =87时，求BC 的长；（2）当点C 为劣弧AP 的中点，且△EDP 与△AOP 相似时，求∠ABC 的度数；（3）当AD =2DP ，且△BEO 为直角三角形时，求四边形AOED 的面积.备用图备用图A B图10PA BC D EO A B13．（崇明）如图，Rt△ABC 中，90ACB ∠=︒，6AC =，8BC =．点D 为斜边AB 的中点，ED ⊥AB ，交边BC 于点E ．点P 为射线AC 上的动点，点Q 为边BC 上的动点，且运动过程中始终保持PD QD ⊥．（1）求证：△ADP ∽△EDQ ；（2）设AP x =，BQ y =．求y 关于x 的函数解析式，并写出该函数的定义域；（3）联结PQ ，交线段ED 于点F ．当△PDF 为等腰三角形时，求线段AP 的长．A D BCPEQ 第25题图A D B C P E Q 第25题备用图F14.（宝山）如图3，已知Rt△ABC 中，∠ACB =90°，AC =BC ，点D、E 在边AB 上，∠DCE =45°，过点A 作AB 的垂线交CE 的延长线于点M ，联结MD.（1）求证：DE BE CE ⋅=2；（2）当AC =3，AD =2BD 时，求DE 的长；（3）过点M 作射线CD 的垂线，垂足为点F .设x BCBD =，y FMD =∠tan ，求y 关于x 的函数关系式，并写出定义域.EM DCAB （图3）15．（青浦）在△ABC 中，∠C=90°，AC =2，BC =23，点D 为边AC 的中点（如图），点P 、Q 分别是射线BC 、BA 上的动点，且BQ =32BP ，联结PQ 、QD 、DP ．（1）求证：PQ ⊥AB ；（2）如果点P 在线段BC 上，当△PQD 是直角三角形时，求BP 的长；（3）将△PQD 沿直线QP 翻折，点D 的对应点为点'D ，如果点'D 位于△ABC 内，请直接写出BP 的取值范围．（第25题图）（备用图）A C O 第25题备用图16.（金山）定理：一条弧所对的圆周角等于这条弧所对的圆心角的一半.如图1中，O A ∠=∠21.已知：如图2，AC 是⊙O 的一条弦，点D 在⊙O 上（与A 、C 不重合），联结DC 交射线AO 于点E ，联结OD ，⊙O 的半径为5，43tan =∠OAC .(1)求弦AC 的长.(2)当点E 在线段OA 上时，若DOE ∆与AEC ∆相似，求DCA ∠的正切值.(3)当1=OE 时，求点A 与点D 之间的距离（直接写出答案）.AB CO第25题图1第25题图2E D C A O。

2021年上海市闵行区部分学校中考数学一模试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列各数中，无理数是（ ）A B ．912 C D ．2272．不等式﹣2x ＞3的解集是（ ）A ．23x >-B ．23x <-C ．32x >-D ．32x <- 3．下列方程中，有实数根的是（ ）A xB 0C ．22111x x x =--D ．x 2+2020x ﹣1＝04．已知反比例函数y ＝k x，当x ＞0时，y 的值随x 的值增大而增大，下列四个选项中，可能是二次函数y ＝2kx 2﹣x ﹣k 图象的选项是（ ）A ．B ．C ．D ．5．要判断一个四边形门框是否为矩形，在下面四个拟定方案中，正确的方案是（ ） A ．测量对角线是否相互平分B ．测量两组对边是否分别相等C ．测量对角线是否互相垂直D ．测量其中三个角是否是直角6．如果两个圆的圆心距为3，其中一个圆的半径长为4，另一个圆的半径长大于1，那么这两个圆的位置关系不可能是（ ）A ．内含B ．内切C ．外切D ．相交二、填空题7．计算：a2•a3=_____．8．在实数范围内分解因式：222--=______.x x9．已知f（x）＝2x2﹣1，且f（a）＝3，那么a＝_____．10．已知一次函数y=kx+b的图象如图，则关于x的不等式kx+b＞0的解集是______.11．某同学计划购买一双运动鞋，在网站上浏览时发现如表所示的男鞋尺码对照表．如果美码（y）与中码（x）之间满足一次函数关系，那么y关于x的函数关系式为_____．12．一个不透明的袋子中装有8个大小、形状、都一样的小球，其中有3个红球与5个黄球，从这8个球中任取一个球是红球的概率是：_____．13．如果一段斜坡的坡角是30°，那么这段斜坡的坡度是_______．（请写成1︰m的形式）．14．如图，在△ABC中，AD是边BC上的中线，设向量AB＝a，AC＝b，如果用向量a，b表示向量AD，那么向量AD可以表示为_____．15．已知正三角形的边长为2，那么该三角形的半径长为_____．16．如果两点A（2，a）和B（x，b）在抛物线y＝x2﹣4x+m上，那么a和b的大小关系为：a_____b．（从“＞”“≥”“＜”“≤”中选择）．17．平移抛物线y＝2x2﹣4x，可以得到抛物线y＝2x2+4x，请写出一种平移方法_____．18．如果三角形的两个内角∠α与∠β满足2α+β＝90°，那么，我们将这样的三角形称为“准互余三角形”．在△ABC中，已知∠C＝90°，BC＝3，AC＝4（如图所示），点D在AC边上，联结BD．如果△ABD为“准互余三角形”，那么线段AD的长为_____（写出一个答案即可）．三、解答题192318- 20．解方程组：2228560x y x xy y +=⎧⎨+-=⎩21．如图，在△ABC 中，∠C ＝90°，∠A ＝30°，BC ＝1，点D 在边AC 上，且∠DBC ＝45°，求sin ∠ABD 的值．22．某电脑公司2021年的各项经营收入中，经营电脑配件的收入为800万元，占全年经营总收入的40%，该公司预计2021年经营总收入要达到2880万元，且计划从2021年到2021年，每年经营总收入的年增长率相同，问2021年预计经营总收入为多少万元？ 23．已知：如图，△ABC 中，∠ACB ＝90°，D 在斜边AB 上，DE ⊥AC ，DF ⊥BC ，垂足分别为E ，F ．（1）当∠ACD ＝∠BCD 时，求证：四边形DECF 是正方形；（2）当∠BCD ＝∠A 时，求证：CD CF CA AD=． 24．如图，已知一个抛物线经过A （0，1），B （1，3），C （﹣1，1）三点．（1）求这个抛物线的表达式及其顶点D的坐标；（2）联结AB、BC、CA，求tan∠ABC的值；（3）如果点E在该抛物线的对称轴上，且以点A、B、C、E为顶点的四边形是梯形，直接写出点E的坐标．25．在圆O中，弦AB与CD相交于点E，且弧AC与弧BD相等．点D在劣弧AB上，联结CO并延长交线段AB于点F，联结OA、OB．当OA tan∠OAB＝12．（1）求弦CD的长；（2）如果△AOF是直角三角形，求线段EF的长；（3）如果S△CEF＝4S△BOF，求线段AF的长．参考答案1．C【分析】根据无理数的概念及其三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数，结合选项解答即可．【详解】解：A．2=-，是整数，属于有理数；B．192，是分数，属于有理数；CD．227是分数，属于有理数．故选：C．【点睛】本题主要考查了无理数的概念，解答本题的关键是掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数．2．D【分析】直接把x的系数化为1即可．【详解】解：不等式的两边同时除以﹣2得，x＜﹣32．故选：D．【点睛】本题考查的是解一元一次不等式，熟知不等式的基本性质是解答此题的关键．3．D【分析】A，﹣x＜0，则方程无实数根；B选项中，当x＝1有最小值1，则方程无实数根；C选项中，解得x＝1是方程的增根，则方程无实数根；D选项中，△＞0，则方程有两个不相等的实数根．【详解】解：，x ﹣1≥0，∴x ≥1，∴﹣x ＜0，﹣x ，∴A 不正确；≥0，当x ＝11，≥1，∴B 不正确；22111x x x =--两边同时乘以x 2﹣1，得x ＝1， 经检验x ＝1是方程的增根，∴方程无解；∴C 不正确；x 2+2020x ﹣1＝0，∵△＝20202+4＞0，∴方程有两个不相等的实数根，∴D 正确；故选：D ．【点睛】本题考查分式方程、无理方程、一元二次方程；熟练掌握分式方程解法、一元二次方程根的判别式、掌握二次根式成立的条件是解题的关键．4．D【分析】直接利用反比例函数的性质得出k 的符号，再利用二次函数的性质得出答案．【详解】解：∵反比例函数y ＝k x，当x ＞0时，y 的值随x 的值增大而增大， ∴k ＜0，∴二次函数y＝2kx2﹣x﹣k中，2k＜0，则图象开口向下，﹣k＞0，则图象与y轴交在正半轴上，又∵b＝﹣1＜0，∴二次项与一次项系数相同，则对称轴在y轴左侧，符合题意的只有选项D．故选：D．【点睛】此题主要考查了反比例函数的性质以及二次函数的性质，正确掌握系数与图象的关系是解题关键．5．D【分析】由矩形的判定即可得出结论．【详解】解：∵对角线相互平分的四边形是平行四边形，故A错误；∵两组对边分别相等的四边形是平行四边形，故B错误；∵对角线互相垂直的四边形不一定是矩形，故C错误；∵三个角是直角的四边形是矩形，故D正确；∴在这四个拟定方案中，正确的方案是D，故选：D．【点睛】本题考查了矩形的判定；熟记三个角是直角的四边形为矩形是解题的关键．6．C【分析】首先利用一个圆的半径为4，另一个圆的半径大于1来求得两圆的半径之差的范围，然后根据圆心距d与两半径的关系判断即可．【详解】解：∵一个圆的半径R为4，另一个圆的半径r大于1，∴R﹣r＜4﹣1，R+r＞5即：R﹣r＜3，∵圆心距为3，∴两圆不可能外切，故选：C ．【点睛】本题考查了圆与圆的位置关系，解题的关键是根据两圆的半径的大小或取值范围求得两圆的半径之差，然后根据圆心距与半径的关系确定本题的答案．7．a 5．【解析】【分析】根据同底数的幂的乘法，底数不变，指数相加，计算即可．【详解】a 2•a 3=a 2+3=a 5，故答案为：a 5．【点睛】本题考查了同底数幂的乘法，熟练掌握同底数的幂的乘法的运算法则是解题的关键．8．(11x x --【分析】可将x 2-2x 先配成一个完全平方式，再应用平方差公式进行分解即可.【详解】原式=2(1)3x --(11x x =-+--故填：(11x x -+--【点睛】本题考查配方法的应用，用平方差公式因式分解.能想到分组因式分解是解决此题的关键.9．【分析】由已知可得f （a ）＝2a 2﹣1＝3，解出a 即可．【详解】解：∵f （x ）＝2x 2﹣1，f （a ）＝3，∴f （a ）＝2a 2﹣1＝3，∴2a 2﹣1＝3时，a ＝，故答案为．【点睛】本题考查函数值；理解题意，能够将所求问题转化为一元二次方程求解是关键．10．2x<【分析】直接利用一次函数图象，结合式kx+b＞0时，则y的值＞0时对应x的取值范围，进而得出答案．【详解】如图所示：关于x的不等式kx+b＞0的解集是：x＜2．故答案为：x＜2．【点睛】此题主要考查了一次函数与一元一次不等式，正确利用数形结合是解题关键．11．y＝0.1x﹣17.5【分析】设y关于x的函数关系式为：y＝kx+b，利用待定系数法求解析式．【详解】解：设y关于x的函数关系式为：y＝kx+b，由题意可得：5225 8255k bk b =+⎧⎨=+⎩解得：0.117.5 kb=⎧⎨=-⎩∴y关于x的函数关系式为y＝0.1x﹣17.5，故答案为：y＝0.1x﹣17.5．【点睛】本题考查了一次函数的应用，利用待定系数法求解析式，理解题意是本题的关键．12．3 8【分析】让红球的个数除以球的总数即为摸到红球的概率．【详解】解：在口袋中放有3个红球与5个黄球，共8个，这两种球除颜色外完全相同，随机从口袋中任取一个球，从这8个球中任取一个球是红球的概率是：38．故答案为：38．【点睛】本题考查随机事件概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）＝mn．13．【详解】试题分析：因为斜坡的坡角是30°，所以这段斜坡的坡度=tan30°：3=1故答案为：【点睛】本题考查坡度与坡角．14．12a+12b【分析】如图，延长AD到E，使得DE＝AD，连接BE，CE．证明四边形ABEC是平行四边形，利用三角形法则求出AE即可解决问题．【详解】解：如图，延长AD到E，使得DE＝AD，连接BE，CE．∵AD＝DE，BD＝CD，∴四边形ABEC是平行四边形，∴BE AC b==，∵AE AB BE a b=+=+，∴111222AD AE a b==+．故答案为：12a+12b．【点睛】本题考查平面向量，平行四边形的判定和性质，三角形法则等知识，解题的关键是学会添加常用辅助线，构造平行四边形解决问题，属于中考常考题型．15．3【分析】根据题意作出图形，构造直角三角形求得外接圆的半径即可求得本题的答案．【详解】解：如图所示：连接OA、OB、OC，过O作OD⊥BC于D，∵△ABC是边长为2的等边三角形，∴AB＝AC＝BC＝2，∠ABC＝60°，∴∠OBD＝30°，∵OD⊥BC，∴∠ODB＝90°，BD＝CD＝12BC＝1，∴OD＝BD•tan30°＝∴OB＝2OD＝，3∴该三角形的半径长为，3．【点睛】本题考查的是正三角形的性质、边心距、半径、周长和面积的计算；熟练掌握正三角形的性质，根据题意画出图形，利用数形结合求解是解答此题的关键．16．≤【分析】由已知可得当x＝2时函数有最小值，则可求b≥a．【详解】解：∵抛物线y＝x2﹣4x+m的对称轴为x＝2，∴当x＝2时函数有最小值，∴b≥a，故答案为：≤．【点睛】本题考查二次函数图象上点的特征；熟练掌握二次函数的图象及性质是解题的关键．17．向左平移2个单位【分析】把y＝2x2﹣4x和y＝2x2+4x改写成顶点式，进而解答即可．【详解】解：∵y＝2x2﹣4x＝2（x﹣1）2﹣2，y＝2x2+4x＝2（x+1）2﹣2，∴两抛物线的顶点坐标分别为（1，﹣2）和（﹣1，﹣2），∴将抛物线y＝2x2﹣4x先向左平移2个单位长度，可以得到抛物线y＝2x2+4x．故答案为：向左平移2个单位．【点睛】本题考查了二次函数图象与几何变换：先把二次函数的解析式配成顶点式，然后把抛物线的平移问题转化为顶点的平移问题．18．52或74【分析】作DM⊥AB于M．设∠ABD＝α，∠A＝β．分两种情形：①当2α+β＝90°时．②当α+2β＝90°时，分别求解即可．【详解】解：过点D作DM⊥AB于M．设∠ABD＝α，∠A＝β．①当2α+β＝90°时，∵α+β+∠DBC＝90°，∴∠DBC＝∠DBA，∵DM⊥AB，DC⊥BC，∴DM＝DC，∵∠DMB＝∠C＝90°，DM＝DC，BD＝BD，∴Rt△BDC≌Rt△BDM（HL），∴BM＝BC＝3，∵∠C＝90°，BC＝3，AC＝4，∴AB5，∴AM＝5﹣3＝2，设AD＝x，则CD＝DM＝4﹣x，在Rt△ADM中，则有x2＝（4﹣x）2+22，解得x＝52．∴AD＝52．②当α+2β＝90°时，∵α+β+∠DBC＝90°，∴∠DBC＝β＝∠A，∵∠C＝∠C，∴△CBD∽△CAB，∴BC2＝CD•CA，∴CD＝94，∴AD＝AC﹣CD＝4﹣94＝74．故答案为：52或74．【点睛】本题考查的是勾股定理，角平分线的性质，全等三角形的判定和性质，相似三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题．19．-3.【解析】【分析】根据绝对值的性质，二次根式的混合运算，进行运算即可【详解】1243-+=-【点睛】此题考查二次根式的混合运算，解题关键在于掌握运算法则20．1112 2x y =⎧⎨=-⎩，228383xy⎧=⎪⎪⎨⎪=⎪⎩【分析】先将第2个方程变形为x +6y ＝0，x ﹣y ＝0，从而得到两个二元一次方程组，再分别求解即可．【详解】解：2228560x y x xy y +=⎧⎨+-=⎩①②， 由②得：x +6y ＝0，x ﹣y ＝0，原方程组可化为2860x y x y +=⎧⎨+=⎩或280x y x y +=⎧⎨-=⎩， 故原方程组的解为11122x y =⎧⎨=-⎩，228383x y ⎧=⎪⎪⎨⎪=⎪⎩． 【点睛】本题考查的是高次方程，关键是通过分解，把高次方程降次，得到二元一次方程组，用到的知识点是因式分解、加减法．21【分析】如图，作DM ⊥AB 于M ，在BA 上取一点H ，使得BH ＝DH ，连接DH ．设DM ＝a ．解直角三角形求出BD 即可解决问题．【详解】解：如图，过点D 作DM ⊥AB 于M ，在BA 上取一点H ，使得BH ＝DH ，连接DH ．设DM ＝a ．∵∠C ＝90°，∠A ＝30°，∴∠ABC ＝90°﹣30°＝60°，∵∠DBC ＝45°，∴∠ABD ＝60°﹣45°＝15°，∵HB ＝HD ，∴∠HBD ＝∠HDB ＝15°，∴∠DHM ＝∠HBD +∠HDB ＝30°，∴DH ＝BH ＝2a ，MH ，BM ＝2a ，∴BD a =，∴sin ∠ABD ＝DM DB =． 【点睛】本题考查解直角三角形，直角三角形30度角的性质等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．22．2400万【分析】设从2021年到2021年，平均经营总收入增长率为x ，根据等量关系：2021年经营总收入×（1+增长率）2＝2021年经营总收入，列出方程求解即可．【详解】解：从2021年到2021年，平均经营总收入增长率为x ，根据题意可得：800÷40%（1+x ）2＝2880，解得：x 1＝0.2＝20%，x 2＝2.2（不合题意舍去），则800÷40%×（1+20%）＝2400（万元），答：2021年预计经营总收入为2400万元．【点睛】此题主要考查了一元二次方程的应用，属于增长率的问题，一般公式为原来的量×（1±x ）2＝后来的量，其中增长用+，减少用﹣．23．（1）见解析；（2）见解析【分析】（1）由垂直的定义可得出∠DEC ＝∠DFC ，结合∠ECF ＝90°可得出四边形DECF 为矩形，由∠ACD ＝∠BCD 可得出CD 平分∠ACB ，利用角平分线的性质可得出DE ＝DF ，再利用“邻边相等的矩形是正方形”可证出四边形DECF 是正方形；（2）由∠BCD+∠ACD＝∠ACB＝90°，∠BCD＝∠A可得出∠A+∠ACD＝90°，利用三角形内角和定理可求出∠ADC＝90°，由∠DCF＝∠A，∠DFC＝∠ADC＝90°可证出△CDF∽△ACD，再利用相似三角形的性质可证出CD CF CA AD=．【详解】证明：（1）∵DE⊥AC，DF⊥BC，∴∠DEC＝∠DFC＝90°，又∵∠ECF＝90°，∴四边形DECF为矩形．∵∠ACD＝∠BCD，∴CD平分∠ACB，∴DE＝DF，∴四边形DECF是正方形．（2）∵∠BCD+∠ACD＝∠ACB＝90°，∠BCD＝∠A，∴∠A+∠ACD＝90°，∴∠ADC＝180°﹣90°＝90°．∵∠DCF＝∠A，∠DFC＝∠ADC＝90°，∴△CDF∽△ACD，∴CD CF CA AD=．【点睛】本题考查了相似三角形的判定与性质以及正方形的判定，解题的关键是：（1）利用“邻边相等的矩形是正方形”，证出四边形DECF是正方形；（2）利用“两角对应相等两三角形相似”证出△CDF∽△ACD．24．（1）y＝x2+x+1，顶点D的坐标（﹣12，34）；（2）tan∠ABC＝13；（3）点E的坐标为（﹣12，3）或（﹣12，2）或（﹣12，12）【分析】（1）设抛物线的解析式为y＝ax2+bx+c，将A（0，1）、B（1，3）、C（﹣1，1）代入，求a、b、c的值，可得结果；（2）如图，过点B作BF⊥x轴于F，延长CA交BF于点D，过点A作AM⊥BC于M，通过勾股定理和等腰直角三角形的性质可求AM 和BM 的长，即可求解；（3）分三种情况讨论，由梯形的性质可求解．【详解】解：（1）设抛物线的解析式为y ＝ax 2+bx +c （a ≠0）．由题意可得：311a b c a b c c =++⎧⎪=-+⎨⎪=⎩解得：111a b c =⎧⎪=⎨⎪=⎩∴抛物线的解析式为：y ＝x 2+x +1，∵y ＝x 2+x +1＝213()24x ++， ∴顶点D 的坐标（﹣12，34）； （2）如图，过点B 作BF ⊥x 轴于F ，延长CA 交BF 于点D ，过点A 作AM ⊥BC 于M ，∴BF ＝3，∵A （0，1），C （﹣1，1），∴AC ∥x 轴，∴CD ⊥BF ，∴CD ＝BD ＝2，AD ＝1，CA ＝1，∴BC ＝，∠BCD ＝∠CBD ＝45°，∵AM ⊥BC ，∴∠MAC ＝∠MCA ＝45°，∴CM ＝AM ，∴CM ＝AM=，∴BM ＝BC ﹣CM ＝2， ∴tan ∠ABC ＝AM BM ＝13； （3）∵A （0，1），B （1，3），C （﹣1，1），∴直线AC 解析式为：y ＝1，直线AB 解析式为：y ＝2x +1，直线BC 解析式为：y ＝x +2，若BE ∥AC ，则点E 的纵坐标为3，且点E 在对称轴上，∴点E （﹣12，3）； 若CE ∥AB ，则CE 的解析式为；y ＝2x +3，∵点E 在对称轴上，∴x ＝﹣12， ∴y ＝2， 即点E （﹣12，2）； 若AE ∥BC ，则AE 解析式为：y ＝x +1，∵点E 在对称轴上，∴x ＝﹣12， ∴y ＝12， 即点E （﹣12，12）， 综上所述：点E 的坐标为（﹣12，3）或（﹣12，2）或（﹣12，12）． 【点睛】本题是二次函数综合题，考查了待定系数法求解析式，等腰直角三角形的性质，勾股定理，梯形的性质等知识，利用分类讨论思想解决问题是本题的关键．25．（1）4；（2）32；（3） 【分析】（1）如图，过点O作OH⊥AB于点H，由锐角三角函数可求OH＝1，AH＝2，由垂径定理可得AB＝4，即可求CD＝4（2）分两种情况讨论，由相似三角形的性质可求解；（3）先利用面积关系得出53COFO=，进而利用△OAF∽△EFC得出比例式，即可得出结论．【详解】解：（1）如图，过点O作OH⊥AB于点H，∵tan∠OAB＝12OHAH =，∴设OH＝a，AH＝2a，∵AO2＝OH2+AH2＝5，∴a＝1，∴OH＝1，AH＝2，∵OH⊥AB，∴AB＝2AH＝4，∵弧AC＝弧BD∴AB CD=，∴AB＝CD＝4；（2）∵OA＝OB，∴∠OAF＝∠OBA，∴∠OAF＝∠ECF，①当∠AFO＝90°时，∵OA tan∠OBA＝12，∴OC＝OA OF＝1，AB＝4，∴EF＝CF•tan∠ECF＝CF•tan∠OBA；②当∠AOF＝90°时，∵OA＝OB，∴∠OAF＝∠OBA，∴tan ∠OAF ＝tan ∠OBA ＝12， ∵OA∴OF ＝OA •tan ∠OAF， ∴AF ＝52， ∵∠OAF ＝∠OBA ＝∠ECF ，∠OF A ＝∠EFC ，∴△OF A ∽△EFC ，∴EF OC OF OF AF +=， ∴EF32=， 即：EF ＝32或12； （3）如图，连接OE ，∵∠ECB ＝∠EBC ，∴CE ＝EB ，∵OE ＝OE ，OB ＝OC ，∴△OEC ≌△OEB ，∴S △OEC ＝S △OEB ，∵S △CEF ＝4S △BOF ，∴S △CEO +S △EOF ＝4（S △BOE ﹣S △EOF ）， ∴53CEO EFO S S ∆∆=， ∴53CO FO =， ∴FO＝35CO ， ∵△OF A ∽△EFC ， ∴53CE AO OC EF FO OF ===， ∴BF ＝BE ﹣EF ＝CE ﹣EF ＝23EF ， ∴AF ＝AB ﹣BF ＝4﹣23EF ，∵△OAF∽△EFC，∴CF EF FA FO=，∴5243EF= -∴EF＝3，∴AF＝4﹣23EF＝．【点睛】此题是圆的综合题，主要考查了圆的性质，锐角三角函数，全等三角形的判定和性质，相似三角形的判定和性质，分类讨论的思想，判断出53CE AO OCEF FO OF===是解本题的关键．。

2021年上海市闵行区中考数学模拟试卷解析版一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上.】 1．（4分）下列各数中，无理数是（ ） A ．−√4B ．912C ．√93D ．227【解答】解：A .−√4=−2，是整数，属于有理数； B .912=√9=3，是整数，属于有理数； C .√93是无理数； D .227是分数，属于有理数．故选：C ．2．（4分）不等式﹣2x ＞3的解集是（ ） A ．x ＞−23B ．x ＜−23C ．x ＞−32D ．x ＜−32【解答】解：不等式的两边同时除以﹣2得，x ＜−32． 故选：D ．3．（4分）下列方程中，有实数根的是（ ） A ．√x −1=−x B ．√x −1+√x =0C ．x x 2−1=1x 2−1D ．x 2+2020x ﹣1＝0【解答】解：∵√x −1≥0，x ﹣1≥0， ∴x ≥1， ∴﹣x ＜0， ∴√x −1≠−x ， ∴A 不正确；∵√x −1≥0，√x ≥0，当x ＝1时√x −1+√x 有最小值1， ∴√x −1+√x ≥1， ∴B 不正确；x x 2−1=1x 2−1两边同时乘以x 2﹣1，得x ＝1，经检验x＝1是方程的增根，∴方程无解；∴C不正确；x2+2020x﹣1＝0，∵△＝20202+4＞0，∴方程有两个不相等的实数根，∴D正确；故选：D．4．（4分）已知反比例函数y=kx，当x＞0时，y的值随x的值增大而增大，下列四个选项中，可能是二次函数y＝2kx2﹣x﹣k图象的选项是（）A．B．C．D．【解答】解：∵反比例函数y=kx，当x＞0时，y的值随x的值增大而增大，∴k＜0，∴二次函数y＝2kx2﹣x﹣k中，2k＜0，则图象开口向下，﹣k＞0，则图象与y轴交在正半轴上，又∵b＝﹣1＜0，∴二次项与一次项系数相同，则对称轴在y轴左侧，符合题意的只有选项D．故选：D．5．（4分）要判断一个四边形门框是否为矩形，在下面四个拟定方案中，正确的方案是（）A．测量对角线是否相互平分B．测量两组对边是否分别相等C．测量对角线是否互相垂直D．测量其中三个角是否是直角【解答】解：∵三个角是直角的四边形是矩形，∴在下面四个拟定方案中，正确的方案是D，故选：D．6．（4分）如果两个圆的圆心距为3，其中一个圆的半径长为4，另一个圆的半径长大于1，那么这两个圆的位置关系不可能是（）A．内含B．内切C．外切D．相交．【解答】解：∵一个圆的半径R为4，另一个圆的半径r大于1，∴R﹣r＜4﹣1，R+r＞5即：R﹣r＜3，∵圆心距为3，∴两圆不可能外切，故选：C．二、填空题：（本大题共12题，每题4分，满分48分）7．（4分）计算：a2•a3＝a5．【解答】解：a2•a3＝a2+3＝a5．故答案为：a5．8．（4分）在实数范围内分解因式：x2﹣2x﹣2＝(x−1+√3)(x−1−√3)．【解答】解：原式＝（x﹣1）2﹣3=(x−1+√3)(x−1−√3)故填：(x−1−√3)(x−1−√3)．9．（4分）已知f（x）＝2x2﹣1，且f（a）＝3，那么a＝±√2．【解答】解：∵f（x）＝2x2﹣1，f（a）＝3，∴f（a）＝2a2﹣1＝3，∴2a2﹣1＝3时，a＝±√2，故答案为±√2．10．（4分）如图．函数y＝kx+b（k、b为常数，k≠0）的图象如图，则关于x的不等式kx+b ＞0的解集为x＜2．【解答】解：函数y ＝kx +b 的图象经过点（2，0），并且函数值y 随x 的增大而减小， 所以当x ＜2时，函数值小于0，即关于x 的不等式kx +b ＞0的解集是x ＜2． 故答案为：x ＜2．11．（4分）某同学计划购买一双运动鞋，在网站上浏览时发现如表所示的男鞋尺码对照表．中码CHN 220 225 230 … 250 255 260 … 美码USA4.555.5…7.588.5…如果美码（y ）与中码（x ）之间满足一次函数关系，那么y 关于x 的函数关系式为 y ＝0.1x ﹣17.5 ．【解答】解：设y 关于x 的函数关系式为：y ＝kx +b ， 由题意可得：{5=225k +b 8=255k +b解得：{k =0.1b =−17.5∴y 关于x 的函数关系式为y ＝0.1x ﹣17.5， 故答案为：y ＝0.1x ﹣17.5．12．（4分）一个不透明的袋子中装有8个大小、形状、都一样的小球，其中有3个红球与5个黄球，从这8个球中任取一个球是红球的概率是：38．【解答】解：在口袋中放有3个红球与5个黄球，共8个，这两种球除颜色外完全相同，随机从口袋中任取一个球，从这8个球中任取一个球是红球的概率是：38．故答案为：38．13．（4分）如果一段斜坡的坡角是30°，那么这段斜坡的坡度是 1：√3 ．（请写成1：m 的形式）【解答】解：i ＝tan α＝tan30°=√33=1：√3， 故答案是：1：√3．14．（4分）如图，在△ABC 中，AD 是边BC 上的中线，设向量AB →=a →，AC →=b →，如果用向量a →，b →表示向量AD →，那么向量AD →可以表示为12a →+12b → ．【解答】解：如图，延长AD 到E ，使得DE ＝AD ，连接BE ，CE ．∵AD ＝DE ，BD ＝CD ， ∴四边形ABEC 是平行四边形， ∴BE →=AC →=b →，∵AE →=AB →+BE →=a →+b →，∴AD →=12AE →=12a →+12b →．故答案为12a →+12b →．15．（4分）已知正三角形的边长为2，那么该三角形的半径长为 2√33． 【解答】解：如图所示：连接OA 、OB 、OC ，过O 作OD ⊥BC 于D ， ∵△ABC 是边长为2的等边三角形， ∴AB ＝AC ＝BC ＝2，∠ABC ＝60°， ∴∠OBD ＝30°， ∵OD ⊥BC ，∴∠ODB ＝90°，BD ＝CD =12BC ＝1， ∴OD ＝BD •tan30°＝1×√33=√33，∴OB ＝2OD =2√33， ∴该三角形的半径长为2√33， 故答案为：2√33．16．（4分）如果两点A （2，a ）和B （x ，b ）在抛物线y ＝x 2﹣4x +m 上，那么a 和b 的大小关系为：a ≤ b ．（从“＞”“≥”“＜”“≤”中选择）． 【解答】解：∵抛物线y ＝x 2﹣4x +m 的对称轴为x ＝2， ∴当x ＝2时函数有最小值， ∴b ≥a ， 故答案为≤．17．（4分）平移抛物线y ＝2x 2﹣4x ，可以得到抛物线y ＝2x 2+4x ，请写出一种平移方法 向左平移2个单位 ．【解答】解：∵y ＝2x 2﹣4x ＝2（x ﹣1）2﹣2，y ＝2x 2+4x ＝2（x +1）2﹣2， ∴两抛物线的顶点坐标分别为（1，﹣2）和（﹣1，﹣2），∴将抛物线y ＝2x 2﹣4x 先向左平移2个单位长度，可以得到抛物线y ＝2x 2+4x ． 故答案为：向左平移2个单位．18．（4分）如果三角形的两个内角∠α与∠β满足2α+β＝90°，那么，我们将这样的三角形称为“准互余三角形”．在△ABC 中，已知∠C ＝90°，BC ＝3，AC ＝4（如图所示），点D 在AC 边上，联结BD ．如果△ABD 为“准互余三角形”，那么线段AD 的长为52或74（写出一个答案即可）．【解答】解：过点D 作DM ⊥AB 于M ．设∠ABD ＝α，∠A ＝β．①当2α+β＝90°时，∵α+β+∠DBC ＝90°， ∴∠DBC ＝∠DBA ， ∵DM ⊥AB ，DC ⊥BC ， ∴DM ＝DC ，∵∠DMB ＝∠C ＝90°，DM ＝DC ，BD ＝BD ， ∴Rt △BDC ≌Rt △BDM （HL ）， ∴BM ＝BC ＝3，∵∠C ＝90°，BC ＝3，AC ＝4， ∴AB =√BC 2+AC 2=5，∴AM ＝5﹣3＝2，设AD ＝x ，则CD ＝DM ＝4﹣x ， 在Rt △ADM 中，则有x 2＝（4﹣x ）2+22， 解得x =52． ∴AD =52．②当α+2β＝90°时，∵α+β+∠DBC ＝90°， ∴∠DBC ＝β＝∠A ， ∵∠C ＝∠C ， ∴△CBD ∽△CAB ， ∴BC 2＝CD •CA ， ∴CD =94，∴AD ＝AC ﹣CD ＝4−94=74． 故答案为52或74．三、解答题：（本大题共7题，满分78分）19．（10分）计算：|√3−1|−√2×√6+2−3823【解答】解：|√3−1|−√2×√62−3−823=√3−1﹣2√3+2+√3−4 ＝﹣320．（10分）解方程组：{x +2y =8x 2+5xy −6y 2=0【解答】解：{x +2y =8①x 2+5xy −6y 2=0②，由②得：x +6y ＝0，x ﹣y ＝0，原方程组可化为{x +2y =8x +6y =0或{x +2y =8x −y =0，故原方程组的解为{x 1=12y 1=−2，{x 2=83y 2=83． 21．（10分）如图，在△ABC 中，∠C ＝90°，∠A ＝30°，BC ＝1，点D 在边AC 上，且∠DBC ＝45°，求sin ∠ABD 的值．【解答】解：如图，过点D 作DM ⊥AB 于M ，在BA 上取一点H ，使得BH ＝DH ，连接DH ．设DM ＝a ．∵∠C ＝90°，∠A ＝30°， ∴∠ABC ＝90°﹣30°＝60°， ∵∠DBC ＝45°，∴∠ABD ＝60°﹣45°＝15°， ∵HB ＝HD ，∴∠HBD ＝∠HDB ＝15°， ∴∠DHM ＝∠HBD +∠HDB ＝30°，∴DH ＝BH ＝2a ，MH =√3a ，BM ＝2a +√3a ，∴BD =√DM 2+BM 2=√a 2+(2a +√3a)2=（√2+√6）a ， ∴sin ∠ABD =DM DB =(2+6)a =√6−√24． 22．（10分）某电脑公司2019年的各项经营收入中，经营电脑配件的收入为800万元，占全年经营总收入的40%，该公司预计2021年经营总收入要达到2880万元，且计划从2019年到2021年，每年经营总收入的年增长率相同，问2020年预计经营总收入为多少万元？ 【解答】解：从2019年到2021年，平均经营总收入增长率为x ，根据题意可得： 800÷40%（1+x ）2＝2880，解得：x 1＝0.2＝20%，x 2＝2.2（不合题意舍去）， 则800÷40%×（1+20%）＝2400（万元）， 答：2020年预计经营总收入为2400万元．23．（12分）已知：如图，△ABC 中，∠ACB ＝90°，D 在斜边AB 上，DE ⊥AC ，DF ⊥BC ，垂足分 别为E ，F ．（1）当∠ACD ＝∠BCD 时，求证：四边形DECF 是正方形； （2）当∠BCD ＝∠A 时，求证：CD CA=CF AD．【解答】证明：（1）∵DE ⊥AC ，DF ⊥BC ， ∴∠DEC ＝∠DFC ＝90°， 又∵∠ECF ＝90°， ∴四边形DECF 为矩形． ∵∠ACD ＝∠BCD ，∴CD 平分∠ACB ， ∴DE ＝DF ，∴四边形DECF 是正方形．（2）∵∠BCD +∠ACD ＝∠ACB ＝90°，∠BCD ＝∠A ， ∴∠A +∠ACD ＝90°，∴∠ADC ＝180°﹣90°＝90°．∵∠DCF ＝∠A ，∠DFC ＝∠ADC ＝90°， ∴△CDF ∽△ACD ， ∴CD CA=CF AD．24．（12分）如图，已知一个抛物线经过A （0，1），B （1，3），C （﹣1，1）三点． （1）求这个抛物线的表达式及其顶点D 的坐标； （2）联结AB 、BC 、CA ，求tan ∠ABC 的值；（3）如果点E 在该抛物线的对称轴上，且以点A 、B 、C 、E 为顶点的四边形是梯形，直接写出点E 的坐标．【解答】解：（1）设抛物线的解析式为y ＝ax 2+bx +c （a ≠0）． 由题意可得：{3=a +b +c 1=a −b +c c =1解得：{a =1b =1c =1∴抛物线的解析式为：y＝x2+x+1，∵y＝x2+x+1＝（x+12）2+34，∴顶点D的坐标（−12，34）；（2）如图，过点B作BF⊥x轴于F，延长CA交BF于点D，过点A作AM⊥BC于M，∴BF＝3，∵A（0，1），C（﹣1，1），∴AC∥x轴，∴CD⊥BF，∴CD＝BD＝2，AD＝1，CA＝1，∴BC＝2√2，∠BCD＝∠CBD＝45°，∵AM⊥BC，∴∠MAC＝∠MCA＝45°，∴CM＝AM，∴CM＝AM=2=√22，∴BM＝BC﹣CM=3√2 2，∴tan∠ABC=AMBM=13；（3）∵A（0，1），B（1，3），C（﹣1，1），∴直线AC解析式为：y＝1，直线AB解析式为：y＝2x+1，直线BC解析式为：y＝x+2，若BE∥AC，则点E的纵坐标为3，且点E在对称轴上，∴点E（−12，3）；若CE∥AB，则CE的解析式为；y＝2x+3，∵点E在对称轴上，∴x=−1 2，∴y＝2，即点E（−12，2）；若AE∥BC，则AE解析式为：y＝x+1，∵点E在对称轴上，∴x=−1 2，∴y=1 2，即点E（−12，12），综上所述：点E的坐标为（−12，3）或（−12，2）或（−12，12）．25．（14分）在圆O中，弦AB与CD相交于点E，且弧AC与弧BD相等．点D在劣弧AB上，联结CO并延长交线段AB于点F，联结OA、OB．当OA=√5，且tan∠OAB=1 2．（1）求弦CD的长；（2）如果△AOF是直角三角形，求线段EF的长；（3）如果S△CEF＝4S△BOF，求线段AF的长．【解答】解：（1）如图，过点O作OH⊥AB于点H，∵tan∠OAB=12=OHAH，∴设OH＝a，AH＝2a，∵AO2＝OH2+AH2＝5，∴a＝1，∴OH＝1，AH＝2，∵OH⊥AB，∴AB＝2AH＝4，∵弧AC＝弧BD∴AB̂=CD̂，∴AB＝CD＝4；（2）∵OA＝OB，∴∠OAF＝∠OBA，∴∠OAF＝∠ECF，①当∠AFO＝90°时，∵OA=√5，tan∠OBA=1 2，∴OC＝OA=√5，OF＝1，AB＝4，∴EF＝CF•tan∠ECF＝CF•tan∠OBA=√5+1 2；②当∠AOF＝90°时，∵OA＝OB，∴∠OAF＝∠OBA，∴tan∠OAF＝tan∠OBA=1 2，∵OA=√5，∴OF＝OA•tan∠OAF=√5 2，∴AF=5 2，∵∠OAF＝∠OBA＝∠ECF，∠OF A＝∠EFC，∴△OF A∽△EFC，∴EFOF =OC+OFAF=3√55，∴EF=3√55OF=32，即：EF=32或√5+12；（3）如图，连接OE，∵∠ECB ＝∠EBC ， ∴CE ＝EB ，∵OE ＝OE ，OB ＝OC ， ∴△OEC ≌△OEB ， ∴S △OEC ＝S △OEB ， ∵S △CEF ＝4S △BOF ， ∴S △CEO +S △EOF ＝4（S △BOE ﹣S △EOF ）， ∴S △CEO S △EFO =53， ∴CO FO =53，∴FO =35CO =3√55，∵△OF A ∽△EFC ， ∴CE EF =AO FO =OC OF =53， ∴BF ＝BE ﹣EF ＝CE ﹣EF =23EF ，∴AF ＝AB ﹣BF ＝4−23EF ， ∵△OAF ∽△EFC ， ∴CF FA =EF FO ，∴85√54−23EF =3√55，∴EF ＝3−3√55， ∴AF ＝4−23EF ＝2+2√55．。

2020-2021学年上海市闵行区九年级（上）期末数学试卷（一模）第I卷（选择题）一、选择题（本大题共6小题，共24.0分）1.下列函数中，y是x二次函数的是()A. y=x+2B. y=2x2+1x−10C. y=x2+5xD. y2=x−12.在Rt△ABC中，∠C=90°，∠B=35°，AB=7，则BC的长为()A. 7sin35°B. 7cos35°C. 7tan35°D. 7cos35∘3.二次函数y=ax2+bx−2(a≠0)的图象的顶点在第三象限，且过点(1,0)，设t=a−b−2，则t值的变化范围是()A. −2<t<0B. −3<t<0C. −4<t<−2D. −4<t<04.已知e⃗是单位向量，且a⃗=−2e⃗，b⃗ =4e⃗，那么下列说法错误的是()A. a⃗//b⃗B. |a⃗|=2C. |b⃗ |=−2|a⃗|D. a⃗=−12b⃗5.已知⊙O1与⊙O2的半径分别是2和6，若⊙O1与⊙O2相交，那么圆心距O1O2的取值范围是()A. 2<O1O2<4B. 2<O1O2<6C. 4<O1O2<8D. 4<O1O2<106.美是一种感觉，当人体下半身长与身高比值越接近0.618，越给人一种美感，某女士身高165厘米，下半身长X与身高I的比值是0.6，为尽可能达到好的效果，她应该穿的高跟鞋的高度大约为A. 4厘米B. 6厘米C. 8厘米D. 10厘米第II卷（非选择题）二、填空题（本大题共12小题，共48.0分）7.如果x2=y3≠0，那么xy=______．8.计算：32(a⃗−2b⃗ )−4b⃗ =______．9.在直角坐标系平面内，抛物线y=3x2+2x在对称轴的左侧部分是______的(填“上升”或“下降”)10.将抛物线y=(x+2)2−3向右平移3个单位长度，得到的抛物线与y轴的交点坐标是()A.(0,−2)B.(0,−1)C.(0.2)D.(0,3)11.已知两个相似三角形的面积之比是1：4，那么这两个三角形的周长之比是______ ．12.如图所示，△ABC中，点D、E分别在AB、AC上，DE//BC，，则BC=______若AE=3，EC=1，且知DE=7213.在直角坐标系中，已知点P在第一象限内，点P与原点O的距离OP=2，点P与原点O的连线与x轴的正半轴的夹角为60°，则点P的坐标是______ ．14.若B地在A地的南偏东50∘方向5km处，则A地在B地的方向处.15.已知正六边形的半径为4cm，则它的边长等于________cm．16.如图，已知△ABC和△DEC的面积相等，点E在BC边上，DE//AB交AC于点F，AB=12，EF=9，则DF的长是．17.在△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径画圆．(1)若⊙C与线段AB没有公共点，则r满足的条件是____________；(2)若⊙C 与线段AB 只有一个公共点，则r 满足的条件是___________； (3)若⊙C 与线段AB 有两个公共点，则r 满足的条件是___________． 18. 如图，在△ABC 中，∠ACB =90°，sinB =35，将△ABC 绕顶点C 顺时针旋转，得到△A 1B 1C ，点A 、B 分别与点A 1、B 1对应，边A 1B 1分别交边AB 、BC 于点D 、E ，如果点E 是边A 1B 1的中点，那么BDB1C=______．三、解答题（本大题共7小题，共78.0分）19. 计算：cos30°+sin60°−(tan45°−1)201820. 已知：如图，在平行四边形ABCD 中，E 、F 分别是对角线BD 上的两点，且BE =DF ，AB ⃗⃗⃗⃗⃗ =a ⃗ ，BC ⃗⃗⃗⃗⃗ =b ⃗ ，AF ⃗⃗⃗⃗⃗ =c ⃗ ． (1)用向量a ⃗ 、b ⃗ 、c ⃗ 表示下列向量：向量CE ⃗⃗⃗⃗⃗ =______，向量BD ⃗⃗⃗⃗⃗⃗ =______，向量DE⃗⃗⃗⃗⃗⃗ =______； (2)求作：b ⃗ +c ⃗ ．21.如图，⊙O是△ABC的外接圆，∠A=45°，BD是直径，且BC=2，连接CD，求BD的长．22.某数学小组在郊外的水平空地上对无人机进行测高实验．如图，两台测角仪分别放在A、B位置，且离地面高均为1米(即AD=BE=1米)，两台测角仪相距100米(即AB=100米).在某一时刻无人机位于点C(点C与点A、B在同一平面内)，A处测得其仰角为30°，B处测得其仰角为45°.求该时刻无人机的离地高度；(单位：米，结果保留整数)；(参考数据：√2≈1.41，√3≈1.73)23.已知：如图，△ABC中，AD是角平分线，点E在AC上，∠ADE=∠B，求证：AD2=AE⋅AB．24.已知：抛物线y=ax2+bx−3经过点A(7,−3)，与x轴正半轴交于点B(m,0)、C(6m、0)两点，与y轴交于点D．(1)求m的值；(2)求这条抛物线的表达式；(3)点P在抛物线上，点Q在x轴上，当∠PQD=90°且PQ=2DQ时，求点P、Q的坐标．25.已知锐角∠MBN的余弦值为3，点C在射线BN上，BC=25，点A在∠MBN的内部，5且∠BAC=90°，∠BCA=∠MBN.过点A的直线DE分别交射线BM、射线BN于点D、E.点F在线段BE上(点F不与点B重合)，且∠EAF=∠MBN．(1)如图1，当AF⊥BN时，求EF的长；(2)如图2，当点E在线段BC上时，设BF=x，BD=y，求y关于x的函数解析式并写出函数定义域；(3)联结DF，当△ADF与△ACE相似时，请直接写出BD的长．答案和解析1.【答案】C【解析】【分析】本题考查了二次函数的定义，形如y=ax2+bx+c(a≠0)是二次函数．根据二次函数的定义，可得答案．【解答】A. y=x+2，是一次函数，不合题意；−10，不是二次函数，不合题意；B.y=2x2+1xC.y=x2+5x，是二次函数，符合题意；D.y2=x−1，y不是x的二次函数，不合题意．故选C．2.【答案】B【解析】解：在Rt△ABC中，cosB=BC，AB∴BC=AB⋅cosB=7cos35°，故选：B．根据余弦的定义列出算式，计算即可．本题考查的是锐角三角函数的定义，掌握锐角A的邻边b与斜边c的比叫做∠A的余弦是解题的关键．3.【答案】D【解析】解：y=ax2+bx−2，当x=0时，y=−2，即抛物线与y轴的交点是(0,−2)，过点(1,0)和点(0,−2)的直线的解析式是y=2x−2，当x=−1时，y=2x−2=−4，而x=−1时，y=ax2+bx+c=a−b+c，∵t=a−b−2，∴−4<a−b+c<0，即−4<t<0，故选：D．先利用待定系数法求出经过点(1,0)和(0,−2)的直线解析式为y=2x−2，则当x=−1时，y=2x−2=−4，再利用抛物线的顶点在第三象限，所以x=−1时，对应的二次函数值为负数，从而得到所以−4<a−b+c<0，再根据抛物线的顶点坐标得出即可．本题考查了二次函数图象与系数的关系：二次项系数a决定抛物线的开口方向和大小．当a>0时，抛物线向上开口；当a<0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时，对称轴在y轴左；当a与b异号时，对称轴在y轴右．常数项c决定抛物线与y轴交点：抛物线与y轴交于(0,c).抛物线与x 轴交点个数由判别式确定：△=b2−4ac>0时，抛物线与x轴有2个交点；△=b2−4ac=0时，抛物线与x轴有1个交点；△=b2−4ac<0时，抛物线与x轴没有交点．4.【答案】C【解析】解：∵a⃗=−2e⃗，b⃗ =4e⃗，b⃗ ，∴a⃗//b⃗ ，|a⃗|=2，a⃗=−12∴A、B、D正确，故选：C．根据平面向量的性质即可一一判断．本题考查平面向量，熟练掌握平面向量的基本性质的解题的关键．5.【答案】C【解析】解：两圆半径差为4，半径和为8，两圆相交时，圆心距大于两圆半径差，且小于两圆半径和，所以，4<O1O2<8．故选C．本题直接告诉了两圆的半径及两圆相交，求圆心距范围内的可能取值，根据数量关系与两圆位置关系的对应情况便可直接得出答案．相交，则R−r<P<R+r.(P表示圆心距，R，r分别表示两圆的半径)．本题考查了由数量关系及两圆位置关系确定圆心距范围内的数的方法，属于基础题，比较简单．6.【答案】C【解析】【分析】本题考查了黄金分割的应用．关键是明确黄金分割所涉及的线段的比．先求得下半身的实际高度，再根据黄金分割的定义求解．【解答】解：根据已知条件得下半身长是165×0.60=99cm，设需要穿的高跟鞋是ycm，则根据黄金分割的定义得：99+y165+y=0.618，解得：y≈8cm．故选C．7.【答案】23【解析】【试题解析】解：∵x2=y3≠0，∴xy =23．故答案为：23．直接利用已知将比例式变形得出答案．此题主要考查了比例的性质，正确将比例式变形是解题关键．8.【答案】32a⃗−7b⃗【解析】【分析】实数的运算法则同样适用于平面向量的计算．本题考查了平面向量的有关概念，是基础题．【解答】解：：32(a⃗−2b⃗ )−4b⃗ =32a⃗−32×2b⃗ −4b⃗ =32a⃗−7b⃗ ．a⃗−7b⃗ ．故答案是：329.【答案】下降【解析】解：∵在y=3x2+2x中，a=3>0，∴抛物线开口向上，∴在对称轴左侧部分y随x的增大而减小，即图象是下降的，故答案为：下降．由抛物线解析式可求得其开口方向，再结合二次函数的增减性则可求得答案．本题主要考查二次函数的性质，利用二次函数的解析式求得抛物线的开口方向是解题的关键．10.【答案】A【解析】【分析】此题主要考查了二次函数的几何变换，正确得出平移后解析式是解题关键．直接利用二次函数的平移规律进而得出函数关系式，进而求出答案．【解答】解：将抛物线y=(x+2)2−3向右平移3个单位长度，得抛物线y=(x−1)2−3，当x=0时，y=−2，∴得到的抛物线与y轴的交点坐标是(0,−2)．故选A．11.【答案】1：2【解析】解：∵两个相似三角形的面积比是1：4，∴这两个相似三角形的相似比是1：2，∴它们的周长比是1：2．故答案为：1：2．由两个相似三角形的面积比是1：4，根据相似三角形的面积比等于相似比的平方，即可求得它们的相似比，又由相似三角形周长的比等于相似比，即可求得它们的周长比．此题考查了相似三角形的性质．此题比较简单，解题的关键是掌握相似三角形的面积比等于相似比的平方与相似三角形周长的比等于相似比性质的应用．12.【答案】143【解析】解：∵DE//BC，∴∠ADE=∠B，∠AED=∠C，∴△ADE∽△ABC，可知：AEAC =DEBC将AE=3，AC=3+1=4DE=7 2代入得：34=72BC∴BC=143故答案为：143根据相似三角形的性质与判定即可求出答案．本题考查相似三角形的性质与判定，解题的关键是熟练运用相似三角形的性质与判定，本题属于基础题型．13.【答案】(1,√3)【解析】解：作PM⊥x轴于点M，如图所示：∵OP=2，∴sin60°=PMOP =√32，cos60°=OMOP=12，∴PM=√3，OM=1．故P点坐标为：(1,√3).故答案为：(1,√3).作PM⊥x轴于点M，构造直角三角形，根据三角函数的定义求解．本题考查了解直角三角形和坐标与图形性质的知识，难度不大，注意掌握一个角的余弦和正弦的计算方法．14.【答案】北偏西50°，5km【解析】【分析】本题考查的是方向角，解答此类题需要从运动的角度，正确画出方位角，找准中心是解答此类题的关键．根据方位角的概念，画图正确表示出方位角，即可求解．【解答】解：从图中发现∠CAB=50°，故A地在B地的北偏西50°方向5km．故答案为北偏西50°，5km．15.【答案】【解析】【分析】此题主要考查了正多边形和圆，利用正六边形的外接圆半径和正六边形的边长将组成一个等边三角形得出是解题关键.根据正六边形的外接圆半径和正六边形的边长将组成一个等边三角形，即可求解．【解答】解：正六边形的中心角为360°÷6=60°，那么外接圆的半径和正六边形的边长将组成一个等边三角形，故正六边形的外接圆半径等于4cm，则正六边形的边长是4cm．故答案为4．16.【答案】7【解析】【分析】本题考查相似三角形的判定与性质，三角形的面积，关键是根据题意，易得△CDF与四边形AFEB的面积相等，再根据相似三角形的相似比求得它们的面积关系比，从而求DF的长．【解答】解：∵△ABC与△DEC的面积相等，∴△CDF与四边形AFEB的面积相等，∵AB//DE，∴△CEF∽△CBA，∵EF=9，AB=12，∴EF:AB=9:12=3:4，∴△CEF和△CBA的面积比=9:16，设△CEF的面积为9k，则四边形AFEB的面积=7k，∵△CDF与四边形AFEB的面积相等，∴S△CDF=7k，∵△CDF与△CEF是同高不同底的三角形，∴面积比等于底之比，∴DF:EF=7k:9k=7:9，∵EF=9，∴DF=7．故答案为：7．17.【答案】(1)0<r<2.4或r>4(2)3<r≤4或r=2.4(3)2.4<r≤3．【解析】【分析】(1)要使圆和斜边没有公共点，则有两种情况：①直线和圆相离；②直线和圆相交，但交点不在斜边上，根据题意，求出直角三角形斜边上的高，便可直观得出半径的取值范围；(2)两种情况：①圆与AB相切时；②点A在园内部，点B在圆上或圆外时；(3)要使圆与斜边AB有两个交点，则应满足直线和圆相交，且半径不大于AC即可．【解答】(1)如图，根据勾股定理求得AB=5．∵BC>AC，r=CD=3×4÷5=2.4，若⊙C与线段AB没有公共点，0<r<2.4，或r>4．(2)以C为圆心，r为半径所作的圆与斜边AB只有一个公共点，分两种情况：①圆与AB相切时，即r=CD=3×4÷5=2.4;②点A在圆内部，点B在圆上或圆外时，此时AC<r≤BC，即3<r≤4，∴r=2.4或3≤4;(3)以C为圆心，r为半径所作的圆与斜边AB有两个交点，则圆的半径应大于CD，小于或等于AC，即r的取值范围是2.4<r≤3．故答案为(1)0<r<2.4或r>4；(2)3<r≤4或r=2.4；(3)2.4<r≤3．18.【答案】35【解析】【分析】本题考查了旋转的性质，解直角三角形，相似三角形的判定和性质，证△CEB1∽△DEB 是本题的关键．设AC=3x，AB=5x，可求BC=4x，由旋转的性质可得CB1=BC=4x，A1B1=5x，∠ACB=∠A1CB1，由题意可证△CEB1∽△DEB，可得BDB1C =BEB1E=1.5x2.5x=35，即可求解．【解答】解：∵∠ACB=90°，sinB=ACAB =35，∴设AC=3x，AB=5x，∴BC=√AB2−AC2=4x，∵将△ABC绕顶点C顺时针旋转，得到△A1B1C，∴CB1=BC=4x，A1B1=5x，∠ACB=∠A1CB1，∵点E是A1B1的中点，∴CE=12A1B1=2.5x=B1E，∴BE=BC−CE=1.5x，∵∠B=∠B1，∠CEB1=∠BED∴△CEB1∽△DEB∴BDB1C =BEB1E=1.5x2.5x=35，故答案为：35．19.【答案】解：原式=√32+√32−(1−1)2018=√3．【解析】根据特殊角三角函数值，可得答案．本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键． 20.【答案】(1)−c ⃗ a ⃗ −b ⃗ a⃗ −c ⃗ (2)延长EC 到K ，使得CK =EC ，连接BK ，则向量BK⃗⃗⃗⃗⃗⃗ 即为所求；【解析】解：(1)∵四边形ABCD 是平行四边形， ∴AD//BC ，AD =BC ， ∴∠ADF =∠CBE ， ∵DF =BE ， ∴△ADF≌△CBE ，∴∠AFD =∠CEB ，AF =CE ， ∴∠AFB =∠CED ， ∴AF//CE ，∴CE ⃗⃗⃗⃗⃗ =−EC ⃗⃗⃗⃗⃗ =−AF ⃗⃗⃗⃗⃗ =−c ⃗ ， BD ⃗⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ =a ⃗ −b ⃗ ， DE ⃗⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ +CE ⃗⃗⃗⃗⃗ =a ⃗ −c ⃗ ， 故答案为−c ⃗ ，a ⃗ −b ⃗ ，a ⃗ −c ⃗ ．(2)见答案． 【分析】(1)根据平面向量的加法法则计算即可；(2)延长EC 到K ，使得CK =EC ，连接BK ，则向量BK⃗⃗⃗⃗⃗⃗ 即为所求； 本题考查平行四边形的性质、三角形法则等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．21.【答案】解：∵∠A 和∠D 所对的弧都是弧BC ，∴∠D =∠A =45°， ∵BD 是直径，∴∠D=∠DBC=45°，∴CB=CD=2，由勾股定理得：BD=√BC2+CD2=2√2．【解析】根据圆周角定理求出∠D=∠A=45°，BD是直径，根据勾股定理计算即可．本题考查的是三角形的外接圆，掌握圆周角定理、勾股定理是解题的关键．22.【答案】解：如图，过点C作CH⊥AB，垂足为点H，∵∠CBA=45°，∴BH=CH，设CH=x，则BH=x．∵在Rt△ACH中，∠CAB=30°，AH=√3CH=√3x∴.√3x+x=100解得：x=√3+1=36.6≈37∴37+1=38m.答：无人机的离地的高约为38m.【解析】本题考查解直角三角形的应用−仰角、俯角问题，解题的关键是学会添加常用辅助线，构造直角三角形解决问题.过点C作点CH⊥AB于H.设AH=CH=x，根据AB= 100，构建方程即可解决问题．23.【答案】证明：∵AD是角平分线，∴∠BAD=∠DAE，又∵∠ADE=∠B，∴△ABD∽△ADE，∴ABAD =ADAE，【解析】本题考查的是相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．证明△ABD∽△ADE，根据相似三角形的性质列出比例式，计算即可证明．24.【答案】解：(1)当x=0时，y=−3，∴D(0,−3)．设抛物线的解析式为y=a(x−m)(x−6m)．把点D和点A的坐标代入得：6am2=−3①，a(7−m)(7−6m)=−3②，∴a(7−m)(7−6m)=6am2．∵a≠0，∴(7−m)(7−6m)=m2．解得：m=1．(2)∵6am2=−3，∴a=−36m2=−12．将a=−12，m=1代入得：y=−12x2+72x−3．∴抛物线的表达式为y=−12x2+72x−3．(3)如图所示：过点P作PE⊥x轴，垂足为E．设点Q的坐标为(a,0)则OQ=−a−∵∠DQP=90°，∴∠PQO+∠OQD=90°．又∵∠ODQ+∠DQO=90°，∴∠PQE=∠ODQ．又∵∠PEQ=∠DOQ=90°，∴△ODQ∽△EQP．∴QOPE =ODQE=QDQP=12，即−a3=PE6=12，∴QE=6，PE=−2a．∴P的坐标为(a+6,−2a)将点P的坐标代入抛物线的解析式得：−12(a+6)2+72(a+6)−3=−2a，整理得：a2+a=0，解得a=−1或a=0．当a=−1时，Q(−1,0)，P(5,2)；当a=0时，Q(0,0)，P(6,0)．综上所述，Q(−1,0)，P(5,2)或者Q(0,0)，P(6,0)．【解析】(1)先求得点D的坐标，然后设抛物线的解析式为y=a(x−m)(x−6m)，把点D和点A的坐标代入可求得m的值；(2)由6am2=−3，m=1可求得a的值，然后代入抛物线的解析式即可；(3)过点P作PE⊥x轴，垂足为E.设点Q的坐标为(a,0)则OQ=−a，然后证明△ODQ∽△EQP，依据相似三角形的性质可求得QE=6，PE=−2a.，则P的坐标为(a+6,−2a)，将点P的坐标代入抛物线的解析式可求得a的值．本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式、相似三角形的性质和判定，用含a的式子表示出点P的坐标是解题的关键．25.【答案】解：(1)∵在Rt△ABC中，∠BAC=90°，∴cos∠BCA=cos∠MBN=ACBC =35=，∴AC=3∴AC=15∴AB=√BC2−AC2=20∵S△ABC=12×AB×AC=12×BC×AF，∴AF=20×1525=12，∵AF⊥BC∴cos∠EAF=cos∠MBN=35=AFAE∴AE=20∴EF=√AE2−AF2=16(2)如图，过点A作AH⊥BC于点H，由(1)可知：AB=20，AH=12，AC=15，∴BH=√AB2−AH2=16，∵BF=x，∴FH=16−x，CF=25−x，∴AF2=AH2+FH2=144+(16−x)2=x2−32x+400，∵∠EAF=∠MBN，∠BCA=∠MBN∴∠EAF=∠BCA，且∠AFC=∠AFC，∴△FAE∽△FCA∴AFFC =EFAF，∠AEF=∠FAC，∴AF2=FC×EF∴x2−32x+400=(25−x)×EF，∴EF=x2−32x+40025−x∴BE=BF+EF=400−7x 25−x∵∠MBN=∠ACB，∠AEF=∠FAC，∴△BDE∽△CFA∴BDFC=BEAC∴y=400−7x25−x∴y=400−7x15(0<x≤252)(3)如图，若△ADF∽△CEA，∵△△ADF∽△CEA，∴∠ADF=∠AEC，∵∠EAF=∠MBN，∠EAF+∠DAF=180°，∴∠DAF+∠MBN=180°，∴点A，点F，点B，点D四点共圆，∴∠ADF=∠ABF，∴∠ADF=∠AEC=∠ABF，∴AB=AE，∵∠BAC=90°，∴∠ABC+∠ACB=90°，且∠ABF=∠AEC，∠ACB=∠MBN=∠EAF，∴∠AEC+∠EAF=90°，∠AEC+∠MBN=90°，∴∠BDE=90°=∠AFC，∵S△ABC=12×AB×AC=12×BC×AF，∴AF=20×1525=12，∴BF=√AB2−AF2=16，∵AB=AE，∠AFC=90°，∴BE=2BF=32，∴cos∠MBN=BDBE =35，∴BE=965，如图，若△ADF∽△CAE，∵△ADF∽△CAE ，∴∠ADF =∠CAE ，∠AFD =∠AEC ，∴AC//DF∴∠DFB =∠ACB ，且∠ACB =∠MBN ，∴∠MBN =∠DFB ，∴DF =BD ，∵∠EAF =∠MBN ，∠EAF +∠DAF =180°，∴∠DAF +∠MBN =180°，∴点A ，点F ，点B ，点D 四点共圆，∴∠ADF =∠ABF ，∴∠CAE =∠ABF ，且∠AEC =∠AEC ，∴△ABE∽△CAE∴AB AC =AE CE =BE AE =2015=43设CE =3k ，AE =4k ，(k ≠0)∴BE =163k ，∵BC =BE −CE =25∴k =757∴AE =3007，CE =2257，BE =4007∵∠ACB =∠FAE ，∠AFC =∠AFE ，∴△AFC∽△EFA ，∴AF EF =CF AF =AC AE =153007=720， 设AF =7a ，EF =20a ，∴CF =4920a ，∵CE =EF −CF =35120a =2257，∴a =15007×117，∴EF =30000117×7， ∵AC//DF ，∴AC DF =CE EF ，∴15DF =2257300007×117， ∴DF =2000117，综上所述：当BD 为965或2000117时，△ADF 与△ACE 相似【解析】(1)由锐角三角函数可求AC =15，根据勾股定理和三角形面积公式可求AB ，AF 的长，即可求EF 的长；(2)通过证△FAE∽△FCA 和△BDE∽△CFA ，可得y 关于x 的函数解析式；(3)分△ADF∽△CEA ，△ADF∽△CAE 两种情况讨论，通过等腰三角形的性质和相似三角形性质可求BD 的长．本题是相似综合题，考查了相似三角形的判定和性质，勾股定理，锐角三角函数等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．。

中考数学模拟试卷一、选择题（本题包括10个小题，每小题只有一个选项符合题意）1．甲、乙两船从相距300km 的A 、B 两地同时出发相向而行，甲船从A 地顺流航行180km 时与从B 地逆流航行的乙船相遇，水流的速度为6km/h ，若甲、乙两船在静水中的速度均为xkm/h ，则求两船在静水中的速度可列方程为（ ）A ．1806x +=1206x -B ．1806x -=1206x + C ．1806x +=120x D ．180x =1206x - 【答案】A 【解析】分析：直接利用两船的行驶距离除以速度=时间，得出等式求出答案．详解：设甲、乙两船在静水中的速度均为xkm/h ，则求两船在静水中的速度可列方程为：1806x +=1206x -． 故选A ．点睛：此题主要考查了由实际问题抽象出分式方程，正确表示出行驶的时间和速度是解题关键． 2．在一幅长80cm ，宽50cm 的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整幅挂图的面积是25400cm ，设金色纸边的宽为xcm ，那么x 满足的方程是（ ）A ．213014000x x +-=B ．2653500x x +-=C ．213014000x x --=D ．2653500x x --=【答案】B 【解析】根据矩形的面积=长×宽，我们可得出本题的等量关系应该是：（风景画的长+2个纸边的宽度）×（风景画的宽+2个纸边的宽度）=整个挂图的面积，由此可得出方程.【详解】由题意，设金色纸边的宽为xcm ，得出方程：（80+2x ）（50+2x ）=5400，整理后得：2653500x x +-=故选：B.【点睛】本题主要考查了由实际问题得出一元二次方程，对于面积问题应熟记各种图形的面积公式，然后根据等量关系列出方程是解题关键.3．如图，已知AB＝AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是( )A．CB＝CD B．∠BCA＝∠DCAC．∠BAC＝∠DAC D．∠B＝∠D＝90°【答案】B【解析】由图形可知AC＝AC，结合全等三角形的判定方法逐项判断即可.【详解】解：在△ABC和△ADC中∵AB＝AD，AC＝AC，∴当CB＝CD时，满足SSS，可证明△ABC≌△ACD，故A可以；当∠BCA＝∠DCA时，满足SSA，不能证明△ABC≌△ACD，故B不可以；当∠BAC＝∠DAC时，满足SAS，可证明△ABC≌△ACD，故C可以；当∠B＝∠D＝90°时，满足HL，可证明△ABC≌△ACD，故D可以；故选：B.【点睛】本题考查了全等三角形的判定方法，熟练掌握判定定理是解题关键.4．如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB＝1，CD＝3，那么EF的长是( )A．13B．23C．34D．45【答案】C【解析】易证△DEF∽△DAB，△BEF∽△BCD，根据相似三角形的性质可得EFAB=DFDB,EFCD=BFBD，从而可得EFAB+EFCD=DFDB+BFBD=1．然后把AB=1，CD=3代入即可求出EF的值．【详解】∵AB、CD、EF都与BD垂直，∴AB∥CD∥EF，∴△DEF∽△DAB,△BEF∽△BCD，∴EFAB =DFDB,EFCD=BFBD，∴EF AB +EF CD =DF DB +BF BD =BD BD=1. ∵AB=1，CD=3， ∴1EF +3EF =1， ∴EF=34. 故选C.【点睛】本题考查了相似三角形的判定及性质定理，熟练掌握性质定理是解题的关键.5．如图，能判定EB ∥AC 的条件是( )A ．∠C=∠ABEB ．∠A=∠EBDC ．∠A=∠ABED ．∠C=∠ABC【答案】C 【解析】在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角，被判断平行的两直线是否由“三线八角”而产生的被截直线．【详解】A 、∠C=∠ABE 不能判断出EB ∥AC ，故本选项错误；B 、∠A=∠EBD 不能判断出EB ∥AC ，故本选项错误；C 、∠A=∠ABE ，根据内错角相等，两直线平行，可以得出EB ∥AC ，故本选项正确；D 、∠C=∠ABC 只能判断出AB=AC ，不能判断出EB ∥AC ，故本选项错误．故选C ．【点睛】本题考查了平行线的判定，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．6．如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是( )A ．1，2，3B ．1，12C ．1，13D ．1，23【答案】D【解析】根据三角形三边关系可知，不能构成三角形，依此即可作出判定；B 、根据勾股定理的逆定理可知是等腰直角三角形，依此即可作出判定；C 、解直角三角形可知是顶角120°，底角30°的等腰三角形，依此即可作出判定；D 、解直角三角形可知是三个角分别是90°，60°，30°的直角三角形，依此即可作出判定．【详解】∵1+2=3，不能构成三角形，故选项错误；B 、∵12+12=(2)2，是等腰直角三角形，故选项错误；C 、底边上的高是2231-2（）=12，可知是顶角120°，底角30°的等腰三角形，故选项错误； D 、解直角三角形可知是三个角分别是90°，60°，30°的直角三角形，其中90°÷30°=3，符合“智慧三角形”的定义，故选项正确．故选D ．7．世界上最小的鸟是生活在古巴的吸蜜蜂鸟，它的质量约为0.056盎司．将0.056用科学记数法表示为（ ） A ．5.6×10﹣1B ．5.6×10﹣2C ．5.6×10﹣3D ．0.56×10﹣1【答案】B【解析】0.056用科学记数法表示为：0.056=-25.610⨯，故选B. 8．运用图形变化的方法研究下列问题：如图，AB 是⊙O 的直径，CD ，EF 是⊙O 的弦，且AB ∥CD ∥EF ，AB=10，CD=6，EF=8.则图中阴影部分的面积是（ ）A ．252πB ．10πC ．24+4πD ．24+5π【答案】A【解析】作直径CG ，连接OD 、OE 、OF 、DG ，则根据圆周角定理求得DG 的长，证明DG=EF ，则S 扇形ODG =S 扇形OEF ，然后根据三角形的面积公式证明S △OCD =S △ACD ，S △OEF =S △AEF ，则S 阴影=S 扇形OCD +S 扇形OEF =S 扇形OCD +S 扇形ODG =S 半圆，即可求解．【详解】作直径CG ，连接OD 、OE 、OF 、DG ．∵CG 是圆的直径，∴∠CDG=90°，则2222106CG CD -=-=8，又∵EF=8，∴DG=EF ，∴DG EF =，∴S 扇形ODG =S 扇形OEF ，∵AB ∥CD ∥EF ，∴S △OCD =S △ACD ，S △OEF =S △AEF ，∴S 阴影=S 扇形OCD +S 扇形OEF =S 扇形OCD +S 扇形ODG =S 半圆=12π×52=252π， 故选A ．【点睛】本题考查扇形面积的计算，圆周角定理．本题中找出两个阴影部分面积之间的联系是解题的关键．9．若数a ，b 在数轴上的位置如图示，则（ ）A ．a+b ＞0B ．ab ＞0C ．a ﹣b ＞0D ．﹣a ﹣b ＞0 【答案】D【解析】首先根据有理数a ，b 在数轴上的位置判断出a 、b 两数的符号，从而确定答案．【详解】由数轴可知：a ＜0＜b ，a<-1，0<b<1,所以,A.a+b<0，故原选项错误；B. ab ＜0，故原选项错误；C.a-b<0，故原选项错误；D. 0a b -->,正确.故选D ．【点睛】本题考查了数轴及有理数的乘法，数轴上的数：右边的数总是大于左边的数，从而确定a ，b 的大小关系．10．已知关于x 的不等式3x ﹣m+1＞0的最小整数解为2，则实数m 的取值范围是（ ）A ．4≤m ＜7B ．4＜m ＜7C ．4≤m≤7D ．4＜m≤7 【答案】A【解析】先解出不等式，然后根据最小整数解为2得出关于m 的不等式组，解之即可求得m 的取值范围．【详解】解:解不等式3x ﹣m+1＞0，得：x ＞13m -， ∵不等式有最小整数解2，∴1≤13m -＜2， 解得：4≤m ＜7，故选A ．【点睛】本题考查了一元一次不等式的整数解，解一元一次不等式组，正确解不等式，熟练掌握一元一次不等式、一元一次不等式组的解法是解答本题的关键．二、填空题（本题包括8个小题）11．分解因式：32a 4ab -= ．【答案】()()a a 2b a 2b +- 【解析】分析：要将一个多项式分解因式的一般步骤是首先看各项有没有公因式，若有公因式，则把它提取出来，之后再观察是否是完全平方公式或平方差公式，若是就考虑用公式法继续分解因式．因此， 先提取公因式a 后继续应用平方差公式分解即可：()()()3222a 4ab a a 4b a a 2b a 2b -=-=+-． 12．若一个圆锥的底面圆的周长是5πcm ，母线长是6cm ，则该圆锥的侧面展开图的圆心角度数是_____．【答案】150【解析】利用圆锥的底面周长和母线长求得圆锥的侧面积，然后再利用圆锥的面积的计算方法求得侧面展开扇形的圆心角的度数即可【详解】∵圆锥的底面圆的周长是45cm ，∴圆锥的侧面扇形的弧长为5π cm ，65180n ππ⨯∴=， 解得：150n =故答案为150．【点睛】此题考查弧长的计算，解题关键在于求得圆锥的侧面积13．如图，直线y 1＝mx 经过P(2，1)和Q(－4，－2)两点，且与直线y 2＝kx ＋b 交于点P ，则不等式kx ＋b ＞mx ＞－2的解集为_________________．【答案】－4＜x ＜1【解析】将P （1，1）代入解析式y 1=mx ，先求出m 的值为12，将Q 点纵坐标y=1代入解析式y=12x ，求出y 1=mx 的横坐标x=-4，即可由图直接求出不等式kx+b ＞mx ＞-1的解集为y 1＞y 1＞-1时，x 的取值范围为-4＜x ＜1．故答案为-4＜x ＜1．点睛：本题考查了一次函数与一元一次不等式，求出函数图象的交点坐标及函数与x 轴的交点坐标是解题的关键．142的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC ，用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为 米．【答案】14【解析】先利用△ABC 为等腰直角三角形得到AB=1，再设圆锥的底面圆的半径为r ，则根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到2πr=901180π⨯，然后解方程即可． 【详解】∵⊙O 的直径BC=2，∴AB=22BC=1， 设圆锥的底面圆的半径为r ，则2πr=901180π⨯，解得r=14， 即圆锥的底面圆的半径为14米故答案为14． 15．已知点A （4，y 1），B （，y 2），C （-2，y 3）都在二次函数y=（x-2）2-1的图象上，则y 1，y 2，y 3的大小关系是 .【答案】y 3>y 1>y 2.【解析】试题分析：将A,B,C 三点坐标分别代入解析式，得：y 1=3,y 2=5-4,y 3=15,∴y 3>y 1>y 2. 考点：二次函数的函数值比较大小.16．已知a ，b ，c ，d 是成比例的线段，其中3cm a =，2cm b =，6cm c =，则d =_______cm ．【答案】4【解析】如果其中两条线段的乘积等于另外两条线段的乘积，则四条线段叫成比例线段．根据定义ad ＝cb ，将a ，b 及c 的值代入即可求得d ．【详解】已知a ，b ，c ，d 是成比例线段，根据比例线段的定义得：ad ＝cb ，代入a ＝3，b ＝2，c ＝6，解得：d ＝4，则d ＝4cm ．故答案为：4【点睛】本题主要考查比例线段的定义．要注意考虑问题要全面．17．如图，在平面直角坐标系中，已知点A （1，1），以点O 为旋转中心，将点A 逆时针旋转到点B 的位置，则AB 的长为_____．【答案】24π． 【解析】由点A(1，1)，可得OA 的长，点A 在第一象限的角平分线上，可得∠AOB=45°，，再根据弧长公式计算即可．【详解】∵A(1，1)，∴OA=22112+=，点A 在第一象限的角平分线上，∵以点O 为旋转中心，将点A 逆时针旋转到点B 的位置，∴∠AOB=45°，∴AB 的长为452180π⨯=24π， 故答案为：24π． 【点睛】本题考查坐标与图形变化——旋转，弧长公式，熟练掌握旋转的性质以及弧长公式是解题的关键.本题中求出OA=2以及∠AOB=45°也是解题的关键．18．如图，AB 、CD 相交于点O ，AD ＝CB ，请你补充一个条件，使得△AOD ≌△COB ，你补充的条件是_____．【答案】∠A ＝∠C 或∠ADC ＝∠ABC【解析】本题证明两三角形全等的三个条件中已经具备一边和一角，所以只要再添加一组对应角或边相等即可．【详解】添加条件可以是：∠A ＝∠C 或∠ADC ＝∠ABC ．∵添加∠A ＝∠C 根据AAS 判定△AOD ≌△COB ，添加∠ADC ＝∠ABC 根据AAS 判定△AOD ≌△COB ，故填空答案：∠A ＝∠C 或∠ADC ＝∠ABC ．【点睛】本题考查了三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解题的关键．三、解答题（本题包括8个小题）19．如图，已知A（﹣4，n），B（2，﹣4）是一次函数y＝kx+b的图象和反比例函数y＝mx的图象的两个交点．求反比例函数和一次函数的解析式；求直线AB与x轴的交点C的坐标及△AOB的面积；直接写出一次函数的值小于反比例函数值的x的取值范围．【答案】（1）y＝﹣x﹣2；（2）C（﹣2，0），△AOB=6，,（3）﹣4＜x＜0或x＞2.【解析】（1）先把B点坐标代入代入y＝mx，求出m得到反比例函数解析式，再利用反比例函数解析式确定A点坐标，然后利用待定系数法求一次函数解析式；（2）根据x轴上点的坐标特征确定C点坐标，然后根据三角形面积公式和△AOB的面积＝S△AOC+S△BOC 进行计算；（3）观察函数图象得到当﹣4＜x＜0或x＞2时，一次函数图象都在反比例函数图象下方．【详解】解：∵B（2，﹣4）在反比例函数y＝mx的图象上，∴m＝2×（﹣4）＝﹣8，∴反比例函数解析式为：y＝﹣8x，把A（﹣4，n）代入y＝﹣8x，得﹣4n＝﹣8，解得n＝2，则A点坐标为（﹣4，2）．把A（﹣4，2），B（2，﹣4）分别代入y＝kx+b，得4224k bk b-+=⎧⎨+=-⎩，解得12kb=-⎧⎨=-⎩，∴一次函数的解析式为y＝﹣x﹣2；（2）∵y＝﹣x﹣2，∴当﹣x﹣2＝0时，x＝﹣2，∴点C的坐标为：（﹣2，0），△AOB 的面积＝△AOC 的面积+△COB 的面积 ＝12×2×2+12×2×4 ＝6；（3）由图象可知，当﹣4＜x ＜0或x ＞2时，一次函数的值小于反比例函数的值．【点睛】本题考查的是一次函数与反比例函数的交点问题以及待定系数法的运用，灵活运用待定系数法是解题的关键，注意数形结合思想的正确运用．20．2019年我市在“展销会”期间，对周边道路进行限速行驶.道路AB 段为监测区，C 、D 为监测点(如图).已知C 、D 、B 在同一条直线上，且AC BC ⊥，CD=400米，tan 2ADC ∠=，35ABC ∠=︒.求道路AB 段的长；(精确到1米)如果AB 段限速为60千米/时，一辆车通过AB 段的时间为90秒，请判断该车是否超速，并说明理由.(参考数据：sin350.57358︒≈，cos350.8195︒≈，tan350.7︒≈)【答案】 (1)AB≈1395 米；(2)没有超速．【解析】（1）先根据tan ∠ADC ＝2求出AC ，再根据∠ABC ＝35°结合正弦值求解即可（2）根据速度的计算公式求解即可.【详解】解：(1)∵AC ⊥BC ，∴∠C ＝90°，∵tan ∠ADC ＝AC CD ＝2， ∵CD ＝400，∴AC ＝800，在Rt △ABC 中，∵∠ABC ＝35°，AC ＝800，∴AB ＝sin 35AC ︒＝8000.57358≈1395 米； (2)∵AB ＝1395， ∴该车的速度＝139590＝55.8km/h ＜60千米/时， 故没有超速．【点睛】此题重点考察学生对三角函数值的实际应用，熟练掌握三角函数值的实际应用是解题的关键.21．某商场销售一批名牌衬衫，平均每天可以销售20件，每件盈利40元，为了扩大销售，增加利润，尽量减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫降价1元，商场平均每天多售出2件，若商场平均每天要盈利1200元，每件衬衫应降价多少元？【答案】每件衬衫应降价1元.【解析】利用衬衣平均每天售出的件数×每件盈利=每天销售这种衬衣利润列出方程解答即可.【详解】解：设每件衬衫应降价x元.根据题意，得（40-x）（1+2x）=110,整理，得x2-30x+10=0,解得x1=10，x2=1．∵“扩大销售量，减少库存”，∴x1=10应舍去，∴x=1.答：每件衬衫应降价1元.【点睛】此题主要考查了一元二次方程的应用，利用基本数量关系：平均每天售出的件数×每件盈利=每天销售的利润是解题关键.22．如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）. 请画出△ABC向左平移5个单位长度后得到的△A B C；请画出△ABC关于原点对称的△A B C；在轴上求作一点P，使△PAB 的周长最小，请画出△PAB，并直接写出P的坐标.【答案】（1）图形见解析；（2）图形见解析；（3）图形见解析，点P的坐标为：（2，0）【解析】(1)按题目的要求平移就可以了关于原点对称的点的坐标变化是:横、纵坐标都变为相反数，找到对应点后按顺序连接即可(3)AB的长是不变的，要使△PAB的周长最小，即要求PA+PB最小，转为了已知直线与直线一侧的两点，在直线上找一个点，使这点到已知两点的线段之和最小，方法是作A、B两点中的某点关于该直线的对称点，然后连接对称点与另一点．【详解】（1）△A1B1C1如图所示；（2）△A2B2C2如图所示；（3）△PAB如图所示，点P的坐标为：（2，0）【点睛】1、图形的平移；2、中心对称；3、轴对称的应用23．随着社会的发展，通过微信朋友圈发布自己每天行走的步数已经成为一种时尚．“健身达人”小陈为了了解他的好友的运动情况．随机抽取了部分好友进行调查，把他们6月1日那天行走的情况分为四个类别：A（0～5000步）（说明：“0～5000”表示大于等于0，小于等于5000，下同），B（5001～10000步），C（10001～15000步），D（15000步以上），统计结果如图所示：请依据统计结果回答下列问题：本次调查中，一共调查了位好友．已知A类好友人数是D类好友人数的5倍．①请补全条形图；②扇形图中，“A”对应扇形的圆心角为度．③若小陈微信朋友圈共有好友150人，请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步？【答案】（1）30；（2）①补图见解析；②120；③70人.【解析】分析：（1）由B类别人数及其所占百分比可得总人数；（2）①设D类人数为a，则A类人数为5a，根据总人数列方程求得a的值，从而补全图形；②用360°乘以A类别人数所占比例可得；③总人数乘以样本中C、D类别人数和所占比例．详解：（1）本次调查的好友人数为6÷20%=30人，故答案为：30；（2）①设D类人数为a，则A类人数为5a，根据题意，得：a+6+12+5a=30，解得：a=2，即A类人数为10、D类人数为2，补全图形如下：②扇形图中，“A”对应扇形的圆心角为360°×1030=120°，故答案为：120；③估计大约6月1日这天行走的步数超过10000步的好友人数为150×12230+=70人．点睛：此题主要考查了条形统计图、扇形统计图的综合运用，读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．24．先化简，再求值：2441x xx+++÷（31x+﹣x+1），其中x=sin30°+2﹣14．【答案】-5【解析】根据分式的运算法则以及实数的运算法则即可求出答案．【详解】当x=sin30°+2﹣14时，∴x=12+12+2=3，原式=2(x2)x1++÷24xx1-+=x2x2+--=﹣5.【点睛】本题考查分式的运算法则，解题的关键是熟练运用分式的运算法则，本题属于基础题型．25．在矩形ABCD中，AB＝6，AD＝8，点E是边AD上一点，EM⊥EC交AB于点M，点N在射线MB上，且AE是AM和AN的比例中项．如图1，求证：∠ANE＝∠DCE；如图2，当点N在线段MB之间，联结AC，且AC与NE互相垂直，求MN的长；连接AC，如果△AEC与以点E、M、N为顶点所组成的三角形相似，求DE的长．【答案】（1）见解析；（2）4924；（1）DE的长分别为92或1．【解析】（1）由比例中项知AM AEAE AN＝，据此可证△AME∽△AEN得∠AEM＝∠ANE，再证∠AEM＝∠DCE可得答案；（2）先证∠ANE＝∠EAC，结合∠ANE＝∠DCE得∠DCE＝∠EAC，从而知DE DCDC AD＝，据此求得AE＝8﹣9 2＝72，由（1）得∠AEM＝∠DCE，据此知AM DEAE DC＝，求得AM＝218，由求得AM AEAE AN＝MN＝4924；（1）分∠ENM＝∠EAC和∠ENM＝∠ECA两种情况分别求解可得．【详解】解：（1）∵AE是AM和AN的比例中项∴AM AEAE AN＝，∵∠A＝∠A，∴△AME∽△AEN，∴∠AEM＝∠ANE，∵∠D＝90°，∴∠DCE＋∠DEC＝90°，∵EM⊥BC，∴∠AEM＋∠DEC＝90°，∴∠AEM＝∠DCE，∴∠ANE＝∠DCE；（2）∵AC与NE互相垂直，∴∠EAC＋∠AEN＝90°，∵∠BAC＝90°，∴∠ANE＋∠AEN＝90°，∴∠ANE＝∠EAC，由（1）得∠ANE＝∠DCE，∴∠DCE＝∠EAC，∴tan∠DCE＝tan∠DAC，∴DE DCDC AD＝，∵DC＝AB＝6，AD＝8，∴DE＝92，∴AE＝8﹣92＝72，由（1）得∠AEM＝∠DCE，∴tan∠AEM＝tan∠DCE，∴AM DEAE DC＝，∴AM＝218，∵AM AEAE AN＝，∴AN＝143，∴MN＝4924；（1）∵∠NME＝∠MAE＋∠AEM，∠AEC＝∠D＋∠DCE，又∠MAE＝∠D＝90°，由（1）得∠AEM＝∠DCE，∴∠AEC＝∠NME，当△AEC与以点E、M、N为顶点所组成的三角形相似时①∠ENM＝∠EAC，如图2，∴∠ANE＝∠EAC，由（2）得：DE＝92；②∠ENM＝∠ECA，如图1，过点E作EH⊥AC，垂足为点H，由（1）得∠ANE＝∠DCE，∴∠ECA＝∠DCE，∴HE＝DE，又tan∠HAE＝68 EH DCAH AD＝＝，设DE＝1x，则HE＝1x，AH＝4x，AE＝5x，又AE＋DE＝AD，∴5x＋1x＝8，解得x＝1，∴DE＝1x＝1，综上所述，DE的长分别为92或1．【点睛】本题是相似三角形的综合问题，解题的关键是掌握相似三角形的判定与性质、三角函数的应用等知识点．26．观察猜想：在Rt△ABC中，∠BAC=90°，AB=AC，点D在边BC上，连接AD，把△ABD绕点A逆时针旋转90°，点D 落在点E处，如图①所示，则线段CE和线段BD的数量关系是，位置关系是．探究证明：在（1）的条件下，若点D在线段BC的延长线上，请判断（1）中结论是还成立吗？请在图②中画出图形，并证明你的判断．拓展延伸：如图③，∠BAC≠90°，若AB≠AC，∠ACB=45°，AC=2，其他条件不变，过点D作DF⊥AD交CE于点F，请直接写出线段CF长度的最大值．【答案】（1）CE=BD，CE⊥BD．（2）（1）中的结论仍然成立．理由见解析；（3）1 4 .【解析】分析：（1）线段AD绕点A逆时针旋转90°得到AE，根据旋转的性质得到AD=AE，∠BAD=∠CAE，得到△BAD≌△CAE，CE=BD，∠ACE=∠B，得到∠BCE=∠BCA+∠ACE=90°，于是有CE=BD，CE⊥BD．（2）证明的方法与（1）类似．（3）过A作AM⊥BC于M，EN⊥AM于N，根据旋转的性质得到∠DAE=90°，AD=AE，利用等角的余角相等得到∠NAE=∠ADM，易证得Rt△AMD≌Rt△ENA，则NE=MA，由于∠ACB=45°，则AM=MC，所以MC=NE，易得四边形MCEN为矩形，得到∠DCF=90°，由此得到Rt△AMD∽Rt△DCF，得MD AMCF DC，设DC=x，MD=1-x，利用相似比可得到CF=-x2+1，再利用二次函数即可求得CF的最大值．详解：（1）①∵AB=AC，∠BAC=90°，∴线段AD绕点A逆时针旋转90°得到AE，∴AD=AE，∠BAD=∠CAE，∴△BAD≌△CAE，∴CE=BD，∠ACE=∠B，∴∠BCE=∠BCA+∠ACE=90°，∴BD⊥CE；故答案为CE=BD，CE⊥BD．（2）（1）中的结论仍然成立．理由如下：如图，∵线段AD绕点A逆时针旋转90°得到AE，∴AE=AD，∠DAE=90°，∵AB=AC，∠BAC=90°∴∠CAE=∠BAD，∴△ACE≌△ABD，∴CE=BD，∠ACE=∠B，∴∠BCE=90°，即CE⊥BD，∴线段CE，BD之间的位置关系和数量关系分别为：CE=BD，CE⊥BD．（3）如图3，过A作AM⊥BC于M，EN⊥AM于N，∵线段AD绕点A逆时针旋转90°得到AE∴∠DAE=90°，AD=AE，∴∠NAE=∠ADM，易证得Rt△AMD≌Rt△ENA，∴NE=AM，∵∠ACB=45°，∴△AMC为等腰直角三角形，∴AM=MC，∴MC=NE，∵AM⊥BC，EN⊥AM，∴NE∥MC，∴四边形MCEN为平行四边形，∵∠AMC=90°，∴四边形MCEN为矩形，∴∠DCF=90°，∴Rt△AMD∽Rt△DCF，∴MD AM，CF DC设DC=x，∵∠ACB=45°，2，∴AM=CM=1，MD=1-x，∴11x CF x-=， ∴CF=-x 2+x=-（x-12）2+14， ∴当x=12时有最大值，CF 最大值为14． 点睛：本题考查了旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．也考查了等腰直角三角形的性质和三角形全等及相似的判定与性质．中考数学模拟试卷一、选择题（本题包括10个小题，每小题只有一个选项符合题意）1．甲、乙两名同学在一次用频率去估计概率的实验中，统计了某一结果出现的频率绘出的统计图如图，则符合这一结果的实验可能是（ ）A ．掷一枚正六面体的骰子，出现1点的概率B ．抛一枚硬币，出现正面的概率C ．从一个装有2个白球和1个红球的袋子中任取一球，取到红球的概率D ．任意写一个整数，它能被2整除的概率【答案】C【解析】解：A ．掷一枚正六面体的骰子，出现1点的概率为16，故此选项错误； B ．掷一枚硬币，出现正面朝上的概率为12，故此选项错误； C ．从一装有2个白球和1个红球的袋子中任取一球，取到红球的概率是：11123=+≈0.33；故此选项正确； D ．任意写出一个整数，能被2整除的概率为12，故此选项错误． 故选C ．2．cos30°=（ ）A ．12B ．22C 3D 3【答案】C【解析】直接根据特殊角的锐角三角函数值求解即可. 【详解】3cos30︒=故选C.【点睛】考点：特殊角的锐角三角函数点评：本题属于基础应用题，只需学生熟练掌握特殊角的锐角三角函数值，即可完成.3．对于命题“如果∠1+∠1＝90°，那么∠1≠∠1．”能说明它是假命题的是（ ）A ．∠1＝50°，∠1＝40°B ．∠1＝40°，∠1＝50°C．∠1＝30°，∠1＝60°D．∠1＝∠1＝45°【答案】D【解析】能说明是假命题的反例就是能满足已知条件，但不满足结论的例子．【详解】“如果∠1+∠1＝90°，那么∠1≠∠1．”能说明它是假命题为∠1＝∠1＝45°．故选：D．【点睛】考查了命题与定理的知识，理解能说明它是假命题的反例的含义是解决本题的关键．4．甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m，先到终点的人原地休息．已知甲先出发2s．在跑步过程中，甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示，给出以下结论：①a＝8；②b＝92；③c＝1．其中正确的是（）A．①②③B．仅有①②C．仅有①③D．仅有②③【答案】A【解析】解：∵乙出发时甲行了2秒，相距8m，∴甲的速度为8/2＝4m/ s．∵100秒时乙开始休息．∴乙的速度是500/100＝5m/ s．∵a秒后甲乙相遇，∴a＝8/(5－4)＝8秒．因此①正确．∵100秒时乙到达终点，甲走了4×(100＋2)＝408 m，∴b＝500－408＝92 m．因此②正确．∵甲走到终点一共需耗时500/4＝125 s，，∴c＝125－2＝1 s．因此③正确．终上所述，①②③结论皆正确．故选A．5．某商店有两个进价不同的计算器都卖了80元，其中一个赢利60%，另一个亏本20%，在这次买卖中，这家商店（）A．赚了10元B．赔了10元C．赚了50元D．不赔不赚【答案】A【解析】试题分析：第一个的进价为：80÷(1+60%)=50元，第二个的进价为：80÷(1－20%)=100元，则80×2－(50+100)=10元，即盈利10元.考点：一元一次方程的应用6．轮船沿江从A港顺流行驶到B港，比从B港返回A港少用3小时，若船速为26千米/时，水速为2千米/时，求A港和B港相距多少千米. 设A港和B港相距x千米. 根据题意，可列出的方程是（）.A ．32824x x =- B ．32824x x =+ C ．2232626x x +-=+ D ．2232626x x +-=- 【答案】A 【解析】通过题意先计算顺流行驶的速度为26+2=28千米/时，逆流行驶的速度为：26-2=24千米/时．根据“轮船沿江从A 港顺流行驶到B 港，比从B 港返回A 港少用3小时”，得出等量关系，据此列出方程即可．【详解】解：设A 港和B 港相距x 千米，可得方程：32824x x =- 故选：A ．【点睛】本题考查了由实际问题抽象出一元一次方程，抓住关键描述语，找到等量关系是解决问题的关键．顺水速度=水流速度+静水速度，逆水速度=静水速度-水流速度．7．4-的相反数是( )A ．4B ．4-C ．14-D ．14 【答案】A【解析】直接利用相反数的定义结合绝对值的定义分析得出答案．【详解】-1的相反数为1，则1的绝对值是1．故选A ．【点睛】本题考查了绝对值和相反数，正确把握相关定义是解题的关键．8．计算－3－1的结果是（ ）A ．2B ．－2C ．4D ．－4【答案】D【解析】试题解析：-3-1=-3+（-1）=-（3+1）=-1．故选D.9．中国幅员辽阔，陆地面积约为960万平方公里，“960万”用科学记数法表示为（ ）A ．0.96×107B ．9.6×106C ．96×105D ．9.6×102 【答案】B【解析】试题分析：“960万”用科学记数法表示为9.6×106，故选B ．考点：科学记数法—表示较大的数．10．如图，在▱ABCD 中，AC ，BD 相交于点O ，点E 是OA 的中点，连接BE 并延长交AD 于点F ，已知S △AEF =4，则下列结论：①12AF FD =；②S △BCE =36；③S △ABE =12；④△AEF ～△ACD ，其中一定正确的是（ ）A ．①②③④B ．①④C ．②③④D ．①②③【答案】D 【解析】∵在▱ABCD 中，AO=12AC ， ∵点E 是OA 的中点，∴AE=13CE ， ∵AD ∥BC ，∴△AFE ∽△CBE ， ∴AF AE BC CE ==13， ∵AD=BC ，∴AF=13AD ， ∴12AF FD =；故①正确； ∵S △AEF =4， AEF BCE S S =（AF BC ）2=19， ∴S △BCE =36；故②正确；∵EF AE BE CE = =13， ∴AEF ABE S S =13， ∴S △ABE =12，故③正确；∵BF 不平行于CD ，∴△AEF 与△ADC 只有一个角相等，∴△AEF 与△ACD 不一定相似，故④错误，故选D ．二、填空题（本题包括8个小题）11．若使代数式212x x -+有意义，则x 的取值范围是_____． 【答案】x≠﹣2【解析】直接利用分式有意义则其分母不为零，进而得出答案．【详解】∵分式212x x -+有意义， ∴x 的取值范围是：x+2≠0，解得：x≠−2.故答案是：x≠−2.【点睛】本题考查了分式有意义的条件，解题的关键是熟练的掌握分式有意义的条件.12．如图，是由一些小立方块所搭几何体的三种视图，若在所搭几何体的基础上（不改变原几何体中小立方块的位置），继续添加相同的小立方块，以搭成一个大正方体，至少还需要________个小立方块．【答案】54【解析】试题解析：由主视图可知，搭成的几何体有三层，且有4列；由左视图可知，搭成的几何体共有3行；第一层有7个正方体，第二层有2个正方体，第三层有1个正方体，共有10个正方体，∵搭在这个几何体的基础上添加相同大小的小正方体，以搭成一个大正方体，∴搭成的大正方体的共有4×4×4=64个小正方体，∴至少还需要64-10=54个小正方体．【点睛】先由主视图、左视图、俯视图求出原来的几何体共有10个正方体，再根据搭成的大正方体的共有4×4×4=64个小正方体，即可得出答案．本题考查了学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查，关键是求出搭成的大正方体共有多少个小正方体．13．计算32)3_____2【解析】根据二次根式的运算法则进行计算即可求出答案．【详解】(323=323=2，2.【点睛】本题考查二次根式的运算，解题的关键是熟练运用二次根式的运算法则.14．我们定义：关于x的函数y=ax2+bx与y=bx2+ax（其中a≠b）叫做互为交换函数．如y=3x2+4x与y=4x2+3x 是互为交换函数．如果函数y=2x2+bx与它的交换函数图象顶点关于x轴对称，那么b=_____．。

2021-2022中考数学模拟试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．数轴上分别有A、B、C三个点，对应的实数分别为a、b、c且满足，|a|＞|c|，b•c＜0，则原点的位置（）A．点A的左侧B．点A点B之间C．点B点C之间D．点C的右侧2．如图，在矩形ABCD中，连接BD，点O是BD的中点，若点M 在AD边上，连接MO并延长交BC边于点M’，连接MB,DM’则图中的全等三角形共有（）A．3对B．4对C．5对D．6对3．图为一根圆柱形的空心钢管，它的主视图是( )A．B．C．D．4．如图，AB是定长线段，圆心O是AB的中点，AE、BF为切线，E、F为切点，满足AE=BF，在EF上取动点G，国点G作切线交AE、BF的延长线于点D、C，当点G运动时，设AD=y，BC=x，则y与x所满足的函数关系式为（）A．正比例函数y=kx（k为常数，k≠0，x＞0）B．一次函数y=kx+b（k，b为常数，kb≠0，x＞0）C．反比例函数y=kx（k为常数，k≠0，x＞0）D．二次函数y=ax2+bx+c（a，b，c为常数，a≠0，x＞0）5．如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（）A．613B．513C．413D．3136．如果边长相等的正五边形和正方形的一边重合，那么∠1的度数是( )A．30°B．15°C．18°D．20°7．如图，△ABC的面积为8cm2，AP垂直∠B的平分线BP于P，则△PBC的面积为（）A．2cm2B．3cm2C．4cm2D．5cm28．下列图形中，既是轴对称图形又是中心对称图形的是()A．B．C．D．9．如图，在ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，DE：EC=2:3，则S △DEF:S△ABF=（）A．2：3 B．4：9 C．2：5 D．4：2510．下列事件是确定事件的是（）A．阴天一定会下雨B．黑暗中从5把不同的钥匙中随意摸出一把，用它打开了门C．打开电视机，任选一个频道，屏幕上正在播放新闻联播D．在五个抽屉中任意放入6本书，则至少有一个抽屉里有两本书11．在Rt△ABC中，∠C=90°，如果sinA=12，那么sinB的值是（）A．32B．12C．2D．2212．如图，已知AB∥CD，DE⊥AF，垂足为E，若∠CAB=50°，则∠D的度数为（）A．30°B．40°C．50°D．60°二、填空题：（本大题共6个小题，每小题4分，共24分．）13．如图，已知圆柱底面周长为6cm，圆柱高为2cm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为_____cm．14．反比例函数y=2mx-的图象是双曲线，在每一个象限内，y随x的增大而减小，若点A（–3，y1），B（–1，y2），C（2，y3）都在该双曲线上，则y1、y2、y3的大小关系为__________．（用“<”连接）15．如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m．水面下降2.5m，水面宽度增加_____m．16．已知A(x1，y1)，B(x2，y2)都在反比例函数y＝6x的图象上．若x1x2＝﹣4，则y1⋅y2的值为______．17．桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图所示，这个几何体最多可以由___________个这样的正方体组成.18．如图，△ABC与△DEF位似，点O为位似中心，若AC＝3DF，则OE：EB＝_____．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上的两点，∠EAD＝45°，将△ADC绕点A顺时针旋转90°，得到△AFB，连接EF．求证：EF＝ED；若AB＝22，CD＝1，求FE的长．20．（6分）已知：四边形ABCD是平行四边形，点O是对角线AC、BD的交点，EF过点O且与AB、CD分别相交于点E、F，连接EC、AF．（1）求证：DF=EB；（2）AF与图中哪条线段平行？请指出，并说明理由．21．（6分）如图，△ABC内接与⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于AC点E，交PC于点F，连接AF．判断AF与⊙O的位置关系并说明理由；若⊙O的半径为4，AF=3，求AC 的长．22．（8分）先化简，再求值：a（a﹣3b）+（a+b）2﹣a（a﹣b），其中a=1，b=﹣1 223．（8分）计算：12 ＋ (12)－2 - 8sin60° 24．（10分）如图，已知△ABC 内接于O ，AB 是直径，OD ∥AC ，AD=OC ． (1)求证：四边形OCAD 是平行四边形；(2)填空：①当∠B= 时，四边形OCAD 是菱形；②当∠B= 时，AD 与O 相切.25．（10分）如今很多初中生购买饮品饮用，既影响身体健康又给家庭增加不必要的开销，为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查，大致可分为四种：A ：自带白开水；B ：瓶装矿泉水；C ：碳酸饮料；D ：非碳酸饮料．根据统计结果绘制如下两个统计图（如图），根据统计图提供的信息，解答下列问题：（1）请你补全条形统计图；（2）在扇形统计图中，求“碳酸饮料”所在的扇形的圆心角的度数；（3）为了养成良好的生活习惯，班主任决定在自带白开水的5名同学（男生2人，女生3人）中随机抽取2名同学担任生活监督员，请用列表法或树状图法求出恰好抽到一男一女的概率．26．（12分）已知：AB 为⊙O 上一点，如图，12AB =，43BC=BH 与⊙O 相切于点B ，过点C 作BH 的平行线交AB 于点E.（1）求CE 的长；（2）延长CE 到F ，使2EF =，连结BF 并延长BF 交⊙O 于点G ，求BG 的长；（3）在（2）的条件下，连结GC 并延长GC 交BH 于点D ，求证：BD BG =27．（12分）如图1，四边形ABCD 中，AB BC ⊥，//AD BC ，点P 为DC 上一点，且AP AB =，分别过点A 和点C 作直线BP 的垂线，垂足为点E 和点F ．()1证明：ABE ∽BCF ； ()2若34AB BC =，求BP CF 的值；()3如图2，若AB BC =，设DAP ∠的平分线AG 交直线BP 于.G 当1CF =，74PD PC =时，求线段AG 的长．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1、C【解析】分析：根据题中所给条件结合A、B、C三点的相对位置进行分析判断即可.详解：<，这与已知不符，故不能选A；A选项中，若原点在点A的左侧，则a cB选项中，若原点在A、B之间，则b>0，c>0，这与b·c<0不符，故不能选B；>且b·c<0，与已知条件一致，故可以选C；C选项中，若原点在B、C之间，则a cD选项中，若原点在点C右侧，则b<0，c<0，这与b·c<0不符，故不能选D.故选C.点睛：理解“数轴上原点右边的点表示的数是正数，原点表示的是0，原点左边的点表示的数是负数，距离原点越远的点所表示的数的绝对值越大”是正确解答本题的关键.2、D【解析】根据矩形的对边平行且相等及其对称性，即可写出图中的全等三角形的对数.【详解】图中图中的全等三角形有△ABM≌△CDM’，△ABD≌△CDB, △OBM≌△ODM’,△OBM’≌△ODM, △M’BM≌△MDM’, △DBM≌△BDM’,故选D.【点睛】此题主要考查矩形的性质及全等三角形的判定，解题的关键是熟知矩形的对称性.3、B【解析】试题解析：从正面看是三个矩形，中间矩形的左右两边是虚线，故选B.4、C【解析】延长AD，BC交于点Q，连接OE，OF，OD，OC，OQ，由AE与BF为圆的切线，利用切线的性质得到AE与EO 垂直，BF与OF垂直，由AE=BF，OE=OF，利用HL得到直角三角形AOE与直角BOF全等，利用全等三角形的对应角相等得到∠A=∠B，利用等角对等边可得出三角形QAB为等腰三角形，由O为底边AB的中点，利用三线合一得到QO垂直于AB，得到一对直角相等，再由∠FQO与∠OQB为公共角，利用两对对应角相等的两三角形相似得到三角形FQO与三角形OQB相似，同理得到三角形EQO与三角形OAQ相似，由相似三角形的对应角相等得到∠QOE=∠QOF=∠A=∠B ，再由切线长定理得到OD 与OC 分别为∠EOG 与∠FOG 的平分线，得到∠DOC 为∠EOF 的一半，即∠DOC=∠A=∠B ，又∠GCO=∠FCO ，得到三角形DOC 与三角形OBC 相似，同理三角形DOC 与三角形DAO 相似，进而确定出三角形OBC 与三角形DAO 相似，由相似得比例，将AD=x ，BC=y 代入，并将AO 与OB 换为AB 的一半，可得出x 与y 的乘积为定值，即y 与x 成反比例函数，即可得到正确的选项．【详解】延长AD ，BC 交于点Q ，连接OE ，OF ，OD ，OC ，OQ ，∵AE ，BF 为圆O 的切线，∴OE ⊥AE ，OF ⊥FB ，∴∠AEO=∠BFO=90°，在Rt △AEO 和Rt △BFO 中，∵{AE BF OE OF＝ ， ∴Rt △AEO ≌Rt △BFO （HL ），∴∠A=∠B ，∴△QAB 为等腰三角形，又∵O 为AB 的中点，即AO=BO ，∴QO ⊥AB ，∴∠QOB=∠QFO=90°，又∵∠OQF=∠BQO ，∴△QOF ∽△QBO ，∴∠B=∠QOF ，同理可以得到∠A=∠QOE ，∴∠QOF=∠QOE ，根据切线长定理得：OD 平分∠EOG ，OC 平分∠GOF ，∴∠DOC=12∠EOF=∠A=∠B ， 又∵∠GCO=∠FCO ，∴△DOC∽△OBC，同理可以得到△DOC∽△DAO，∴△DAO∽△OBC，∴AD AO OB BC，∴AD•BC=AO•OB=14AB2，即xy=14AB2为定值，设k=14AB2，得到y=kx，则y与x满足的函数关系式为反比例函数y=kx（k为常数，k≠0，x＞0）．故选C．【点睛】本题属于圆的综合题，涉及的知识有：相似三角形的判定与性质，切线长定理，直角三角形全等的判定与性质，反比例函数的性质，以及等腰三角形的性质，做此题是注意灵活运用所学知识．5、B【解析】解：∵根据轴对称图形的概念，轴对称图形两部分沿对称轴折叠后可重合，白色的小正方形有13个，而能构成一个轴对称图形的有4个情况，∴使图中黑色部分的图形仍然构成一个轴对称图形的概率是：513．故选B．6、C【解析】∠1的度数是正五边形的内角与正方形的内角的度数的差，根据多边形的内角和定理求得角的度数，进而求解．【详解】∵正五边形的内角的度数是15×（5-2）×180°=108°，正方形的内角是90°，∴∠1=108°-90°=18°．故选C【点睛】本题考查了多边形的内角和定理、正五边形和正方形的性质，求得正五边形的内角的度数是关键．7、C【解析】延长AP交BC于E，根据AP垂直∠B的平分线BP于P，即可求出△ABP≌△BEP，又知△APC和△CPE等底同高，可以证明两三角形面积相等，即可求得△PBC的面积．【详解】延长AP交BC于E．∵AP垂直∠B的平分线BP于P，∴∠ABP＝∠EBP，∠APB＝∠BPE＝90°．在△APB和△EPB中，∵，∴△APB≌△EPB（ASA），∴S△APB＝S△EPB，AP＝PE，∴△APC和△CPE 等底同高，∴S△APC＝S△PCE，∴S△PBC＝S△PBE+S△PCE S△ABC＝4cm1．故选C．【点睛】本题考查了三角形面积和全等三角形的性质和判定的应用，关键是求出S△PBC＝S△PBE+S△PCE S△ABC．8、D【解析】根据轴对称图形和中心对称图形的定义逐项识别即可，在平面内，把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形.【详解】解：A. 是轴对称图形，但不是中心对称图形，故不符合题意；B. 不是轴对称图形，是中心对称图形，故不符合题意；C. 是轴对称图形，但不是中心对称图形，故不符合题意；D. 既是轴对称图形又是中心对称图形，故符合题意．故选D.【点睛】本题考查了轴对称图形和中心对称图形的识别，熟练掌握轴对称图形和中心对称图形的定义是解答本题的关键.9、D【解析】试题分析：先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF，从而DE：AB=DE：DC=2：5，所以S△DEF:S△ABF=4：25试题解析:∵四边形ABCD是平行四边形，∴AB∥CD，BA=DC∴∠EAB=∠DEF，∠AFB=∠DFE，∴△DEF∽△BAF，∴DE：AB=DE：DC=2：5，∴S△DEF：S△ABF=4：25，考点：1.相似三角形的判定与性质；2.三角形的面积；3.平行四边形的性质．10、D【解析】试题分析：找到一定发生或一定不发生的事件即可．A、阴天一定会下雨，是随机事件；B、黑暗中从5把不同的钥匙中随意摸出一把，用它打开了门，是随机事件；C、打开电视机，任选一个频道，屏幕上正在播放新闻联播，是随机事件；D、在学校操场上向上抛出的篮球一定会下落，是必然事件．故选D．考点：随机事件．11、A【解析】∵Rt△ABC中，∠C=90°，sinA=12，∴2=，∴∠A+∠B=90°，∴sinB=cosA=2．故选A．12、B【解析】试题解析：∵AB ∥CD ，且50CAB ∠=︒，50ECD ∴∠=︒，ED AE ，⊥ 90CED ∴∠=︒，∴在Rt CED 中，905040D ．∠=︒-︒=︒故选B ．二、填空题：（本大题共6个小题，每小题4分，共24分．）13、213 【解析】要求丝线的长，需将圆柱的侧面展开，进而根据“两点之间线段最短”得出结果，在求线段长时，根据勾股定理计算即可．【详解】解：如图，把圆柱的侧面展开，得到矩形，则这圈金属丝的周长最小为2AC 的长度．∵圆柱底面的周长为6cm ，圆柱高为2cm ，∴AB ＝2cm ，BC ＝BC′＝3cm ，∴AC 2＝22+32＝13，∴AC ＝13cm ，∴这圈金属丝的周长最小为2AC ＝213cm ．故答案为213．【点睛】本题考查了平面展开−最短路径问题，圆柱的侧面展开图是一个矩形，此矩形的长等于圆柱底面周长，高等于圆柱的高，本题就是把圆柱的侧面展开成矩形，“化曲面为平面”，用勾股定理解决．14、y 2＜y 1＜y 1．【解析】先根据反比例函数的增减性判断出2-m 的符号，再根据反比例函数的性质判断出此函数图象所在的象限，由各点横坐标的值进行判断即可．【详解】∵反比例函数y=2-mx的图象是双曲线，在每一个象限内，y随x的增大而减小，∴2−m>0，∴此函数的图象在一、三象限，∵−1<−1<0，∴0>y1>y2，∵2>0，∴y1>0，∴y2<y1<y1.故答案为y2<y1<y1.【点睛】本题考查的知识点是反比例函数图像上点的坐标特征，解题的关键是熟练的掌握列反比例函数图像上点的坐标特征.15、1.【解析】根据已知建立平面直角坐标系，进而求出二次函数解析式，再通过把y=-1.5代入抛物线解析式得出水面宽度，即可得出答案【详解】解：建立平面直角坐标系，设横轴x通过AB，纵轴y通过AB中点O且通过C点，则通过画图可得知O为原点，抛物线以y轴为对称轴，且经过A，B两点，OA和OB可求出为AB的一半1米，抛物线顶点C坐标为（0，1），设顶点式y=ax1+1，把A点坐标（-1，0）代入得a=-0.5，∴抛物线解析式为y=-0.5x1+1，当水面下降1.5米，通过抛物线在图上的观察可转化为：当y=-1.5时，对应的抛物线上两点之间的距离，也就是直线y=-1与抛物线相交的两点之间的距离，可以通过把y=-1.5代入抛物线解析式得出：-1.5=-0.5x1+1，解得：x=±3，1×3-4=1，所以水面下降1.5m，水面宽度增加1米．故答案为1．本题考查了二次函数的应用，根据已知建立坐标系从而得出二次函数解析式是解决问题的关键，学会把实际问题转化为二次函数，利用二次函数的性质解决问题，属于中考常考题型．16、﹣1．【解析】 根据反比例函数图象上点的坐标特征得到121266,y y x x ==， 再把它们相乘，然后把124x x =-代入计算即可． 【详解】 根据题意得121266,y y x x ==， 所以1212126636369.4y y x x x x =⋅===-- 故答案为:−1.【点睛】考查反比例函数图象上点的坐标特征，把点,A B 的坐标代入反比例函数解析式得到121266,,y y x x ==是解题的关键. 17、1【解析】主视图、左视图是分别从物体正面、左面看，所得到的图形．【详解】易得第一层最多有9个正方体，第二层最多有4个正方体，所以此几何体共有1个正方体．故答案为1．18、1:2【解析】△ABC 与△DEF 是位似三角形，则DF ∥AC ，EF ∥BC ，先证明△OAC ∽△ODF ，利用相似比求得AC ＝3DF ，所以可求OE ：OB ＝DF ：AC ＝1：3，据此可得答案．【详解】解：∵△ABC 与△DEF 是位似三角形，∴DF ∥AC ，EF ∥BC∴△OAC ∽△ODF ，OE ：OB ＝OF ：OC∴OF ：OC ＝DF ：AC∴OE：OB＝DF：AC＝1：3，则OE：EB＝1：2故答案为：1：2【点睛】本题考查了位似的相关知识，位似是相似的特殊形式，位似比等于相似比，位似图形的对应顶点的连线平行或共线．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19、（1）见解析；（2）EF＝5 3 .【解析】（1）由旋转的性质可求∠FAE＝∠DAE＝45°，即可证△AEF≌△AED，可得EF＝ED；（2）由旋转的性质可证∠FBE＝90°，利用勾股定理和方程的思想可求EF的长．【详解】（1）∵∠BAC＝90°，∠EAD＝45°，∴∠BAE+∠DAC＝45°，∵将△ADC绕点A顺时针旋转90°，得到△AFB，∴∠BAF＝∠DAC，AF＝AD，CD＝BF，∠ABF＝∠ACD＝45°，∴∠BAF+∠BAE＝45°＝∠FAE，∴∠FAE＝∠DAE，AD＝AF，AE＝AE，∴△AEF≌△AED（SAS），∴DE＝EF（2）∵AB＝AC＝，∠BAC＝90°，∴BC＝4，∵CD＝1，∴BF＝1，BD＝3，即BE+DE＝3，∵∠ABF＝∠ABC＝45°，∴∠EBF＝90°，∴BF2+BE2＝EF2，∴1+（3﹣EF）2＝EF2，∴EF＝5 3【点睛】本题考查了旋转的性质，等腰直角三角形的性质，全等三角形的判定和性质，勾股定理等知识，利用方程的思想解决问题是本题的关键．20、（1）见解析；（2）AF ∥CE ，见解析.【解析】（1）直接利用全等三角三角形判定与性质进而得出△FOC ≌△EOA （ASA ），进而得出答案；（2）利用平行四边形的判定与性质进而得出答案．【详解】（1）证明：∵四边形ABCD 是平行四边形，点O 是对角线AC 、BD 的交点，∴AO=CO ，DC ∥AB ，DC=AB ，∴∠FCA=∠CAB ，在△FOC 和△EOA 中FCO EAO CO AOCOF AOE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△FOC ≌△EOA （ASA ），∴FC=AE ，∴DC-FC=AB-AE ，即DF=EB ；（2）AF ∥CE ，理由：∵FC=AE ，FC ∥AE ，∴四边形AECF 是平行四边形，∴AF ∥CE ．【点睛】此题主要考查了平行四边形的判定与性质以及全等三角形的判定与性质，正确得出△FOC ≌△EOA （ASA ）是解题关键．21、解：（1）AF 与圆O 的相切．理由为：如图，连接OC ，∵PC为圆O切线，∴CP⊥OC．∴∠OCP=90°．∵OF∥BC，∴∠AOF=∠B，∠COF=∠OCB．∵OC=OB，∴∠OCB=∠B．∴∠AOF=∠COF．∵在△AOF和△COF中，OA=OC，∠AOF=∠COF，OF=OF，∴△AOF≌△COF（SAS）．∴∠OAF=∠OCF=90°．∴AF为圆O的切线，即AF与⊙O的位置关系是相切．（2）∵△AOF≌△COF，∴∠AOF=∠COF．∵OA=OC，∴E为AC中点，即AE=CE=12AC，OE⊥AC．∵OA⊥AF，∴在Rt△AOF中，OA=4，AF=3，根据勾股定理得：OF=1．∵S△AOF=12•OA•AF=12•OF•AE，∴AE=245．∴AC=2AE=．【解析】试题分析：（1）连接OC，先证出∠3=∠2，由SAS证明△OAF≌△OCF，得对应角相等∠OAF=∠OCF，再根据切线的性质得出∠OCF=90°，证出∠OAF=90°，即可得出结论；（2）先由勾股定理求出OF，再由三角形的面积求出AE，根据垂径定理得出AC=2AE．试题解析：（1）连接OC，如图所示：∵AB是⊙O直径，∴∠BCA=90°，∵OF∥BC，∴∠AEO=90°，∠1=∠2，∠B=∠3，∴OF ⊥AC ，∵OC=OA ，∴∠B=∠1，∴∠3=∠2，在△OAF 和△OCF 中，{32OA OCOF OF=∠=∠=，∴△OAF ≌△OCF （SAS ），∴∠OAF=∠OCF ，∵PC 是⊙O 的切线，∴∠OCF=90°，∴∠OAF=90°，∴FA ⊥OA ，∴AF 是⊙O 的切线；（2）∵⊙O 的半径为4，AF=3，∠OAF=90°，∴=∵FA ⊥OA ，OF ⊥AC ，∴AC=2AE ，△OAF 的面积=12AF•OA=12OF•AE ， ∴3×4=1×AE ， 解得：AE=125， ∴AC=2AE=245． 考点：1.切线的判定与性质；2.勾股定理；3.相似三角形的判定与性质．22、54【解析】原式去括号合并得到最简结果，把a 与b 的值代入计算即可求出值；【详解】解：原式=a 2﹣3ab+a 2+2ab+b 2﹣a 2+ab=a 2+b 2，当a=1、b=﹣12时， 原式=12+（﹣12）2 =1+14=54． 【点睛】考查了整式的加减-化简求值，以及非负数的性质，熟练掌握运算法则是解本题的关键．23、【解析】试题分析：原式第一项利用二次根式的化简公式进行化简，第二项利用负指数公式化简，第三项利用特殊角的三角函数值化简，合并即可得到结果试题解析：原式＋4- 8×224、（1）证明见解析；（2）① 30°，② 45°【解析】试题分析：（1）根据已知条件求得∠OAC =∠OCA ，∠AOD =∠ADO ，然后根据三角形内角和定理得出∠AOC =∠OAD ，从而证得OC ∥AD ，即可证得结论；（2）①若四边形OCAD 是菱形，则OC =AC ，从而证得OC =OA =AC ，得出∠60AOC ∠=，即可求得1302B AOC ∠=∠=； ②AD 与O 相切，根据切线的性质得出90OAD ∠=，根据AD ∥OC ，内错角相等得出90AOC ∠=，从而求得145.2B AOC ∠=∠= 试题解析：(方法不唯一)(1)∵OA =OC ，AD =OC ，∴OA =AD ，∴∠OAC =∠OCA ，∠AOD =∠ADO ，∵OD ∥AC ，∴∠OAC =∠AOD ，∴∠OAC =∠OCA =∠AOD =∠ADO ，∴∠AOC =∠OAD ，∴OC∥AD，∴四边形OCAD是平行四边形；(2)①∵四边形OCAD是菱形，∴OC=AC，又∵OC=OA，∴OC=OA=AC，∴60AOC∠=，∴1302B AOC∠=∠=；故答案为30.②∵AD与O相切，∴90OAD∠=，∵AD∥OC，∴90AOC∠=，∴145.2B AOC∠=∠=故答案为45.25、（1）详见解析；（2）72°；（3）【解析】（1）由B类型的人数及其百分比求得总人数，在用总人数减去其余各组人数得出C类型人数，即可补全条形图；（2）用360°乘以C类别人数所占比例即可得；（3）用列表法或画树状图法列出所有等可能结果，从中确定恰好抽到一男一女的结果数，根据概率公式求解可得．【详解】解：（1）∵抽查的总人数为：（人）∴类人数为：（人）补全条形统计图如下：（2）“碳酸饮料”所在的扇形的圆心角度数为：（3）设男生为、，女生为、、，画树状图得：∴恰好抽到一男一女的情况共有12 种，分别是∴（恰好抽到一男一女）．【点睛】本题考查的是条形统计图和扇形统计图的综合运用以及概率的求法，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．26、2；（2）2；（3）证明见解析.【解析】（1）只要证明△ABC∽△CBE，可得BC ABCE AC=，由此即可解决问题；（2）连接AG,只要证明△ABG∽△FBE，可得BG BEAB BF=，由BE22(43)(42)-4，再求出BF，即可解决问题；（3）通过计算首先证明CF＝FG，推出∠FCG＝∠FGC，由CF∥BD，推出∠GCF＝∠BDG，推出∠BDG＝∠BGD 即可证明．【详解】解：（1）∵BH 与⊙O 相切于点B ，∴AB ⊥BH ，∵BH ∥CE ，∴CE ⊥AB ，∵AB 是直径，∴∠CEB=∠ACB=90°，∵∠CBE=∠ABC ，∴△ABC ∽△CBE ， ∴BC AB CE AC=，∵=∴．（2）连接AG ．∵∠FEB=∠AGB=90°，∠EBF=∠ABG ，∴△ABG ∽△FBE ， ∴BG BE AB BF=，∵，∴=， ∴12BG =，∴．（3）易知，∴GF=BG ﹣，∴CF=GF ，∴∠FCG=∠FGC ，∵CF ∥BD ，∴∠GCF=∠BDG ，∴∠BDG=∠BGD ，∴BG=BD ．【点睛】本题考查的是切线的性质、相似三角形的判定和性质、勾股定理的应用，掌握圆的切线垂直于经过切点的半径是解题的关键．27、（1）证明见解析；（2）32BP CF =；（3）3AG =. 【解析】 ()1由余角的性质可得ABE BCF ∠∠=，即可证ABE ∽BCF ； ()2由相似三角形的性质可得AB BE 3BC CF 4==，由等腰三角形的性质可得BP 2BE =，即可求BP CF 的值；()3由题意可证DPH ∽CPB ，可得HP PD 7BP PC 4==，可求32AE =由等腰三角形的性质可得AE 平分BAP ∠，可证1EAG BAH 452∠∠==，可得AEG 是等腰直角三角形，即可求AG 的长． 【详解】证明：()1AB BC ⊥，ABE FBC 90∠∠∴+=又CF BF ⊥，BCF FBC 90∠∠∴+=ABE BCF ∠∠∴=又AEB BFC 90∠∠==，ABE ∴∽BCF()2ABE ∽BCF ， AB BE 3BC CF 4∴==又AP AB =，AE BF ⊥，BP 2BE ∴= BP 2BE 3CF CF 2∴== ()3如图，延长AD 与BG 的延长线交于H 点AD //BC ，DPH ∴∽CPB ∴HP PD 7BP PC 4== AB BC =，由()1可知ABE ≌BCFCF BE EP 1∴===，BP 2∴=，代入上式可得7HP 2=，79HE 122=+= ABE ∽HAE ，BE AE AE HE ∴=，1AE 9AE 2=， ∴32AE =AP AB =，AE BF ⊥，AE ∴平分BAP ∠又AG 平分DAP ∠，1EAG BAH 452∠∠∴==， AEG ∴是等腰直角三角形．∴AG 2AE 3==.【点睛】本题考查的知识点是全等三角形的判定和性质，相似三角形的判定和性质，解题关键是添加恰当辅助线构造相似三角形．。

2021-2022学年上海市闵行区九年级上学期期末数学试卷(一模)一、选择题（本大题共6小题，共24.0分）1. 二次函数y =12(x −2)2−3的二次项系数、一次项系数和常数项分别是( ) A. 12，−2，−3B. 12，−2，−1C. 12，4，−3D. 12，−4，1 2. 如图，在Rt △ABC 中，∠C =90°，AB =10，AC =8，则sinA 等于( )A. 35B. 45C. 34D. 433. 在抛物线y =x 2−4x −4上的一个点是( ) A. (4,4)B. (3,−1)C. (−2,8)D. (1,7) 4. 在梯形ABCD 中，AD//BC ，AB =CD ，那么下列结论中正确的是( )A. AB ⃗⃗⃗⃗⃗ 与DC ⃗⃗⃗⃗⃗ 是相等向量B. AC ⃗⃗⃗⃗⃗ 与BD ⃗⃗⃗⃗⃗⃗ 是相等向量C. AD ⃗⃗⃗⃗⃗⃗ 与CB⃗⃗⃗⃗⃗ 是相反向量 D. AD ⃗⃗⃗⃗⃗⃗ 与CB ⃗⃗⃗⃗⃗ 是平行向量 5. 若两圆外切，半径分别为4和7，则它们的圆心距是( )A. 2B. 3C. 6D. 11 6. 已知a 为任意整数，且(a +7)2−a 2的值总可以被n(n 为自然数，且n ≠1)整除，则n 的值为( )A. 14B. 7C. 7或14D. 7的倍数二、填空题（本大题共12小题，共48.0分）7.若x y =32，则x+y y 的值为______． 8. 如图，已知点G 是△ABC 的重心，过点G 作DE//BC ，分别交边AB 、AC 于点D 、E ，那么用向量BC ⃗⃗⃗⃗⃗ 表示向量ED ⃗⃗⃗⃗⃗ 为______ ．9. 已知二次函数y =mx m 2−2的图象开口向上，则m 的值为______．10.将抛物线y=2(1−x)2−3向左平移3个单位，再向下平移2个单位后的抛物线的顶点坐标为______．11.已知△ABC∽△A′B′C′，AD和A′D′是它们的对应中线，若AD=8，A′D′=6，则△ABC与△A′B′C′的周长比是______．12.如图，在Rt△ABC中，∠ABC=90°，BA=BC，点D、E在射线AC上且∠DBC=∠E，3AD=4CE，CD=2，则BE=______．13.在平面直角坐标系xOy中，已知点A(2,3)，在坐标轴上找一点P，使得△AOP是等腰三角形，则这样的点P共有_______个．14.如图，一条船从灯塔C南偏东42°的A处出发，以每小时8海里的速度向正北航行到达B处，灯塔C在B的北偏西84°方向且距离B处16海里，则船从A到B航行了______小时．15.正多边形的一个中心角为36度，那么这个正多边形的一个内角等于______度．16.如图，在Rt△BAD中，延长斜边BD到点C，使DC=13BC，连接AC，若tanB=35，则tan∠CAD的值为______．17.如图，在四边形ABCD中，AD//BC，∠B=90°，AD=8cm，AB=6cm，BC=10cm，点Q从点A出发以1cm/s的速度向点D运动，点P从点B出发以2cm/s的速度向C点运动，P、Q两点同时出发，其中一点到达终点时另一点也停止运动．若DP≠DQ，当t=______s时，△DPQ是等腰三角形．18.如图，四边形ABCD中，A(1,1)，B(8,2)，C(6,6)，D(3,5)，E在四边形内，E(5,3)，以下结论正确的是______(填写编号)．①△ABE≌△ACD；②AE⊥BC；③∠ADC=135°；④tan∠EBA=1．2三、解答题（本大题共7小题，共78.0分）)−1−2cos45°．19.(1)计算：|−√2|+(π−3)0+(12(2)解不等式组{2x−1>x+1x+8≥4x−1，并把它的解集在数轴上表示出来．20.如图，在Rt△ABC中，∠ACB=90°，AC=12，AB=13．(1)作△ABC的高CD，(要求：尺规作图，不写作法，保留作图痕迹)；(2)在(1)的条件下，求CD的长．21.如图，△ABC内接于⊙O，直径AD⊥BC于点E，连结CO．(1)求证：∠COD=∠CAB；(2)若CD⏜=2AC⏜，AB=3，求图中阴影部分面积．22.如图是某个园区部分景点(景点A，B，C，D，E)示意图，景点A，D之间是一个荷花池，景点E，D和景点B，D之间正在维修，不能通行．已知AB= 400√3米，BC=l000米，CE=600米，CD⊥AD，∠BDC=45°，∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E，D之间的距离．23. 如图，P 是平行四边形ABCD 的边BC 的延长线上任意一点，AP 分别交BD 、CD 于点M 、N ，求证：AM 2=MN ⋅MP ．24. 如图，在平面直角坐标系中，抛物线y =−12x 2+x +4与x 轴交于A ，C 两点(点A 在点C 左侧)，与y 轴交于点B ，P 是抛物线上一动点，设点P 的横坐标为m ，连结PO ，PB ，PC ．(1)当m =2√2时，求证：△OPB≌△OPC ．(2)直线BC 交直线OP 于点Q ，当P 为OQ 中点时，求点Q 坐标．(3)当S △OPB =S △OPC ，求所有满足条件的点P 坐标．25. (1)如图1，点C 在线段AB 上，点D 、E 在直线AB 同侧，∠A =∠DCE =∠CBE ，DC =CE.求证：AC =BE ．(2)如图2，点C 在线段AB 上，点D 、E 在直线AB 同侧，∠A =∠DCE =∠CBE =90°．①求证：AC BE =AD BC ；②连接BD ，若∠ADC =∠ABD ，AC =3，BC =163，求tan∠CDB 的值；(3)如图3，在△ABD 中，点C 在AB 边上，且∠ADC =∠ABD ，点E 在BD 边上，连接CE ，∠BCE +∠BAD =180°，AC =3，BC =163，CE =125，直接写出BECD 的值．参考答案及解析1.答案：B解析：根据平方可化简二次函数，可得二次函数的一般形式，可得答案．本题考查了二次函数的定义，化成一般形式，再判断二次项系数、一次项系数和常数项．解：y =12x 2−2x −1，二次项系数是12，一次项系数是−2，常数项是−1，故选：B ． 2.答案：A解析：解：在Rt △ABC 中，∵AB =10、AC =8，∴BC =√AB 2−AC 2=√102−82=6，∴sinA =BC AB =610=35，故选：A ．先根据勾股定理求得BC =6，再由正弦函数的定义求解可得．本题主要考查锐角三角函数的定义，解题的关键是掌握勾股定理及正弦函数的定义． 3.答案：C解析：解：A 、x =4时，y =x 2−4x −4=−4≠4，点(4,4)不在抛物线上；B 、x =3时，y =x 2−4x −4=−7≠−1，点(3,−1)不在抛物线上；C 、x =−2时，y =x 2−4x −4=8，点(−2,8)在抛物线上；D 、x =1时，y =x 2−4x −4=−7，点(1,7)不在抛物线上．故选：C ．把各点的横坐标代入函数式，比较纵坐标是否相符，逐一检验．本题考查了函数图象上的点的坐标与函数解析式的关系．4.答案：D解析：解：A 、∵AB =CD ，但AB 不平行于CD ，AB ⃗⃗⃗⃗⃗ ≠CD ⃗⃗⃗⃗⃗ ，故本选项错误；B 、∵AD//BC ，AB =CD ，∴AC =BD ，但AC 不平行于BD ，∴AC ⃗⃗⃗⃗⃗ ≠BD⃗⃗⃗⃗⃗⃗ ，故本选项错误；C 、∵AD ≠BC ，∴AD ⃗⃗⃗⃗⃗⃗ 与CB⃗⃗⃗⃗⃗ 不是相反向量，故本选项错误； D 、∵AD//BC ，∴AD ⃗⃗⃗⃗⃗⃗ 与CB⃗⃗⃗⃗⃗ 是平行向量，故本选项正确．根据等腰梯形的性质，即可得AC=BD，然后根据相等向量与相反向量，以及平行向量的定义，即可求得答案．此题考查了平面向量的知识．此题难度不大，解题的关键是熟记相等向量与相反向量，以及平行向量的定义．5.答案：D解析：解：∵两圆外切，它们的半径分别是4和7，∴圆心距=4+7=11．故选D．依据两圆外切时，圆心距等于两圆半径之和即可求解．本题考查了两圆的位置关系，利用了两圆外切时，圆心距等于两圆半径之和求解．6.答案：B解析：解：(a+7)2−a2=(a+7+a)(a+7−a)=7(2a+7)∴(a+7)2−a2的值总可以被7整除，∴n的值为7．故选：B．应用平方差公式，把(a+7)2−a2分解因式，判断出n的值为多少即可．此题主要考查了因式分解的应用，要熟练掌握，注意平方差公式的应用．7.答案：52解析：本题主要考查了比列的合比性质，对比例的性质的记忆是解题的关键．解：∵x y=32，∴x+yy=3+22=52故答案为52．8.答案：−23BC ⃗⃗⃗⃗⃗解析：解：连接AG，并延长AG交BC于点F．∴AG ：AF =DE ：BC ；又∵点G 是△ABC 的重心，∴AG ：AF =2：3，∴DE ：BC =2：3；即|ED⃗⃗⃗⃗⃗ |：|BC ⃗⃗⃗⃗⃗ |=2：3； ∵向量BC ⃗⃗⃗⃗⃗ 与向量ED ⃗⃗⃗⃗⃗ 的方向相反，∴ED ⃗⃗⃗⃗⃗ =−−23BC ⃗⃗⃗⃗⃗ ； 故答案为：−23BC ⃗⃗⃗⃗⃗． 先根据三角形重心的性质(重心到顶点的距离与重心到对边中点的距离之比为2：1)，求得|BC⃗⃗⃗⃗⃗ |与|ED ⃗⃗⃗⃗⃗ |的数量关系，然后再根据平面向量BC ⃗⃗⃗⃗⃗ 与ED ⃗⃗⃗⃗⃗ 的方向来确定它们之间的关系．本题主要考查了三角形的重心、平面向量．在解答此题时要注意两点：①三角形的重心的性质：重心到顶点的距离与重心到对边中点的距离之比为2：1，即AG ：GF =2：1，而不是AG ：AF =2：1；②平面向量是有方向的． 9.答案：2解析：解：∵二次函数y =mx m2−2的图象开口向上，∴{m >0m 2−2=2， 解得，m =2，故答案为：2．根据二次函数y =mx m 2−2的图象开口向上，可以求得m 的值，本题得以解决．本题考查二次函数的性质、二次函数的定义，解答本题的关键是明确题意，利用二次函数的性质解答．10.答案：(−2,−5)解析：解：抛物线y =2(1−x)2−3的顶点坐标为(1,−3)，∵向左平移3个单位，再向下平移2个单位，∴平移后的抛物线的顶点坐标为(−2,−5)．故答案为：(−2,−5)．先求出抛物线的顶点坐标，再根据向左平移横坐标减，向下平移纵坐标减求出平移后的抛物线的顶点坐标即可．本题考查了二次函数图象与几何变换，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．11.答案：4：3解析：解：∵AD=8，A′D′=6，∴AD：A′D′=4：3，∵△ABC∽△A′B′C′，AD和A′D′是它们的对应中线，∴△ABC与△A′B′C′的相似比=AD：A′D′=4：3，∴△ABC与△A′B′C′的周长比是4：3，故答案为：4：3．根据相似三角形周长的比等于相似比、对应中线的比等于相似比解答．本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比、相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比是解题的关键．12.答案：3√5解析：解：过点B作BF⊥AC于点F．∵∠DBC=∠E，∠BDE=∠BDE，∴△DCB～△DBE，∴DCDB =DBDE=BCBE，∴BD2=DC⋅DE．∵3AD=4CE，∴可设AD=4a，CE=3a，则AC=4a+2，BF=2a+1，DF=2a−1，∴BD2=(2a+1)2+(2a−1)2=8a2+2，BC=√2(2a+1)，∴8a2+2=2×(2+3a)，解得a=1或a=−0.25(负值舍去)，∴BC=3√2，BD=√10，代入比例式中得：√10=3√2BE，解得BE=3√5．故答案为：3√5．过点B作BF⊥AC于点F.由已知易证△DCB～△DBE，∴DCDB =DBDE=BCBE，由3AD=4CE，可设AD=4a，CE=3a，用含a的代数式表示出比例式中各线段长，解方程即可求出a的值和BE的长．本题主要考查了相似三角形的判定与性质，等腰直角三角形的性质，难度中等，解题的关键在于构造出直角三角形从而用含a的代数式表示出比例式中各线段长．13.答案：8解析：本题考查等腰三角形的性质和作图，体现分类讨论的思想，难度较大．本题应考虑点P在x轴和y轴上两种情形，(1)点P在x轴上：若OA=OP，则以点O为圆心，OA长为半径作弧交x轴于两点P 1，P 2，点P 1，P 2符合题意；若OA=AP，则以点A为圆心，AO长为半径作弧交x轴于两点O，P 3，点P 3符合题意；若OP=AP，则作OA的垂直平分线交x轴于点P 4，点P 4符合题意，故在x轴上有符合条件的4个点，同理在y轴上也有符合条件的4个点，故这样的点P共有8个．【易错分析】本题不仅要对等腰三角形加以讨论，还要对坐标轴加以讨论．14.答案：2解析：解：如图，∵AB//CD，∴∠A=∠ACD=42°，∵∠NBC=∠A+∠ACB，∴∠ACB=84°−42°=42°，∴∠ACB=∠A，∴BC=BA=16，即船距离灯塔16海里．则航行的时间是168=2(小时)．故答案是：2．先利用平行线的性质得到∠A=∠ACD=42°，再利用三角形外角性质可求出∠ABC=42°，则∠ACB=∠A，于是可判断△BAC为等腰三角形，所以BC=BA.然后求得航行的时间．本题考查了等腰三角形的判定与方向角问题，根据三角形外角的性质求得∠BCA的度数，从而证明△ABC是等腰三角形，正确理解方向角的定义是解题的关键．15.答案：144解析：解：由于正多边形的中心角等于36°，360÷36°=10，所以正多边形为正10边形，又因为其外角和为360°，所以其外角为360÷10=36°，其每个内角为180°−36°=144°．故答案为144．根据正多边形的中心角为36°，求出正多边形的边数，再求出其每个外角，即可根据内角和外角的和为180度求出每个内角的度数．本题考查学生对正多边形的概念掌握和计算的能力．解答这类题往往一些学生因对正多边形的基本知识不明确，将多边形的中心角和外角、内角混淆．16.答案：59解析：解：过点C 作CE ⊥AD ，垂足为E ，∵tanB =35，即AD AB =35， ∴设AD =3x ，则AB =5x ，∵∠CDE =∠BDA ，∠CED =∠BAD =90°，∴△CDE∽△BDA ，∵DC =13BC ，∴BD =2DC ，∴CEAB =DC BD=DE AD =12， ∴CE =52x ，DE =32x ，∴AE =92x ，∴tan∠CAD =CE AE =52x 92x =59， 故答案为：59．过点C 作CE ⊥AD ，垂足为E ，根据tanB =35，设AD =3x ，AB =5x ，证△CDE∽△BDA ，得出比例式，求出CE 、DE 长，求出AE ，再解直角三角形求出即可．本题考查了相似三角形的判定和性质，解直角三角形的应用，能构造直角三角形是解此题的关键． 17.答案：83或74解析：解：由运动知，AQ =t ，BP =2t ，∵AD =8，BC =10，∴DQ =AD −AQ =(8−t)(cm)，PC =BC −BP =(10−2t)(cm)，∵△DPQ 是等腰三角形，且DQ ≠DP ，∴①当DP =QP 时，∴点P 在DQ 的垂直平分线上，∴AQ +12DQ =BP ，∴t +12(8−t)=2t ，∴t =83，②当DQ =PQ 时，如图，Ⅰ、过点Q 作QE ⊥BC 于E ，∴∠BEQ =∠OEQ =90°，∵AD//BC ，∠B =90°，∴∠A =∠B =90°，∴四边形ABEQ 是矩形，∴EQ =AB =6，BE =AQ =t ，∴PE =BP −BE =t ，在Rt △PEQ 中，PQ =√PE 2+EQ 2=√t 2+36，∵DQ =8−t∴√t 2+36=8−t ，∴t =74，∵点P 在边BC 上，不和C 重合，∴0≤2t <10，∴0≤t <5，∴此种情况符合题意，即t =83或74s 时，△DPQ 是等腰三角形． 故答案为：83或74．先由运动速度表示出AQ ，BP ，再分两种情况讨论计算，求出时间，判断时间是否符合题意． 主要考查了勾股定理，平行线的性质，等腰三角形的判定，关键是分情况讨论，是一道中等难度的题目． 18.答案：①②③④解析：解：①∵AB =√49+1=5√2，AE =√16+4=2√5，BE =√9+1=√10，AC =√25+25=5√2，AD =√4+16=2√5，CD =√9+1=√10，∴AB =AC ，AE =AD ，BE =CD ，∴△ABE≌△ACD(sss)，故①正确；②由①知△ABE≌△ACD ，∴AB =AC ，连接CE ，∵CE =√9+1=√10，∴BC =CE ，∵AE =AE ，∴△ABE≌△ACE(SSS)，∴∠BAE =∠CAE ，∠AEB =∠AEC ，∴AE ⊥BC ，故②正确；∵BC 2═16+4=20∴BE 2+CE 2=10+10=20=BC 2，∴∠BEC =90°，∴∠AEB=360°−90°2=135°，∵△ABE≌△ACD，∴∠ADC=∠AEB=135°，故③正确；④延长CD与y轴交于点F，连接AF，如图2，则AF=√10，CF=2√10，∴AF2+CF2=10+40=50=AC2，∴∠AFC=90°，∴tan∠ABE=tan∠ACD=AFCF =12，故④正确．故答案为：①②③④．①利用两点距离公式求出△AB和△ACD的各边之长，便可根据三角形全等的判定方法进行判断；②连接CE，证明△ABE≌△ACE，得AE平分∠BAC，再根据等腰三角形性质进行判断；③证明△BCE是直角三角形，得∠BEC的度数，进而求得∠AEB的度数便可∠ADC的度数是否正确；④延长CD与y轴交于点F，证明AF⊥CF，再利用直角三角形的三角形函数定义求得tan∠ACF，便可进行判断．本题主要考查了点的坐标，三角形全等的性质与判定，直角三角形的判定，解直角三角形的应用，两点的距离公式，等腰三角形的性质与判定，关键是构造直角三角形．19.答案：解：(1)原式=√2+1+2−2×√22=√2+3−√2=3；(2)解不打呢个是2x−1>x+1，得：x>2，解不等式x+8≥4x−1，得：x≤3，则不等式组的解集为2<x≤3，将解集表示在数轴上如下：解析：(1)分别计算绝对值、零指数幂、负整数指数幂及三角函数值代入，再计算乘法和加减法可得；(2)分别求出各不等式的解集，再求出其公共解集即可．本题主要考查了实数的混合运算和解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．20.答案：解：(1)以C为圆心适当的长为半径画弧交AB于M、N，分别以M、N为圆心大于12MN为半径画弧，两弧交于点K，作直线CK交AB于D，线段CD即为所求；(2)在Rt△ABC中，BC=√AB2−AC2=5，∵12×AC×BC=12×AB×CD，∴CD=6013．解析：(1)以C为圆心适当的长为半径画弧交AB于M、N，分别以M、N为圆心大于12MN为半径画弧，两弧交于点K，作直线CK交AB于D，线段CD即为所求；本题考查的是作图−基本作图，熟知三角形高线的作法是解答此题的关键．21.答案：(1)证明：∵AD是⊙O的直径，AD⊥BC，∴CD⏜=BD⏜=12CDB ⏜，∵∠CAB的度数=12CDB⏜的度数，∠COD的度数=12CDB⏜的度数，∴∠COD=∠CAB；(2)解：∵CD⏜=2AC⏜，∴∠AOC=12∠COD，∵直径AD⊥BC于点E，∴AC⏜=AB⏜，∴AC =AB =3，∴OC =2，∴S 阴影=2×(60⋅π×32360−√34×32)=6π−9√32．解析：(1)根据垂径定理得到CD ⏜=BD ⏜=12CDB ⏜，求得∠CAB 的度数=12CDB ⏜的度数，∠COD 的度数=12CDB⏜的度数，于是得到结论； (2)根据已知条件得到∠AOC =12∠COD ，根据垂径定理得到AC⏜=AB ⏜，求得OC =2，根据扇形和三角形的面积公式即可得到结论．本题考查了三角形的外接圆与外心，垂径定理，圆周角定理，扇形面积的计算，正确的识别图形是解题的关键．22.答案：解：过B 作BF ⊥AD 交DA 的延长线于点F ，∵CD ⊥AD ，∴BF//DC ．∵∠BDC =45°，∴∠FBD =45°．又∵∠ABD =15°，∴∠FBA =30°．∴在Rt △BFA 中，BF =AB ⋅cos∠FBA =400√3×√32=600米．AF =AB ⋅sin∠FBA =400√3×12=200√3米．在Rt △BFD 中，DF =BF =600米，∴AD =DF −AF =(600−200√3)米．过B 作BG ⊥CD 于G ，则四边形BFDG 为矩形，又BF =DF ，∴四边形BFDG 为正方形，∴BG =FB =600.在Rt △BGC 中，CG =√BC 2−BG 2=800米，∴CD =CG +GD =1400米，ED =CD −CE =1400−600=800米．∴荷花池AD 宽(600−200√3)米，景点E ，D 之间的距离为800米．解析：过B 作BF ⊥AD 交DA 的延长线于点F ，过B 作BG ⊥CD 于G ，则四边形BFDG 为矩形，在Rt △BFA 中可求出BF ，AF 的长，进而可求出AD 的长，在Rt △BGC 中，利用勾股定理可求出CG =800米，所以CD =CG +GD =1400米，进而可求出ED =CD −CE =1400−600=800米．本题考查了勾股定理在直角三角形中的运用，特殊角的三角函数值的计算，三角函数在直角三角形中的运用，解题的关键正确作出高线构造直角三角形．23.答案：证明：∵四边形ABCD是平行四边形，∴AD//BP，AB//CD，∴△ABM∽△NDM，△MBP∽△MDA，∴AMMN =MBMD，MBMD=MPAM，∴AMMN =MPAM，∴AM2=MN⋅MP．解析：可证明△ABM∽△NDM，△MBP∽△MDA，利用相似三角形的性质可证得结论．本题主要考查相似三角形的判定和性质，由平行四边形的性质证明三角形相似是解题的关键，化乘积为比例再证明三角形相似是这类问题的一般思路．24.答案：解：(1)在抛物线y=−12x2+x+4中，当x=0时，y=4，∴B(0,4)，当y=0时，x1=−2，x2=4，∵点A在点C左侧，∴C(4,0)，∴OB=OC=4，∵P是抛物线上一动点，点P的横坐标为m，∴P(m,−12m2+m+4)，∴当m=2√2时，−12m2+m+4=2√2，∴P(2√2,2√2)，过点P作PH⊥x轴于H，则PH=OH，∴△OPH是等腰直角三角形，∴∠POH=45°，∴∠BOP=90°−∠POH=45°，∴∠BOP=∠POH，又∵OB=OC，OP=OP，∴△OPB≌△OPC(SAS)；(2)设直线BC的解析式为y=kx+4，将点C(4,0)代入，得0=4k+4，∴k=−1，∴y BC=−x+4，∵O(0,0)，P(m,−12m2+m+4)，且点P是OQ的中点，∴Q(2m,−m2+2m+8)，∴又∵点Q是直线OP与直线BC的交点，∴将Q(2m,−m2+2m+8)代入y BC=−x+4，得−m2+2m+8=−2m+4，解得m1=2+2√2，m2=2−2√2，∴点Q的坐标为(4+4√2,−4√2)或(4−4√2,4√2)；(3)∵S△OPB=S△OPC，∴12OB⋅|x P|=12OC⋅|y P|，即|x P|=|y P|，∴x P=±y P，当x P=y P时，m=−12m2+m+4，解得，m1=2√2，m2=−2√2，∴P1(2√2,2√2)，P2(−2√2,−2√2)；当x P=−y P时，m=12m2−m−4，解得，m1=2+2√3，m2=2−2√3，∴P3(2+2√3,−2−2√3)，P4(2−2√3,−2+2√3)；综上所述：点P的坐标为P1(2√2,2√2)，P2(−2√2,−2√2)，P3(2+2√3,−2−2√3)，P4(2−2√3,−2+ 2√3).解析：(1)分别求出B，C，P的坐标，推出OB=OC及∠BOP=∠POC即可证出结论；(2)求出直线BC的解析式，用含m的代数式表示出点Q的坐标，再代入直线BC的解析式即可；(3)由S△OPB=S△OPC可推出|x P|=|y P|，可列出关于m的方程，解方程即可求出点P的坐标．本题考查了全等三角形的判定，三角形的面积等，解题关键是由点的坐标取线段的长度应该是非负的，需加绝对值符号等．25.答案：解：(1)如图1中，∵∠DCA+∠DCE+∠ECB=180°，∠DCA+∠A+∠CDA=180°，∠A=∠DCE，∴∠ADC=∠ECB，∵∠A=∠B，∴△DAC∽△CBE，∴ACBE =ADBC．(2)如图2中，设CE交BD于G．∵∠ADC=∠DBA，∠A=∠A，∴△ADC∽△ABD，∴ACAD =ADAB，即3AD=AD253，解得AD=5，∴DC=√34，DB=5√343，设∠DBA=∠CDA=α，∴∠CDG=90−2α，∴∠CGD=2α，∴∠GCB=∠GBC=α，∴CG=GB，设CG=GB=x，∴DG=5√343−x，∴(√34)2+x2=(5√343−x)2，解得x=8√3415，∴tan∠CDB=815．(3)如图3中，以E为圆心，EC长为半径画弧，交BC于点H，连接EH，∵∠ADC=∠B，∠A=∠A，∴△ADC∽△ADB，∴ADAC =ABAD，∴AD3=253AD解得AD=5，∵∠BCE+∠BAD=180°，∠ADC+∠DCA+∠BAD=180°，∴∠ADC+∠DCA=∠BCE，∴EH=EC，∠EHC=∠ECB=∠ADC+∠DCA，∵∠B=∠ADC，∴∠BEH=∠ACD，∴△BEH∽△ADC，∴BECD =EHAC=1253=45．解析：(1)根据∠A=∠DCE=∠CBE，可推出∠ADC=∠ECB，从而得到△ADC∽△ECB，则ACBE =ADBC．(2)根据∠A=∠DCE=∠CBE=90°，∠ADC=∠ABD，可推出△ADC∽△ADB，从而求出相应的线段长度，得到tan∠CDB的值．(3)根据∠ADC=∠ABD，可推出△ADC∽△ADB，从而得到AD的长，根据∠BCE+∠BAD=180°，以E为圆心，EC长为半径画弧，交BC于点H，连接EH，可得EH=EC，∠EHC=∠ECB=∠ADC+∠DCA，可得△BEH∽△ADC，则BECD =EHAC=1253=45．本题属于相似形综合题，考查了相似三角形得性质和判定，勾股定理，锐角三角函数等知识，解题的关键是正确寻找相似三角形解决问题，学会添加常用辅助线，构造相似三角形解决问题，属于中考常考题型．。

一、选择题（每题3分，共30分）1. 下列数中，既是整数又是正数的是（）A. -3.14B. 0.5C. -2D. 32. 下列图形中，不是轴对称图形的是（）A. 正方形B. 等边三角形C. 长方形D. 梯形3. 已知x + 2 = 5，则x的值为（）A. 3B. 4C. 5D. 64. 下列代数式中，能表示“a比b多5”的是（）A. a - b = 5B. a + b = 5C. a ÷ b = 5D. a × b = 55. 若a > b，则下列不等式正确的是（）A. a + 1 > b + 1B. a - 1 < b - 1C. a ÷ 1 > b ÷ 1D. a × 1 < b × 16. 下列函数中，是反比例函数的是（）A. y = 2x + 3B. y = x²C. y = 3/xD. y = x³7. 一个长方体的长、宽、高分别是4cm、3cm、2cm，那么它的体积是（）A. 12cm³B. 24cm³C. 36cm³D. 48cm³8. 下列分数中，最大的是（）A. 1/2B. 3/4C. 5/6D. 7/89. 下列运算正确的是（）A. (a + b)² = a² + b²B. (a - b)² = a² - b²C. (a + b)² = a² + 2ab + b²D. (a - b)² = a² - 2ab + b²10. 下列图形中，内角和为360°的是（）A. 正三角形B. 正方形C. 正五边形D. 正六边形二、填空题（每题3分，共30分）11. 计算：3.5 × 2.5 - 1.5 × 1.5 = ______12. 解方程：2(x - 3) = 4x + 613. 一个等腰三角形的底边长为6cm，腰长为8cm，那么它的面积是______ cm²。