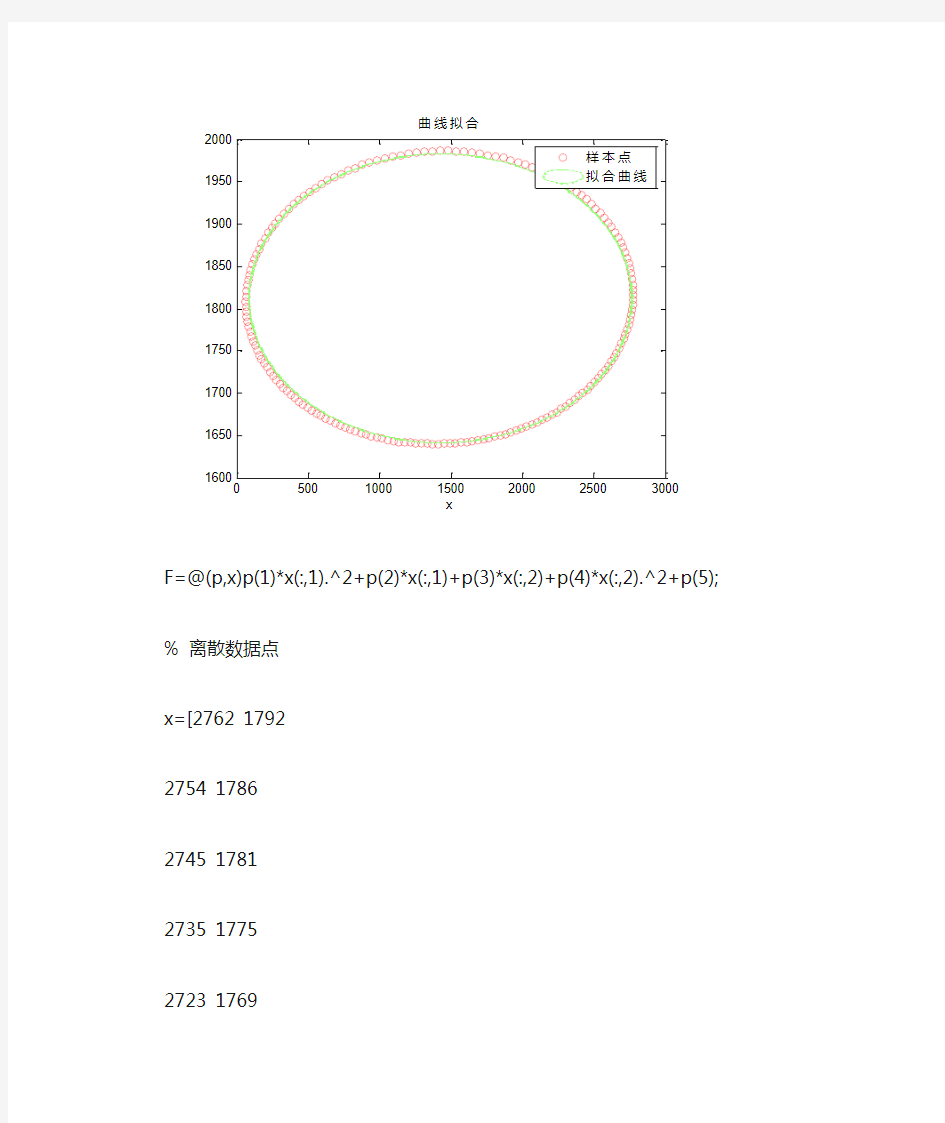
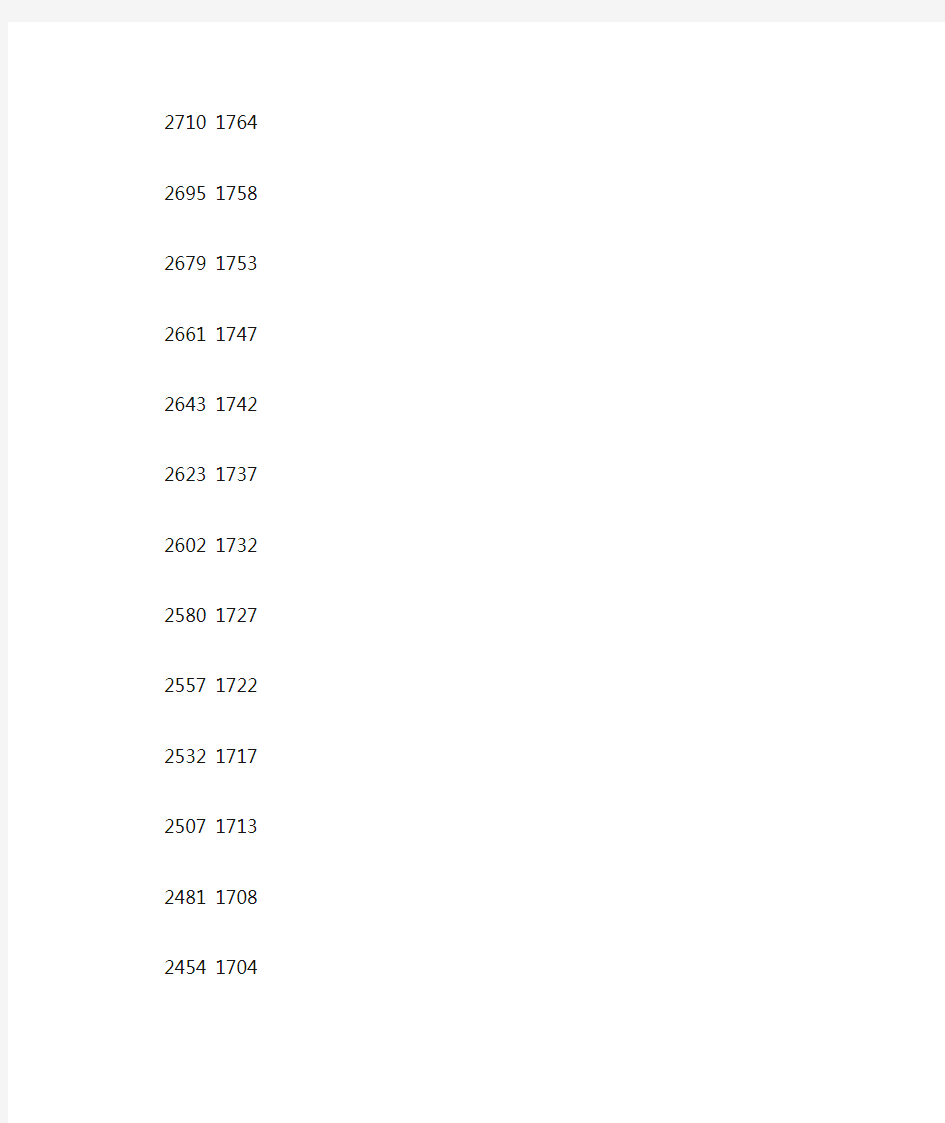
F=@(p,x)p(1)*x(:,1).^2+p(2)*x(:,1)+p(3)*x(:,2)+p(4)*x(:,2).^2+p(5);
% 离散数据点
x=[2762 1792
2754 1786
2745 1781
2735
1775 2723
1769 2710
1764 2695
1758 2679
1753 2661
1747 2643
1742 2623
1737 2602
1732 2580
1727 2557
1722 2532
1717 2507
1713 2481
1708 2454
1704 2425
1700 2396
1696 2367
1692 2336 1688
050010001500
20002500300016001650
1700
1750
1800
1850
1900
1950
2000
x y 曲线拟合
2305 1684 2273 1681 2240 1677 2207 1674 2173 1671 2138 1668 2103 1665 2068 1663 2032 1660 1995 1658 1959 1655 1921 1653 1884 1651 1846 1650 1807 1648 1769 1646 1730 1645 1691 1644 1652 1643 1613 1642 1573 1641 1534 1640 1494 1640 1454 1640 1415 1639 1375 1639 1336 1640 1296 1640 1256 1640 1217 1641 1178 1641 1139 1642 1100 1643 1061 1644 1023 1646 985 1647 947 1649 910 1651 873 1652 836 1654 800 1657 764 1659 729 1661 694 1664
626 1670 593 1673 561 1676 529 1679 499 1683 468 1686 439 1690 410 1694 383 1698 356 1702 330 1706 305 1711 281 1715 259 1720 237 1725 216 1730 197 1735 179 1740 162 1745 146 1750 132 1756 119 1761 107 1767 97 1773 89 1778 82 1784 76 1790 72 1796 70 1802
69 1808
70 1814 73 1821 77 1827 84 1833 92 1839 102 1845 113 1852 127 1858 143 1864 160 1870 179 1877 201 1883 224 1889
276 1900 304 1906 335 1912 367 1917 401 1923 438 1928 475 1933 514 1938 555 1942 598 1947 642 1951 687 1955 734 1959 782 1963 832 1966 882 1970 933 1972 986 1975 1039 1977 1093 1979 1148 1981 1203 1983 1259 1984 1315 1985 1371 1985 1427 1986 1484 1986 1540 1985 1596 1985 1652 1984 1707 1983 1761 1981 1815 1980 1868 1978 1921 1975 1972 1973 2022 1970 2072 1967 2120 1963 2166 1960 2212 1956 2255 1952 2297 1948
2339 1943
2378 1938
2415 1934
2450 1929
2484 1923
2516 1918
2547 1913
2575 1907
2602 1901
2626 1896
2649 1890
2670 1884
2689 1878
2706 1872
2722 1866
2735 1859
2746 1853
2756 1847
2764 1841
2770 1835
2774 1828
2776 1822
2777 1816
2776 1810
2773 1804
2769 1798
];
p0=[0.005 0.005 0.005 0.005 0.005];
warning off
% 拟合系数,最小二乘方法
p=nlinfit(x,zeros(size(x,1),1),F,p0);
plot(x(:,1),x(:,2),'ro');
hold on;
xmin=min(x(:,1));
xmax=max(x(:,1));
ymin=min(x(:,2));
ymax=max(x(:,2));
% 作图
ezplot(@(x,y)F(p,[x,y]),[-1+xmin,1+xmax,-1+ymin,1+ymax]); title('曲线拟合');
legend('样本点','拟合曲线')
F=@(p,x)p(1)*x(:,1).^2+p(2)*x(:,1)+p(3)*x(:,2)+p(4)*x(:,2).^2+p(5);
% 离散数据点
x=[2737 214
2727 217
2715
220 2701
224 2687
227 2671
231 2653
234 2635
237 2615
240 2594
243 2572
246 2549
249 2525
252 2500
255 2474
257 2447
260 2419
262 2390
265 2360
267 2330
269 2299 271
050010001500
20002500300050100
150
200
250
300
x y
曲线拟合
2267 274 2235 275 2202 277 2168 279 2134 281 2099 283 2064 284 2028 285 1992 287 1955 288 1918 289 1881 290 1843 291 1805 292 1767 293 1728 294 1690 294 1651 295 1612 295 1573 296 1533 296 1494 296 1455 296 1415 296 1376 296 1337 296 1297 296 1258 295 1219 295 1180 294 1141 293 1103 293 1064 292 1026 291 988 290 951 289 914 288 877 286 841 285 805 283 769 282 734 280 700 278 666 277
600 273 568 271 536 268 506 266 476 264 447 261 418 259 391 256 364 254 339 251 314 248 291 245 268 242 247 239 227 236 207 233 190 230 173 226 158 223 144 219 131 216 120 212 110 209 102 205 95 202 90 198 86 194 84 190 83 187 85 183 88 179 92 175 99 171 107 167 117 164 129 160 143 156 158 152 176 148 195 145 217 141 240 137 265 134
320 127 351 123 383 120 417 117 453 114 490 110 529 108 570 105 612 102 656 100 701 97
747 95
795 93
844 91
893 89
944 87
996 86 1049 85 1103 84 1157 83 1211 82 1267 81 1322 81 1378 81 1434 81 1489 81 1545 81 1600 82 1655 83 1710 83 1764 84 1817 86 1870 87 1922 89 1973 91 2023 92 2071 95 2119 97 2165 99 2210 102 2253 104 2295 107 2336 110
2374 113
2412 116
2447 119
2480 123
2512 126
2542 130
2570 133
2596 137
2621 140
2643 144
2664 148
2683 152
2699 156
2714 159
2727 163
2739 167
2748 171
2756 175
2761 179
2765 183
2768 186
2768 190
2767 194
2765 198
2760 201
2754 205
2747 209
];
p0=[1 1 1 1 1];
warning off
% 拟合系数,最小二乘方法
p=nlinfit(x,zeros(size(x,1),1),F,p0);
plot(x(:,1),x(:,2),'ro');
hold on;
xmin=min(x(:,1));
xmax=max(x(:,1));
ymin=min(x(:,2));
ymax=max(x(:,2));
% 作图
ezplot(@(x,y)F(p,[x,y]),[-1+xmin,1+xmax,-1+ymin,1+ymax]); title('曲线拟合');
legend('样本点','拟合曲线')
首先用excel对下椭圆的纵坐标进行排序,找出最小值为81,再用matlab程序求出横坐标1497.5,最后把横坐标代入椭圆方程中求出B,C,D点的值,function f=fx(x);
f=8.5236e-038*x*x-2.4333e-034*x-4.9894e-033*81+1.3252e-035*81*81+4.9044e-031;
>> z=fzero(@fx,1450)
z =
1.4975e+003
function f=fx(y);
f=8.5236e-038*1497.5*1457.5-2.4333e-034*1457.5-4.9894e-033*y+1.3252e-035*y*y+4.9044e-031;
B=fzero(@fx,300)
B =
293.8610
>> function f=fx(y);
f=5.7344e-032*1497.5*1457.5-1.6323e-028*1457.5-1.2744e-026*y+3.516e-030*y*y+1.1562e-0 23;
C=fzero(@fx,1650)
C=
1.6448e+003
D=fzero(@fx,1980)
D=
1.9798e+003
function q=myfun2(p)
x=p(1);
y=p(2);
q(1)=0.127*1351*(x+y)-97543.41;
q(2)=1899*(x-y)*0.127-97543.41;
>> options=optimset('Display','off'); >> x=fsolve(@myfun2,[487,84]',options)
x =
486.4825
82.0284
第三章 曲线拟合算法的研究 3.1 引言 随着航空、汽车等现代工业与计算机技术的发展,圆锥曲线与列表点曲线已经成为形状数学描述的常用方法,得到了广泛的应用。为了满足激光切割加工任务的需要,自动编程系统集成了多种曲线拟合算法,这样利用现有的激光切割机,即可实现特殊曲线的插补功能,极大地丰富系统的插补能力,满足复杂的生产要求。 3.2 圆锥曲线拟合算法的研究 在经济型数控系统中,对于圆锥曲线即平面二次曲线的加工是数控加工中经常遇到的问题,随着数控加工对圆锥曲线插补的需求,近年来有关各种圆锥曲线的插补算法应运而生[26]。常用的解决方法是先用低次的有理参数曲线拟合或将其离散,再用直线、圆弧逼近,然后才能进行数控加工[28]。本章从一个新的视角利用双圆弧方法,提出先对圆锥曲线进行标准化处理,再用双圆弧拟合逼近,然后再进行数控加工。这样的优点是:圆弧样条的等距曲线还是圆弧;双圆弧样条能达到C 1连续,基本上能满足要求;所有数控系统都具有直线插补和圆弧插补功能,无需增加额外负担。 由于工程应用不同,对曲线拟合的要求也不同。有的只要求拟合曲线光滑,有的要求光顺[9-10]。本章中开发的软件要求是:支持多种常用圆锥曲线的拟合;拟合曲线要求光滑;拟合曲线与函数曲线间的误差应控制在允许的范围之内,且拟合圆弧段数较少。 本章提出的对圆锥曲线的插补,是建立在对平面任意二次曲线可以进行分类的基础上,先将二次曲线进行分类,然后对各类曲线分别进行双圆弧拟合,这样就可以直接利用数控系统的圆弧插补功能进行插补。 3.2.1 圆锥曲线的一般理论[9] 在平面直角坐标系中,二元二次方程所表示的曲线称为二次曲线。其中系数A 、B 、 C 、 D 、 E 、 F 为实常数,且A 、B 、C 不同时为零。 022=+++++F Ey Dx Cy Bxy Ax (3.1) 式(3.1)称为圆锥曲线的隐式方程。令 AC B 42-=? (3.2) 称上式为二元二次方程(3.1)的判别式。 0
曲线拟合的数值计算方法实验 【摘要】实际工作中,变量间未必都有线性关系,如服药后血药浓度与时间的关系;疾病疗效与疗程长短的关系;毒物剂量与致死率的关系等常呈曲线关系。曲线拟合(curve fitting)是指选择适当的曲线类型来拟合观测数据,并用拟合的曲线方程分析两变量间的关系。曲线直线化是曲线拟合的重要手段之一。对于某些非线性的资料可以通过简单的变量变换使之直线化,这样就可以按最小二乘法原理求出变换后变量的直线方程,在实际工作中常利用此直线方程绘制资料的标准工作曲线,同时根据需要可将此直线方程还原为曲线方程,实现对资料的曲线拟合。常用的曲线拟合有最小二乘法拟合、幂函数拟合、对数函数拟合、线性插值、三次样条插值、端点约束。 关键词曲线拟合、最小二乘法拟合、幂函数拟合、对数函数拟合、线性插值、三次样条插值、端点约束 一、实验目的 1.掌握曲线拟合方式及其常用函数指数函数、幂函数、对数函数的拟合。 2.掌握最小二乘法、线性插值、三次样条插值、端点约束等。 3.掌握实现曲线拟合的编程技巧。 二、实验原理 1.曲线拟合 曲线拟合是平面上离散点组所表示的坐标之间的函数关系的一种数据处理方法。用解析表达式逼近离散数据的一种方法。在科学实验或社会活动中,通过 实验或观测得到量x与y的一组数据对(X i ,Y i )(i=1,2,...m),其中各X i 是彼此不同的。人们希望用一类与数据的背景材料规律相适应的解析表达式,y=f(x,c)来反映量x与y之间的依赖关系,即在一定意义下“最佳”地逼近或 拟合已知数据。f(x,c)常称作拟合模型,式中c=(c 1,c 2 ,…c n )是一些待定参 数。当c在f中线性出现时,称为线性模型,否则称为非线性模型。有许多衡量拟合优度的标准,最常用的一种做法是选择参数c使得拟合模型与实际观测值在
最小二乘法拟合圆公式推导及vc实现[r] 最小二乘法(least squares analysis)是一种数学优化技术,它通过最小化 误差的平方和找到一组数据的最佳函数匹配。最小二乘法是用最简的方法求得一些绝对不可知的真值,而令误差平方之和为最小。最小二乘法通常用于曲线拟合 (least squar es fitting) 。这里有拟合圆曲线的公式推导过程和 vc实现。
此处使用平方差与最小二乘法差的平方不一样,但是仍然具有实用估计价值,并且可以化简公式。
VC实现的代码:C++类 void CViewActionImageTool::LeastSquaresFitting() { if(m_nNum<3) { return; } int i=0; double X1=0; double Y1=0; double X2=0; double Y2=0; double X3=0;
double Y3=0; double X1Y1=0; double X1Y2=0; double X2Y1=0; for(i=0;i 椭圆弧等误差直线拟合的算法研究 为实现椭圆弧的等误差直线拟合,提出了一种基于罗尔定理和二分法的曲线节点计算新算法。该算法通过二分角度迭代求解弦与对应的弧之间的误差,逐步逼近程序要求的允差。最后,总结了具体的算法流程并进行了轨迹仿真验证。 标签:等误差拟合;二分法;罗尔定理 引言 本文提出了一种基于罗尔定理与二分法的曲线等误差直线拟合新算法,适用于椭圆弧的拟合节点计算,该算法通过二分角度迭代求解弦与对应的弧之间的误差,逐步逼近程序要求的允差,避免了高次方程组的求解[1][2],可广泛应用于数控加工。 1 基于罗尔定理与二分法的曲线等误差直线拟合新算法 图1 椭圆弧等误差直线拟合新算法 如图1所示,在本节讨论中不妨设椭圆弧AB夹角∠AOB≤180°。用直线连接曲线的两个端点A、B,我们称直线AB为曲线的弦。只要该曲线上的点到弦AB的最大距离hmax小于程序设定的允许误差res,就可以用直线段AB来拟合曲线AB。而当hmax大于res时,就需要用二分法在∠AOB范围内搜索拟合点F[3]。 1.1 擬合误差的求解 如图1所示,弦AB斜率为k,椭圆弧的AB段为凹凸性一致的单值区间,由罗尔定理可知,在弧AB上有且仅有一点C,使得过C点的椭圆弧切线斜率与弦AB斜率相等。设过C点的该切线为lc,则线段AB拟合椭圆弧AB的误差为直线lc与直线AB之间的距离。 设A点坐标为A(xa,ya),则直线AB的方程为: y-ya=k(x-xa)(1) 由椭圆弧AB方程x2/a2+y2/b2=1,得到椭圆上的点C(xc,yc)处切线斜率为: k=-b2xc/a2yc (2) 可求得切点C的坐标为: 曲线拟合(curve-fitting ):工程实践中,用测量到的一些离散的数据},...2,1,0),,{(m i y x i i =求一个近似的函数)(x ?来拟合这组数据,要求所得的拟合曲线能最好的反映数据的基本趋势(即使)(x ?最好地逼近()x f ,而不必满足插值原则。因此没必要取)(i x ?=i y ,只要使i i i y x -=)(?δ尽可能地小)。 原理: 给定数据点},...2,1,0),,{(m i y x i i =。求近似曲线)(x ?。并且使得近似曲线与()x f 的偏差最小。近似曲线在该点处的偏差i i i y x -=)(?δ,i=1,2,...,m 。 常见的曲线拟合方法: 1.使偏差绝对值之和最小 2.使偏差绝对值最大的最小 3.使偏差平方和最小 最小二乘法: 按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。 推导过程: 1. 设拟合多项式为: 2. 各点到这条曲线的距离之和,即偏差平方和如下: 3. 问题转化为求待定系数0a ...k a 对等式右边求i a 偏导数,因而我们得到 了: ....... 4、 把这些等式化简并表示成矩阵的形式,就可以得到下面的矩阵: 5. 将这个范德蒙得矩阵化简后可得到: 6. 也就是说X*A=Y,那么A = (X'*X)-1*X'*Y,便得到了系数矩阵A,同时,我们也就得到了拟合曲线。 MATLAB实现: MATLAB提供了polyfit()函数命令进行最小二乘曲线拟合。 调用格式:p=polyfit(x,y,n) [p,s]= polyfit(x,y,n) [p,s,mu]=polyfit(x,y,n) x,y为数据点,n为多项式阶数,返回p为幂次从高到低的多项式系数向量p。x必须是单调的。矩阵s包括R(对x进行QR分解的三角元素)、df(自由度)、normr(残差)用于生成预测值的误差估计。 [p,s,mu]=polyfit(x,y,n)在拟合过程中,首先对x进行数据标准化处理,以在拟合中消除量纲等影响,mu包含标准化处理过程中使用的x的均值和标准差。 polyval( )为多项式曲线求值函数,调用格式: y=polyval(p,x) [y,DELTA]=polyval(p,x,s) y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。 [y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计Y DELTA。它假设polyfit函数数据输入的误差是独立正态的,并且方差为常数。则Y DELTA将至少包含50%的预测值。 如下给定数据的拟合曲线: x=[0.5,1.0,1.5,2.0,2.5,3.0], y=[1.75,2.45,3.81,4.80,7.00,8.60]。 解:MATLAB程序如下: x=[0.5,1.0,1.5,2.0,2.5,3.0]; y=[1.75,2.45,3.81,4.80,7.00,8.60]; p=polyfit(x,y,2) x1=0.5:0.05:3.0; y1=polyval(p,x1); plot(x,y,'*r',x1,y1,'-b') 运行结果如图1 计算结果为: p =0.5614 0.8287 1.1560 即所得多项式为y=0.5614x^2+0.08287x+1.15560 图1 最小二乘法曲线拟合示例 对比检验拟合的有效性: 例:在[0,π]区间上对正弦函数进行拟合,然后在[0,2π]区间画出图形,比较拟合区间和非拟合区间的图形,考察拟合的有效性。 在MATLAB中输入如下代码: clear x=0:0.1:pi; y=sin(x); [p,mu]=polyfit(x,y,9) 曲线拟合算法: 本人进行测试通过,完全正常使用。 #region splined private void splined(PointF[] temp, ref ArrayList splinedPt) { double x, y, t; double px, py; int q = 3; int phi; int kaw; int naw; int n = temp.Length; int add; phi = 5; naw = n; add = 5 * (naw + q - 1) + 1; for (t = -phi + 1.0; t < naw + phi; t = t + 0.2) { x = 0.0; y = 0.0; for (kaw = -2 * phi + 1; kaw < naw + 2 * phi; kaw++) { px = 0; py = 0; if (kaw < 1) { px = temp[0].X; py = temp[0].Y; } if (kaw > naw) { px = temp[naw - 1].X; py = temp[naw - 1].Y; } if (kaw > 0 && kaw <= naw) { px = temp[kaw - 1].X; py = temp[kaw - 1].Y; } x = x + nqt(q, t - kaw) * px; y = y + nqt(q, t - kaw) * py; } PointF Point1 = new PointF((float)x, (float)y); splinedPt.Add(Point1); 第三章数据拟合回顾 keywords 最小二乘法 转化的思想 使误差的平方和为最小: 按最小二乘法, 作直线拟合应使 ∑=+-=N i i i x y b a b a Q 1 2 )]([),(为最小,极小值点一阶导数为0:0,0=??=??b Q a Q 最小二乘法(least squares method ) 2min, ()i i e e y a bx i i i =∑=-+2i i i i i i aN b x y a x b x x y ?+=??+=??∑∑∑∑∑得正规方程组: 2i i i i i i i i i i i i a b x y a x b x x y ωωωωωω?+=??+=??∑∑∑∑∑∑加权正规方程组: IF Y*=a0+a1X1+a2X2+a3X3+……+akXk (n>k ),THEN? 最小二乘法的几何意义(p51) y=a0x0+a1x1+a2x2+a3x3+……+akxk(n>k)其中x0=(1,1,1,.....1),x i=(xi1,xi2,xi3,.....,xin),i=1,2,3.....n 数据拟合方法一览表 线性关系直线拟合非线性关系曲线拟合 单变量直线拟合多 变 量 直 线 拟 合 多项式拟合非多项式拟合 变量 替换 转换 为直 线拟 合 多项 式拟 合的 最小 二乘 法 变量 替换 为多 变量 直线 拟合 方程 两边 取对 数转 换为 直线 拟合 正 交 多 项 式 拟 合 Y*=a0+a1X1+a2X2+a3X3+……+akXk(n>k)本 thank u 最小二乘法的基本原理和多项式拟合 一 最小二乘法的基本原理 从整体上考虑近似函数)(x p 同所给数据点),(i i y x (i=0,1,…,m)误差 i i i y x p r -=)((i=0,1,…,m) 的大小,常用的方法有以下三种:一是误差 i i i y x p r -=)((i=0,1,…,m)绝对值的最大值i m i r ≤≤0max ,即误差 向量 T m r r r r ),,(10 =的∞—范数;二是误差绝对值的和∑=m i i r 0 ,即误差向量r 的1— 范数;三是误差平方和∑=m i i r 02 的算术平方根,即误差向量r 的2—范数;前两种方法简单、自然,但不便于微分运算 ,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合中常采用误差平方和∑=m i i r 02 来 度量误差i r (i=0,1,…,m)的整 体大小。 数据拟合的具体作法是:对给定数据 ),(i i y x (i=0,1,…,m),在取定的函数类Φ中,求Φ∈)(x p ,使误差i i i y x p r -=)((i=0,1,…,m)的平方和最小,即 ∑=m i i r 2 = 从几何意义上讲,就是寻求与给定点),(i i y x (i=0,1,…,m)的距离平方和为最 小的曲线 )(x p y =(图6-1)。函数)(x p 称为拟合函数或最小二乘解,求拟合函数)(x p 的方法称为曲线拟合的最小二乘法。 在曲线拟合中,函数类Φ可有不同的选取方法 . 6—1 二 多项式拟合 假设给定数据点),(i i y x (i=0,1,…,m),Φ为所有次数不超过)(m n n ≤的多项式构成的函数类,现求一 Φ ∈=∑=n k k k n x a x p 0 )(,使得 [] min )(0 02 02 =??? ??-=-=∑∑∑===m i m i n k i k i k i i n y x a y x p I (1) [ ] ∑ = = - m i i i y x p 0 2 min ) ( 1 20/"geometry.cfg" 20/"natbib.cfg" 20/"bblopts.cfg" 20/"english.cfg"20/"____________.aux" 插值算法February3,2020 需要根据已知的函数点进行数据,模型的处理和分析,有时候现有的数据是极少的,不足以分析支撑的比较,这时候需要数学的方法,模拟产生一些洗呢但又比较靠谱的值来满足需求。 一维插值问题多项式插值分段插值 拉格朗日插值多项式公式 L n(x)= n ∑ k=0 y k ωn+1(x) (x?x k)ω′ n+! (x k) 其中ωn+1(x)=(x?x0)(x?x1)....(x?x n) 龙格现象(runge phenomenon)高次插值会产生龙格现象,在两端处的波动计大,产生明显的震荡.在不熟悉曲线的运动趋势下,不要轻易使用高次插值. 采用分段低次插值的思路:在随便两个点之间,采用分段二次或者三次插值的方法/又叫分段抛物插值. 牛顿插值法:f(x)=f(x0)+f|x0,x1|(x?x0)+f|x0,x1,x2|(x?x0)(x?x1)+.....差商的定义:称f|x0,x k|=f(x k)?f(x0) x k?x0 两种插值的区别在于没有体现在导数的一致上 埃尔米特插值法:要求节点处的函数值相同,同时要求对应的导数值也相同分段三次埃尔米特插值法: matlab里有内存的函数pchip(x,y,new_w)x是已知样本点的横坐标,y是已知样本点的纵坐标,new_x是要插入的对应的横坐标 n维数据的插值了解:p=interpn(x1,x2,...xn,y,new_x1,newx_2,....newx_n,method) x1,x2,x3...是样本点的横坐标 y是样本点的纵坐标 输入的new是要输入点的横坐标 method是要插值的方法拟合算法 拟合和插值的区别:找到一个确定的曲线保证误差足够小,不要求曲线经过每一个样本点,只要足够接近就可以. 最小二乘法拟合椭圆 设平面任意位置椭圆方程为: x 2+Axy +By 2+Cx +Dy +E =0 设P i (x i ,y i )(i =1,2,…,N )为椭圆轮廓上的N (N ≥5) 个测量点,依据最小二乘原理,所拟合的目标函数为: F (A,B,C,D,E )=∑(x i 2+Ax i y i +By i 2+Cx i +Dy i +E)2 N i=1 欲使F 为最小,需使 ?F ?A =?F ?B =?F ?C =?F ?D =?F ?E =0 由此可以得方程: [ ∑x i 2y i 2∑x i y i 3∑x i 2y i ∑x i y i 2∑x i y i ∑x i y i 3∑y i 4∑x i y i 2∑y i 3∑y i 2∑x i 2y i ∑x i y i 2∑x i 3∑x i y i ∑x i ∑x i y i 2∑y i 3∑x i y i ∑y i 2∑y i 2∑x i y i ∑y i 2∑x i ∑y i N ] [ A B C D E ] =-[ ∑x i 3y i ∑x i 2y i 2∑ x i 3∑x i 2y i ∑ x i 2] 解方程可以得到A ,B ,C ,D ,E 的值。 根据椭圆的几何知识,可以计算出椭圆的五个参数:位置参数(θ,x 0,y 0)以及形状参数(a,b )。 x 0=2BC?AD A 2?4B y 0=2D ?AD A 2?4B a =√2(ACD ?BC 2?D 2+4BE ?A 2E )(A 2?4B )(B ?√A 2+(1?B 2)+1) b =√2(ACD ?BC 2?D 2+4BE ?A 2E )(A 2?4B )+√A 2+(1?B 2)+1) θ=tan ?1√ a 2? b 2B a 2B ?b 2 椭圆的目标函数: F(A,B,C,D,E)=XiGeMa(xi^2+A*xiyi+B*yi^2+C*xi+D*yi+E)^2 分别对A,B,C,D,E求一阶偏导并令其等于0 得到线性方程组: |A1B1C1D1E1||A|=|resul1| |A2B2C2D2E2||B|=|resul2| |A3B3C3D3E3||C|=|resul3| |A4B4C4D4E4||D|=|resul4| |A5B5C5D5E5||E|=|resul5| 求得A,B,C,D,E. 椭圆的五个参数: center.x=(2*B*C-A*D)/(A*A-4*B); center.y=(2*D-A*D)/(A*A-4*B); fenzi=2*(A*C*D-B*C*C-D*D+4*E*B-A*A*E); fenmu=(A*A-4*B)*(B-sqrt(A*A+(1-B)*(1-B))+1); femmu2=(A*A-4*B)*(B+sqrt(A*A+(1-B)*(1-B))+1); long=sqrt(fabs(fenzi/fenmu)); short=sqrt(fabs(fenzi/femmu2)); theta=atan(sqrt((center.x*center.x-center.y*center.y*B)/(center.x*center.x *B-center.y*center.y))+0.0001)*180/cv_pi;; vector 曲线拟合——最小二乘法算法 一、目的和要求 1)了解最小二乘法的基本原理,熟悉最小二乘算法; 2)掌握最小二乘进行曲线拟合的编程,通过程序解决实际问题。 二、实习内容 1)最小二乘进行多项式拟合的编程实现。 2)用完成的程序解决实际问题。 三、算法 1)输入数据节点数n ,拟合的多项式次数m ,循环输入各节点的数据x j , y j (j=0,1,…,n-1) 2)由x j 求S ;由x j ,y j 求T : S k = ∑-=10n j k j x ( k=0,1,2, … 2*m ) T k = ∑-=1 0n j k j j x y ( k=0,1,2,… m ) 3)由S 形成系数矩阵数组c i,j :c[i][j]=S[i+j] (i=0,1,2,…m, j=0,1,2,…,m);由T 形成系数矩阵增广部分c i,m+1:c[i][m+1]=T[i] (i=0,1,2,…m) 4)对线性方程组CA=T[或A C ],用列主元高斯消去法求解系数矩阵A=(a 0,a 1,…,a m )T 四、实验步骤 1)完成最小二乘法进行曲线拟合的程序设计及录入、编辑; 2)完成程序的编译和链接,并进行修改; 3)用书上P105例2的例子对程序进行验证,并进行修改; 4)用完成的程序求解下面的实际问题。 5)完成实验报告。 五、实验结果 1. 经编译、链接及例子验证结果正确的源程序: #include 最小二乘法拟合一条直线(C语言代码) #include 实验题目: 用多项式模型进行数据拟合实验 1 实验目的 本实验使用多项式模型对数据进行拟合,目的在于: (1)掌握数据拟合的基本原理,学会使用数学的方法来判定数据拟合的情况; (2)掌握最小二乘法的基本原理及计算方法; (3)熟悉使用matlab 进行算法的实现。 2 实验步骤 2.1 算法原理 所谓拟合是指寻找一条平滑的曲线,最不失真地去表现测量数据。反过来说,对测量 的实验数据,要对其进行公式化处理,用计算方法构造函数来近似表达数据的函数关系。由于函数构造方法的不同,有许多的逼近方法,工程中常用最小平方逼近(最小二乘法理论)来实现曲线的拟合。 最小二乘拟合利用已知的数据得出一条直线或曲线,使之在坐标系上与已知数据之间的距离的平方和最小。模型主要有:1.直线型2.多项式型3.分数函数型4.指数函数型5.对数线性型6.高斯函数型等,根据应用情况,选用不同的拟合模型。其中多项式型拟合模型应用比较广泛。 给定一组测量数据()i i y x ,,其中m i ,,3,2,1,0Λ=,共m+1个数据点,取多项式P (x ),使得 min )]([020 2=-=∑∑==m i i i m i i y x p r ,则称函数P (x )为拟合函数或最小二乘解,此时,令 ∑==n k k k n x a x p 0 )(,使得min ])([02 002=??? ? ??-=-=∑∑∑===m i n k i k i k m i i i n y x a y x p I ,其中 n a a a a ,,,,210Λ为待求的未知数,n 为多项式的最高次幂,由此该问题化为求),,,(210n a a a a I I Λ=的极值问题。 由多元函数求极值的必要条件:0)(200 =-=??∑∑==m i j i n k i k i k i x y x a a I ,其中n j ,,2,1,0Λ= 得到: ∑∑∑===+=n k m i i j i k m i k j i y x a x )(,其中n j ,,2,1,0Λ=,这是一个关于n a a a a ,,,,210Λ的线 性方程组,用矩阵表示如下所示: 最小二乘拟合 在物理实验中经常要观测两个有函数关系的物理量。根据两个量的许多组观测数据来确定它们的函数曲线,这就是实验数据处理中的曲线拟合问题。这类问题通常有两种情况:一种是两个观测量x 与y 之间的函数形式已知,但一些参数未知,需要确定未知参数的最佳估计值;另一种是x 与y 之间的函数形式还不知道,需要找出它们之间的经验公式。后一种情况常假设x 与y 之间的关系是一个待定的多项式,多项式系数就是待定的未知参数,从而可采用类似于前一种情况的处理方法。 一、最小二乘法原理 在两个观测量中,往往总有一个量精度比另一个高得多,为简单起见把精度较高的观测量看作没有误差,并把这个观测量选作x ,而把所有的误差只认为是y 的误差。设x 和y 的函数关系由理论公式 y =f (x ;c 1,c 2,……c m ) (0-0-1) 给出,其中c 1,c 2,……c m 是m 个要通过实验确定的参数。对于每组观测数据(x i ,y i )i =1,2,……,N 。都对应于xy 平面上一个点。若不存在测量误差,则这些数据点都准确落在理论曲线上。只要选取m 组测量值代入式(0-0-1),便得到方程组 y i =f (x ;c 1,c 2,……c m ) (0-0-2) 式中i =1,2,……,m.求m 个方程的联立解即得m 个参数的数值。显然N 最小二乘法数据拟合 设给定数据),(i i f x ,),,2,1(m i = 在集合},,,{Span 10n ??? =Φ中找一个函数 )()(* 0** x a x S k n k k ?∑==,)(m n < (1) 其误差是 i i i f x S -=)(*δ,),,2,1(m i = (2) 使)(* x S 满足 2 1 )(2 *1 1 2 ])()[(min ])()[(i i m i i x S i i m i i m i i f x S x f x S x -=-=∑∑∑=Φ ∈==ωωδ (3) 0)(≥x ω是],[b a 上给定的权函数。上述求逼近函数)(*x S 的方法就称为曲线拟合的最小二 乘法。满足关系式(3)的函数)(* x S 称为上述最小二乘问题的最小二乘解。 并且有结论: 1)对于给定的函数表),(i i f x ,),,2,1(m i =,在函数类},,,{Span 10n ??? =Φ中存在唯一的函数)()(*0** x a x S k n k k ?∑== ,使得关系式(3)成立。 2)最小二乘解的系数* *1*0,,,n a a a 可以通过解法方程 ),(),(0 ???f a k n k j k =∑=,),,2,1,0(n j = (4) 作为曲线拟合的一种常用的情况,如果讨论的是代数多项式拟合,即取 },,,,1{},,,{210n n x x x =??? 那么相应的法方程(4)就是 ??????????????=???????????????????????? ??∑∑∑∑∑∑∑∑∑∑∑∑++i n i i i i i i i n n i i n i i n i i n i i i i i i n i i i i i f x f x f a a a x x x x x x x x ωωωωωωωωωωωω 102112 (5) Random Walks and Rehab: Analyzing the Spread of the Opioid Crisis Ellen Considine Suyog Soti Emily Webb University of Colorado Boulder Boulder,Colorado USA ellen.considine@https://www.doczj.com/doc/5114788371.html, Advisor:Anne Dougherty Summary We classify69types of opioid substances into four categories based on synthesis and availability.Plotting use rates of each category over time re-veals that use of mild painkillers and natural alkaloids has stayed relatively constant over time,semi-synthetic drugs have declined slightly,and syn-thetic drugs such as fentanyl and heroin have increased dramatically.These ?ndings align with reports from the CDC.We select54of149socioeconomic variables based on their variance in?ation factor score(a common measure of multicollinearity)as well as on their relevance based on the public health literature. To model the spread of the opioid crisis across Kentucky,Ohio,Penn-sylvania,West Virginia,and Virginia,we develop two completely different models and then compare them. Our?rst model is founded on common modeling approaches in epidemi-ology:SIR/SIS models and stochastic simulation.We design an algorithm that simulates a random walk between six discrete classes,each of which represents a different stage of the opioid crisis,using thresholds for opioid abuse prevalence and rate of change.We penalize transitions between cer-tain classes differentially based on realistic expectations.Optimization of parameters and coef?cients for the model is guided by an error function in-spired by the global spatial autocorrelation statistic Moran’s I.Testing our model via both error calculation and visual mapping illustrates high accu-racy over many hundreds of trials.However,this model does not provide much insight into the in?uence of socioeconomic factors on opioid abuse The UMAP Journal40(4)(2018)353–380.c Copyright2019by COMAP,Inc.All rights reserved. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for pro?t or commercial advantage and that copies bear this notice.Abstracting with credit is permitted,but copyrights for components of this work owned by others than COMAP must be honored.To copy otherwise, to republish,to post on servers,or to redistribute to lists requires prior permission from COMAP. 实验三 函数逼近与曲线拟合 一、问题的提出: 函数逼近是指“对函数类A 中给定的函数)(x f ,记作A x f ∈)(,要求在另一类简的便于计算的函数类B 中求函数A x p ∈)(,使 )(x p 与)(x f 的误差在某中度量意义下最小”。函数类A 通常是区间],[b a 上的连续函数,记作],[b a C ,称为连续函数空间,而函数类B 通常为n 次多项式,有理函数或分段低次多项式等,函数逼近是数值分析的基础。主要内容有: (1)最佳一致逼近多项式 (2)最佳平方逼近多项式 (3)曲线拟合的最小二乘法 二、实验要求: 1、构造正交多项式; 2、构造最佳一致逼近; 3、构造最佳平方逼近多项式; 4、构造最小二乘法进行曲线拟合; 5、求出近似解析表达式,打印出逼近曲线与拟合曲线,且打印出其在数据点上的偏差; 6、探讨新的方法比较结果。 三、实验目的和意义: 1、学习并掌握正交多项式的MATLAB 编程; 2、学习并掌握最佳一致逼近的MATLAB 实验及精度比较; 3、学习并掌握最佳平方逼近多项式的MATLAB 实验及精度比较; 4、掌握曲线拟合的最小二乘法; 5、最小二乘法也可用于求解超定线形代数方程组; 6、 探索拟合函数的选择与拟合精度之间的关系; 四、 算法步骤: 1、正交多项式序列的生成 {n ?(x )}∞ 0:设n ?(x )是],[b a 上首项系数a ≠n 0的n 次多项式,)(x ρ为],[b a 上权函数,如果多项式序列{n ?(x )} ∞0 满足关系式???=>≠==?.,0,, 0)()()()(),(k j A k j x d x x x k k j b a k j ??ρ?? 则称多项式序列{n ?(x )}∞ 0为在],[b a 上带权)(x ρ正交,称n ?(x )为],[b a 上带权)(x ρ 的n 次正交多项式。 1)输入函数)(x ρ和数据b a ,; 2)分别求))(),(()),(,(x x x x j j j n ???的内积; 3)按公式①)()) (),(()) (,()(,1)(1 0x x x x x x x x j n j j j j n n n ??? ???∑-=- ==计算)(x n ?,生成正交多项式; 流程图: 开始椭圆弧等误差直线拟合的算法研究
最小二乘法曲线拟合 原理及matlab实现
曲线拟合算法
计算方法_数据拟合回顾
最小二乘法的基本原理和多项式拟合
插值拟合数学建模算法
(完整版)最小二乘法拟合椭圆附带matlab程序
椭圆拟合算法实现
曲线拟合——最小二乘法算法
线性拟合C语言算法
用多项式模型进行数据拟合实验报告(附代码)
(2020年编辑)最小二乘法拟合原理
最小二乘法数据拟合
回归拟合算法优秀论文2
曲线拟合的最小二乘法讲解