生物统计学教案

生物统计学教案

第十章一元回归及简单相关分析

教学时间：5学时

教学方法：课堂板书讲授

教学目的：重点掌握一元线性回归方程,掌握一元线性回归方程的检验和相关，了解一元非线性回归和多元回归与相关。

讲授难点：一元线性回归方程的检验和相关

10.1 回归与相关的基本概念

函数关系：F＝ma

相关关系：单位面积的施肥量、播种量和产量；血压和年龄；胸径和高度；玉米的穗长和穗重；身高和体重。

相关：设有两个随机变量X和Y，对于任一随机变量的每一个可能的值，另一个随机变量都有一个分布与之相对应，称X和Y存在相关。

回归：对于变量X的每一个可能的值x i，都有随机变量Y的一个分布相对应，则称随机变量Y对变量X存在回归。X称为自变量，Y称为因变量。

条件平均数：当X＝x i时Y的平均数μY.X＝xi，称为条件平均数。

10.2 一元线性回归方程

10.2.1 散点图

例不同NaCl含量对单位叶面积干物质的影响

NaCl

含量X(g/kg土壤) 0 0.8 1.6 2.4 3.2 4.0 4.8

干重Y(mg/dm2) 80 90 95 115 130 115 135

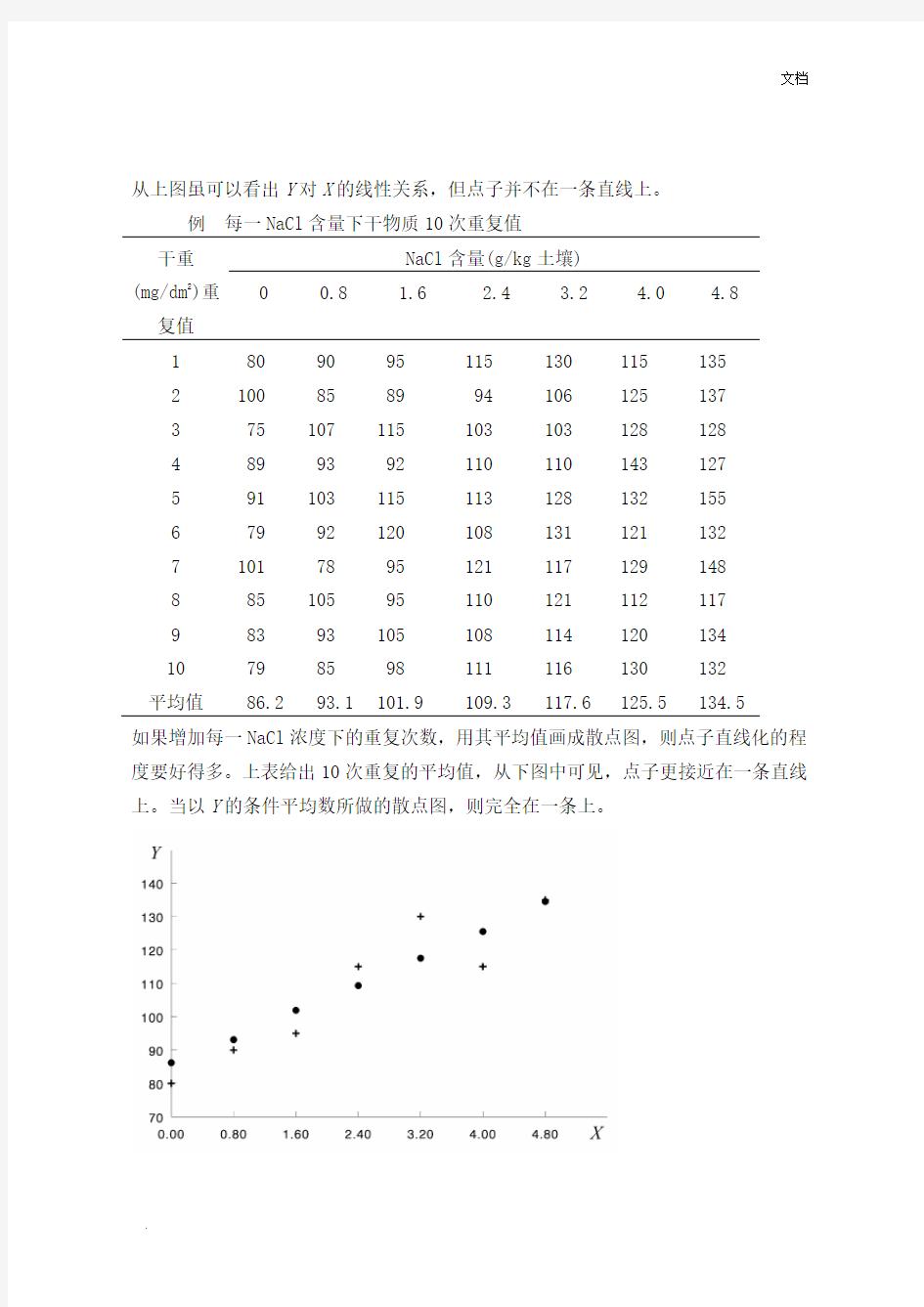
从上图虽可以看出Y对X的线性关系，但点子并不在一条直线上。

例每一

NaCl含量下干物质10次重复值

干重(mg/dm2)重

复值

NaCl含量(g/kg土壤)

0 0.8 1.6 2.4 3.2 4.0 4.8

1 80 90 95 115 130 115 135

2 100 85 89 94 106 125 137

3 75 107 115 103 103 128 128

4 89 93 92 110 110 143 127

5 91 103 115 113 128 132 155

6 79 92 120 108 131 121 132

7 101 78 95 121 117 129 148

8 85 105 95 110 121 112 117

9 83 93 105 108 114 120 134

10 79 85 98 111 116 130 132

平均值 86.2 93.1 101.9 109.3 117.6 125.5 134.5

如果增加每一NaCl浓度下的重复次数，用其平均值画成散点图，则点子直线化的程度要好得多。上表给出10次重复的平均值，从下图中可见，点子更接近在一条直线上。当以Y的条件平均数所做的散点图，则完全在一条上。

10.2.2 一元正态线性回归模型

x i 和各x i 上Y 的条件平均数μy.x 可构成一条直线：

μY ＝α＋βX

对于变量X 的每一个值，都有一个Y 的分布，其平均数是上式所示的线性函数。对于随机变量Y ：

Y ＝α＋βX ＋ε

ε：NID (0,σ2) Y ：NID (α+βX ,σ2) 上式称为一元正态线性回归模型。 10.2.3 参数α和β的估计

在实际工作中，我们是无法得到α和β的，只能得到它们的估计值a 和b ，从而得到一条估计的回归线：

bX a Y

+=?

上式称为Y 对X 的回归方程，所画出的直线称为回归线。a 是直线的截距，称为常数项；b 是直线的斜率，称为回归系数。

对于因变量Y 的每一个观测值y i ： y i = a + bx i + e i

y i 的回归估计值i y

?是对i x Y ?μ的估计，因此i y ?也是平均数。 在各种离差平方和中，以距平均数的离差平方和为最小。因此我们就把e i =

y i -i y

?平方和为最小的直线作为最好的回归线。 记()∑=-=n

i i i y y L 12

?,求出使L 达到最小时的a 和b ，

这种方法称为最小二乘法。

为使()()[]

∑∑==+-=-=

n

i n

i i

i

i i

bx a y y

y

L 1

1

2

2

?达到最小，令：

可以得到以下一组联立方程：

解该方程组，得到β的最小二乘估计：

及a 的最小二乘估计：

公式的分子部分称为X 和Y 的校正交叉乘积和，以S XY 表示。分母部分称为X 的校正平方和，以S XX 表示。因变量Y 的 平方和称为总平方和，以S YY 表示。因此，b 又可以表示为：

10.2.4 回归方程的计算

??????

?=??=??00b

L a l

()()[]()()[]???????=+--=+--∑∑==n i i i i n

i i i bx a y x bx a y 1

10202XX

XY

S S b =

()()

()

∑∑∑∑

∑∑∑=======---=

???

?

??--

=

n

i i

n

i i i

n i i

n

i i n

i n

i i

n i i

i i

x x

y y x x

n

x x n y

x y x

b 1

2

1

2

1

1

21

1

1

x

b y a -=

由此得出回归方程：

回归系数的含义是：当自变量X 每变动一个单位，因变量Y 平均变动11.16个单位。

X X ’=X-2.4 X ’2

Y Y ’=Y-110 Y ’2

X ’Y ’ 0 -2.4 5.76 80 -30 900 72 0.8 -1.6 2.56 90 -20 400 32 1.6 -0.8 0.64 95 -15 225 12 2.4 0 0 115 5 25 0 3.2 0.8 0.64 130 20 400 16 4.0 1.6 2.56 115 5 25 8 4.8 2.4 5.76 135 25 625 60 和 0

17.92

-10

2600

200

79

.814.216.1157.10816

.1192.1700.20071

.25957

10260092

.177092.17200710

02002

2

=?-=-====--==-===-?-

==''''''x b y a S S b S S S S S S XX XY Y Y YY X X XX Y X XY X Y

16.1179.81?+=

10.3 一元线性回归的检验 10.3.1 b 和a 的数学期望和方差

上式中的σ2是由ε得到的，ε是实际观测值与总体回归估计值的离差i i i x y βαε--=。由于α和β都是未知的，因此无法得到εi ，只能用εi 的估计值e i

，i i i bx a y e --=。∑=n

i i

e

1

2

称为误差平方和即为SS e

()()XX

S b b E 2

var σ

β=

=()()???

? ?

?+==XX S x n a a E 22

1var σ

α

()()()()()[]

()()()()

[

]

XY

YY XY XY YY n

i i i i i n

i i i n i n i n

i i i n i i i i i i e bS S bS bS S x x b x x y y b y y x x b y y bx x b y y bx a y y

y e SS -=+-=-+----=---=-+-=--=-==∑∑∑∑∑∑======22?1

2

22

12

11

1

212

2

可以证明

MS e 是σ2的无偏估计量，因此样本回归系数b 的方差

a 的方差

根据表10－2中的7套重复数据（细线所示），和它们的平均数（粗虚线所示）所绘出的回归线。如果无限增加重复次数，最终将得到一条直线μY ＝α＋βX 。实际上这条直线是无法获得的，只能得到它的估计直线（由一套或几套数据获得），

bX a Y

+=?。这些估计直线是总体回归线的无偏估计。它们有自己的分布，因此有自己的期望和方差。

10.3.2 b 和a 的显著性检验

()2

2σ=??

? ??-=

n SS E MS E e e

XX

e

b

S MS s =

2???

?

??+=XX e a

S

x n MS s

2

21

10.3.2.1 b 的显著性检验

b 的显著性检验原理与第五章所讲的假设检验原理类似。β决定回归线的倾斜程度，当β＝0时两变量间不存在回归关系。b

有自己的分布，

????

??XX S

N b 2

,:σβ。

根据b 的分布，在β＝0这一假设下计算出，获得回归系数为b 的这一事件出现的概率很小，而实际上它却出现了，说明假设的条件不正确，从而拒绝假设。

上面已经说过，σb 2无法得到，只能用s b 2估计，因此需用t 检验。所使用的检验统计量为：

服从n －2自由度的t 分布。因回归系数是由μY.X 的估计值y ?得到的，因此s b 是标准误差，而不是标准差。

例 对前述回归方程的回归系数的显著性作检验。 解 H 0：β＝0 H A ：β≠0 计算MS e ，

检验统计量 61.599

.116

.11===

b s b t t 5,0.005=4.032，t > t 0.005，P < 0.01，拒绝H 0。结论是干物重在NaCl 含量上的回归极显著。

t 检验还可以检验β具有某一给定值的假设。 例 对前述方程的以下假设做检验 H 0：β＝7 H A ：β≠7 检验统计量

b

b b s b

s b s b t =-=-=

00β99.192

.1774

.7074

.705200

16.1171.25852===

=?-=--=XX e b XY YY e S MS s n bS S MS 09

.2716.110=-=-=b t β

t 5,0.025=2.571，t < t 0.025，P >0.05，接受H 0。b 很可能抽自β＝7的总体。 10.3.2.2 a 的显著性检验

检验统计量a

s a t α

-=，在H 0：α＝0的假设下

a

s a

t =, 具n - 2自由度

在H 0：α＝α0的假设下 a

s a t 0

α-=

， 具n - 2自由度 例 对前述方程的a 的显著性做检验 解 H 0: α = 0 H A : α≠0

先计算s a , 计算统计量的值

t 5,0.025=2.571，t > t 5,0.025，P <0.05，拒绝H 0：α＝0。

例 对前述方程的a =100这一假设做检验

解 H 0: α =100 H A : α≠100

s a 在上例中已经求出，计算统计量的值

t 5,0.025=2.571，|t |>t 0.025，P < 0.05，结论是拒绝H 0：α＝100的假设。

73

.592.174.27174.70122=???

? ??+=???? ??+=

XX e a s x n MS s 27.1473

.579.81===a s a t 18.373

.510079.810-=-=-=

a s a t α

10.3.4 一元回归的方差分析

10.3.4.1 无重复时一元回归的方差分析

回归方程方差分析的基本思想与第八章所述方差分析的基本思想是相同的。即将总变差的平方和分解为各个分量的平方和。

从图中可见，()()

y y y

y y y -+-=-??，将等式两边平方，然后对全部n 个点求和。

其中的第三项等于0，因此

等号左边一项是Y 的平方和，称为总校正平方和，记为S YY 。等号右边的第二项称为回归平方和，是由于X 对Y 的线性贡献而产生的平方和，记为SS R 。等号右边的第一项是观测值距回归估计值离差的平方和，称为误差平方和或剩余平方和，记为SS e 。“剩余平方和”的含义是，该平方和表示除了X 对Y 的线性影响外，一切因素对Y

()

()()[]()()()()[]

()()()()∑∑∑∑∑∑======--+-+-=-+--+-=-+-=-n

i i i i n

i i n

i i i n

i i i i i i i n

i i i i n

i i y y y y y y y

y y y y y y y y

y y y y

y y y 1

1

2

1

2

122121

2

??2?????2???()()()∑∑∑===-+-=

-n

i n

i n

i i i i

i

y y y

y

y y

1

1

1

22

2

??

的变差的作用，包括X 对Y 的非线性影响及实验误差等。

S YY 具n – 1自由度，SS R 具1自由度，SS e 具n – 2自由度。由此可以得到相

应的均方。2,-==n SS MS SS MS e e R R ，以及检验统计量,e

R

MS MS F =方差分析的

零假设H 0：β＝0，备择假设H A ：β≠0。当F >F 1,n -2,α时拒绝H 0。在实际计算时，可以利用以下二式求出误差平方和及回归平方和。

SS e ＝S YY －bS xy SS R ＝S YY －SS e ＝bS XY 最后，将计算结果列成方差分析表。

例 对前例的方程做方差分析。

已知 S YY ＝2585.71，S XY ＝200，b ＝11.16。 由此计算出 SS R ＝bS XY ＝11.16×200＝2232，

SS e ＝S YY －bS XY =2585.71－2232=353.71。 将上述结果列成方差分析表 变差来源 平方和 自由度 均 方 F 回归 2232 1 2232 31.55** 剩余 353.71 5 70.74 总和

2585.71

6

**α＝0.01

F >F 1,5,0.01，结果是回归极显著。

10.3.4.2 有重复时的一元回归的方差分析

如果同一自变量，因变量重复观测两次以上，则称为有重复观测。这时误差平方和可以通过重复平方和获得，因此总平方和可以做如下分解：

S YY ＝SS R ＋SS LOF ＋SS pe

其中SS pe 称为纯实验误差平方和，是通过重复观测获得的。SS LOF 称为失拟平方和，是剩余平方和除掉纯实验误差平方和之后的剩余部分，这部分是由于模型选择不当造成的。各项平方和的计算如下：

()

()()

()∑∑∑∑∑∑=??==?

=??==?

?-=-=

-=-=

n

i i i LOF n

i m

j i ij

pe n

i i R n i m

j ij

YY y

y m SS y y

SS y y

m SS y y

S 1

211

2

1

2

11

2

??

设实验共收集i =1,2,…,n 对数据，在每一x i 下做了j =1,2,…,m 次重复，各平方和由以下各式给出

自由度分别为：回归项为1，失拟项为n －2，纯误差项为mn －n ，总和为mn -1。从而得出各项均方。

在作检验时，首先用纯误差均方对失拟均方作检验

如果结果是显著的，可能有以下几个原因：①除X 外，还有其它影响Y 的因素。②模型选择不当，X 、Y 之间可能是非线性关系。③X 和Y 无关。这时没有必要用SS LOF 对MS R 做检验。

若结果是不显著的，说明失拟平方和基本是由实验误差造成的，这时需将失拟平方和与纯误差平方和合并，用合并的平方和对回归平方和做检验。

若检验的结果仍不显著，可能的原因有：①X 和Y 不存在回归关系。②实验误差过大。

例 以10.2节所给出的前两次重复为例，做方差分析。

NaCl 含量 0 0.8 1.6 2.4 3.2 4.0 4.8 干 重复I 80 90 95 115 130 115 135 重

重复II 100

85

89

94

106

125

137

和

∑=m

j ij y 1

2

16400 15325 16946 22061 28136 28850 36994 164712

2

1??

? ??∑=m j ij y 32400 30625 33856 43681 55696 57600 73984 327842

由以上数据计算出回归方程：X

Y

22.1032.82?+=，以及S YY ＝4853.71和

pe

LOF MS MS F =

pe

LOF pe

LOF R

df df SS SS MS F ++=

SS R ＝3744.61。纯误差平方和

代入上表右下角数字，得00.7912

327842

164712=-=pe

SS 。失拟平方和

SS LOF ＝S YY －SS R －SS pe ＝4853.71－3744.61－791.00＝318.10。将以上结果列成方差分析表： 变差来源

平方和 自由度 均 方 F 回 归 3744.61 1 3744.61 40.52 失 拟 318.10 5 63.62 0.56 纯误差 791.00 7 113.00 总 和

4853.71

13

对失拟做检验的结果，F ＝0.56。将失拟平方和与误差平方和合并后对回归做检验的结果F ＝40.52。F >F 0.01，Y 与X 存在极显著的回归关系。 10.3.6 一元回归分析的意义 1、预报 2、减少实验误差 10.4 一元非线性回归 10.4.2 对数变换

例 用X 射线照射大麦种子，记处理株第一叶平均高度占对照株高度的百分数为X ，存活百分数为Y ，得到以下结果。

X 28 32 40 50 60 72 80 80 85 Y

8

12

18

28

30

55

61

85

80

在直角坐标纸上做成的散点图和线性回归线如下：

()

∑∑∑∑∑∑======?

???

? ??-=-=n

i m

j n

i m j ij ij

n i m

j i ij pe y m y y y SS 1112

1

2

11

2

1

可以明显看出用直线拟合散点是不合适的。为了能够以直线拟合散点，对X和Y进行坐标变换，取X’=lg X，Y’=lg Y，重新作图如下：

这时可按直线回归，求出线性方程：

将X ’=lg X ，Y ’=lg Y 代入上式，经整理得到如下回归方程：

例 钩虫病人的重复治疗次数X 和复查阳性率Y 如下表： 治疗次数 X 1

2

3

4

5

6 7 8 复查阳性率 Y 63.9 36.0 17.1 10.5 7.3

4.5

2.8

1.7

散点图如下：

X Y

'+-='9928.19577.1?9928.1011.0?X Y

=

从散点图可见，Y 和X 显然不是线性关系，很可能呈指数函数关系。令Y '=ln Y ，变换后的散点图可用直线拟合，求出

Y ’和X 的线性方程

X Y 506248.0526053.4?-='，以ln Y 代替Y '?，整理后得到以下回归方程：

X e Y 506248.0526053.4?-=

图中的实线就是根据该方程绘出的。 10.4.3 概率对数变换

在寻找半致死剂量时，常用到这种变换。

例 用不同剂量的γ射线照射小麦品种库班克调查死苗率，得到以下结果： 剂量(Kr)X 14 16 18 20 22 24 26 死苗率(%)Y 6

10

40

70

80

93

95

散点图和拟合曲线如下：

上图为一S形曲线，曲线的下半部比较陡峭，上半部比较平缓。将剂量X作对数变换，变换后的图形，成为对称的S形曲线。

该曲线的形状与正态分布累积分布曲线的形状是一样的。因此，只要把死亡率的百分率坐标变换为概率坐标，S形曲线便化作为直线。有时为了防止出现负值，将变换后的每一个值都加上5。当然，不做这样处理也可以。

本例中，剂量是自变量，死亡率是因变量，因此剂量为横坐标，死亡率为纵坐标。但是在计算半致死剂量时，要求在死亡50％时的剂量，这时经常将死亡率作为横坐标，剂量作为纵坐标。经概率坐标变换的图形如下：

于是可以得到一个线性方程，X b a Y '+='

?。在半致死剂量处，X ＝50，X ’＝

0，回归方程变为a Y ='?。半致死剂量LD 50

可由下式得到：a Y 10?=。上例经

变换后所得回归方程为：

半致死剂量的估计为：

92.1810?277.1==Y 。 10.4.5 曲线拟合优劣的检验

10.4.5.1 通过比较剩余均方来判断曲线拟合好坏

对于一个未知的曲线，可以用几种不同的方法拟合。在几种不同的拟合曲线中，必然有一种是最好的。为了得到最优拟合曲线，可以计算各种拟合曲线的剩余平方和，哪一个剩余平方和最小，哪一个就是最优拟合。但在计算剩余平方和时一定要用实测点与回归估计点离差的平方和来计算，这一点至关重要。 10.4.5.2 根据失拟均方的大小判断曲线拟合优劣

对于有重复的实验数据，可以采取多种方法直线化，求出直线方程，按有重复

X Y

'+='075.0277.1?

实验方差分析方法进行分析。用纯误差均方对失拟均方做检验，所得F 值不显著的拟合最好。

10.4.5.3 根据相关指数做判断

相关指数记为R 2。 YY

2

S 1剩余SS R

-

=

在计算上式的SS 剩余时，不能使用变换后的X ’和Y ’根据Y X Y Y e bS S SS '

'''-=来计算，而应由实测值与回归估计值之差的平方和来计算。R 2越大拟合的越好。 10.5 相 关 10.5.1 相关系数

由回归所引起的变差占总变差分数的平方根称为相关系数。

10.5.2 相关系数的性质

相关系数的平方

r 2只能小于等于1，或|r |≤1。当0

10.5.3 相关系数的计算 （略） 10.5.4 相关系数的检验

利用相关系数检验表检验相关系数的显著性。对于简单相关系数，附表12中的独立自变量的个数为1，相关系数检验的自由度为剩余自由度，即n －2。当相关系数大于表中给出的值时，相关显著。回归系数的显著性，也可通过相关系数的显著性做检验。

YY

XX XY YY

XX XY

YY

XY

YY R

S S S S S S S bS S SS r =

===

2YY

e YY e YY YY XX XY

S SS S SS S S S S r -

=-==12

2