
一、初一数学几何模型部分解答题压轴题精选(难)
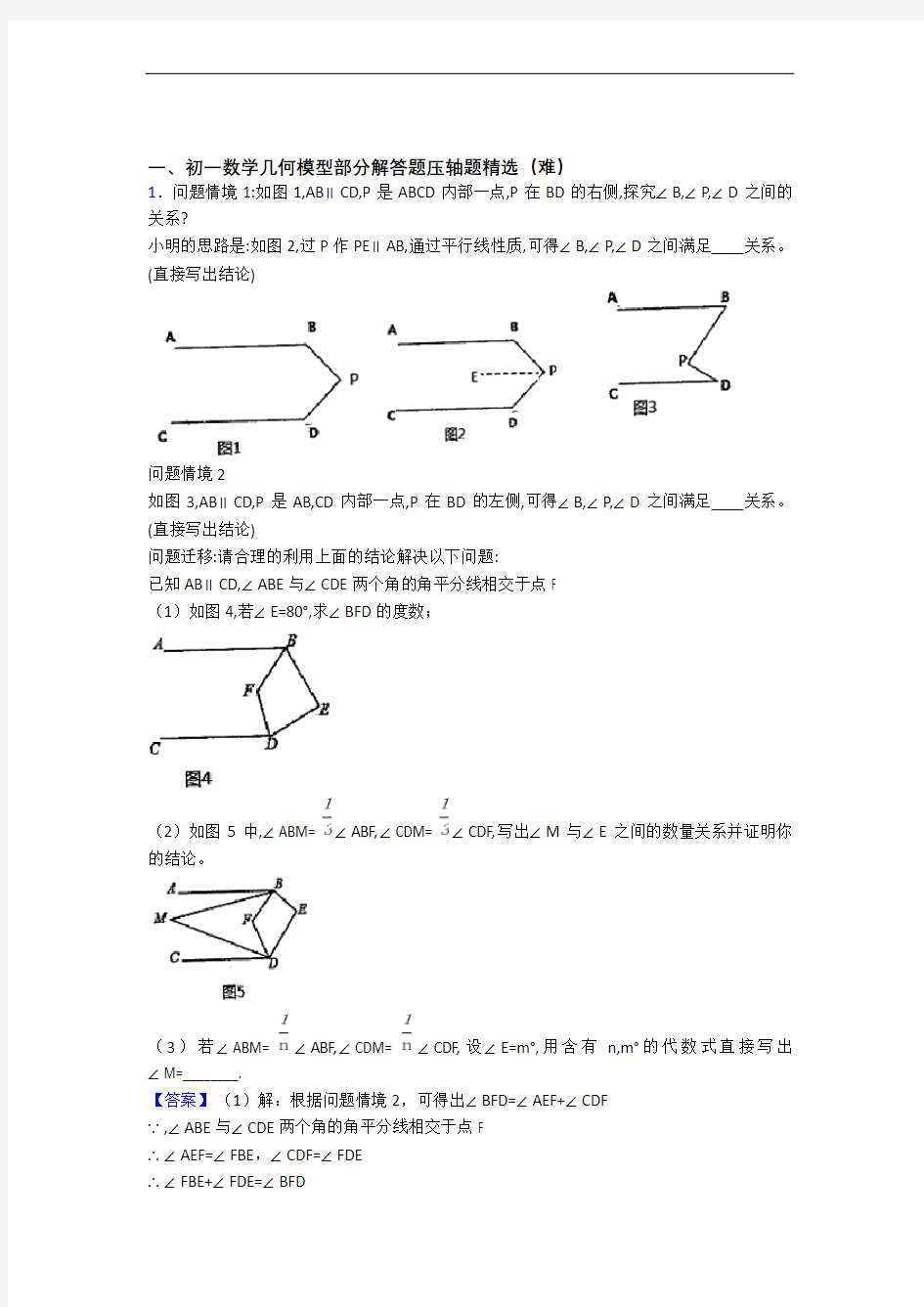
1.问题情境1:如图1,AB∥CD,P是ABCD内部一点,P在BD的右侧,探究∠B,∠P,∠D之间的关系?
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠B,∠P,∠D之间满足____关系。(直接写出结论)
问题情境2
如图3,AB∥CD,P是AB,CD内部一点,P在BD的左侧,可得∠B,∠P,∠D之间满足____关系。(直接写出结论)
问题迁移:请合理的利用上面的结论解决以下问题:
已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F
(1)如图4,若∠E=80°,求∠BFD的度数;
(2)如图5中,∠ABM= ∠ABF,∠CDM= ∠CDF,写出∠M与∠E之间的数量关系并证明你的结论。
(3)若∠ABM= ∠ABF,∠CDM= ∠CDF,设∠E=m°,用含有n,m°的代数式直接写出∠M=________.
【答案】(1)解:根据问题情境2,可得出∠BFD=∠AEF+∠CDF
∵,∠ABE与∠CDE两个角的角平分线相交于点F
∴∠AEF=∠FBE,∠CDF=∠FDE
∴∠FBE+∠FDE=∠BFD
∵∠E+∠BFD+∠FBE+∠FDE=360°
∴80°+∠BFD+∠BFD=360°
∴∠BFD=140°
(2)结论为:6∠M+∠E=360°
证明:∵∠ABM= ∠ABF,∠CDM= ∠CDF
∴∠ABF=3∠ABM,∠CDF=3∠CDM
∵∠ABE与∠CDE两个角的角平分线相交于点F
∴∠ABE=6∠ABM,∠CDE=6∠CDM
∵∠ABE+∠CDE+∠E=360°
∴6(∠ABM+∠CDM)+∠E=360°
∵∠M=∠ABM+∠CDM
∴6∠M+∠E=360°
(3)证明:根据(2)的结论可知
2n∠ABM+2n∠CDM+∠E=360°
2n(∠ABM+∠CDME)+∠E=360°
∵∠M=∠ABM+∠CDM
∴2n∠M+m°=360°
∴∠M=
【解析】问题情境1: 图1中∠B,∠P,∠D之间关系是:∠P+∠B+∠D=360°,问题情境2:图3中∠B,∠P,∠D之间关系是:∠P=∠B+∠D;
【分析】问题情境1和2 过点P作EP∥AB,利用平行线的性质,可证得结论。
(1)利用问题情境2的结论,可得出∠BFD=∠AEF+∠CDF,再根据角平分线的定义得出∠AEF=∠FBE,∠CDF=∠FDE,再证明∠E+∠BFD+∠FBE+∠FDE=360°,就可建立方程80°+∠BFD+∠BFD=360°,解方程求出∠BFD的度数即可。
(2)根据已知可得出∠ABF=3∠ABM,∠CDF=3∠CDM,再根据角平分线的定义得出,∠ABE=6∠ABM,∠CDE=6∠CDM,然后根据问题情境1的结论∠ABE+∠CDE+∠E=360°,可推出6(∠ABM+∠CDM)+∠E=360°,变形即可证得结论。
(3)根据已知得出2n∠ABM+2n∠CDM+∠E=360°,再根据∠M=∠ABM+∠CDM,代入变形即可得出结论。
2.如图(1),将两块直角三角板的直角顶点C叠放在一起.
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
【答案】(1)解:∠ACE=∠BCD,理由如下:
∵∠ACD=∠BCE=90°,∠ACE+∠ECD=∠ECB+∠ECD=90°,
∴∠ACE=∠BCD
(2)解:若∠DCE=30°,∠ACD=90°,
∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°,
∵∠BCE=90°且∠ACB=∠ACE+∠BCE,
∠ACB=90°+60°=150°
(3)解:猜想∠ACB+∠DCE=180°.理由如下:
∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°
(4)解:成立
【解析】【分析】(1)根据同角的余角相等即可求证;
(2)根据余角的定义可先求得∠ACE=∠ACD-∠DCE,再由图可得∠ACB=∠ACE+∠BCE,把∠ACE和∠BCE 的度数代入计算即可求解;
(3)由图知,∠ACB=∠ACD+∠BCE-∠ECD,则∠ACB+∠ECD=∠ACD+∠BCE,把∠ACD和∠BCE的度数代入计算即可求解;
(4)根据重叠的部分实质是两个角的重叠可得。。
3.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,另一边ON仍在直线AB
的下方.
(1)若OM恰好平分∠BOC,求∠BON的度数;
(2)若∠BOM等于∠COM余角的3倍,求∠BOM的度数;
(3)若设∠BON=α(0°<α<90°),试用含α的代数式表示∠COM.
【答案】(1)解:∵∠BOC=120°,OM恰好平分∠BOC
∴∠BOM=∠BOC=60°
又∵∠MON=90°
∴∠BON=∠MON?∠BOM
=90°?60°=30°
(2)解:设的余角为x°,
则
由题意得:,
x=15,
3x=45,
所以的度数为45°
(3)解:(0°< <90°).
.
【解析】【分析】(1)利用角平分线的定义求出∠BOM的度数,再根据∠BON=∠MON?∠BOM,即可求出结果。
(2)设∠ C O M 的余角为x°,表示出∠COM的度数,再根据∠BOM=∠COM余角的3倍,建立方程求解即可。
(3)根据角的和与差计算即可。
4.根据下图回答问题:
(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,G为线段AC上一定点,点H为直线CD上一动点且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外)∠CGH+∠CHG与∠BAC有何数量关系?猜想结论并说明理由.
【答案】(1)∵CM平分∠ACD,AM平分∠BAC,
∴∠BAC=2∠MAC,∠ACD=2∠ACM,
∵∠MAC+∠ACM=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAM+∠MCD=90°,
理由:如图,过M作MF∥AB,
∵AB∥CD,
∴MF∥AB∥CD,
∴∠BAM=∠AMF,∠FMC=∠DCM,
∵∠M=90°,
∴∠BAM+∠MCD=90°;
(3)∠BAC=∠CHG+∠CGH.
理由:过点G作GP∥AB,
∵AB∥CD
∴GP∥CD,
∴∠BAC=∠PGC,∠CHG=∠PGH,
∴∠PGC=∠CHG+∠CGH,
∴∠BAC=∠CHG+∠CGH.
【解析】【分析】(1)已知CM平分∠ACD,AM平分∠BAC,根据角平分线的定义可得∠BAC=2∠MAC,∠ACD=2∠ACM,再由∠MAC+∠ACM=90°,即可得∠BAC+∠ACD=180°,根据同旁内角互补,两直线平行即可得AB∥CD;(2)∠BAM+∠MCD=90°,过M作MF∥AB,即可得MF∥AB∥CD,根据平行线的性质可得∠BAM=∠AMF,∠FMC=∠DCM,再由∠M=90°,即可得∠BAM+∠MCD=90°;(3)∠BAC=∠CHG+∠CGH,过点G作GP∥AB,即可得GP∥CD,根据平行线的性质可得∠BAC=∠PGC,∠CHG=∠PGH,所以PGC=∠CHG+∠CGH,即可得∠BAC=∠CHG+∠CGH.
5.已知,与两角的角平分线交于点P,D是射线上一个动点,过点D的直线分别交射线,,于点E,F,C.
(1)如图1,若,,,求的度数;
(2)如图2,若,请探索与的数量关系,并证明你的结论;
(3)在点运动的过程中,请直接写出,与这三个角之间满足的数量关系:________.
【答案】(1)解:∵PA、PB是∠BAM、∠ABN的角平分线,
∴∠BAP=∠PAE= ∠BAM= ,
∠ABP=∠PBE= ∠ABN= ,
∴∠BPC=∠BAP+∠ABP= ;
(2)解:,理由如下:
∵PA、PB是∠BAM、∠ABN的角平分线,
∴设,,
∵,
∴,
∵,
∴,
又∵,
∴,
∴;
(3)
【解析】【解答】解:(3)∵PA、PB是∠BAM、∠ABN的角平分线,
∴设,,
∵,
∴,
如图,当点P在线段BD上时,
,
∴;
如图,当点P在线段BD的延长线上时,
,即,
∴,
即;
故答案为:.
【分析】(1)根据角平分线的性质结合三角形外角的性质即可求解;
(2)设,,根据角平分线的性质结合四边形内角和定理即可求解;
(3)分点P在线段BD上和点P在线段BD的延长线上两种情况讨论即可求解.
6.如图,已知DC∥FP,∠1=∠2,∠FED=28°,∠AGF=80°,FH平分∠EFG.
(1)说明:DC∥AB;
(2)求∠PFH的度数.
【答案】(1)证明:∵DC∥FP,
∴∠3=∠2,又∵∠1=∠2,∴∠3=∠1,
∴DC∥AB
(2)解:∵DC∥FP,DC∥AB,∠DEF=30°,
∴∠DEF=∠EFP=30°,AB∥FP,
又∵∠AGF=80°,
∴∠AGF=∠GFP=80°,
∴∠GFE=∠GFP+∠EFP=80°+30°=110°,
又∵FH平分∠EFG,
∴∠GFH= ∠GFE=55°,
∴∠PFH=∠GFP﹣∠GFH=80°﹣55°=25°
【解析】【分析】(1)根据二直线平行,同位角相等得出,又∠1=∠2,故∠1=∠3,根据同位角相等,两直线平行得出DC∥AB;
(2)根据平行于同一直线的两条直线互相平行得出AB∥FP,根据二直线平行,内错角相等得出,,根据角的和差,由
算出∠GFE的度数,根据角平分线的定义得出∠GFH的度数,最后根据即可算出答案。
7.如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN.
(1)求∠ABN的度数
(2)当点P运动时,∠CBD的度数是否随之发生变化?若不变化,请求出它的度数。若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数。
【答案】(1)证明:∵AM//BN
∴∠A+∠ABN=180°
∵∠A=60°
∴∠ABN=180°?∠A=180°?60=120°
(2)解:如图,
没有变化。
∵CB平分∠ABP, BD平分∠PBN
∴∠1= ∠ABP, ∠2= ∠PBN
∴∠CBD=∠1 +∠2 = ∠ABP+∠PBN)
= ×1200=600
(3)解:如图,
∵AM//BN
∴∠ACB=∠CBN
∵∠ACB=∠ABD
∴∠CBN=∠ABD
∴∠CBN?∠CBD=∠ABD?∠CBD
即∠1=∠4
又∵CB平分∠ABP, BD平分∠PBN
∴∠1=∠2 ∠3=∠4
∴∠1=∠2=∠3=∠4=120°÷4=30°
即∠ABC=30°
【解析】【分析】(1)根据两直线平行,同旁内角互补即可求出答案;
(2)根据角平分线的性质以及角度相加减即可得证;
(3)根据两直线平行,同旁内角互补以及已知条件得到∠CBN=∠ABD,根据角度的相加减得到∠1=∠4,再根据角平分线的性质得到∠1=∠2=∠3=∠4,最后根据∠ABN=120°即可得到答案.
8.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断AB与CD的位置关系,并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD.当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?并说明理由;(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外),∠CPQ+∠CQP与∠BAC有何数量关系?直接写出结论,其数量关系为________.
【答案】(1)解:AB∥CD;理由如下:
∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD
(2)解:∠BAE+∠MCD=90°;理由如下:
过E作EF∥AB,如图2所示:
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠AEC=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD
∴∠ECD=∠MCD
∴∠BAE+∠MCD=90°
(3)∠BAC=∠CPQ+∠CQP
【解析】【解答】解:(3)∠BAC=∠CPQ+∠CQP;理由如下:
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠CPQ+∠CQP+∠PCQ=180°,
即(∠CPQ+∠CQP)+∠ACD=180°,
∴∠BAC=∠CPQ+∠CQP.
故答案为:∠BAC=∠CPQ+∠CQP.
【分析】(1)由角平分线的性质得出∠BAC=2∠EAC,∠ACD=2∠ACE,推出∠BAC+∠ACD=180°,即可得出结论;
(2)过E作EF∥AB,则EF∥AB∥CD,得出∠BAE=∠AEF,∠FEC=∠DCE,由∠AEC=
90°,推出∠BAE+∠ECD=90°,∠ECD=∠MCD,得出∠BAE+∠MCD=90°;
(3)由平行线的性质得出∠BAC+∠ACD=180°,由三角形内角和定理得出∠CPQ+∠CQP +∠PCQ=180°,即可得出结果.
9.如图,直线,点E、F分别是AB、CD上的动点(点E在点F的右侧);点M为线段EF上的一点,点N为射线FD上的一点,连接MN;
(1)如图1,若,,则 ________;
(2)作的角平分线MQ,且,求与之间的数量关系;(3)在(2)的条件下,连接EN,且EN恰好平分,;求的度数.
【答案】(1)60°
(2)解:如图,
∵,
∴∠EMQ=∠AEF,
∵,AB∥CD,
∴MQ∥CD,
∴∠NMQ=∠MNF,
∵MQ平分∠EMN,
∴∠EMQ=∠NMQ,
∴ = ;
(3)解:设∠ENM=x,则∠MNF=2x,
∴∠ENF=3x,
∵AB∥MQ,
∴∠BEN=∠ENF=3x,
∵EN平分∠BEF,
∴∠BEF=2∠BEN=6x,
∵∠AEF=∠MNF=2x,∠AEF+∠BEF=180°,
∴2x+6x=180°,
解得x=22.5°,
∴,∠EFN=∠AEF=∠MNF=45°,∴∠EMN=∠EFN+∠MNF=90°.
【解析】【解答】解:(1)∵AB∥CD,
∴∠BEF+∠EFD=180°,
∵ ,
∴∠EFD=30°,
∵,
∴∠NMF=90°,
∴∠MNF=180°-∠NMF-∠EFD=60°,
故答案为:60°;
【分析】(1)根据AB∥CD得到∠BEF+∠EFD=180°,由求出∠EFD=30°,
根据得到∠NMF=90°,再利用三角形的内角和定理得到∠MNF=180°-∠NMF-
∠EFD=60°;(2)根据得到∠EMQ=∠AEF,由,AB∥CD推出MQ∥CD,证得∠NMQ=∠MNF,根据角平分线的性质得到∠EMQ=∠NMQ,即可得到 =
;(3)设∠ENM=x,则∠MNF=2x,根据AB∥MQ得到∠BEN=∠ENF=3x,由EN平分∠BEF,证得∠BEF=2∠BEN=6x,再根据∠AEF=∠MNF=2x,∠AEF+∠BEF=180°,列式求出x=22.5°,即可求出∠EMN=∠EFN+∠MNF=90°.
10.如图1,将一副直角三角板的两顶点重合叠放于点O,其中一个三角板的顶点C落在另一个三角板的边OA上,已知∠ABO=∠DCO=90°,∠AOB=45°,∠COD=60°作∠AOD的平分线交边CD于点E。
(1)求∠BOE的度数。
(2)如图2,若点C不落在边OA上,当∠COE=15°时,求∠BOD的度数。
【答案】(1)解:∵∠COD=60°,OE为∠COD的平分线,
∴∠COE=30°,
∴∠BOE=∠AOB+∠COE
=45°+30°
=75°;
(2)解:∵∠COE=15°,
∴∠DOE=∠DOC-∠OCE=60°-15°=45°,
∵OE平分∠AOD,
∴∠AOD=2∠DOE=2×45°=90°,
∴∠BOD=∠AOD+∠AOB=90°+45°=135°.
【解析】【分析】(1)OE为∠COD的平分线,求出∠COE的度数,则∠BOE的度数等于∠AOB和∠COE的度数之和;
(2)现知∠COE的度数,则∠DOE度数可求,结合OE平分∠AOD,则∠AOD可求,于是∠BOD的度数可得;
11.如图①,点为直线上一点,过点作射线,使,将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的上方.
(1)在图①中, ________度;
(2)将图①中的三角板绕点按逆时针方向旋转,使得在的内部,如图②,若,求的度数;
(3)将图①中的三角板绕点以每秒的速度沿逆时针方向旋转一周,在旋转的过程中,当直线恰好平分锐角时,旋转的时间是________秒.(直接写出结果)
【答案】(1)30
(2)解:设∠BON=α,
∵∠BOC=60°,
∴∠NOC=60°-α,
∵∠MON=90°,
∴∠MOC=∠MON-∠NOC=90°-60°+α=30°+α,
∠MOA=180°-∠MON-∠BON=180°-90°-α=90°-α,
∵∠NOC= ∠MOA,
∴60°-α= (90°-α),
解得:α=54°,
即∠BON=54°;
(3)3或21
【解析】【解答】(1)∵将一直角三角板的直角顶点放在点O处,一边ON在射线OB 上,另一边OM在直线AB的上方,
∴∠MON=90°,
∴∠COM=∠MON-∠BOC=90°-60°=30°,(3)∵直线ON平分∠BOC,∠BOC=60°,
∴∠BON=30°或∠BON=210°,
∵三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,
∴直线ON平分∠BOC时,旋转的时间是3或21秒,
故答案为:3或21.
【分析】(1)由题意得出∠MON=90°,得出∠COM=∠MON-∠BOC=90°-60°=30°;(2)设∠BON=α,则∠NOC=60°-α,∠MOC=∠MON-∠NOC=90°-60°+α=30°+α,∠MOA=180°-
∠MON-∠BON=180°-90°-α=90°-α,由题意得出60°-α= (90°-α),解得α=54°即可;(3)求出∠BON=30°或∠BON=210°,即可得出答案.
12.以直线上点为端点作射线,使,将直角的直角顶点放在点处.
(1)若直角的边在射线上(图①),求的度数;
(2)将直角绕点按逆时针方向转动,使得所在射线平分(图②),说明所在射线是的平分线;
(3)将直角绕点按逆时针方向转动到某个位置时,恰好使得(图③),求的度数.
【答案】(1)解:∵,
又∵,
∴ .
(2)解:∵平分,
∴,
∵,
∴,,
∴,
∴所在直线是的平分线.
(3)解:设,则,
∵,,
①若∠COD在∠BOC的外部,
∴,解得x=10,
∴∠COD=10°,
∴∠BOD=60°+10°=70°;
②若∠COD在∠BOC的内部,
,解得x=30,
∴∠COD=30°,
∴∠BOD=60°-30°=30°;
即或,
∴或 .
【解析】【分析】(1)代入∠BOE=∠COE+∠COB求出即可;(2)求出∠AOE=∠COE,根据∠DOE=90°求出∠AOE+∠DOB=90°,∠COE+∠COD=90°,推出∠COD=∠DOB,即可得出答案;(3)要分情况讨论,一种是∠COD在∠BOC的内部,另一种是∠COD在∠BOC的外部,再根据平角等于180°可通过列方程求出即可.