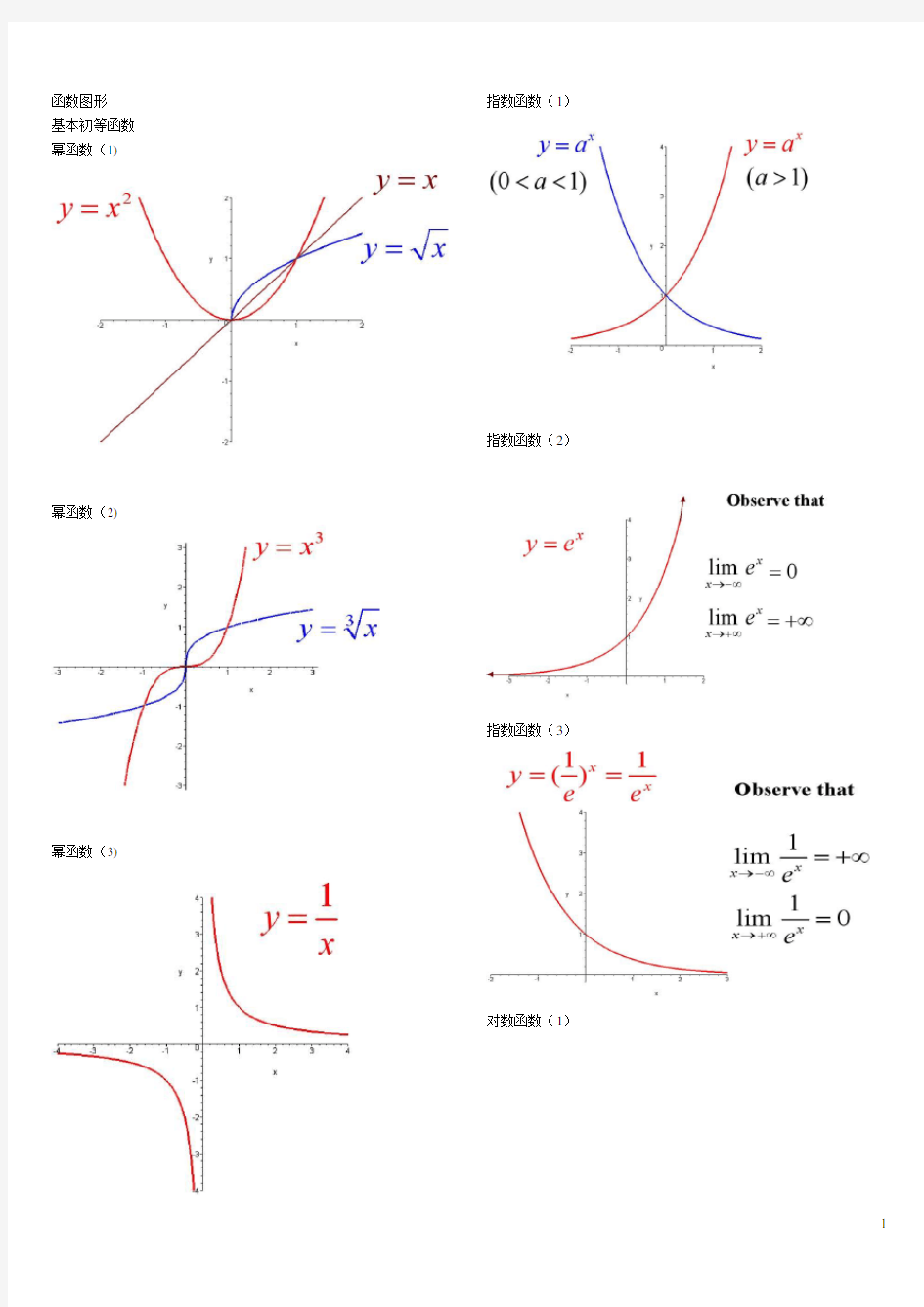
函数图形 基本初等函数 幂函数(
1)
幂函数(
2)
幂函数(
3)
指数函数(1)
指数函数(2)
指数函数(3)
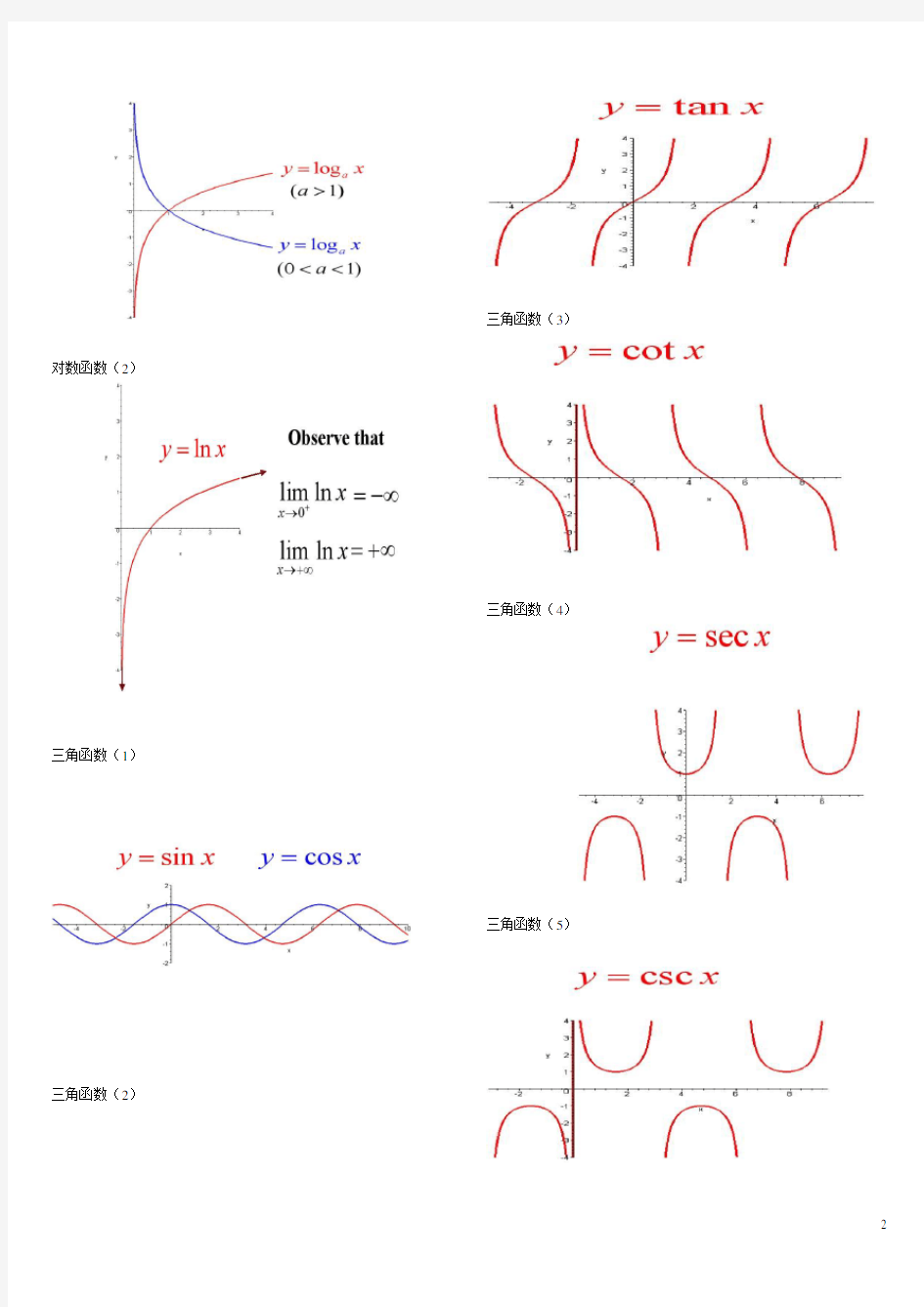
对数函数(1)
对数函数(2)
三角函数(1)
三角函数(2)
三角函数(3)
三角函数(4)三角函数(5)
反三角函数(1)
反三角函数(2)
反三角函数(3)
反三角函数(4)
反三角函数(5)
反三角函数(6)
反三角函数(7)
反三角函数(8)
双曲函数(1)
双曲函数(2)
双曲函数(3)
双曲函数(4)
双曲函数(5)
双曲函数(6)
双曲函数(7)
反双曲函数(1)
反双曲函数(2)
反双曲函数(3)
反双曲函数(4)
反双曲函数(5)
反双曲函数(6)
y=sin(1/x) (1)
y=sin(1/x) (2)
y=sin(1/x) (3)
y=sin(1/x) (4)
y = [1/x](1)
y = [1/x](2)
y=21/x
y=21/x (2)
y=xsin(1/x)
y=arctan(1/x) y=e1/x
y=sinx (x->∞)
绝对值函数 y = |x|
符号函数 y = sgnx
取整函数 y= [x]
极限的几何解释
(1)
极限的几何解释
(2)
极限的几何解释
(3)
极限的性质 (1) (局部保号性)
极限的性质 (2) (局部保号性
)
极限的性质 (3) (不等式性质
)
极限的性质 (4) (局部有界性
)
极限的性质 (5) (局部有界性
)
两个重要极限
y=sinx/x (1)
y=sinx
/x (2)
limsinx/x 的一般形式
y=(1+1/x)^x (1)
y=(1+1/x)^x (2)
lim(1+1/x)^x 的一般形式
(1)
lim(1+1/x)^x 的一般形式
(2)
lim(1+1/x)^x 的一般形式
(3)
e 的值(1)
等价无穷小 (x->0)
sinx 等价于x
arcsinx 等价于
x
tanx 等价于
x
arctanx 等价于x
1-cosx 等价于
x^2/2
sinx 等价于x
数列的极限的几何解释
海涅定理
渐近线
水平渐近线
铅直渐近线
y=(x+1)/(x-1)
y=sinx/x (x->∞
) 夹逼定理(1)
夹逼定理
(2)
数列的夹逼性
(1)
数列的夹逼性
(2)
pi 是派的意思(如果你没有切换到公式版本) ^是次方的意思,
$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了
高中数学常见函数图像1. 2.对数函数:
3.幂函数: 定义形如αx y=(x∈R)的函数称为幂函数,其中x是自变量,α是常数. 图像 性质过定点:所有的幂函数在(0,) +∞都有定义,并且图象都通过点(1,1).单调性:如果0 α>,则幂函数的图象过原点,并且在[0,) +∞上为增函数.如果0 α<,则幂函数的图象在(0,) +∞上为减函数,在第一象限内,图象无限接近x轴与y轴.
函数 sin y x = cos y x = tan y x = 图象 定义域 R R ,2x x k k ππ??≠+∈Z ???? 值域 []1,1- []1,1- R 最值 当 22 x k π π=+ () k ∈Z 时, max 1y =; 当22 x k π π=- ()k ∈Z 时,min 1y =-. 当()2x k k π =∈Z 时, max 1y =; 当2x k π π=+ ()k ∈Z 时,min 1y =-. 既无最大值也无最小值 周期性 2π 2π π 奇偶性 奇函数 偶函数 奇函数 单调性 在 2,222k k ππππ? ?-+???? ()k ∈Z 上是增函数;在 32,222k k π πππ??++???? ()k ∈Z 上是减函数. 在[]() 2,2k k k πππ-∈Z 上 是 增 函 数 ; 在 []2,2k k πππ+ ()k ∈Z 上是减函数. 在,2 2k k π ππ π? ? - + ?? ? ()k ∈Z 上是增函数. 对称性 对称中心 ()(),0k k π∈Z 对称轴 ()2 x k k π π=+ ∈Z 对称中心 (),02k k ππ??+∈Z ?? ? 对称轴()x k k π =∈Z 对称中心(),02k k π?? ∈Z ??? 无对称轴
函数与图形经典好题 一、选择题 1、若一次函数y=kx+1与两坐标轴围成的三角形面积为3,则k 为( ) A 、16 B 、-16 C 、±16 D 、±13 2、若 11m n -=3, 2322m mn n m mn n +---的值是( ) A 、1.5 B 、35 C 、-2 D 、-75 3、判断下列真命题有( ) ①任意两个全等三角形可拼成平行四边形②两条对角线垂直且相等的四边形是正方形③四边形ABCD ,AB=BC=CD ,∠A=90°,那么它是正方形④在同一平面内,两条线段不相交就会平行⑤有一条对角线平分一个内角的平行四边形是菱形 A 、②③ B 、①②④ C 、①⑤ D 、②③④ 4、如图,矩形ABCD 中,已知AB=5,AD=12,P 是AD 上的动点,PE ⊥AC ,E,PF ⊥BD 于F,则PE+PF=( ) A 、5 B 、6013 C 、245 D 、55 12 5、在直角坐标系中,已知两点A (-8,3)、B (-4,5)以及动点C (0,n )、D(m,0),则当四边形ABCD 的周长最小时,比值为 m n ( ) A 、-23 B 、-32 C 、-34 D 、34 二、填空题 6、当x= 时, ||3x x -与3x x -互为倒数。9、已知x 2 -3x+1=0,求(x-1 x ) 2 = 7、一个人要翻过两座山到另外一个村庄,途中的道路不是上山就是下山,已知他上山的速度为v ,下山的速度为v ′,单程的路程为s .则这个人往返这个村庄的平均速度为 8、将点A (4,0)绕着原点O 顺时针方向旋转30°角到对应点 A ',则点A '的坐标是 9、菱形ABCD 的一条对角线长为6,边AB 的长是方程(X-3)(X-4)=0的解,则菱形ABCD 的周长为 10、△ABC 中,∠A=90°,AB=AC ,BD 是△ABC 的中线,△CDB 内以CD 为边的等腰直角三角形周长是 11. 如图,边长为6的菱形ABCD 中,∠DAB=60°,AE=AB ,F 是AC?上一动点,EF+BF 的最小值为 12、如图,边长为3的正方形ABCD 顺时针旋转30°,得上图,交DE 于D ’,阴影部分面积是
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C(其中C 为常数); α
1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称; 2)当α为负整数时。函数的定义域为除去x=0的所有实数; 3)当α为正有理数 n m 时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1); 4)如果m>n 图形于x 轴相切,如果m 3.(选,补充)指数函数值的大小比较* N ∈a ; a.底数互为倒数的两个指数函数 x a x f =)(, x a x f ? ? ? ??=1)( 的函数图像关于y 轴对称。 b.1.当1>a 时,a 值越大,x a y = 的图像越靠近y 轴; b.2.当10<∈>=n Z n m a a a n m n m (2)) 1,,,0(1 1*>∈>= =- n Z n m a a a a n m n m n m y x f x x x x g ? ? ?=1)( 一次函数与几何图形综合专题 思想方法小结: (1)函数方法. 函数方法就是用运动、变化的观点来分析题中的数量关系,抽象、升华为函数的模型,进而解决有关问题的方法?函数的实质是研究两个变量之间的对应关系,灵活运用函数方法可以解决许多数学问题. (2)数形结合法. 数形结合法是指将数与形结合,分析、研究、解决问题的一种思想方法,数形结合法在解决与函数有关的问题时,能起到事半功倍的作用. 知识规律小结: (1)常数k,b对直线y=kx+b(k工0)位置的影响. ①当b>0时,直线与y轴的正半轴相交; 当b=0时,直线经过原点; 当b< 0时,直线与y轴的负半轴相交. ②当k,b异号时,即-b> 0时,直线与x轴正半轴相交; k 当b=0时,即-b =0时,直线经过原点; k 当k,b同号时,即-b< 0时,直线与x轴负半轴相交. k ③当k>O, b>O时,图象经过第一、二、三象限; 当k>0,b=0时,图象经过第一、三象限; 当b>O, b< O时,图象经过第一、三、四象限; 当k< O, b>0时,图象经过第一、二、四象限; 当k< O, b=0时,图象经过第二、四象限; 当b< O, b< O时,图象经过第二、三、四象限. (2)直线y=kx+b (k工0)与直线y=kx(k工0)的位置关系. 直线y=kx+b(k工0)平行于直线y=kx(k工0) 当b>0时,把直线y=kx向上平移b个单位,可得直线y=kx+b; 当b< O时,把直线y=kx向下平移|b|个单位,可得直线y=kx+b . (3)直线与直线y2=k2X+b2 (匕工0 , k?工0)的位置关系. ①k i工k2:= y i与y2相交; ②k i *2 := y i与y2相交于y轴上同一点(0, b i)或(0, b2); b i =b2 ③k i_k2, := y i 与y2 平行; b i我2 ④ki =k2, := y i 与y2 重合. b i电 例题精讲: i、直线y=-2x+2与x轴、y轴交于A B两点,C在y轴的负半轴上,且OC=OB -i - / i8 五、基本初等函数及其性质和图形 1.幂函数 函数称为幂函数。如,,,都是幂函数。没有统一的定义域,定义域由值确定。如,。但在内总是有定义的,且都经过(1,1 )点。当时,函数在上是单调增加的,当时,函数在内是单调减少的。下面给出几个常用的幂函数:的图形,如图1-1-2、图1-1-3 图1-1-3 2.指数函数 函数称为指数函数,定义域,值域;当时函数为单调增加的;当时为单调减少的,曲线过点。高等数学中常用的指数函数是时,即。以与为例绘出图形,如图1-1-4 。 图1-1-4 3.对数函数 函数称为对数函数,其定义域,值域。当时单调增加,当时单调减少,曲线过(1,0)点,都在右半平面内。与互为反函数。当时的对数函数称为自然对数,当时,称为常用对数。以为例绘出图形,如图1-1-5 。 图1-1-5 4.三角函数有 :|1」 "「. 1” ;■-■? - 它们都是周期函数。对三角函数作简要的叙述: (1)正弦函数与余弦函数:与定义域都是,值域都是。它们都是有界函数,周期都是,为奇函数,为偶函数。图形为图1-1-6、图1-1-7。 图1-1-6 正弦函数图形 图1-1-7 余弦函数图形 (2)正切函数,定义域,值域为。周期,在其定义域内单调增加的奇函数,图形为图1-1-8 (3)余切函数,定义域,值域为,周期。在定义域内是单调减少的奇函数,图形如图1-1-9。 (4)正割函数,定义域,值域为,为无界函数,周期的偶函数,图形如图1-1-10 。 (5)余割函数,定义域,值域为,为无界函数,周期在定义域为奇函数,图形如图1-1-11。 5.反三角函数 反正弦函数,定义域,值域,为有界函数,在其定义域内是单调增加的奇函数,图形如图1-1-12 ; 图1-1-12 高中常用函数性质及图像 一次函数 (一)函数 1、确定函数定义域的方法: (1)关系式为整式时,函数定义域为全体实数; (2)关系式含有分式时,分式的分母不等于零; (3)关系式含有二次根式时,被开放方数大于等于零; (4)关系式中含有指数为零的式子时,底数不等于零; (5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。 (二)一次函数 1、一次函数的定义 一般地,形如y kx b =+(k ,b 是常数,且0k ≠)的函数,叫做一次函数,其中x 是自变量。当0b =时,一次函数y kx =,又叫做正比例函数。 ⑴一次函数的解析式的形式是y kx b =+,要判断一个函数是否是一次函数,就是判断是否能化成以上形式. ⑵当0b =,0k ≠时,y kx =仍是一次函数. ⑶当0b =,0k =时,它不是一次函数. ⑷正比例函数是一次函数的特例,一次函数包括正比例函数. 2、正比例函数及性质 一般地,形如y=kx(k 是常数,k≠0)的函数叫做正比例函数,其中k 叫做比例系数. 注:正比例函数一般形式 y=kx (k 不为零) ① k 不为零 ② x 指数为1 ③ b 取零 当k>0时,直线y=kx 经过三、一象限,从左向右上升,即随x 的增大y 也增大;当k<0时,?直线y=kx 经过二、四象限,从左向右下降,即随x 增大y 反而减小. (1) 解析式:y=kx (k 是常数,k ≠0) (2) 必过点:(0,0)、(1,k ) (3) 走向:k>0时,图像经过一、三象限;k<0时,?图像经过二、四象限 (4) 增减性:k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小 (5) 倾斜度:|k|越大,越接近y 轴;|k|越小,越接近x 轴 3、一次函数及性质 一般地,形如y=kx +b(k,b 是常数,k≠0),那么y 叫做x 的一次函数.当b=0时,y=kx +b 即y=kx ,所以说正比例函数是一种特殊的一次函数. 注:一次函数一般形式 y=kx+b (k 不为零) ① k 不为零 ②x 指数为1 ③ b 取任意实数 一次函数y=kx+b 的图象是经过(0,b )和(- k b ,0)两点的一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx 平移|b|个单位长度得到.(当b>0时,向上平移;当b<0时,向下平移) 第五节 函数图形的描绘 分布图示 ★ 引言 ★ 渐近线 ★ 函数图形描绘的步骤 ★ 例1 ★ 例2 ★ 例3 ★ 例4 ★ 内容小结 ★ 课堂练习 ★ 习题3-5 内容要点 一、渐近线的概念 水平渐近线 铅直渐近线 斜渐近线; 二、函数图形的描绘:对于一个函数,若能作出其图形,就能从直观上了解该函数的性态特征,并可从其图形清楚地看出因变量与自变量之间的相互依赖关系. 在中学阶段,我们利用描点法来作函数的图形. 这种方法常会遗漏曲线的一些关键点,如极值点、拐点等. 使得曲线的单调性、凹凸性等一些函数的重要性态难以准确显示出来. 本节我们要利用导数描绘函数)(x f y =的图形,其一般步骤如下: 第一步 确定函数)(x f 的定义域, 研究函数特性如: 奇偶性、周期性、有界性等, 求出函数的一阶导数)(x f '和二阶导数)(x f ''; 第二步 求出一阶导数)(x f '和二阶导数)(x f ''在函数定义域内的全部零点,并求出函数)(x f 的间断点和导数)(x f '和)(x f ''不存在的点, 用这些点把函数定义域划分成若干个部分区间; 第三步 确定在这些部分区间内)(x f '和)(x f ''的符号, 并由此确定函数的增减性和凹凸性,极值点和拐点; 第四步 确定函数图形的水平、铅直渐近线以及其它变化趋势; 第五步 算出)(x f '和)(x f ''的零点以及不存在的点所对应的函数值,并在坐标平面上定出图形上相应的点;有时还需适当补充一些辅助作图点(如与坐标轴的交点和曲线的端点等); 然后根据第三、四步中得到的结果,用平滑曲线联接而画出函数的图形. 例题选讲 求曲线渐近线 例1 作函数1)(23+--=x x x x f 的图形. 解 定义域为),,(+∞-∞无奇偶性及周期性. ),1)(13()(-+='x x x f ).13(2)(-=''x x f 令,0)(='x f 得,3/1-=x .1=x 令,0)(=''x f 得.3/1=x 列表综合如下: - 1 - 函数与几何图形 1. 如图4,正方形ABCD 的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上,且它们的各边与正方形ABCD 各边平行或垂直.若小正方形的边长为x ,且0 【例1】小明外出散步,从家走了20分钟后到达了一个离家900米的报亭,看了10分钟的 报纸然后用了15分钟返回到家.则下列图象能表示小明离家距离y 与时间x 关系的是( ) 选择D 答案 【例2】打开某洗衣机开关(洗衣机内无水),在洗涤衣服时,洗衣机经历了进水、清洗、 排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y (升)与时间x (分钟)之间满足某种函数关系,其函数图象大致为( ) D 答案。 【练习一】 1.(2010黑龙江绥化)六月P 市连降大雨,某部队前往救援,乘车行进一段路程之后,由于道路受阻,汽车无法通行,部队短暂休整后决定步行前往. 则能反映部队离开驻地的距离s (千米)与时间t (小时)之间函数关系的大致图象是( ) 【答案】A 2.(2010广东深圳)升旗时,旗子的高度h (米)与时间t (分)的函数图像大致为( ) A . / B . C . D . 【答案】B 3.(2010 河南模拟)如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图像是 ( ) 4.(2010四川巴中)如图3所示,以恒定的速度向此容器注水,容器内水的高度(h)与注水时间(t)之间的函数关系可用下列图像大致描述的是() 5.(2010 湖北孝感)均匀地向如图所示的一个容器注水,最后把容器注满,在注水过程中,能大致反映水面高度h随时间t变化的图像是() 【答案】C 6.(2010内蒙呼和浩特)均匀的地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC位一折线),则这个容器的形状为( ) 图 3 A B C D 高中数学常见函数图像 1.指数函数: 定义 函数 (0x y a a =>且1)a ≠叫做指数函数 图象 1a > 01a << 定义域 R 值域 (0,)+∞ 过定点 图象过定点(0,1),即当0x =时,1y =. 奇偶性 非奇非偶 单调性 在R 上是增函数 在R 上是减函数 2.对数函数: 定义 函数 log (0a y x a =>且1)a ≠叫做对数函数 图象 1a > 01a << 定义域 (0,)+∞ 值域 R 过定点 图象过定点(1,0),即当1x =时,0y =. 奇偶性 非奇非偶 单调性 在(0,)+∞上是增函数 在(0,)+∞上是减函数 x a y =x y (0,1) O 1 y =x a y =x y (0,1) O 1 y =x y O (1,0) 1 x =log a y x =x y O (1,0) 1 x =log a y x = 3.幂函数: 定义形如αx y=(x∈R)的函数称为幂函数,其中x是自变量,α是常数. 图像 性质过定点:所有的幂函数在(0,) +∞都有定义,并且图象都通过点(1,1).单调性:如果0 α>,则幂函数的图象过原点,并且在[0,) +∞上为增函数.如果0 α<,则幂函数的图象在(0,) +∞上为减函数,在第一象限内,图象无限接近x轴与y轴. 4. 函数 sin y x = cos y x = tan y x = 图象 定义域 R R ,2x x k k ππ??≠+∈Z ???? 值域 []1,1- []1,1- R 最值 当 22 x k π π=+ () k ∈Z 时, max 1y =; 当22 x k π π=- ()k ∈Z 时,min 1y =-. 当()2x k k π =∈Z 时, max 1y =; 当2x k ππ=+ ()k ∈Z 时,min 1y =-. 既无最大值也无最小值 周期性 2π 2π π 奇偶性 奇函数 偶函数 奇函数 单调性 在 2,222k k ππππ? ?-+???? ()k ∈Z 上是增函数;在 32,222k k π πππ? ?++??? ? ()k ∈Z 上是减函数. 在[]() 2,2k k k πππ-∈Z 上 是 增 函 数 ; 在 []2,2k k πππ+ ()k ∈Z 上是减函数. 在,2 2k k π ππ π? ? - + ?? ? ()k ∈Z 上是增函数. 对称性 对称中心 ()(),0k k π∈Z 对称轴 ()2 x k k π π=+ ∈Z 对称中心 (),02k k ππ??+∈Z ?? ? 对称轴()x k k π =∈Z 对称中心(),02k k π?? ∈Z ??? 无对称轴 常见函数性质汇总及简单评议对称变换 常数函数 f (x )=b (b ∈R) 1)、y=a 和 x=a 的图像和走势 2)、图象及其性质:函数f (x )的图象是平行于x 轴或与x 轴重合(垂直于y 轴)的直线 一次函数 f (x )=kx +b (k ≠0,b ∈R) 1)、两种常用的一次函数形式:斜截式—— 点斜式—— 2)、对斜截式而言,k 、b 的正负在直角坐标系中对应的图像走势: 3)、|k|越大,图象越陡;|k|越小,图象越平缓 4)、定 义 域:R 值域:R 单调性:当k>0时 ;当k<0时 奇 偶 性:当b =0时,函数f (x )为奇函数;当b ≠0时,函数f (x )没有奇偶性; 例题:y=f (x ); y=g (x )都有反函数,且f (x-1)和g -1 (x)函数的图像关于y=x 对称,若g (5)=2016,求)= 周 期 性:无 5)、一次函数与其它函数之间的练习 1、常用解题方法: b 反比例函数 f (x )= x k (k ≠0,k 值不相等永不相交;k 越大,离坐标轴越远) 图象及其性质:永不相交,渐趋平行;当k>0时,函数f (x )的图象分别在第一、第三 象限;当k<0时,函数f (x )的图象分别在第二、第四象限; 双曲线型曲线,x 轴与y 轴分别是曲线的两条渐近线; 既是中心对成图形也是轴对称图形 定 义 域:),0()0,(+∞-∞ 值 域:),0()0,(+∞-∞ 单 调 性:当k> 0时;当k< 0时 周 期 性:无 奇 偶 性:奇函数 反 函 数:原函数本身 补充:1、反比例函数的性质 2、与曲线函数的联合运用(常考查有无交点、交点围城图行的面积)——入手点常有两个——⑴直接带入,利用二次函数判别式计算未知数的取值;⑵利用斜率,数形结合判断未知数取值(计算面积基本方法也基于此) 3、反函数变形(如右图) 1)、y=1/(x-2)和y=1/x-2的图像移动比较 2)、y=1/(-x)和y=-(1/x )图像移动比较 3)、f (x )= d cx b ax ++ (c ≠0且 d ≠0)(补充一下分离常数) (对比标准反比例函数,总结各项内容) 二次函数 一般式:)0()(2 ≠++=a c bx ax x f 顶点式:)0()()(2 ≠+-=a h k x a x f 两根式:)0)()(()(21≠--=a x x x x a x f 图象及其性质:①图形为抛物线,对称轴为 ,顶点坐标为 ②当0>a 时,开口向上,有最低点 当00时,函数图象与x 轴有两个交点( );当<0时,函数图象与x 轴有一个交点( );当=0时,函数图象与x 轴没有交点。 ④)0()(2 ≠++=a c bx ax x f 关系 )0()(2 ≠=a ax x f 定 义 域:R 值 域:当0>a 时,值域为( );当0a 时;当0 基本初等函数 . 幂函数(a为实数) 要记住最常见的几个幂函数的定义域及图形 . 1.当u为正整数时,函数的定义域为区间 ) , (+∞ -∞ ∈ x,他们的图形都经过原点,并当u>1 时在原点处与X轴相切。且u为奇数时,图形关于原点对称;u为偶数时图形关于Y轴对称; 2.当u为负整数时。函数的定义域为除去x=0的所有实数。 3.当u为正有理数m/n时,n为偶数时函数的定义域为(0, +∞),n为奇数时函数的定义域为(-∞+∞)。函数的图形均经过原点和(1 ,1). 如果m>n图形于x轴相切,如果m 奇数时,跟原点对称 .4.当u为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n为奇数时,定义域为去除x=0以外的一切实数. . 指数函数 定义域:, 值域:, 图形过(0,1)点,a>1时,单调增加;a时,单调减少。今后用的较多。 1.当a>1时函数为单调增,当a<1时函数为单调减. 2.不论x为何值,y总是正的,图形在x轴上方. 3.当x=0时,y=1,所以他的图形通过(0,1)点. . 对数函数 定义域:, 值域:, 4.与指数函数互为反函数,图形过(1,0)点,a>1时,单调增加;a<1时,单调减少。 1.他的图形为于y轴的右方.并通过点(1,0) 5.当a>1时在区间(0,1),y的值为负.图形位于x的下方,在区间(1, + ),y值为正,图形 位于x轴上方.在定义域是单调增函数.a<1在实用中很少用到 . 三角函数 ,奇函数、有界函数、周期函数; ,偶函数、有界函数、周期函数; ,的一切实数,奇函数、 周期函数 函数与几何图形 华罗庚说:数与形,本是相倚依,焉能分作两边飞。数缺形时少直观,形少数时难入微。数形结合百般好,隔裂分家万事非。切莫忘,几何代数统一体,永远联系,切莫分离! 一.以函数为背景研究几何图形: 例1.已知322 --=x x y 与x 轴交于点A 、B, (A 点在B 点的左侧),与y 轴交于点C ,顶点为D , P 为对称轴上一点. ⑴当△PAC 是等腰三角形时,求P 点坐标; ⑵当△PAC 是直角三角形时,求P 点坐标; ⑶当∠APC =∠ABC 时,求P 点坐标; ⑷当四边形ACBP 是梯形时,求P 点坐标;(引伸) ⑸当△PAC 的周长最短时,求P 点坐标;(引伸) ⑹当△PAC 的面积是4时,求P 点坐标; ⑺当ABC PAC S S ??=2 1时,求P 点坐标; ⑻若Q 为线段AB 上一点,过Q 平行于CD 的直线交B C 、BD 于E 、F ,当BEF ACD S S ??=4时,求Q 点坐标. 二.以几何图形为背景研究变量之间的关系: 例2. 如图,在Rt △ABC 中,∠C =90°,AC = 3,AB = 5.点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动,到达点A 后立刻以原来的速度沿AC 返回;点Q 从点A 出发沿AB 以每秒1个 单位长的速度向点B 匀速运动.伴随着P 、Q 的运动,DE 保持垂直平分PQ ,且交PQ 于点D ,交折线QB -BC -CP 于点E .点P 、Q 同时出发,当点Q 到达点B 时停止运动,点P 也随之停止.设点P 、Q 运动的时间是t 秒(t >0). (1)当t = 2时,AP = ,点Q 到AC 的距离是 ; (2)在点P 从C 向A 运动的过程中,求△APQ 的面积S 与 t 的函数关系式;(不必写出t 的取值范围) (3)在点E 从B 向C 运动的过程中,四边形QBED 能否成 为直角梯形?若能,求t 的值.若不能,请说明理由; (4)当DE 经过点C 时,请直接..写出t 的值. 常见函数性质汇总 常数函数 f (x )=b (b ∈R) 图象及其性质:函数f (x )的图象是平行于x 轴或与x 轴重合(垂直于y 轴)的直线 一次函数 f (x )=kx +b (k ≠0,b ∈R) |k|越大,图象越陡;|k|越小,图象越平缓; 图象及其性质:直线型图象。b=0;k>0;k<0 定 义 域:R 值域:R 单调性:当k>0时, 当k<0时 奇 偶 性:当b =0时,函数f (x )为奇函数;当b ≠0时,函数f (x )没有奇偶性; 反 函 数:有反函数。K=±1、b=0的时候 周 期 性:无 补充:一次函数与其它函数之间的lianxi 1、与一元一次函数之间的联系 2、与曲线函数的联合运用 反比例函数 f (x )= x k (k ≠0,k 值不相等永不相交;k 越大,离坐标轴越远) 图象及其性质:永不相交,渐趋平行;当k>0时,函数f (x )的图象分别在第一、第三象限; 当k<0时,函数f (x )的图象分别在第二、第四象限; 双曲线型曲线,x 轴与y 轴分别是曲线的两条渐近线; 既是中心对成图形也是轴对称图形 定 义 域:),0()0,(+∞-∞ 值 域:),0()0,(+∞-∞ 单 调 性:当k> 0时;当k< 0时 奇 偶 性:奇函数 反 函 数:原函数本身 周 期 性:无 补充:1、反比例函数的性质 2、与曲线函数的联合运用(常考查有无交点、交点围城图行的面积)——入手点常有两个——⑴直接带入,李永二次函数判别式计算未知数的取值;⑵利用斜率,数形结合判断未知数取值(计算面积基本方法也基于此) 3、反函数变形(如右图) f (x )= d cx b ax ++ (c ≠0且 d ≠0) x y b O f (x )=b x y O f (x )=kx +b x y O f (x )=x k y f (x )= d cx b ax ++ 一次函数的图像与性质知识点总结 知识点1 、 一次函数和正比例函数的概念 若两个变量x ,y 间的关系式可以表示成y=kx+b (k ,b 为常数,k ≠0)的形式,则称y 是x 的一次函数(x 为自变量),特别地,当b=0时,称y 是x 的正比例函数.例如:y=2x+3,y=-x+2,y=21x 等都是一次函数,y=2 1x ,y=-x 都是正比例函数. 知识点2、 函数的图象 把一个函数的自变量x 与所对应的y 的值分别作为点的横坐标和纵坐标在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象.画函数图象一般分为三步:列表、描点、连线. 知识点 3、一次函数的图象 由于一次函数y=kx+b (k ,b 为常数,k ≠0)的图象是一条直线,所以一次函数y=kx+b 的图象也称为直线y=kx+b . 由于两点确定一条直线,因此在今后作一次函数图象时,只要描出适合关系式的两点,再连成直线即可,一般选取两个特殊点:直线与y 轴的交点(0,b ),直线与x 轴的交点(-k b ,0).但也不必一定选取这两个特殊点.画正比例函数y=kx 的图象时,只要描出点(0,0),(1,k )即可. 知识点4 、 一次函数y=kx+b (k ,b 为常数,k ≠0)的性质 (1)k 的正负决定直线的倾斜方向; ①k >0时,y 的值随x 值的增大而增大; ②k ﹤O 时,y 的值随x 值的增大而减小. (2)|k|大小决定直线的倾斜程度,即|k|越大,直线与x 轴相交的锐角度数越大(直线陡),|k|越小,直线与x 轴相交的锐角度数越小(直线缓); (3)b 的正、负决定直线与y 轴交点的位置; ①当b >0时,直线与y 轴交于正半轴上; ②当b <0时,直线与y 轴交于负半轴上; ③当b=0时,直线经过原点,是正比例函数. (4)由于k ,b 的符号不同,直线所经过的象限也不同; ①当k >0,b >0时,直线经过第一、二、三象限(直线不经过 第四 象限); ②当k >0,b ﹥O 时,直线经过第一、三、四象限(直线不经过 第二象限); ③当k ﹤O ,b >0时,直线经过第一、二、四象限(直线不经过第三 指数函数 概念:一般地,函数y=a^x(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。 注意:⒈指数函数对外形要求严格,前系数要为1,否则不能为指数函数。 ⒉指数函数的定义仅是形式定义。 指数函数的图像与性质: 规律:1. 当两个指数函数中的a互为倒数时,两个函数关于y轴对称,但这两个函数都不具有奇偶 性。 2.当a>1时,底数越大,图像上升的越快,在y轴的右侧,图像越靠近y轴; 当0<a<1时,底数越小,图像下降的越快,在y轴的左侧,图像越靠近y轴。 在y轴右边“底大图高”;在y轴左边“底大图低”。 3.四字口诀:“大增小减”。即:当a >1时,图像在R 上是增函数;当0<a <1时,图像在R 上是减函数。 4. 指数函数既不是奇函数也不是偶函数。 比较幂式大小的方法: 1. 当底数相同时,则利用指数函数的单调性进行比较; 2. 当底数中含有字母时要注意分类讨论; 3. 当底数不同,指数也不同时,则需要引入中间量进行比较; 4. 对多个数进行比较,可用0或1作为中间量进行比较 底数的平移: 在指数上加上一个数,图像会向左平移;减去一个数,图像会向右平移。 在f(X)后加上一个数,图像会向上平移;减去一个数,图像会向下平移。 对数函数 1.对数函数的概念 由于指数函数y=a x 在定义域(-∞,+∞)上是单调函数,所以它存在反函数, 我们把指数函数y=a x (a >0,a ≠1)的反函数称为对数函数,并记为y=log a x(a >0,a ≠1). 因为指数函数y=a x 的定义域为(-∞,+∞),值域为(0,+∞),所以对数函数y=log a x 的定义域为(0,+∞),值域为(-∞,+∞). 2.对数函数的图像与性质对数函数与指数函数互为反函数,因此它们的图像对称于直线y=x . 据此即可以画出对数函数的图像,并推知它的性质. 为了研究对数函数y=log a x(a >0,a ≠1)的性质,我们在同一直角坐标系中作出函数 y=log 2x ,y=log 10x ,y=log 10x,y=log 2 1x,y=log 10 1x 的草图 考研高等数学常用公式及函数图象 导数公式: 基本积分表: 三角函数的有理式积分: 2 22212211cos 12sin u du dx x tg u u u x u u x +==+-=+=, , , a x x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22= '='?-='?='-='='2 2 22 11 )(11 )(11 )(arccos 11 )(arcsin x arcctgx x arctgx x x x x +- ='+= '-- ='-= '? ?????????+±+=±+=+=+=+-=?+=?+-==+==C a x x a x dx C shx chxdx C chx shxdx C a a dx a C x ctgxdx x C x dx tgx x C ctgx xdx x dx C tgx xdx x dx x x )ln(ln csc csc sec sec csc sin sec cos 222 22 22 2C a x x a dx C x a x a a x a dx C a x a x a a x dx C a x arctg a x a dx C ctgx x xdx C tgx x xdx C x ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=????????arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 2 2222222? ????++-=-+-+--=-+++++=+-= ==-C a x a x a x dx x a C a x x a a x x dx a x C a x x a a x x dx a x I n n xdx xdx I n n n n arcsin 22ln 22)ln(221 cos sin 22 2222222 2222222 22 2 22 2 π π 高中常见函数图像及基 本性质 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN 常见函数性质汇总及简单评议对称变换 常数函数 f (x )=b (b ∈R) 1)、y=a 和 x=a 的图像和走势 2)、图象及其性质:函数f (x )的图象是平行于x 轴或与x 轴重合(垂直于y 轴)的直线 一次函数 f (x )=kx +b (k ≠0,b ∈R) 1)、两种常用的一次函数形式:斜截式—— 点斜式—— 2)、对斜截式而言,k 、b 的正负在直角坐标系中对应的图像走势: 3)、|k|越大,图象越陡;|k|越小,图象越平缓 4)、定 义 域:R 值域:R 单调性:当k>0时 ;当k<0时 奇 偶 性:当b =0时,函数f (x )为奇函数;当b ≠0时,函数f (x )没有奇偶性; 反 函 数:有反函数(特殊情况下:K=±1并且b=0的时候)。 补充:反函数定义: 例题:定义在上的函数y=f (x ); y=g (x )都有反函数,且f (x-1)和g -1(x)函数的图像关于y=x 对称,若g (5)=2016,求f (4)= x y b O f (x )=b x y O f (x )=kx +b R 周期性:无 5)、一次函数与其它函数之间的练习 1、常用解题方法: 2、与曲线函数的联合运用 反比例函数f(x)= x k (k≠0,k值不相等永不相交;k越大,离坐标轴越远) 图象及其性质:永不相交,渐趋平行;当k>0时,函数f(x)的图象分别在 第一、第三象限;当k<0时,函数f(x)的图象分别在第 二、第四象限; 双曲线型曲线,x轴与y轴分别是曲线的两条渐近线; 既是中心对成图形也是轴对称图形 定义域:) ,0( )0, (+∞ -∞ 值域:) ,0( )0, (+∞ -∞ 单调性:当k> 0时;当k< 0时周期性:无 奇偶性:奇函数 反函数:原函数本身 补充:1、反比例函数的性质 2、与曲线函数的联合运用(常考查有无交点、交点围城图行的面积)——入手点常有两个——⑴直接带入,利用二次函数判别式计算未知数的取值;⑵利用斜率,数形结合判断未知数取值(计算面积基本方法也基于此) x y O f(x)= d cx b ax + + 2)点关于直线(点)对称,求点的坐标 《一次函数与几何图形综合》专题 总论:函数与几何是初中数学中的重点内容,是中考命题重点考查的内容之一;函数中的几何问题,能使代数知识图形化,而几何中的函数问题,能使图形性质代数化;由于函数与几何结合的综合题的形式灵活、立意新颖,能更好地考查学生的思维水平和数学思想方法,因而成为近几年各地中考的一类热门试题; 函数知识与几何知识有机结合的综合题,根据构成命题的主要要素可分为以下两类: 一类是几何元素间的函数关系问题(这类问题不妨称简称为“几函”问题),这类问题的特点是:根据已知几何图形间的位置和数量关系(如平行、全等、相似,特别是成比例)建立自变量与函数所表示的几何元素间的等量关系,求出函数关系式,运用函数的性质解决几何图形中的问题; 另一类是函数图像中的几何图形的问题(如三角形、四边形,特别是圆)(这类问题不妨简称为“函几”问题),这类问题的特点是:根据已知函数图像中的几何图形的位置特征,运用数形结合方法解决有关函数、几何问题。 一次函数与几何综合题是八年级学生初次接触一种用代几综合解决问题的方法,这种方法和能力是九年级解决中考压轴题所必须具备的。 1.代数 (1)表达什么函数(包括其系数的代数意义、几何意义、物理意义) (2)显现怎样的图形(自身、与坐轴、与其他图形) (3)既是一个方程,也是一个坐标 4)藏有那些数据,含有什么些关系(5)要建立某种代数关系缺少那些数据 2.几何 (1)基本图象有几个 (2)图象之间有怎样关系(3)图象与所要证明(求解)的结论怎样的关联(4)要建立图象与图象之间的关系缺少那些数据 3.代数与几何 (1)代数(几何)在那些地方为几何(代数)提供了怎样的数据 (2)几何(代数)通过什么方式为几何(代数)提供关系式 (3)怎样设数据(坐标或线段长) 函数与几何综合题的解题思想方法: “函几问题”与“几函问题”涉及的知识面广、知识跨度大、综合性强,应用数学方法多、纵横联系较复杂、结构新颖灵活、注重基础能力、探索创新和数学思想方法,它要求学生有良好的心理素质和过硬的数学基本功,能从已知所提供的信息中提炼出数学问题,从而灵活地运用所学知识和掌握的基本技能创造性的解决问题,正因如此,解决这类问题时,要注意解决问题的策略,常用的解题策略一般有以下几种: 1.综合使用分析法和综合法。就是从条件与结论出发进行联想、推理,“由已知得可知”,“从要求到需求”,通过对问题的“两边夹击”,使它们在中间的某个环节上产生联系,从而使问题得以解决。 2.运用方程的思想。就是寻找要解决的问题中量与量之间的等量关系,建立已知量与未知量间的方程,通过解方程从而使问题得到解决;在运用这种思想时,要注意充分挖掘问题的的隐藏条件,寻找等量关系建立方程或方程组; 3.注意使用分类讨论的思想(函数方法)。函数方法就是用运动、变化的观点来分析题中的数量关系,抽象、 第六节 函数图形的描绘 ㈠本课的基本要求 会求水平、铅直和斜渐近线,会描绘函数的图形 ㈡本课的重点、难点 重点是函数图形的描绘,难点是求渐近线 ㈢教学内容 随着现代计算机技术的发展,借助于计算机和许多数学软件,可以方便地画出各种函数的图形。但是,如何识别机器作图中的误差,如何掌握图形上的关键点,如何选择作图的范畴等,从而进行人工干预,仍然需要我们有运用微分学的方法描绘函数图形的基本知识。因此,本节讨论手工绘制函数的简图。所谓简图是指图形的基本样式是正确的,但细微之处可以不太深究。在函数图形中,下述特征是必不可少的:定义域、奇偶性、对称性、周期性、连续性、单调性、凹凸性、极值和最大最小值、渐近线以及一些特殊点特别是临界点的函数值等。画一张函数的简图几乎用到了前面几节的全部知识。 一.曲线的渐近线 定义 若),()(y x M x f y 上的动点=沿着曲线无限远离坐标原点,它与某直线L 的距离趋向于0,则称L 为该曲线的渐近线。 L 可以是各种位置的直线,我们只讨论几种特殊情况 ⑴垂直(铅直)渐近线 若∞=∞=∞=→→→+-)()()(lim lim lim 000x f x f x f x x x x x x 或或,则称直线 )(0x f y x x ==为曲线的垂(铅)直渐近线。 例 )2 (t a n ),0(1ππ+====k x x y x x y 分析垂直渐近线可能出现的情况 ⑵水平渐近线 若b x f b x f b x f x x x ===∞→+∞→-∞→)()()(lim lim lim 或或,则称直线b y =为曲线)(x f y =的水平渐近线。 例 )0(1),2(arctan ==±==y x y y x y π 介绍水平渐近线的求法 ⑶斜渐近线 若b kx x f k x y x x =-=∞ →∞→])([,lim lim (这里的∞也可以分别是+∞,-∞) ,则称直线b kx y +=为曲线)(x f y =的斜渐近线。 例 23 ) 1()1(+-=x x y 的斜渐近线为5-=x y 二.函数图形的描绘 步骤: ⑴确定函数的定义域并讨论其对称性和周期性 ⑵讨论函数的单调性、极值点和极值 ⑶讨论函数图形的凹凸区间和拐点一次函数与几何图形综合专题
五大基本初等函数性质和图像
高中常用函数性质及图像汇总
第五节--函数图形的描绘
函数与几何图形
初中数学函数与图像汇总
高中数学常见函数图像
高中的常见函数图像及基本性质
基本初等函数与图像大全
函数与几何图形
高中数学函数常用函数图形及其基本性质
一次函数图像与性质的知识点整理
高中函数图像大全
考研高等数学常用公式以及函数图像
高中常见函数图像及基本性质
《一次函数与几何图形综合》 专题
第六节 函数图形的描绘