1-8章习题参考答案全

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出，P2=6W吸收，P3=16W吸收，P4=-lOW发出，PS=-7W发出，PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开：UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合：12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。

第3章静定梁与静定刚架习题解答
习题3.1是非判断题
(1) 在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。（ ）
(2) 区段叠加法仅适用于弯矩图的绘制，不适用于剪力图的绘制。（ ）
(3) 多跨静定梁在附属部分受竖向荷载作用时，必会引起基本部分的内力。（ ）
(4)习题3.1(4)图所示多跨静定梁中，CDE和EF部分均为附属部分。（ ）
(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故原体系是几何可变体系。( )
习题 2.1(6)图
习题2.2填空
(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2) 习题2.2(2)图所示体系为__________体系。
习题 2-2(2)图
（4）习题5.1(3)图(a)和(b)所示两结构的变形相同。（ ）
习题7.2填空题
（1）习题5.2(1)图(a)所示超静定梁的支座A发生转角，若选图(b)所示力法基本结构，则力法方程为_____________，代表的位移条件是______________，其中1c=_________；若选图(c)所示力法基本结构时，力法方程为____________，代表的位移条件是______________，其中1c=_________。
(3) 习题7.2(3)图所示刚架各杆的线刚度为i，欲使结点B产生顺时针的单位转角，应在结点B施加的力矩MB=______。
习题 7.2(1)图习题 7.2(2)图 习题 7.2(3)图
(4) 用力矩分配法计算习题7.2(4)图所示结构（EI=常数）时，传递系数CBA=________，CBC=________。

A
35.采用几何平均法计算平均发展速度的理由是（ ）。
A.各年环比发展速度之和等于总速度B.各年环比发展速度之积等于总速度
C.各年环比增长速度之积等于总速度D.各年环比增长速度之和等于总速度
B
36.计算平均发展速度应用几何平均法的目的在于考察（ ）。
A.最初时期发展水平B.全期发展水平
C.最末时期发展水平D.期中发展水平
B
3.发展速度属于( )
A比例相对数B比较相对数C动态相对数D强度相对数
C
4.计算发展速度的分母是( )
A报告期水平B基期水平C实际水平D计划水平
B
5.某车间月初工人人数资料如下：
月份
1
2
3
4
5
6
7
月初人数(人)
280
284
280
300
302
304
320
则该车间上半年的平均人数约为( )
A 296人B 292人C 295人D 300人
A.0.33倍B.0.50倍C.0.75倍D.2倍
D
16.已知一个数列的环比增长速度分别为3%、5%、8%，则该数列的定基增长速度为（）
A.3%×5%×8%B.103%×105%×108%
C.（3%×5%×8%）＋1D.（103%×105%×108%）－1
D
17.企业生产的某种产品2002年比2001年增长了8%，2003年比2001年增长了12%，则2003年比2002年增长了（）。
时间第一年第二年第三年第四年第五年销售额万元10001100130013501400根据上述资料计算的下列数据正确的有a第二年的环比增长速度二定基增长速度10b第三年的累计增长量二逐期增长量200万元c第四年的定基发展速度为135d第五年增长1绝对值为14万元e第五年增长1绝对值为135万元ace7

第六章课后练习题1、三通公司拟发行5年期、利率6%、面额1000元债券一批；预计发行总价格为550元，发行费用率2%；公司所得税率33%。

要求：试测算三通公司该债券的资本成本率。

参考答案：可按下列公式测算：=1000*6%*（1-33%）/550*（1-2%）=7.46%2、四方公司拟发行优先股50万股，发行总价150万元，预计年股利率8%，发行费用6万元。

要求：试测算四方公司该优先股的资本成本率。

参考答案：可按下列公式测算：其中：=8%*150/50=0.24=（150-6）/50=2.88=0.24/2.88=8.33%3、五虎公司普通股现行市价为每股20元，现准备增发8万份新股，预计发行费用率为5%，第一年每股股利1元，以后每年股利增长率为5%。

要求：试测算五虎公司本次增发普通股的资本成本率。

参考答案：可按下列公式测算：=1/19+5%=10.26%4、六郎公司年度销售净额为28000万元，息税前利润为8000万元，固定成本为3200万元，变动成本为60%；资本总额为20000万元，其中债务资本比例占40%，平均年利率8%。

要求：试分别计算该公司的营业杠杆系数、财务杠杆系数和联合杠杆系数。

参考答案：可按下列公式测算：DOL=1+F/EBIT=1+3200/8000=1.4DFL=8000/（8000-20000*40%*8%）=1.09DCL=1.4*1.09=1.535、七奇公司在初创时准备筹集长期资本5000万元，现有甲、乙两个备选筹资方案，有关资料如下表：筹资方式筹资方案甲筹资方案乙筹资额（万元）个别资本成本率（%）筹资额（万元）个别资本成本率（%）长期借款公司债券普通股800120030007.08.514.0110040035007.58.014.0合计5000 —5000 —要求：试分别测算该公司甲、乙两个筹资方案的综合资本成本率，并据以比较选择筹资方案。

参考答案：（1）计算筹资方案甲的综合资本成本率：第一步，计算各种长期资本的比例：长期借款资本比例=800/5000=0.16或16% 公司债券资本比例=1200/5000=0.24或24%普通股资本比例 =3000/5000=0.6或60%第二步，测算综合资本成本率：Kw=7%*0.16+8.5%*0.24+14%*0.6=11.56%（2）计算筹资方案乙的综合资本成本率：第一步，计算各种长期资本的比例：长期借款资本比例=1100/5000=0.22或22% 公司债券资本比例=400/5000=0.08或8%普通股资本比例 =3500/5000=0.7或70%第二步，测算综合资本成本率：Kw=7.5%*0.22+8%*0.08+14%*0.7=12.09%由以上计算可知，甲、乙两个筹资方案的综合资本成本率分别为11.56%、12.09%，可知，甲的综合资本成本率低于乙，因此选择甲筹资方案。

严新华主编《水力学（修订本）》教材（科技文献出版社2001年版）部分习题参考答案第一章 习题答案1-1 水的运动粘性系数s m /10006.126-⨯=ν；空气的动力粘性系数s Pa ⋅⨯=-51081.1μ。

1-2 活塞移动速度s m V /49.0=。

1-3 动力粘性系数s Pa ⋅=151.0μ。

1-4 2/5.11m N =τ。

1-5 阻力矩m N M ⋅=6.39。

第二章 习题答案2-1（a ）图中2/6.68m KN p A =；绝对压强2/93.169m KN p A='。

（b ）图中22/4.29,0,/6.19m KN p p m KN p A B C -===；绝对压强222/93.71,/33.101,/93.120m KN p m KN p m KN p AB C ='='='。

2-2 20/4900m N p -=；液面真空值20/4900m N p V =。

2-3（1）2/54.115m KN p A ='；2/47.17m KN p A =。

（2）压力表读数m h m KN p M 213.1,/63.92==。

2-4 A 点表压强2/8.9m KN p A -=；液面空气真空度2/6.19m KN p V =。

2-5 m H 40.0=。

2-6 cm h 1284=。

2-7 O H 84.172mmh V =。

2-8 ①2/22.185m KN p p B A =-；②2/42.175m KN p p B A =-。

2-9 ⑴21/86.1m KN p p B A -=-为油时：ρ；⑵21/784.0m KN p p B A -=-为空气时：ρ。

2-10 ⎪⎭⎫⎝⎛-='b a 1ρρ；gH b a p p BA ρ=-。

2-11 241/1084.118m N p ⨯=。

2-12 )/3.101(/84.37822m KN p m KN p a =='取：。

固体物理习题参考答案（部分）第一章 晶体结构1.氯化钠：复式格子，基元为Na +，Cl -金刚石：复式格子，基元为两个不等价的碳原子 氯化钠与金刚石的原胞基矢与晶胞基矢如下：原胞基矢)ˆˆ()ˆˆ()ˆˆ(213212211j i a a i k a a k j a a +=+=+= ， 晶胞基矢 ka a j a a ia a ˆˆˆ321===2. 解：31A A O '：h:k;l;m==-11:211:11:111:1:-2:1 所以（1 1 2 1） 同样可得1331B B A A ：（1 1 2 0）； 5522A B B A ：（1 1 0 0）；654321A A A A A A ：（0 0 0 1）3.简立方： 2r=a ，Z=1,()63434r 2r a r 3333πππ===F体心立方：()πππ833r4r 342a r 3422a 3r 4a r 4a 33333=⨯=⨯=∴===F Z ，，则面心立方：()πππ622r 4r 34434442r 4a r 4a 233ar 33=⨯=⨯=∴===F Z ，，则 六角密集：2r=a, 60sin 2c a V C = a c 362=,πππ622336234260sin 34223232=⨯⨯⨯=⨯=⎪⎭⎫ ⎝⎛a a c a r F a金刚石：()πππ163r 38r 348a r 3488Z r 8a 33333=⨯=⨯===F ，， 4. 解：'28109)31arccos(312323)ˆˆˆ()ˆˆˆ(cos )ˆˆˆ()ˆˆˆ(021*******12211=-=-=++-⋅+-=⋅=++-=+-=θθa a k j i a k j i a a a a a kj i a a kj i a a 5.解：对于（110）面：2a 2a a 2S =⋅=所包含的原子个数为2，所以面密度为22a2a22=对于（111）面：2a 2323a 22a 2S =⨯⨯= 所包含的原子个数为2，所以面密度为223a34a 232=8.证明：ABCD 是六角密堆积结构初基晶胞的菱形底面，AD=AB=a 。

第5章S7-200 PLC的指令系统习题与思考题7-200指令参数所用的基本数据类型有哪些？：S7-200 PLC的指令参数所用的基本数据类型有1位布尔型(BOOL)、8位无符号字节型(BYTE)、8位有符号字节型(SIMATIC模式仅限用于SHRB指令)、16位无符号整数(WORD)、16位有符号整数(INT)、32位无符号双字整数(DWORD)、32位有符号双字整数(DINT)、32位实数型(REAL)。

实数型(REAL)是按照ANSI/IEEE 754-1985标准(单精度)的表示格式规定。

2~255字节的字符串型（STRING）即I/O指令有何特点？它应用于什么场合？：立即指令允许对输入和输出点进行快速和直接存取。

当用立即指令读取输入点的状态时，相应的输入映像寄存器中的值并未发生更新；用立即指令访问输出点时，访问的同时，相应的输出映像寄存器的内容也被刷新。

由于立即操作指令针对的是I/O端口的数字输入和数字输出信号，所以它们的位操作数地址只能是物理输入端口地址Ix.x和物理输出端口地址Qx.x。

辑堆栈指令有哪些？各用于什么场合？：复杂逻辑指令，西门子称为逻辑堆栈指令。

主要用来描述对触点进行的复杂连接，并可以实现对逻辑堆栈复杂的操作。

杂逻辑指令包括：ALD、OLD、LPS、LRD、LPP和LDS。

这些指令中除LDS外，其余指令都无操作数。

这些指令都是位逻辑指令。

装载与指令ALD用于将并联子网络串联起来。

装载或指令OLD用于将串联子网络并联起来。

辑推入栈指令LPS，在梯形图中的分支结构中，用于生成一条新的母线，左侧为主控逻辑块时，第一个完整的从逻辑行从此处开始。

辑读栈指令LRD，在梯形图中的分支结构中，当左侧为主控逻辑块时，该指令用于开始第二个和后边更多的从逻辑块。

辑栈弹出指令LPP，在梯形图中的分支结构中，用于恢复LPS指令生成的新母线。

入堆栈指令LDS，复制堆栈中的第n级值，并将该值置于栈顶。

习题参考答案第1章绪论1. 见教材2. 略3. 答：（1）羟基，饱和脂环醇；（2）羟基，不饱和脂环醇；（3）羟基，苯酚；（4）醚键，芳香混醚；（5）醛基，脂肪醛；（6）酮基，脂肪酮；（7）氨基，脂肪胺；（8）磺酸基，芳香磺酸；（9）酮基，酮；（10）羧基与羟基，羟基酸；（11）酯键，酯；（12）羟基与硝基，硝基酚；（13）氨基，芳香胺；（14）卤素，脂肪卤代烃；（15）酰胺键，脂肪酰胺。

4. 答：（1）（2）（3）（4）（5）酸：硫酸和质子化醚水和质子化胺乙酸和水合质子三氟化硼溴负离子碱：乙醚与硫酸氢根胺与氢氧根乙酸根与水甲醚甲基正碳离子5. 答：（2）、（5）、（6）、（7）和（9）属于羧酸类化合物；（1）、（4）、（3）和（8）属于醇类化合物；（2）和（7）同为芳香族羧酸；（6）和（9）同为脂肪酸；（5）为脂环族羧酸；（4）为脂环醇；（1）、（3）和（8）为脂肪醇。

第2章烷烃1.（1）2-甲基丁烷（2）3,3-二甲基己烷（3）2,4,6-三甲基-4-乙基辛烷（4）4,5-二甲基辛烷（5）2,2,4-三甲基戊烷（6）2,3-二甲基己烷（7）3-甲基庚烷（8）2,3-二甲基戊烷2.(1) CH3CHCH2CHCH2CH3CH3CH3(2)C(CH3)4(3)CH3CCHCH3CH3CH3CH3CH(4)CH3CH2CHCH2CH2CH2CH3CH3(5) CH3CHCH2CH3CH3(6)CH3CHCH2CCH2CH2CH3CH3CH2CH3CH33. CH 2CH 3C2CHCH 3CH 3CH 3CH 3C4. (1)(CH 3)2CHCH 2CH 3(2)(CH 3)4C(3)CH 3CH 2CH 2CH 2CH 35.(1) 正庚烷 正己烷 异己烷 新己烷 （2）二十一烷 十八烷 十七烷 十六烷 （3）水 丁烷 甲烷6.CH 3CH 2CH 2CH 2CH 2CH 3(CH 3)2CHCH 2CH 2CH 3CH 3CH 2CH(CH 3)CH 2CH 3(CH 3)3CCH 2CH 3(CH 3)2CHCH(CH 3)27.解答提示：结合甲烷取代反应机理解释。

解 令x a cos t, y a sin t,
I
2 0
1 a2
[a 2
(cos
t
sin
t
)(
sin
t
)
(cos
t
sin
t
)
cos
t
]dt
2
0 dt 2 .
p55. 2.计算 ( x2 2xy)dx ( y2 2xy)dy,其中 L
L为抛物线y x2上从点(1,1)到点(1,1)的一段弧.
C
(2)曲线弧C的重心坐标为
xG
1 x( x, y)ds
MC
,yG
1 y( x, y)ds .
MC
p51.2.设光滑曲线L关于x轴对称, L1是L在x轴上方的部分, (1)若f ( x, y)在L上连续,且关于y为奇函数,则Biblioteka f ( x, y)ds 0 ; L
(2)若f ( x, y)在L上连续,且关于y为偶函数,
(1)当p点从点A(a , 0)经位于第一象限的弧段到 B(0,b)时, F所作的功;
(2)当p点经过全椭圆时,F所作的功.
p56. 解 F | F | F 0 x2 y2 ( x , y ) x2 y2 x2 y2
( x, y),
(1) W F d s ( x)dx ( y)dy
0
22
a2
2
| cos
t
| dt
2a 2
2 cos udu 2a2 .
20
2
0
p52. 3.计算 | xy | ds,其中L :圆周x2 y2 a2. L
解法1
I 4
2
a3
sin t

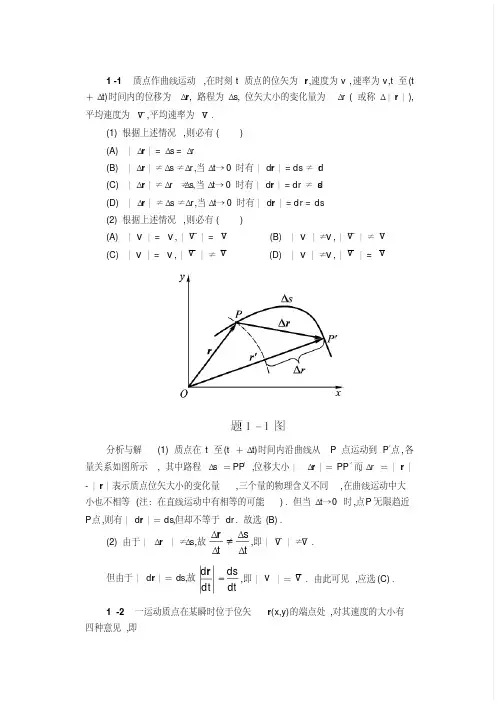
1 -1质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v,t 至(t ＋Δt)时间内的位移为Δr , 路程为Δs, 位矢大小的变化量为Δr ( 或称Δ｜r ｜),平均速度为v ,平均速率为v ．(1) 根据上述情况,则必有()(A) ｜Δr ｜= Δs = Δr(B) ｜Δr ｜≠　Δs ≠　Δr ,当Δt →0 时有｜d r ｜= ds ≠ d r(C) ｜Δr ｜≠　Δr ≠　Δs,当Δt →0 时有｜d r ｜= dr ≠ d s(D) ｜Δr ｜≠　Δs ≠　Δr ,当Δt →0 时有｜d r ｜= dr = ds(2) 根据上述情况,则必有()(A) ｜v ｜= v ,｜v ｜= v (B) ｜v ｜≠v ,｜v ｜≠v(C) ｜v ｜= v ,｜v ｜≠　v (D) ｜v ｜≠v ,｜v ｜= v分析与解(1) 质点在t 至(t ＋Δt)时间内沿曲线从P 点运动到P ′点,各量关系如图所示, 其中路程Δs ＝PP ′, 位移大小｜Δr ｜＝PP ′，而Δr ＝｜r ｜-｜r ｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt →0 时,点P ′无限趋近P 点,则有｜d r ｜＝ds,但却不等于dr ．故选(B)．(2) 由于｜Δr ｜≠Δs,故t st ΔΔΔΔr ,即｜v ｜≠v ．但由于｜d r ｜＝ds,故t st d d d d r ,即｜v ｜＝v ．由此可见,应选(C)．1 -2一运动质点在某瞬时位于位矢r (x,y)的端点处,对其速度的大小有四种意见,即(1)t r d d ；(2)t d d r；(3)t s d d ；(4)22d d d d t y t x．下述判断正确的是()(A) 只有(1)(2)正确(B) 只有(2)正确(C) 只有(2)(3)正确(D) 只有(3)(4)正确分析与解t rd d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量；t d d r表示速度矢量；在自然坐标系中速度大小可用公式t sd d v 计算,在直角坐标系中则可由公式22d d d d t yt x v 求解．故选(D)．1 -3一个质点在做圆周运动时,则有()(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解加速度的切向分量a ｔ起改变速度大小的作用,而法向分量a n 起改变速度方向的作用．质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的．至于a ｔ是否改变,则要视质点的速率情况而定．质点作匀速率圆周运动时, a ｔ恒为零；质点作匀变速率圆周运动时,a ｔ为一不为零的恒量,当a ｔ改变时,质点则作一般的变速率圆周运动．由此可见,应选(B)．1 -4质点的运动方程为23010t t x 和22015t t y ，式中x,y 的单位为m,t 的单位为ｓ。

第1章网上开店概述一、名词解释1．支付宝实名认证支付宝实名认证服务是由浙江支付宝网络科技有限公司与公安部门联合推出的一项身份识别服务。

支付宝实名认证除了核实身份信息以外，还核实了银行账户等信息。

通过支付宝实名认证后，相当于拥有了一张互联网身份证，可以在淘宝网等众多电子商务网站开店、出售商品。

2．淘宝开店认证淘宝开店认证是在淘宝网上开店时注册了账户，支付宝实名认证后进行的确认开店的认证。

需要按照系统提示进行操作，并设置有效经营地址等信息。

3．店铺动态评分店铺动态评分也称卖家服务评级（Detailed Seller Ratings，DSR），只有使用支付宝完成的交易才能进行店铺动态评分。

包括宝贝与描述相符、卖家的服务态度和物流服务的质量，每项店铺动态评分取连续6个月内所有买家给予评分的算术平均值。

4．主图打标打标，“标”是标签的意思，主图打标即在商品的主图上打上促销标识。

淘宝主图打标应该注意：（1）淘宝平台只有主图支持编辑打标，其他图片不支持该功能。

（2）打标在主图上要生效，网店必须开通打标功能，而且需要特定的标签、价格、优惠券等，然后系统会自动填写。

5．分销网站除了淘宝的官方供货平台外，还有很多提供批发服务的分销网站，适合中小卖家选择货源，如购途网（go2）、爱买卖（2mm）、四季星座网（571xz）、杭州女装网（hznzcn）、衣联网（eelly）等。

6．产业带产业带是一条带状的链条产业集中区域，是相关或相同产业的基地。

在此区域内可以形成产业集聚效应，从而更好地壮大产业，如杭州的女装、扬州的毛绒玩具、深圳的3C数码产品、佛山的卫浴产品等。

按阿里巴巴→“源头好货”的顺序查看“产地地图”即可看到不同类目、不同产品的产业带，以及每个产业带工厂的联系信息。

二、单项选择题1～5 A B C B D三、判断题1～6：√√×√×√四、简答题1．常见的网上开店平台有哪些？各有什么特点？答：目前，网店平台有很多，根据其经营性质的不同可以划分为不同类型，如B2B、B2C、C2C等。

（）7. short，int都是C++语言的关键字。

（）8. C++编译系统对源程序编译时，可以检查出注释语句中的语法错误。

（）9. 将一个字符常量放到一个字符变量中，并不是把该字符本身放到内存变量中去，而是将该字符相应的ASCII代码放到存储单元中。

（）10. 语句int answer=3+2 9/(10-6)；执行完毕后，变量answer的值是7.5。

三、单项选择题1. C++源程序文件的扩展名为（）。

（A）.CPP（B）.OBJ（C）.C（D）.EXE2. 下列变量名中，（）是合法的。

（A）double（B）A+a（C）CHINA（D）5s3. 下列符号能用作C++标识符的是（）（A）xyz/2 （B）2xsale （C）x-sale （D）x_sale4. 下列各运算符中，（）只能用于整型数据的运算。

（A）+（B）/（C） （D）%5.（）不是C++的基本数据类型。

（A）字符类型（B）数组类型（C）整数类型（D）布尔类型6. 下列运算符中，优先级最高的是（）。

（A）%（B）！（C）>=（D）/7. 字符串常量“ME”的字符个数是（）。

（A）4（B）3（C）2（D）18. 在C++语言中，080是（）。

（A）八进制数（B）十进制数（C）十六进制数（D）非法数9. 整型变量i定义后赋初值的结果是（）。

int i=2.8 6;（A）12（B）16（C）17（D）1810.如有int m=31;则表达式（m++*1/2）的值是（）。

（A）0 （B）15 （C）15.5 （D）1611.每个C++程序都必须有且仅有一个（）。

（A）预处理命令（B）主函数（C）函数（D）语句12.在C++语言中，自定义的标志符（）。

（A）能使用关键字并且不区分大小写（B）不能使用关键字并且不区分大小写（C）能使用关键字并且区分大小写（D）不能使用关键字并且区分大小写13.下列C++标点符号中表示一条语句结束的是（）。

第一章课后习题及参考答案一、单项选择题1.团队成员能积极主动地补位，这主要体现了团队的（）基本特点。

A．思考性 B．自主性C．凝聚力 D．协作性2.团队最核心的力量是（）。

A．目标 B．人 C．定位D．权限3.能为团队出谋划策，充当创新者和发明者的角色是（）。

A．凝聚者B．实干者C．智多星 D．监督者二、多项选择题1.团队与群体的区别有（）。

A．目标差异 B．协同程度差异 C．责任差异 D．技能差异2.团队的作用有（）。

A．优化的人员组合 B．优化的资源整合C．优化的组织效能 D．优化的成员凝聚力3.团队角色包括（）。

A．推进者 B．完美主义者 C．实干者 D．领导者三、思考题1.团队在现实中有哪些体现？能否举例说明？2.群体可以向团队转化吗？如果可以转化，需要经历哪些阶段？3.你怎么理解贝尔宾团队角色理论？对现实工作、生活有何指导意义？习题答案一、单项选择题1.B2.B3. C二、多项选择题1.ABCD2.ABCD3. ABC三、思考题1.结合现实生活及团队理论，学生要进行案例阐述。

2.群体可以向团队转化。

转化过程一般要经历群体、伪团队、潜在团队、真正团队、高效团队五个阶段。

3.贝尔宾团队角色理论将团队划分为8个角色，分别是推进者、实干者、完美主义者、协调者、凝聚者、外交者、智多星及监督者。

团队角色理论在现实工作、生活中具有很强的指导意义，能指导团队更好组合。

第二章课后习题及参考答案一、单项选择题1.在团队激荡期，比较适宜的团队领导风格是（）。

A．指挥式领导B．参与型领导C．教练型领导 D．委任型领导2.企业所开展的“质量圈”团队形式，属于（）团队类型。

A．问题解决型团队 B．自我管理型团队 C．多功能型团队D．跨组织团队3.在虚拟组织中所存在的新型团队组织形式是（）。

A．电子商务团队B．学习型团队C．创客团队 D．虚拟团队二、多项选择题1.下列属于团队高产期的行为特征有（）。

A．团队成员信心大增 B．协力解决问题 C．分享领导权 D．自我定位模糊2.下列属于自我管理型团队的特征有（）。

++++++++++++++++++++++++++第一章习题答案1-1解：1-2解：1-3解：1-4 解：1-5 解：1-6 解：1-7 解：1-8 解：第二章习题答案2-1 解：群延迟特性曲线略2-2 解：2-3 解：2-4 解：二径传播时选择性衰落特性图略。

2-5 解：2-6 解：2-7 解：2-8 解：第三章习题答案3-4 解：3-5 解：3-6 解：3-7 解：3-8 解：3-9 解：3-10 解：3-11 解：第四章习题答案4-2 解：4-3 解：4-4 解：4-6 解：4-8 解：4-9 解：4-10 解：4-11 解：4-12 解：4-13 解：4-15 解：4-16 解：4-17 解：第五章习题答案5-1 解：，，，（1）波形（2）5-2 解：，，（1）（2）相干接收时5-3 解：，，（1）相干解调时（2）非相干解调时5-4 解：，，，（1）最佳门限：而：所以：（2）包检：5-5 解：系统，，5-6 解：（1）信号与信号的区别与联系：一路可视为两路（2）解调系统与解调系统的区别与联系：一路信号的解调，可利用分路为两路信号，而后可采用解调信号的相干或包检法解调，再进行比较判决。

前提：信号可分路为两路信号谱不重叠。

5-7 解：系统，，，（1）（2）5-8 解：系统，，，，（1）（2）所以，相干解调时：非相干解调时：5-9 解：5-10 解：（1）信号时1 0 0 1 0（2）1 0 1 0 0，5-12 解：时：相干解调码变换：差分相干解调：，，（1）：a：相干解调时解得：b：非相干解调时解得：（2）：（同上）a：相干解调时，b：非相干解调时，（3）相干解调时即在保证同等误码率条件下，所需输入信号功率为时得1/4，即（4）a：差分相干解调时即在保证同等误码率条件下，所需输入信号功率为时得1/4，即b：相干解调的码变换后解得：5-16 解：（A方式）0 1 1 0 0 1 1 1 0 1 0 0 ，5-17 解：（1）时所以（2）时所以5-18 解：5-19 解：，：：一个码元持续时间，含：个周波个周波。

离散数学答案屈婉玲版第二版高等教育出版社课后答案第一章部分课后习题参考答案16设p、q的真值为0；r、s的真值为1，求下列各命题公式的真值。

（1）p∨(q∧r)⇔0∨(0∧1)⇔0（2）（p?r）∧(﹁q∨s)⇔（0?1）∧(1∨1)⇔0∧1⇔0.（3）（⌝(4)（176能被2q:3r:2s:619（4）(p（5）(p（6）((p答：（pqp→q⌝0011111011011110010011110011所以公式类型为永真式（5）公式类型为可满足式（方法如上例）（6）公式类型为永真式（方法如上例）第二章部分课后习题参考答案3.用等值演算法判断下列公式的类型，对不是重言式的可满足式，再用真值表法求出成真赋值.(1)⌝(p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)答：(2)（p→(p∨q)）∨(p→r)⇔(⌝p∨(p∨q))∨(⌝p∨r)⇔⌝p∨p∨q∨r⇔1所以公式类型为永真式(3)P qrp∨qp∧r（p∨q）→(p∧r)0000010010014.(2)(p→(4)(p∧证明（2（45.(1)(⌝p→q)→(⌝q∨p)(2)⌝(p→q)∧q∧r(3)(p∨(q∧r))→(p∨q∨r)解：（1）主析取范式(⌝p→q)→(⌝q∨p)⇔⌝(p∨q)∨(⌝q∨p)⇔(⌝p∧⌝q)∨(⌝q∨p)⇔(⌝p∧⌝q)∨(⌝q∧p)∨(⌝q∧⌝p)∨(p∧q)∨(p∧⌝q)⇔(⌝p∧⌝q)∨(p∧⌝q)∨(p∧q)⇔∑(0,2,3)主合取范式：(⌝p→q)→(⌝q∨p)⇔⌝(p∨q)∨(⌝q∨p)⇔(⌝p∧⌝q)∨(⌝q∨p)⇔(⌝p⇔1∧(p⇔(p∨⇔∏(2)⌝(p→q)⇔(p∧(3)⇔⌝⇔1∧1⇔1所以该式为永真式.永真式的主合取范式为1主析取范式为∑(0,1,2,3,4,5,6,7)第三章部分课后习题参考答案14.在自然推理系统P中构造下面推理的证明：(2)前提：p→q,⌝(q∧r),r结论：⌝p(4)前提：q→p,q↔s,s↔t,t∧r结论：p∧q证明：（2）①⌝(q∧r)前提引入②⌝q∨⌝r①置换③q→⌝r②蕴含等值式④r⑤⌝q⑥p→q⑦￢p（3证明（4①t②t③q④s⑤q⑥（⑦（⑧q⑨q⑩p15在自然推理系统P中用附加前提法证明下面各推理：(1)前提：p→(q→r),s→p,q结论：s→r证明①s附加前提引入②s→p前提引入③p①②假言推理④p→(q→r)前提引入⑤q→r③④假言推理⑥q前提引入⑦r⑤⑥假言推理16在自然推理系统P中用归谬法证明下面各推理：(1)前提：p→⌝q,⌝r∨q,r∧⌝s结论：⌝p证明：①p②p③﹁④￢⑤￢⑥r⑦r⑧r3.:(1)均有2=(x+)(x).(2)其中(a)(b)解：F(x):2=(x+)(x).G(x):x+5=9.(1)在两个个体域中都解释为)(x∀，在（a）中为假命题，在(b)中为真命题。

第1-5章和第8-10章习题和复习题参考答案第1章函数、极限与连续习题⒈下列各组函数，哪些是同一函数，哪些不是？（1）yx =与是同一函数 （2）y x =与y=（3）2111x y x x -=-+与y=不是同一函数 （4）22ln ln y x x =与y=不是同一函数⒉指出下列函数的定义域. （1）43)(+=x x f 的定义域是),34[+∞- （2）xx f -=11ln )(的定义域是)1,(-∞（3）)1ln()(2-=x x f 的定义域是),2[]2,(+∞⋃-∞（4）)arcsin(ln )(x x f =的定义域是],1[e e-（5）若)(x f 的定义域是]4,4[-，则)(2x f 的定义域是]2,2[-（6）若)(x f 的定义域是]3,0[a ，则)()(a x f a x f -++的定义域是]2,[a a 3.判别下列函数的奇偶性.（1）()sin f x x x =+是奇函数 （2）()cos f x x x =⋅是奇函数（3）()2f x x x =-是非奇非偶函数 （4）()1lg 1x f x x-=+是奇函数（5）()cos(sin )f x x =是偶函数 （6）()sin x f x x=是偶函数（7）())f x x =是奇函数 （8）()f x =是偶函数⒋下列函数哪些在其定义域内是单调的. （1）sin y x =在其定义域内不是单调的（2）arcsin y x =在其定义域内是单调递增的 （3）2y x x =-在其定义域内不是单调的 （4）0≠a 时，ax y e =在其定义域内是单调的，其中 0<a 时，ax y e =在其定义域内是单调递减的， 0>a 时，ax ye =在其定义域内是单调递增的5.下列函数在给定区间中哪个区间上有界. （1）),1(1+∞=在区间xy 上有界（2）)10,1()12ln(在区间-=x y 上有界 （3）)4,3(3-=在区间x y 上有界（4）)1,1(),,(),0,(sin -+∞-∞-∞=在区间x y 上分别有界 6.下列函数哪些是周期函数，如果是求其最小正周期. （1）sin 3yx =是周期函数，最小正周期是32π （2）cos y x =是周期函数，最小正周期是π （3）tan 2y x =是周期函数，最小正周期是2π （4）ln(cos 2)y x =+是周期函数，最小正周期是π 7.下列各对函数中，哪些可以构成复合函数.（1）2),2arcsin()(x u u u f =+=不可以构成复合函数 （2）x u u u f 2sin ),1ln()(=-=不可以构成复合函数（3）221ln,)(x u u u f +==不可以构成复合函数（4）212,arccos )(xxu u u f +==可以构成复合函数 8.将下列复合函数进行分解. （1）对复合函数43)(2--=x x x f 的分解结果是：43,)(2--==x x u u x f（2）对复合函数32)(-=x ex f 的分解结果是：32,)(-==x u e x f u（3）对复合函数()ln(23)f x x =-的分解结果是：32,ln )(-==x u u x f（4）对复合函数()arcsin(1)f x x =+的分解结果是：1,sin )(+==x u u acc x f 9.求函数值或表达式. （1）已知函数12)(,2)0(,4-)2(,0)2(,12)(222+-===-=+-=x x x f f f f x x x f 则.（2）已知函数0)(,22)4(,0)1(,1,01,sin )(===⎩⎨⎧≥<=ππf f f x x xx f 则.（3）已知函数21-)21arcsin (,sin )(=-=f x x f 则. （4）已知函数x x f 2cos )(sin =，则[]1,1,21)(2-∈-=x x x f习题1.用观察法判断下列数列是否有极限，若有，求其极限. （1）Λ,67,51,45,31,23,1:n x 没有极限（2）n x n 1=有极限，01lim =∞→nn （3）2sinπn x n =没有极限 （4）1)1(3+-=n n x nn 有极限，0]1)1[(lim 3=+-∞→n n n n2.分析下列函数的变化趋势，求极限 （1）01lim2=∞→x x （2）011lim =++∞→x x （3）+∞=++∞→)2ln(lim x x （4）2232lim=++-∞→x x x3.图略，)(lim 0x f x →不存在4.下列变量中，哪些是无穷小量，哪些是无穷大量？（1）0→x 时，2100x 是无穷小量 （2）+→0x 时，x2是无穷大量（3）∞→x 时，112--x x 是无穷小量 （4）+∞→x 时，xe 是无穷大量 （5）∞→n 时，3)1(2+-n n n是无穷大量 （6）∞→x 时，xxsin 是无穷小量（7）∞→x 时，x1sin 是无穷小量 （8）0→x 时，12-x是无穷小量 5.已知函数2)3(1)(--=x x x f ，则)(x f 在-∞→x 或+∞→x 或∞→x 的过程中是无穷小量，在-→3x 或+→3x 或3→x 的过程中是无穷大量？6. 当1x →-时，无穷小1x +与下列无穷小是否同阶？是否等价？ （１）当1x →-时，无穷小1x +与无穷小31x +同阶，但不等价 （２）当1x →-时，无穷小1x +与无穷小21(1)2x -同阶，而且等价习题1.设函数x x f =)(，则xt x f t x f t 21)()(lim=-+→2.设函数⎩⎨⎧<+≥+=2,122,1)(2x x x x x f ，则5)(lim ,5)(lim ,5)(lim 222===→→→+-x f x f x f x x x .3.求下列各式的极限：（1）15)52(lim 22=+--→x x x （2）3213lim 2421-=++-→x x x x（3）35)321(lim 0=--→x x （4）242lim 22=+-∞→x x x x （5）2111lim 220-=+-→x x x （6）21)21(lim 222=+++∞→n n n n n Λ （7）1122lim2=-+++∞→x x x x （8）311lim 31=--→x x x（9）61)319(lim 2=-++∞→x x x x （10）112lim1=---→x x x x （11）201020101032)53()32()1(lim =---+∞→x x x x 4.已知516lim21-=-+-→x ax x x ，则7=a . 5.2)(lim 2=-++∞→x kx x x ，则4=k .6.求下列极限：（1）252sin 5sin lim0=→x x x （2）1sin 2tan lim 0=-→xxx x（3）43cos cos lim 20=-→x x x x （4）2)sin()2tan(lim 230=-+→x x x x x （5）11sin lim =⋅∞→xx x （6）0sin sin lim 0=+-→x x xx x（7）323arcsin 2lim 0=→x x x （8）21sin tan lim 30=-→x x x x7.求下列极限： （1）82)41(lim e x x x =+∞→ （2）21)21(lim --∞→=-e xx x（3）3220)33(lim -→=-e x x x （4）21)11(lim --∞→=+-e x x x x（5）5ln 51)ln 1(lim e x xx =++→ （6）e x x x =+→sec 2)cos 1(lim π8.用等价无穷小替换计算下列各极限：（1）236arctan lim0=→x x x （2）214lim 20=-→x x e x（3）22cos 1lim 20=-→x x x （4）21)21ln(lim 0=-+→x x e x 习题1.设函数⎪⎩⎪⎨⎧=≠--=1,31,11)(2x x x x x f ，则()f x 在1=x 处不连续．2.指出下列函数的间断点，并指明是哪一类间断点？ （1）函数11)(2-=x x f 的间断点有点1-=x 和点1=x ，它们都是第二类间断点中的无穷间断点（2）函数xe xf 1)(=的间断点有点0=x ，它是第二类间断点（3）函数xx x x f )1(1)(2--=的间断点有点0=x 和点1=x ，其中点0=x 是第二类间断点中的无穷间断点，点1=x 是第一类间断点（4）函数⎪⎩⎪⎨⎧-=-≠+-=1,01,11)(2x x x x x f 的间断点有点1-=x ，它是第一类间断点中的可去间断点（5）函数⎩⎨⎧>≤+=0,2,2)(2x x x x f x 的间断点有点0=x ，它是第一类间断点中的跳跃间断点（6）函数⎪⎩⎪⎨⎧=≠--=2,32,24)(2x x x x x f 的间断点有点2=x ，它是第一类间断点中的可去间断点3.设函数⎪⎪⎪⎩⎪⎪⎪⎨⎧>+=<=0,11sin 0,0,sin )(x x x x k x xxx f ，当1=k 时，函数)(x f 在其定义域内是连续的.4.求下列极限：（1）42arccoslim 21π=+→x x x （2）0sin lg lim 2=→x x π （3）021lim cos sin 0=+-→x x x e e （4）2ln ln )1ln(lim 1=-+→xxx x（5）2121lim 224=+++∞→x x x x （6）11lim 1=--→x xx x（7）e x x e x 1ln lim=→ （8）4arctan lim 1π=→x x5.（略）6.（略）复习题1一、单项选择题1.下列函数中（C ）是初等函数.（A ）)2arcsin(2+=x y （B ）⎩⎨⎧∈∉=Qx Qx x f 10)(（C ）12+-=x y （D ）⎩⎨⎧>+<≤=1110)(2x x x x x f2.下列极限存在的是（B ）.（A ）xx 4lim ∞→ （B ）131lim 33-+∞→x x x （C ）xx ln lim 0+→ （D ）11sin lim 1-→x x3.当0x →时，2tan x 与下列（D ）不是等价无穷小.（A ）2tan x （B ）2x （C ）2sin x （D ）2cos x 4.函数在某点连续是该函数在此点有定义的（B ）.（A ）必要条件 （B ）充分条件 （C ）充分必要条件 （D ）无关条件 5.已知0sin lim2x axx→=,则常数=a （C ）.（A ）0 （B ）1 （C ）2 （D ）4 6.闭区间[,]a b 上的连续函数()y f x =在[,]a b 上一定是（C ）.（A ）单调函数 （B ）奇函数或偶函数（C ）有界函数 （D ）周期函数 二、填空题 1.设10()20xx x f x x +-∞<≤⎧=⎨<<+∞⎩， 则(2)f = 4 . 2.函数5cos 3y x =是由简单函数 x v v u u y 3,cos ,3=== 复合而成的. 3.点1x =是函数1,1()3,1x x f x x x -≤⎧=⎨->⎩ 的第一类间断点中的跳跃 间断点.4.当x ∞- 时，函数3xy =是无穷小.5.极限 2lim 1xx x →∞⎛⎫- ⎪⎝⎭= 2e .6.函数ln(4)y x =-+的连续区间为 [)4,1 .三、计算下列极限1.24231x x x x -++=0 2.223lim 2x x x →--不存在 3.2211lim 21x x x x →---21= 4.22356lim 815x x x x x →-+-+ 5.1)2(1lim 22=---∞→x x x x 6.4281lim5x x x x →∞-++ 不存在 7.63132lim1=--+→x x x 8.231lim (3cos )1x x x x →∞+++=09.21sin cos 1lim0=-→θθθθ 10.1cos lim =-∞→x x x x 11.212sin )1ln(lim0=+→x x x 12.21)81221(lim 32=---→x x x13.320lim(12)xx x →-3-=e 14.122lim(1)xx x-→∞- 1-=e15.11lim x x x x +→+⎛⎫⎪⎝⎭e = 16.1lim()1xx x x →∞-+ 2-=e 四、综合题1.函数2101()11x x f x x x ⎧-≤≤=⎨+>⎩在点1=x 处不连续，在点2=x 处连续，函数的图像略。

第一章教育与教育学一、选择题1．原始社会末期，担负教育年轻一代主要任务的是（B）A．学校教育B．家庭教育C．社区教育D．社会教育2．我国奴隶社会的教育内容是（B）A．四书五经B．六艺C．自然科学D．生产技能3．我国最早使用“教育”一词的是（B）A．孔子B．孟子C．许慎D．朱熹4．构成教育活动最基本的要素是（D）。

A．教育者、受教育者、教育形式B．受教育者、教育内容、教育形式C．教育内容、教育形式D．教育者、受教育者、教育中介系统5．人的教育活动和动物的“教育活动”的本质区别是（B）。

A．模仿性B．目的性C．规律性D．社会性E．复杂性6．中国历史上最早提出“教学相长”的著作是（ C ）A．《大学》B．《中庸》C．《学记》D．《春秋》7．教育的“心理起源论”认为教育起源于（ B ）。

A．生产劳动B．模仿C．语言D．动物本能8．我国当前教育最薄弱的环节是（D）。

A．普通教育B．职业教育C．高等教育D．学前教育9．“官守学业”、“学在官府”体现了教育的( D)。

A．强迫性B．民主性 C.基础性D．阶级性10．教育是年轻一代成长和社会延续与发展不可缺少的条件，为一切社会所必需，与人类社会共始终。

从这个意义上说，教育具有（B）。

A．生物性B．永恒性C．历史性D．阶级性11．学校教育产生于（B）。

A．原始社会B．奴隶社会C．封建社会D．资本主义社会12．人类最早的学校产生于（A）。

A．公元前2500年的埃及B．公元前21世纪的夏朝C．公元前3000年的古巴比伦D．公元前2500年的印度二、辨析题1、教育是人类社会永恒的普遍的现象。

(√)解析：教育是年轻一代成长和社会延续与发展不可缺少的条件，为一切社会所必需，与人类社会共始终。

从这个意义上说，教育具有永恒性。

2、教育同生产劳动相分离是现代教育的基本特征。

(×)解析：教育同生产劳动相分离是古代教育的基本特征，教育与生产劳动相结合才是现代教育的特征。

3、终身教育和全民教育已经成为当代社会两大教育思潮。