“中考数学专题复习 圆来如此简单”经典几何模型之隐圆专题(含答案)

经典几何模型之隐圆”“圆来如此简单”

一.名称由来

在中考数学中，有一类高频率考题，几乎每年各地都会出现，明明图形中没有出现“圆”，但是解题中必须用到“圆”的知识点，像这样的题我们称之为“隐圆模型”。

正所谓：有“圆”千里来相会，无“圆”对面不相逢。“隐圆模型”的题的关键突破口就在于能否看出这个“隐藏的圆”。一旦“圆”形毕露，则答案手到擒来！

二.模型建立

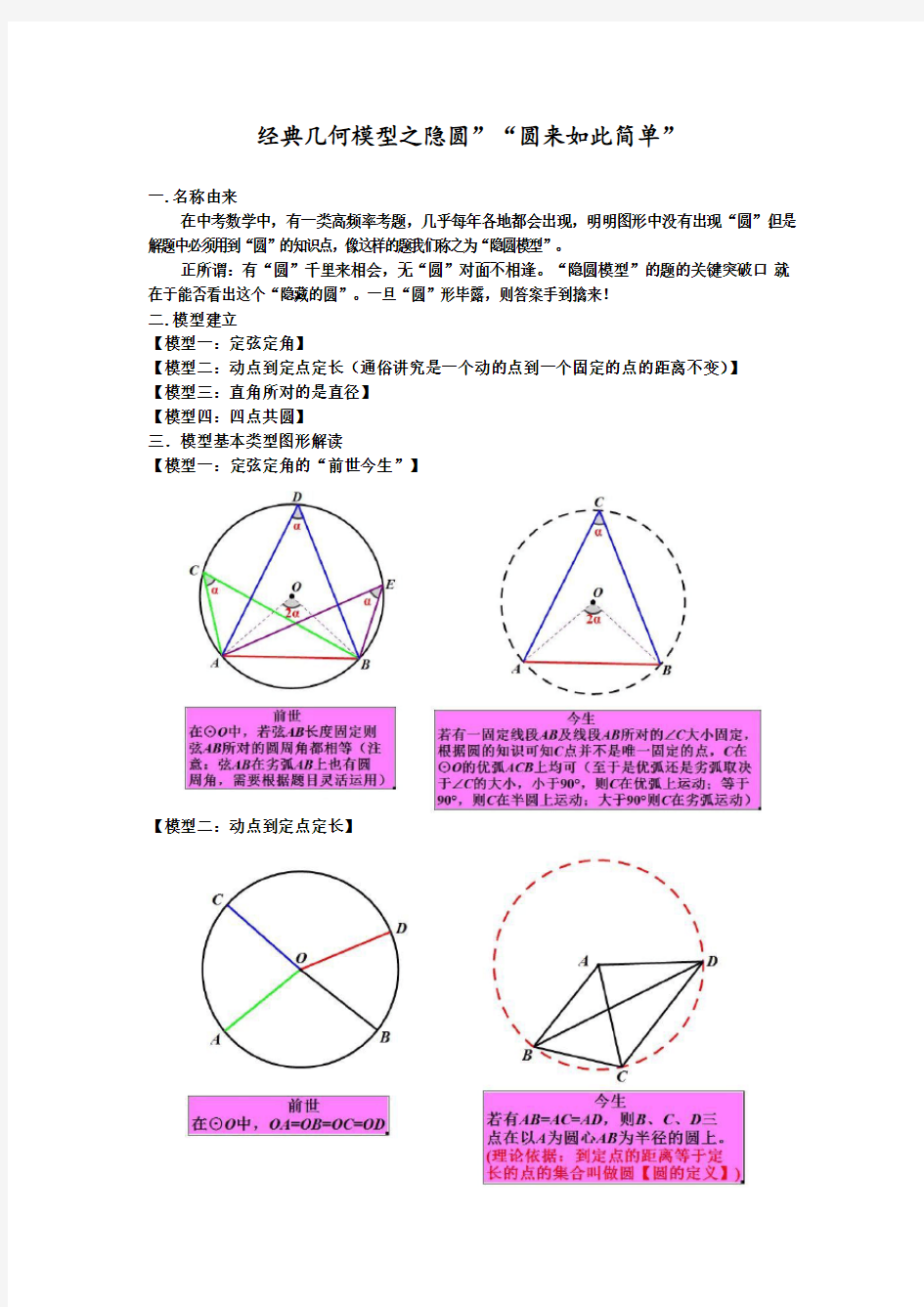
【模型一：定弦定角】

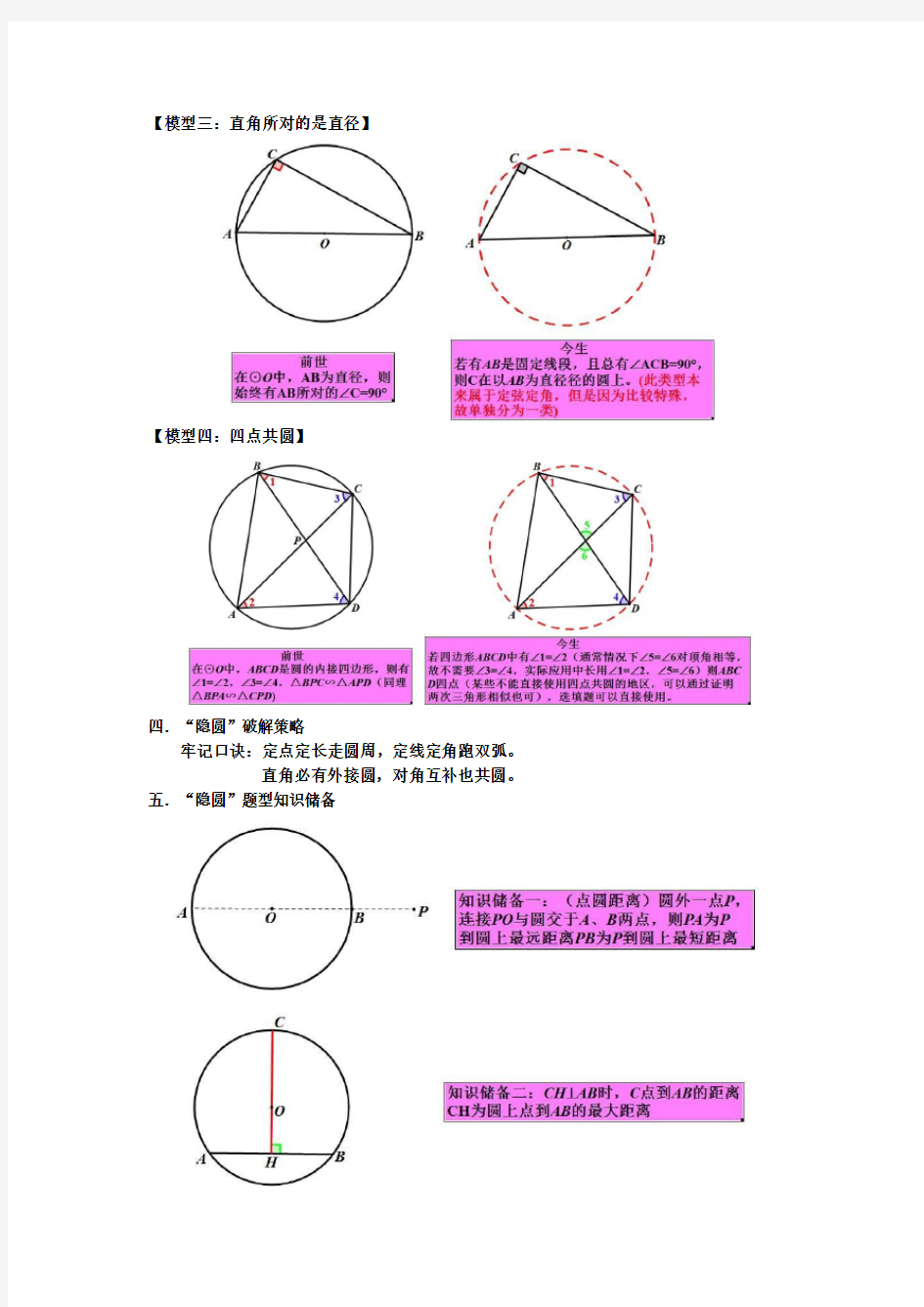
【模型二：动点到定点定长（通俗讲究是一个动的点到一个固定的点的距离不变）】

【模型三：直角所对的是直径】

【模型四：四点共圆】

三．模型基本类型图形解读

【模型一：定弦定角的“前世今生”】

【模型二：动点到定点定长】

【模型三：直角所对的是直径】

【模型四：四点共圆】

四．“隐圆”破解策略

牢记口诀：定点定长走圆周，定线定角跑双弧。

直角必有外接圆，对角互补也共圆。五．“隐圆”题型知识储备

3

六．“隐圆”典型例题 【模型一：定弦定角】

1.（2017 威海）如图 1，△ABC 为等边三角形，AB =2，若 P 为△ABC 内一动点，且满足 ∠PAB =∠ACP ，则线段 PB

长度的最小值为_

。

简答：因为∠PAB =∠PCA ，∠PAB +∠PAC =60°，所以∠PAC +∠PCA =60°，即∠APC =120°。因为 AC 定长、∠APC =120°定角，故满足“定弦定角模型”，P 在圆上，圆周角∠APC =120°，通过简单推导可知圆心角∠AOC =60°，故以 AC 为边向下作等边△AOC ，以 O 为圆心，OA 为半径作⊙O ，P 在⊙O 上。当 B 、P 、O 三点共线时，BP 最短（知识储备一：点圆距离），

此时 BP =2 -2

2. 如图 1 所示，边长为 2 的等边△ABC 的原点 A 在 x 轴的正半轴上移动，∠BOD =30°，

顶点 A 在射线 OD 上移动，则顶点 C 到原点 O 的最大距离为 。

3 2 2 简答：因为∠AOB =30°（定角），AB =2（定弦），故 A 、B 、O 三点共圆，圆心角为 60°，故以 AB 为边向 O 方向作等边△ABQ ，∠AQB =60°为圆心角，Q 为圆心，以 QA 为半径作 ⊙ Q （ 如 图 2 ）， 由 知 识 储 备 二 可 知 当 OC ⊥ AB 时 ， OC 距 离 最 大 ，

OC =OQ +QH +HC =2+ + =2+2 【思考：若∠BOD =45°呢？（提示：需要构造倍角

模型）】 3. 如图 1，点 A 是直线 y =-x 上的一个动点，点 B 是 x 轴上的动点，若 AB =2，则△AOB 面积最大值为（ ） A. 2 B . + 1

C. -1

D.

2

简答：因为 AB =2（定弦），∠AOB =135°（定角），因为∠AOB 是圆周角，故圆心角为 90°，以 AB 为斜边向上方作等腰直角△QAB ，则 Q 为圆心（如图 2），由“知识储备二”可知，当 OQ ⊥ AB 时 ， 此 时 △ OAB 的 高 OH 最 大 ， 面 积 最 大 。 面 积 为 1 AB ? OH = 1

? 2 ? ( 2 - 1) = 2 2

2 - 1 ，所以此题选择 B 。 同学：老师，你说错答案了，选 C 。 小段老师：没错啊，就选 B 啊。同学：你是老师，你说了算，你开心就好...

3 3 2

3

3

小段老师：题目有告诉你们A、B 在哪里吗，为什么想当然觉得∠AOB=135°呢，难道不可

能等于 45°吗？如图 3，构建⊙Q，由“知识储备二”可知当OQ⊥AB 时，此时△OAB 的

面积最大为

1

AB ?OH =

1

? 2 ? ( 2 +1) =

2 2

2 +1 ，故答案选B

4.如图 1，AC 为边长为2 的菱形ABCD 的对角线，∠ABC=60°，点M、N 分别从点B、

C 同时出发，以相同速度沿BC、CA 向终点C 和A 运动，连接AM 和BN，求△APB 周长

的最大值

简答：如图 2，由M、N 点速度相同可知BM=CN，易证△ABM≌△BCN，故∠NBC=∠BAM （如图2），又因为∠NBC+∠ABN=60°，所以∠BAM+∠ABN=∠APN=60°（外角性质），

所以∠APB=120°（定角），又因为AB长度固定（定弦），故以AB为底向左侧构建等腰△ QAB，∠AQB=120°，则P 在⊙Q 上，由“知识储备三”可知，当△ABP 是等腰三角形时，

△ABP 周长最短。又由△APB 是定角为120°的等腰三角形，故AP:BP:AB=1:1: ，

AB=AC=2，故PB=PA=2，故△ABP 的周长最大值为 4+2

【模型二：动点到定点定长】

1.如图1，四边形ABCD 中，AB=AC=AD,若∠CAD=76°，则∠CBD= 度。

简答：如图 2，因为AB=AC=AD，故B、C、D 三点在以 A 为圆心的圆上，故∠CBD=

1

∠

2

CAD=38°

2.如图，在△ABC 内有一点D，使得DA=DB=DC，若∠DAB=20°，则∠ACB= 。

33

简答：如图 2，因为DA=DB=DC，故A、B、C 三点在⊙D 上，∠DAB=∠DBA=20°，故∠

ADB=140°，故∠ACB= 1

∠ADB=70°

2

3.如图 1，已知四边形ABCD 中，AB∥CD，AB=AC=AD=5，BC=6，求BD

简答：因为∠1=∠2，AD∥BC，故∠3=∠1，∠4=∠2，故易证△AEB≌△ACD，故EB=CD=6，ED=2AD=10，故BD=8

4.如图 1，长 2 米的梯子AB 竖直放在墙角，在沿着墙角缓慢下滑直至水平地面过程中，梯子AB 的中点P 的移动轨迹长度为？

.

简答：由斜边上的中点等于斜边的一半可知，OP=1，动点P 到定点O 的距离始终等于 1，满足圆的定义（到定点的距离等于定长的点的集合叫做圆），故P的运动轨迹是圆弧，圆心角为90°，轨迹长度为四分之一圆的长度，省略。

5.在矩形ABCD 中，已知AB=2，BC=3，现有一根长为 2 的木棒EF 紧贴着矩形的边（即

两个端点始终落在矩形的边上），接逆时针方向滑动一周，则木棒 EF 的中点 P 在运动过程中所围成的围形的面积为？

如图 1 如图 2

简答：由上一题可知，P 的运动轨迹是圆弧，因为滑动一周，故有四个圆弧，则点 P 所围

成的图形为中间的图形，用矩形的面积减去四个四分之一圆的面积即可，答案： 6 -π

6. 如图 1，在矩形 ABCD 中，AB =2，AD =3，点 E ，F 分别为 AD 、DC 边上的点，且 EF =2， G 为 EF 的中点，P 为 BC 边上一动点，则 PA +PG 的最小值为？

如图 1 如图 2

简单：G 的运动轨迹为圆，求 AP +PG 典型的“将军饮马”问题，故做 A 关于 BC 的对称点A ＇，则 AP +PG =A ＇P +PG ，当 A ＇、P 、G 三点共线时，最短，又因为 A ＇为固定点，G 在圆上运动，由“知识储备一”可知当 A ＇、G 、D 三点共线时，此时 A ＇G 最短，为 4

7. 在平面直角坐标系中，点 A 的坐标为（3，0），B 为 y 轴正半轴上的点，C 为第一象限内

的点，且 AC =2.设 t AN ∠BOC =M ，则 M 的取值范围为？

简答：因为 AC =2，A 是定点，通过圆的定义（到定点的距离等于定长的点的集合叫做圆） 可知，C 在⊙A 上运动，当 OC 与⊙A 相切时，此时∠BOC 最小，t AN ∠BOC 也最小，此

时∠BOC +∠AOC =∠AOC +∠CAO =90°，故∠BOC =∠CAO ，此时 t AN ∠CAO = OC = 5

，

AC 2

3 3 又因为角度越大，正切值越大，故 t AN ∠BOC =M ≥ 5

2

8. 如图 1，在 R t△ABC 中，∠C =90°，AC =7，BC =8，点 F 在边 AC 上，并且 CF =2，点 E

为边 BC 上的动点，将△CEF 沿直线 EF 翻折，点 C 落在点 P 处，则点 P 到边 AB 距离的最小值是？

简答：E 是动点，导致 EF 、EC 、EP 都在变化，但是 FP =FC =2 不变，故 P 点到 F 点的距离永远等于 2，故 P 在⊙F 上运动，如图 2。由垂线段最短可知，FH ⊥AB 时，FH 最短， 当 F 、P 、H 三点共线时，PH 最短，又因为△AFH ∽△ABC ，所以 AF :FH :AH =5:4:3，又因为 AF =5，故 FH =4，又因为 FP =2，故 PH 最短为 2 9. 如图，在□ABCD 中，∠BCD ＝30°，BC ＝4，CD ＝ 3 3 ，M 是 AD 边的中点，N 是 AB 边上一动点，将△AMN 沿 MN 所在直线翻折得到△PMN ，连接 PC ，则 PC 长度的最小值是？

简答：翻折过程中，MP =MA =2，故 P 在⊙M 上运动，当 M 、P 、C 三点共线时，PC 最短。

PC =MC -MP ，要求 MP 需要过 M 作 MH ⊥CD 于 H ，∠HDM =30°，故 HM =1，HD = ，

故 HC =4 ，故易求 MC =7，则 PC =7-2=5

【模型三：直角所对的是直径】

1. 如图 1，R t△ABC 中，AB ⊥BC ，AB =6，BC =4，P 是△ABC 内部的一个动点，且始终有 AP ⊥BP ，则线段 CP 长的最小值为？

2 2

简答：如图 2，因为 AP ⊥BP ，∠P =90°（定角），AB =6（定弦），故 P 在以 AB 为直径的 ⊙H 上，当 H 、P 、C 三点共线时 CP 最短，HB =3，BC =4 则 HC =5，故 CP =5-3=2 2. 如图 1，A （1,0）、B （3,0），以 AB 为直径作圆 M ，射线 OF 交圆 M 于 E 、F 两点，C 为弧 AB 的中点，D 为弦 EF 的中点，当射线绕 O 旋转时，CD 的最小值为？

简答：因为 D 是 EF 中点，故 MD ⊥EF ，故∠ODM 始终等于 90°，故 D 在以 OM 为直径的圆上，如图 2。易知 A 为圆心，当 A 、D 、C 三点共线时，CD 最短，CD =AC -AD ，又易

知 C （2,1），故 AC = ，故 CD = -1

3. 在△ABC 中,∠ABC =90,AB =6,BC =8,O 为 AC 的中点,过 O 作 OE ⊥OF ,OE 、OF 分别交

射线 AB ,BC 于 E 、F ，则 EF 的最小值为？

简答：因为∠EOF=90°，∠C=90°，故C、O均在以EF为直径的圆上（也称四点共圆），因为EF 是圆的直径，O、C 均在圆上，且OC 长度固定，要使得EF 最短，则圆最小，要使圆最小，OC 为固定长度，则OC 为直径时，圆最小（此处比较难，思维量比较大，大家慢慢琢磨），此时CO=EF=OA=OB=5（斜边上中线等于斜边一半）

4.如图 1，已知R t△ABC 中，AC＝5，BC＝12，∠ACB＝90°，P 是边AB 上的动点，Q 是边BC 上的动点，且∠CPQ＝90°，求线段CQ 的取值范围．

简答：以CQ 为直径作⊙O，根据直径所对的圆周角是直角，若AB 边上的动点P 在圆上，∠CPQ就为直角．当⊙O与AB相切时（如图2），直径CQ最小．由切线长定理，得AP＝

AC＝5，所以BP＝13―5＝8．再根据△BPO∽△BCA，所以OP

＝10

，CQ＝

20

．当点Q 3 3

与点B重合时（如图3），直径CQ最大，此时ＣＱ＝１２．综上所述，20

≤CQ≤12 3

5.如图 1，半径为 4 的⊙O 中，CD 为直径，弦AB⊥CD 且过半径OD 的中点，点E 为⊙O

上一动点，CF⊥AE 于点F．当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径

长为？

简答：因为∠CFA=90°（定角），AC=4（定弦），故F在以AC为直径的⊙Q上，当E

在B 处时，F 在G 处，当 E 在 D 处时，F 在 A 处，故 F 的运动路径为弧AG 的长度，易求

60

出∠ACD=30°，故∠AQG=60°，故弧AG 长度=? 2π? 2 3= 2 3

360 3

6.（2013 武汉）如图 1，E，F 是正方形ABCD 的边AD 上两个动点，满足AE=DF．连接CF 交BD 于点G，连接BE 交AG 于点H．若正方形的边长为 2，则线段DH 长度的最小

3

5 3 值是？

简答：易证△ABE ≌△DCF ，△DAG ≌△DCG ，故∠DAG =∠DCG =∠ABE ，又因为∠ABE + ∠AEB =90°，故∠EAH +∠AEH =90°，故∠AHB =90°，故 H 在以 AB 为直径的⊙O 上，

当 O 、H 、D 三点共线的时候 DH 最小，DH =OD -OH = -1

7.如图 1，在 R t△ABC 中，∠B =90°，∠C =30°，AB =1，D 为线段 AC 上一动点，将△ BDC 沿着 BD 翻折，点 C 的对应点为 F ，E 为 AC 的中点，在 D 从 C 到 A 的运动过程中， 当 EF 最短时，CD 为？

简答：在折叠过程中，BF 始终等于 BC ，故 F 到 B 点的距离是定值，F 在⊙B 上，当 EF 最短时，B 、E 、F 三点共线（如图 2），此时∠BFD =∠BCD =30°，∠FBD =∠CBD =15°（因为 BE =CE ，故∠EBC =∠BCE =30°），故∠FDH =∠CDH =45°，∠FED =60°，故 FD ⊥CE ，

EF =BF -BE = -1 ， 又 因 为 DF =DC ， 在 R t △ EDF 中 ED = 1

EF = 3 -1 ， 故

CD =1-ED =1 -

2 2

3 -1 = 3 - 3

2 2

8.（2017 宿迁）如图，在矩形纸片 ABCD 中，已知 AB =1，BC = ，点 E 在边 CD 上移动， 连接 AE ，将多边形 ABCE 沿直线 AE 翻折，得到多边形 AB ′C ′E ，点 B 、C 的对应点分

别为点 B ′、C ′．

（1） 当 B ′C ′恰好经过点 D 时（如图 1），求线段 CE 的长；

（2） 若 B ′C ′分别交边 AD ，CD 于点 F ，G ，且∠DAE =22.5°（如图 2），求△DFG 的

面积；

3

6 （3） 在点 E 从点 C 移动到点 D 的过程中，求点 C ′运动的路径长．

简答：（1）“K 字形”秒杀，过程略，答案： - 2

（2） 由翻折全等可知∠B ′AE =∠BAE =67.5°，又因为∠DAE =22.5°，故∠B ′

AF =45°，故△AB ′F 、△DFE

均为等腰直角三角形，后面略，答案：

5 - 2

（3）

折叠过程中始终有 AC ＇=AC ，故 C ＇在以 A 为圆心，AC 为半径的圆上。根据点 E 在 C 时，C ＇在 C 点，点 E 移动到 D 时，C ＇在如图 3 位置，

易求 C ′运动的圆弧的圆心角为 60°，故 C ′运动的轨迹为 60 ? 2π? 2= 2

【模型四：四点共圆】

360 3 1. 如图 1，正方形 ABCD 中，∠EAF =45°，AF 与 BD 交于 N ，AE 与 BD 交于 M ，连接MF 、NE ，求证△ANE 、△AMF 是等腰直角三角形

6

π

简答：因为∠1=∠2=45°，∠3=∠4，故 A 、B 、E 、N 四点共圆，因为∠ABE =90°，故 AE 为直径，故∠ANE =90°，故△ANE 是等腰直角三角形，同理可证△AMF 是等腰直角三角形

（此题也是很经典的“半角模型”问题之一）

2. 如图 1，等边△ABC 中，AB =6，P 为 AB 上一动点，PD ⊥BC ，PE ⊥AC ，则 DE 的最小值为？

简答：因为∠PEC =∠PDC =90°，故四边形 PDCE 对角互补，故 PDCE 四点共圆，如图 2。 ∠EOD =2∠ECD =120°，故 ED = 3R ，要使得 DE 最小则要使圆的半径 R 最小，故直径 PC

最小，当 CP ⊥AB 时，PC 最短为3 ，故 R

=

3 3

，故 DE = 2

3R = 3 ? 3 3 = 9

2 2 3. 如图，正方形 ABCD 绕点 A 逆时针旋转到正方形 APQR ，连接 CQ ，延长 BP 交于 CQ 于点 E ，求证：E 是线段 CQ 的中点

3

3

简答：因为 AC =AQ ，AB =AP 且∠BAP =∠CAQ （旋转角相等）故△APB ∽△AQC ，故∠ABP = ∠ACQ 又因为∠1=∠2，故 A 、B 、C 、E 四点共圆（如图 2），因为∠ABC =90°，故 AC 是直径，故∠AEC =90°，又因为 AQ =AC ，所以 AE 垂直且平分 QC （三线合一）

4. 如图 1，已知△ABC 是边长为 4 的等边三角形，取 AC 的中点 E ，△ABC 绕 E 点旋转任意角度得到△GMN ，直线 BN 、GC 相交于点 H 。△GMN 绕点 E 旋转的过程中，线段 AH 的最大值是？

简答：因为 EB =EN （分别是△ABC 、△GMN 的高），EC =EG ，且∠GEC =∠NEB （旋转角相等），故△GEC ∽△NEB ，故∠GCE =∠EBH （前面相似主要目的是为了得到此处角相等， 故不一定要说明相似，用内角和说明角相等亦可），又因为∠GCE +∠ECH =180°，所以∠ EBH +∠ECH =180°，故 E 、B 、H 、C 四点共圆，因为∠BEC =90°，所以 BC 为直径，圆 心 O 是 BC 中点，R =2，当 A 、O 、H 三点共线时，AH 长度最大，AH =AO +OH = 2 2

思考题：如图，点 D 为∠ABC 的一遍 BC 上一丁点，且 BD =5，线段 PQ 在∠ABC 另一边

3

AB 上移动，且 PQ =2，若 si NB = 5 ，则当∠PDQ 达到最大值时，PD 的长为？

10

简单：当DH 垂直平分PQ 时，∠PDQ 最大，答案：PD= （w Hy？自行思考）

中考数学专题训练圆专题复习

——圆 ◆知识讲解 一．圆的定义 1、在一个平面内，线段OA绕着它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆。 2、圆是到定点的距离等于定长的所有点的集合。 3、确定一个圆需要两个要素：一是位置二是大小，圆心确定其位置，半径确定其大小。 4、连接圆上任意两点的线段叫弦，经过圆心的弦叫直径。圆上任意两点间的部分叫做圆弧，简称弧。以A、B为端点的弦记作“圆弧AB”，或者“弧AB”。大于半圆的弧叫作优弧（用三个字母表示，如ABC）叫优弧；小于半圆的弧（如AB）叫做劣弧。 二、垂直于弦的直径、弧、弦、圆心角 1、垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弦。 2、垂径定理逆定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧。 3、在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。 在同圆或等圆中，等弧所对的圆心角相等。 在等圆中，弦心距相等的弦相等。 三、圆周角 1、定义：顶点在圆上，并且角的两边和圆相交的角。 2、定理：一条弧所以的圆周角等于这条弧所对的圆心角的一半。 3、推论：（1）在同圆或等圆中，同弧或等弧所以的圆周角相等。 （2）直径所对的圆周角是直角，90°的圆周角所对的弦是直径。 四、点和圆的位置关系 1、设⊙O的半径为r，点到圆心的距离为d。 则d>r ?点在圆外，d=r ?点在圆上，d

中考数学专题复习圆的综合的综合题

一、圆的综合真题与模拟题分类汇编（难题易错题） 1．如图，点P在⊙O的直径AB的延长线上，PC为⊙O的切线，点C为切点，连接AC，过点A作PC的垂线，点D为垂足，AD交⊙O于点E． (1)如图1，求证：∠DAC=∠PAC； (2)如图2，点F（与点C位于直径AB两侧）在⊙O上，BF FA =，连接EF，过点F作AD 的平行线交PC于点G，求证：FG=DE+DG； (3)在(2)的条件下，如图3，若AE=2 3 DG，PO=5，求EF的长． 【答案】（1）证明见解析；（2）证明见解析；（3）EF=32． 【解析】 【分析】 （1）连接OC，求出OC∥AD，求出OC⊥PC，根据切线的判定推出即可； （2）连接BE交GF于H，连接OH，求出四边形HGDE是矩形，求出DE=HG，FH=EH，即可得出答案； （3）设OC交HE于M，连接OE、OF，求出∠FHO=∠EHO=45°，根据矩形的性质得出 EH∥DG，求出OM=1 2 AE，设OM=a，则HM=a，AE=2a，AE= 2 3 DG，DG=3a， 求出ME=CD=2a，BM=2a，解直角三角形得出tan∠MBO＝ 1 2 MO BM =，tanP= 1 2 CO PO =,设 OC=k，则PC=2k，根据OP=5k=5求出k=5，根据勾股定理求出a，即可求出答案．【详解】 （1）证明：连接OC， ∵PC为⊙O的切线，

∴OC⊥PC， ∵AD⊥PC， ∴OC∥AD， ∴∠OCA=∠DAC， ∵OC=OA， ∴∠PAC=∠OCA， ∴∠DAC=∠PAC； （2）证明：连接BE交GF于H，连接OH， ∵FG∥AD， ∴∠FGD+∠D=180°， ∵∠D=90°， ∴∠FGD=90°， ∵AB为⊙O的直径， ∴∠BEA=90°， ∴∠BED=90°， ∴∠D=∠HGD=∠BED=90°， ∴四边形HGDE是矩形， ∴DE=GH，DG=HE，∠GHE=90°， ∵BF AF =， ∴∠HEF=∠FEA=1 2 ∠BEA=190 2 o ?=45°， ∴∠HFE=90°﹣∠HEF=45°， ∴∠HEF=∠HFE， ∴FH=EH， ∴FG=FH+GH=DE+DG； （3）解：设OC交HE于M，连接OE、OF， ∵EH=HF，OE=OF，HO=HO， ∴△FHO≌△EHO， ∴∠FHO=∠EHO=45°，

2015中考数学分类汇编圆综合题学生版

2015中考数学真题分类汇编圆综合题 一．解答题（共30小题） 1．（2015?大连）如图，AB是⊙O的直径，点C，D在⊙O上，且AD平分∠CAB，过点D作AC的垂线，与AC的延长线相交于点E，与AB的延长线相交于点F． （1）求证：EF与⊙O相切； （2）若AB=6，AD=4，求EF的长． 2．（2015?潍坊）如图，在△ABC中，AB=AC，以AC为直径的⊙O交BC于点D，交AB于点E，过点D作DF⊥AB，垂足为F，连接DE． （1）求证：直线DF与⊙O相切； （2）若AE=7，BC=6，求AC的长． 3．（2015?枣庄）如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心、OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE． （1）判断DE与⊙O的位置关系，并说明理由； （2）求证：BC2=CD?2OE； （3）若cos∠BAD=，BE=6，求OE的长． 4．（2015?西宁）如图，已知BC为⊙O的直径，BA平分∠FBC交⊙O于点A，D是射线BF上的一点，且满足=，过点O作OM⊥AC于点E，交⊙O于点M，连接BM， AM． （1）求证：AD是⊙O的切线；

（2）若sin∠ABM=，AM=6，求⊙O的半径． 5．（2015?广元）如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA交弦于点E，交⊙O于点F，且CE=CB． （1）求证：BC是⊙O的切线； （2）连接AF、BF，求∠ABF的度数； （3）如果CD=15，BE=10，sinA=，求⊙O的半径． 6．（2015?北海）如图，AB、CD为⊙O的直径，弦AE∥CD，连接BE交CD于点F，过点E作直线EP与CD的延长线交于点P，使∠PED=∠C． （1）求证：PE是⊙O的切线； （2）求证：ED平分∠BEP； （3）若⊙O的半径为5，CF=2EF，求PD的长． 7．（2015?莆田）如图，在四边形ABCD中，AB=AD，对角线AC，BD交于点E，点O 在线段AE上，⊙O过B，D两点，若OC=5，OB=3，且cos∠BOE=．求证：CB是⊙O的切线．

中考数学专题训练圆的证明与计算(含答案)

圆的证明与计算 1.如图，已知△ABC 内接于△O ， P 是圆外一点，P A 为△O 的切线，且P A ＝PB ，连接 OP ，线段 AB 与线段 OP 相交于点D . （1）求证：PB 为△O 的切线； （2）若P A ＝4 5PO ，△O 的半径为10，求线段 PD 的长. 第1题图 (1)证明：△△△△△△OA △OB △ 第1题解图 △P A △PB △OA △OB △OP △OP △ △△OAP △△OBP (SSS)△ △△OAP △△OBP △ △P A △△O △△△△ △△OAP △90°△ △△OBP △90°△ △OB △△O △△△△ △PB △△O △△△△

△△Rt△AOP △△OA △PO 2 △△4 5PO △2△10△ △△PO △50 3△ △cos△AOP △AO OP △OD AO △ △OD △6△ △PD △PO △OD △32 3. 2. △△△△△ABC △△AB △AC △△D △BC △△△△△AD △DC △△A △B △D △△△△O △AE △△O △△△△△△DE . △1△△△△AC △△O △△△△ △2△△cos C △3 5△AC △24△△△△AE △△. 第2题图 (1)证明：△AB △AC △AD △DC △ △△C △△B △△DAC △△C △ △△DAC △△B △ △△△E △△B △ △△DAC △△E △ △AE △△O △△△△ △△ADE △90°△ △△E △△EAD △90°△ △△DAC △△EAD △90°△ △△EAC △90°△

△OA △△O △△△△ △AC △△O △△△△ (2)解：△△△△△△D △DF △AC △△F △ 第2题解图 △DA △DC △ △CF △1 2AC △12△ △Rt△CDF △△△cos C △CF CD △3 5△ △DC △20△ △AD △20△ △Rt△CDF △△△△△△△△1622==CF CD DF －△ △△ADE △△DFC △90°△△E △△C △ △△ADE △△DFC △ △AE DC △AD DF △ △AE 20△1620 △△△AE △25△ △△O △△△AE △25. 3．如图，在△ABC 中，AB =BC ，以AB 为直径作△O ，交BC 于点D ，交AC 于点E ，过点E 作△O 的切线EF ，交BC 于点F ． （1）求证：EF △BC ； （2）若CD =2，tan C =2，求△O 的半径．

中考数学圆的综合-经典压轴题及答案

中考数学圆的综合-经典压轴题及答案 一、圆的综合 1．如图，点A、B、C分别是⊙O上的点， CD是⊙O的直径，P是CD延长线上的一点，AP=AC． （1）若∠B=60°，求证：AP是⊙O的切线； （2）若点B是弧CD的中点，AB交CD于点E，CD=4，求BE·AB的值． 【答案】（1）证明见解析；（2）8． 【解析】 （1）求出∠ADC的度数，求出∠P、∠ACO、∠OAC度数，求出∠OAP=90°，根据切线判定推出即可； （2）求出BD长，求出△DBE和△ABD相似，得出比例式，代入即可求出答案． 试题解析：连接AD，OA， ∵∠ADC=∠B，∠B=60°， ∴∠ADC=60°， ∵CD是直径， ∴∠DAC=90°， ∴∠ACO=180°-90°-60°=30°， ∵AP=AC，OA=OC， ∴∠OAC=∠ACD=30°，∠P=∠ACD=30°， ∴∠OAP=180°-30°-30°-30°=90°， 即OA⊥AP， ∵OA为半径， ∴AP是⊙O切线． （2）连接AD，BD，

∵CD是直径， ∴∠DBC=90°， ∵CD=4，B为弧CD中点， ∴BD=BC=， ∴∠BDC=∠BCD=45°， ∴∠DAB=∠DCB=45°， 即∠BDE=∠DAB， ∵∠DBE=∠DBA， ∴△DBE∽△ABD， ∴， ∴BE?AB=BD?BD=． 考点：1．切线的判定；2．相似三角形的判定与性质． 2．如图，已知△ABC内接于⊙O，BC交直径AD于点E，过点C作AD的垂线交AB的延长线于点G，垂足为F．连接OC． （1）若∠G=48°，求∠ACB的度数； （2）若AB=AE，求证：∠BAD=∠COF； （3）在（2）的条件下，连接OB，设△AOB的面积为S1，△ACF的面积为S2．若 tan∠CAF= 1 2，求1 2 S S的值． 【答案】（1）48°（2）证明见解析（3）3 4

深圳中考数学专题--圆

2017届深圳中考数学专题——圆 一．解答题（共30小题） 1．如图，AB是⊙O的直径，点C，D在⊙O上，且AD平分∠CAB，过点D作AC的垂线，与AC的延长线相交于点E，与AB的延长线相交于点F． （1）求证：EF与⊙O相切； （2）若AB=6，AD=4，求EF的长． 2．如图，在△ABC中，AB=AC，以AC为直径的⊙O交BC于点D，交AB于点E，过点D作DF⊥AB，垂足为F，连接DE． （1）求证：直线DF与⊙O相切； （2）若AE=7，BC=6，求AC的长． 3．如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心、OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE． （1）判断DE与⊙O的位置关系，并说明理由； （2）求证：BC2=CD?2OE； （3）若cos∠BAD=，BE=6，求OE的长．

4．如图，已知BC为⊙O的直径，BA平分∠FBC交⊙O于点A，D是射线BF上的一点，且满足=，过点O作OM⊥AC于点E，交⊙O于点M，连接BM，AM． （1）求证：AD是⊙O的切线； （2）若sin∠ABM=，AM=6，求⊙O的半径． 5．如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA交弦于点E，交⊙O 于点F，且CE=CB． （1）求证：BC是⊙O的切线； （2）连接AF、BF，求∠ABF的度数； （3）如果CD=15，BE=10，sinA=，求⊙O的半径．

6.如图，AB、CD为⊙O的直径，弦AE∥CD，连接BE交CD于点F，过点E作直线EP与CD的延长线交于点P，使∠PED=∠C． （1）求证：PE是⊙O的切线； （2）求证：ED平分∠BEP； （3）若⊙O的半径为5，CF=2EF，求PD的长． 8．如图，△ABC中，以AC为直径的⊙O与边AB交于点D，点E为⊙O上一点，连接CE并延长交AB于点F，连接ED． （1）若∠B+∠FED=90°，求证：BC是⊙O的切线； （2）若FC=6，DE=3，FD=2，求⊙O的直径． 9．如图，△ABC为等边三角形，以边BC为直径的半圆与边AB，AC分别交于D，F两点，过点D作DE⊥AC，垂足为点E． （1）判断DF与⊙O的位置关系，并证明你的结论； （2）过点F作FH⊥BC，垂足为点H，若AB=4，求FH的长（结果保留根号）．

中考数学综合题专题【圆】专题训练含答案

中考数学综合题专题【圆】专题训练含答案 一、选择题 1．（北京市西城区）如图，BC 是⊙O 的直径，P 是CB 延长线上一点，PA 切⊙O 于点A ，如果PA ＝3，PB ＝1，那么∠APC 等于 （ ） （A ） 15 （B ） 30 （C ） 45 （D ） 60 2．（北京市西城区）如果圆柱的高为20厘米，底面半径是高的 41，那么这个圆柱的侧面积是 （ ） （A ）100π平方厘米 （B ）200π平方厘米 （C ）500π平方厘米 （D ）200平方厘米 3．（北京市西城区）“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题，“今在圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”用 现在的数学语言表述是：“如图，CD 为⊙O 的直径，弦AB ⊥CD ，垂足为E ，CE ＝1寸，AB ＝寸，求直径CD 的长”．依题意，CD 长为 （ ） （A ）2 25寸 （B ）13寸 （C ）25寸 （D ）26寸 4．（北京市朝阳区）已知：如图，⊙O 半径为5，PC 切⊙O 于点C ，PO 交⊙O 于点A ，PA ＝4，那么PC 的长等于 （ ） （A ）6 （B ）25 （C ）210 （D ）214 5．（北京市朝阳区）如果圆锥的侧面积为20π平方厘米，它的母线长为5厘 米，那么此圆锥的底面半径的长等于 （ ） （A ）2厘米 （B ）22厘米 （C ）4厘米 （D ）8厘米 6．（天津市）相交两圆的公共弦长为16厘米，若两圆的半径长分别为10厘 米和17厘米，则这两圆的圆心距为 （ ） （A ）7厘米 （B ）16厘米 （C ）21厘米 （D ）27厘米 7．（重庆市）如图，⊙O 为△ABC 的内切圆，∠C ＝ 90，AO 的延长线交BC 于点D ，AC ＝4，DC ＝1，，则⊙O 的半径等于 （ ）

中考数学圆综合题汇编

25题汇编 1. 如图，AB 是⊙O 的直径，BC 是⊙O 的切线，切点为B ，AD 为弦，OC ∥AD 。 （1）求证：DC 是⊙O 的切线； （2）若OA=2，求OC AD 的值。 2. 如图，⊙O 是△ABC 的外接圆，∠B=60°，CD 是⊙O 的直径，P 是CD 延长线上的一点，且AP=AC （1）求证：直线AP 是⊙O 的切线； （2）若AC=3，求PD 的长。 D C B A O C B

3. 如图，已知AB 是⊙O 的直径，AM 和BN 是⊙O 的两条切线，点E 是⊙O 上一点，点D 是AM 上一点，连接DE 并延长交BN 于点C ，连接OD 、BE ，且OD ∥BE 。 （1）求证：DE 是⊙O 的切线； （2）若AD=1，BC=4，求直径AB 的长。 4. 如图，△ABC 内接于⊙O ，弦AD ⊥AB 交BC 于点E ，过点B 作⊙O 的切线交DA 的延长线于点F ，且∠ABF=∠ABC 。 （1）求证：AB=AC ； （2）若EF=4，2 3 tan F ，求DE 的长。 M N E D C B A O

5. 在△ABC 中，AB=AC ，以AB 为直径作⊙O ，交BC 于点D ，过点D 作DE ⊥AC ，垂足为E 。 （1）求证：DE 是⊙O 的切线； （2）若AE=1，52=BD ，求AB 的长。 6. 如图，AB 是⊙O 的直径，C 是⊙O 上一点，AD 垂直于过点C 的直线，垂足为D ，且AC 平分 ∠BAD 。 （1）求证：CD 是⊙O 的切线； （2）若62=AC ，AD=4，求AB 的长。 A

中考数学圆的综合综合经典题及详细答案

中考数学圆的综合综合经典题及详细答案 一、圆的综合 1．如图，四边形OABC 是平行四边形，以O 为圆心，OA 为半径的圆交AB 于D ，延长AO 交O 于E ，连接CD ，CE ，若CE 是⊙O 的切线，解答下列问题： （1）求证：CD 是⊙O 的切线； （2）若BC=4，CD=6，求平行四边形OABC 的面积． 【答案】（1）证明见解析（2）24 【解析】 试题分析：（1）连接OD ，求出∠EOC=∠DOC ，根据SAS 推出△EOC ≌△DOC ，推出∠ODC=∠OEC=90°，根据切线的判定推出即可； （2）根据切线长定理求出CE=CD=4，根据平行四边形性质求出OA=OD=4，根据平行四边形的面积公式=2△COD 的面积即可求解． 试题解析：（1）证明：连接OD ， ∵OD=OA ， ∴∠ODA=∠A ， ∵四边形OABC 是平行四边形， ∴OC ∥AB ， ∴∠EOC=∠A ，∠COD=∠ODA ， ∴∠EOC=∠DOC ， 在△EOC 和△DOC 中， OE OD EOC DOC OC OC =?? ∠=∠??=? ∴△EOC ≌△DOC （SAS ）， ∴∠ODC=∠OEC=90°， 即OD ⊥DC ， ∴CD 是⊙O 的切线； （2）由（1）知CD 是圆O 的切线， ∴△CDO 为直角三角形， ∵S △CDO = 1 2 CD?OD ， 又∵OA=BC=OD=4，

∴S△CDO=1 2 ×6×4=12， ∴平行四边形OABC的面积S=2S△CDO=24． 2．如图，⊙M交x轴于B、C两点，交y轴于A，点M的纵坐标为2．B（﹣33，O），C（3，O）． （1）求⊙M的半径； （2）若CE⊥AB于H，交y轴于F，求证：EH=FH． （3）在（2）的条件下求AF的长． 【答案】（1）4；（2）见解析;（3）4． 【解析】 【分析】 （1）过M作MT⊥BC于T连BM，由垂径定理可求出BT的长，再由勾股定理即可求出BM的长； （2）连接AE，由圆周角定理可得出∠AEC=∠ABC，再由AAS定理得出△AEH≌△AFH，进而可得出结论； （3）先由（1）中△BMT的边长确定出∠BMT的度数，再由直角三角形的性质可求出CG 的长，由平行四边形的判定定理判断出四边形AFCG为平行四边形，进而可求出答案．【详解】 （1）如图（一），过M作MT⊥BC于T连BM， ∵BC是⊙O的一条弦，MT是垂直于BC的直径， ∴BT=TC=1 2 3 ∴124 ； （2）如图（二），连接AE，则∠AEC=∠ABC，∵CE⊥AB， ∴∠HBC+∠BCH=90°

天津市2020版中考数学专题练习：圆50题_含答案

、选择题： 1. 如图，小明同学设计了一个测量圆直径的工具，标有刻度的尺子 3. 已知圆内接正三角形的边心距为 1，则这个三角形的面积为( ) A ．2 B ．3 C ．4 D ．6 4. 如图，点 A ， B ， C ，在⊙ O 上，∠ ABO=32°，∠ ACO=38°，则∠ BOC 等于 ( 6.如图, ⊙O 是△ ABC 的外接圆 ,弦AC 的长为 3,sinB=0.75, 则⊙ O 的半径为( ) 圆 50 题 垂直，在测直径时，把 A ． O 点靠在圆周上，读得刻度 OE=8个单位， 12 个单位 B ． 10 个单位 C CD 是⊙ O 的两条弦，连结 AD 、BC ．若∠ BCD=70°， OF=6个单位，则圆的直径为 ( 1 个单位 D ． 15 个单位 则∠ BAD 的度数为( 2. 如图， AB 、 A ． 40° B ．50° C ． 60° D ． 70° B ．70° C ．120° D ． 140° 5. 如图 , 点 A,B,C 在⊙ O 上, ∠A=36° , ∠ C=28° , 则∠ B=( A.100 B.72 C.64 D.36 OA 、 OB 在 O 点钉在一起，并使它们保持

AD 切⊙ O 于点 A ，点 C 是弧 BE 的中点，则下列结论不成立的是( B ． EC=B C C ．∠ DAE=∠ABE D ．AC ⊥OE 10. 如图 , △ABC 中,AB=5,BC=3,AC=4, 以点 C 为圆心的圆与 AB 相切 ,则⊙ C 半径为( 11. 数学课上，老师让学生尺规作图画 Rt △ABC ，使其斜边 AB=c ，一条直角边 BC=a ，小明的作法如图所 示， 你认为这种作法中判断∠ ACB 是直角的依据是( ) A.4 B.3 C.2 D. OB=6cm,高 OC=8cm 则. 这个圆锥的侧面 积是 7. 如图，圆锥的底面半径 22 A.30cm 2 B.30 π cm 2 C.60 2 π cm D.120cm 9. 如图,AB 是⊙ O 的直径 ,C 、D 是⊙ O 上两点 , 分别连接 AC 、BC 、CD 、OD ．∠ DOB=140° A.20° B.30 C.40 D.70 ，则∠ ACD (= B.2.5 C.2.4 D.2.3

“中考数学专题复习 圆来如此简单”经典几何模型之隐圆专题(含答案)

经典几何模型之隐圆”“圆来如此简单” 一.名称由来 在中考数学中，有一类高频率考题，几乎每年各地都会出现，明明图形中没有出现“圆”，但是解题中必须用到“圆”的知识点，像这样的题我们称之为“隐圆模型”。 正所谓：有“圆”千里来相会，无“圆”对面不相逢。“隐圆模型”的题的关键突破口就在于能否看出这个“隐藏的圆”。一旦“圆”形毕露，则答案手到擒来！ 二.模型建立 【模型一：定弦定角】 【模型二：动点到定点定长（通俗讲究是一个动的点到一个固定的点的距离不变）】 【模型三：直角所对的是直径】 【模型四：四点共圆】 ` 三．模型基本类型图形解读 【模型一：定弦定角的“前世今生”】 【模型二：动点到定点定长】

【模型三：直角所对的是直径】 【模型四：四点共圆】 四．“隐圆”破解策略 牢记口诀：定点定长走圆周，定线定角跑双弧。 直角必有外接圆，对角互补也共圆。五．“隐圆”题型知识储备

3 六．“隐圆”典型例题 【模型一：定弦定角】 1.（2017 威海）如图 1，△ABC 为等边三角形，AB=2，若P 为△ABC 内一动点，且满足 ∠PAB=∠ACP，则线段P B 长度的最小值为_ 。 简答：因为∠PAB=∠PCA，∠PAB+∠PAC=60°，所以∠PAC+∠PCA=60°，即∠APC=120°。因为A C定长、∠APC=120°定角，故满足“定弦定角模型”，P在圆上，圆周角∠APC=120°，通过简单推导可知圆心角∠AOC=60°，故以AC 为边向下作等边△AOC，以O 为圆心，OA 为半径作⊙O，P在⊙O 上。当B、P、O三点共线时，BP最短（知识储备一：点圆距离）， 此时B P=2 -2 2.如图1所示，边长为2的等边△ABC 的原点A在x轴的正半轴上移动，∠BOD=30°，顶点A 在射线O D 上移动，则顶点C到原点O的最大距离为。

中考数学圆的综合提高练习题压轴题训练附详细答案

中考数学圆的综合提高练习题压轴题训练附详细答案 一、圆的综合 1．如图，点P在⊙O的直径AB的延长线上，PC为⊙O的切线，点C为切点，连接AC，过点A作PC的垂线，点D为垂足，AD交⊙O于点E． (1)如图1，求证：∠DAC=∠PAC； (2)如图2，点F（与点C位于直径AB两侧）在⊙O上，?? BF FA =，连接EF，过点F作AD 的平行线交PC于点G，求证：FG=DE+DG； (3)在(2)的条件下，如图3，若AE=2 3 DG，PO=5，求EF的长． 【答案】（1）证明见解析；（2）证明见解析；（3）EF=32． 【解析】 【分析】 （1）连接OC，求出OC∥AD，求出OC⊥PC，根据切线的判定推出即可； （2）连接BE交GF于H，连接OH，求出四边形HGDE是矩形，求出DE=HG，FH=EH，即可得出答案； （3）设OC交HE于M，连接OE、OF，求出∠FHO=∠EHO=45°，根据矩形的性质得出 EH∥DG，求出OM=1 2 AE，设OM=a，则HM=a，AE=2a，AE= 2 3 DG，DG=3a， 求出ME=CD=2a，BM=2a，解直角三角形得出tan∠MBO＝ 1 2 MO BM =，tanP= 1 2 CO PO =,设 OC=k，则PC=2k，根据OP=5k=5求出k=5，根据勾股定理求出a，即可求出答案．【详解】 （1）证明：连接OC， ∵PC为⊙O的切线，

∴OC⊥PC， ∵AD⊥PC， ∴OC∥AD， ∴∠OCA=∠DAC， ∵OC=OA， ∴∠PAC=∠OCA， ∴∠DAC=∠PAC； （2）证明：连接BE交GF于H，连接OH， ∵FG∥AD， ∴∠FGD+∠D=180°， ∵∠D=90°， ∴∠FGD=90°， ∵AB为⊙O的直径， ∴∠BEA=90°， ∴∠BED=90°， ∴∠D=∠HGD=∠BED=90°， ∴四边形HGDE是矩形， ∴DE=GH，DG=HE，∠GHE=90°， ∵?? BF AF =， ∴∠HEF=∠FEA=1 2 ∠BEA=190 2 o ?=45°， ∴∠HFE=90°﹣∠HEF=45°， ∴∠HEF=∠HFE， ∴FH=EH， ∴FG=FH+GH=DE+DG； （3）解：设OC交HE于M，连接OE、OF， ∵EH=HF，OE=OF，HO=HO， ∴△FHO≌△EHO， ∴∠FHO=∠EHO=45°，

中考数学培优专题复习圆的综合练习题附详细答案

一、圆的综合 真题与模拟题分类汇编（难题易错题） 1．如图，四边形OABC 是平行四边形，以O 为圆心，OA 为半径的圆交AB 于D ，延长AO 交O 于E ，连接CD ，CE ，若CE 是⊙O 的切线，解答下列问题： （1）求证：CD 是⊙O 的切线； （2）若BC=4，CD=6，求平行四边形OABC 的面积． 【答案】（1）证明见解析（2）24 【解析】 试题分析：（1）连接OD ，求出∠EOC=∠DOC ，根据SAS 推出△EOC ≌△DOC ，推出∠ODC=∠OEC=90°，根据切线的判定推出即可； （2）根据切线长定理求出CE=CD=4，根据平行四边形性质求出OA=OD=4，根据平行四边形的面积公式=2△COD 的面积即可求解． 试题解析：（1）证明：连接OD ， ∵OD=OA ， ∴∠ODA=∠A ， ∵四边形OABC 是平行四边形， ∴OC ∥AB ， ∴∠EOC=∠A ，∠COD=∠ODA ， ∴∠EOC=∠DOC ， 在△EOC 和△DOC 中， OE OD EOC DOC OC OC =?? ∠=∠??=? ∴△EOC ≌△DOC （SAS ）， ∴∠ODC=∠OEC=90°， 即OD ⊥DC ， ∴CD 是⊙O 的切线； （2）由（1）知CD 是圆O 的切线， ∴△CDO 为直角三角形， ∵S △CDO = 1 2 CD?OD ， 又∵OA=BC=OD=4，

∴S △CDO = 1 2 ×6×4=12， ∴平行四边形OABC 的面积S=2S △CDO =24． 2．已知 O 的半径为5，弦AB 的长度为m ，点C 是弦AB 所对优弧上的一动点． ()1如图①，若m 5=，则C ∠的度数为______； ()2如图②，若m 6=． ①求C ∠的正切值； ②若ABC 为等腰三角形，求ABC 面积． 【答案】()130；()2C ∠①的正切值为3 4 ；ABC S 27=②或 432 25 . 【解析】 【分析】 ()1连接OA ，OB ，判断出AOB 是等边三角形，即可得出结论； ()2①先求出10AD =，再用勾股定理求出8BD =，进而求出tan ADB ∠，即可得出结 论； ②分三种情况，利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论． 【详解】 ()1如图1，连接OB ，OA ，

中考数学圆专题练习

中考数学圆 专题练习-- 一、选择题 1.（2010年 湖里区 二次适应性考试）已知半径分别为5 cm 和8 cm 的两圆相交，则它们的圆心距可能是（ ） A ．1 cm B ．3 cm C ．10 cm D ．15 cm 答案：C 2.（2010年教育联合体）如图，已知AB 是⊙O 的直径，⊙O 交BC 的中点于D ，DE ⊥AC 于E ，连接AD ，则下列结论 正确的个数是（ ） ①AD ⊥BC ，②∠EDA ＝∠B ，③OA ＝ 1 2AC ，④DE 是⊙O 的切线． A ．1个 B ．2个 C ．3个 D ．4个 答案：D 3.（2010安徽省模拟）如图，AB 是⊙O 的直径，点D 、E 是圆的三等分点，AE 、BD 的延长线交于点C ，若CE=2,则 ⊙O 中阴影部分的面积是（ ） A ．433π- B ．2 3π C ．2 23 π- D ．1 3 π 答案：A 4.（2010年重庆市綦江中学模拟1）.在直角坐标系中，⊙A 、⊙B 的 位置如图所示.下列四个点中，在⊙A 外部且在⊙B 内部的是（ ） A.（1，2） B.(2,1). C.(2,-1). D.(3,1) 答案C 5.(2010年聊城冠县实验中学二模)如下图，将半径为2cm 的圆形纸片 第4题图 O D B C E A 第3题 A O B C D E

折叠后，圆弧恰好经过圆心O ，则折痕AB 的长为（ ） A ．2cm B ．3cm C ．32cm D ．52cm 答案C 6.（2010年广州市中考六模）、如果圆锥的母线长为6cm ，底面圆半径为3cm ，则这个圆锥的侧面积为（ ） A. 2 9cm π B. 2 18cm π C. 2 27cm π D. 2 36cm π 答案：B 7.（2010年广州市中考六模）如图，已知⊙O 的弦AB 、CD 相交于点E ， 的度数为60°， 的度数为100°，则∠AEC 等于（ ） A. 60° B. 100° C. 80° D. 130° 答案：C 8.（2010年广西桂林适应训练）如图，圆弧形桥拱的跨度AB ＝ 12米，拱高CD ＝4米，则拱桥的半径为（ ）． A.6.5米 B.9米 C.13米 D.15米 答案：A 9.（2010年广西桂林适应训练）如图，BD 是⊙O 的直径，∠CBD=30o ， 则∠A 的度数为（ ）．[来 A.30o B.45o C.60o D.75o 答案：C 10.（2010山东新泰）已知⊙O 1的半径为5cm ，⊙O 2的半径为3cm ，圆心距O 1O 2＝2，那么⊙O 1与⊙O 2的位置关系是（ ） A ．相离 B ．外切 C ．相交 D ．内切 答案：D 11.（2010年济宁师专附中一模）如图，A B C D ，，，为⊙O 的四等分点，动点P 从圆心O 出发，沿O C D O ---路 7题图 8题图 9题图

中考数学圆的综合-经典压轴题附答案解析

中考数学圆的综合-经典压轴题附答案解析 一、圆的综合 1．如图，点A、B、C分别是⊙O上的点， CD是⊙O的直径，P是CD延长线上的一点，AP=AC． （1）若∠B=60°，求证：AP是⊙O的切线； （2）若点B是弧CD的中点，AB交CD于点E，CD=4，求BE·AB的值． 【答案】（1）证明见解析；（2）8． 【解析】 （1）求出∠ADC的度数，求出∠P、∠ACO、∠OAC度数，求出∠OAP=90°，根据切线判定推出即可； （2）求出BD长，求出△DBE和△ABD相似，得出比例式，代入即可求出答案． 试题解析：连接AD，OA， ∵∠ADC=∠B，∠B=60°， ∴∠ADC=60°， ∵CD是直径， ∴∠DAC=90°， ∴∠ACO=180°-90°-60°=30°， ∵AP=AC，OA=OC， ∴∠OAC=∠ACD=30°，∠P=∠ACD=30°， ∴∠OAP=180°-30°-30°-30°=90°， 即OA⊥AP， ∵OA为半径， ∴AP是⊙O切线． （2）连接AD，BD，

∵CD 是直径， ∴∠DBC=90°， ∵CD=4，B 为弧CD 中点， ∴BD=BC= ， ∴∠BDC=∠BCD=45°， ∴∠DAB=∠DCB=45°， 即∠BDE=∠DAB ， ∵∠DBE=∠DBA ， ∴△DBE ∽△ABD ， ∴ ， ∴BE?AB=BD?BD= ． 考点：1．切线的判定；2．相似三角形的判定与性质． 2．如图，△ABC 是⊙O 的内接三角形，点D 在BC uuu r 上，点E 在弦AB 上（E 不与A 重 合），且四边形BDCE 为菱形． （1）求证：AC=CE ； （2）求证：BC 2﹣AC 2=AB?AC ； （3）已知⊙O 的半径为3． ①若AB AC =5 3 ，求BC 的长； ②当 AB AC 为何值时，AB?AC 的值最大？ 【答案】（1）证明见解析；（2）证明见解析；（3）2；② 32

中考数学专题：圆.(学生版)

中考数学试题专题复习：圆 【学生版】 一、选择题 1. （天津3分）已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ，若12O O =7 cm ，则⊙1O 与⊙2O 的位置关系是 (A) 相交 (B) 相离 (C) 内切 (D) 外切 2.（内蒙古包头3分）已知两圆的直径分别是2厘米与4厘米，圆心距是3厘米，则这两个圆的位置关系是 A 、相交 B 、外切 C 、外离 D 、内含 3,（内蒙古包头3分）已知AB 是⊙O 的直径，点P 是AB 延长线上的一个动点， 过P 作⊙O 的切线，切点为C ，∠APC 的平分线交AC 于点D ，则∠CDP 等于 A 、30° B 、60° C 、45° D 、50° 4.（内蒙古呼和浩特3分）如图所示，四边形ABCD 中，DC∥AB，BC=1， AB=AC=AD=2．则BD 的长为 A. 14 B. 15 C. 32 D. 23 5.（内蒙古呼伦贝尔3分）⊙O 1的半径是cm 2，⊙2的半径是cm 5，圆心距是cm 4，则两圆的位置关系为 A. 相交 B. 外切 C.外离 D. 内切 6.（内蒙古呼伦贝尔3分）如图，⊙O 的半径为5，弦AB 的长为8，M 是弦AB 上的动点, 则线段OM 长的最小值为. A. 5 B. 4 C. .3 D. 2 7.（内蒙古呼伦贝尔3分）如图，AB 是⊙O 的直径，点C 、D 在⊙O 上 ，∠BOD=110°， AC∥OD，则∠AOC 的度数 A. 70° B. 60° C. 50° D. 40° 8.（内蒙古乌兰察布3分）如图， AB 为 ⊙ O 的直径， CD 为弦， AB ⊥ CD ， 如果∠BOC = 700 ，那么∠A 的度数为 A 70 0 B. 350 C. 300 D . 200 17．填空题 1.（天津3分）如图，AD ，AC 分别是⊙O 的直径和弦．且∠CAD=30°．OB⊥AD，交AC 于点B ．若OB=5，则BC 的长等于 ▲ 。

中考数学圆综合题(含答案)

一.圆地概念 集合形式地概念：1. 圆可以看作是到定点地距离等于定长地点地集合； 2.圆地外部：可以看作是到定点地距离大于定长地点地集合； 3.圆地内部：可以看作是到定点地距离小于定长地点地集合 轨迹形式地概念： 1.圆：到定点地距离等于定长地点地轨迹就是以定点为圆心,定长为半径地圆； （补充）2.垂直平分线：到线段两端距离相等地点地轨迹是这条线段地垂直平分线（也叫中垂线）； 3.角地平分线：到角两边距离相等地点地轨迹是这个角地平分线； 4.到直线地距离相等地点地轨迹是：平行于这条直线且到这条直线地距离等于定长地两条直线； 5.到两条平行线距离相等地点地轨迹是：平行于这两条平行线且到两条直线距离都相等地一条直线. 二.点与圆地位置关系 1.点在圆内?d r?点A在圆外； 三.直线与圆地位置关系 1.直线与圆相离?d r>?无交点； 2.直线与圆相切?d r=?有一个交点； 3.直线与圆相交?d r+； A

外切（图2）? 有一个交点 ? d R r =+； 相交（图3）? 有两个交点 ? R r d R r -<<+； 内切（图4）? 有一个交点 ? d R r =-； 内含（图5）? 无交点 ? d R r <-； 图1 五.垂径定理 垂径定理：垂直于弦地直径平分弦且平分弦所对地弧. 推论1：（1）平分弦（不是直径）地直径垂直于弦,并且平分弦所对地两条弧； （2）弦地垂直平分线经过圆心,并且平分弦所对地两条弧； （3）平分弦所对地一条弧地直径,垂直平分弦,并且平分弦所对地另一条弧 以上共4个定理,简称2推3定理：此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即： ①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论. 推论2：圆地两条平行弦所夹地弧相等. 即：在⊙O 中,∵AB ∥CD ∴弧AC =弧BD 六.圆心角定理 图2 图4 图5 B D

2021中考数学专题训练——圆 (解析版)

2021中考数学专题训练——圆 考点一 圆的有关概念及性质 1.(2018衢州,10,3分)如图,AC 是☉O 的直径,弦BD ⊥AO 于E,连接BC,过点O 作OF ⊥BC 于F,若BD=8 cm,AE=2 cm,则OF 的长度是?( ) A.3 cm B.6cm C. 2.5cm D.5cm 答案 D ∵AC ⊥BD,∴BE=DE=2 1BD=4 cm. 设☉O 的半径为r cm. 连接OB,则在Rt △BOE 中,r 2=42+(r-2)2,解得r=5. ∴CE=8 cm.∴BC=54 cm. 又∵OF ⊥BC,∴CF=2 1BC=52 cm, ∵OC=5 cm,∴OF=5 cm.故选D. 2.(2016杭州,8,3分)如图,已知AC 是☉O 的直径,点B 在圆周上(不与A,C 重合),点D 在AC 的延长线上,连接BD 交☉O 于点E.若∠AOB=3∠ADB,则?( ) A.DE=EB B.?DE=2EB C.3DE=DO D.DE=OB 答案 D 连接OE,∠AOB=∠ADB+∠B=3∠ADB, ∴∠B=2∠ADB,∵OE=OB, ∴∠OEB=∠B=2∠ADB=∠ADB+∠EOC, ∴∠ADB=∠EOC,∴DE=EO,∴DE=OB.故选D. 3. (2019台州,14,5分)如图,AC 是圆内接四边形ABCD 的一条对角线,点D 关于AC 的对称点E 在边BC 上,连接AE,若∠ABC=64°,则∠BAE 的度数为_______ . 答案 52° 解析 由题意得∠D=180°-∠ABC=116°, ∵点D 关于AC 的对称点E 在边BC 上, ∴∠D=∠AEC=116°, ∴∠BAE=116°-64°=52°. ? 4.(2018杭州,14,4分)如图,AB 是☉O 的直径,点C 是半径OA 的中点,过点C 作DE ⊥AB,交☉O

中考数学圆综合练习题含答案

数学中考圆综合题附参考答案 1．如图，△ABC 中，以BC 为直径的圆交AB 于点D ，∠ACD =∠ABC ． （1）求证：CA 是圆的切线； （2）若点E 是BC 上一点，已知BE =6，tan ∠ABC = 32，tan ∠AEC =3 5 ，求圆的直径． 2. 如图右，已知直线PA 交⊙0于A 、B 两点，AE 是⊙0的直径．点C 为⊙0上一点，且AC 平分∠PAE ，过C 作CD ⊥PA ，垂足为D 。 (1)求证：CD 为⊙0的切线； (2)若DC+DA=6，⊙0的直径为l0，求AB 的长度. 1. (1)证明：连接OC, ∵点C 在⊙0上，0A=OC,∴∠OCA=∠OAC ，∵CD ⊥PA ，∴∠CDA=90°， 有∠CAD+∠DCA=90°，∵AC 平分∠PAE ，∴∠DAC=∠CAO 。 ∴∠DC0=∠DCA+∠ACO=∠DCA+∠CAO=∠DCA+∠DAC=90°。 又∵点C 在⊙O 上，OC 为⊙0的半径，∴CD 为⊙0的切线． (2)解：过0作0F ⊥AB ，垂足为F ，∴∠OCA=∠CDA=∠OFD=90°， ∴四边形OCDF 为矩形，∴0C=FD ，OF=CD. ∵DC+DA=6，设AD=x ，则OF=CD=6-x ，∵⊙O 的直径为10，∴DF=OC=5，∴AF=5-x ， 在Rt △AOF 中，由勾股定理得222AF +OF =OA .即22(5)(6)25x x -+-=，化简得：211180x x -+= 解得2x =或9x =。由AD

中考数学总复习专题训练及答案(圆)

2008年中考总复习专题训练(圆) 一、选择题（每小题3分，共45分） 1．在△ABC 中，∠C=90°，AB ＝3cm ，BC ＝2cm,以点A 为圆心，以2.5cm 为半径作圆，则点C 和⊙A 的位置关系是（ ）。 A ．C 在⊙A 上 Ｂ．C 在⊙A 外 C ．C 在⊙A 内 Ｄ．C 在⊙A 位置不能确定。 2．一个点到圆的最大距离为11cm ，最小距离为5cm,则圆的半径为（ ）。 A ．16cm 或6cm Ｂ．3cm 或8cm C ．3cm Ｄ．8cm 3．AB 是⊙O 的弦，∠AOB ＝80°则弦AB 所对的圆周角是（ ）。 A ．40° Ｂ．140°或40° C ．20° Ｄ．20°或160° 4．O 是△ABC 的内心，∠BOC 为130°，则∠A 的度数为（ ）。 A ．130° Ｂ．60° C ．70° Ｄ．80° 5．如图1，⊙O 是△ABC 的内切圆，切点分别是D 、E 、F ，已知∠A = 100°，∠C = 30°， 则∠DFE 的度数是（ ）。 A ．55° Ｂ．60° C ．65° Ｄ．70° 6．如图2，边长为12米的正方形池塘的周围是草地，池塘边A 、B 、C 、D 处各有一棵树， 且AB=BC=CD=3米．现用长4米的绳子将一头羊拴在其中的一棵树上．为了使羊在草地上活动区域的面积最大，应将绳子拴在（ ）。 A ． A 处 B ． B 处 C ．C 处 D ．D 处 图1 图2 7．已知两圆的半径分别是2和4，圆心距是3，那么这两圆的位置是（ ）。 A ．内含 Ｂ．内切 C ．相交 Ｄ． 外切 8．已知圆锥的底面半径为3，高为4，则圆锥的侧面积为（ ）。 Ａ．10π B ．12π Ｃ．15π Ｄ．20π 9．如果在一个顶点周围用两个正方形和n 个正三角形恰好可以进行平面镶嵌，则n 的值是 （ ）。 A ．3 B ．4 C ．5 D ．6 10．下列语句中不正确的有（ ）。 ①相等的圆心角所对的弧相等 ②平分弦的直径垂直于弦 ③圆是轴对称图形，任何一条直径都是它的对称轴 ④长度相等的两条弧是等弧 A ．3个 Ｂ．2个 C ．1个 Ｄ．4个 11．先作半径为2 3的第一个圆的外切正六边形，接着作上述外切正六边形的外接圆，再作上述外接圆的外切正六边形，…，则按以上规律作出的第8个外切正六边形的边长为（ ）。