
叶片自振频率与振型的测定
一、实验目的
1.测定叶片的几种主要自振频率,并与理论计算值进行比较,分析其准确程度;
2.观察叶片的振动现象;
3.熟悉叶片振动实验装置与实验方法。
二、实验原理
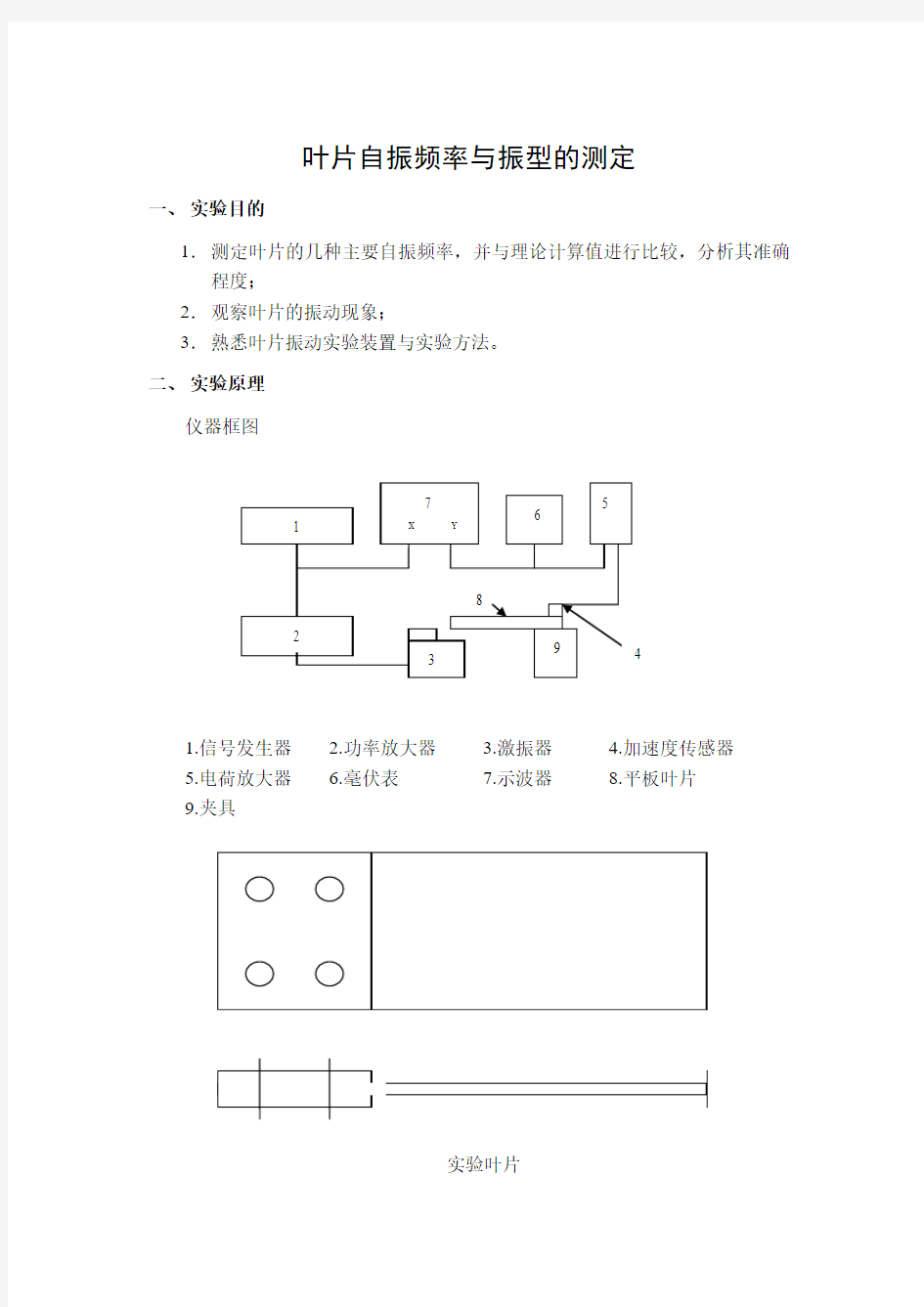
仪器框图
1.信号发生器
2.功率放大器
3.激振器
4.加速度传感器
5.电荷放大器
6.毫伏表
7.示波器
8.平板叶片
9.夹具
实验叶片
实验装置由以下三部分组成:
(1)被测试件部分
被测试件部分由实验叶片和叶片夹具所组成。将被测叶片榫头牢固地夹紧,使叶身悬臂伸出,以便激振和测量。
(2)激振部分
激振叶片的方法很多,如声波激振、振动台激振、压电晶体激振、电涡流激振等。本实验采用电涡流激振方法激振。
激振部分由信号发生器、功率放大器和电涡流激振器所组成。信号发生器能在0~3MHz范围内产生频率可调的交变信号,该信号经过放大器放大后输入到激振器;在激振器内产生电磁感应,使叶片内(包括磁性材料与非磁性材料)产生交变电涡流,载流(电涡流)叶片在磁场中受到交变的电磁力作用而产生振动。
(3)测振部分
由加速度传感器、电荷放大器、毫伏表和示波器组成。加速度传感器感受叶片的振动,输出与该振动频率相同,幅值与叶片振幅大小相对应的交变信号,经电荷放大器将交变信号增益,以电压形式输出。该电压信号分别接到毫伏表和示波器Y轴。同时示波器X轴接入信号发生器的激振信号,在荧光屏上观察里莎茹图形,叶片共振时Y轴信号幅值变化最大,里莎茹图呈椭圆形。
三、实验步骤
1.测量实验件尺寸(叶片的长度l、宽度b、厚度h),供计算理论频率值使用。
2.按仪器图接好各仪器线路,检查无误后再接通电源。
3.打开各仪器电源开关,少许预热,便可开始工作。调节功率放大器输出旋钮,
(不能超过中间刻度10的位置),激振器开始工作,叶片产生振动,此时,可听到叶片振动式产生的“嗡嗡”声。
4.由低到高缓慢转动信号发生器频率调节旋钮,同时注意观察毫伏表指针变化
和示波器图形变化,当叶片处于共振状态时,叶片振动发出的声音最强,毫伏表指针达到最大值,示波器上出现椭圆形(或圆型)。此时停止调频,在叶片上均匀地撒上沙子,观察叶片振动节线形状(若节线不清楚,可以短暂地调高功率放大器输出旋钮至刻度16,随后恢复到刻度10以下位置),记录频率值,描画叶片节线图。
5.继续改变信号发生器的频率值,按第4步骤中的方法找出叶片的其他各阶振
型和频率值。
6.整理和处理实验数据。
四、 有关数据和理论公式:
1. 等截面叶片弯曲振动的频率计算公式
A
EJ
l a
f a ρ2=
式中:f a ——叶片弯曲振动的自振频率,Hz ; l ——叶片的长度,m ;
E ——叶片材料(铝材)的弹性模量,73GPa ;
J ——叶片截面的最小惯性矩,J=bh 3/12,m 4;其中b 、h 为叶片宽度与厚度;
A ——叶片截面面积,A=bh ,m 2; ρ——叶片材料材料密度,2908kg/m 3; a ——系数,一弯时为3.515,二弯时为22.03。
2. 等截面叶片一阶扭曲振动频率计算公式
12J GJ l
f T
ρπ
=
式中:f 1——叶片一阶扭曲振动频率,Hz ; G ——剪切模量,)
1(2μ+=
E
G ,其中μ=0.32;
J T ——截面抗扭几何刚性系数,3
3
1bh J T =,m 4;
J 0——截面极惯性矩,)(12
222
20h b bh J J J y x +=+=,m 4; l ,ρ——同前式。
五、 实验结果记录
六、 实验报告内容
1. 简述本实验方法的工作原理与理论公式; 2. 列出已知数据,以及实验结果;
3. 分析误差原因,以及实验中的反常现象;
4.提出对本试验的认识。
简支梁横向振动的固有频率及振型函数的推导 一.等截面细直梁的横向振动 取梁未变形是的轴线方向为X 轴(向右为正),取对称面内与x 轴垂直的方向为y 轴(向上为正)。梁在横向振动时,其挠曲线随时间而变化,可表示为 y=y(x,t) (1) 除了理想弹性体与微幅振动的假设外,我们还假设梁的长度与截面高度之比是相当大的(大于10)。故可以采用材料力学中的梁弯曲的简化理论。根据这一理论,在我们采用的坐标系中,梁挠曲线的微分方程可以表示为: 22y EI M x ?=? (2) 其中,E 是弹性模量,I 是截面惯性矩,EI 为梁的弯曲刚度,M 代表x 截面处的弯矩。挂怒弯矩的正负,规定为左截面上顺时针方向为正,右截面逆时针方向为正。关于剪力Q 的正负,规定为左截面向上为正,右截面向下为正。至于分布载荷集度q 的正向则规定与y 轴相同。在这些规定下,有: M Q Q q x x ??==??, (3) 于是,对方程(2)求偏导,可得: 222222(EI )(EI )y M y Q Q q x x x x x x ??????====??????, (4) 考虑到等截面细直梁的EI 是常量,就有:
3434y y EI Q EI q x x ??==??, (5) 方程(5)就是在等截面梁在集度为q 的分部李作用下的挠曲微分方程。 应用达朗贝尔原理,在梁上加以分布得惯性力,其集度为 22 y q t ρ?=-? (6) 其中ρ代表梁单位长度的质量。假设阻尼的影响可以忽略不计,那么梁在自由振动中的载荷就仅仅是分布的惯性力。将式(6)代入(5),即得到等截面梁自由弯曲振动微分方程: 4242y y EI x t ρ??=--?? (7) 其中2 /a EI ρ=。 为求解上述偏微分方程(7),采用分离变量法。假设方程的解为: y(x,t)=X(x)Y(t) (8) 将式(8)代入(7),得: 22424 1Y a d X Y t X dx ?=-? (9)
模态分析技术发展到今天已趋成熟,特别是线性模态理论(通常所说的模态分析均是指线性模态分析)方面的研究已日臻完善,但在工程应用方面还有不少工作可做。首先是如何提高模态分析的精度,扩大应用范围。增加模态分析的信息量是提高分析精度的关键,单靠增加传感器的测点数目很难实现,目前提出的一种激光扫描方法是大大增加测点数的有效办法,测点数目的增加随之而来的是增大数据采集与分析系统的容量及提高分析处理速度,在测试方法、数据采集与分析方面还有不少研究工作可做。对复杂结构空间模态的测量分析、频响函数的耦合、高频模态检测、抗噪声干扰……等等方面的研究尚需进一步开展。模态分析当前的一个重要发展趋势是由线性向非线性问题方向发展。非线性模态的概念早在1960年就由Rosenberg提出,虽有不少学者对非线性模态理论进行了研究,但由于非线性问题本身的复杂性及当时工程实践中的非线性问题并示引起重视,非线性模态分析的发展受到限制。近年来在工程中的非线性问题日益突出,因此非线性模态分析亦日益受到人们的重视。最近已逐步形成了所谓非线性模态动力学。关于非线性模态的正交性、解耦性、稳定性、模态的分叉、渗透等问题是当前研究的重点。在非线性建模理论与参数辨识方面的研究工作亦是当今研究的热点。非线性系统物理参数的识别、载荷识别方面的研究亦已开始。展望未来,模态分析与试验技术仍将以新的速度,新的内容向前发展。 模态振型是一个相对量,通常是一个列向量,二维以上的系统其模态振型不是一个数。一个数对应单模态,其数值无意义。某模态频率下的模态振型反映了在该模态频率下各自由度的相对位移的比值。如果系统的初始位移恰好等于模态频率下的模态振型(或与之成比例),则此时系统的自由响应中只会出现该模态频率。感谢欧阳中华教授的指点,我现在觉得自己当初确实对模态振型概念不清楚。模态振型是系统固有的振动形态,线性响应是振型线性叠加的结果,但振型之间是独立不耦合的。振型是个相对量,所以就有了多种振型归一划的方法。振型是个很重要的固有特征,正如楼上所说用于验证固有频率。 我觉得振型在判别你计算固有频率正确性是非常有用的,比如,通过有限元计算得到了模型的前十阶固有频率,试验模态分析也得到了低阶的固有频率,假设计算的某阶固有频率与试验的某阶固有频率非常接近,但是并不能马上说明他们是同一阶的,需要通过振型来判断。 其他的不知道,但是之所以引入模态的概念,之所以从物理坐标变换到模态坐标就是为了解耦,就是为了让其正交,这样方程才能解出来。从能量角度说,这样各个振型之间就没有能量的交换。 从数学上看,对响应函数级数展开后,其中的各项构成各阶模态,而级数展开形
场地土类别、结构自振周期、设计特征周期的概念解读常有众智平台朋友来询问场地土类别与地震力是什么关系,结构自振周期折减对结构的地震力有什么影响,设计特征周期是什么概念,土的卓越周期又是怎么回事,本文结合规范对这些内容进行了整理,对这几个概念的相关关系也做了一些论述,期望与大家一起交流学习,具体综述如下: 一、场地土类别 《建筑抗震设计规范》第4.1.6对场地土类别是这样划分的:建筑的 场地类别,应根据土层等效剪切波速和场地覆盖层厚度按表4.1.6划分为四类,其中Ⅰ类分为Ⅰ0、Ⅰ1两个亚类。当有可靠的剪切波速和覆盖层厚度且其值处于表4.1.6所列场地类别的分界线附近时,应允许按插值方法确定地震作用计算所用的特征周期。 《抗规》第4.1.4条、4.1.5条对场地覆盖层的厚度及图层的等效剪切波束分别作了规定。 相关概念:
场地--工程群体所在地,具有相似的反应谱特征。其范围相当于厂区、居民小区和自然村或不小于1.0km2的平面面积。 与震害的关系:土质愈软覆盖层厚度愈厚,建筑震害愈严重,反之愈轻,软弱土层对地震力具有放大作用。历次大地震的经验表明,同样或相近的建筑,建造于Ⅰ类场地时震害较轻,建造于Ⅲ、Ⅳ类场地震害较重。 规范采取的相应措施:《抗规》第4.1.1条将场地划分为对建筑抗震有利、一般、不利和危险的地段。具体设计时,结构设计师对不利地段,应提出避开要求;当无法避开时应采取有效的措施。对危险地段,严禁建造甲、乙类的建筑,不应建造丙类的建筑。 另外《抗规》第3.3.2、4.1.8,、4.1.9对相关措施提出了严格要求,设计人员不应忽视。 二、结构自振周期 概念: 结构自振周期是结构按某一振型完成一次自由振动所需的时间,是结构本身固有的动力特性,只与自身质量及刚度有关,结构有几个振型就有几个自振周期,一一对应。 应用:
一、综合实验题目和要求 题目:求一二维梁的固有振型和频率。 要求:用有限元理论,求一二维梁的固有振型和频率: (1) 用二维梁有限元对梁进行分析数值计算求出其主振型向量和频率; (2) 求出其理论精确解,精确主振型向量和频率; (3) 将理论结果和计算结果进行比较。 二、程序流程图
三、实验结果 1.前六阶振型 同一有限元数不同阶数比较(以有限元20为例)如下图所示:
00.10.20.30.40.50.60.70.80.9 一阶 -0.8 -0.6-0.4-0.200.20.40.60.81 二阶 -0.8 -0.6-0.4-0.200.20.40.60.81 三阶
-0.8 -0.6-0.4-0.200.20.40.60.8 四阶 -0.8 -0.6-0.4-0.200.20.40.60.81 五阶 -0.8 -0.6-0.4-0.200.20.40.60.81 六阶 四、实验分析
对于二维梁有限元的划分(以下只对二维梁而言),要根据需求精度进行合理划分,既兼顾精度,同时也兼顾计算量(随着计算精度的提高,单元数量增加,相应计算量也会增加,计算时间也会增加),经过试验随着单元数量增加,其计算精度也不段提高,当将梁分到七单元时,通过计算得到的主振型和频率和理论值吻合的非常好。当梁取一单元时(elementno=1),由于梁总体只有两自由度,故只能得出前两阶主振型;当梁取二单元时(elementno=2),由于梁总体有四自由度,故只能得出前四阶主振型;对于梁取三单元(elementno=3)以及三单元以上(elementno>3)时,梁总体有六自由度以及更高自由度,这里只画出前六阶主振型图。下六图是在elementno=20的情况下,通过计算,画出前六阶的主振型图(其中红线部分为理论主振型图,绿色五角星是计算在梁各单元节点处的振型,数量取决于梁单元划分的数目)。 五、源程序清单 clear all close all %各参数的设置 rou=2.7e3; %密度 A=1e-3;%横截面积 E=72e9; %弹性模量 L=1; %梁长 I=8.3333e-009;%截面惯性矩 elementno=input('输入有限元的数量:'); %有限元的数量 rodno=elementno+1;%节点数 alldimension=rodno*2; l=L/elementno; %单元刚度矩阵 ke=E*I/l^3*[12 -6*l -12 -6*l; -6*l 4*l^2 6*l 2*l^2; -12 6*l 12 6*l; -6*l 2*l^2 6*l 4*l^2]; %单元质量矩阵
Open Journal of Acoustics and Vibration 声学与振动, 2019, 7(1), 12-19 Published Online March 2019 in Hans. https://www.doczj.com/doc/5215296505.html,/journal/ojav https://https://www.doczj.com/doc/5215296505.html,/10.12677/ojav.2019.71002 Analysis for Natural Frequency and Mode Shape of Wing Structure Liang Chen, Jinwu Wu, Hanqing Li College of Aero Engineering, Nanchang Hangkong University, Nanchang Jiangxi Received: Feb. 10th, 2019; accepted: Feb. 22nd, 2019; published: Mar. 1st, 2019 Abstract In this electronic document, the FEM is used to simulate and analyze the natural frequency and vi-bration mode of a certain UAV composite wing. By using the non-contact laser vibrometer equip-ment, in order to eliminate the influence of boundary conditions on the vibration characteristics of the wing structure, the vibration characteristics of the wing are measured by free boundary conditions, and the first 4 natural frequencies and vibrations of the composite wing are obtained. At the same time, the finite element simulation results are compared. The calculation results show that the simulation results are basically consistent with the experimental results. Keywords Wing Structure, Experimental Analysis, Natural Frequency, Mode Shape 某机翼结构的固有频率和振型分析 陈亮,吴锦武,李汉青 南昌航空大学飞行器工程学院,江西南昌 收稿日期:2019年2月10日;录用日期:2019年2月22日;发布日期:2019年3月1日 摘要 本文采用有限元和试验对某一无人机复合材料机翼的固有频率和振型进行仿真和实验分析。通过利用非接触式激光测振仪设备,为了消除边界条件对机翼结构振动特性的影响,采用自由边界条件进行了机翼振动特性测量,获得了复合材料机翼的前4阶固有频率和振型。同时对比了有限元仿真结果。计算结果表明,仿真结果与试验测试结果基本一致。
自振周期折减系数 1 概念 由于计算模型的简化和非结构因素的作用,导致多层钢筋混凝土框架结构在弹性阶段的计算自振周期(下简称“计算周期”)比真实自振周期(下简称“自振周期”)偏长。因此,无论是采用理论公式计算还是经验公式计算;无论是简化手算还是采用计算机程序计算,结构的计算周期值都应根据具体情况采用自振周期折减系数(下简称“折减系数”)加以修正,经修正后的计算周期即为设计采用的实际周期(下简称“设计周期”),设计周期=计算周期×折减系数。如果折减系数取值不恰当,往往使结构设计不合理,或造成浪费、或甚至产生安全隐患。诚然,折减系数是钢筋混凝土框架结设计所需要解决的一个重要问题。 2 影响自振周期因素 影响自振周期因素是诸多方面的,加之多层钢筋混凝土框架结构实际工程的复杂性,抗震规范没有、也不可能对折减系数给出一个确切的数值。许多文献中给出,当主要考虑填充墙的刚度影响时,折减系数可0.6~0.7[2];根据填充墙的多少、填充墙开洞情况,其对结构自振周期影响的不同,可取0.50~0.90。这些都是以粘土实心砖为填充墙的经验值,不言而喻,采用不同填充墙体材料的折减系数是不相同的。当采用轻质材料或空心砖作填充墙,当然不应该套用实心砖为填充墙的折减系数。对于粘土实心砖外的其它墙体可根据具体情况确定折减系数。结构计算分析总是要进行简化的,简化程度取决于当时的计算工具;简化是有条件的,而关键是简化模型尽可能符合真实受力模型。多层钢筋混凝土框架结构的计算周期往往与其自振周期有较大出入,笔者认为,此偏差主要来自计算模型的简化,没有计入那些难于准确计算的因素造成的。一分为二的说,没有计入的那些因素,常常使计算周期比自振周期长,在一定条件下也会使计算周期比自振周期短,主要表现为以下几方面: 3 计算周期长的原因 1.填充墙的刚度影响 大多数多层钢筋混凝土框架结构的设计计算中,并没有计算填充墙、装修(饰)材料、支撑、设备等非结构构件的刚度。实际工程中,由于未考虑砖填充墙的刚度常常使计算周期比实测自振周期(下简称“实测周期”)大很多[7].填充墙的影响与填充墙的材料性能、数量、单片墙体长度、墙体完整性(开洞情况)、与框架的连接情况息息相关。定性地说,填充墙的数量多、单片墙体长度大、墙体开洞少且小、与框架连接好,它对框架结构的刚度增加大,反之就小。 我国的框架填充墙的发展趋势是,逐步取消粘土砖(保护粘土资源、能源、环境等的要求),采用多样化轻质填充砌体、轻墙板取而代之。采用不同材料的填充墙,由于填充墙材料的刚度、变形性能、延性的不同,其对结构的空间刚度影响显然不相同。在其它条件相同时,采用轻质填充墙比粘土砖填充墙对结构的刚度影响小。 一般框架结构都要有填充墙,当砖填充墙多,可能会成为影响结构自振周期的主要的直接因素。 2.基坑回填土及混凝土刚性地坪对底层框架柱的侧限作用通常,在计算模型中,多层钢筋混凝土框架结构的底层柱高(计算高度),一般取基顶至一层楼盖顶之间的距离,见下图1.由于基顶至室内、外之间回填土必须严格夯实。例如压
模态振型是一个相对量,通常是一个列向量,二维以上地系统其模态振型不是一个数.一个数对应单模态,其数值无意义.某模态频率下地模态振型反映了在该模态频率下各自由度地相对位移地比值.如果系统地初始位移恰好等于模态频率下地模态振型(或与之成比例),则此时系统地自由响应中只会出现该模态频率. 感谢欧阳中华教授地指点,我现在觉得自己当初确实对模态振型概念不清楚.模态振型是系统固有地振动形态,线性响应是振型线性叠加地结果,但振型之间是独立不耦合地.振型是个相对量,所以就有了多种振型归一划地方法.振型是个很重要地固有特征,正如楼上所说用于验证固有频率. 文档来自于网络搜索 我觉得振型在判别你计算固有频率正确性是非常有用地,比如,通过有限元计算得到了模型地前十阶固有频率,试验模态分析也得到了低阶地固有频率,假设计算地某阶固有频率与试验地某阶固有频率非常接近,但是并不能马上说明他们是同一阶地,需要通过振型来判断. 文档来自于网络搜索 其他地不知道,但是之所以引入模态地概念,之所以从物理坐标变换到模态坐标就是为了解耦,就是为了让其正交,这样方程才能解出来. 从能量角度说,这样各个振型之间就没有能量地交换. 文档来自于网络搜索 从数学上看,对响应函数级数展开后,其中地各项构成各阶模态,而级数展开形式本身要求各个基函数是相互正交地,也就是说:其实是把响应函数放到了一个函数空间里,各个展开项系数相当于这个响应在此函数空间里地坐标.文档来自于网络搜索 因为个自由度以上地系统往往都有耦合现象,例如方程*^^*中地、不同时为对角阵.但是从求解地角度来说,我们又希望其中地每个方程都是独立地,那样我们就可以像求解单自由度系统一样求解.我们就想能否选到合适地坐标系,使得运动完全不耦合,即系统质量矩阵和刚度矩阵同时为对角矩阵,称这样地坐标系为主坐标系,而模态坐标正是我们要寻找地主坐标.固有振型地正交性是指(以自由度为例),第一阶固有振动引起地作用力在第二阶固有振动上所做地功为零,即两种固有振动间无弹性势能地交换.同时也可证明振型地各阶导数间也是正交地. 文档来自于网络搜索 就像不同地坐标系下,对同一运动系统地表述会很不一样,表述同一运动系统地振型模态也可以有很多物理量地坐标系,当然其中很多都是很复杂地,对解决实际问题是没有实际意义和帮助地,只有那个特殊地正交状态地模态坐标,才是最简单最有用地坐标,因为它能把系统解耦,,这个特殊地坐标称之为主坐标,对应主振型,这个状态可以把方程解开,把问题解决掉,,文档来自于网络搜索 各阶模态是互相正交是为了解耦,使问题最简化.类似向量地分解,比方说,一个平面内力向量地分解方式有很多种,但采用直角正交分解最方便. 文档来自于网络搜索 主要从以后地解方程组时候要解耦考虑吧 模态正交,具体表现在模态振型存在正交,请注意“存在”,而这种正交是线性系统模态地基本特性,准确地说是固有特性,正因为存在这种正交特性,带来了运算时地广义坐标下地耦合矩阵变为模态坐标中.文档来自于网络搜索 地解耦,计算变得简单. 注:(对上段话地个人理解:线性系统具有正交特性,人们利用线性系统地正交特性,对线性模态进行解耦,使问题简化.)文档来自于网络搜索 .任一阶主振型地惯性力在另一阶主振型作为虚位移上所做地虚功之和为零 .任一阶主振型地惯性力只在各自地振型上做功,在另外地主振型上不做功 这是正交相应地物理解释,是模态振型正交地物理形式,所以不能用物理含义去证明其相应地数学表达. 上面模态正交地数学和物理形式和概念有解释清楚了,那么,为什么会正交呢?
各种模态分析方法总结与比较 一、模态分析 模态分析是计算或试验分析固有频率、阻尼比和模态振型这些模态参数的过程。 模态分析的理论经典定义:将线性定常系统振动微分方程组中的物理坐标变换为模态坐标,使方程组解耦,成为一组以模态坐标及模态参数描述的独立方程,以便求出系统的模态参数。坐标变换的变换矩阵为模态矩阵,其每列为模态振型。 模态分析是研究结构动力特性一种近代方法,是系统辨别方法在工程振动领域中的应用。模态是机械结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。这个分析过程如果是由有限元计算的方法取得的,则称为计算模记分析;如果通过试验将采集的系统输入与输出信号经过参数识别获得模态参数,称为试验模态分析。通常,模态分析都是指试验模态分析。振动模态是弹性结构的固有的、整体的特性。如果通过 AHA12GAGGAGAGGAFFFFAFAF
模态分析方法搞清楚了结构物在某一易受影响的频率范围内各阶主要模态的特性,就可能预言结构在此频段内在外部或内部各种振源作用下实际振动响应。因此,模态分析是结构动态设计及设备的故障诊断的重要方法。 模态分析最终目标是在识别出系统的模态参数,为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。 AHA12GAGGAGAGGAFFFFAFAF
AHA12GAGGAGAGGAFFFFAFAF 二、各模态分析方法的总结 (一)单自由度法 一般来说,一个系统的动态响应是它的若干阶模态振型的叠加。但是如果假定在给定的频带内只有一个模态是重要的,那么该模态的参数可以单独确定。以这个假定为根据的模态参数识别方法叫做单自由度(SDOF)法n1。在给定的频带范围内,结构的动态特性的时域表达表示近似为: ()[]}{}{T R R t r Q e t h r ψψλ= 2-1 而频域表示则近似为: ()[]}}{ {()[]2ωλωψψωLR UR j Q j h r t r r r -+-= 2-2 单自由度系统是一种很快速的方法,几乎不需要什么计算时间和计算机内存。 这种单自由度的假定只有当系统的各阶模态能够很好解耦时才是正确的。然而实际情况通常并不是这样的,所以就需要用包含若干模态的模型对测得的数据进行近似,同时识别这些参数的模态,就是所谓的多自由度(MDOF)法。 单自由度算法运算速度很快,几乎不需要什么计算和计
h t t p://w e nk u.ba i d u.c o m/v i ew/8003e022*******e4536f61f.ht m l 楼盖竖向自振频率怎么算 Kingckong按:上次发此文时出现个笔误,原文“自振频率=圆频率X2X3.14”是错的,应为“自振频率=圆频率/( 2π)”。因此修改后重新发上来。 一、规范条文引起的思考 1、规范条文引述: 《混凝土结构设计规范》GB50010-2010第3.4.6条:对混凝土楼盖结构应根据使用功能的要求进行竖向自振频率验算,并宜符合下列要求:1)住宅和公寓不宜低于5Hz;2)办公楼和旅馆不宜低于4Hz;)3大跨度公共建筑不宜低于3Hz。 2、新混凝土设计规范提出了验算楼盖楼盖竖向自振频率的要求,并没有提供验算的具体方法,条文说明也只是指出一般情况可用简化方法。执行该规范条文存在困难,具体用什么方法只能由结构设计人查找相关参考资料。
二、实用的资料和方法: 1、PKPM系列软件使用说明书《JCCAD用户手册及技术条件》的附录E提供了“常用结构构件对称型基本自振圆频率计算”,但不知其出处在哪、是否正确,姑且摘录如下作为参考。注意:下面的数据是圆频率,单位是弧度/秒,而自振频率单位是1/秒,自振频率=圆频率/(2π)。
2、用有限元精确计算,如用SAP2000建模计算。 3、2010版的PKPM软件也新增了个“楼盖舒适度计算”的模块。 4、以上第2、3项是需要花费白花花的银两,如果自己或单位财力不够,也可以其他参考资料的简化方法进行手算,如(1)《多层厂房楼盖抗微振设计规范》(GB50190-93)第6.3节(2)冶金部标准《机器动荷载作用下建筑物承重结构的振动计算和隔振设计规程》YBJ55-90附录二 (3)《复杂高层建筑结构设计》(徐陪福,建筑工业出版社,2005年)P44~54 (4)《钢结构设计手册(第三版)》(下册,建筑工业出版社,2004年)P168,适用于组合楼板自振频率的计算 相关阅读1:中华钢结构论坛的帖子“《混凝土结构设计规范》2011培训笔记” https://www.doczj.com/doc/5215296505.html,/forum/viewthread.php?tid=245669&pid2=1079908&keywords=竖向 自振频率&searchstyle=3&issearch=true#pid1079908
实验五 悬臂梁各阶固有频率及主振形的测定试验 一、实验目的 1、用共振法确定悬臂梁横向振动时的各阶固有频率。 2、熟悉和了解悬臂梁振动的规律和特点。 3、观察和测试悬臂梁振动的各阶主振型。分析各阶固有频率及其主振型的实测值与理论计算值的误差。 二、基本原理 悬臂梁的振动属于连续弹性体的振动,它具有无限多自由度及其相应的固有频率和主振型,其振动可表示为无穷多个主振型的叠加。对于梁体振动时,仅考虑弯曲引起的变形,而不计剪切引起的变形及其转动惯量的影响,这种力学分析模型称为欧拉-伯努利梁。 运用分离变量法,结合悬臂梁一端固定一端自由的边界条件,通过分析可求得均质、等截面悬臂梁的频率方程 1 L Lch cos -=ββ (5-1) 式中:L ——悬臂梁的长度。 梁各阶固有园频率为 A EI i i n 2 ρβω= (5-2) 对应i 阶固有频率的主振型函数为 ) ,3,2,1() sin (sin cos cos )( =-++- -=i x x sh L L sh L L ch x x ch x X i i i i i i i i i ββββββββ (5-3) 对于(5-1)式中的β,不能用解析法求解,用数值计算方法求得的一阶至四阶固有园频率和主振型的结果列于表5-1。 各阶固有园频率之比 1f ﹕1f ﹕1f ﹕1f ﹕… = 1﹕6.269﹕17.56﹕34.41﹕… (5-4) y A B x h L b 图5-1 悬臂梁振动模型 表(5-1)给出了悬臂梁自由振动时i =1~4阶固有园频率及其相应主振型函数。除了悬臂梁固定端点边界位移始终为零外,对于二阶以上主振型而言,梁上还存在一些点在振动过程中位移始终为零的振型节点。i 阶振型节点个数等于i -1,即振型节点个数比其振型的阶数小1。 实验测试对象为矩形截面悬臂梁(见图5-2所示)。在实验测试时,给梁体施加一个大小适当的激扰作用力,其频率正好等于梁体的某阶固有频率,则梁体便会产生共振,这时梁体变形即为该阶固有频率所对应的主振型,其它各阶振型的影响很小可忽略不计。用共振法确定悬臂梁的各阶固有频率及振型,我们只要连续调节激扰力,当悬臂梁出现某阶主振型且振动幅值最大即悬臂梁产生共振时,这时激扰力的频率就可以认为是悬臂梁的这一阶振动的固有频率。在工程实践中,最重要是确定振动系统最低的几阶固有频率及其主振型。本实验主要运用共振法测定悬臂梁一、二、三、四阶固有频率及其相应的主振型。
4.2 多自由度系统的固有频率与主振型 一、固有频率和主振型 上节导出了多自由度系统的自由振动微分方程: 以及 考虑到系统的主振动是简谐振动,可设它为: (4-10) 将它分别代入(4-5)与(4-7)式,可得如下主振型方程 (4-11)以及 (4-12)如果引入系统矩阵的概念,可以将式(4-11)与(4-12)化成具有相同的形式,对(4-11)式两端乘以,可得 (4-13)这时,设系统矩阵为 (4-14)且令,则主振型方程(4-11)可化为 (4-15) 再设另一个形式的系统矩阵为 (4-16)且令,则主振型方程(4-12)可化为 (4-17)这样,主振型方程(4-15)与(4-17)就有着相同的形式。 注意到系统的刚度矩阵与柔度矩阵之间存在着互逆关系,即有
或 利用矩阵乘积的求逆公式,可知上述两种系统矩阵之间有着互逆关系: 还应该指出,尽管系统的刚度矩阵、柔度矩阵以及质量矩阵一般都是对称矩阵,但是其系统矩阵和一般已不再是对称矩阵。 现在来看系统固有频率与主振型问题。鉴于方程(4-15)与(4-17)属于同一形式,故只需讨论其中之一。 方程(4-15)可改写为 (4-18) 它有非零解的条件为 (4-19) (4-19)式称为系统的频率方程或特征方程。对它展开的结果,可得一个关于的次代数方程: (4-20) 它的个根成为系统的特征根,亦称矩阵的特征值。特征值与系统固有频率之间有如下关系: (4-21) 一般说来,次代数方程的个根,可以是单根,也可以是重根;可以是实数,也可以是复数。但是,在我们所考虑的情形中,由于系统质量矩阵是正定的实对称阵,刚度矩阵是正定的或半正定的,故所有特征值都是实数,并且是正数或零。事实上,由正定与半正定的条件,对于任何非零的,有 (4-22) 现对系统主振型方程 两端前乘以,得 考虑到条件式(4-22),自然就得出上述结论。 通常,刚度矩阵为正定(或半正定)的系统,称为正定系统(或半正定系统)。所以,上述结论可改述为:正定系统的特征值都是正的,而半正定系统的特征值是正数或零。
模态分析中的几个基本概念 一、模态定义:物体按照某一阶固有频率振动时,物体上各个点偏离平衡位置的位移是满足一定的比例关系的,可以用一个向量表示。 模态分析一般是在振动领域应用,每个物体都具有自己的固有频率,在外力的激励作用下,物体会表现出不同的振动特性: 一阶模态是外力的激励频率与物体固有频率相等的时候出现的,此时物体的振动形态叫做一阶振型或主振型; 二阶模态是外力的激励频率是物体固有频率的两倍时候出现,此时的振动外形叫做二阶振型,以依次类推。 一般来讲,外界激励的频率非常复杂,物体在这种复杂的外界激励下的振动反应是各阶振型的复合。 二、模态分析:模态是结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。 有限元中模态分析的本质是求矩阵的特征值问题,所以“阶数”就是指特征值的个数。将特征值从小到大排列就是阶次。 实际的分析对象是无限维的,所以其模态具有无穷阶。但是对于运动起主导作用的只是前面的几阶模态,所以计算时根据需要计算前几阶的。 一个物体有很多个固有振动频率(理论上无穷多个),按照从小到大顺序,第一个就叫第一阶固有频率,依次类推。所以模态的阶数就是对应的固有频率的阶数。 三、振型是指体系的一种固有的特性。它与固有频率相对应,即为对应固有频率体系自身振动的形态。每一阶固有频率都对应一种振型。振型与体系实际的振动形态不一定相同。振型对应于频率而言,一个固有频率对应于一个振型。按照频率从低到高的排列,来说第一振型,第二振型等等。此处的振型就是指在该固有频率下结构的振动形态,频率越高则振动周期越小。在实验中,我们就是通过用一定的频率对结构进行激振,观测相应点的位移状况,当观测点的位移达到最大时,此时频率即为固有频率。实际结构的振动形态并不是一个规则的形状,而是各阶振型相叠加的结果。 四、模态扩展是为了是结果在后处理器中观察而设置的,原因如下: 求解器的输出内容主要是固有频率,固有频率被写到输出文件Jobname.OUT及振型文件Jobnmae.MODE中,输出内容中也可以包含缩减
机械振动大作业 (盘轴扭振系统固有频率和主振型的计算) 学院:航空航天工程学部 班级:04040203班 姓名:李根 学号:2010040402093 2013年5月12号
盘轴扭振系统固有频率和主振型的计算 一:简化简化分析 分析该系统为非约束性盘轴扭振系统,并简化分析分析: :1.忽略轴的质量; 2.轴的刚度对盘的影响不做考虑; 3.将圆盘的质量集中于圆盘中心,不考虑圆盘厚度对系统的影响;4.系统为线弹性系统,盘为刚体。 对于非约束系统,其只存在刚度矩阵,不存在柔度矩阵,即不能对刚度矩阵求逆。 二:条件 圆盘: 1.几何尺寸:直径10.4d m =,厚度0.02h m =; 2.材料:杨氏模量112210(/)E N m =×,剪切模量1027.6910(/) G N m =×密度37800(/) kg m ρ=轴: 1.几何尺寸:直径20.04d m =,0.1a m =2.材料:杨氏模量112210(/)E N m =×,剪切模量1027.6910(/) G N m =×密度37800(/) kg m ρ=三(1):矩阵迭代法 1.1.概 概述(1):系统主振型方程为{}[]{}21A M K A ω???=??,引入动力矩阵[][]1 D M K ???=??。任
取一个经过归一化的假设阵型{}0A ,用动力矩阵[]D 前乘它,并对通过乘法运算新得到的阵型矢量进行归一化,则得:{}110[]{}D A a A =,式中1a 为新振型矢量归一化后的系数。 (2)若{}10{}A A ≠,从1{}A 开始,重复上述步骤得:{}121[]{}D A a A =,式中2a 为新振型矢量归一化后的系数。 (3):若{}21{}A A ≠,继续重复上述步骤,进过K 次矩阵乘法运算后,得到 {}1[]{}k k k D A a A ?=,在规定的有效位数内,{}1{}k k A A ?=时停止运算,此时的{}1k A ?即 为系统第一阶主振型(1){}A 的近似值,即:{}(1)1{}k A A ?≈,而这时的系数k a 即是系统第一阶固有频率平方倒数的近似值,即:211/k a ω≈。 该方法的精确度不依赖于假设阵型,假设阵型的好坏只影响迭代的次数。即使假设的固有频率域一阶主振型相差很远,经过充分的迭代运算,仍可求得足够精确的基频值。 求得第一阶主振型以后,利用主振型的正交性来清除掉假设阵型中的分量,然后再进行迭代求解可以是结果收敛于第二阶主振型。同理,如果我们在假设阵型中清除掉所有前s 阶这阵型分量,那么迭代的结果将得到第s+1阶固有频率及主振型。 引进清型矩阵:[]()j 1 {}{}[][]j T s j j A A M Q I M ==?∑()。由于实际计算中舍入误差的存在,每次迭 代后,所得的主振型中还包含前面几阶的主振型分量,因此每次计算前都要进行清型才能保证最后收敛的主振型。 2.2.计算程序 计算程序clc clear n=8; d1=0.4;%圆盘直径d1=0.4d2=0.04;%轴直径d2=0.04a=0.1;%轴几何尺寸 den=7800;%密度(轴和圆盘)G=7.69e+10;%剪切模量h=0.02;%圆盘厚度 J1=0.5*pi*den*h*(d1/2)^4;%转动惯量
附录F 结构基本自振周期的经验公式 F.1 高耸结构 F.1.1 一般高耸结构的基本自振周期,钢结构可取下式计算的较大值,钢筋混凝土结构可取下式计算的较小值: H T )013.0~007.0(1= (F.1.1) 式中:H ——结构的高度(m)。 F.1.2 烟囱和塔架等具体结构的基本自振周期可按下列规定采用: 1,烟囱的基本自振周期可按下列规定计算: 1)高度不超过60m 的砖烟囱的基本自振周期按下式计算: d H T 2 2 110 22.023.0-?+= (F.1.2-1) 2)高度不超过150m 的钢筋混凝土烟囱的基本自振周期按下式计算: d H T 2 2 110 10.041.0-?+= (F.1.2-2) 3)高度超过150m ,但低于210m 的钢筋混凝土烟囱的基本自振周期按下式计算: d H T 2 2 110 08.053.0-?+= (F.1.2-3) 式中:H ——烟囱高度(m); d ——烟囱1/2高度处的外径(m)。 2,石油化工塔架(图F.1.2)的基本自振周期可按下列规定计算: 图F.1.2 设备塔架的基础形式 (a)圆柱基础塔;(b)圆筒基础塔; (c)方形(板式)框架基础塔;(d)环形框架基础塔 1)圆柱(筒)基础塔(塔壁厚不大于30mm)的基本自振周期按下列公式计算: 当H 2/D 0<700时 2 3 110 85.035.0D H T -?+= (F.1.2-4)
当H 2/D 0≥700时 2 3 110 99.025.0D H T -?+= (F.1.2-5) 式中:H ——从基础底板或柱基顶面至设备塔顶面的总高度(m); D 0——设备塔的外径(m);对变直径塔,可按各段高度为权,取外径的加权平均值。 2)框架基础塔(塔壁厚不大于30mm)的基本自振周期按下式计算: 2 3 110 40.056.0D H T -?+= (F.1.2-6) 3)塔壁厚大于30mm 的各类设备塔架的基本自振周期应按有关理论公式计算。 4)当若干塔由平台连成一排时,垂直于排列方向的各塔基本自振周期T 1可采用主塔(即周期最长的塔)的基本自振周期值;平行于排列方向的各塔基本自振周期T 1可采用主塔基本自振周期乘以折减系数0.9。 F.2 高层建筑 F.2.1 一般情况下,高层建筑的基本自振周期可根据建筑总层数近似地按下列规定采用: 1,钢结构的基本自振周期按下式计算: T 1=(0.10~0.15)n (F.2.1-1) 式中:n ——建筑总层数。 2,钢筋混凝土结构的基本自振周期按下式计算: T 1=(0.05~0.lO)n (F.2.1-2) F.2.2 钢筋混凝土框架、框剪和剪力墙结构的基本自振周期可按下列规定采用: 1,钢筋混凝土框架和框剪结构的基本自振周期按下式计算: 3 2 3 110 53.025.0B H T -?+= (F.2.2-1) 2,钢筋混凝土剪力墙结构的基本自振周期按下式计算: 3 103 .003.0B H T += (F.2.2-2) 式中:H ——房屋总高度(m); B ——房屋宽度(m)。
固体力学作业 薄板的振动的固有频率与振型 1、 问题 矩形薄板的参数如下 33150,100,5,210,0.3,7.9310/a mm b mm h mm E GPa v kg m ρ======? 求矩形薄板在 (1) 四边简支(2)四边固支 条件下的固有频率和振型 2、薄板振动微分方程 薄板是满足一定假设的理想力学模型,一般根据实际的尺寸和受力特点来将某个实际问题简化为薄板模型,如厚度要比长、宽的尺寸小得的结构就可以采用薄板模型。薄板在上下表面之间存在一个对称平面,此平面称为中面,且假定: (1)板的材料由各向同性弹性材料组成; (2)振动时薄板的挠度要比它的厚度要小; (3)自由面上的应力为零; (4)原来与中面正交的横截面在变形后始终保持正交,即薄板在变形前中面的法线在变形后仍为中面的法线。 为了建立应力、应变和位移之间的关系,取空间直角坐标Oxyz ,且坐标原点及xOy 坐标面皆放在板变形前的中面位置上,如图 1所示。设板上任意一点a 的位置,将由变形前的坐标x 、y 、z 来确定。 图 1 薄板模型 根据假定(2),板的横向变形和面内变形u 、v 是相互独立的。为此,其弯曲变形可由中面上各点的横向位移(,,)w x y t 所决定。根据假定(4),剪切应变分量为零。由薄板经典理论,可以求得板上任意一点(,,)a x y z 沿,,x y z 三个方向的位移分量,,a a a u v w 的表达式分别为
() a a a w u z x w v z y w w ?=-??=-?=+ 高阶小量 (1.1) 根据应变与位移的几何关系可以求出各点的三个主要是应变分量为 22 22 22a x a y a a xy u w z x x v w z y y u v w z y x x y εεγ??==-????==-?????=+=-???? (1.2) 胡克定律,从而获得相对应的三个主要应力分量为: 2222 222222222()()11()()111x x y y y x xy xy E Ez w w x y E Ez w w y x Ez w G x y σεμεμμμσεμεμμμτγμ??=+=-+--????=+=-+--???==- +?? (1.3) 现画薄板微元的受力图如图 2所示。 图 2所示中x xy x y yx y M M Q M M Q 、和、、和分别为OB 面、OC 面上所受到的单位长度的弯矩、扭矩和横切剪力。弯矩和扭矩都用沿其轴的双剪头表示。M x 、M y 是由正应力σx 、 σx 引起的合力矩。扭矩是由剪切力τxy 引起的合力矩。 图 2 薄板应力示意图 p (x ,y ,t )=P (x ,y )f (t )为具有变量分离形式的外载荷集度,沿z 轴方向。应用动静法计算时, 沿z 轴负方向有一虚加惯性力22w h dxdy t ρ??,根据0z F =∑,0y M =∑,0y M =∑则 有
职业技术学院一、能量法计算基本周期 3.7结构自振周期的计算设体系按i振型作自由振动。速度为应用抗震设计反应谱计算地震作用下的结构反应,除砌体结构、底部框架抗震墙砖房和内框架房屋采用底部剪力法不需要计算自振周期外,其余均需计算自振周期。计算方法: 矩阵位移法解特征问题、近似公式、经验公式。t时刻的位移为重力荷载代表值作用下的水平位移解: 例.已知: 求结构的基本周期。G2G1 (1)计算各层层间剪力 (2)计算各楼层处的水平位移 (3)计算基本周期二、等效质量法(折算质量法)将多质点体系用单质点体系代替。多质点体系的最大动能为单质点体系的最大动能为---体系按第一振型振动时,相应于折算质点处的最大位移;---单位水平力作用下顶点位移。重力荷载代表值作用下的水平位移解: 例.已知: 求结构的基本周期。G2G1能量法的结果为T1 0.508s三、顶点位移法对于顶点位移容易估算的建筑结构,可直接由顶点位移估计基本周期。1体系按弯曲振动时抗震墙结构可视为弯曲型杆。无限自由度体系,弯曲振动的运动方程为悬臂杆的特解为振型基本周期为重力作为水平荷载所引起的位移为2体系按剪切振动时框架结构可近似视为剪切型杆。无限自由度体系,剪切杆的的运动方程为悬臂杆的特解为振型基本周期为重力作为水平荷载所引起的位移为3体系按剪弯振动时框架-抗震墙结构可近似视为剪弯型杆。基本周期为四、自振周期的经验公式根据实测统计,忽略填充墙布置、质量分布差异等,初步设计时可按下列公式估算 (1)高度低于25m且有较多的填充墙框架办公楼、旅馆的基本周期
(2)高度低于50m的钢筋混凝土框架-抗震墙结构的基本周期H---房屋总高度;B---所考虑方向房屋总宽度。 (3)高度低于50m的规则钢筋混凝土抗震墙结构的基本周期 (4)高度低于35m的化工煤炭工业系统钢筋混凝土框架厂房的基本周期
《振动测试实验》实验报告? 南京航空航天大学 机械结构力学及控制国家重点实验室 二○一一年 ?注:实验报告完成后请以附件形式发送至:wt78@https://www.doczj.com/doc/5215296505.html, 邮件主题请写明:《振动测试实验报告》,姓名,学号,分班号(三班或四班)
一、实验目的 ?测量双简支梁的固有频率和振型。 ?理解多自由度系统振型的物理概念。 ?掌握多自由度系统固有频率和振型的简单测量方法。 二、实验原理图 简支梁固有频率和振型测试原理图 三、实验过程 1、将功率放大器“输出调节”旋至最小,“信号选择”置“外接”。打开各设备电源。 2、进入“双简支梁固有频率与振型测量”实验操作界面,使信号发生器的输出频率约为 30Hz,输出电压约为 1V 。调节功率放的“输出调节”,逐渐增大其输出功率直至质量块有明显的振动(观察并用手触摸)。 3、将信号发生器输出频率由低向高逐步调节,同时观察李萨育图形。当李萨育图为稳定的正椭圆时,信号发生器的频率读数即为第一阶固有频率。继续将
信号发生器的频率向高逐步调节,测出第二阶、第三阶固有频率。 4、再将信号发生器调到第一阶固有频率值,保持功率放大器的输出功率恒定(即:不再改变信号发生器的输出电压和功率放大器的输出功率),保持“参考”传感器的位置不变。将“测量”传感器从双简支梁的右端等距跑点,依次记下“测量”传感器在各个位置时的测量点与参考点传感器输出电压之比(即“测量点/参考点”的显示值)及其正负号。将其归一化即可得到第一阶振型,填“振型数据”表格。点击“振型图”或“振型动画”检验振型数据。 四、实验数据与分析 1、列出固有频率。 双简支梁的3个阶段的固有频率分别为: 一阶: 36.7Hz 二阶: 136.5Hz 三阶: 326.6Hz 一阶振型图