
三角函数的图像与性质
二. 教学目标:
了解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图,理解A、ω、φ的物理意义。
三. 知识要点:
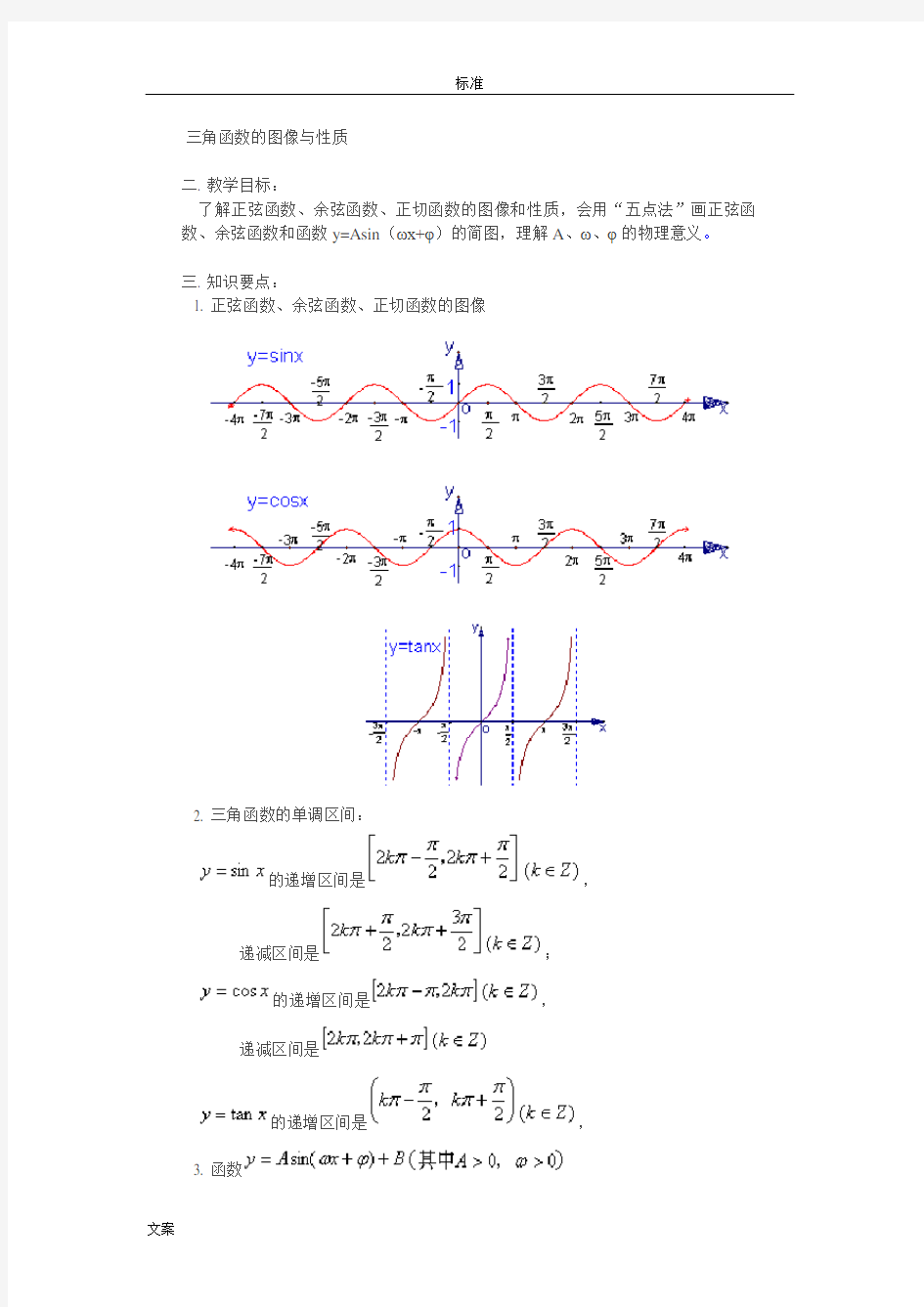
1. 正弦函数、余弦函数、正切函数的图像
2. 三角函数的单调区间:
的递增区间是,
递减区间是;
的递增区间是,
递减区间是
的递增区间是,
3. 函数
最大值是,最小值是,周期是,频率是,相位是,初相是;其图象的对称轴是直线,凡是该图象与直线的交点都是该图象的对称中心。
4. 由y=sin x的图象变换出y=sin(ωx+)的图象一般有两个途径,只有区别开这两个途径,才能灵活地进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现.无论哪种变形,请切记每一个变换总是对字母x而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
途径一:先平移变换再周期变换(伸缩变换)
先将y=sin x的图象向左(>0)或向右(<0=平移||个单位,
再将图象上各点的横坐标变为原来的倍(ω>0),便得到y=sin(ωx+)的图象。
途径二:先周期变换(伸缩变换)再平移变换。
先将y=sin x的图象上各点的横坐标变为原来的倍(ω>0),再沿x
轴向左(>0)或向右(<0,平移个单位,便得到y=sin(ωx+)的图象。
5. 对称轴与对称中心:
的对称轴为,对称中心为;
的对称轴为,对称中心为;
对于和来说,对称中心与零点相联系,对称轴与最值点相联系。
6. 五点法作y=A sin(ωx+)的简图:
五点法是设X=ωx+,由X取0、、π、、2π来求相应的x值及对应的y值,再描点作图。
【典型例题】
例1. 把函数y=cos(x+)的图象向左平移个单位,所得的函数为偶函数,则的最小值是()
A. B. C. D.
解:先写出向左平移4个单位后的解析式,再利用偶函数的性质求解。
向左平移个单位后的解析式为y=cos(x++)
则cos(-x++)=cos(x++),
cos x cos(+)+sin x sin(+)=cos x cos(+)-sin x sin(+)∴sin x sin(+)=0,x∈R.
∴+=kπ,∴=kπ->0
∴k>,∴k=2,∴=
答案:B
例2. 试述如何由y=sin(2x+)的图象得到y=sin x的图象。
解:y=sin(2x+)
另法答案:
(1)先将y=sin(2x+)的图象向右平移个单位,得y=sin2x的图象;
(2)再将y=sin2x上各点的横坐标扩大为原来的2倍(纵坐标不变),得y=sin x的图象;
(3)再将y=sin x图象上各点的纵坐标扩大为原来的3倍(横坐标不变),即可得到y=sin x的图象。
例3. 求函数y=sin4x+2sin x cos x-cos4x的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间。
解:y=sin4x+2sin x cos x-cos4x
=(sin2x+cos2x)(sin2x-cos2x)+sin2x
=sin2x-cos2x
=2sin(2x-).
故该函数的最小正周期是π;最小值是-2;单调递增区间是[0,],[,
π]
点评:把三角函数式化简为y=A sin(ωx+)+k(ω>0)是解决周期、最值、单调区间问题的常用方法。
例4. 已知电流I与时间t的关系式为。
(1)下图是(ω>0,)
在一个周期内的图象,根据图中数据求
的解析式;
(2)如果t在任意一段秒的时间内,电流都能取得最
大值和最小值,那么ω的最小正整数值是多少?
解:本小题主要考查三角函数的图象与性质等基础知识,考查运算能力和逻辑推理能力。
(1)由图可知A=300
设t1=-,t2=
则周期T=2(t2-t1)=2(+)=
∴ω==150π
将点代入
∴=
故所求的解析式为
(2)依题意,周期T≤,即≤,(ω>0)
∴ω≥300π>942,又ω∈N*
故最小正整数ω=943.
点评:本题解答的开窍点是将图形语言转化为符号语言.其中,读图、识图、用图是形数结合的有效途径。
【模拟试题】
1. 在(0,2π)内,使sin x>cos x成立的x的取值范围是()
A. (,)∪(π,)
B. (,π)
C. (,)
D. (,π)∪(,)
2. 如果函数f(x)=sin(πx+θ)(0<θ<2π=的最小正周期是T,且当x=2时取得最大值,那么()
A. T=2,θ=
B. T=1,θ=π
C. T=2,θ=π
D. T=1,θ=
3. 设函数f(x)=A+B sin x,若B<0时,f(x)的最大值是,最小值是-,则A=_______,B=_______。
4. 已知函数y=tan(2x+)的图象过点(,0),则可以是()
A. -
B.
C. -
D.
5. 函数y=sin(-2x)+sin2x的最小正周期是()
A. 2π
B. π
C.
D. 4π
6. 若f(x)sin x是周期为π的奇函数,则f(x)可以是()
A. sin x
B. cos x
C. sin2x
D. cos2x
7. 函数y=2sin(-2x)(x∈[0,π])为增函数的区间是()
A. [0,]
B. [,]
C. [,]
D. [,π]
8. 把y=sin x的图象向左平移个单位,得到函数__________的图象;再把所得
图象上的所有点的横坐标伸长到原来的2倍,而纵坐标保持不变,得到函数__________的图象。
9. 函数y=lg(cos x-sin x)的定义域是_______.
10. f(x)=2cos2x+sin2x+a(a为实常数)在区间[0,]上的最小值为-4,
那么a的值等于()
A. 4
B. -6
C. -4
D. -3
【试题答案】
1. 答案:C
2. 解析:T==2,又当x=2时,sin(π·2+θ)=sin(2π+θ)=sinθ,要使
上式取得最大值,可取θ=。
答案:A
3. 解析:根据题意,由可得结论
答案:-1
4. 解析:将(,0)代入原函数可得,tan(+)=0,再将A、B、C、D代入
检验即可。
答案:A
5. 解析:y=cos2x-sin2x+sin2x=cos2x+sin2x=sin(+2x),T=π.
答案:B
6. 答案:B
7. 解析:对于y=2sin(-2x)=-2sin(2x-),其增区间可由y=2sin(2x -)的减区间得到,即2kπ+≤2x-≤2kπ+,k∈Z。
∴kπ+≤x≤kπ+,k∈Z.令k=0,故选C.
答案:C
8. 解析:向左平移个单位,即以x+代x,得到函数y=sin(x+),再把所得图象上所有点的横坐标伸长到原来的2倍,即以x代x,得到函数:y=sin(
x+)。
答案:y=sin(x+)y=sin(x+)
9. 解析:由cos x-sin x>0cos x>sin x.由图象观察,知2kπ-<x<2kπ+(k∈Z)
答案:2kπ-<x<2kπ+(k∈Z)
10. 解析:f(x)=1+cos2x+sin2x+a=2sin(2x+)+a+1.
∵x∈[0,],∴2x+∈[,].
∴f(x)的最小值为2×(-)+a+1=-4
∴a=-4.