
第三章离散傅里叶变换
离散傅里叶变换不仅具有明确的物理意义,相对于DTFT他更便于用计算机处理。但是,直至上个世纪六十年代,由于数字计算机的处理速度较低以及离散傅里叶变换的计算量较大,离散傅里叶变换长期得不到真正的应用,快速离散傅里叶变换算法的提出,才得以显现出离散傅里叶变换的强大功能,并被广泛地应用于各种数字信号处理系统中。近年来,计算机的处理速率有了惊人的发展,同时在数字信号处理领域出现了许多新的方法,但在许多应用中始终无法替代离散傅里叶变换及其快速算法。
§ 3-1 引言
一.DFT是重要的变换
1.分析有限长序列的有用工具。
2.在信号处理的理论上有重要意义。
3.在运算方法上起核心作用,谱分析、卷积、相关都可以通DFT在计算机上实现。
二.DFT是现代信号处理桥梁
DFT要解决两个问题:
一是离散与量化,
二是快速运算。
傅氏变换
§ 3-2 傅氏变换的几种可能形式
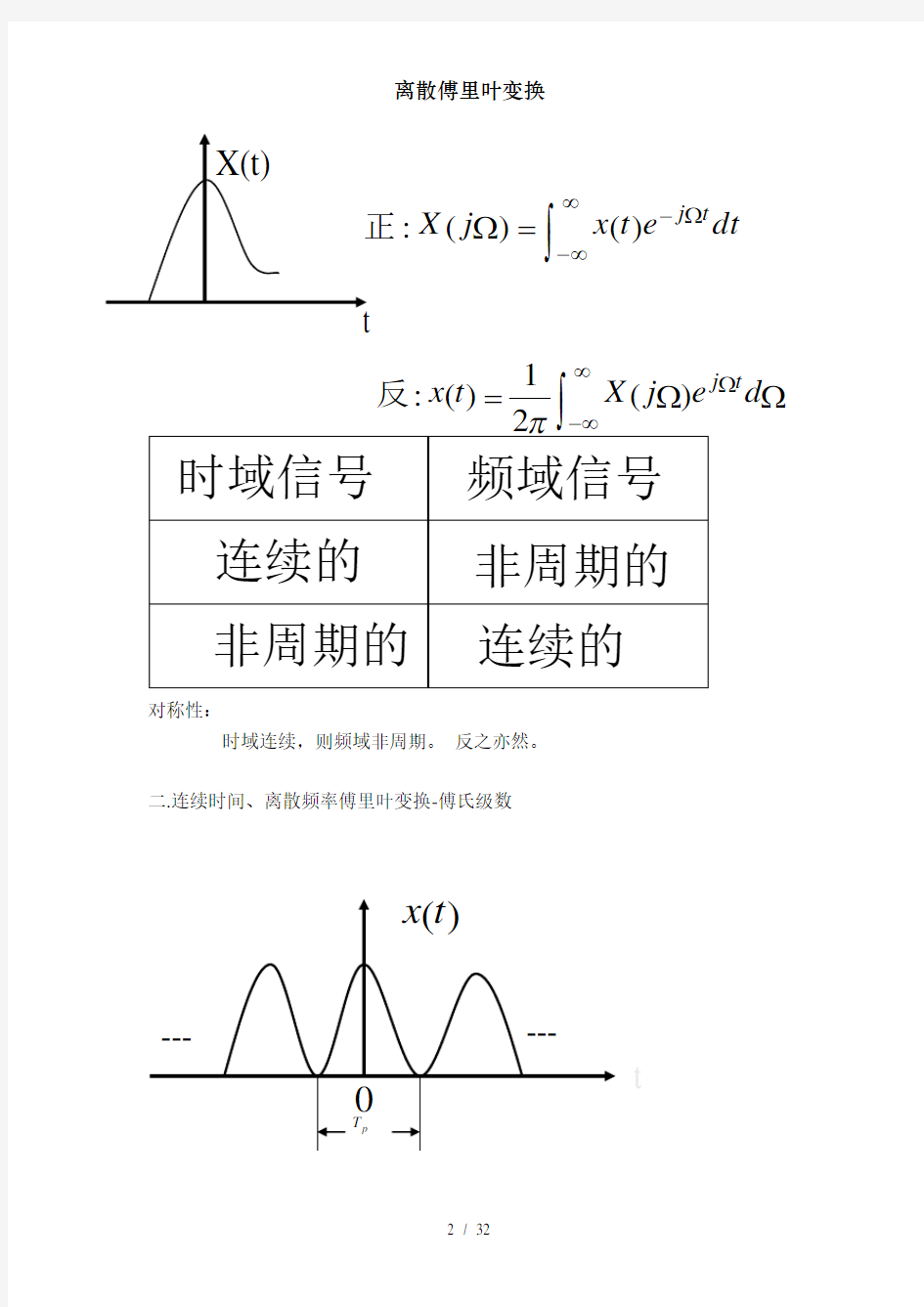
一.连续时间、连续频率的傅氏变换-傅氏变换
对称性: 时域连续,则频域非周期。 反之亦然。
二.连续时间、离散频率傅里叶变换-傅氏级数
时域信号 频域信号 连续的 非周期的
非周期的 连续的
t
?
∞
∞
-Ω-=
Ωdt
e
t x j X t
j )()(:?
∞
∞
-ΩΩ
Ω=
d e j X t x t j )(21
)(:π
反
*时域周期为Tp, 频域谱线间隔为2π/Tp
三.离散时间、连续频率的傅氏变换
--序列的傅氏变换
p
T 0=
Ω时域信号 频域信号 连续的 周期的
非周期的 离散的
?
-Ω-=
Ω2
/2
/00)(1
)(:p p T T t jk p
dt
e t x T jk X 正∑
∞
-∞
=ΩΩ=
k t
jk e jk X t x 0)()(:0反
0 T 2T
t
时域信号 频域信号 离散的 非周期的
周期的 连续的
∑∞
-∞
=Ω-Ω=
n T
jn T
j e
nT x e
X )()(:正?
ΩΩ-ΩΩΩ
Ω=
2
/2
/)(1
)(:s s d e
e
X nT x T
jn T
j s
反T
T s π
2,*=
Ω频域的周期为时域抽样间隔为
四.离散时间、离散频率的傅氏变换--DFT
由上述分析可知,要想在时域和频域都是离散的,那么两域必须是
周期的。
t
0 T 2T 1 2 N
n 时域信号 频域信号 离散的 周期的
周期的 离散的
)
1()1(0
-Ω-N N .
2,;
2*0T
T T T s p p π
π=Ω=Ω频域的周期为时域的离散间隔为为函数,频域的离散间隔时域是周期为
DFT 的简单推演:
在一个周期内,可进行如下变换:
02
/2
/:1~0,2:1
~0:)(1)()()(Ω=?Ω=ΩΩ-=?=Ω=ΩΩ-Ω
Ω=
=
?
∑ΩΩ-ΩΩ∞-∞
=Ω-Ωd d N k F k k N n d e e X nT x e nT x e X s s T jn T j s
n T
jn T j π从∑∑∑
∑
-=-=--=ΩΩ-=Ω-Ω=
=
=
Ω?Ω=?=ΩΩΩ=
=1
2210
22001
1
0)(1
)()()
(222)()()()(0000N k nk N
j k N j
N n nk N
j k N j s p N k T
jnk T jk s
N n T jnk T jk e e
X N
nT x e
nT x e
X N T T T e e X nT x e nT x e X πππππ
ππ因此又
视作n 的函数,
视作k 的函数,
这样,
§ 3-3 周期序列的DFS
一.周期序列DFS 的引入
导出周期序列DFS 的传统方法是从连续的周期信号的复数傅氏级数
开始的:
对上式进行抽样,得: ,代入
又由于
∑∑-=-=-=
=
10
21
2)(1
)()()(N k nk N
j
N n nk N
j
e
k X N
n x e
n x k X π
π
)
()
(2k N j
e
X nT x π)
()
()()(2k X e
X n x nT x k N j →→π∑
∞
-∞
=ΩΩ=k t
jk e k X t x 0)(~)(~0∑
∑
∞
-∞
=∞
-∞
=ΩΩ=
Ω=k nk N
j k nT
jk e
k X e k X nT x π200)(~
)(~
)(~0N
T π20=
Ωkn N
j rn j nk N
j
n rN k N
j
e
e e
e
ππππ
222)(2=?=+
所以求和可以在一个周期内进行,即
这就是说,当在k=0,1,..., N-1求和与在k=N,...,2N-1求和所得的结果是一致的。
二. 的k 次谐波系数 的求法
1.预备知识 同样,当 时,p 也为任意整数,则
亦即
()()∑
-=Ω=
1
20~
~N k nk N
j
e
k X nT x π∑
-==
Ω1
20)(~
)(~)(~~)(~)(~~)(~N k nk N
j
e
k X n x k X k X n x nT x π则有,;,考虑到:)(~
n x )(~k X ??
?==∑
-=r
m mN r N e N n rn
N j ,其他为任意整数0,,10
2π)
(11122)1(222210
2时mN r N e
e
e
e e e
r N j N r N
j
N r N
j
r N
j r N
j N n rn N j
==--=
++++=?-??-=∑πππ
πππ
pN
r k =-]
)[()0(10
)(2pN r k N N N e N n n r k N
j --===∑
-=-δδπ[][]
)()()(11
)(2pN r k pN r k pN r k e
N
N n n r k N
j
+-=--=--=∑-=-δδδπ
所以 2. 的表达式
将式 的两端乘
,然后从 n=0到N-1求和,则:
[])
(~)(~)()(~10
r X pN r X pN r k k X N k =+=+-∑
-=δ)(~k X ∑
-==1
2)(~)(~N k nk N j e k X n x πnr N
j e π2-∑
-=-1
2)(~N n nr N
j
e
n x π
∑∑
-=-=-=
101
)(2)(~N n N k n r k N
j
e
k X π
[]
)
(~)
(~
)()(~
)(~
)(~)(~1
1
010)(2101
)(21
2r X N pN r X N pn r k N k X e k X e
k X e
n x N k N k N n n r k N
j N n N k n r k N
j
N n nr N
j
=+=+-?=
???
?????==
∑
∑∑
∑∑
∑
-=-=-=--=-=--=-δππ
π
通常将定标因子1/N 移到 表示式中。
即:
3.离散傅氏级数的习惯表示法
通常用符号 代入,则:
∑
-=-=
1
2)(~1)(~
,N n nr N
j
e
n x N
r X π
因此∑
∑
∑
-=-=--=-=
=
=
1
21
21
2)(~
)(~)(~1)(~
,)(~1)(~
N k kn N
j N n kn
N
j N n kn N
j
e k X n x e n x N k X e
n x N
k X k r π
π
π
对于周期序列所以则有换成将)
(~n x ∑
∑
-=-=-==
1
21
2)(~1)(~)(~)(~
N k kn N
j
N n kn N
j
e
k X N
n x e
n x k X ππ
N j
N e W π
2-=
正变换: 反变换: 4. 的周期性与用Z 变换的求法 周期性: 用Z 变换的求 :
对
作Z 变换,
[]∑
∑
-=-=-=
=
=1
1
2)(~)(~)(~)(~
N n nk N
N n nk N
j
W n x e
n x n x DFS k X π
[]
∑
∑
-=--====1
1
2)(~1)(~1
)(~)(~N k nk N
N k nk N
j
W k X N
e
k X N
k X IDFS n x π)
(~)(~)(~)(~)(~
10
210
221
0)(2k X e
n x e e n x e
n x mN k X N n kn N
j
N n mn j kn
N j N n n mN k N
j
==
?==+∑
∑
∑
-=--=---=+-π
πππ
个不同值。
只有这就是说,N k X )(~
)(~
k X )(n x )(~
k
X
如果 ,则有
可见, 是Z 变换 在单位圆上抽样,抽样点在单位圆上的
N 个等分点上,且第一个抽样点为k =0。
∑
∑
-=-∞
-∞
=-=
=
1
)()()(N n n
n n Z n x Z n x Z X
[]
Z j Im []
Z
k
N j
e Z π2=)
(~)()
(1
22k X e
n x e
X N n kn N
j
k N j
==
∑-=-ππ
)(~k X )(Z X
第一章 离散傅里叶变换(DFT ) 填空题 (1) 某序列的DFT 表达式为 ∑-==1 )()(N n kn M W n x k X ,由此可以看出,该序列时域的长 度为 ,变换后数字频域上相邻两个频率样点之间的间隔是 。 解:N ; M π 2 (2)某序列DFT 的表达式是 ∑-==1 0)()(N k kl M W k x l X ,由此可看出,该序列的时域长度 是 ,变换后数字频域上相邻两个频率样点之间隔是 。 解: N M π 2 (3)如果希望某信号序列的离散谱是实偶的,那么该时域序列应满足条件 。 解:纯实数、偶对称 (4)线性时不变系统离散时间因果系统的系统函数为2 52) 1(8)(22++--=z z z z z H ,则系统 的极点为 ;系统的稳定性为 。系统单位冲激响应)(n h 的初值为 ;终值 )(∞h 。 解: 2,2 1 21-=- =z z ;不稳定 ;4)0(=h ;不存在 (5) 采样频率为Hz F s 的数字系统中,系统函数表达式中1 -z 代表的物理意义是 ,其中时域数字 序列)(n x 的序号 n 代表的样值实际位置是 ;)(n x 的N 点DFT )k X (中,序号k 代表的样值实际 位置又是 。 解:延时一个采样周期F T 1=,F n nT =,k N k πω2= (6)已知 }{}{4,3,2,1,0;0,1,1,0,1][,4,3,2,1,0;1,2,3,2,1][=-===k n h k n x ,则][n x 和 ][n h 的5点循环卷积为 。 解:{}]3[]2[][][][][---+?=?k k k k x k h k x δδδ {}4,3,2,1,0;2,3,3,1,0])3[(])2[(][55==---+=k k x k x k x (7)已知}{}{3,2,1,0;1,1,2,4][,3,2,1,0;2,0,2,3][=--=== k n h k n x 则][][n h n x 和的 4点循环卷积为 。
XXXX大学 2012届学士学位论文 离散傅里叶变换的分析与研究 学院、专业物理与电子信息学院 电子信息工程 研究方向数字信号处理 学生姓名XX 学号 XXXXXXXXXXX 指导教师姓名XXX 指导教师职称讲师 2012年4月26日
离散傅里叶变换的分析与研究 XX 淮北师范大学物理与电子信息学院 235000 摘要离散傅里叶变换是连续傅里叶变换在时域和频域上都离散的形式,是对连续时间信号频谱分析的逼近。离散傅里叶变换不仅在理论上有重要意义,而且在各种信号的处理中亦起着核心作用。 本文首先介绍了离散傅里叶变换的定义及性质,然后介绍了离散傅里叶变换的应用,主要包括对线性卷积的计算和对连续信号的谱分析。在理解理论的基础上,在matlab环境下实现了线性卷积和对连续信号频谱分析的仿真。仿真结果表明:当循环卷积长度大于或等于线性卷积长度时,可利用循环卷积计算线性卷积;利用DFT对连续信号进行频谱分析必然是近似的,其近似的结果与信号带宽,采样频率和截取长度都有关。 关键词离散傅里叶变换;线性卷积;谱分析
The Analysis and Research of Discrete Fourier Transform XX School of Physics and Electronic Information, Huai Bei Normal University, Anhui Huaibei, 235000 Abstract The discrete Fourier transform is the form that the continuous Fourier transform are discrete both in the time domain and frequency domain,it is a approach to the analysis of continuous time signal spectrum . The discrete Fourier transform not only has important significance in theory, but also plays a central role in all kinds of signal processing . This paper introduced the definition and properties of the discrete Fourier transform first of all.Then introduced the application of the discrete Fourier transform, which mainly including the calculation of linear convolution and analysis of continuous signal the spectral. On the basement of understanding theory, we realized the linear convolution and analysis of continuous signal spectrum on the Matlab environment . The simulation results show that when the length of the cyclic convolution is equal to or greater than linear convolution,we can use cyclic convolution to calculate linear convolution;It is approximately use continuous DFT spectrum to analyze the frequency domain of continuous time signal, the approximation of the results is related to the signal bandwidth, sampling frequency and intercept length. Keywords The discrete Fourier transform; Linear convolution; Spectrum analysis
一、概述 FFT(Fast Fourier Transformation),即为快速傅氏变换,是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。DFT对于X(K)的每个K值,需要进行4N次实数相乘和(4N-2)次相加,对于N个k值,共需N*N乘和N(4N-2)次实数相加。改进DFT算法,减小它的运算量,利用DFT中的周期性和对称性,使整个DFT的计算变成一系列迭代运算,可大幅度提高运算过程和运算量,这就是FFT的基本思想。虽然它对傅氏变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是进了一大步。 虽然FFT大幅度地降低了常规傅立叶变换的运算量,但对于一般的单片机而言,处理FFT运算还是力不从心。主要原冈是FFT计算过程中的蝶形运算是复数运算,要分开实部和虚部分别计算。在这里利用LabVIEW来实现快速傅立叶变化。LabVIEW是一种程序开发环境,类似于BASIC开发环境;但LabVIEW与其它计算机语言相比,有一个特别重要的不同点:其它计算机语言都是采用基于文本的语言产生代码行;而LabVIEW使用图形化编程语言G编写程序,产生.的程序是框图的形式。像C或BASIC一样,LabVIEW也是通用的编程系统,有一个可完成任何编程任务的庞大的函数库。LabVIEW的函数库包括数据采集、GPIB、串口控制、数据分析、数据显示及数据存储等。LabVIEW也有传统的程序调试工具,如设置断点、以动画方式显示数据及其通过程序(子V1)的结果、单步执行等,便于程序的调试。 二、方案论证 1:单一频率正弦信号的FFT 采用Labview的信号产生模板提供的常用的信号发生器,从中找到正弦信号发生器,使其产生一个正弦信号。将此正弦信号输入到实数FFT.vi中的X端进行快速傅里叶变换处理,使时域信号转换为频域信号。然后经过复数至极坐标转换后将其显示出来。其结构如图1所示。 图1 单一频率正弦信号的FFT结构图
第三章离散傅里叶变换 离散傅里叶变换不仅具有明确的物理意义,相对于DTFT他更便于用计算机处理。但是,直至上个世纪六十年代,由于数字计算机的处理速度较低以及离散傅里叶变换的计算量较大,离散傅里叶变换长期得不到真正的应用,快速离散傅里叶变换算法的提出,才得以显现出离散傅里叶变换的强大功能,并被广泛地应用于各种数字信号处理系统中。近年来,计算机的处理速率有了惊人的发展,同时在数字信号处理领域出现了许多新的方法,但在许多应用中始终无法替代离散傅里叶变换及其快速算法。 § 3-1 引言 一.DFT是重要的变换 1.分析有限长序列的有用工具。 2.在信号处理的理论上有重要意义。 3.在运算方法上起核心作用,谱分析、卷积、相关都可以通DFT在计算机上实现。 二.DFT是现代信号处理桥梁 DFT要解决两个问题: 一是离散与量化, 二是快速运算。 傅氏变换 § 3-2 傅氏变换的几种可能形式 一.连续时间、连续频率的傅氏变换-傅氏变换
对称性: 时域连续,则频域非周期。 反之亦然。 二.连续时间、离散频率傅里叶变换-傅氏级数 时域信号 频域信号 连续的 非周期的 非周期的 连续的 t ? ∞ ∞ -Ω-= Ωdt e t x j X t j )()(:? ∞ ∞ -ΩΩ Ω= d e j X t x t j )(21 )(:π 反
*时域周期为Tp, 频域谱线间隔为2π/Tp 三.离散时间、连续频率的傅氏变换 --序列的傅氏变换 p T 0= Ω时域信号 频域信号 连续的 周期的 非周期的 离散的 ? -Ω-= Ω2 /2 /00)(1 )(:p p T T t jk p dt e t x T jk X 正∑ ∞ -∞ =ΩΩ= k t jk e jk X t x 0)()(:0反
数字信号处理设计报告书 课题名称 应用MATLAB 对信号进行频谱分析及 滤波 姓 名 何 晨 学 号 20076089 院、系、部 电气系 专 业 电子信息工程 指导教师 刘鑫淼 2010年 6 月27日 ※※※※※※※※※ ※※ ※ ※ ※※ ※※ ※※※※※ ※※ 2007级数字信号处理 课程设计
应用MATLAB对信号进行频谱分析及滤波 20076089 何晨 一、设计目的
要求学生会用MATLAB语言进行编程,绘出所求波形,并且运用FFT求对连续信号进行分析。 二、设计要求 1、用Matlab产生正弦波,矩形波,并显示各自的时域波形图; 2、进行FFT变换,显示各自频谱图,其中采样率、频率、数据长度自选,要求注明; 3、绘制三种信号的均方根图谱; 4、用IFFT回复信号,并显示恢复的正弦信号时域波形图。 三、系统原理 用FFT对信号作频谱分析是学习数字信号处理的重要内容。经常需要进行频谱分析的信号是模拟信号和时域离散信号。频谱分辨率直接和FFT的变换区间N 有关,因为FFT能够实现频率分辨率是2π/N。 x(n)是一个长度为M的有限长序列,则x(n)的N点离散傅立叶变换为: X(k)=DFT[x(n)]= kn N W N n n x ∑ - = 1 ) ( ,k=0,1,...,N-1 N j e N Wπ2- = 逆变换:x(n) =IDFT[X(k)]= kn N W k X N n N - ∑ - = 1 ) ( 1 ,k=0,1,...,N-1 但FFT是一种比DFT更加快速的一种算法,提高了DFT的运算速率,为数字信号处理技术应用于各种信号处理创造了条件,大大提高了数字信号处理技术的发展。本实验就是采用FFT,IFFT对信号进行谱分析。 四、程序设计 fs=input('please input the fs:');%设定采样频率 N=input('please input the N:');%设定数据长度 t=0:0.001:1; f=100;%设定正弦信号频率 %生成正弦信号
本科学生毕业论文(设计)开题报告题目离散傅里叶变换的分析与研究 姓名XX 专业电子信息工程 学号XXXXXXXXXX 学院物理与电子信息学院 指导教师XXX 淮北师范大学教务处制
一、本课题研究现状及可行性分析 离散傅里叶变换,其实质是有限长序列傅立叶变换的有限点离散采样,从而实现了频域离散化,使数字信号处理可以在频域采用数值运算的方法进行,这样就大大增加了数字信号处理的灵活性。更为重要的是,离散傅里叶变换有多种快速算法,统称为快速傅里叶变换,从而使信号的实时处理和设备的简化得以实现。所以说,离散傅立叶变换不仅在理论上有重要意义,而且在各种信号的处理中亦起着核心作用。 离散傅里叶变换在数字通信、语音信号处理、图像处理、功率谱估计、系统分析与仿真、雷达信号处理、光学、医学、地震以及数值分析等各个领域都有着广泛的应用。 目前,我们已具备有关的大量参考文献和基本的原始程序,对本论文的开展不存在根本性的问题,我们的研究方法是可行的。 二、本课题研究的关键问题及解决问题的思路 关键问题: 线性卷积与循环卷积之间的关系,及对信号的频谱分析。并在MA TLAB环境下的编程实现。 解决思路: 在理解和掌握线性卷积,循环卷积以及信号频谱分析的基础上,用MA TLAB语言编写线性卷积,循环卷积以及频谱分析的设计程序,最后通过仿真结果验证理论的正确性。 三、论文纲要 1 绪论 1.1 DFT的定义 1.2 DFT与傅里叶变换和Z变换的关系 2 DFT的基本性质 2.1 线性性质 2.2 循环卷积性质 2.3循环卷积定理 3 DFT的应用 3.1 用DFT计算线性卷积 3.2 用DFT对信号进行谱分析 3.3 用DFT进行谱分析的误差问题
第3章 离散傅里叶变换 在第二章讨论了利用序列的傅里叶变换和z 变换来表示序列和线性时不变系统的 方法,公式分别为:∑∞ -∞ =-= n n z n x z X )()(和∑∞ -∞ =-= n jwn jw e n x e X )()(。对于有限长序列, 也可以用序列的傅里叶变换和z 变换来分析和表示,但还有一种方法更能反映序列的有限长这个特点,即离散傅叶里变换。这就是我们这一章要讨论的问题。离散傅里叶变换除了作为有限长序列的一种傅里叶表示法在理论上相当重要之外,而且由于存在着计算离散傅里叶变换的有效快速算法,因而离散傅里叶变换在各种数字信号处理的算法中起着核心的作用。这一章讨论的问题有: 1、 傅里叶变换的几种可能形式:至今学过很多种傅里叶变换形式,到底之间有什么 不 同,需要分析一下; 2、 周期序列的离散傅里叶级数(DFS):通常的周期信号都可以表示成傅里叶级数,然 后根据傅里叶级数可以得到傅里叶变换;也就是说傅里叶级数与傅里叶变换之间有一定的关系; 3、 有限长序列的离散傅里叶变换(DFT):这是我们的重点,我们会对其性质等作分析 讨论; 4、 DFT 的应用:学习了这种傅里叶变换,怎么用?计划作一个实验。 3.1 傅里叶变换的几种形式 傅里叶变换就是建立以时间为自变量的"信号"与以频率为自变量的"频率函数"之间的某种变换关系。都是指在分析如何综合一个信号时,各种不同频率的信号在合成信号时所占的比重。 如连续时间周期信号)()(mT t f t f +=,可以用指数形式的傅里叶级数来表示,可以分解成不同次谐波的叠加,每个谐波都有一个幅值,表示该谐波分量所占的比重。 傅里叶表示形式为:∑∞ -∞ =Ω= n t jn n e F t f )(? - Ω-= ?2 2 )(1T T t jn n dt e t f T F (Fn 离散、衰减、 非周期)。例如周期性矩形脉冲,其频谱为 ,1,0,/) /sin(±==n T n T n T F n πτπττ。画出图 形。
MATLAB 离散傅里叶变换及应用 一、DFT 与IDFT 、DFS 、DTFT 的联系 1、 序列的傅里叶变换(DFT)和逆变换(IDFT) 在实际中常常使用有限长序列。如果有限长序列信号为x(n),则该序列的离散傅里叶变换对可以表示为 1N ,0,1,k , W x (n)DFT[x (n)]X(k)1 N 0n nk N -===∑-=Λ (12-1) 1 N ,0,1,n , W X(k)N 1IDFT[X(k)]x (n)1N 0 k nk N -===∑-=-Λ (12-2) 已知x(n)=[0,1,2,3,4,5,6,7],求x(n)的DFT 和IDFT 。要求: (1)画出序列傅里叶变换对应的|X(k)|和arg [X(k)]图形。 (2)画出原信号与傅里叶逆变换IDFT [X(k)]图形进行比较。 程序源代码: xn=[0,1,2,3,4,5,6,7]; N=length(xn); n=0:(N-1);k=0:(N-1); Xk=xn*exp(-j*2*pi/N).^(n'*k); x=(Xk*exp(j*2*pi/N).^(n'*k))/N;
subplot(2,2,1),stem(n,xn); title('x(n)'); subplot(2,2,2),stem(n,abs(x)); title('IDFT|X(k)|'); subplot(2,2,3),stem(k,abs(Xk)); title('|X(k)|'); subplot(2,2,4),stem(k,angle(Xk)); title('arg|X(k)|'); 运行图如下: x(n) IDFT|X (k)| 2 4 6 8 |X (k)| 2 4 6 8 arg|X (k)| 从得到的结果可见,与周期序列不同的是,有限长序列本身是仅有N 点的离散序列,相当于周期序列的主值部分。因此,其频谱也对应序列的主值部分,是含N 点的离散序列。
离散傅里叶变换的物理含义 不知道为什么,我们的教科书总是不把读者最希望了解的东西告诉他们。这里可能有专业与非专业的区别。浸淫多年的专家认为必须让读者理解的东西其实读者并不关心,读者想要知道的简单答案课本上就是不说。 以离散傅里叶变换为例,许多书都会从用一系列正弦波逼近方波开始,好的,这我们都好理解,但是从此以后大堆的公式就开始上场了,以及卷积呀,皱褶呀,截断呀,延拓呀,中间经历了傅里叶变换,拉普拉斯变换,以及Z变换,时间域从连续到离散,频域从离散到连续,最终在离散傅里叶变换里时域和频域都离散了,这时频域里的幅值与相位和我们的原始信号有何联系,物理含义是什么,现在没人说了。 其实作为一个普通的,数学不怎么样的工程师,真的不关心离散傅里叶变换背后的数学原理,但是我们现在的教科书往往是告诉了他,这确实是极有用的工具,却不告诉他如何简单有效地使用它。 我在网上搜索答案,发现许多作答的人其实自己也不了解。直到找到一篇说得比较明白,但是在我读它的时候,早把网页关了,也不致应向谁致谢和致敬。下面举的例子,就基于那篇文章,有的部分是原文,在此基础上改写。 例子: 假设我们有一个信号,它含有a、2V的直流分量,b、频率为50Hz、相位为-30度、幅度为3V的交流信号,以及c、频率为75Hz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下: S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)。 式中cos参数为弧度,所以-30度和90度要分别换算成弧度。 我们以256Hz的采样率对这个信号进行采样,采样时间为1秒,数据长度为256点。按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第n 个点的频率就是n-1。我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第50个点、第76个点上出现峰值,其它各点应该接近0。实际情况如何呢?我们来看看FFT的(部分)结果的模值如下所示,我们把在第1点、第51点、和第76点附近的数据拿上来细看: 1点:512+0i 2点:-2.6195E-14 - 1.4162E-13i 3点:-2.8586E-14 - 1.1898E-13i 50点:-6.2076E-13 - 2.1713E-12i 51点:332.55 - 192i 52点:-1.6707E-12 - 1.5241E-12i 75点:-2.2199E-13 -1.0076E-12i 76点:3.4315E-12 + 192i 77点:-3.0263E-14 +7.5609E-13i 很明显,1点、51点、76点的值都比较大,它附近的点值都很小,可以认为是0,即在那些频率点上的信号幅度为0。接着,我们来计算各点的幅度值。分别计算这三个点的模值,结果如下: 1点:512 51点:384 76点:192
实验2 离散傅里叶变换(DFT) 一、实验目的 (1)加深对离散傅里叶变换(DFT)基本概念的理解。 (2)了解有限长序列傅里叶变换(DFT)与周期序列傅里叶级数(DFS)、离散时间傅里叶变换(DTFT)的联系。 (3)掌握用MA TLAB 语言进行离散傅里叶变换和逆变换的方法。 二、实验内容 1.有限长序列的傅里叶变换(DFT)和逆变换(IDFT) 2.有限长序列DFT 与周期序列DFS 的联系 3.有限长序列DFT 与离散时间傅里叶变换DTFT 的联系 三、实验环境 MA TLAB7.0 四、实验原理 1.有限长序列的傅里叶变换(DFT)和逆变换(IDFT) 在实际中常常使用有限长序列。如果有限长序列信号为x(n),则该序列的离散傅里叶变换对可以表示为 1N ,0,1,k , W x (n)DFT[x (n)]X(k)1 N 0n nk N -===∑-= (2-1) 1 N ,0,1,n , W X(k)N 1IDFT[X(k)]x (n)1N 0 k nk N -===∑-=- (2-2) 从离散傅里叶变换定义式可以看出,有限长序列在时域上是离散的,在频域上也是离散 的。式中,N π2j N e W -=即仅在单位圆上N 个等间距的点上取值,这为使用计算机进行 处理带来了方便。 由有限长序列的傅里叶变换和逆变换定义可知,DFT 和DFS 的公式非常相似,因此在程序编写上也基本一致。 例2-1 已知x(n)=[0,1,2,3,4,5,6,7],求x(n)的DFT 和IDFT 。要求: (1)画出序列傅里叶变换对应的|X(k)|和arg [X(k)]图形。 (2)画出原信号与傅里叶逆变换IDFT [X(k)]图形进行比较。 解 MA TLAB 程序如下:
离散傅里叶变换基础知识 傅里叶是一位法国数学家,他发现任何周期函数都可以用正弦函数和余弦函数构成的无穷级数做为基函数来表示,也就是我们数学上面学到的傅里叶级数,设一个周期函数f(t),其周期为T,则其角频率为w0=2π T ,则该函数可以展开为一系列三角函数的累加: f(t)=a0+a1cosw0t+b1sinw0t+a2cos2w0t+b2sinw2t+? =a0 2 +∑a n cosnw0t+b n sinnw0t ∞ n=1 其中,上式中的各个系数: a0=2 T ∫f(t)dt T2 ? ?T2 ? a n=2 T ∫f(t)cosnw0tdt T2 ? ?T2 ? b n=2 T ∫f(t)sinnw0tdt T2 ? ?T2 ? 但这个形式不太好用,因为正弦和余弦项是分开的,我们要考虑把他们两个整合起来,这样对每一个频率nw0我们就可以得到一个系数项(比如上式的a n或者b n),这其实就是该频率对应的幅值。然后我们以频率为X轴,以其对应的幅值为Y轴,就可以得到该函数在频域里面的图像了。对于周期函数,其频域里面的图像是不连续的,只在w=0,±w0,±2w0…才有图像。 那么我们该如何将上面的正弦项和余弦项整合到一块呢?答案是欧拉公式。下面就是鼎鼎大名的欧拉公式: e iwt=coswt+isinwt 换个表达方式: coswt=1 2 (e iwt+e?iwt) sinwt=1 2i (e iwt?e?iwt) 将上面的公式代入傅里叶级数中: f(t)=a0+a1cosw0t+b1sinw0t+a2cos2w0t+b2sinw2t+? =a0 2 +∑a n cosnw0t+b n sinnw0t ∞ n=1