高一数学第15周周练

高中数学教学进度表高一上学期教学进度安排如下：1.第1周：集合的含义及其表示；子集、全集、补集；交集、并集；题课。

2.第2周：一元二次不等式的解法。

3.第3周：简单高次不等式及分式不等式的解法。

4.第4周：简单绝对值不等式的解法；复课。

5.第5周：函数的概念和图像；函数的表示方法；函数的简单性质。

6.第6周：函数的简单性质；映射的概念。

7.第7周：函数题课。

8.第8周：二次函数图像、概念和性质；二次函数在给定区间上的最值问题。

9.第9周：分数指数幂；指数函数。

10.第10周：指数函数；对数。

11.第11周：对数；对数函数。

12.第12周：幂函数；题课。

13.第13周：简单复合函数的研究。

14.第14周：二次函数与一元二次方程；用二分法求方程的近似解；函数模型及其应用；题课。

15.第15周：复与期中考试。

16.第16周：任意角；弧度制；题课（角范围的表示）。

高一下学期教学进度安排如下：1.第1周：任意角的三角函数的概念；三角函数线（补充简单的三角不等式）。

2.第2周：同角三角函数的基本关系；同角三角函数的基本关系；诱导公式；题课。

3.第3周：三角函数的周期性；正、余弦函数的图象及五点法；正、余弦函数的性质（补充对称性）。

4.第4周：正、余弦函数的性质题课；正切函数的图象与性质；题课。

5.第5周：函数y=Asin(ωx+φ)的图像；三角函数的应用。

6.第6周：向量的概念及其表示；向量的加法；向量的减法；向量的数乘；题课。

7.第7周：平面向量的基本定理；平面向量的座标表示及运算；向量平行的座标表示；向量的数量的概念。

8.第8周：向量数量积的座标表示；题课；复与小结。

9.第9周：两角和与差的余弦；两角和与差的正弦；题课（补asinx+bcosx的内容）；两角和与差的正切；题课。

10.第10周：二倍角的三角函数，明确降幂公式；题课；几个三角恒等式。

11.第11周：三角函数的化简、求值和证明；复与小结。

12.第12周：期末复。

七一中学高一年级第15周周练一 、选择题（本大题共12小题，每小题5分，共60分）1.为提高我校高一年级学生的学习成绩，年级决定开设数学和英语两科的培优班。

已知某班级共有学生60人，其中参加数学、英语培优的人数分别为32、23人，同时参加数学和英语两科培优的有 9人，则该班级没有参加数学和英语任何一科培优的人数是（ ）A ． 4人B ． 9人C ． 13人D ． 14人2.cos 300= （ ）A ．1B ．12CD 3.若2cos sin 2cos sin =-+αααα，则=αtan （ ） A ．1 B ． - 1 C ．43 D ．34- 4.在 (0，2π)内，使sin x >cos x 成立的x 取值范围为A ．(π4，π2)∪(π，5π4)B ．(π4，π)C ．(π4，5π4)D ．(π4，π)∪(5π4，3π2) 5.设f ，g 都是由A 到A 的映射（其中A={1,2,3}），其对应法则如下表：则f (g (3)) = （ ）A ．1B ．2C ．3D ．不存在6.同时具有性质：“①最小正周期为π；②图象关于直线3x π=对称；③在,63ππ⎡⎤-⎢⎥⎣⎦上是增函数”的一个函数是（ ） A ．sin()26x y π=+B ．sin(2)3y x π=+ C ．sin(2)6y x π=- D ．5sin(2)6y x π=+ 7.1sin ，1cos ，1tan 的大小关系是 （ ） A ．1sin ＜1cos ＜1tanB ．1tan ＜1sin ＜1cosC ．1cos ＜1tan ＜1sinD ．1cos ＜1sin ＜1tan8.若角α的终边与直线y =3x 重合且sin α＜0，又P （m ，n ）是角α终边上一点，且|OP |=10，则m －n 等于( )A ．2B ．－2C ．4D ．－49.tan300°+00765sin )405cos(-的值是 （ ） A ．1＋3 B ．1－3 C ．－1－3 D ．－1＋310.函数32tan()26y x π=-的最小正周期是（ ） A ．π B ．2π C ．23π D ．43π11.函数,(,0)(0,)sin x y x xππ=∈-的图象可能是下列图象中的（ ）12.函数()()122-+-+=a x b a ax x f 是定义在()()22,00,--a a 上的偶函数，则=⎪⎪⎭⎫ ⎝⎛+522b a f A ．1 B ．3 C ．25 D ．不存在二 、填空题（本大题共4小题，每小题4分，共16分）13.设全集U=R ，集合{}|214,M x a x a a R =-<<∈，{}|12N x x =<<，若N M ⊆，则实数a 的取值范围是________14.若0≤θ＜2π，则使tan θ≤1成立的角θ的取值范围是_________．15.设定义在R 上的函数)(x f 同时满足以下条件：①0)()(=-+x f x f ；②)2()(+=x f x f ；③当10<≤x 时，12)(-=x x f 。

第15练 函数的奇偶性培优第一阶——基础过关练一、单选题1．下列命题正确的是（ ）A ．奇函数的图象关于原点对称，且()00f =B ．偶函数的图象关于y 轴对称，且()00f =C ．存在既是奇函数又是偶函数的函数D ．奇､偶函数的定义域可以不关于原点对称 2．下列函数是奇函数的是（ ） A ．y x =B ．223y x =+C ．1y x=-D ．2,(1,1)y x x =-∈-3．定义在R 上的奇函数()y f x =，满足当0x >时，2()1f x x x =-+．当0x ≤时的表示式是（ ）A ．2()1f x x x =---B ．2()1f x x x =-+-C ．()20,01,0x f x x x x =⎧=⎨---<⎩D ．()20,01,0x f x x x x =⎧=⎨-+-<⎩4．定义在R 上的偶函数()f x 满足：对任意的[)1212,0,(),x x x x ∈+∞≠有()()12120f x f x x x -<-，则（ ）A ．()()()321f f f <-<B ．()()()123f f f <-<C ．()()()213f f f -<<D ．()()()312f f f <<-5．若函数()(21)()xf x x x a =+-为奇函数，则a =（ ）A ．12B ．23C ．34D ．16．已知()f x 是偶函数，()g x 是奇函数，定义域均为[]1,1-，二者在[]0,1上的图象如图所示，则关于x 的不等式()()0f x g x <的解集为（ ）课后培优练级练A ．111,0,22⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭B ．11,00,22⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭C ．11,0,122⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭D ．111,,122⎛⎫⎛⎫--⋃ ⎪ ⎪⎝⎭⎝⎭7．已知()f x 为R 上的奇函数，()g x 为R 上的偶函数，且()0g x ≠，则下列说法正确的是（ ） A ．()()f x g x +为R 上的奇函数 B ．()()f x g x -为R 上的奇函数 C ．()()f xg x 为R 上的偶函数D ．()()f x g x 为R 上的偶函数8．若定义域为R 的奇函数()f x 在(0,)+∞内单调递减，且(2)0f -=，则满足(10)xf x -≥的x 的取值范围是（ ） A ．[][)1,14,-+∞ B ．[][]2,10,1--C ．[][)1,01,-⋃+∞D ．[][]1,01,3-二、多选题9．已知()f x 是定义在[]3,3-上的奇函数，()()12f f <，则下列各式一定成立的是（ ） A ．()00f =B ．()()02f f <C ．()()12f f ->-D ．()()13f f <10．下列哪个函数是其定义域上的偶函数（ ） A ．2y x =-+B ．23y x =-C ．21y x -D ．y x =11．已知函数()f x 是定义在R 上的奇函数，当0x ≤时，()f x 单调递减，则（ ） A ．()00f =B ．当0x ≥时，()f x 单调递减C ．当0x ≥时，()0f x ≥D ．R x ∀∈，()0xf x ≤12．已知函数()f x 是定义在R 上的偶函数，当0x ≥时，()22f x x x =-，则（ ）A ．()f x 的最小值为1-B ．()f x 在()2,0-上单调递减C ．()0f x ≤的解集为[]22-,D ．存在实数x 满足()()20f x f x ++-=三、填空题13．若函数()22,00,0,0x x x f x x ax x x ⎧-+>⎪==⎨⎪+<⎩是奇函数，则实数a 的值为___________.14．已知函数()y f x =是定义在R 上的奇函数，在()0,∞+上的图象如图所示，则使()0f x <的x 的取值集合为______．15．已知函数()f x 的定义域为R ，且()f x 为奇函数，其图象关于直线2x =对称．当[]0,4x ∈时，()24f x x x =-，则()2022f =____.16．奇函数()2f x +是定义在()3,1--上的减函数，若()()1230f m f m ---<，则实数m 的取值范围为______．四、解答题17．已知函数2()2,f x x mx x =-++∈R ． (1)当3m =时，求(1)f 值；(2)若()f x 是偶函数，求()f x 的最大值．18．已知函数()f x 是定义在R 上的奇函数，且当0x ≤时，()22f x x x =+．(1)求当x ＞0时，函数()f x 的解析式；(2)解不等式()()30x f x f x -->⎡⎤⎣⎦．19．已知函数()22x x af x x++=.(1)若()()2g x f x =-，判断()g x 的奇偶性并加以证明. (2)若对任意[)()1,,0x f x ∞∈+>恒成立，求实数a 的取值范围.20．已知f (x )是定义在区间[－1，1]上的奇函数，且f (1)＝1，当a ，b ∈[－1，1]，a ＋b ≠0时，有()()f a f b a b++＞0成立.(1)判断f (x )在区间[－1，1]上的单调性，并证明；(2)若f (x )≤m 2－2am ＋1对所有的a ∈[－1，1]恒成立，求实数m 的取值范围.培优第二阶——拓展培优练一、单选题1．已知函数21()x f x -= ）A ．是奇函数，但不是偶函数B ．既不是奇函数也不是偶函数C ．是偶函数但不是奇函数D ．既是奇函数也是偶函数2．设函数()f x ,()g x 的定义域为R ，且()f x 是奇函数，()g x 是偶函数，则下列结论中正确的是（ ）A ．()()f x g x 是偶函数B ．|()|()f x g x 是奇函数C ．()()f x g x 是奇函数D ．()()f x g x 是奇函数3．已知()f x 是定义在R 上的偶函数，且满足下列两个条件：①对任意的[]12,4,8x x ∈，且12x x ≠，都有()()12120f x f x x x ->-；②任取实数x ，都有()()8f x f x +=.若()()()7,11,2022a f b f c f =-==，则,,a b c 的大小关系正确的是（ ）A ．a b c <<B ．b a c <<C ．b c a <<D ．c b a <<4．若函数对于任意实数,x y R ∈满足()()2()()f x y f x y f x f y ++-=，则下列关于函数奇偶性说法一定正确的是（ ） A ．是偶函数但不是奇函数 B ．是奇函数但不是偶函数 C ．是非奇非偶函数D ．可能是奇函数也可能是偶函数5．关于函数22()44f x x x --()44h x x x =--（ ） A ．两函数均为偶函数B ．两函数都既是奇函数又是偶函数C ．函数()f x 是偶函数，()h x 是非奇非偶函数D ．函数()f x 既是奇函数又是偶函数，()h x 是非奇非偶函数6．设函数()f x 定义域为R ，()1f x -为奇函数，()1f x +为偶函数，当()1,1x ∈-时，()21f x x =-+，则下列结论错误的是（ ）A ．7324f ⎛⎫=- ⎪⎝⎭B ．()7f x +为奇函数C ．()f x 在()6,8上为减函数D ．()f x 的一个周期为87．设函数()f x 的定义域为R ，()1f x -为奇函数，()2f x +为偶函数，当[]1,2x ∈-时，()2.f x ax b =+若()()130f f +=，且()()433f f -+=-，则132f ⎛⎫⎪⎝⎭=（ ）A ．32B ．32-C ．34D ．34-8．若关于x 的函数()32222021x ax x a f x x a+++=+的最大值为M ，最小值为N ，且4M N +=，则实数a 的值为（ ） A ．4- B ．2-C ．2D ．1二、多选题9．下列判断错误的是：（ ）A ．如果一个函数的定义域关于坐标原点对称，那么这个函数为偶函数；B ．对于定义域为实数集R 的任何奇函数()f x 都有()()0f x f x ⋅-≤；C ．解析式中含自变量的偶次幂而不含常数项的函数必是偶函数；D ．既是奇函数又是偶函数的函数存在且唯一．10．已知()y f x =是定义在R 上的偶函数，但不是奇函数，则下列函数中为偶函数的有（ ）A ．()y f x =B ．()=y xf xC ．()()y f x f x =+-D ．()y f x x =+11．已知f (x )是定义在R 上的奇函数，若()()4f x f x +=且()12f =，则()()()12f f f n +++*(N n ∈)的值可能为（ ）A ．－2B ．0C ．2D ．412．函数()f x 是定义在R 上的奇函数，当0x >时，()1f x xx=+，则下列结论正确的是（ ）A ．()22f -=B ．关于x 的不等式()()10f x f x +-<的解集为1,2⎛⎫-∞ ⎪⎝⎭C ．若关于x 的不等式()f x ax <在()0,∞+上恒成立，则a 的取值范围为1a >D ．12,x x ∀∈R ，()()212f x f x -<三、填空题13．已知()y f x =是定义在R 上的奇函数，当0x ≥时，2()4f x x x =-，则0x <时，()f x 的解析式为________．14．已知定义域为R 的函数()f x 在(],0-∞上单调递增，且()()0f x f x +-=，若()112f -=-，则不等式()1212f x -≤的解集为___________. 15．已知函数()()22,f x mx nx m n =++∈R 是定义在[]2,3m m +上的偶函数，则函数()()2g x f x x =+在[]22-,上的最小值为______． 16．已知函数()f x 是定义在R 上的奇函数，若对任意给定的实数1x ，2x ，()()()()11221221x f x x f x x f x x f x +<+恒成立，则不等式()()1120x f x +-<的解集是______．四、解答题17．已知()y f x =是定义在(,)-∞+∞上的偶函数，当0x ≥时，2()23f x x x =--. (1)用分段函数形式写出()y f x =的解析式； (2)写出()y f x =的单调区间； (3)求出函数()f x 的最小值.18．已知函数()21ax bf x x +=+是定义在()1,1-上的奇函数，且1225f ⎛⎫= ⎪⎝⎭. (1)求函数()f x 的解析式；(2)判断函数()f x 在()1,1-上的单调性，并用定义证明； (3)解不等式：11022f t f t ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝+⎭+-≤.19．函数()y f x =的图象关于坐标原点成中心对称的充要条件是函数()y f x =为奇函数，有同学发现可以将其推广为：函数()y f x =的图象关于点(),P a b 成中心对称的充要条件是函数()y f x a b =+-是奇函数.(1)依据推广结论，求函数()323f x x x =-的图象的对称中心； (2)请利用函数()323f x x x =-的对称性()()()201920172015f f f -+-+-+⋅⋅⋅()()()()()()()()31135201720192021f f f f f f f f +-+-++++⋅⋅⋅+++的值；(3)类比上述推广结论，写出“函数()y f x =的图像关于y 轴成轴对称的充要条件是函数()y f x =为偶函数”的一个推广结论.（不需要证明）20．二次函数()f x 满足()()123f x f x x +-=+，且()02f = (1)求()f x 的解析式; (2)求()f x 在[]3,4-上的最值;(3)若函数()f x m +为偶函数，求()f f m ⎡⎤⎣⎦的值; (4)求()f x 在[],2m m +上的最小值.培优第三阶——高考沙场点兵一、单选题1．（2022·天津·高考真题）函数()21x f x x-=的图像为（ ）A ．B ．C ．D ．2．（2015·山东·高考真题）已知函数()f x 是奇函数，当0x >时，()22f x x =+，那么()1f -的值是（ ） A ．3-B ．1-C ．1D ．33．（2021·全国·高考真题）已知函数()f x 的定义域为R ，()2f x +为偶函数，()21f x +为奇函数，则（ ） A ．102f ⎛⎫-= ⎪⎝⎭B ．()10f -=C ．()20f =D ．()40f =4．（2021·全国·高考真题（文））设()f x 是定义域为R 的奇函数，且()()1f x f x +=-.若1133f ⎛⎫-= ⎪⎝⎭，则53f ⎛⎫= ⎪⎝⎭（ ） A ．53-B ．13-C ．13D ．535．（2021·全国·高考真题（理））设函数1()1xf x x-=+，则下列函数中为奇函数的是（ ） A ．()11f x --B ．()11f x -+C ．()11f x +-D ．()11f x ++6．（2020·海南·高考真题）若定义在R 的奇函数f (x )在(,0)-∞单调递减，且f (2)=0，则满足(10)xf x -≥的x 的取值范围是（ ）A ．[)1,1][3,-+∞B ．3,1][,[01]--C ．[1,0][1,)-⋃+∞D ．[1,0][1,3]-⋃7．（2008·湖北·高考真题（文））已知()f x 在R 上是奇函数，且(4)()f x f x +=，当(0,2)x ∈时，2()2f x x =，则(7)f =A ．-2B ．2C ．-98D ．98。

高一数学周练七（满分100分）班别 ： 姓名：一、选择题（共50分，每道题5分）1、函数12log (32)y x =-的定义域是 （ ） （A ）[1,+∞] (B) (23,)+∞ (C) [23,1] (D) (23,1]2、下列四个函数中,在(0,+∞)上为增函数的是( )A. f (x )=3-xB. f (x )=x 2-3xC. f (x )=—11+x D. f (x )=-|x | 3、方程x 2-px +6=0的解集为M ,方程x 2+6x -q =0的解集为N ,且M ∩N ={2},那么p +q 等于( )A. 21B. 8C. 6D. 74、已知函数f(x)14x a -=+的图象恒过定点p ，则点p 的坐标是 （ ）（A ）（ 1，5 ） （B ）（ 1, 4） （C ）（ 0，4） （D ）（ 4，0）5、已知函数f (n )=⎩⎨⎧<+≥-),10)](5([),10(3n n f f n n 其中n ∈N ，则f (8)等于（ ）A. 2B. 4C. 6D. 76、某算法的程序框如图所示，若输出结果为12，则输入的实数x 的值是 （ ）A ．32-B ．2C ．52D ．4 7、设a,b,c 都是正数，且346a b c ==，则下列正确的是 （ ） (A)111c a b =+ (B) 221C a b=+ (C) 122C a b =+ (D) 212c a b =+ 8、已知偶函数()f x 在区间[0,)+∞单调递增，则满足)(x f ＜)1(f 的x 取值范围是( )A ．（-1，1）B ．(-1，0）C ．（0，1）D ．[-1，1)9、a y x y =-=与函数|1|2的图象有4个交点，则实数a 的取值范围是（ ）A ．（0，+∞）B ．(-1，1）C ．（0，1）D ．（1，+∞）10、下面四个结论：①偶函数的图象一定与y轴相交；②奇函数的图象一定通过原点；③偶函数的图象关于y轴对称；④既是奇函数又是偶函数的函数一定是()f x ＝0（x∈R），其中正确命题的个数是（）A 4B 3C 2D 1选择题答案：1 2 3 4 5 6 7 8 9 10二、填空题（共20分，每道题5分）11、已知集合}0=x-xA.若A中至多有一个元素，则a的取值范围ax+2{2=3|是12、按照程序框图(如右图)执行，第3个输出的数是.13、执行下图所示的程序，输出的结果为48，则判断框中应填入的条件为．(12题图) （13题图）14、函数f(x)＝a x＋log a(x＋1)在[0,1]上的最大值与最小值之和为a，则a的值为_________.三、解答题(共30分，每道题15分)15、（1）用辗转相除法和更相减损术求三个数 324 , 243 , 135 的最大公约数.（2）把“五进制”数)5(1234转化为“十进制”数，再把它转化为“八进制”数。

上蔡一高2022-2022学年优班专用试题高一数学 周练一命题时间：2022年09月06日考试时间：90分钟 试卷满分：150分本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分 第Ⅰ卷 一、选择题（共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1、如图中阴影部分所表示的集合是（ ） A ．()U B C A C B ．()()AB B CC ．()()A B C B D ．()U BC A C ⎡⎤⎣⎦2、设集合},412|{Z k k x x M ∈+==，},214|{Z k k x x N ∈+==，则（ ）A ．N M =B ．C ．D ．M N φ=3、已知22(1)()(12)2(2)x x f x x x x x +≤-⎧⎪=-<<⎨⎪≥⎩，若()3f x =，则的值是（ ）A ．B ．或32C ．，32或 D ．4、判断下列各组中的两个函数是同一函数的为（ ）⑴3)5)(3(1+-+=x x x y ，52-=x y ；⑵111-+=x x y ，)1)(1(2-+=x x y ；⑶x x f =)(，2)(x x g =；⑷343()f x x x =-3()1F x x x =-⑸21)52()(-=x x f ，52)(2-=x x f 。

A ．⑴、⑵B ．⑵、⑶C ．⑷D ．⑶、⑸5、设集合{}1,2,3, (10)A =集合的所有非空子集元素的和为（ ）。

A ．28100B ．28160C ．28260D ． 283006、已知集合{}2|10,A x x A R =++==∅若，则实数的取值范围是（ ）A ．4<mB ．4>mC ．40<≤mD ．40≤≤m7、已知集合{}{}421,2,3,,4,7,,3A k B a a a ==+，且,,a N x A y B +∈∈∈使中元素31y x =+和中的元素对应，则的值分别为（ ） A ． B ． C ． D ．8、设⎩⎨⎧<+≥-=)10()],6([)10(,2)(x x f f x x x f 则的值为（ ） A ． B ． C ． D ．9、函数)23(,32)(-≠+=x x cx x f 满足,)]([x x f f =则常数等于（ ）A ．B ．C ．33-或D ．35-或10、若函数234y x x =--的定义域为[0,]m ,值域为25[4]4--，，则的取值范围是（ ）A．B．3 []2，4C．3[3]2，D．3[2+∞，）11、函数xxxy+=的图象是（）12、若函数2()f x x=，则对任意实数，下列不等式总成立的是（）A．12()2x xf+≤12()()2f x f x+B．12()2x xf+<12()()2f x f x+C．12()2x xf+≥12()()2f x f x+D．12()2x xf+>12()()2f x f x+二、填空题：（本大题共4小题，每小题5分，共20分．把答案填在题中横线上．）13、设全集{}(,),U x y x y R=∈,集合2(,)12yM x yx⎧+⎫==⎨⎬-⎩⎭，{}(,)4N x y y x=≠-, 那么()()U UC M C N等于________________。

高一数学周测（2）一．单选题（每小题5分，满分100分）1.已知α为第三象限角，则α2所在的象限是( )A.第一或第二象限B.第二或第三象限C.第一或第三象限D.第二或第四象限2.集合⎩⎨⎧⎭⎬⎫α⎪⎪k π＋π4≤α≤k π＋π2，k ∈Z 中角所表示的范围(阴影部分)是( )3.已知sin θ＋cos θ＝43⎝⎛⎭⎫0<θ<π4，则sin θ－cos θ等于( ) A.23 B.－23 C.13 D.－134.若1＋cos αsin α＝3,则cos α－2sin α＝( )A ．－1B ．1C ．－25D ．－1或－255．已知tan θ＝2,则sin ⎝⎛⎭⎫π2＋θ－cos (π－θ)sin ⎝⎛⎭⎫π2＋θ－sin (π－θ)＝( )A ．2B ．－2C ．0D ．236.已知sin(α+π6)=,则sin(α+)+cos(π3－α)= ( )A ．-B ．C ．0D ．7.函数f (x )＝的定义域为( )A. [2k π+],k ∈ZB. [2k π+],k ∈ZC. [k π+],k ∈ZD. [k π+],k ∈Z8.函数的定义域为( )A.{x|2k π+π4<x ≤2k π+5π6,k ∈Z }B. {x|2k π+π4≤x ≤2k π+5π6,k ∈Z }C. {x|k π+π4<x ≤k π+5π6,k ∈Z }D. {x|k π+π4≤x ≤k π+5π6,k ∈Z }9.函数f (x )＝lgcos x ＋25－x 2的定义域为( )A.⎣⎡⎭⎫－5，－32π∪⎝⎛⎭⎫－π2，π2∪⎝⎛⎦⎤32π，5B.⎣⎡⎭⎫－5，－32π∪⎝⎛⎦⎤32π，5 C.⎝⎛⎭⎫－π2，π2∪⎝⎛⎦⎤32π，5 D.⎣⎡⎭⎫－5，－32π∪⎝⎛⎭⎫－π2，π210.函数y ＝cos(x ＋π3),x ∈(0, π]的值域是( )A ．(－1,12)B ．[－1,12)C ．[－1,12] D ．[－1,1]11.函数f (x )＝－2cos 2x ＋2sin x ＋3，x ∈⎣⎡⎦⎤π6，5π6的值域是( )A. [12,54]B.[52,5]C. [12,5]D. [1,54]12.函数y ＝tan 2⎝⎛⎭⎫3x ＋π3＋tan ⎝⎛⎭⎫3x ＋π3＋1的定义域和值域分别是( ) A. ⎩⎨⎧⎭⎬⎫x |x ≠k π3＋π18，k ∈Z ,{y |y ≥34} B.{x |x ≠k π3－,( k ∈Z )},{y |y ≥34}C.R,{y |y ≥34}D. ⎩⎨⎧⎭⎬⎫x |x ≠k π3＋π18，k ∈Z ,R13．设函数f (x )＝sin(2x －π2),x ∈R,则f (x )是( )A ．最小正周期为π的奇函数B ．最小正周期为π的偶函数C ．最小正周期为π2的奇函数D ．最小正周期为π2的偶函数14．设f (x )是周期为2的奇函数，当0<x <1时，f (x )＝sin x ＋x ，则1<x <2时，f (x )＝( )A.sin(x －2)＋x －2B.－sin(x －2)＋x －2C. sin(x －2)＋2－xD. －sin(x －2)＋2－x15.已知函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4(ω>0)的最小正周期为π,则函数f (x )的图象( ) A ．关于直线x ＝π4对称 B ．关于直线x ＝π8对称C ．关于点⎝⎛⎭⎫π4，0对称D ．关于点⎝⎛⎭⎫π8，0对称16．下列函数中,周期为π,且在[π4,π2]上为减函数的是( )A ．y ＝sin(2x ＋π2)B ．y ＝cos(2x ＋π2)C ．y ＝sin(x ＋π2)D ．y ＝cos(x ＋π2)17．已知函数f (x )＝f (π－x ),且当x ∈⎝⎛⎭⎫－π2，π2时,f (x )＝x ＋sin x ．设a ＝f (1),b ＝f (2),c ＝f (3),则( )A ．a <b <cB ．b <c <aC ．c <b <aD ．c <a <b18．方程2x ＝cos x 解的个数为( )A ．1B ．2C ．0D ．无数个19．已知函数f (x )=2sin(2x+φ)(|φ|≤π2),的部分图像如图,则φ等于( )A ．π6B ．π4C ．π3D ．π220．函数y ＝11－x的图象与函数y ＝2sinπx (－2≤x ≤4)的图象所有交点的横坐标之和等于( )A ．2B ．4C ．6D ．8二．多选题（每小题5分，满分30分） 21.下列转化结果正确的是( )A.67°30′化成弧度是3π8 B.－10π3化成角度是－600°C.－150°化成弧度是－7π6D.π12化成角度是15°22.若sin αcos α<0，则角α的终边可能在( )A.第一象限B.第二象限C.第三象限D.第四象限23.已知扇形的周长是6 cm ，面积是2 cm 2，下列对该扇形性质的描述可能正确的是( )A.扇形所在圆的半径为2 cmB.扇形所在圆的半径为1 cmC.扇形所在圆的圆心角的弧度数是1D.扇形所在圆的圆心角的弧度数是224.对于函数f (x )＝a sin x ＋b tan x ＋c (其中a ，b ∈R ，c ∈Z )，选取a ，b ，c 的一组值计算f (1)和f (－1)，所得出的结果可能是( )A.4和6B.3和1C.2和4D.1和225.若tan α＋1tan α＝3,则下列一定正确的是( )A ． sin αcos α＝13B ． tan 2α＋1tan 2α＝7C ． tan α－＝D ． tan 2α－1tan 2α＝326．函数f (x )=cos x +|cos x|是( )A ．最小正周期是πB ．区间[0,1]上的减函数C ．图象关于点(k π,0)(k ∈Z)对称D ．周期函数且图象有无数条对称轴三．填空题（每小题5分，满分20分） 27.化简(1＋tan 215°)·cos 215°＝________.28.函数y ＝sin ⎝⎛⎭⎫x 2－π3的单调递增区间为____________．29.若方程sin x ＝1－a 2在x ∈⎣⎡⎦⎤π3，π上有两个实数根，则a 的取值范围是 .30.若f (x )＝sin 2x ＋a cos 2x 的图象关于直线x ＝－π8对称，则实数a 的值为________.高一数学周测（2）答案一．单选题（每小题5分，满分100分）1.解析:选D 法一 如图所示，将每个象限二等分，标号Ⅲ所在的区域即为α2所在的区域，故选D.法二 ∵180°＋k ·360°<α<270°＋k ·360°，k ∈Z ，∴90°＋k · 180°<α2<135°＋k ·180°，k ∈Z ，∴α2为第二或第四象限角，故选D.2.解析：选C k 为偶数时，集合对应的区域为第一象限内直线y ＝x 左上部分(包含边界)， k 为奇数时集合对应的区域为第三象限内直线y ＝x 的右下部分(包含边界).故选C.3.解析：选B 由(sin θ＋cos θ)2＝1＋2sin θcos θ＝169，得2sin θcos θ＝79，则(sin θ－cos θ)2＝1－2sin θcos θ＝29，由0<θ<π4，知sin θ－cos θ<0，所以sin θ－cos θ＝－23.4.解析：选C 由已知得sin α≠0,且3sin α＝1＋cos α＞0,即cos α＝3sin α－1,则cos 2α＝1－sin 2α＝(3sin α－1)2,解得sin α＝35,∴cos α－2sin α＝3sin α－1－2sin α＝sin α－1＝－25,故选C ．5．解析：选B sin ⎝⎛⎭⎫π2＋θ－cos (π－θ)sin ⎝⎛⎭⎫π2＋θ－sin (π－θ)＝cos θ＋cos θcos θ－sin θ＝21－tan θ＝21－2＝－2．6.解析：选C sin(α+)+cos(π3－α)= sin[π＋(α+π6)+cos[π2－(α+π6)]=－sin(α+π6)+sin(α+π6)=0 ．7.解析：选C 由sin(2x +π6)≥32,得2k π+π3≤2x +π6≤2k π+2π3,k ∈Z ，得k π+≤2x +π6≤k π+π4,k ∈Z ，故所求定义域为[k π+],k ∈Z8.解析：选A {x|2k π+π4<x ≤2k π+5π6,k ∈Z }9.解析：选A 由题意，得x 满足不等式组⎩⎪⎨⎪⎧cos x >0，25－x 2≥0，即⎩⎪⎨⎪⎧cos x >0，－5≤x ≤5，作出y ＝cos x 的图象，如图所示.结合图象可得：x ∈⎣⎡⎭⎫－5，－32π∪⎝⎛⎭⎫－π2，π2∪⎝⎛⎦⎤32π，5.10.解析：选B11.解析：选Bf (x )＝－2(1－sin 2x )＋2sin x ＋3＝2sin 2x ＋2sin x ＋1＝2⎝⎛⎭⎫sin x ＋122＋12.因为x ∈⎣⎡⎦⎤π6，5π6，所以12≤sin x ≤1.当sin x ＝1时，y max ＝5；当sin x ＝12时，y min ＝52. 所以，f (x )在⎣⎡⎦⎤π6，5π6上的最大值和最小值分别为5，52.12.解析：选A 由3x ＋π3≠k π＋π2，k ∈Z ，得x ≠k π3＋π18，k ∈Z ，所以函数的定义域为⎩⎨⎧⎭⎬⎫x |x ≠k π3＋π18，k ∈Z .设t ＝tan ⎝⎛⎭⎫3x ＋π3，则t ∈R ，y ＝t 2＋t ＋1＝⎝⎛⎭⎫t ＋122＋34≥34， 所以原函数的值域是⎣⎡⎭⎫34，＋∞.13．解析：选B14．解析：选A 当1<x <2时，－2<－x <－1，则0<2－x <1， 因为当0<x <1时，f (x )＝sin x ＋x ，所以f (2－x )＝sin(2－x )＋2－x .因为f (x )是周期为2的奇函数，所以f (x )＝－f (－x )＝－f (2－x )＝－sin(2－x )＋x －2＝sin(x －2)＋x －2.15.解析：选B ∵f (x )＝sin ⎝⎛⎭⎫ωx ＋π4的最小正周期为π,∴2πω＝π,ω＝2,∴f (x )＝sin ⎝⎛⎭⎫2x ＋π4．当x ＝π4时,2x ＋π4＝3π4,∴A 、C 错误；当x ＝π8时,2x ＋π4＝π2,∴B 正确,D 错误．16．解析：选A17．解析：选D 由已知函数f (x )在⎝⎛⎭⎫－π2，π2上是增函数． 因为π－2∈⎝⎛⎭⎫－π2，π2,π－3∈⎝⎛⎭⎫－π2，π2,π－3<1<π－2, 所以f (π－3)<f (1)<f (π－2),即f (3)<f (1)<f (2),c <a <b ．18．解析：选D 方程2x＝cos x ⇔⎩⎪⎨⎪⎧y ＝2x ，y ＝cos x ，作出y ＝2x 与y ＝cos x 的图象如图所示,由图可知,两曲线有无数个交点．19．解析：选A 将(0,1)代入f (x )=2sin(2x +φ),得sin φ=12,又|φ|≤π2,∴φ=π6．20．解析：选D 令1－x ＝t ,则x ＝1－t ．由－2≤x ≤4,知－2≤1－t ≤4,所以－3≤t ≤3且t ≠0．又y ＝2sin πx ＝2sin π(1－t )＝2sin πt ．在同一坐标系下作出y ＝1t和y ＝2sin πt 的图象．由图可知两函数图象在[－3,3]上共有8个交点,且这8个交点两两关于原点对称． 因此这8个交点的横坐标的和为0, 即t 1＋t 2＋…＋t 8＝0．也就是1－x 1＋1－x 2＋…＋1－x 8＝0, 因此x 1＋x 2＋…＋x 8＝8．二．多选题（每小题5分，满分30分）21.解析：选ABD －150°＝－150×π180＝－5π6，只有选项C 错误.22.解析：选BD 由sin αcos α<0可知sin α与cos α异号， 故角α的终边可能在第二象限或第四象限.23.解析：选ABC 设扇形所在圆的半径为r ，圆心角的弧度数为α，则由题意得⎩⎪⎨⎪⎧2r ＋αr ＝6，12αr 2＝2，解得⎩⎪⎨⎪⎧r ＝1，α＝4或⎩⎪⎨⎪⎧r ＝2，α＝1，则圆心角的弧度是4或1.故选ABC.24.解析:选ABC 设g (x )＝a sin x ＋b tan x ，显然g (x )为奇函数. ∵f (1)＝g (1)＋c ，f (－1)＝g (－1)＋c ，∴f (1)＋f (－1)＝2c . ∵c ∈Z ，∴f (1)＋f (－1)为偶数.因此ABC 均适合.25.解析：选AB 对于A,∵tan α＋1tan α＝3,∴sin αcos α＋cos αsin α＝3,即sin 2α＋cos 2αsin αcos α＝3,∴sin αcos α＝13, 对于B,tan 2α＋1tan 2α＝⎝⎛⎭⎫tan α＋1tan α2－2tan α·1tan α＝9－2＝7． 对于C,(tan α－)2＝(tan α+)2-4=9-4=5,∴tan α－＝对于D,tan 2α－1tan 2α＝(tan α＋1tan α)(tan α－)=26．解析：选BD，则对应的图象如图：A 中由图象知函数的最小正周期为2π，故A 错误，B 中函数在[0,]2π上为减函数，故B 正确，C 中函数关于x k π=对称，故C 错误，D 中函数由无数条对称轴，且周期是2π，故D 正确．三．填空题（每小题5分，满分20分） 27.答案：1解析：(1＋tan 215°)cos 215°＝⎝⎛⎭⎫1＋sin 215°cos 215°·cos 215°＝cos 215°＋sin 215°cos 215°·cos 215°＝1.28. 答案：⎣⎡⎭⎫4k π＋5π3，4k π＋8π3，k ∈Z . 解析：要求函数y ＝sin ⎝⎛⎭⎫x 2－π3的单调递增区间，即求使y ＝sin ⎝⎛⎭⎫x 2－π3>0且单调递减的区间.令2k π＋π2≤x 2－π3<2k π＋π，k ∈Z ，整理得4k π＋5π3≤x <4k π＋8π3，k ∈Z .故函数y ＝log 12sin ⎝⎛⎭⎫x 2－π3的单调递增区间为⎣⎡⎭⎫4k π＋5π3，4k π＋8π3，k ∈Z .29. 答案：(－1，1－3].解析：在同一直角坐标系中作出y ＝sin x ，x ∈⎣⎡⎦⎤π3，π的图象，y ＝1－a 2的图象， 由图象可知，当32≤1－a2<1，即－1<a ≤1－3时，y ＝sin x ，x ∈⎣⎡⎦⎤π3，π的图象与y ＝1－a 2的图象有两个交点，即方程sin x ＝1－a 2在x ∈⎣⎡⎦⎤π3，π上有两个实根. 故所求a 的取值范围为(－1，1－3].30. 答案：－1解析：因为f (x )的图象关于x ＝－π8对称，所以f ⎝⎛⎭⎫－π8＋x ＝f ⎝⎛⎭⎫－π8－x ，即f (x )＝f ⎝⎛⎭⎫－π4－x . 令x ＝0，则f (0)＝f ⎝⎛⎭⎫－π4，所以a ＝－1.。

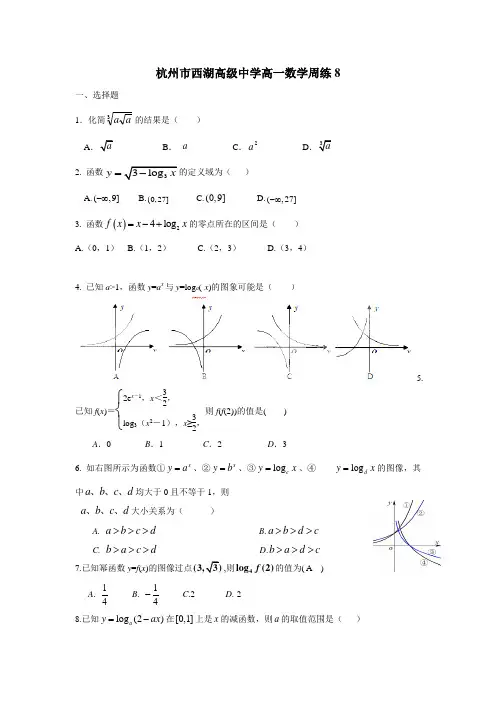
杭州市西湖高级中学高一数学周练8一、选择题1．化简3a a 的结果是（ ）A B ． a C ．2a D2. 函数y =）A.(,9]-∞B.(0,27]C.(0,9]D.(,27]-∞ 3. 函数()24log f x x x =-+的零点所在的区间是（ ）A.（0，1）B.（1，2）C.（2，3）D.（3，4）4. 已知a >1，函数y =a x 与y =log a (-x )的图象可能是（ ）5.已知f (x )＝⎩⎨⎧2e x －1，x ＜32，log 3（x 2－1），x ≥32，则f (f (2))的值是( )A ．0B ．1C ．2D ．36. 如右图所示为函数①xy a =、②xy b =、③log c y x =、④ log d y x =的图像，其中a b c d 、、、均大于0且不等于1，则a b c d 、、、大小关系为（ ）A. a b c d >>>B.a b d c >>>C. b a c d >>> D .b a d c >>>7.已知幂函数y =f (x )的图像过点,则4log (2)f 的值为( A ) A .14B . 14-C .2D .-28.已知log (2)a y ax =-在[0,1]上是x 的减函数，则a 的取值范围是（ ）A ．（0，1）B ．（1，2）C ．（0，2）D ．∞[2，+）9.给定函数①x 2x y += ，②12log (1)y x =+，③1x y +=，④12x y +=，其中在区间（0，1）上单调递减的函数序号是（ ）A. ①④B. ①②C. ②③D.③④ 10.已知12)(-=x x f ，该函数在区间[],a b 上的值域为[]1,2，记满足该条件的实数,a b a 、b 所形成的实数对为点P （a,b ），则由点P 构成的点集组成的图形为（ ） A.线段AD 与线段CD B.线段ABC.线段ADD.线段AB 与BC 二、填空题11.函数()12221+-⎪⎭⎫⎝⎛=x x x f 的单调增区间为__________________.12.已知2510x y ==,则x 1+y1=13.函数f (x )在R 上为奇函数，且()0f x x =≥，则当x <0时，()f x = ____14. 已知01a a >≠且，函数()log 23a y x =-P ， 若点P 在指数函数()f x 的图象上，则()8f =__________；15. 直线1y =与曲线2y x x a =-+有四个交点，则a 的取值范围是 .16. 已知2()2y f x x =+为奇函数，且()()1g x f x =+. 若(2)2f =，则(2)g -= ； 17. 已知函数()33xxf x -=-,则不等式(21)(4)0f x f x -++>的解集为 三、解答题18.（1）计算41320.75344(4)16---++-的值.（2）计算211log 522lg 5lg 2lg 502+++的值.19.已知函数⎪⎪⎪⎩⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡∈-⎪⎭⎫⎢⎣⎡-∈---∈+=2,21,121,1,2)1,2[,1)(x x x x x x x x f (1)判断当x ∈[-2,1)时，函数f (x )的单调性，并用定义证明之； (2)求f (x )的值域220.()lg()lg10109),8a f x ax x f a x f x a =⋅=≤设函数（1）若（），求的值；（2）若对一切正实数恒有（求的取值范围.21. 设函数122a 2a )x (f x x +-+=,（1）对任意,R x ,x 21∈且21x x <,是否有0x x )x (f )x (f 2121>--成立？如果成立，请证明你的结论；如果不成立，请说明理由；（2）当1a =时，若对任意t ∈[1,2]有0)2()22(≥+-t t f m f ，求m 的取值范围。

高一级2014-2015年度第一学期第15周数学小测班级 姓名 学号 成绩一、选择题（每小题5分，共50分）题号 12345678910答案1．已知集合A ＝{0,1,2,3,4,5}，B ＝{1,3,6,9}，C ＝{3,7,8}，则(A ∩B )∪C 等于 A ．{0,1,2,6,8} B ．{3,7,8} C ．{1,3,7,8} D ．{1,3,6,7,8}2.函数()23log (1)f x x x =-++的定义域为 ( )A ．[)1,3-B ．()1,3-C ．(1,3]-D ．[]1,3- 3．下列函数中，在区间(0，2)上为增函数的是 ( )A ．1y x =-+B ．32xy ⎛⎫= ⎪⎝⎭C ．245y x x =-+ D ．2y x = 4．设5.1348.029.01)21(,8,4-===y y y ，则( ) A 、123y y y >>2 B 、 321y y y >> C 、231y y y >> D 、 312y y y >> 5．一个正方体的顶点都在球面上，它的棱长为cm 2，则球的表面积是A ．π82cmB ．π122cmC ．π162cmD ．π202cm6．一个直角三角形直角边分别为3与4，以其直角边为旋转轴，旋转而成的圆锥的侧面积为( )A ．15πB ．20πC ．12πD ．15π或20π7．一个无盖的正方体盒子展开后的平面图形(如图)，A 、B 、C 是展开图上的三点，若回复到正方体盒子中，∠ABC 的大小是（ ）.A 、 90°B 、45°C 60°D 、30°8．一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底长均为1的等腰梯形，则该平面图形的面积等于( . )A ．B ．C ．D ．9．如图，在四面体ABCD 中，E ，F 分别是AC 与BD 的中点，若CD ＝2AB ＝4，EF ⊥BA ，则EF 与CD 所成的角为( )A ．90°B ．45°C ．60°D ．30°10.判断下列命题，正确的个数为（ ）①直线a 与平面α没有公共点，则//a α； ②直线a 平行于平面α内的一条直线，则//a α； ③直线a 与平面α内的无数条直线平行，则//a α； ④平面α内的两条直线分别平行于平面β，则//αβ A 、0 B 、1 C 、2个D 、3个二、填空题(本大题共4小题，每小题5分，共20分)11.lg 5lg 20+的值是___________.112．如图，四棱锥S －ABCD 中，底面ABCD 为平行四边形，E 是SA 上一点，当点E 满足条件：________时，SC ∥平面EBD .点E 是SA 的中点13．函数1)(2-+=x x x f 在[]2,2-的最大值是_________________514．右图是一个几何体的三视图，则该 几何体的表面积为 ．π)7212(+三、解答题：（本大题共5小题，每小题10分，共50分） 15．如图，一个圆锥形的空杯子上面放着一个半球形 的冰淇淋，如果冰淇淋融化了，会溢出杯子吗? 请用你的计算数据说明理由．16．如图，已知点E ，F ，G ，H 分别为正方体ABCD －A1B1C1D1的棱AB ，BC ，CC1，C1D1的中点，求证：EF ，HG ，DC 三线共点．17．已知函数)1(122>-+=a a a y x x 在区间[－1,1]上的最大值是14，求a 的值._ 12cm _4cm18．如图是一个几何体的三视图，其中正视图与左视图都是全等的腰为3的等腰三角形，俯视图是边长为2的正方形，（1）画出该几何体；（2）求此几何体的表面积与体积．正视图左视图俯视图19．如图中，是一个长方体截去一个角所得多面体的直观图．它的正视图和侧视图在右面画出(单位：cm)．(1)在正视图下面，按照画三视图的要求画出该多面体的俯视图；(2)按照给出的尺寸，求该多面体的体积；(3)在所给直观图中连接BC′，证明：BC′∥面EFG.15．解：因为)(134434213421333cm R V ≈⨯⨯=⨯=ππ半球 ………………5分)(2011243131322cm h r V ≈⨯⨯==ππ圆锥 ………………10分因为圆锥半球V V <所以，冰淇淋融化了，不会溢出杯子． ………………12分16．证明 ∵点E ，F ，G ，H 分别为所在棱的中点，连接BC 1，GF ，如图．∴GF 是△BCC 1的中位线，∴GF ∥BC 1.∵BE ∥C1H ，且BE ＝C 1H ， ∴四边形EBC 1H 是平行四边形． ∴EH ∥BC 1，∴GF ∥EH . ∴E ，F ，G ，H 四点共面． ∵GF ≠EH ，故EF 与HG 必相交． 设EF ∩HG ＝I .∵I ∈GH ，GH ⊂平面CC 1D 1D ， ∴I ∈平面CC 1D 1D . 同理可证I ∈平面ABCD .∴点I 在交线DC 上．即EF ，HG ，DC 三线共点．17．解： )1(122>-+=a a a y x x ， 换元为)1(122a t at t y ≤≤-+=，……5分对称轴为1-=t . ………7分 当1>a ，a t=，即x =1时取最大值14，………10分得到14122=-+a a ………12分 解得 a =3 (a = －5舍去) ………14分18．解：（1）该几何体的直观图如右。

高一下数学周测试卷一、选择题（共8题，每题5分，8题少选得2分，选错不得分；共40分）1.已知正方体的表面积为54，则正方体的体积为( )A. 18B. 27C. 36D. 452.已知两条不同的直线m ，n 和两个不同的平面α，β，且m ⊂α，n ⊂α，则“m∥β且n∥β”是“α∥β”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3.已知a ，b 是不同的直线，α，β是不同的平面，若a∥α，b∥β，α∥β，则a 与b 的位置关系是( )A. 平行B. 平行或异面C. 相交D. 平行或异面或相交4.如图，矩形O'A'B'C'是用斜二测画法画出的一个水平放置的平面图形的直观图，其中O'A'=6，O'C'=3，则该平面图形的面积是( )A.36√2B.9√22C.9D. 365.用一个平行于圆锥底面的平面截这个圆锥，截得圆台上、下底面半径的比是1∶4，且该圆台的母线长为9，则截去的圆锥的母线长为( )A. 94B. 3C. 12D. 366.设三棱柱的侧棱垂直于底面，所有棱的长都为a ，顶点都在一个球面上，则该球的表面积为( )A. πa 2B. 73πa 2C. 113πa 2D. 5πa 27.（多选）如图是正方体的平面展开图，在这个正方体中：下列命题中，所有正确命题的是（ ）A.BM∥平面DE ；∥平面AF ；C.平面BDM∥平面AFN ；D.平面BDE∥平面NCF.8.(多选) l 1，l 2，l 3是空间三条不同的直线，则下列结论不正确的是( )A ．l 1⊥l 2，l 2⊥l 3⇒l 1∥l 3B ．l 1⊥l 2，l 2∥l 3⇒l 1⊥l 3C ．l 1∥l 2∥l 3⇒l 1，l 2，l 3共面D ．l 1，l 2，l 3共点⇒l 1，l 2，l 3共面三、填空题(共4题，每题5分；共20分)9.已知球 O 的半径为4，圆M 与圆N 为该球的两个小圆， AB 为圆M 与圆N 的公共弦，AB =4，若 OM =ON =3，则两圆圆心的距离MN = .10.若某圆锥的高等于其底面圆的半径，则它的底面积和侧面积之比为 .11.已知正四棱锥P-ABCD 的所有棱长都相等，高2√2，则该正四棱锥的表面积为 .12.如图，在正方体ABCD-A1B1C1D1中，AB=2，点E为AD的中点，点F在CD上.若EF∥平面AB1C，则线段EF的长度等于.四、计算题（共3题，共计40分）13.（10分）如图所示，已知E，F，G，H分别是正方体ABCD－A1B1C1D1的棱AB，BC，CC1，C1D1的中点．求证：FE，HG，DC三线共点．14.（15分)四边形ABCD是平行四边形，点P是平行四边形外一点，M是PC的中点，在DM上取一点G，过点G和AP作平面交平面BDM于GH，求证：AP∥GH.15.（15分）如图，在正方体ABCD-A1B1C1D1中，E为BB1的中点，F为DD1的中点.求证：平面BC1F∥平面AD1E.。

高一数学第15周测试题（统计Ⅰ、Ⅱ节）1、从高一D 级1000名学生中抽取60名学生进行体重的统计分析，在这个问题中，60名学生的体重是（ ）A 、总体B 、个体C 、从总体中抽取的一个样本D 、样本容量 2、从162人中抽取一个样本容量为16的样本，采用系统抽样的方法则必须从这162人中剔除（ ）人A 、1B 、2C 、3D 、43、一批热水器共有98台，其中甲厂生产的有56台，乙厂生产的有42台，用分层抽样从中抽出一个容量为14的样本，那么甲、乙两厂各抽得的热水器的台数是（ ）A 、甲厂9台，乙厂5台B 、甲厂7台，乙厂7台C 、甲厂10台，乙厂4台D 、甲厂8台，乙厂6台4、频率分布直方图中，各小长方形高的比不．等于（ ） A 、组距比 B 、频率比 C 、面积比 D 、频数比5、一个容量为10的样本数据，分组后，组距与频数如下：［10，20），2；［20，30），3；［30，40），4；［40，50），1则样本在［20，30）上的频率为（ ）A 、0.2B 、0.4C 、0.1D 、0.36、计算40个数据的平均数时，错将其中的一个数据115输入为15，那么由此求出的平均数与实际平均数的差是（ ）A 、－2.5B 、2.5C 、3.25D 、－3.257、阅读如图1的程序框图，如果两次输入的值分别为1和3，则输出y 的值分别为（ ）A 、1和6B 、2和9C 、2x 和x 2D 、3和68、某商场一天中售出MK 牌运动鞋12双，其中各种尺码的鞋的销售量如下表所9、在频率分布直方图中共有11个小矩形，其中中间小矩形的面积是其余小矩形面积之和的4倍，若样本容量为220，则该组的频数是（ ）A 、176B 、44C 、20D 、以上答案都不对10、一组数据X 1，X 2，…，Xn 的平均数是3，方差是5，则数据3X 1＋2，3X 2＋2，…，3Xn ＋2 的平均数和方差分别是（ ）A 、3 ，5B 、5 ，15C 、11 ，45D 、5 ，4511、从参加数学竞赛的100名学生中抽取一个容量为10的样本，按系统抽样的方法分成10组，第一组随机抽取一个号码为05，则抽取的第8个号码为12、观察某县新生婴儿的体重，其频率分布直方图如图2所示，则新生婴儿体重在[2.6，2.8）的频率为图113、某班学生父母年龄的茎叶图如图3所示，则该班学生的母亲的平均年龄是________；父亲的平均年龄是_________14、如图4所示的程序运行后输出的结果是班级 学号 姓名 分数二、填空题（5×4＝20）11、 12、 13、（1） （2） 14、三、计算题（30）15、某赛季甲、乙两名NBA 球员在5场比赛中的盖帽数如下： 甲 2，3，4，5，6 乙 3，4，5，3，5根据上述数据，试判断谁更优秀．父 母 2 3 8 4 7 2 3 1 2 83 1 7 1 2 345 图3图22.8 2.4 2.6 33.2 3.4图4高一数学第15周测试题（统计Ⅰ、Ⅱ节）参考答案二、填空题11、75 12、 0.3 13、（1） 41 （2） 44 14、 2 三、 15、分故乙比甲更优秀，但乙比甲更稳定，两人的平均盖帽数相同由此可以说明，甲、乙＞ ＝　分 ］）－＋（）－＋（）－＋（）－＋（）－［（＝分 ］）－＋（）－＋（）－＋（）－＋（）－［（＝分 ＝＋＋＋＋＝分＝＋＋＋＋＝乙甲乙甲乙甲乙甲30 . s s 24 8.0454********1s 172464544434251s 10 4553543 5 4565432 22222222222222x x x x ∴==。