
圆
目录
圆的定义及相关概念
垂经定理及其推论
圆周角与圆心角
圆心角、弧、弦、弦心距关系定理
圆内接四边形
会用切线, 能证切线
切线长定理
三角形的内切圆
了解弦切角与圆幂定理(选学)
圆与圆的位置关系
圆的有关计算
一.圆的定义及相关概念
【考点速览】
考点1:
圆的对称性:圆既是轴对称图形又是中心对称图形。经过圆心的每一条直线都是它的对称轴。圆心是它的对称中心。
考点2:
确定圆的条件;圆心和半径
①圆心确定圆的位置,半径确定圆的大小;
②不在同一条直线上的三点确定一个圆;
考点3:
弦:连结圆上任意两点的线段叫做弦。经过圆心的弦叫做直径。直径是圆中最大的弦。
弦心距:圆心到弦的距离叫做弦心距。
弧:圆上任意两点间的部分叫做弧。弧分为半圆,优弧、劣弧三种。
(请务必注意区分等弧,等弦,等圆的概念)
弓形:弦与它所对应的弧所构成的封闭图形。
弓高:弓形中弦的中点与弧的中点的连线段。
(请务必注意在圆中一条弦将圆分割为两个弓形,对应两个弓高)
固定的已经不能再固定的方法:
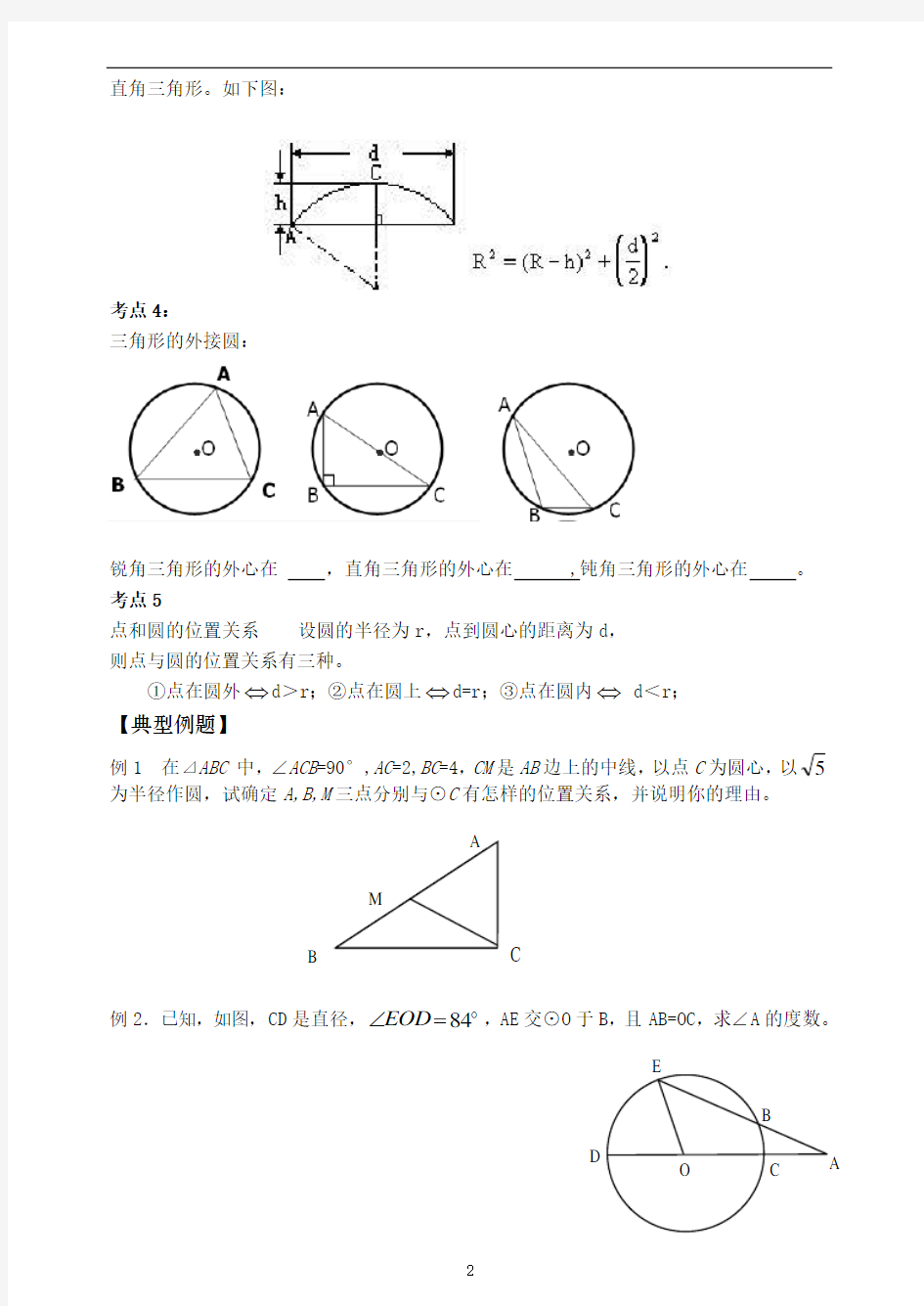
求弦心距,弦长,弓高,半径时通常要做弦心距,并连接圆心和弦的一个端点,得到
直角三角形。如下图:
考点4:
三角形的外接圆:
锐角三角形的外心在,直角三角形的外心在 ,钝角三角形的外心在。
考点5
点和圆的位置关系设圆的半径为r,点到圆心的距离为d,
则点与圆的位置关系有三种。
①点在圆外?d>r;②点在圆上?d=r;③点在圆内? d<r;
【典型例题】
例1 在⊿ABC中,∠ACB=90°,AC=2,BC=4,CM是AB边上的中线,以点C为圆心,以5为半径作圆,试确定A,B,M三点分别与⊙C有怎样的位置关系,并说明你的理由。
例2.已知,如图,CD是直径,?
=
∠84
EOD,AE交⊙O于B,且AB=OC,求∠A的度数。
M
A
B C
D
O
E
B
C
例3 ⊙O 平面内一点P 和⊙O 上一点的距离最小为3cm ,最大为8cm ,则这圆的半径是_________cm 。
例4 在半径为5cm 的圆中,弦AB ∥CD ,AB=6cm ,CD=8cm ,则AB 和CD 的距离是多少?
例5 如图,⊙O 的直径AB 和弦CD 相交于点E ,已知AE=6cm ,EB=2cm,ο30=∠CEA , 求CD 的长.
例6.已知:⊙O 的半径0A=1,弦AB 、AC 的长分别为3,2,求BAC ∠的度数.
二.垂径定理及其推论
【考点速览】
考点1
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条孤. 推论1:
①平分弦(不是直径)的直径重直于弦,并且平分弦所对的两条孤. ②弦的垂直平分线经过圆心,并且平分弦所对的两条孤.
③平分弦所对的一条孤的直径,垂直平分弦,并且平分弦所对的另一条孤. 推论2.圆的两条平行弦所夹的孤相等.垂径定理及推论1中的三条可概括为:
① 经过圆心;②垂直于弦;③平分弦(不是直径);④平分弦所
对的优弧;⑤平分弦所对的劣弧.以上五点已知其中的任意两点,都可以推得其它两点
A
B D
C
O
· E
【典型例题】
例1 如图AB 、CD 是⊙O 的弦,M 、N 分别是AB 、CD 的中点,且CNM AMN ∠=∠. 求证:AB=CD .
例2已知,不过圆心的直线l 交⊙O 于C 、D 两点,AB 是⊙O 的直径,AE ⊥l 于E ,BF ⊥l 于F 。求证:CE=DF .
l
?
问题一图1
O
H
F
E D C
B
A l
?
问题一图2
O H F E D
C B
A
l
?
问题一图3
O
H F
E D C B
A
【考点速练】
1.已知⊙O 的半径为2cm ,弦AB 长cm 32,则这条弦的中点到弦所对劣孤的中点的距离为( ).
A .1cm B.2cm C.cm 2 D.cm 3cm
3.如图1,⊙O 的半径为6cm ,AB 、CD 为两弦,且AB ⊥CD ,垂足为点E ,若CE=3cm ,DE=7cm ,则AB 的长为( )
A .10cm B.8cm C.cm 24 D.cm 28
4.有下列判断:①直径是圆的对称轴;②圆的对称轴是一条直径;③直径平分弦与弦所对的孤;④圆的对称轴有无数条.其中正确的判断有( ) A .0个 B.1个 C.2个 D.3个
5.如图2,同心圆中,大圆的弦交AB 于C 、D 若AB=4,CD=2,圆心O 到AB 的距离等于1,那么两个同心圆的半径之比为( )
A B
D
C O
· N
M
A
B
D
C
O 800
A .3:2 B.5:2 C.5:2 D.5:4
6.如图,⊙O 的直径为10,弦AB=8,P 是弦AB 上的一个动点,那么OP 长的取值范围是 .
7.如图,已知有一圆弧形拱桥,拱的跨度AB=16cm,拱高CD=4cm,那么拱形的半径是_ ___m.
8.如图,直径为1000mm 的圆柱形水管有积水(阴影部分),水面的宽度AB 为800mm ,求水的最大深度CD .
三.圆周角与圆心角
【考点速览】 考点1
圆心角:顶点在圆心的角叫圆心角,圆心角的度数等于它所对的弧的度数。 Eg: 判别下列各图中的角是不是圆心角,并说明理由。
圆周角:顶点在圆周上,角两边和圆相交的角叫圆周角。两个条件缺一不可. Eg: 判断下列图示中,各图形中的角是不是圆周角,并说明理由
B
P
A
O D C
A
考点2
定理:一条弧所对的圆周角等于它所对的圆心角的一半.
Eg: 如下三图,请证明。
考点3
4. 推论:
①同弧或等弧所对的圆周角相等,同圆或等圆中,相等的圆周角所对的弧也相等.
90的圆周角所对的弦是直径.
②半圆(或直径)所对的圆周角是直角,
③如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
经典例题
例1:下图中是圆周角的有 .是圆心角的有。
例2:如图,∠A 是⊙O 的圆周角,且∠A =35°,则∠OBC=_____.
例3:如图,圆心角∠AOB=100°,则∠ACB= .
例4:如图1,AB 是⊙O 的直径,点C D E ,,都在⊙O 上,若C D E ==∠∠∠,则
A B +=∠∠ o
.
例如
图2,⊙O 的直径CD 过弦EF 的中点G ,40EOD ∠=o
,则DCF ∠= . 例6:已知:如图,AD?是⊙O?的直径,∠ABC=?30?°,则∠CAD=_______.
例7:已知⊙O 中,30C ∠=o
,2cm AB =,则⊙O 的半径为 cm
O
A
B
C
(例1)
B E
F C
D G O 例2
四.圆心角、弧、弦、弦心距关系定理【考点速览】
圆心角, 弧,弦,弦心距之间的关系定理:
在同圆或等圆中,相等的圆心角所对的孤相等,所对的弦相等,所对的弦的弦心距相等
推论:在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
(务必注意前提为:在同圆或等圆中)
例1.如图所示,点O是∠EPF的平分线上一点,以O为圆心的圆和角的两边分别交于A、B和C、D,求证:AB=CD.
例2、已知:如图,EF为⊙O的直径,过EF上一点P作弦AB、CD,且∠APF=∠CPF。
求证:PA=PC。
A
B
E
F
O
P
C
1
2
D
例3.如图所示,在ABC ?中,∠A=?72,⊙O 截ABC ?的三条边长所得的三条弦等长,求∠BOC.
例4.如图,⊙O 的弦CB 、ED 的延长线交于点A ,且
例5.如图所示,已知在⊙O 中,弦AB=CB ,∠ABC=?120,OD ⊥AB 于D ,OE ⊥BC 于E . 求证:ODE ?是等边三角形.
五.圆内接四边形
【考点速览】
圆内接四边形对角互补,外角等于内对角。 圆内接梯形为等腰梯形,圆内接平行四边形为矩形。 判断四点共圆的方法之一:四边形对角互补即可。
【典型例题】
例1 (1)已知圆内接四边形ABCD 中,∠A:∠B:∠C=2:3:4,求∠D 的度数.
·O
A
B
C
O ·
C
A
E B D
·
O A D
E B
C
(2)已知圆内接四边形ABCD 中,如图所示,AB 、BC 、CD 、AD 的度数之比为1:2:3:4,求∠A 、∠B 、∠C 、∠D 的度数.
例2 四边形ABCD 内接于⊙O ,点P 在CD 的延长线上,且AP ∥BD .求证:AD AB BC PD ?=?
例3 如图所示,ABC ?是等边三角形,D 是BC 上任一点.求证:DB+DC=DA .
六.会用切线,能证切线
考点速览:
考点1
直线与圆的位置关系
·
A
D
C
B
O P
A
·
B
C
D
O · A
B
D
O
考点2
切线:经过半径外端并且垂直于这条半径的直线是圆的切线。
符号语言
∵ OA ⊥ l 于A , OA 为半径
∴ l 为⊙O 的切线
考点3
判断直线是圆的切线的方法:
①与圆只有一个交点的直线是圆的切线。
②圆心到直线距离等于圆的半径的直线是圆的切线。 ③经过半径外端,垂直于这条半径的直线是圆的切线。
(请务必记住证明切线方法:有交点就连半径证垂直;无交点就做垂直证半径) 考点4
切线的性质定理:
圆的切线垂直于经过切点的半径。
推论1:经过圆心且垂直于切线的直线必经过切点。 推论2:经过切点且垂直于切线的直线必经过圆心。
(请务必记住切线重要用法: 见切线就要连圆心和切点得到垂直)
经典例题:
例1.如图,△ABC 内接于⊙O , AB 是 ⊙O 的直径,∠CAD = ∠ABC ,判断直线AD 与⊙O 的位置关系,并说明理由。
A B
B
C
例2.如图,OA=OB=13cm ,AB=24cm ,⊙O 的半径为5cm ,AB 与⊙O 相切吗?为什么?
例3.如图,PA 、PB 是⊙O 的切线,切点为A 、B ,C 是⊙O 上一点,若∠P =40。
, 求∠C 的度数。
例4.如图所示,ABC Rt ?中,?=∠90C ,以AC 为直径作⊙O 交AB 于D ,E 为BC 中点。
求证:DE 是⊙O 的切线.
中考链接
1.如图,在以O 为圆心的两个同心圆中,AB 经过圆心O ,且与小圆相交于点A ,与大圆相交于点B ,小圆的切线AC 与大圆相交于点D ,且CO 平分∠ACB.
试判断BC 所在直线与小圆的位置关系,并说明理由。
2. 如图,在Rt △ABC 中,∠C=90。 ,点O 在AB 上,以O 为圆心,OA 长为半径的圆与AC 、AB 分别交于点D 、E ,且∠CBD= ∠A ,
判断BD 与⊙O 的位置关系,并证明你的结论。
B
B
· A
B
C E
O
D
七.切线长定理
考点速览: 考点1
切线长概念:
经过圆外一点做圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长. 切线长和切线的区别
切线是直线,不可度量;而切线长是切线上一条线段的长,而圆外一已知点到切点之间的距离,可以度量. 考点2 切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
要注意:此定理包含两个结论,如图,PA 、PB 切⊙O 于A 、B 两点,
①PA=PB ②PO 平分APB ∠. 考点3 两个结论:
圆的外切四边形对边和相等;
圆的外切等腰梯形的中位线等于腰长. 经典例题:
例1 已知PA 、PB 、DE 分别切⊙O 于A 、B 、C 三点,若PO=13㎝,PED ?的周长为24㎝, 求:①⊙O 的半径;②若40APB ∠=?,EOD ∠的度数.
例2 如图,⊙O 分别切ABC ?的三边
AB 、BC 、CA 于点D 、E 、F ,若,,BC a AC b AB c ===. (1)求AD 、BE 、CF 的长;(2)当90C ∠=?,求内切圆半径r .
例3.如图,一圆内切四边形ABCD ,且AB=16,CD=10,则四边形的周长为?
考点速练1:
1.如图,⊙O 是ABC ?的内切圆,D 、E 、F 为切点,
::4:3:2A B C ∠∠∠=,则DEF ∠= . FEC ∠= .
2.直角三角形的两条直角边为5㎝、12㎝,则此直角三角形的外接圆半径为 ㎝,内切圆半径为 ㎝.
3.如图,直线AB 、BC 、CD 分别与⊙O 相切于点E 、F 、G ,且AB ∥CD ,若OB=6㎝,OC=8㎝,则BOC ∠= ,⊙O 的半径= ㎝,BE+CG= ㎝.
· F
D
O
A
B
· E
F
D
C
O
A
B
·
A O C
D
B
E
F
· A
O C D B E F
G
八.三角形内切圆
考点速览
考点1
概念:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.
概念推广:和多边形各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形.
考点2
三角形外接圆与内切圆比较:
名称
确定方法
图形
性质
外心(三角形外接圆的圆心)
三角形三边中垂线的交点
(1)OA=OB=OC ;
(2)外心不一定在三角形的内部.
内心(三角形内切圆的圆心)
三角形三条
角平分线的
交点
(1)到三边的距离相等;
(2)OA 、OB 、OC 分别平
分∠BAC 、∠ABC 、∠ACB ;
(3)内心在三角形内部.
考点3
求三角形的内切圆的半径
1、直角三角形△ABC 内切圆⊙O 的半径为2
c
b a r -+=.
2、一般三角形
①已知三边,求△ABC 内切圆⊙O 的半径r.
c
b a S r ++?=2
(海伦公式S △=)c s )(b s )(a s (s --- , 其中s=
2
c
b a ++) B
O D
c
a B
O E F D
经典例题:
例1.阅读材料:如图(1),△ABC的周长为L,内切圆O的半径为r,连结OA,OB,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积.
∵S△ABC =S△OAB +S△OBC +S△OCA
又∵S△OAB =1
2
AB·r,S△OBC =
1
2
BC·r,S△OCA =
1
2
AC·r
∴S△ABC =1
2
AB·r+
1
2
BC·r+
1
2
CA·r
=1
2
L·r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5,12,13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(2)?且面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1,a2,a3,…a n,合理猜想其内切圆半径公式(不需说明理由).
例2.如图,△ABC中,∠A=m°.
(1)如图(1),当O是△ABC的内心时,求∠BOC的度数;
(2)如图(2),当O是△ABC的外心时,求∠BOC的度数;
(3)如图(3),当O是高线BD与CE的交点时,求∠BOC的度数.
例3.如图,Rt△ABC中,AC=8,BC=6,∠C=90°,⊙I分别切AC,BC,AB于D,E,F,求Rt△ABC的内心I与外心O之间的距离.
考点速练1:
1.如图1,⊙O内切于△ABC,切点为D,E,F.已知∠B=50°,∠C=60°,?连结OE,OF,DE,DF,那么∠EDF等于()
A.40° B.55° C.65° D.70°
图1 图2 图3
2.如图2,⊙O是△ABC的内切圆,D,E,F是切点,∠A=50°,∠C=60°,?则∠DOE=()
A.70° B.110° C.120° D.130°
3.如图3,△ABC中,∠A=45°,I是内心,则∠BIC=()
A.112.5° B.112° C.125° D.55°
4.下列命题正确的是()
A.三角形的内心到三角形三个顶点的距离相等
B.三角形的内心不一定在三角形的内部
C.等边三角形的内心,外心重合
D.一个圆一定有唯一一个外切三角形
5.在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为() A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.5
6.如图,在△ABC中,AB=AC,内切圆O与边BC,AC,AB分别切于D,E,F.(1)求证:BF=CE;
(2)若∠C=30°,CE=23,求AC的长.
7.如图,⊙I切△ABC的边分别为D,E,F,∠B=70°,∠C=60°,M是弧DEF上的动点(与D,E不重合),∠DMF的大小一定吗?若一定,求出∠DMF的大小;若不一定,请说明理由.
九.了解弦切角与圆幂定理
(选学)
【考点速览】
考点1
1. 弦切角的概念:
顶点在圆上,一边和圆相交,另一边和圆相切的角
叫做弦切角。
注意:弦切角必须具备三个条件:(1)顶点在圆上
(切点),(2)一边和圆相切,(3)一边和圆相交(弦),三者缺一不可。
2. 弦切角定理:
弦切角等于它所夹的弧对的圆周角。
3. 弦切角定理的推论:
如果两个弦切角所夹的弧相等,那么这两个弦切角也相等。
考点2
圆幂定理:圆幂定理是对相交弦定理、切割线定理及割线定理(切割线定理推论)以及它们推论统一归纳的结果。
1、相交弦定理:圆内两条相交弦,被交点分成的两条线段长的积相等。
2、相交弦定理的推论:如果弦与直径相交,那么弦的一半是它分直径所成的两条线段的比例中项。
3、切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
4、切割线定理的推论(或称割线定理):
从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
典型例题:
例1. 如图,经过⊙O上的点T的切线和弦AB的延长线相交于点C。
求证:∠ATC=∠TBC
O
T
A B C
E
例2. 已知:如图,AB是⊙O的弦,P是AB上的一点,AB=10cm,PA=4cm,OP=5cm,求⊙O的半径。
B A
O
P
例3. AB是半圆O的直径,C是AB延长线上一点,CD切半圆于D,连结AD,若AD=15,sin C=
3
5
,求BC的长。
十.圆与圆位置的关系
考点速览:
外离外切相交内切内含图形
公共
点
0个1个2个1个0个
d、r、
R的关
d R r
>+d R r
=+R r d R r
-<<+d R r
=-d R r
<-O1O
2
O1O
2
O1O
2
O1
O2
O1
O2
九年级数学上册 圆 几何综合(提升篇)(Word 版 含解析) 一、初三数学 圆易错题压轴题(难) 1.如图,二次函数y=x 2-2mx+8m 的图象与x 轴交于A 、B 两点(点A 在点B 的左边且OA≠OB ),交y 轴于点C ,且经过点(m ,9m ),⊙E 过A 、B 、C 三点。 (1)求这条抛物线的解析式; (2)求点E 的坐标; (3)过抛物线上一点P (点P 不与B 、C 重合)作PQ ⊥x 轴于点Q ,是否存在这样的点P 使△PBQ 和△BOC 相似?如果存在,求出点P 的坐标;如果不存在,说明理由 【答案】(1)y=x 2 +2x-8(2)(-1,- 72)(3)(-8,40),(-15 4,-1316),(-174 ,-25 16 ) 【解析】 分析:(1)把(),9m m 代入解析式,得:22289m m m m -+=,解这个方程可求出m 的值; (2)分别令y =0和x =0,求出OA ,OB ,O C 及AB 的长,过点E 作EG x ⊥轴于点 G ,EF y ⊥轴于点F ,连接CE ,AE ,设OF =GE =a ,根据AE CE = ,列方过程求出a 的值, 从而求出点E 的坐标; (3)设点P (a , a 2+2a -8), 则2 28,2PQ a a BQ a =+-=-,然后分PBQ ∽CBO 时 和PBQ ∽BCO 时两种情况,列比例式求出a 的值,从而求出点P 的坐标. 详解:(1)把(),9m m 代入解析式,得:22289m m m m -+= 解得:121,0m m =-=(舍去) ∴228y x x =+-
一.圆的定义及相关概念 【考点速览】 考点1: 圆的对称性:圆既是轴对称图形又是中心对称图形。经过圆心的每一条直线都是它的对称轴。圆心是它的对称中心。 考点2: 确定圆的条件;圆心和半径 ①圆心确定圆的位置,半径确定圆的大小; ②不在同一条直线上的三点确定一个圆; 考点3: 弦:连结圆上任意两点的线段叫做弦。经过圆心的弦叫做直径。直径是圆中最大的弦。 弦心距:圆心到弦的距离叫做弦心距。 弧:圆上任意两点间的部分叫做弧。弧分为半圆,优弧、劣弧三种。 (请务必注意区分等弧,等弦,等圆的概念) 弓形:弦与它所对应的弧所构成的封闭图形。 弓高:弓形中弦的中点与弧的中点的连线段。 (请务必注意在圆中一条弦将圆分割为两个弓形,对应两个弓高) 固定的已经不能再固定的方法: 求弦心距,弦长,弓高,半径时通常要做弦心距,并连接圆心和弦的一个端点,得到直角三角形。如下图: 考点4: 三角形的外接圆: 锐角三角形的外心在,直角三角形的外心在 ,钝角三角形的外心在。 考点5 点和圆的位置关系设圆的半径为r,点到圆心的距离为d,
则点与圆的位置关系有三种。 ①点在圆外?d >r ;②点在圆上?d=r ;③点在圆? d <r ; 【典型例题】 例1 在⊿ABC 中,∠ACB =90°,AC =2,BC =4,CM 是AB 边上的中线,以点C 为圆心,以5为半径作圆,试确定A,B,M 三点分别与⊙C 有怎样的位置关系,并说明你的理由。 例2.已知,如图,CD 是直径,?=∠84EOD ,AE 交⊙O 于B ,且AB=OC ,求∠A 的度数。 例3 ⊙O 平面一点P 和⊙O 上一点的距离最小为3cm ,最大为8cm ,则这圆的半径是_________cm 。 例4 在半径为5cm 的圆中,弦AB ∥CD ,AB=6cm ,CD=8cm ,则AB 和CD 的距离是多少? 例5 如图,⊙O 的直径AB 和弦CD 相交于点E ,已知AE=6cm ,EB=2cm, 30=∠CEA , 求CD 的长. 例6.已知:⊙O 的半径0A=1,弦AB 、AC 的长分别为3,2,求BAC ∠的度数. A B D C O · E
圆 目录 圆的定义及相关概念 垂经定理及其推论 圆周角与圆心角 圆心角、弧、弦、弦心距关系定理 圆内接四边形 会用切线, 能证切线 切线长定理 三角形的内切圆 了解弦切角与圆幂定理(选学) 圆与圆的位置关系 圆的有关计算 一.圆的定义及相关概念 【考点速览】 考点1: 圆的对称性:圆既是轴对称图形又是中心对称图形。经过圆心的每一条直线都是它的对称轴。圆心是它的对称中心。 考点2: 确定圆的条件;圆心和半径 ①圆心确定圆的位置,半径确定圆的大小; ②不在同一条直线上的三点确定一个圆; 考点3: 弦:连结圆上任意两点的线段叫做弦。经过圆心的弦叫做直径。直径是圆中最大的弦。 弦心距:圆心到弦的距离叫做弦心距。 弧:圆上任意两点间的部分叫做弧。弧分为半圆,优弧、劣弧三种。 (请务必注意区分等弧,等弦,等圆的概念) 弓形:弦与它所对应的弧所构成的封闭图形。 弓高:弓形中弦的中点与弧的中点的连线段。 (请务必注意在圆中一条弦将圆分割为两个弓形,对应两个弓高) 固定的已经不能再固定的方法:
求弦心距,弦长,弓高,半径时通常要做弦心距,并连接圆心和弦的一个端点,得到直角三角形。如下图: 考点4: 三角形的外接圆: 锐角三角形的外心在,直角三角形的外心在,钝角三角形的外心在。 考点5 点和圆的位置关系设圆的半径为r,点到圆心的距离为d, 则点与圆的位置关系有三种。 ①点在圆外?d>r;②点在圆上?d=r;③点在圆内? d<r; 【典型例题】 例1 在⊿ABC中,∠ACB=90°,AC=2,BC=4,CM是AB边上的中线,以点C为圆心,以5为半径作圆,试确定A,B,M三点分别与⊙C有怎样的位置关系,并说明你的理由。 例2.已知,如图,CD是直径,? = ∠84 EOD,AE交⊙O于B,且AB=OC,求∠A的度数。 M A B C
九年级上册数学圆章节知 识点总结 Prepared on 21 November 2021
与圆相关的基本知识和计算 一、知识梳理: (一):圆及圆的有关概念 1.圆:到顶点的距离等于定长的点的集合叫做圆; 2.弧:圆上任意两点间的部分叫做圆弧,简称弧。圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆,大于半圆的弧叫做优弧,小于半圆的叫做劣弧; 3.弦:连接圆上任意两点的线段叫做弦。经过圆心的弦叫做直径,它是圆的最长的弦; 4.等圆:能够完全重合的两个圆叫做等圆;等弧:在同圆或等圆中,能够互相重合的弧叫做等弧; 5.圆心角:顶点在圆心的角叫做圆心角;圆周角:顶点在圆上且两边与圆相交的角叫做圆周角; (二)圆的有关性质: 1.对称性:圆是中心对称图形,其对称中心是圆心;圆是轴对称图形,其对称轴是直径所在的直线; 2.垂径定理及其推论: (1)、垂径定理:垂直弦的直径平分弦,并且平分弦所对的弧; (2)、推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧;3.圆心角、弧、弦之间的关系 (1)定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;(2)推论:在同圆或等圆中,如果两条弧相等,那么他们所对的圆心角相等、所对的弦相等。在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等、所对的弧相等。 4.圆周角与圆心角的关系 (1)在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;
(2)推论:半圆(或直径)所对的圆周角是直角,0 90的圆周角所对的弦是直径; 5.圆内接四边形对角互补。 (三)点与圆的位置关系 1、点和圆的位置关系 如果圆的半径为r,已知点到圆心的距离为d,则可用数量关系表示位置关系. (1)d>r点在圆外;(2)d=r点在圆上;(3)d<r点在圆内. 2、确定圆的条件:不在同一直线上的三个点确定一个圆. (四)直线与圆的位置关系 1、(1)直线与圆的位置关系有关概念 ①相交与割线:直线和圆有两个公共点时,叫做直线和圆相交,这条直线叫做圆的割线. ②切线与切点:直线和圆有惟一公共点时,叫做直线和圆相切,这条直线叫做圆的切线,惟一的公共点叫做切点. ③相离,当直线和圆没有公共点时,叫做直线和圆相离. (2)用数量关系判断直线与圆的位置关系 如果⊙O的半径为r,圆心O到直线l的距离为d,那么: (1)直线l和⊙O相交d<r(如图(1)所示); (2)直线l和⊙O相切d=r(如图(2)所示); (3)直线l和⊙O相离d>r(如图(3)所示). 2、切线 (1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. (2)切线的性质:圆的切线垂直于过切点的半径. (3)切线长:圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长. (4)切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角. (五)三角形的外接圆和内切圆 1、三角形的外接圆 (1)定义:经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆.
欢迎来主页下载---精品文档 九年级数学第二十四章圆测试题(A) 一、选择题(每小题3分,共33分) ,最aO上的点的最大距离为·资阳)若⊙O所在平面内一点P到⊙1.(2005 ),则此圆的半径为(小距离为b(a>b)b?baa?.A B.221 ——A图24ba?a?b ba?a?b或或 D .C.22,则弦的长为3到弦AB的距离OM1A—,⊙O的直径为10,圆心O2.(2005·浙江)如图24—)AB的长是( .8 DC.7 B.6 A.4 )°,则∠BOC的度数为(3.已知点O为△ABC的外心,若∠A=80120°D.80°C.160°A.40°B.)OBC的度数为(,△ABC内接于⊙O,若∠A=40°,则∠4.如 图24—A—270°D.°C.50°A.20°B.40 4 —AA——3 图图24—A—242 图24—5 —A—图24 点钉OB在O—3,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA、5.如图24—A个OE=8个单位,OF=6在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度)单位,则圆的直径为(B.10个单位A.12个单位 15个单位D.个单位C.1 )等于(°,则∠A 为⊙O的直径,点C在⊙O上,若∠B=60—6.如图24A—4,AB°D.30.50°C.40°A.80°B、PA 于点E,分别交A、B,CD切⊙O,—A—5P为⊙O外一点,PA、PB分别切⊙O于7.如图24 )的周长为(、D,若PA=5,则△PCDPB于点C10 D.7 C.8 .A.5 B,为防雨需在粮仓顶部铺上,母线长为3m8.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m )油毡,则这块油毡的面积是(
圆 目录 一.圆的定义及相关概念 二.垂经定理及其推论 三.圆周角与圆心角 四.圆心角、弧、弦、弦心距关系定理五.圆内接四边形 六.会用切线, 能证切线 七.切线长定理 八.三角形的内切圆 九.了解弦切角与圆幂定理(选学)十.圆与圆的位置关系 十一.圆的有关计算 十二.圆的基础综合测试 十三.圆的终极综合测试
一.圆的定义及相关概念 【考点速览】 考点1: 圆的对称性:圆既是轴对称图形又是中心对称图形。经过圆心的每一条直线都是它的对称轴。圆心是它的对称中心。 考点2: 确定圆的条件;圆心和半径 ①圆心确定圆的位置,半径确定圆的大小; ②不在同一条直线上的三点确定一个圆; 考点3: 弦:连结圆上任意两点的线段叫做弦。经过圆心的弦叫做直径。直径是圆中最大的弦。 弦心距:圆心到弦的距离叫做弦心距。 弧:圆上任意两点间的部分叫做弧。弧分为半圆,优弧、劣弧三种。 (请务必注意区分等弧,等弦,等圆的概念) 弓形:弦与它所对应的弧所构成的封闭图形。 弓高:弓形中弦的中点与弧的中点的连线段。 (请务必注意在圆中一条弦将圆分割为两个弓形,对应两个弓高) 固定的已经不能再固定的方法: 求弦心距,弦长,弓高,半径时通常要做弦心距,并连接圆心和弦的一个端点,得到直角三角形。如下图:
考点4: 三角形的外接圆: 锐角三角形的外心在 ,直角三角形的外心在 ,钝角三角形的外心在 。 考点5 点和圆的位置关系 设圆的半径为r ,点到圆心的距离为d , 则点与圆的位置关系有三种。 ①点在圆外?d >r ;②点在圆上?d=r ;③点在圆内? d <r ; 【典型例题】 例1 在⊿ABC 中,∠ACB =90°,AC =2,BC =4,CM 是AB 边上的中线,以点C 为圆心,以5为半径作圆,试确定A,B,M 三点分别与⊙C 有怎样的位置关系,并说明你的理由。 例2.已知,如图,CD 是直径,?=∠84EOD ,AE 交⊙O 于B ,且AB=OC ,求∠A M A B C
圆所有经典难题 一,选择题 1.下列命题中正确的有( )个 (1) 平分弦的直径垂直于弦 (2)经过半径一端且与这条半径垂直的直线是圆的切线 (3)在同圆或等圆中,圆周角等于圆心角的一半 (4)平面内三点确定一个圆 (5)三角形的外心到各个顶点的距离相等 (A) 1个 (B) 2个 (C) 3个 (D) 4个 2.AC 平分∠BAD 且交BD 于F 点.若∠ADE =19°,则∠AFB 的度数为何?( ) A .97° B .104° C .116° D .142° 3.下列说法正确的是 ( ) A 、三点确定一个圆。 B 、一个三角形只有一个外接圆。 C 、和半径垂直的直线是圆的切线。 D 、三角形的内心到三角形三个顶点距离相等。 4.在半径等于5cm 的圆内有长为35cm 的弦,则此弦所对的圆周角为( ) A 、60o或120o B. 30o或120o C. 60o D. 120o 5.如图4,⊙O 的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为( ) A、2 B、3 C、4 D、5 6.与三角形三个顶点距离相等的点,是这个三角形的 ( ) A 、 三条中线的交点, B 、三条角平分线的交点, C 、三条高的交点, D 、三边的垂直平分线的交点。 7.圆的半径为5cm ,圆心到一条直线的距离是7cm ,则直线与圆( ) A 、有两个交点, B 、有一个交点, C 、没有交点, D 、交点个数不定。 8.两圆的半径比为 2 cm 与3cm ,圆心距等于小圆半径的2倍,则两圆的关系为 ( ) A 、相离, B 、外切, C 、相交, D 、内切或内含 9.若⊙O 所在平面内一点P 到⊙O 上的点的最大距离为a ,最小距离为b (a>b ), A B P O
初中数学试卷 金戈铁骑整理制作 圆 章节测试 时间:40分钟 满分:120分 姓名: 得分: 一、选择题(本大题共9小题,共54分) 1. 如图,圆锥的底面半径为2,母线长为6,则侧面积为( ) A. 4π B. 6π C. 12π D. 16π 2. 一个扇形的弧长是10πcm ,面积是60πcm 2,则此扇形的圆心角的度数是( ) A. 300° B. 150° C. 120° D. 75° 3. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( ) A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形 4. 如图,AB 是⊙O 的直径,C ,D 是⊙O 上位于AB 异侧的两点.下列四个角中,一定与∠ACD 互余的角是( ) A. ∠ADC B. ∠ABD C. ∠BAC D. ∠BAD 5. 如图,在⊙O 中,AB 是直径,AC 是弦,连接OC ,若∠ACO =30°,则∠BOC 的度数是( ) A. 30° B. 45° C. 55° D. 60°
6.如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12, OM:MD=5:8,则⊙O的周长为() A. 26π B. 13π C. D. 7.如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的 对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是() A. B. 2- C. 2- D. 4- 8.如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°, 则阴影部分的面积是() A. 4π-4 B. 2π-4 C. 4π D. 2π
初三数学 有关圆的经典例题 1. 在半径为的⊙中,弦、的长分别为和,求∠的度数。132O AB AC BAC 分析:根据题意,需要自己画出图形进行解答,在画图时要注意AB 与AC 有不同的位置关系。 解:由题意画图,分AB 、AC 在圆心O 的同侧、异侧两种情况讨论, 当AB 、AC 在圆心O 的异侧时,如下图所示, 过O 作OD ⊥AB 于D ,过O 作OE ⊥AC 于E , ∵,,∴,AB AC AD AE = == = 32322 2 ∵,∴∠,OA OAD AD OA == =132 cos cos ∠OAE AE OA = = 22 ∴∠OAD=30°,∠OAE=45°,故∠BAC=75°, 当AB 、AC 在圆心O 同侧时,如下图所示, 同理可知∠OAD=30°,∠OAE=45°, ∴∠BAC=15° 点拨:本题易出现只画出一种情况,而出现漏解的错误。 例2. 如图:△ABC 的顶点A 、B 在⊙O 上,⊙O 的半径为R ,⊙O 与AC 交于D , 如果点既是的中点,又是边的中点,D AB AC ? (1)求证:△ABC 是直角三角形; ()22 求的值AD BC 分 析 : ()1由为的中点,联想到垂径定理的推论,连结交于,D AB OD AB F ? 则AF=FB ,OD ⊥AB ,可证DF 是△ABC 的中位线;
(2)延长DO 交⊙O 于E ,连接AE ,由于∠DAE=90°,DE ⊥AB ,∴△ADF ∽△,可得·,而,,故可求DAE AD DF DE DF BC DE R AD BC 2 2 122=== 解:(1)证明,作直径DE 交AB 于F ,交圆于E ∵为的中点,∴⊥,D AB AB DE AF FB ? = 又∵AD=DC ∴∥,DF BC DF BC = 12 ∴AB ⊥BC ,∴△ABC 是直角三角形。 (2)解:连结AE ∵DE 是⊙O 的直径 ∴∠DAE=90° 而AB ⊥DE ,∴△ADF ∽△EDA ∴ ,即·AD DE DF AD AD DE DF ==2 ∵,DE R DF BC ==21 2 ∴·,故AD BC R AD BC R 2 2 == 例3. 如图,在⊙O 中,AB=2CD ,那么( ) A A B CD B AB CD ..?>? ?
圆中的基本概念及定理(讲义) 课前预习 在小学的时候,我们知道“一中同长”表示的是圆,中心称为,固定的线段长称为,还知道半径为r 的圆的周长为,面积为 . 在七年级我们学习了圆的另外一种说法:平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆.固定的端点O 称为圆心,线段OA 称为半径. 一条弧AB 和经过这条弧的两条半径OA,OB 所组成的图形叫做扇形.顶点在圆心的角叫做圆心角.
知识点睛 1.在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另一个 端点A 所形成的图形叫做.其固定的端点O叫做,线段OA 叫做.以点O 为圆心的圆,记作,读作“圆O”. 2.圆中概念: 弧:,弧包括和; 弦:; 圆周角:; 圆心角:; 弦心距:; 等圆:; 等弧:. 3.圆的对称性: 圆是轴对称图形,其对称轴是; 圆是中心对称图形,其对称中心为.4.圆中基本定理: *(1)垂径定理: .推论: .(2)四组量关系定理:在中,如果 、、、 中有一组量相等,那么它们所对应的其余各组量都分别相等. (3)圆周角定理:.推论1:. 推论2:, .推论3:. 注:如果一个多边形的所有顶点都在同一个圆上,那么这个多边 形叫做圆内接多边形,这个圆叫做这个多边形的外接圆. 圆中处理问题的思路: ①找圆心,连半径,转移边; ②遇弦,作垂线,垂径定理配合勾股定理建等式; ③遇直径,找直角,由直角,找直径; ④由弧找角,由角看弧.
C D A R B 精讲精练 1. 如图,AB 是⊙O 的直径,弦 CD ⊥AB ,垂足为 M ,下列结论不一定成立 的是( ) ︵ ︵ A .CM =DM B . C B =B D C .∠ACD =∠ADC D .OM =MB 第 1 题图 第 2 题图 2. 如图,⊙O 的弦 AB 垂直平分半径 OC ,若 AB = 的半径为 . ,则⊙O 3. 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是 10 mm ,测得钢珠顶端离零件表面的距离为 8 mm ,如图所示,则这个小圆孔的宽口 AB 的长度为 mm . 第 3 题图 第 4 题图 4. 如图,圆拱桥桥拱的跨度 AB =12 m ,桥拱高 CD =4 m ,则拱桥的直径为 . 5. 如图,在⊙O 中,直径 CD 垂直于弦 AB ,垂足为 E ,连接 OB , CB .已知⊙O 的半径为 2,AB = 2 ,则∠BCD = . 6 3
圆的相关练习题(含答案) 1、已知:弦AB 把圆周分成1:5的两部分,这弦AB 所对应的圆心角的度数为 。 2、如图:在⊙O 中,∠AOB 的度数为1200,则 的长是圆周的 。 3、已知:⊙O 中的半径为4cm ,弦AB 所对的劣弧为圆的3 1,则弦AB 的长为 cm , AB 的弦心距为 cm 。 4、如图,在⊙O 中,AB ∥CD , 的度数为450,则∠COD 的度数为 。 5、如图,在三角形ABC 中,∠A=700,⊙O 截△ABC 的三边所得的弦长相等,则 ∠BOC=( )。 A .140° B .135° C .130° D .125° (第2题图) (第4题图) (第5题图) 6、下列语句中,正确的有( ) (1)相等的圆心角所对的弧相等; (2)平分弦的直径垂直于弦; (3)长度相等的两条弧是等弧; (4) 圆是轴对称图形,任何一条直径都是对称轴 A .0个 B .1个 C .2个 D .3个 7、已知:在直径是10的⊙O 中, 的度数是60°,求弦AB 的弦心距。 8、已知:如图,⊙O 中,AB 是直径,CO ⊥AB ,D 是CO 的中点,DE ∥AB , 求证:
600 9. 已知:AB 交圆O 于C 、D ,且AC =BD.你认为OA =OB 吗?为什么? 10. 如图所示,是一个直径为650mm 的圆柱形输油管的横截面,若油面宽AB=600mm ,求油面的最大深度。 11. 如图所示,AB 是圆O 的直径,以OA 为直径的圆C 与圆O 的弦AD 相交于点E 。你认为图中有哪些相等的线段?为什么? 答案:1.60度 2. 3 2 3. 1 3 4 4.90度 5.D 6.A 7.2.5 8.提示:连接OE ,求出角COE 的度数为60度即可 9.略 10.100毫米 11.AC=OC , OA=OB , AE=ED B
24.1.1 圆 知识点一圆的定义 o叫作圆圆的定义:第一种:在一个平面内,线段0A绕它固定的一个端点0旋转一周,另一个端点A所形成的图形叫作圆。固定的端点 心,线段0A叫作半径。第二种:圆心为0,半径为r的圆可以看成是所有到定点0的距离等于定长r的点的集合。 比较圆的两种定义可知:第一种定义是圆的形成进行描述的,第二种是运用集合的观点下的定义,但是都说明确定了定点与定长, 也就确定了圆。 知识点二圆的相关概念 (1)弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫作直径。 (2)弧:圆上任意两点间的部分叫做圆弧,简称弧。圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。( 等圆:等够重合的两个圆叫做等圆。 (4)等弧:在同圆或等圆中,能够互相重合的弧叫做等弧。 弦是线段,弧是曲线,判断等弧首要的条件是在同圆或等圆中,只有在同圆或等圆中完全重合的弧才是等弧,而不是长度相等的弧。 24.1.2垂直于弦的直径 知识点一圆的对称性 圆是轴对称图形,任何一条直径所在直线都是它的对称轴。 知识点二垂径定理 (1)垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。如图所示,直径为CD, AB是弦,且CDLAE, C ~|M A B AM=BM 垂足为M AC=BC AD=BD D 垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧如 上图所示,直径CD与非直径弦AB相交于点M CDLABAM=BMAC=BC AD=BD 注意:因为圆的两条直径必须互相平分,所以垂径定理的推论中,被平分的弦必须不是直径,否则结论不成立。 24.1.3弧、弦、圆心角 知识点弦、弧、圆心角的关系(1)弦、弧、圆心角之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相 等,所对的弦也相等。 (2)在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余的各组量也相等。 (3)注意不能忽略同圆或等圆这个前提条件,如果丢掉这个条件,即使圆心角相等,所对的弧、弦也不一定相等,比如两个同心 圆中,两个圆心角相同,但此时弧、弦不一定相等。 24.1.4圆周角 知识点一圆周角定理
九年级数学第二十四章圆测试题(A ) 一、选择题(每小题3分,共33分) 1.(2005·资阳)若⊙O 所在平面内一点P 到⊙O 上的点的 最大距离为a ,最小距离为b (a>b ),则此圆的半径为( ) A .2b a + B .2 b a - C .2 2b a b a -+或 D .b a b a -+或 2.(2005·浙江)如图24—A —1,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,则弦AB 的长是( ) A .4 B .6 C .7 D .8 3.已知点O 为△ABC 的外心,若∠A=80°,则∠BOC 的度数为( ) A .40° B .80° C .160° D .120° 4.如图24—A —2,△ABC 内接于⊙O ,若∠A=40°,则∠OBC 的度数为( ) A .20° B .40° C .50° D .70° 图24—A
5.如图24—A —3,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( ) A .12个单位 B .10个单位 C .1个单位 D .15个单位 6.如图24—A —4,AB 为⊙O 的直径,点C 在⊙O 上,若∠B=60°,则∠A 等于( ) A .80° B .50° C .40° D .30° 7.如图24—A —5,P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B ,CD 切⊙O 于点E ,分别交PA 、PB 于点C 、D ,若PA=5,则△PCD 的周长为( ) A .5 B .7 C .8 D .10 8.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m ,母线长为3m ,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是( ) A .26m B .26m π C .212m D .212m π 9.如图24—A —6,两个同心圆,大圆的弦AB 与小圆相切 于点P ,大圆的弦CD 经过点P ,且CD=13,PC=4,则两圆 组成的圆环的面积是( ) A .16π B .36π C .52π D .81π
第11讲与圆有关的位置关系 知识定位 讲解用时:3分钟 A、适用范围:人教版初三,基础偏上 B、知识点概述:本讲义主要用于人教版初三新课,本节课我们首先学习与圆有 关的三类位置关系:点与圆的位置关系、直线与圆的位置关系以及圆与圆的位置关系,重点掌握各种与圆位置关系的判断方法,其次学习切线的有关性质与判定以及切线长定理及应用,能够结合已知题意证明相关切线,最后掌握圆的外接三角形与三角形内切圆概念。本节课的重点是三类位置关系的判断方法以及切线的性质与判定定理,属于中考重点内容,也是难点之一,希望同学们能够好好学习,扎实基础。 知识梳理 讲解用时:25分钟 与圆有关的位置关系 (1)点与圆的位置关系 点与圆的位置关系有3种,设⊙O的半径为r,点P到圆心的距离OP=d,则有: ⊙点P在圆外⊙d>r ⊙点P在圆上⊙d=r ⊙点P在圆内⊙d<r 注意: 点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆 心距离与半径的关系可以确定该点与圆的位置关系。
(2)直线与圆的位置关系 直线和圆的3种位置关系: ⊙相离:一条直线和圆没有公共点; ⊙相切:一条直线和圆只有一个公共点,这条直线叫圆的切线,唯一的公共点叫切点; ⊙相交:一条直线和圆有两个公共点,这条直线叫圆的割线; 判断直线和圆的位置关系: ⊙直线l和⊙O相交⊙d<r ⊙直线l和⊙O相切⊙d=r ⊙直线l和⊙O相离⊙d>r (3)圆与圆的位置关系 ⊙外离:两个圆没有公共点,并且每个圆上的点都在另一个圆的外部; ⊙外切:两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部; ⊙相交:两个圆有两个公共点; ⊙内切:两个圆有唯一公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部; ⊙内含:两个圆没有公共点,并且一个圆上的点都在另一个圆的内部。 判断圆和圆的位置关系: ⊙两圆外离⊙d>R+r; ⊙两圆外切⊙d=R+r; ⊙两圆相交⊙R﹣r<d<R+r(R≥r); ⊙两圆内切⊙d=R﹣r(R>r); ⊙两圆内含⊙d<R﹣r(R>r).
一、圆的综合真题与模拟题分类汇编(难题易错题) 1.如图,△ABC的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD于E,交AB于F,交⊙O于G. (1)判断直线PA与⊙O的位置关系,并说明理由; (2)求证:AG2=AF·AB; (3)若⊙O的直径为10,AC=25,AB=45,求△AFG的面积. 【答案】(1)PA与⊙O相切,理由见解析;(2)证明见解析;(3)3. 【解析】 试题分析:(1)连接CD,由AD为⊙O的直径,可得∠ACD=90°,由圆周角定理,证得∠B=∠D,由已知∠PAC=∠B,可证得DA⊥PA,继而可证得PA与⊙O相切. (2)连接BG,易证得△AFG∽△AGB,由相似三角形的对应边成比例,证得结论. (3)连接BD,由AG2=AF?AB,可求得AF的长,易证得△AEF∽△ABD,即可求得AE的长,继而可求得EF与EG的长,则可求得答案. 试题解析:解:(1)PA与⊙O相切.理由如下: 如答图1,连接CD, ∵AD为⊙O的直径,∴∠ACD=90°. ∴∠D+∠CAD=90°. ∵∠B=∠D,∠PAC=∠B,∴∠PAC=∠D. ∴∠PAC+∠CAD=90°,即DA⊥PA. ∵点A在圆上, ∴PA与⊙O相切.
(2)证明:如答图2,连接BG , ∵AD 为⊙O 的直径,CG ⊥AD ,∴AC AD =.∴∠AGF=∠ABG. ∵∠GAF=∠BAG ,∴△AGF ∽△ABG. ∴AG :AB=AF :AG. ∴AG 2=AF?AB. (3)如答图3,连接BD , ∵AD 是直径,∴∠ABD=90°. ∵AG 2=AF?AB ,55∴5 ∵CG ⊥AD ,∴∠AEF=∠ABD=90°. ∵∠EAF=∠BAD ,∴△AEF ∽△ABD. ∴ AE AF AB AD =545=,解得:AE=2. ∴221EF AF AE = -=. ∵224EG AG AE = -=,∴413FG EG EF =-=-=. ∴1132322 AFG S FG AE ?=??=??=.
1.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE?CA. (1)求证:BC=CD; (2)分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,若PB=OB,CD =,求DF的长. 2.如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K. (1)求证:KE=GE; (2)若=KD·GE,试判断AC与EF的位置关系,并说明理由; (3)在(2)的条件下,若sinE=,AK=,求FG的长.
3.如图,AB 是⊙O 的直径,点C 是⊙O 上一点,AD 与过点C 的切线垂直,垂足为点D ,直线DC 与AB 的延长线相交于点P ,弦CE 平分∠ACB ,交AB 于点F ,连接BE . (1)求证:AC 平分∠DAB ; (2)求证:△PCF 是等腰三角形; (3)若tan ∠ABC= 3 4,BE=72,求线段PC 的长. 4.
5.已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC,连结DE,DE=。 (1)求证:AM·MB=EM·MC;(2)求EM的长;(3)求sin∠EOB的值。 6.如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知 ∠EAT=30°,AE=3,MN=2. (1)求∠COB的度数; (2)求⊙O的半径R; (3)点F在⊙O上(是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
《圆》 一、圆的概念 概念:1、圆可以看作是到定点的距离等于定长的点的集合; 2、圆的外部:可以看作是到定点的距离大于定长的点的集合; 3、圆的内部:可以看作是到定点的距离小于定长的点的集合 轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆; (补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线); 3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线; 4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线; 5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。 二、点与圆的位置关系 1、点在圆内?d r ?点A在圆外; 三、直线与圆的位置关系 1、直线与圆相离?d r >?无交点; 2、直线与圆相切?d r =?有一个交点; 3、直线与圆相交?d r +; 外切(图2)?有一个交点?d R r =+; 相交(图3)?有两个交点?R r d R r -<<+; 内切(图4)?有一个交点?d R r =-; 内含(图5)?无交点?d R r <-; A
r R d 图3 r R d 五、垂径定理 垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。 推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即: ①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。 推论2:圆的两条平行弦所夹的弧相等。 即:在⊙O 中,∵AB ∥CD ∴弧AC =弧BD 例题1、 基本概念 1.下面四个命题中正确的一个是( ) A .平分一条直径的弦必垂直于这条直径 B .平分一条弧的直线垂直于这条弧所对的弦 C .弦的垂线必过这条弦所在圆的圆心 D .在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心 2.下列命题中,正确的是( ). A .过弦的中点的直线平分弦所对的弧 B .过弦的中点的直线必过圆心 C .弦所对的两条弧的中点连线垂直平分弦,且过圆心 D .弦的垂线平分弦所对的弧 例题2、垂径定理 1、 在直径为52cm 的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大 深度为16cm ,那么油面宽度AB 是________cm. r R d 图4 r R d 图5 r R d O E D C A O C D A B
九年级数学第二十四章圆测试题(A) 时间:45分钟分数:100分 一、选择题(每小题3分,共33分) 1 .若O O所在平面内一点P到O O上的点的最大距离为10, A . 14 B . 6 C . 14 或6 D. 7 或3 2. 如图24—A —1 , O O的直径为10,圆心O到弦AB的距离 A . 4 B . 6 C . 7 I 3. 已知点O ABC的外心,若/ A=80 A . 40 4. 如图 A . 20° B . 80 24—A — 2, B . C. 160° △ ABC内接于O 最小距离为 OM的长为 4则此圆的半径为( 3,则弦AB 的长是 D . 8 ,则/ BOC的度数为( D. 120° 若/ A=40 °,则/ OBC的度数为( O 图24—A — 4 图24—A — 3 小明同学设计了一个测量圆直径的工具, 垂直,在测直径时,把O点靠在圆周上, A . 12个单位 B . 10个单位 6. 如图 A . 80° 7. 如图 PB于点 A . 5 24—A —4, AB为O O的直径,点 B. 50° C. 40 ° 24—A —5, P 为O O 外一点, 5 .如图24—A —3, 标有刻度的尺子OA、OB在O点钉在一起, 读得刻度OE=8个单位,OF=6个单位,则圆的直径为( D . 15个单位 ,则/ A等于() 并使它们保持 ) PA 、 C、D,若PA=5,则△ PCD的周长为( B . 7 C . 8 D . 10 C . 1个单位 C 在O O 上,若/ B=60 ° D . 30° PB分别切O O于A、B, ) CD切O O于点E,分别交PA、 &若粮仓顶部是圆锥形,且这个圆锥的底面直径为 毡,则这块油毡的面积是() 4m,母线长为3m,为防雨需在粮仓顶部铺上油 A . 6m2 C . 12m22 D . 12二 m 9.如图24—A —6,两个同心圆,大圆的弦AB 点P,且 CD=13 , PC=4,则两圆组成的圆环的面积是( A. 16 n B . 36 n 10 .已知在△ ABC中, 10 A . 3 11.如图 C、D E、 C. 52 n AB=AC=13 , 与小圆相切于点P,大圆的弦CD经过) D. 81 n BC=10,那么△ ABC的内切圆的半径为( 12 B . 5 24—A —7,两个半径都是4cm的圆外切于点C, 一只蚂蚁由点A开始依A、B、 F、C、G A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这 C. 2 径上不断爬行,直到行走2006 n cm后才停下来, A . D 点 B . E 点 C . F 点D 二、填空题(每小题3分,共30分) 12 .如图24—A —8,在O O中,弦AB等于O 则蚂蚁停的那一个点为( .G点 O的半径,0C丄AB交O O于点C,则 8段路 )
九年级数学第二十四章圆测试题(A ) 一、选择题(每小题3分,共33分) 1.(2005·资阳)若⊙O 所在平面内一点P 到⊙O 上的点的最大距离为a ,最小距离为b (a>b ),则此圆的半径为( ) A . 2b a + B .2b a - C .2 2b a b a -+或 D .b a b a -+或 2.(2005·浙江)如图24—A —1,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,则弦 AB 的长是( ) A .4 B .6 C .7 D .8 3.已知点O 为△ABC 的外心,若∠A=80°,则∠BOC 的度数为( ) A .40° B .80° C .160° D .120° 4.如图24—A —2,△ABC 内接于⊙O ,若∠A=40°,则∠OBC 的度数为( ) A .20° B .40° C .50° D .70° 5.如图24—A —3,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( ) A .12个单位 B .10个单位 C .1个单位 D .15个单位 6.如图24—A —4,AB 为⊙O 的直径,点C 在⊙O 上,若∠B=60°,则∠A 等于( ) A .80° B .50° C .40° D .30° 7.如图24—A —5,P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B ,CD 切⊙O 于点E ,分别交PA 、PB 于点C 、D ,若PA=5,则△PCD 的周长为( ) A .5 B .7 C .8 D .10 8.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m ,母线长为3m ,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是( ) A .2 6m B .2 6m π C .2 12m D .2 12m π 9.如图24—A —6,两个同心圆,大圆的弦AB 与小圆相切于点P ,大圆的弦CD 经过点P ,且CD=13,PC=4,则两圆组成的圆环的面积是( ) A .16π B .36π C .52π D .81π 10.已知在△ABC 中,AB=AC=13,BC=10,那么△ABC 的内切圆的半径为( ) A .310 B .5 12 C .2 D . 3 图24—A — 5 图24—A — 6 图24—A — 1 图24—A — 2 图24—A — 3 图24—A —4
四点共圆(一) 模块一辅助圆思想 模块二四点共圆的判定(一)
模块一:辅助圆思想 平面几何中有很多题目的背景中并没有出现圆,但是如果能够适当添加辅助圆,能让题目解起来变得十分简单,因此,辅助圆思想是学习四点共圆的基础.
则 OC __________ (2)如图 2-2,在 △ ABC 中, ?ACB 90?, AC= BC ,点 P 为△ABC 外一点( P 与 C 在直线 AB 异侧),且 ?APB 45?.设点 P 关于 AB 的对称点为 E ,连接 PE 、CE ,试判定线段 AB 与 CE 的数 量关系,并给予证明. 1)如图 1-1,四边形 ABCD 中, AB AC BAC ___________ . AD ,若 CAD 76 , BDC 13 ,则 CBD 2)如图 1-2,已知四边形 ABCD ,AB//CD ,AB AC AD a , BC b ,且 2a b ,求 BD 的值. 1)如图 2-1,平面上有四个点 A 、O 、B 、C ,其中 AOB 120 , ACB 60 ,AO BO ,AB 2 3 , D 图 1-1 图 2-1 E
例题3 如图,E,B,A,F 四点共线,点 D 是等边三角形ABC的边AC的中点,点P是直线AB 上异于A,B 的一个动点,且满足CPD 30 ,则( A.点B.点 P 一定在射线P一定在线段BE 上AB 上 例题 4 如图,AB 是⊙O 的直径,CD 是弦,且CD 线于F.求证:E、F、B、K 四点共 AB于K.E为劣弧AC 上的一点,连接AE交DC延长AB 上 AB 上