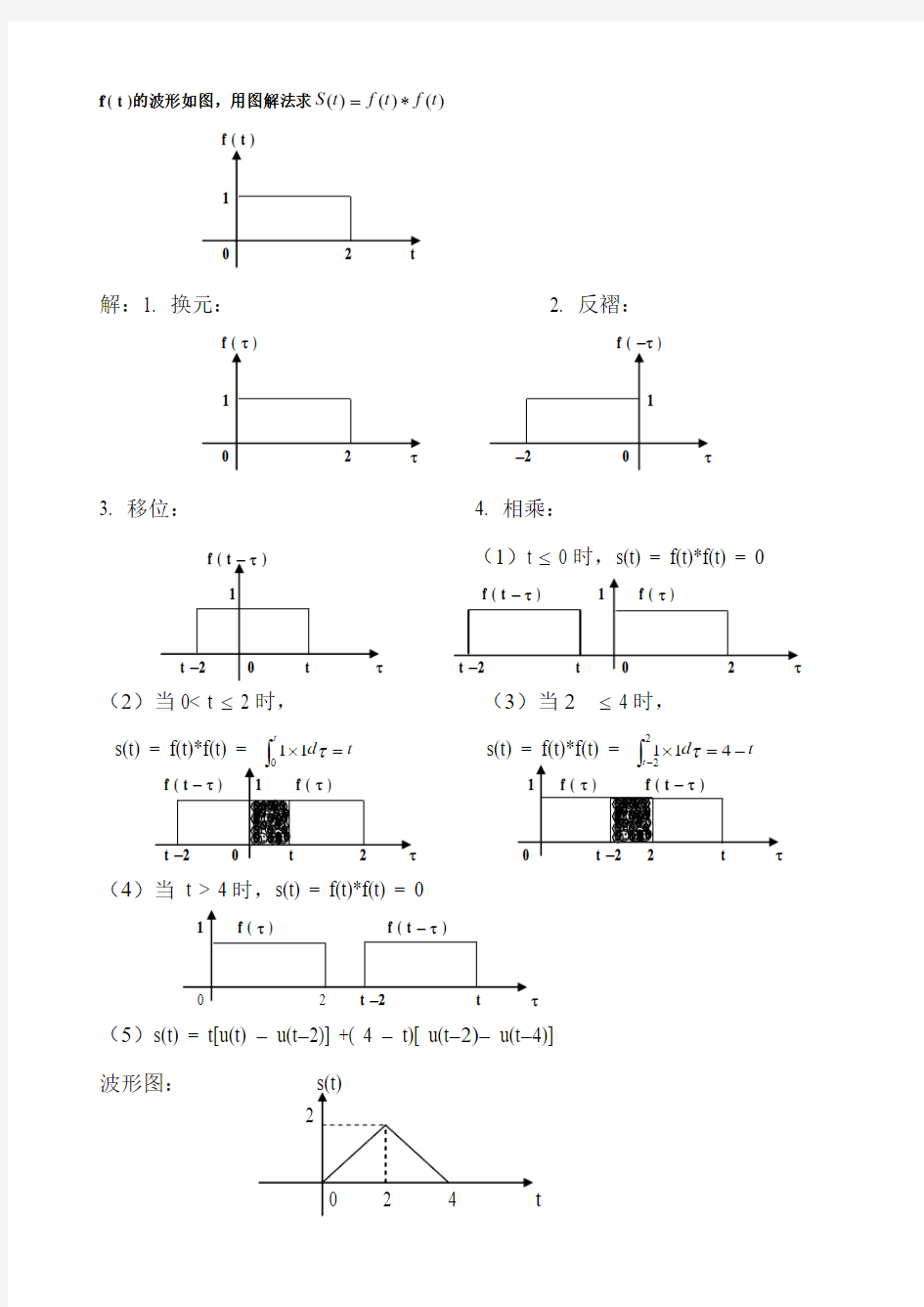
f ( t )的波形如图,用图解法求)()()(t f t f t S *=
f ( t )
1
0 2 t
解:1. 换元: 2. 反褶: f ( τ ) f ( -τ )
1 1
0 2 τ -2 0 τ
3. 移位:
4. 相乘: f ( t - τ ) (1)t ≤ 0时,s(t) = f(t)*f(t) = 0
1 f ( t - τ ) 1 f ( τ )
t -2 0 t τ t -2 t 0 2 τ
(2)当0< t ≤ 2时, (3)当2 2τ f ( t - τ ) 1 f ( τ ) 1 f ( τ ) f ( t - τ ) t -2 0 t 2 τ 0 t -2 2 t τ (4)当 t > 4时,s(t) = f(t)*f(t) = 0 1 f ( τ ) f ( t - τ ) 0 2 t -2 t τ (5)s(t) = t[u(t) - u(t -2)] +( 4 - t)[ u(t -2)- u(t -4)] 波形图: s(t) 2 0 2 4 t 已知x1(n)={2,3,2},x2(n)={1,2,3,4}(1)求出x2(m-n),当m=0,1,2,3时的序列;(2)计算出x1(n)与x2(n)的卷积;(3)用频域方法算出x1(n)与x2(n)的卷积 解:(1)m=0时,x(m-n)=x(-n) , x(-0)=x(-0+4)=1;x(-1)=x(-1+4)=4;x(-2)=3;x(-3)=2; 故x(-n)={1,4,3,2} 同理m=1时;x(m-n)=x(1-n)={2,1,4,3} 同理m=2时;x(m-n)=x(2-n)={3,2,1,4} 同理m=3时;x(m-n)=x(3-n)={4,3,2.1} (2)m=0时 3 =∑[{2,3,2,0}*{1,4,3,2}]=∑{2,12,6,0}=20 n=0 m=1时 3 =∑[{2,3,2,0}*{2,1,4,3}]=∑{4,3,8,0}=15 n=0 m=2时 3 =∑[{2,3,2,0}*{3,2,1,4}]=∑{6,6,2,0}=14 n=0 m=3时 3 =∑[{2,3,2,0}*{4,3,2.1}]=∑{8,9,4,0}=21 n=0 (3) x1(n)={2,3,2=}==> X1(k)={6, -2-2j, 2, 2j-2} x2(n)={1,2,3,4}==>X2(k)={10,-2+2j,-2,-2-2j} X1(k)?X2(k)={60, 8,- 4, 8} 令Y(k)=X1(k)·X2(k) y(n)=x1(n)x2(n) IDFT后 3 3 y(n)=(1/N )∑Y(k)e^(j(2π/4)kn)=(1/N )∑Y(k)(-j)^(kn) k=0 k=0 ={ 18,16,10,21} 卷积运算 信号的卷积运算是信号处理领域中最重要的运算之一。随着对信号与系统理论研究的深入,特别是计算机技术的不断发展,不仅使卷积方法在很我领域得到了很广泛的应用,而且卷积运算的逆运算---反卷积的问题也受到了越来越大的重视和应用。 比如,在语音识别、地震勘探、超声诊断、光学成像、系统辨识及其他诸多信号处理领域中,甚至可以说卷积与反卷积的问题无处不在,而且很多的问题,都是有待深入研究的课题。 所以,大家要切实理解和掌握好卷积分运算的各个方面,打好牢固的基础。下面,我们来看看卷积的定义是怎样的。 信号的卷积积分(简称卷积),定义为: 简记为,其中的星号是卷积运算符。注意不要与我们在编写计算机程序时所用的乘法的表示符号搞混了。在信号处理课程里,乘法往往是用居中的点来表示的,或者干脆不写居中的点,而直接将要进行乘积运算的信号(包括直流信号---它是一个常数)连在一起写。 信号的卷积运算对应着一定的物理背景,这要在我们进一步学习了关于系统的激励与响应的关系之后,才能更深入地理解。 不仅如此,信号的卷积运算还对应着一定的几何解释。从定义式我们可以看出:(1) 在积分式中,信号自变量改变了符号,这对应在几何波形上,就是将信号进行了反褶变换;(2) 并且,信号f2的波形 位置与积分变量的取值有关,积分变量在积分限内的不断变化,将导致信号的波形发生移动,即是对它不断进行平移操作;(3) 最后,每当信号处在一个新位置,都要与信号f1相乘,且依据积分的定义,要将这些乘积加起来,而其结果实际上对应着两信号波形相交部分的面积。所以,卷积运算可以用几何图解方式来直观求解。 下面我们来说明如何用它的几何意义来求解两信号的卷积。 将信号的自变量改为,信号变为。对任意给定的,卷积的计算过程为: (a) 将关于r进行反褶得到; (b) 再平移至t0得到; (c) 与相乘得到; (d) 对r进行积分得,即; 不断变化,就可以得到s(t)。时域和频域法计算4点卷积
卷积运算