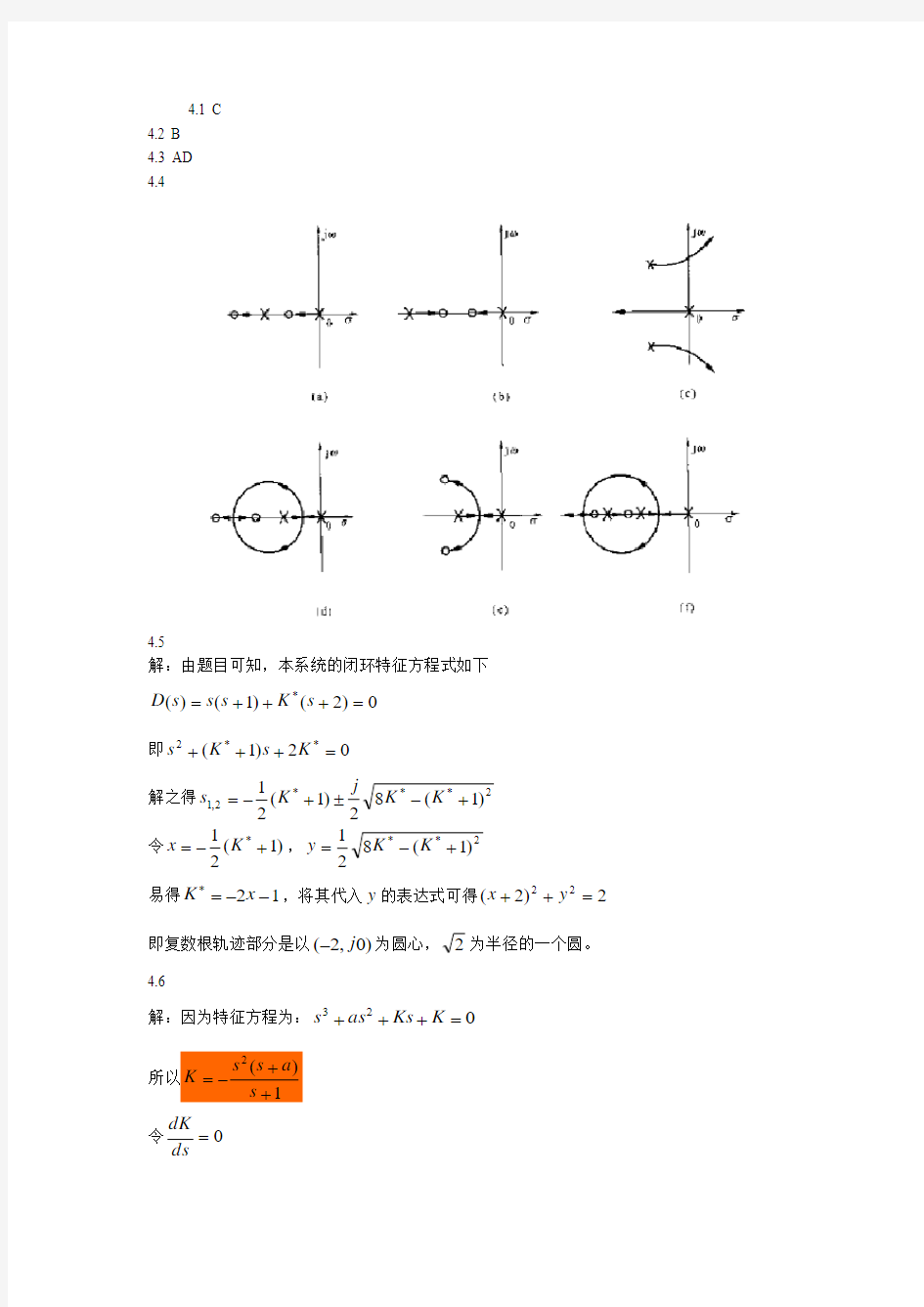
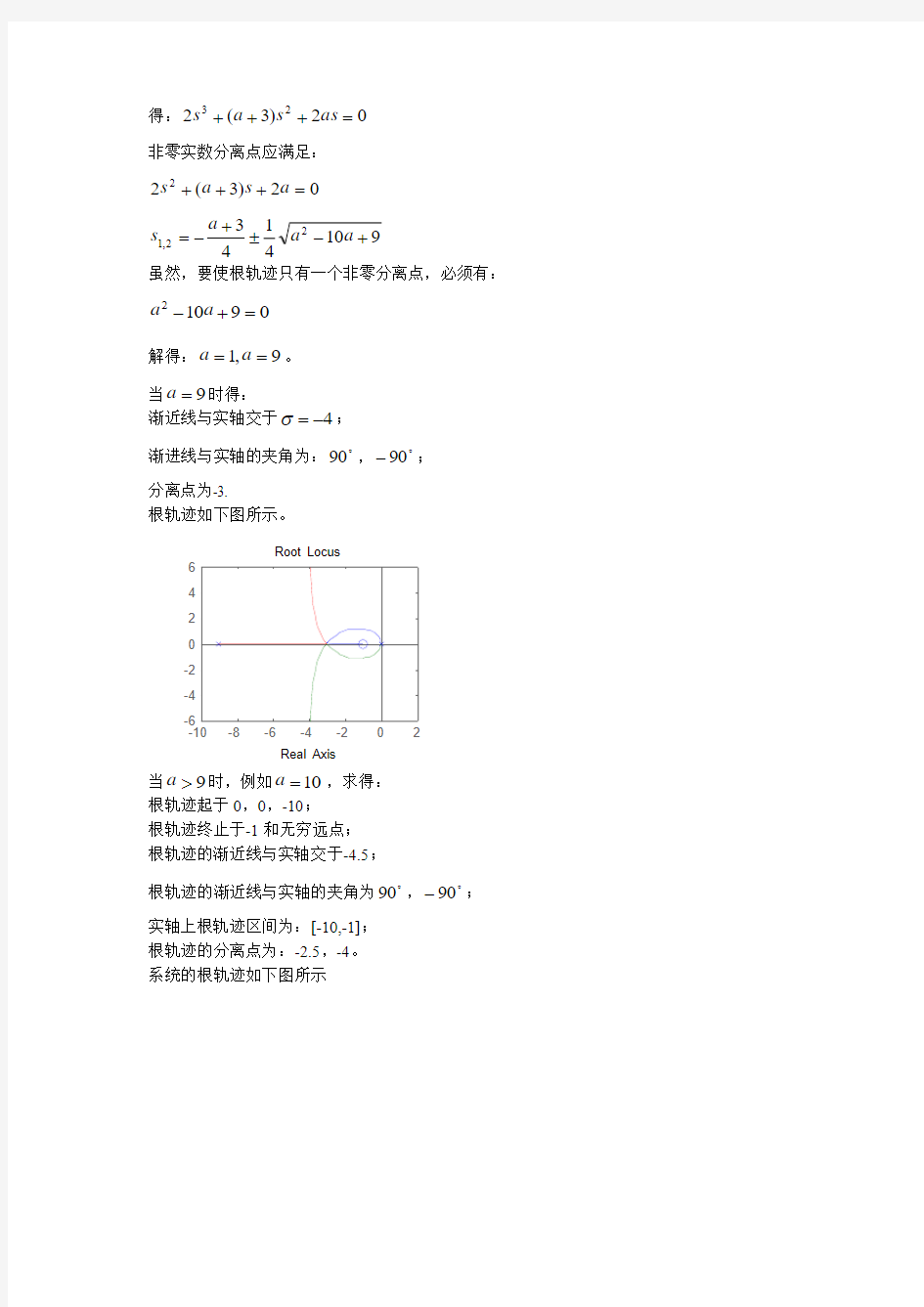
解:先列出系统)258()
256()(2
2++++=s s s s s K s G 的幅值条件如下
1)
258()
256(22=++++s s s s s K 当9.0=K 时利用试凑法可得:101-=s 满足次幅值条件。 系统的闭环特征方程式为:
05.1724.669.14)256(9.6)258()(2322=+++=+++++=s s s s s s s s s D
又已知10-=s 为特征方程式的一个跟,则可得
0)179.4)(10()(2=+++=s s s s D
解之得:j s 1145.23,2±-=
所以,系统的闭环特征根为101-=s ,j s 1145.23,2±-=。 4.11
解:开环传递函数)
2)(1()
1(6)()(+++=
s s s ks s H s G
特征方程式为:
1)
2)(1()
1(6=+++s s s ks
整理后的特征方程式为:
16
)2)(1(6)(1-=+++=
s s s ks
s G
此特征方程式的根轨迹,由)(1s G 的极点出发,其极点是
1)
2)(1(6
-=++s s s 的根。因此,
)(1s G 的根轨迹由)
2)(1()(++=
s s s K
s G 的根轨迹(见图)在6=K 时对应点出发。
由图可知,出发点为j 4.1±与-3. )(1s G 的根轨迹分成3条,其中一条朝向坐标原点,其余2条趋向去穷远处。其渐进线为:5.11
34.14.13-=--+-=j
j a σ, 270,90=a ?。
根据以上分析可得根轨迹如图所示。
4.12
解:由图知,该系统是一个正反馈控制系统,其根轨迹为零度根轨迹。该系统的开环传递函数为
2
2
*)
2()1()()(++=s s K s H s G 根据绘制零度根轨迹图的法则可得 (1)2=n ,即根轨迹有2条分支;
(2)2条根轨迹的起点分别为:21-=p ,22-=p ;2条根轨迹的终点分别为:11-=z ,
12-=z ;
(3)实轴上的根轨迹为),1[],1,2[],2,(∞-----∞。 根据以上分析,可以绘制该系统的零度根轨迹如图所示。
4.13
解:闭环系统特征方程为:
1()()0G s H s +=
因为()1H s =,则1()0G s +=,3
2
320Ts s s +++= 等效的开环传递函数为
3
2()32
Ts G s s s '=++
则开环零点有3个:1230z z z ===,开环极点有2个:121,2p p =-=-。 根据根轨迹的规则,可知:
(1)2,3n m ==,有3条根轨迹。起始于开环有限极点1p ,2p 和无限远极点,终于开环零点1z ,2z 和3z ,实轴上的根轨迹为[1,0]-和(,2]-∞- (2)求分离点坐标d
11
312d d d
+=++
由上式解得:13d =-,23d =-
(3)求与虚轴的交点 闭环系统的特征方程为
32320Ts s s +++=
将s j ω=
代入,解得:ω= 1.5T =。
-5
-4-3-2-101
-3-2-1012
3Root Locus
Real Axis
I m a g i n a r y A x i s
4.14
解:(1)由于本题给出的开环传递函数()G s 并非标准型,故需写出等效的开环传递函数,由题意,已知单位负反馈系统的开环传递函数()G s ,可得到系统的闭环特征方程为:
1()0G s +=
整理后得:
22(44)40K s s s s -+++=
两边同时除以2
4s s +,得系统的等效开环传递函数为
2
(2)()(4)
K s G s s s -'=+
则开环零点有2个:122z z ==,开环极点有2个:124,0p p =-=。 根据根轨迹的规则,可知:
(1)2,2n m ==,有2条根轨迹。起始于开环有限极点1p 和2p ,终于开环零点1z 和2z ,实轴上的根轨迹为[4,0]- (2)求分离点坐标d
1111
422
d d d d +=+
+++
由上式解得:1d =-
由根轨迹的幅值条件,可得分离点对应的根轨迹增益为2
1(4)1
(2)3
d s s s K s =-+==- (3)求与虚轴的交点 闭环系统的特征方程为
2(1)(44)40K s K s K ++-+=,列出劳斯矩阵如下
2s 1K + 4K 1s 44K - 0 0s 4K 0
当1K =时,有全零解,即1K =时,根轨迹与虚轴相交,将1K =代入全零行的上一行,
得2
40s +=
,解出交点为s =
-4
-3-2-1012
Root Locus
Real Axis
I m a g i n a r y A x i s
(2)由%0σ>,得系统为欠阻尼系统,根据欠阻尼系统的瞬态性能指标
%100%e
σ=?,
可得:当% 4.32%σ=时,0.707ζ=,阻尼角0
arccos 45βζ==,由0% 4.32%σ<<,阻尼角4590β<<,
由2(2)s t s ≤?=得:
4
2s n
t ζω≈<,即2n ζω>,
由于系统的特征值为1,2n p j ζωω=-±2s t <,即要求系统的共轭特征根
的实部<-2,而根轨迹的分离点在1s =-处,故不能同时满足0% 4.32%δ<<,
2(2)s t s ≤?=的要求。
4.15
解(1)取s
z s z s s K )
)(()(21++=
,则系统的开环传递函数为
)
1()
)(()()(221+++=
s s z s z s s K s G (Ⅰ型),且闭环系统稳定
所以,系统跟踪斜坡参考输入信号)(s R 时,=ssR e 常值; (2)因为0=ssN e ,所以)(s N 为阶跃信号; (3))
1()
)(()()(221+++=
s s z s z s k s K s G
已知:34.485.52,1j s ±-=?
180)()(2,12,1-=∠s K s G 若取11=z
则
180)()()()(211112111-=+∠-+∠-∠-+∠++∠p s p s s z s z s
42=z
(4)65.1272
.451.674
.692.728.7)
)(()
1()(34.485.52121=???=
+++=
+-=j
s z s z s s s s K
设另一个闭环极点为3p 则
4165.12)34.485.5)(34.485.5(3??=--+-p j j
95.03=p
因为???-=--=-95.013
1p z ?可构成一对闭环偶极子,3p 可忽略。
所以34.485.52,1j s ±-=是一对主导极点 简化后的闭环传函为:
53
7.11)
4(22.13)34.485.5)(34.485.5)(95.0()4)(1(56.12)(2+++=-++++++=
s s s j s j s s s s s K
4.16
解num=[1,2,4];den=conv([1,0],conv([1,4],conv([1,6],[1,1.4,1]))); rlocus(num,den),axis([-10,2,-6,6]); [K,poles]=rlocfind(num,den)
-10
-8
-6
-4-2
2
-6-4-2024
6Root Locus
Real Axis
I m a g i n a r y A x i s
Select a point in the graphics window selected_point = 0.0000 +1.2115i K=
15.5589 poles =
0.0000 + 1.2115i 0.0000 – 1.2115i
使用同样的方法可得相应的与虚轴交点的值 [K,poles]=rlocfind(num,den);
Select a point in the graphics window selected_point = 0.0000 +2.1545i K=
67.7351 poles =
0.0000 +2.1545i 0.0000 –2.1545i
[K,poles]=rlocfind(num,den);
Select a point in the graphics window selected_point = 0.0000 +3.7538i K=
1.6345e+002 poles =
0.0000 + 3.7538i 0.0000 –3.7538i
参看根轨迹图可知,系统稳定性范围是5589.15*
<解num=1;den=conv([1,0],conv([1,4],conv([1,0,4],conv([1,4,8],[1,8,20])))); rlocus(num,den),axis([-6,2,-4,4]);
-6
-4-202
-4-2
2
4
Root Locus
Real Axis
I m a g i n a r y A x i s
num0=1000;den0=conv([1,0],conv([1,4],conv([1,0,4],conv([1,4,8],[1,8,20])))); [numc,denc]=cloop(num0,den0); t=0:0.1:50;
[y,x,t]=step(numc,denc,t); plot(t,y)
M=((max(y)-1)/1)*100;
disp(['最大超调量M=' num2str(M) '%'])
010********
0.5
1
1.5
最大超调量M=11.1368% 4.18
解:系统的开环传递函数为:
)
5()
1(10)5()1()()(22++=++=
s s ks s s ks K s H s G
整理后得等效开环传递函数为:
10
510)()(2
3++=
''s s ks
s H s G (1)MATLAB 程序如下: num=[10,0];den= [1,5,0,10]; rlocus(num,den)
-6
-5
-4
-3
-2
-1
1
-15-10-50510
15Root Locus
Real Axis
I m a g i n a r y A x i s
(2)当1=k 时,系统(a )的闭环传递函数为 num0=[100,10];den0=conv([1,0],conv([1,0],[1,5])); [numa,dena]=cloop(num0,den0) printsys(numa,dena) 执行结果为: num/den =
100 s + 10 ------------------------ s^3 + 5 s^2 + 100 s + 10 系统(a )的闭环极点为 sa=roots(dena) 执行结果为: sa =
-2.4498 + 9.6699i -2.4498 - 9.6699i -0.1005
即系统(a)的闭环极点为:1005.01-=s ,j s 6699.94498.23,2±-= 系统(b )的闭环传递函数为
numg=10;deng= conv([1,0],conv([1,0],[1,5])); numh=[1,1];denh=[0,1];
[numb,denb]=feedback(numg,deng,numh,denh) printsys(numb,denb) 执行结果为: num/den =
10 ----------------------- s^3 + 5 s^2 + 10 s + 10 sb=roots(denb)
执行结果为: sb =
-2.6506 -1.1747 + 1.5469i -1.1747 - 1.5469i
即系统(b)的闭环极点为:6506.21-=s ,j s 5469.11747.13,2±-= t=0:0.1:10;
[ya,xa,t]=step(numa,dena,t); [yb,xb,t]=step(numb,denb,t); plot(t,ya,t,yb)
执行结果如图所示:
0246810
0.5
1
1.5
其中,a 为a 系统的阶跃响应曲线,b 为b 系统的阶跃响应曲线。
通过上图可以看出:a 系统的阶跃响应上升时间小,超调量大,b 系统的阶跃响应上升时间较按系统大,但超调量小