2012高考二轮复习专题限时集训:数学(文)第17讲 概率统计1
- 格式:doc
- 大小:502.05 KB
- 文档页数:12

2012高考数学二轮模拟新题分类汇编--专题六-概率统计、算法、复数概率统计、算法、复数1.(2012唐山市高三上学期期末统一考试文)复数1(1)(1)i i-+= ( )A .2iB .-2iC .2D .-2 2.(2012江西师大附中高三下学期开学考卷文)设复数113iz=-,232iz=-,则21z z 在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限。
3. (2012三明市普通高中高三上学期联考文)已知i 是虚数单位,则(1)i i -= A .1i --B .1i -+C .1i +D .1i -4.(2012三明市普通高中高三上学期联考文)在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其它10个小长方形的面积和的14,且样本容量为160,则中间一组的频数为A .32B .0.2C .40D .0.255.(2012年石家庄市高中毕业班教学质检1文)阅读如图所示的程序框图,输出的S 值为 A .0 B .21+ C .221+D .12-6.(2012唐山市高三上学期期末统一考试文)执行右面的程序框图,如果输出的是341a =,那么判断框( ) A .4?k < B .5?k < C .6?k < D .7?k <7.(2012黄冈市高三上学期期末考试文)复数121ii ++(i 是虚数单位)的虚部是( ) A .1B .3C .12D .32 8.(2012金华十校高三上学期期末联考文)复数31x i z i+=-(,x R i ∈是虚数单位)是实数,则x 的值( ) A .2 450 B .2 550 C .5 050 D .4 90013.(2012武昌区高三年级元月调研文)通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:由22()()()()()n ad bc K a b c d a c b d -=++++,算得22110(40302020)~7.8.60506050K ⨯⨯-⨯=≈⨯⨯⨯附表:参照附表,得到的正确结论是( ) A .有99%以上的把握认为“选择过马路的方式与性别有关”B .有99%以上的把握认为“选择过马路的方式与性别无关”C.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”D.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”14. (2012年西安市高三年级第一次质检文)复数的实部是A.-1B. 1C.OD. -215.(2012年西安市高三年级第一次质检文)执行如图所示的程序框图,输出的s值为A. -3B.C. D. 216. (2012年西安市高三年级第一次质检文)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:则以上两组数据的方差中较小的一个为,则=A. B. C. D.217. (2012•粤西北九校联考理) 已知Ω=+≤≥≥,{(,)|4,0,20}x y x y x y{(,)|6,0,0}=≤≥-≥,若向区域Ω上A x y x y x y开10n S ==, S p<? 是 输入p结输出n12n S S -=+ 否1n n =+随机投一点P ,则点P 落入区域A 的概率为( )A .31 B .32 C .91D .9218. (2012•粤西北九校联考理)执行如图的程序框图,若输出的n =5,则输入整数p 的最小值是( ) A .6 B.7 C.8 D.15(第7题图)19.(2012•宁德质检理)运行如右所示的程序框图,输入下列四个函数,则可以输出的函数是( ) A .2()f x x = B .()cos 2f x x = C .()xf x e = D .()sin f x x π=20.(2012•韶关第一次调研理)在复平面内,复数311i i+-对应的点位于 ( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限21(2012•韶关第一次调研理)执行如图的程序框图,那么输出S 的值是( )A .1-B .12C .1D .222(2012•韶关第一次调研理)某班50名学生在一次百米测试中,成绩全部介于13秒与18秒 之间,将测试结果分成五组:每一组[13,14);第二组[14,15),…,第五组[]17,18.右图是按上述分组方法得到的频率分布直方图若成绩大于或等于14秒且小于16秒认为良好,则该班在这次百米测试中成绩良好的人数是__________. 23.(2012•深圳中学期末理)在右图的程序框图中,输出的s 的值为 ( )A . 12B . 14C . 15D . 2024(2012•黑龙江绥化市一模理)已知复数2(1)(2)z a a i=-+-,(a R ∈),则“1a =”是“z 为纯虚数”的( )A .充分非必要条件 B. 必要非充分条件 C.开s=0 i=5 s=s i=i结i<1 输是 否充要条件 D. 非充分非必要条件25.(2012•黑龙江绥化市一模理)输入ln0.8a =,12b e =,2ec -=,经过下列程序运算后,输出a ,b 的值分别是( )?b a >?c a >?c b >是是是x a=a b =b x=x a =a c =c x=x b=b c =c x=否否否,,a b c输出,,a b c输入开始结束ABC1B 1A 1C26.(2012• 浙江瑞安期末质检理)右图是一算法的程序框图,若输出结果为720=S ,则在判断框中应填入的条件是( ▲ )A .?6≤kB .?7≤kC .8?k ≤D .9?k ≤27(2012• 浙江瑞安期末质检理)设复数z 满足ii z 46)32(+=-,则z = ▲ .【答案】i 228(2012•延吉市质检理)某程序框图如图所示,该程序运行后输出的S 为 ( ) A .2 B .12- C .3- D .1329.(2012浙江宁波市期末文)已知i 为虚数单位,则=+31i i( )(A)(B)i-1(C)i 2 (D)i2-30(2012浙江宁波市期末文)200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60km/h 的汽车数量为( ) (A )65辆 (B )76辆(C )88 辆 (D )辆95 31(2012浙江宁波市期末文)执行如右图所示的程序框图,其输出的结果是 . 32(2012安徽省合肥市质检文)复数11z i=-(i 为虚数单位)的共轭复数z 是( )A .1-iB .1+iC .1122i +D .1122i -33.(2012安徽省合肥市质检文)在正四面体的6条棱中随机抽取2条,则其2条棱互相垂直的概率为 ( ) A .34B .23C .15D .1334.(2012安徽省合肥市质检文)如图所示的程序框图运行的结果是 ( )A .20112012B .20122013C .12012D .1201335.(2012吉林市期末质检文)某地区教育主管部门为了对该地区模拟考试成绩进行分析,抽取了总成绩介于350 分到650分之间的名学生成绩,并 根据这10000名学生的总成绩画了样本的频率分布直方图(如右图),则总成绩在 [400,500)内共有350 400 450 500 550 600 6500.0010.0020.003 0.004频率/组距 总成绩 (分)A. 5000 人B. 4500人C. 3250人D. 2500人36.(2012吉林市期末质检文)执行如图所示的程序框图,输出的M的值为A.17B.53C.161D.485;37.(2012江西南昌市调研文)集合M={4,-3m+(m-3)i} (其中i为虚数单位),N={-9,3},若M∩N≠∅,则实数m的值为()A.-1 B.-3 C.3或-3 D.3【答案】D【解析】由题可知3(3)m m i-+-必为实数,则3m=,检验符合题意。

绝密★启用前2012届高三数学二轮精品专题卷:专题8 概率与统计考试范围:概率与统计一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.要完成下列两项调查:①从某肉联厂的火腿肠生产线上抽取1000根火腿肠进行“瘦肉精”检测;②从某中学的15名艺术特长生中选出3人调查学习负担情况.适合采用的抽样方法依次为 ( ) A .①用分层抽样,②用简单随机抽样 B .①用系统抽样,②用简单随机抽样 C .①②都用系统抽样 D .①②都用简单随机抽样2.将一个骰子抛掷1次,设事件A 表示向上的一面出现偶数,事件B 表示向上的一面出现的点数不超过3,事件C 表示向上的一面出现的点数不小于4,则 ( ) A .A 与B 是互斥而非对立事件 B .A 与B 是对立事件 C .B 与C 是互斥而非对立事件 D .B 与C 是对立事件3.要从编号为01~50的50枚最新研制的某型号导弹中随机抽取5枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定,则选取的5枚导弹的编号可能是 ( ) A .05,10,15,20,25 B .03,13,23,33,43 C .01,02,03,04,05 D .02,04,08,16,324.(理)2011年3月17日上午,日本自卫队选派了两架直升飞机对福岛第一核电站3号机组的染料池进行了4次注水.如果直升飞机有A 、B 、C 、D 四架供选,飞行员有甲、乙、丙、丁四人供选,且一架直升飞机只安排一名飞行员,则选出两名飞行员驾驶两架直升飞机的不同方法数为 ( ) A .18 B .36 C .72 D .108(文)两根相距3m 的木杆上系一根拉直的绳子,并在绳子上挂一伦敦奥运会吉祥物“温洛克”,则“温洛克”与两端距离都大于1m 的概率为 ( )A .21B .31C .41D .325.(理)道路安全交通法规定,驾驶员血液酒精含量在20~80mg /100ml ,属酒后驾车,血液酒精含量在80mg /100ml 以上时,属醉酒驾车,2011年6月1日7:00至22:30,某地查处酒后驾车和醉酒驾车共50起,如图是对这50人的血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数大约为 ( )A .9B .10C .11D .12(文)某农科所研制成功一种产量较高的农作物种子,并对该作物种子在相同条件下发芽与否进行了试验,试验结果如下表,则其发芽的概率大约为 ( )种子粒数 2 5 10 70 130 310 700 1500 2000 3000 发芽粒数 2 4 9 60 116 282 639 1339 1806 2715A .1B .0.7C .0.8D .0.96.(理)某堂训练课上,一射击运动员对同一目标独立地进行了四次射击,已知他至少命中一次的概率为8165,则四次射击中,他命中2次的概率为 ( )A .814B .818C .278 D .以上都不对(文)2011年4月28日,世界园艺博览会(以下简称世园会)在西安顺利开幕,吸引了海内外的大批游客.游客甲、游客乙暑假期间去西安看世园会的概率分别为31、41,假定他们两人的行动相互不受影响,则暑假期间游客甲、游客乙两人都不去西安看世园会的概率为 ( )A .21B .127C .1211D .327.2011年6月,台湾爆出了食品添加有毒塑化剂的案件,令世人震惊.我国某研究所为此开发了一种用来检测塑化剂的新试剂,把500组添加了该试剂的食品与另外500组未添加该试剂的食品作比较,提出假设0H :“这种试剂不能起到检测出塑化剂的作用”,并计算出()01.0635.62≈≥x P .对此,四名同学做出了以下的判断:p :有99%的把握认为“这种试剂能起到检测出塑化剂的作用” q :随意抽出一组食品,它有99%的可能性添加了塑化剂r:这种试剂能检测出塑化剂的有效率为99%s:这种试剂能检测出塑化剂的有效率为1%则下列命题中正确的是()A.p∧q B.﹁p∧q C.(﹁p∧﹁q)∧(r∨s)D.(p∨﹁r)∧(﹁q∨s)8.日本福岛核电站爆炸后,工作人员随机测量了甲、乙两个城镇空气中核辐射的含量,获得的数据如茎叶图所示,则对甲、乙两个城镇的空气质量评价正确的是()A.甲城镇的空气质量优于乙城镇的空气质量B.乙城镇的空气质量优于甲城镇的空气质量C.甲、乙两城镇的空气质量差不多D.无法比较9.给出以下三幅统计图及四个命题:①从折线统计图能看出世界人口的变化情况②2050年非洲人口大约将达到近15亿③2050年亚洲人口比其他各洲人口的总和还要多④从1957年到2050年各洲中北美洲人口增长速度最慢其中正确的个数是()A.1 B.2 C.3 D.410.(理)如图,设D是图中边长为4的正方形区域,E是D内函数y = x2图像上方的点构成的区域(阴影部分).在D内随机取一点,则该点在E中的概率为()(1)31B.41C.32D.21(文)已知函数()xaxf3cosπ=,a等于抛掷一颗骰子得到的点数,则()x fy=在[]4,0上有5个以下或6个以上零点的概率是()A.31B.32C.21D.65二、填空题(本大题共5小题;每小题5分,共25分.将答案填在题中的横线上)11.2011年“两会”期间,某大学组织全体师生,以调查表的形式对温总理的政府工作报告进行讨论.为及时分析讨论结果,该大学从所回收的调查表中,采用分层抽样的方法抽取了300份进行分析.若回收的调查表中,来自于退休教职工、在职教职工、学生的份数之比为3:7:40,则所抽取的调查表中来自于退休教职工的有份. 12.(理)在某项测量中,测量结果x(单位:mm )服从正态分布)2,(2μN且正态分布的密度曲线如图所示,则x在[]3,1-内取值的概率为.(其中:841.0)1(=Φ)(文)小明同学学完统计知识后,随机调查了他所在辖区若干居民的年龄,将调查数据绘制成如图所示的扇形和条形统计图,则ba-= .(60以上含60)12题(文)12题(理)13.(理)若()5cos x +ϕ的展开式中3x 的系数为2,则=⎪⎭⎫ ⎝⎛-ϕπ223sin .(文)某城市供电局为了了解用电量)(度y 与气温)(C x之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:气温(℃)学科网ZXXK] 18 13 10 -1用电量(度) 24 34 38 64 由表中数据,得线性回归方程a x y +-=2.当气温为4-℃时,预测用电量的度数约为 . (1)把容量为100的某组样本数据分为10组,其分组情况及频率如下:[)40,20:0.1;[)60,40:0.25;[)80,60:0.45;[)100,80:0.20.若同一组数据用该组区间的中点(例如:区间[)40,20的中点值为30)表示,则这100个数据的平均值为 . 15.把一颗骰子投掷两次,第一次得到的点数记为a ,第二次得到的点数记为b ,以a 、b 为系数得到直线31=+by ax l :,又已知直线22:2=+y x l ,则直线1l 与2l 相交的概率为 . 三、解答题(本大题共6小题;共75分.解答应写出文字说明、证明过程或演算步骤) 16.(本小题满分12分)在甲、乙两个箱子中分别装有标号为1、2、3、4的四张卡片,现从甲、乙两个箱子中各取出1张卡片,每张卡片被取出的可能性相等. (1)求取出的两张卡片上标号恰好相同的概率;(2)求取出的两张卡片上的标号至少有一个大于2的概率. 17.(本小题满分12分)2011年2月始发生的利比亚内战引起了全球人民的关注,联合国为此多次召开紧急会议讨论应对措施.在某次分组研讨会上,某组有6名代表参加,B A 、两名代表来自亚洲,D C 、两名代表来自北美洲,E 、F 两名代表来自非洲,小组讨论后将随机选出两名代表发言. (1)代表A 不被选中的概率是多少? (2)(理)记选出的两名代表中来自于北美洲或非洲的人数为X ,求X 的分布列及期望. (文)选出的两名代表“恰有1名来自北美洲或2名都来自非洲”的概率是多少? 18.(本小题满分12分)一机器可以按各种不同速度转动,其生产的产品有一些会有缺陷,每小时生产有缺陷产品的多少随机器运转速度而变化,用x 表示转速(单位:转/秒),用y 表示每小时生产的有缺陷产品的个数,现观测得到)(y x ,的4组观测值为(8,5),(12,8),(14,9),(16,11). (1)画出散点图.(2)你能从散点图中发现零件数与加工时间近似成什么关系吗?如果近似成线性相关关系的话,请求出相应的回归直线方程;(3)若实际生产中所容许的每小时最多有缺陷产品数为10,则机器的速度不得超过多少转/秒?(精确到1) 19.(本小题满分12分)(理)某市某社区拟选拔一批综合素质较强的群众,参加社区的义务服务工作.假定符合参加选拔条件的每个选手还需要进行四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮问题的概率分别为31,21,43,54且各轮问题能否正确回答互不影响. (1)求该选手进入第四轮才被淘率的概率.(2)该选手在选拔过程中回答过的问题的总个数记为X ,求随机变量X 的分布列与数学期望.(注:本小题结果可用分数表示) (文)某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了n 人,回答问题统计结果如图表所示.(1)分别求出a ,b ,x ,y 的值;(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.20.(本小题满分13分)为了解大学生观看某电视节目是否与性别有关,一所大学心理学教师从该校学生中随机抽取了50人进行问卷调查,得到了如下的列联表,若该教师采用分层抽样的方法从50份问卷调查中继续抽查了10份进行重点分析,知道其中喜欢看该节目的有6人喜欢看该节目 不喜欢看该节目 合计 女生 5 男生 10 合计 50(1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为喜欢看该节目节目与性别有关?说明你的理由;(3)已知喜欢看该节目的10位男生中,1A 、2A 、3A 、4A 、5A 还喜欢看新闻,1B 、2B 、3B 还喜欢看动画片,1C 、2C 还喜欢看韩剧,现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查,求1B 和1C 不全被选中的概率. 下面的临界值表供参考:()k K p ≥2 0.15 0.10 0.05 0.025 0.010 0.005 0.001k2.072 2.7063.841 5.024 6.635 7.879 10.828 (参考公式:()()()()()d b c a d c b a bc ad n K ++++-=22,其中d c b a n +++=)21.(本小题满分14分)某大学为调查来自南方和北方的同龄大学生的身高差异,从2011级的年龄在18~19岁之间的大学生中随机抽取了一自南方和北方的大学生各10名,测量他们的身高,量出的身高如下(单位:cm ) 南方:158,170,166,169,180,175,171,176,162,163 北方:183,173,169,163,179,171,157,175,178,166 (1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对来自南方和北方的大学生的身高作比较,写出两个统计结论. (2)设抽测的10名南方大学生的平均身高为x ,将10名同学的身高依次输入按程序框图进行运算,问输出的S 大小为多少?并说明S 的统计学意义. (3)(理)若将样本频率视为总体的概率,现从来自南方的大学生中随机抽取3名同学,记其中身高不低于平均身高的同学的人数为X ,求X 的分布列及数学期望EX (均值).(文)为进一步调查身高与生活习惯的关系,现从来自南方这10名大学生中随机抽取两名身高不低于173cm 的同学,求身高为176cm 的同学被抽中的概率.组号 分组回答正确 的人数 回答正确的人数 占本组的概率 第1组 [)25,15 5 0.5第2组 [)35,25 a 0.9第3组[)45,35 27x第4组 [)55,45 b 0.36 第5组 [)65,553 y2012届专题卷数学专题八答案与解析1.【思路点拨】简单随机抽样适用于总体容量较小的情形;总体容量较大且各个体间没有明显差异时选用系统抽样;当组成总体的各部分存在明显差异时,则应选用分层抽样.【答案】B 【解析】①中总体容量较大,且火腿肠之间没有明显差异,故适合采用系统抽样;②中总体容量偏小,故适合采用简单随机抽样. 2.【思路点拨】可从集合角度进行分析:若A 与B 是互斥事件,则φ=⋂B A ,若A 与B 是对立事件,则,Ω=⋃=⋂B A B A ,φ即对立事件是特殊的互斥事件.【答案】D 【解析】由题意知,=B A {出现点数2},所以事件A 、B 不互斥也不对立;,,Ω=∅=C B C B 故事件B ,C 是对立事件,选D . 3.【思路点拨】系统抽样的特点:总体平均分段、选定起始号、等间距、等可能抽样.【答案】B 【解析】采用系统抽样,可先将50个编号分成5组,在第一组随机地抽取一号码,比如抽到3号,则其它各组就依次选取13,23,33,43.四个选择答案中,只有B 属于这种抽取方法. 4.(理)【思路点拔】本题为排列组合的综合题,一般采用“先选后排”的解题策略求解.【答案】C 【解析】选派的所有情形有72222424==A C C N . (文)【思路点拔】几何概型的计算公式为:的长度(面积或体积)的长度(面积或体积)G G A P 1)(=.【答案】B 【解析】如图设线段AB =3,C 、D 是线段A B 的两个三等分点,则当“温洛克”挂在线段CD 上的时候,“温洛克”与两端A 、B 的距离都大于1.所以“温洛克”与两端距离都大于1m 的概率为31==的长度的长度AB CD P .5.(理)【思路点拔】利用频率分布直方图中各组频率之和为1这一性质求解.【答案】C【解析】由图可知数据落在20~80间的累积频率为0.1+0.2+0.2+0.04+0.12+0.12=0.78,故数据落在80~100间频率为1-0.78=0.22,故醉酒驾车人数为50×0.22=11(人). (文)【思路点拔】求出种子发芽的各频率值,发现频率的稳定值,即为概率值.【答案】D 【解析】我们可以用频率的近似值表示随机事件发生的概率,根据表格计算不同情况下的菜籽发芽的频率分别是1,0.8,0.9,0.857,0.892,0.910,0.913,0.903,0.905,由上面的计算结果可知,菜籽发芽的频率接近于0.9,且在它附近摆动,故此可知菜籽在已知条件下发芽的概率大约为0.9.6.(理)【思路点拔】(1)在n 次独立重复试验中,某事件恰好发生k 次的概率为()()()n k p p C k P k n kk nn ,,2,1,01 =-=-,其中p 为该事件在一次试验中发生的概率.(2)本题解题思路为:先设他命中一次的概率为p ,并由已知构造方程求得p ,即可由概率公式得所求.【答案】C 【解析】四次射击可看作4次独立重复试验.设一次射击中,他命中的概率为p ,则他至少命中一次的概率为()8165114=--p ,解得31=p .∴他命中2次的概率为()278812431131222244==⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=C P .(文)【思路点拔】由于甲、乙两人的行动相互不受影响,故他们去西安看世园会为相互独立事件,于是联想到调用概率的乘法公式求解.【答案】A 【解析】分别记甲、乙去西安旅游为事件A 、B ,则()31=A P ,()41=B P ,由题设可知A 、B 相互独立,故所求的概率()()()21411311=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-==⋅=B P A P B A P P . 7.【思路分析】本题中:提出假设0H :“这种试剂不能起到检测出塑化剂的作用”,并计算出()01.0635.62≈≥x P ,因此,在一定程度上说明假设不合理,我们就以99%的把握拒绝假设,故易知p ,r 为真命题,再由真值表即可获解. 【答案】D 【解析】由题设可知命题p ,r 为真命题,q ,s 为假命题,依据复合命题的真值表可知D 为真命题. 8.【思路点拔】先利用茎叶图得到两组数据,并求出其平均值和方差,再利用方差进行比较:方差越小,波动越小,空气质量越高. 【答案】B 【答案】17010182179179171170168168163162158=+++++++++=x .甲城镇核辐射的样本方差为:[()()()()+-+-+-+-2222170168170163170162170158101()+-2170168()+-2170170()+-2170171()2170179-()]571701822=-+, 1.17110181179178176173170168165162159=+++++++++=x ,乙城镇核辐射的样本方差为101[()21.171159-()21.171162-+()21.171165-+()21.171168-+()21.171170-+()21.171173-+()21.171176-+()21.171178-+()21.171179-+()21.171181-+29.51=,由此判断乙城镇的空气质量较好.9.【思路点拔】利用折线图,扇形统计图,条形统计图的特征,解决问题.【答案】B 【解析】①显然正确;从条形统计图中可得到:2050年非洲人口大约将达到近18亿,②错;从扇形统计图中能够明显的得到结论:2050年亚洲人口比其他各洲人口的总和还要多,③正确;由上述三幅统计图并不能得出从1957年到2050年中哪个洲人口增长速度最慢,故④错误.因此正确的命题有①③. 10.(理)【思路点拔】利用定积分求面积时要特别注意函数的选择,对于几何概型则应特别注意基本事件空间和时间A 的几何度量(面积、体积、长度)的计算. 【答案】C 【解析】由定积分的几何意义可得阴影部分面积为33232162-442322=-=⨯=⎰x dx x S 阴,又由几何概型可得点在E 中的概率为3216332===正阴μμP .(文)【答案】D 【解析】抛掷一颗骰子共有6种情况.当a =1,2,3,4,5,6时,利用函数()x f 的图像易知,()x f y =在[]4,0 上的零点分别为1,2,4,5,7,8个.故所求概率为656263=+=P . 11.【思路点拔】确定各层应抽取的个体数是实施分层抽样的最关键步骤,而确定办法主要有二:①利用抽样比k 来确定,当已知各层的个体数时,用此法计算较为简便;②利用结论“样本中各层抽取的个体数之比=总体中各层的个体数之比”来确定,当总体(或样本)中各层个体数以比的形式给出时,一般考虑用此法速解.【答案】18【解析】由题设知:来自于退休教职工、在职教职工、学生的份数之比为3:7:40,故样本中相应的份数之比仍为3:7:40,设所抽取的调查表中来自退休教职工份数为m ,则1840733300=⇒++=m m . (1)(理)【思路点拔】由正态曲线得到μ=1,再利用公式⎪⎭⎫⎝⎛-=σμφx Fx 计算概率. 【答案】0.682【解析】由图可知,2σ=,所以()()()()682.01121121121331=-Φ=-Φ-Φ=⎪⎭⎫⎝⎛--Φ-⎪⎭⎫ ⎝⎛-Φ=≤≤-ξP .(文)【思路点拔】读取统计图解答问题的关键是充分挖掘图中所包含的信息.在条形统计图中,每个直条的高度表示相应样本值出现的次数(即频数)或百分比;扇形统计图中,每个扇形的大小反映所表示的那部分占总体百分比的大小. 【答案】8%【解析】设小明共调查了x 名居民的年龄,由230%46=⋅x ,得500=x ;于是得%20%100500100=⨯=a ;b=12%22%)46%(20%1=++-.故a-b =8%. 13.(理)【思路点拔】(1)涉及二项展开式中的特定项(如常数项、有理项等)、二项式系数、系数的问题一般用通项法求解;(2)由诱导公式知ϕϕπ2cos 223sin -=⎪⎭⎫⎝⎛-.(3)二倍角的余弦公式:ϕϕϕ22sin 211cos 22cos -=-=.【答案】53【解析】由二项式定理得,3x 的系数为2cos 235=ϕC 得51cos 2=ϕ故53cos 212cos 223sin 2=-=-=⎪⎭⎫ ⎝⎛-ϕϕϕπ. (文)【思路点拨】先利用回归直线方程过(y x ,),求出a ,然后再求解. 【答案】68【解析】因为1813101104x ++-==,40464383424=+++=y ,又因为回归直线方程过(y x ,),所以402060a a =-+⇒=,把04-代入回归直线方程,可得用电量的都市约为68.14.【思路点拔】由频率求出频数,便能求得这100个数据的平均值.【答案】65【解析】由题设可知各组及其频数分别为:[)40,20:10;[)60,40:25;[)80,60:45;[)100,80:20.故这100个 数据的期望值(平均值)为[]6520904570255010301001=⨯+⨯+⨯+⨯=x . 15.【思路点拔】由两直线的交点在第一象限,构造出关于a ,b 不等式组,再利用枚举法确定基本事件数,便易得所求.【答案】3613【解析】由题意知,{}6,5,4,3,2,1,∈b a .因为直线1l 与2l 的交点在第一象限,所以由他们的图象可知:3132b a ⎧<⎪⎪⎨⎪>⎪⎩或3132ba⎧>⎪⎪⎨⎪<⎪⎩解得3,1b a >⎧⎨≤⎩或32b a <⎧⎨≥⎩,所以基本事件()b a ,可以是(1,4),(1,5),(1,6),(2,1),(2,2),(3,1),(3,2),(4,1),(4,2),(5,1),(5,2),6,1),(6,2)共13个,而基本事件有3666=⨯种,所以随机事件“直线1l 与2l 的交点在第一象限”的概率为3613=P 16.【思路点拨】根据树脂图列出所有结果或者直接写出所有结果,然后求解.【解析】利用树状图可以列出从甲、乙两个盒子中各取出1个球的所有可能结果(如下图),可以看出,试验的所有可能结果数为16种且每种结果是等可能的.(3分)(1)所取两张卡片上的标号为相同整数的结果有1-1,2-2,3-3,4-4,共4种.故根据古典概型公式,所求概率41164==P .答:取出的两张卡片的标号为相同整数的概率为41.(6分)(2)记事件“取出的两张卡片的标号至少有一个大于2”为A .则A 的对立事件是A =“取出的两张卡片上的标号都不于大2”(8分)所取出的两张卡片上的标号都不大于3的结果有1-1,1-2,2-1,2-2,共4种.43)(1)(41164)(=-=∴==A P A P A P .答:取出的两张卡片上的标号至少有一个大于3的概率为43.(12分) 17.(理)【思路点拔】(1)利用对立事件的概率公式求解;(2)易知X 的可能取值为0,1,2,分别求出对应的概率值,即得分布列,再进一步求期望. 【解析】(1)代表A 被选中的概率为151125=C (2分),所以代表A 不被选中的概率是15141511=-.(4分)(2)X 的可能取值为0,1,2.(5分)()1510262===C C X P ,()1581261412===C C C X P ,()15622624===C C X P (8分)∴X 的分布列为(见右图表)(10分)1864()0121515153E X =⨯+⨯+⨯=.(12分) (文)【思路点拔】先利用枚举法列举出6名代表中随机选出2名的结果总数,再从中找中各事件所包含的结果数,然后代入古典概型、对立事件以及互斥事件的概率公式进行求解. 【解析】(1)从这6名代表中随机选出2名,共有C 种不同的选法,分别为(A ,B ),(A ,C ),(A ,D ),(A ,E ),(A ,F ),(B ,C ),(B ,D ),(B ,E ),(B ,F ),(C ,D ),(C ,E ),(C ,F ),(D ,E ),(D ,F ),(E ,F ).(3分).其中代表A 被选中的选法有(A ,B ),(A ,C ),(A ,D ),(A ,E ),(A ,F )共5种,则代表A 被选中的概率为31155=(6分)所以代表A 不被选中的概率为321551=-=P . (2)随机选出的2名代表“恰有1名来自北美洲或2名都来自非洲”的结果有9种,分别是),(C A ,),(D A ,),(C B ,),(D B ,),(E C ,),(F C ,),(E D ,),(F D ,),(F E .“恰有1名来自北美洲或2名都来自非洲”这一事件的概率为53159=(12分). 18.【思路点拔】先画出散点图,由散点图可知各散点分布成一条直线附近,故零件数与加工时间近似成线性相关关系,再求出回归直线方程,并利用此方程求解.【解析】(1)如图(4分)(2)设回归直线方程为a bx y+=ˆ,则5.1241614128=+++=x ,25.8411985=+++=y ,(3)43811169148125844332211=⨯+⨯+⨯+⨯=+++y x y x y x y x ;6601614128222224232221=+++=+++x x x x ,所以,70515.12466025.85.1244382=⨯-⨯⨯-=b ,765.12705125.8-=⨯-=-=x b y a ;故:y 与x 之间的回归直线方程为767051ˆ-=x y (8分)(3)由10767051≤-=x y ,得1451706≈≤x .即机器的速度不得超过14转/秒.(12分) 19.(理)【思路点拔】对于(1)(2),均可用相互独立事件的概率公式求出相应的概率,从而得出X 的分布列,再利用期望公式求X 期望值.【解析】(1)记“该选手能正确回答第i 轮的问题”的事件为()4,3,2,1=i A i ,则()541=A P ,()432=A P ,()213=A P ,()314=A P .(2分)∴该选手进入第四轮才被淘率的概率()()()()()43214321A P A P A P A P A A A A P P ==5132214354=⨯⨯⨯=.(5分) (2)X 的可能值为4321、、、,()()5111===A P X P ,()()()()51415422121=⨯====A P A P A A P X P ,()()()()()1032143543321321=⨯⨯====A P A P A P A A A P X P 103214354=⨯⨯=,12341234123444313(4)()()()()()()154210P X P A A A A P A A A A P A P A P A P A A ==+=+=⨯⨯⨯=.(9分)X ∴的分布列为(见右侧表格)(11分) ()102710341033512511=⨯+⨯+⨯+⨯=∴X E .(12分) (文)【思路点拔】对于(1),可结合频率分布直方图的性质求解;对于(2),则可利用分层抽样比求解;问题(3)为古典概型问题,可用枚举法求解.X 012P151158 156 X 1 2 3 4P 51 51 103 103【解析】(1)由频率表中第1组数据可知,第1组总人数为105.05=,再结合频率分布直方图可知1001010.010=⨯=n(1分)∴a=100×0.020×10×0.9=18,b=100×0.025×10×0.36=9,(2分)9.03.010027=⨯=x,2.015.01003=⨯=y(4分)(2)第2,3,4组中回答正确的共有54人.(5分)∴利用分层抽样在54人中抽取6人,每组分别抽取的人数为:第2组:265418=⨯人,第3组:365427=⨯人,第4组:16549=⨯人.(8分)(3)设第2组的2人为1A、2A,第3组的3人为1B、2B、2B,第4组的1人为1C,则从6人中抽2人所有可能的结果有:()21,AA,()11,B A,()21,B A,()31,B A,()11,CA,()12,BA,()22,BA,()32,BA,()12,CA,()21,BB,()31,B B,()11,CB,()32,BB,()12,CB,()13,CB,共15个基本事件,(10分)其中第2组至少有1人被抽中的有()21,AA,()11,BA,()21,BA,()31,BA,()11,CA,()12,BA,()22,BA,()32,BA,()12,CA这9个基本事件.(11分)∴第2组至少有1人获得幸运奖的概率为53159=(12分)学科网ZXXK]20.【思路点拔】在独立性检验中,常利用2K来确定“两个分类变量是否有关联”:当706.22≤K时,可以认为变量A、B 是没有关联的;当2K>2.706时,有90%的把握判定变量A、B有关联;当2K>3.841时,有95%的把握判定变量A、B有关联;当2K>6.635时,有99%的把握判定变量A、B有关联.故只需计算出2K的值,利用上述结论即可解决第(2)小题.第(3)小题可用组合知识及枚举法求解.学_科_网Z_X_X_K]【解析】(1)由分层抽样知识知,喜欢看该节目的同学有3010650=⨯,故不喜欢看该节目的同学有50-30=20人,(2分)于是可将列联表补充如右图:(4分)(2)()333.82525203051015205022≈⨯⨯⨯⨯-⨯⨯=K>7.879(7分)∴有99.5%的把握认为喜爱该节目与性别有关.(8分)(3)(理)从10位男生中选出喜欢看韩剧、喜欢看新闻、喜欢看动画片的各1名,其一切可能的结果组成的基本事件共有30121315==CCCN个,(10分)用M表示“11CB、不全被选中”这一事件,则其对立事件M表示“11CB、全被选中”这一事件,由于M由()111,,CBA,()112,,CBA,()113,,CBA,()114,,CBA,()115,,CBA,5个基本事件组成,所以()61305==MP,(12分)由对立事件的概率公式得()()656111=-=-=MPMP.(13分)(文)从10位男生中选出喜欢看韩剧、喜欢看新闻、喜欢看动画片的各1名,其一切可能的结果组成的基本事件如下:()111,,CBA,()211,,CBA,()121,,CBA,()221,,CBA,()131,,CBA,()231,,CBA,()112,,CBA,()212,,CBA,()122,,CBA,()222,,CBA,()132,,CBA,()232,,CBA,()113,,CBA,()213,,CBA,()123,,CBA,()233,,CBA,()223,,CBA,()133,,CBA,()114,,CBA,()214,,CBA,()124,,CBA,()224,,CBA,()134,,CBA,()234,,CBA,()115,,CBA,()215,,CBA,()125,,CBA,()225,,CBA,()135,,CBA,()235,,CBA,基本事件的总数为30,(10分)用M表示“11CB、不全被选中”这一事件,则其对立事件M表示“11CB、全被选中”这一事件,由于M由()111,,CBA,()112,,CBA,()113,,CBA,()114,,CBA,()115,,CBA,5个基本事件组成,所以()61305==MP,(12分)由对立事件的概率公式得()()656111=-=-=MPMP.(13分)21.【思路点拔】(1)可利用给出数据直接画出茎叶图,再根据茎叶图从样本的数字特征等角度来得出统计结论;(2)认真读懂框图,不难看出该框图的功能是计算一组数据的方差;(3)(文)利用枚举法求解;(3)(理)易知X服从二项分布,故调用二项分布的概率及期望公式简解.【解析】(1)茎叶图如右图(2分)统计结论:(给出下述四个供参考,考生只要答对其中两个即给满分,给出其他合理的答案也可给分)①北方大学生的平均身高大于南方大学生的平均身高.②南方大学生身高比北方大学生的身高更整齐;③南方大学生的身高的中位数为169.5cm,北方大学生的身高的中位数是172cm.④南方大学生的高度基本上是对称的,而且大多数集中在均值附近,北方大学生的高度分布较为分散.(4分)(2)169=x,6.42=S(6分),S表示10位南方大学生身高的方差,是描述身高离散程度的量.S值越小,表示身高越整齐,S值越大,表示身高参差不齐.(8分)(1)(理)记“抽取一位同学恰好抽中身高不低于平均身高的同学”为事件A,由(2)知来自南方的大学生平均身高为169cm,故()53106==AP.(9分),随机变量X的可能取值为0,1,2,3,且喜欢看该节目不喜欢看该节目合计女生20 5 25男生10 15 25合计30 2050X0 1 2 3P12581253612554125273(3,)5X B .所以()()3,2,1,0525333=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛==-k C k X P kkk ,所以变量X 的分布列为(见右表格)5912527312554212536112580=⨯+⨯+⨯+⨯=∴EX (或59533=⨯==np EX )(14分)(文)记“身高为176cm 的同学被抽中”为事件A ,从这10名南方大学生中抽出两名身高不低于170cm 的同学有(170,171),(170,175),(170,176),(170,180),(171,175),(171,176),(171,180),(175,176),(175,180),(176,180),共10个基本事件,而事件A 含有4个基本事件,故()52104==A P .(14分)。

高三数学二轮复习微专题精选6 概率统计概率统计是高中数学中的一个重要内容,它涉及到随机事件的概率计算和统计分析。
在高三数学二轮复中,概率统计是一个需要重点复和掌握的知识点。
1. 概率计算概率计算是概率统计的基础,它涉及到事件发生的可能性大小的计算。
在复中,我们应该重点掌握以下几个内容:- 根据样本空间和事件的定义计算概率;- 利用频率定义概率;- 使用排列和组合计算概率;- 利用事件的补集计算概率。
2. 随机变量和概率分布随机变量是概率统计中的重要概念,它表示随机事件的结果。
概率分布则是随机变量取各种可能值的概率分布情况。
在复中,我们应该掌握以下几个重点:- 定义随机变量和概率分布;- 计算离散型随机变量的期望和方差;- 计算连续型随机变量的期望和方差。
3. 统计分析统计分析是概率统计的另一个重要内容,它涉及到数据的收集、整理和分析。
在复中,我们应该重点掌握以下几个内容:- 数据的收集和整理;- 数据的均值和标准差的计算;- 样本估计和参数估计的方法;- 使用统计推断进行判断和决策。
4. 解题技巧和思路在复的过程中,我们还需掌握一些解题技巧和思路:- 注意理解题目中的要求和条件;- 灵活运用概率计算的各种方法;- 注意统计分析中的常见统计指标的计算;- 理解样本和总体的关系,正确进行估计。
总之,对于高三数学二轮复微专题精选6的概率统计内容,我们应该系统性地复和掌握概率计算、随机变量和概率分布以及统计分析的相关知识。
同时,我们还应该注意解题思路和技巧的应用,提高解题效率。
通过充分理解和练,我们可以更好地应对考试中的概率统计题目,取得好成绩。

第十七讲 概率与统计★★★高考在考什么 【考题回放】 1.(重庆卷)从5张100元,3张200元,2张300元的奥运预赛门票中任取3张, 则所取3张中至少有2张价格相同的概率为( )A .41B .12079C . 43D .2423解:可从对立面考虑,即三张价格均不相同,11153231031.4C C C P C ⇒=-= 选C 2.(辽宁卷)一个坛子里有编号为1,2,…,12的12个大小相同的球,其中1到6号球是红球,其余的是黑球. 若从中任取两个球,则取到的都是红球,且至少有1个球的号码 是偶数的概率是( )A .122B .111C .322D .211解: 从中任取两个球共有66212=C 种取法,其中取到的都是红球,且至少有1个球的号码是偶数的取法有122326=-C C 种取法,概率为1126612=,选D.3.(广东卷) 甲、乙两个袋子中均装有红、白两种颜色的小球,这些小球除颜色外完全相同,其中甲袋装有4个红球、2个白球,乙袋装有1个红球、5个白球。
现分别从甲、乙两袋中各随机抽取一个球,则取出的两球是红球的概率为______(答案用分数表示)解:P=64⨯61=914.(上海卷) 在五个数字12345,,,,中,若随机取出三个数字,则剩下两个数字都是奇数的 概率是 (结果用数值表示).解:212335310C C C ==3.05. 某篮球运动员在三分线投球的命中率是12,他投球10次,恰好投进3个球的概率为.(用数值作答)解:由题意知所求概率37310111522128p C ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭ 6.(全国II) 在某项测量中,测量结果ξ服从正态分布2(1)(0)N σσ>,.若ξ在(01),内取值的概率为0.4,则ξ在(02),内取值的概率为 . 解:在某项测量中,测量结果ξ服从正态分布N (1,σ2)(σ>0),正态分布图象的对称轴为x=1,ξ在(0,1)内取值的概率为0.4,可知,随机变量ξ在 (1,2)内取值的概率于ξ在(0,1)内取值的概率相同,也为0.4,这样随机 变量ξ在(0,2)内取值的概率为0.8。

2012高考:概率统计综合 1、(2012全国课标,18)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花当垃圾处理(I )若花店一天购进16枝玫瑰花,求当天利润y (单位:元)关于当天需求量n (单位:支,n N ∈)的函数解析式;(II )花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:以100天记录的各需求量的频率作为各需求量发生的概率(i )若花店一天购进16枝玫瑰花,X 表示当天的利润(单位:元),求X 的分布列、数学期望及方差; (ii )若花店一天计划购进16枝或17枝玫瑰花,你认为应当购进16枝还是17枝?说明理由。
2、(2012山东,19)现有甲、乙两个靶,某射手向甲靶射击一次,命中概率为34,命中得1分,没命中得0分;向乙靶射击两次,每次命中概率为23,每命中一次得2分,没命中得0分,该射手每次射击的结果相互独立,假设该射手完成以上三次射击 (I )求该射手恰好命中一次的概率;(II )求该射手总得分X 的分布列及数学期望EX 。
3、(2012广东,17)某班50位学生期中考试成绩频率分布直方图如图所示,其中成绩分组区间为[4050),,[5060),,[6070),,[7080),,[8090),,[90100],(I )求图中x 的值;(II )从成绩不低于80分的学生中随机抽取2人,该2人中成绩在90分以上(含90分)的人数记为ξ,求ξ的数学期望。
10 20 16 16 15 13 1014 15 16 17 18 19 20 频数日需求量n图44、(2012江苏,22)设ξ为随机变量,从棱长为1的正方体的12条棱中,任取其中的两条,当两条棱相交时,0ξ=;当两条棱平行时,ξ为两条棱间的距离;当两条棱异面时,1ξ= (I )求概率(0)P ξ=;(II )求ξ的分布列,并求其数学期望()E ξ。
5、(2012安徽,17)某单位招聘面试,每次从试题库中随机调用一道试题,若调用的是A 类试题,则使用后该试题回库,并增补一道A 类试题和B 类试题入库,此次调题工作结束;若调用的是B 类试题,则使用后该试题回库,此次调题工作结束。

《计数原理与概率》高考复习指导一、考试说明:1.考试内容(1)分类计数原理与分步计数原理,排列与组合.(2)等可能性事件的概率,互斥事件有一个发生的概率,相互独立事件同时发生的概率.2.考试要求(1)掌握分类计数原理与分步计数原理,并能用它们分析和解决一些简单的应用问题.(2)理解排列与组合的意义,掌握排列数与组合数的计算公式,掌握组合数的两个性质,并能用它们解决一些简单的应用问题.(3)了解等可能性事件的概率的意义,会用排列组合公式计算一些等可能性事件的概率.(4)了解互斥事件的意义,会用互斥事件的概率加法公式计算一些事件的概率.(5)了解相互独立事件的意义,会用相互独立事件的概率乘法公式计算一些事件的概率,会计算事件在n次独立重复试验中恰好发生k次的概率.二、高考试题分析排列与组合、概率与统计是高中数学的重要内容.一方面,这部分内容占用教学时数多达36课时,另一方面,这部分内容是进一步学习高等数学的基础知识,因此,它是高考数学命题的重要内容.从近三年全国高考数学(新材)试题来看,主要是考查排列与组合、概率与统计的基本概念、公式及基本技能、方法,以及分析问题和解决问题的能力.试题特点是基础和全面.题目类型有选择题、填空题、解答题,一般是两小(9分~10分)一大(12分),解答题通常是概率问题.试题难度多为低中档.为了支持高中数学课程的改革,高考数学命题对这部分将进一步重视,但题目数量、难度、题型将会保持稳定.例1.(1999年全国)在一块并排10垄的田地中,选择2垄分别种植A、B两种作物,每种作物种植一垄,为有利于作物生长,要求A、B两种作物间的间隔不小于6垄,则不同的选垄方法共有_______种(用数字作答).[解析]A种植在左边第一垄时,B有3种不同的种植方法;A种植在左边第二垄时,B有两种不同的种植方法;A种植在左边第三垄时,B只有一种种植方法.B在左边种植的情形与上述情形相同.故共有2(3+2+1)=12种不同的选垄方法.∴应填12.例2.(2003年新教材)将3种作物种植在如图所示的5块试验田里,每一块种植一种作物且相邻的试验田不能种植同一作物,不同的种植方法共有______种(以数字作答).[解析]将5块试验田从左到右依次看作甲、乙、丙、丁、戊,3种作物依次看作A、B、C,则3种作物都可以种植在甲试验田里,由于相邻的试验田不能种植同一种作物,从而可知在乙试验田里只能有两种作物.同理,在丙、丁、戊试验田里也只能有两种作物可以种植.由分步计数原理,不同的种植方法共有3×2×2×2=48种.∴应填:48例3.(2003年全国高考题)某城市中心广场建造一个花圃,花圃分为6个部分(如图),现要栽种4种不同颜色的花,每部分栽种1种且相邻部分不能栽种同样颜色的花,不同的栽法有_______种.[解析]由于第1、2、3块两两相邻,我们先安排这三块,给第1、2、3块种花时分别有4、3、2种种法,所以共有4×3×2=24种不同种法.下面给第4块种花,若第4块与第6块同色,只有一种种植方法,则第5块只有2种种法,若第4块与第2块同色时,共有2×1=2种种法.若第4块与第6块不同色,但第4块与第2块同色,则第6块有2种种植的方案,而第5块只有1种种法,共有2种不同的种植方法.若第4块与第6块不同色,但第4块与第2块不同色,则第6块有1种种法,则第5块也有一种不同种法,所以第4块与第6块不同色时,有1种种法.综上共有24×(2+2+1)=120种不同的种植方法.例4.(2003年春季考试题)某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目,如果将这两个节目插入原节目单中,那么不同的插法的种数为A 、42B 、30C 、20D 、12[解析]将两个新节目插入5个固定顺序节目单有两种情况:(1)两个新节目相邻的插法种数为226A ;(2)两个节目不相邻的插法种数为26A ;由分类计数原理共有2226642A A +=种方法,选A.例5.(2004重庆)(本小题满分12分)设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5。


第七部分:计数原理、概率、随机变量及其分步、统计、统计案例(8)(限时:时间45分钟,满分100分)一、选择题1.简单随机抽样、系统抽样、分层抽样之间的共同点是( )A.都是从总体中逐个抽取B.将总体分成几部分,按事先确定的规则在各部分抽取C.抽样过程中每个个体被抽取的机会相同D.将总体分成几层,分层进行抽取【解析】三种抽样方法有共同点也有不同点,它们的共同点就是抽样过程中每个个体被抽取的机会相同.【答案】 C2.(2012年荆州一模)为了检查某超市货架上的奶粉是否含有三聚氰胺,要从编号依次为1到50的袋装奶粉中抽取5袋进行检验,用每部分选取的间隔一样的系统抽样方法确定所选取的5袋奶粉的编号可能是( )A.5,10,15,20,25 B.2,4,8,16,32C.1,2,3,4,5, D.7,17,27,37,47【解析】利用系统抽样,把已编号分为5段,每段10个,每段抽取一个,间隔为10,故选D.【答案】 D3.(2011年某某模拟)某校有老师200人,男学生1 200人,女学生1 人.现用分层抽样的方法抽取一个容量为n的样本,已知从女学生中抽取的人数为80,则n为( ) A.16 B.96C.192 D.112【解析】由801 000=225,∴n2 400=225,∴n=192. 【答案】 C4.(2011年某某模拟)在样本方差的计算公式s2=110[(x1-20)2+(x2-20)2+…+(x10-20)2]中,数字10和20分别表示样本的( )A.容量,方差 B.平均数,容量C.容量,平均数 D.标准差,平均数【解析】方差公式为s 2=1n [(x 1-x )2+(x 2-x )2+…+(x n -x )2],可知,10是样本容量,x =20,20是平均数. 【答案】 C5.在2008年第29届奥运会上,我国代表团的金牌数雄踞榜首.如图是位居金牌榜前十二位的代表团获得的金牌数的茎叶图,则这十二个代表团获得的金牌数的平均数与中位数的差m 的值为( )A .3.5B .4C .4.5D .5【解析】 由茎叶图中的数据可求得这十二个代表团获得的金牌数的平均数为17.5,中位数为13.5,故m =4.【答案】 B 二、填空题6.用系统抽样法从160名学生中抽取容量为20的样本,将160名学生随机地进行1~160的编号,按编号顺序平均分成20组(1~8号,9~16号,…,153~160号),若第16组抽出的为126,则第1组中用抽签的方法确定的是________.【解析】 平均分成20组,每组有8个编号. 因此设第一组抽取的编号为n , 则n +8×15=126,n =6. 【答案】 67.(2011年某某模拟)为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图(如图所示),已知从左到右各长方形高的比为2∶3∶5∶6∶3∶1,则该班学生数学成绩在(80,100)之间的学生人数是________.【解析】 由题意,得数学成绩在(80,100)之间的学生人数是×60=33(人).【答案】 338.在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4 8.4 9.4 9.9 9.6 9.4 9.7,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为________、________.【解析】 去掉最高分9.9,最低分8.4, 则剩下数据为9.4,9.4,9.4,9.6,9.7, 平均数x =3×9.4+9.6+9.75=9.5,s 2=15[3×(9.4-9.5)2+(9.6-9.5)2+(9.7-9.5)2]=0.016.【答案】 9.5 0.016 三、解答题9.某工厂人员及工资构成如表: 人员 经理 管理人员 高级技工 工人 学徒 合计 周工资 2 200 250 220 200 100 人数 1 6 5 10 1 23 合计2 2001 5001 10020001006 900(2)这个问题中,平均数能客观地反映该工厂的工资水平吗?为什么? 【解析】 (1)众数200,中位数220,平均数 x =1×2 200+6×250+5×220+10×200+1×10023=300.(2)平均数受数据中的极端值的影响较大,这个平均数是从一名工资极高(是工人工资的11倍)的经理和其他四类员工的周工资计算出来的,它不能客观地反映该工厂的工资水平.10.从高三学生中抽取50名同学参加数学竞赛,成绩的分组及各组的频数如下:(单位:分)[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100),8.(1)列出样本的频率分布表;(2)画出频率分布直方图;(3)估计成绩在[60,90)分的学生比例;(4)估计成绩在85分以下的学生比例.【解析】(1)频率分布表如下:(2)频率分布直方图如下图所示:(3)74% (4)72%。


考前30天之备战2012高考数学冲刺系列二概率与统计(文)学生版【命题趋势】:概率是高考的必考内容,主要考查的内容有:等可能性事件的概率、互斥事件有一个发生的概率、相互独立事件同时发生的概率、n次独立重复试验中恰好发生k次的概率及离散型随机变量的分布列、期望与方差等.一般会有一道选择题或填空题与一道解答题,在高考中所占的比重大于10%.近年来,高考中的应用题基本是考查离散型随机变量的期望与方差的解答题.统计知识则主要考查抽样方法、频率分布直方图、正态分布等知识,主要以选择题和填空题的形式出现.【方法与技巧】事件A、B的和记作A+B,表示事件A、B至少有一个发生。
当A、B为互斥事件时,事件A+B是由“A发生而B不发生”以及“B发生而A不发生”构成的。
当计算事件A的概率P(A)比较困难时,有时计算它的对立事件A的概率则要容易些,为此有P(A)=1-P(A)。
对于n个互斥事件A1,A2,…,A n,其加法公式为P(A1+A2+…+A n)=P(A1)+P(A2)+…+P (A n)。
分类讨论思想是解决互斥事件有一个发生的概率的一个重要的指导思想。
4.在应用题背景条件下,能否把一个复杂事件分解为若干个互相排斥或相互独立、既不重复又不遗漏的简单事件是解答这类应用题的关键,也是考查学生分析问题、解决问题的能力的重要环节【高考冲刺押题】【押题2】某企业招聘中,依次进行A 科、B 科考试,当A 科合格时,才可考B 科,且两科均有一次补考机会,两科都合格方通过。
甲参加招聘,已知他每次考A 科合格的概率均为32,每次考B 科合格的概率均为21。
假设他不放弃每次考试机会,且每次考试互不影响。
(I)求甲恰好3次考试通过的概率;(II)求甲招聘考试通过的概率. 【押题指数】★★★★★【押题3】已知关于x 的一元二次函数2()4 1.f x ax bx =-+(Ⅰ)设集合{}1,2,3P =和{}1,1,2,3,4Q =-,分别从集合P 和Q 中随机取一个数作为a 和b ,求函数()y f x =在区间[1,)+∞上是增函数的概率;(Ⅱ)设点(,)a b 是区域8000x y x y +-≤⎧⎪>⎨⎪>⎩内的随机点,记{()A y f x ==有两个零点,其中一个大于1,另一个小于1},求事件A 发生的概率.【押题指数】★★★★★【押题4】某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如右图所示.(Ⅰ)下表是年龄的频数分布表,求正整数,a b 的值;(Ⅱ)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?(Ⅲ)在(Ⅱ)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率. 【押题指数】★★★★★【押题5】如图,从参加环保知识竞赛的学生中抽出40名,将其成绩(均为整数....)整理后画出的频率分布直方图如下:观察图形,回答下列问题:(1)80~90这一组的频数、频率分别是多少? (2)估计这次环保知识竞赛成绩的平均数、众数、中位数。
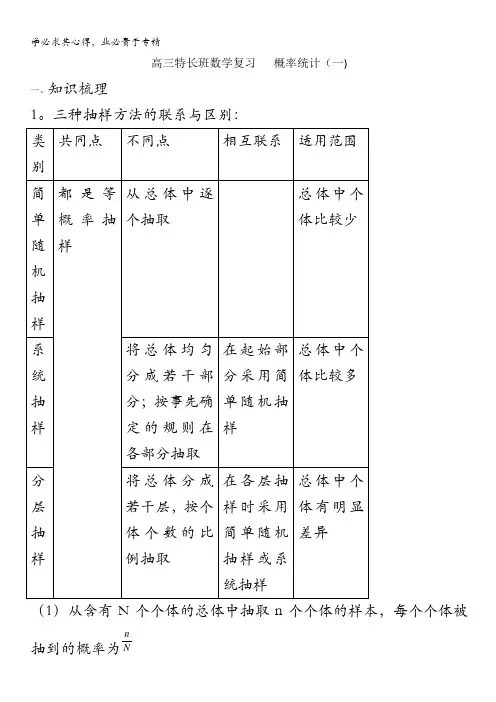
高三特长班数学复习概率统计(一)一、知识梳理1。
三种抽样方法的联系与区别:(1)从含有N个个体的总体中抽取n个个体的样本,每个个体被n抽到的概率为N(2)系统抽样的步骤: ①将总体中的个体随机编号;②将编号分段;③在第1段中用简单随机抽样确定起始的个体编号;④按照事先研究的规则抽取样本。
(3)分层抽样的步骤:①分层;②按比例确定每层抽取个体的个数;③各层抽样;④汇合成样本.(4) 要懂得从图表中提取有用信息如:在频率分布直方图中①小矩形的面积=组距组距频率=频率②众数是最高矩形的中点的横坐标③中位数的左边与右边的直方图的面积相等,可以由此估计中位数的值2.方差和标准差都是刻画数据波动大小的数字特征,一般地,设一组样本数据1x ,2x ,…,n x,其平均数为-x 则方差 ,标准差3.古典概型的概率公式:如果一次试验中可能出现的结果有n 个,而且所有结果都是等可能的,如果事件A 包含m 个结果,那么事件A 的概率P=特别提醒:古典概型的两个共同特点:错误!,即试中有可能出现的基本事件只有有限个,即样本空间Ω中的元素个数是有限的;错误!,即每个基本事件出现的可能性相等。
4. 几何概型的概率公式: P (A )=积)的区域长度(面积或体试验的全部结果所构成积)的区域长度(面积或体构成事件A特别提醒:几何概型的特点:试验的结果是无限不可数的;错误!每个结果出现的可能性相等.二、夯实基础(1)某单位有职工160名,其中业务人员120名,管理人员16名,后勤人员24名。
为了解职工的某种情况,要从中抽取一个容量为20的样本.若用分层抽样的方法,抽取的业务人员、管理人员、后勤人员的人数应分别为____________。
(2)某赛季,11场比赛,, A .19、13 B .13、19 C .20、18 D .18、20(3)统计某校1000及格,不低于80优秀率为 。
(4 9.4 8.4 9.4 9.9 9。
6 9。
专题限时集训(十七)A[第17讲 概率统计](时间:10分钟+35分钟)1.由一组样本数据(x 1,y 1),(x 2,y 2),…,(xn ,yn )得到回归直线方程y ︿=bx +a ,那么下面说法错误的是( )A .直线y ︿=bx +a 必经过点(x ,y ) B .直线y ︿=bx +a 至少经过点(x 1,y 1),(x 2,y 2),…,(xn ,yn )中的一个点C .直线y ︿=bx +a 的斜率b =∑i =1nxiyi -n x y ∑i =1nx 2i -n x 2D .直线y ︿=bx +a 和各点(x 1,y 1),(x 2,y 2),…,(xn ,yn )的偏差∑i =1n[yi -(bxi +a )]2是该坐标平面上所有直线与这些点的偏差中最小的2.从正六边形的6个顶点中随机选择4个顶点,则以它们作为顶点的四边形是矩形的概率等于( )A.110B.18C.16D.15 3.某工厂质检员每隔10分钟从传送带某一位置取一件产品进行检测,这种抽样方法是( )A .分层抽样B .简单随机抽样C .系统抽样D .以上都不对4.有一个容量为66的样本,数据的分组及各组的频数如下: [11.5,15.5) 2;[15.5,19.5) 4;[19.5,23.5) 9; [23.5,27.5) 18;[27.5,31.5) 11;[31.5,35.5) 12; [35.5,39.5) 7;[39.5,43.5) 3.根据样本的频率分布估计,大于或等于31.5的数据约占( ) A.211 B.13 C.12 D.233.为了解儿子身高与其父亲身高的关系,随机抽取5对父子身高数据如下父亲身高x (cm)174 176 176 176 178 儿子身高y (cm)175 175 176 177 177则y 对x 的线性回归方程为( ) A .y =x -1 B .y =x +1C .y =88+12x D .y =1764.某产品的广告费用x 与销售额y 的统计数据如下表:广告费用x (万元)4 2 35 销售额y (万元)49 26 39 54 根据上表可得回归方程y ︿=bx +a 中的b 为9.4,据此模型预报广告费用为6万元时,销售额约为( )A .63.6万元B .65.5万元C .67.7万元D .72.0万元5.博才实验中学共有学生1600名,为了调查学生的身体健康状况,采用分层抽样法抽取一个容量为200的样本.已知样本容量中女生比男生少10人,则该校的女生人数是________.6.曲线C 的方程为x 2m 2+y 2n 2=1,其中m 、n 是将一枚骰子先后投掷两次所得点数,事件A =方程x 2m 2+y 2n 2=1表示焦点在x 轴上的椭圆,那么P (A )=________.7.在一项打鼾与患心脏病的调查中,共调查了1671人,经过计算K 2=27.63,根据这一数据分析,我们有理由认为打鼾与患心脏病是________的(填“有关”或“无关”).8.某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n 小块地,在总共2n 小块地中,随机选n 小块地种植品种甲,另外n 小块地种植品种乙.(1)假设n =2,求第一大块地都种植品种甲的概率;(2)试验时每大块地分成8小块,即n =8,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:品种甲403 397 390 404 388 400 412 406 品种乙419 403 412 418 408 423 400 413 分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?附:样本数据x 1,x 2,…,xn 的样本方差s 2=1n [(x 1-x )2+(x 2-x )2+…+(xn -x )2],其中x 为样本平均数.9.某校高三某班的一次测试成绩的茎叶图、频率分布直方图及频率分布表中的部分数据如下,请据此解答如下问题:(1)求班级的总人数;(2)将频率分布表及频率分布直方图的空余位置补充完整;(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份试卷的分数在[90,100]之间的概率.专题限时集训(十七)B[第17讲 概率统计](时间:10分钟+35分钟)1.关于线性回归,以下说法错误的是( )A .自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系B .在平面直角坐标系中用描点的方法得到的表示具有相关关系的两个变量的一组数据的图形叫做散点图C .线性回归直线方程最能代表观测值x ,y 之间的关系D .任何一组观测值都能得到具有代表意义的回归直线方程 2.对总数为N 的一批零件抽取一个容量为30的样本,若每个零件被抽到的概率为0.25,则N 的值为( )A .120B .200C .150D .1003.在样本的频率分布直方图中,一共有m (m ≥3)个小矩形,第3个小矩形的面积等于其余m -1个小矩形面积之和的14,且样本容量为100,则第3组的频数是( )A .0.2B .25C .20D .以上都不正确4.设(x 1,y 1),(x 2,y 2),…,(xn ,yn )是变量x 和y 的n 个样本点,直线l 是由这些样本点通过最小二乘法得到的线性回归直线(如图17-2),以下结论中正确的是( )图17-2A .直线l 过点(x ,y )B .x 和y 的相关系数为直线l 的斜率C .x 和y 的相关系数在0到1之间D .当n 为偶数时,分布在l 两侧的样本点的个数一定相同1.冶炼某种金属可以用旧设备和改造后的新设备,为了检验用这两种设备生产的产品中所含杂质的关系,对一批产品进行了调查,结果如下表所示:杂质高 杂质低旧设备37 121 新设备22 202根据以上数据,则( )A .含杂质的高低与设备是否改造有关B .含杂质的高低与设备是否改造无关C .设备是否改造决定含杂质的高低D .以上答案都不对2.某校有高一学生300人,高二学生270人,高三学生210人,现教育局督导组欲用分层抽样的方法抽取26名学生进行问卷调查,则下列判断正确的是( )A .高一学生被抽到的概率最大B .高三学生被抽到的概率最大C .高三学生被抽到的概率最小D .每位学生被抽到的概率相等3.在100个零件中,有一级品20个,二级品30个,三级品50个,从中抽取20个作为样本.①采用随机抽样法:抽签取出20个样本;②采用系统抽样法:将零件编号为00,01,…,99,然后平均分组抽取20个样本; ③采用分层抽样法:从一级品,二级品,三级品中抽取20个样本. 下列说法中正确的是( )A .无论采用哪种方法,这100个零件中每一个零件被抽到的概率都相等B .①②两种抽样方法,这100个零件中每一个零件被抽到的概率都相等;③并非如此C .①③两种抽样方法,这100个零件中每一个零件被抽到的概率都相等;②并非如此D .采用不同的抽样方法,这100个零件中每一个零件被抽到的概率是各不相同的 4.某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图17-3).根据频率分布直方图,推测这3000名学生在该次数学考试中成绩小于60分的学生数是________.5.一般来说,一个人脚越长,他的身高就越高.现对10名成年人的脚长x 与身高y 进行测量,得如下数据(单位:cm):x 20 21 22 23 24 25 26 27 28 29 y 141 146 154 160 169 176 181 188 197 203 作出散点图后,发现散点在一条直线附近.经计算得到一些数据:x =24.5,y =171.5,∑i =110x 2i =6085,∑i =110y 2i =298173,∑i =110xiyi =42595. 某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长26.5 cm ,请你估计案发嫌疑人的身高为________cm.6.调查了某地若干户家庭的年收入x (单位:万元)和年饮食支出y (单位:万元),调查显示年收入x 与年饮食支出y 具有线性相关关系,并由调查数据得到y 对x 的回归直线方程:y ︿=0.254x +0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.7.20世纪50年代,日本熊县水俣市的许多居民都感到运动失调、四肢麻木等症状,人们称为水俣病,后经调查是因为人们吃了被甲基汞污染的罗非鱼造成的.法律规定食品的汞含量不得超过1.00 ppm.现从一大批罗非鱼中随机抽取6条做样本,经检验得每条鱼的汞含量的茎叶图(以小数点前一位数字为茎,小数点后一位数字为叶)如图17-4所示,若从这6条鱼中,随机抽出2条.(1)求恰有1条鱼汞超标的概率;(2)求至多有1条鱼汞超标的概率.罗非鱼的汞含量(ppm)0132 111 2图17-48.某校对高三年级800名男生的身高(单位:cm)进行了统计,随机抽取的一个容量为50的样本的频率分布直方图的部分图形如图17-5所示,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.(1)估计这所学校高三年级全体男生身高180 cm以上(含180 cm)的人数;(2)求第六组、第七组的频率并补充完整频率分布直方图;(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x、y,求满足|x-y|≤5的事件概率.专题限时集训(十七)A【基础演练】1.B 【解析】 回归直线方程y ︿=bx +a 经过样本点的中心(x ,y ),可能不经过(x 1,y 1),(x 2,y 2),…,(x n ,y n )中的任何一点,这些点分布在这条直线附近.2.D 【解析】 假设正六边形的六个顶点分别为A 、B 、C 、D 、E 、F ,则从6个顶点中任取4个共有15种基本结果,所取四个点构成矩形四个顶点的结果数为3,所以概率为15.3.C 【解析】 按照一定的规律进行抽取为系统抽样. 4.B 【解析】 根据各组数据有12+7+366=2266=13,所以选B.【提升训练】1.D 【解析】 该题考查线性回归的实际应用.由条件知,消费水平为7.675千元时,人均工资为7.675-1.5620.66≈9.262(千元).故7.6759.262×100%≈83%.2.B 【解析】 该学校共有2000人,抽取一个容量为60的样本,设高三抽x 人,则x 500=602000,因此x =15. 3.C 【解析】 由表中数据知回归直线是上升的,首先排除D.x =176,y =176,由线性回归性质知:点(x ,y )=(176,176)一定在回归直线上,代入各选项检验,只有C 符合,故选C.4.B 【解析】 x =4+2+3+54=3.5,y =49+26+39+544=42,由于回归方程过点(x ,y ),所以42=9.4×3.5+a ,解得a =9.1,故回归方程为y ︿=9.4x +9.1,所以当x =6时,y =6×9.4+9.1=65.5.5.760 【解析】 设该校女生人数为x ,则男生人数为(1600-x ).由已知,2001600×(1600-x )-2001600·x =10,解得x =760.故该校的女生人数是760.6.512【解析】 试验中所含基本事件个数为36;若想表示椭圆则前后两次的骰子点数不能相同,则去掉6种可能,既然椭圆焦点在x 轴上,则m >n ,又只剩下一半情况,即15种,因此P (A )=1536=512.7.有关 【解析】 K 2>10.828,有99.9%的把握说打鼾与患心脏病有关. 8.【解答】 (1)设第一大块地中的两小块地编号为1,2,第二大块地中的两小块地编号为3,4,令事件A 为“第一大块地都种品种甲”.从4小块地中任选2小块地种植品种甲的基本事件共6个: (1,2),(1,3),(1,4),(2,3),(2,4),(3,4). 而事件A 包含1个基本事件:(1,2).所以P (A )=16.(2)品种甲的每公顷产量的样本平均数和样本方差分别为: x 甲=18(403+397+390+404+388+400+412+406)=400,s 2甲=18[32+(-3)2+(-10)2+42+(-12)2+02+122+62]=57.25. 品种乙的每公顷产量的样本平均数和样本方差分别为: x 乙=18(419+403+412+418+408+423+400+413)=412,s 2乙=18[72+(-9)2+02+62+(-4)2+112+(-12)2+12]=56. 由以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两品种的样本方差差异不大,故应该选择种植品种乙.9.【解答】 (1)由茎叶图知分数在[90,100]之间的频数为2.由频率分布直方图知分数在[90,100]之间的频率为0.008×10=0.08.所以全班人数为20.08=25. (2)直方图如下:频率分布表如下:分组 频数 频率 [50,60) 2 0.08 [60,70) 7 0.28 [70,80) 10 0.4 [80,90) 4 0.16 [90,100]20.08(3)将[80,90]之间的4个分数编号为1,2,3,4; [90,100]之间的2个分数编号为5,6.则在[80,100]之间的试卷中任取两份的基本事件为(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15个.其中,至少有一个在[90,100]之间的基本事件有(1,5),(1,6),(2,5),(2,6),(3,5),(3,6),(4,5),(4,6),(5,6),共9个,故至少有一份试卷的分数在[90,100]之间的概率是915=35.专题限时集训(十七)B【基础演练】1.D 【解析】 依据两个变量具有相关关系的意义可知,A 正确;根据散点图的定义得B 正确;根据最小二乘法的思想,所求得的回归直线,满足一组数据对应点到该直线的偏差的平方和最小,即线性回归直线方程最能代表观测值x ,y 之间的关系,故C 正确;D 不正确.2.A 【解析】 因为从含有N 个个体的总体中抽取一个容量为30的样本时,在整个抽样过程中各个个体被抽到的概率为30N ,所以30N=0.25,从而有N =120.故选A.3.C 【解析】 第3组的频率是15,样本容量为100,∴第3组的频数为100×15=20.4.A 【解析】 由题设给出的图象知两变量负相关,则相关系数为负值,则C 错,相关系数r 是研究相关性大小的,b 为直线的斜率,则B 错,回归分析得到的直线为与所有点距离和最小的,与点在直线两边的个数无关,D 错,故答案为A.【提升训练】1.A 【解析】 由已知数据得到如下2×2列联表:杂质高 杂质低 合计 旧设备 37 121 158 新设备 22 202 224 合计59323382由公式K 2=382×(37×202-121×22)2158×224×59×323≈13.11,由于13.11>10.828,故有99.9%的把握认为含杂质的高低与设备是否改造是有关的. 2.D 【解析】 本题考查分层抽样,被抽到的概率一样.3.A 【解析】 三种抽样方法,每一种个体被抽到的概率均等于20100=15.4.600 【解析】 设满足所求条件的学生人数为x 名,由频率分布直方图可知200名学生中60分以下学生为200×(0.002+0.006+0.012)×10=40(名).又x 3000=40200,即x =600.5.185.5 【解析】 由已知得b =10i =1x i y i -10x y 10i =1x 2i -10x2=7,a =y -b x =0,故y ︿=7x .当x =26.5时,y =185.5.6.0.254 【解析】 由题意得y ︿2-y ︿1=[0.254(x +1)+0.321]-[0.254x +0.321]=0.254,即家庭年收入每增加1万元,年饮食支出平均增加0.254万元.7.【解答】 记这4条没被污染的罗非鱼分别为a ,b ,c ,d,2条被污染的罗非鱼分别为e ,f .则选取罗非鱼的所有可能结果为ab ,ac ,ad ,ae ,af ,bc ,bd ,be ,bf ,cd ,ce ,cf ,de ,df ,ef ,基本事件数为15.(1)记“从这6条鱼中,随机地抽出2条,恰有1条鱼汞超标”为事件A ,可能结果为ae,af,be,bf,ce,cf,de,df,基本事件数为8.∴P(A)=815.(2)记“至多有1条鱼汞超标”为事件B,“2条鱼都汞超标”为事件C,其可能结果为ef,故P(C)=1 15,∴P(B)=1-P(C)=1-115=1415.8.【解答】(1)由频率分布直方图知,前五组频率为(0.008+0.016+0.04+0.04+0.06)×5=0.82,后三组频率为1-0.82=0.18,故这所学校高三男生身高在180 cm以上(含180 cm)的人数为800×0.18=144人.(2)由频率分布直方图得第八组频率为0.008×5=0.04,人数为0.04×50=2人,后三组人数为0.18×50=9人,设第六组人数为m,则第七组人数为9-2-m=7-m,又m+2=2(7-m),所以m=4,即第六组人数为4人,第七组人数为3人,频率分别为0.08,0.06.频率除以组距分别等于0.016,0.012,补全频率分布直方图如下:(3)由(2)知身高在第六组的人数为4人,设为a,b,c,d,身高在第八组的人数为2人,设为A,B.若抽取的两人同在第六组,有ab,ac,ad,bc,bd,cd共6种情况,若抽取的两人同在第八组,有AB共一种情况;若抽取的两人分别在两组内时,有aA,bA,cA,dA,aB,bB,cB,dB共8种情况.所以基本事件的总数为6+8+1=15种.事件|x-y|≤5所包含的基本事件个数有6+1=7种,故P(|x-y|≤5)=7 15.。