
全等三角形的判定题型
类型一、全等三角形的判定1——“边边边”
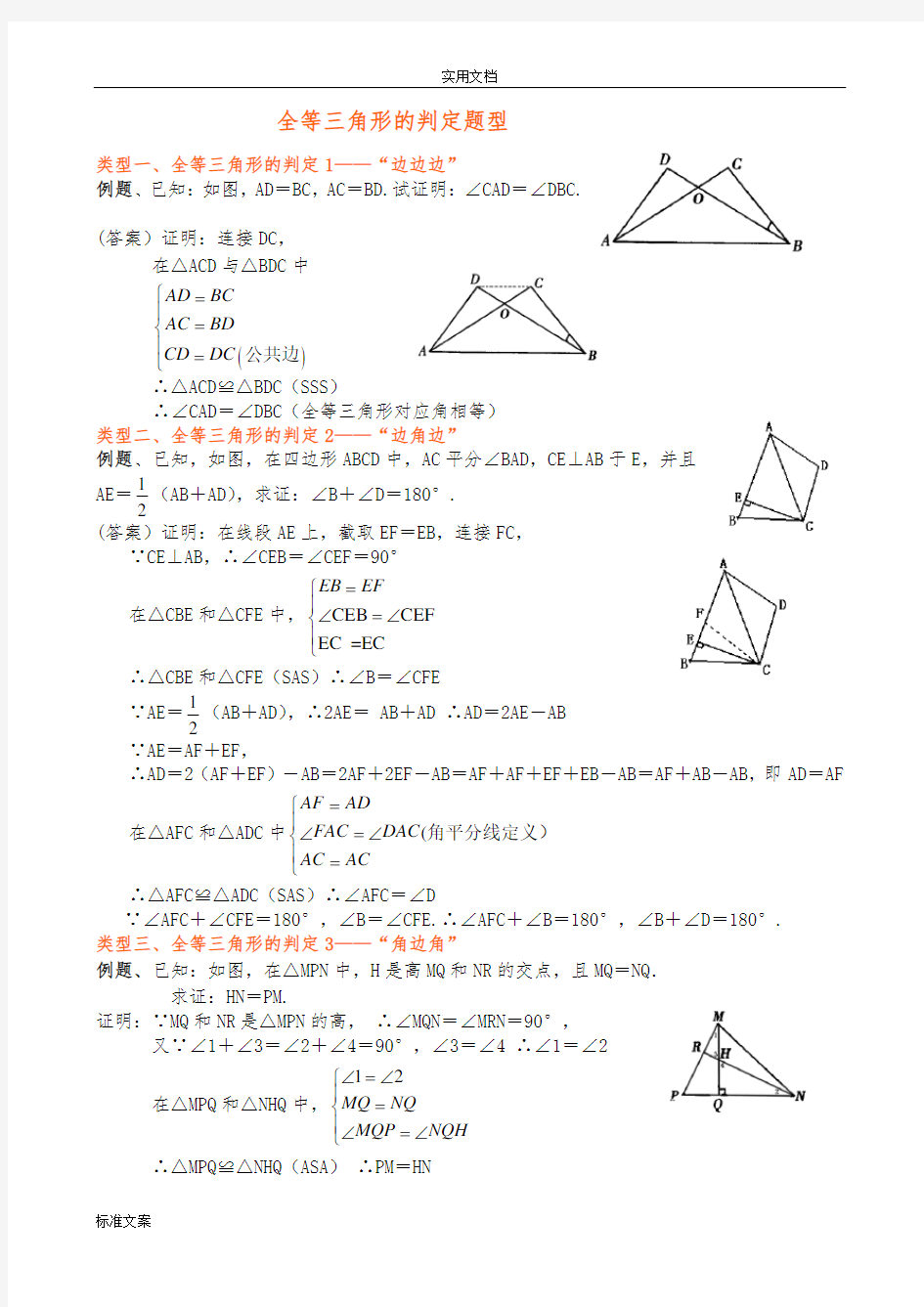
例题、已知:如图,AD =BC ,AC =BD.试证明:∠CAD =∠DBC.
(答案)证明:连接DC ,
在△ACD 与△BDC 中
()AD BC AC BD
CD DC ?=?=??=?
公共边 ∴△ACD ≌△BDC (SSS )
∴∠CAD =∠DBC (全等三角形对应角相等)
类型二、全等三角形的判定2——“边角边”
例题、已知,如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,并且
AE =12
(AB +AD ),求证:∠B +∠D =180°. (答案)证明:在线段AE 上,截取EF =EB ,连接FC ,
∵CE ⊥AB ,∴∠CEB =∠CEF =90°
在△CBE 和△CFE 中,CEB CEF EC =EC EB EF =??∠=∠???
∴△CBE 和△CFE (SAS )∴∠B =∠CFE
∵AE =12
(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB ∵AE =AF +EF ,
∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF
在△AFC 和△ADC 中(AF AD FAC DAC AC AC =??∠=∠??=?
角平分线定义)
∴△AFC ≌△ADC (SAS )∴∠AFC =∠D
∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°. 类型三、全等三角形的判定3——“角边角”
例题、已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .
求证:HN =PM.
证明:∵MQ 和NR 是△MPN 的高, ∴∠MQN =∠MRN =90°,
又∵∠1+∠3=∠2+∠4=90°,∠3=∠4 ∴∠1=∠2
在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠??=??∠=∠?
∴△MPQ ≌△NHQ (ASA ) ∴PM =HN
类型四、全等三角形的判定4——“角角边”
例题、已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D 点旋转,它的两边分别交AC、CB于E、F.当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证
1
2
DEF CEF ABC
S S S
+=
△△△
;当∠EDF绕D点旋转到DE和AC不垂直时,在图2情况下,上述结论是否成立?若成立,请给予证明;若不成立,请写出你的猜想,不需证明.
解:图2成立;证明图2:过点D作DM AC DN BC
⊥⊥
,
则90
DME DNF MDN
∠=∠=∠=°
在△AMD和△DNB中,
AMD=DNB=90
A B
AD BD
∠∠?
?
?
∠=∠
?
?=
?
∴△AMD≌△DNB(AAS)∴DM=DN ∵∠MDE+∠EDN=∠NDF+∠EDN=90°,∴∠ MDE=∠NDF
在△DME与△DNF中,
90
EMD FDN
DM DN
MDE NDF
∠=∠=?
?
?
=
?
?∠=∠
?
∴△DME≌△DNF(ASA)∴
DME DNF
S S
=
△△
∴
DEF CEF
DMCN DECF
S=S=S S.
+
△△
四边形四边形
可知
ABC
DMCN
1
S=S
2△
四边形
,∴
1
2
DEF CEF ABC
S S S
+=
△△△
类型五、直角三角形全等的判定——“HL”
下列说法中,正确的画“√”;错误的画“×”,并举出反例画出图形.
(1)一条直角边和斜边上的高对应相等的两个直角三角形全等.()
(2)有两边和其中一边上的高对应相等的两个三角形全等.()
(3)有两边和第三边上的高对应相等的两个三角形全等.()
(答案)(1)√;(2)×;在△ABC和△DBC中,AB=DB,AE和DF是其中一边上的高,AE=DF
(3)×. 在△ABC和△ABD中,AB=AB,AD=AC,AH为第三边上的高,如下图:
1、已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.求证:AB∥DC.
(答案与解析)证明:∵DE⊥AC,BF⊥AC,
∴在Rt △ADE 与Rt △CBF 中.AD BC DE BF ???
=,=∴Rt △ADE ≌Rt △CBF (HL ) ∴AE =CF ,DE =BF ∴AE +EF =CF +EF ,即AF =CE
在Rt △CDE 与Rt △ABF 中,DE BF DEC BFA EC FA =??∠=∠??=?
∴Rt △CDE ≌Rt △ABF (SAS )∴∠DCE =∠BAF ∴AB ∥DC.
(点评)从已知条件只能先证出Rt △ADE ≌Rt △CBF ,从结论又需证Rt △CDE ≌Rt △ABF.我们可
以从已知和结论向中间推进,证出题目.
2、如图,△ABC 中,∠ACB =90°,AC =BC ,AE 是BC 边上的中线,
过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于D.
(1)求证:AE =CD ;
(2)若AC =12cm ,求BD 的长.
(答案与解析)(1)证明:∵DB ⊥BC ,CF ⊥AE ,∴∠DCB +∠D =∠DCB +∠AEC =90°.
∴∠D =∠AEC .
又∵∠DBC =∠ECA =90°,且BC =CA ,∴△DBC ≌△ECA (AAS ).∴AE =CD .
(2)解:由(1)得AE =CD ,AC =BC ,∴△CDB ≌△AEC (HL ) ∴BD =EC =12BC =12
AC ,且AC =12.
∴BD =6cm .
(点评)三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件
三角形角平分线的性质
三角形三条角平分线交于三角形内部一点,此点叫做三角形的内心且这一点到三角形三边的距离相等.
三角形的一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三
角形的旁心.三角形有三个旁心.所以到三角形三边所在直线距离相等的点共有
4个.如图所示:△ABC 的内心为1P ,旁心为234,,P P P ,这四个点到△ABC 三边所
在直线距离相等.
角的平分线的性质及判定
1、如图,AD 是∠BAC 的平分线,DE ⊥AB ,交AB 的延长线于点E ,DF ⊥AC
于点F ,且DB =DC.求证:BE =CF.
(答案)证明:∵DE ⊥AE ,DF ⊥AC ,AD 是∠BAC 的平分线, ∴DE =DF ,∠BED =∠DFC =90°
在Rt △BDE 与Rt △CDF 中,DB DC DE DF
=??=?,∴Rt △BDE ≌Rt △CDF (HL ) ∴BE =CF
2、如图,AC=DB ,△PAC 与△PBD 的面积相等.求证:OP 平分∠AOB .
(答案与解析)
证明:作PM ⊥OA 于M ,PN ⊥OB 于N
12PAC S AC PM =g △∵,12
PBD S BD PN =g △,且PAC S =△PBD S △ ∴ 12AC PM g 12
BD PN =g 又∵AC =BD ∴PM =PN
又∵PM ⊥OA ,PN ⊥OB ∴OP 平分∠AOB
(点评)观察已知条件中提到的三角形△PAC 与△PBD ,显然与全等无关,而面积相等、底边
相等,于是自然想到可得两三角形的高线相等,联系到角平分线判定定理可得.跟三
角形的高结合的题目,有时候用面积会取得意想不到的效果.
3、如图,DC ∥AB ,∠BAD 和∠ADC 的平分线相交于E ,过E 的直线
分别交DC 、AB 于C 、B 两点. 求证:AD =AB +DC.
(答案) 证明:在线段AD 上取AF =AB ,连接EF ,
∵AE 是∠BAD 的角平分线,∴∠1=∠2,
∵AF =AB AE =AE ,∴△ABE ≌△AFE ,∴∠B =∠AFE
由CD ∥AB 又可得∠C +∠B =180°,∴∠AFE +∠C =180°,
又∵∠DFE +∠AFE =180°,∴∠C =∠DFE ,
∵DE 是∠ADC 的平分线,∴∠3=∠4,
又∵DE =DE ,∴△CDE ≌△FDE ,∴DF =DC ,
∵AD =DF +AF ,∴AD =AB +DC .
类型一、全等三角形的性质和判定
如图,已知:AE ⊥AB ,AD ⊥AC ,AB =AC ,∠B =∠C ,
求证:BD =CE.
(答案)证明:∵AE ⊥AB ,AD ⊥AC , ∴∠EAB =∠DAC =90°
∴∠EAB +∠DAE =∠DAC +∠DAE ,即∠DAB =∠EAC.
在△DAB 与△EAC 中,DAB EAC AB AC B C ∠=∠??=??∠=∠?
∴△DAB ≌△EAC (SAS ) ∴BD =CE.
类型二、巧引辅助线构造全等三角形
(1).作公共边可构造全等三角形:
1、在ΔABC 中,AB =AC.求证:∠B =∠C
(答案)证明:过点A 作AD ⊥BC 在Rt △ABD 与Rt △ACD 中AB AC AD AD =??=?
∴Rt △ABD ≌Rt △ACD (HL ) ∴∠B =∠C.
(2).倍长中线法:
1、已知:如图所示,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.
求证:CD=2CE.
(答案)证明:延长CE至F使EF=CE,连接BF.
∵ EC为中线,∴ AE=BE.
在△AEC与△BEF中,
,
,
,
AE BE
AEC BEF
CE EF
=
?
?
∠=∠
?
?=
?
∴△AEC≌△BEF(SAS).
∴ AC=BF,∠A=∠FBE.(全等三角形对应边、角相等)
又∵∠ACB=∠ABC,∠DBC=∠ACB+∠A,∠FBC=∠ABC+∠A.∴ AC=AB,∠DBC=∠FBC.∴ AB=BF.
又∵ BC为△ADC的中线,∴ AB=BD.即BF=BD.
在△FCB与△DCB中,
,
,
,
BF BD
FBC DBC
BC BC
=
?
?
∠=∠
?
?=
?
∴△FCB≌△DCB(SAS).∴ CF=CD.即CD=2CE.
2、若三角形的两边长分别为5和7, 则第三边的中线长x的取值范围是( )
A.1 <x< 6
B.5 <x< 7
C.2 <x< 12
D.无法确定
(答案)A ;提示:倍长中线构造全等三角形,7-5<2x<7+5,所以选A选
项.
(3).作以角平分线为对称轴的翻折变换构造全等三角形:
如图,AD是ABC
?的角平分线,H,G分别在AC,AB上,且HD=BD.
(1)求证:∠B与∠AHD互补;
(2)若∠B+2∠DGA=180°,请探究线段AG与线段AH、HD之间满足的等量关系,并加以
证明.
(答案)证明:(1)在AB上取一点M, 使得AM=AH, 连接DM.
∵∠CAD=∠BAD, AD=AD, ∴△AHD≌△AMD. ∴ HD=MD, ∠AHD=∠AMD.
∵ HD=DB, ∴ DB= MD. ∴∠DMB=∠B.
∵∠AMD+∠DMB =180?,∴∠AHD+∠B=180?. 即∠B与∠AHD互补.
(2)由(1)∠AHD=∠AMD, HD=MD, ∠AHD+∠B=180?.
∵∠B+2∠DGA =180?,∴∠AHD=2∠DGA.
∴∠AMD=2∠DGM.
∵∠AMD=∠DGM+∠GDM. ∴ 2∠DGM=∠DGM+∠GDM.
∴∠DGM=∠GDM. ∴ MD=MG.
∴ HD= MG.∵ AG= AM+MG, ∴ AG= AH+HD. (3).利用截长(或补短)法作构造全等三角形:
1、如图,AD是△ABC的角平分线,AB>AC,求证:AB-AC>BD-DC
(答案)
证明:在AB上截取AE=AC,连结DE
∵AD是△ABC的角平分线,∴∠BAD=∠CAD
M G
H
D
C
B A
E
A
在△AED 与△ACD 中?????=∠=∠=AD
AD CAD BAD AC
AE
∴△AED ≌△ADC (SAS )∴DE =DC
在△BED 中,BE >BD -DC
即AB -AE >BD -DC ∴AB -AC >BD -DC
2、如图所示,已知△ABC 中AB >AC ,AD 是∠BAC 的平分线,M 是AD 上任意一点,
求证:MB -MC <AB -AC .
(答案与解析)
证明:∵AB >AC ,则在AB 上截取AE =AC ,连接ME .在△MBE 中,MB -ME <BE (三角形两边之差小于第三边).
在△AMC 和△AME 中,()()()AC AE CAM EAM AM AM =??∠=∠??=?所作,
角平分线的定义,公共边,
∴ △AMC ≌△AME (SAS ).∴ MC =ME (全等三角形的对应边相等).
又∵ BE =AB -AE ,∴ BE =AB -AC ,∴ MB -MC <AB -AC .
(点评)因为AB >AC ,所以可在AB 上截取线段AE =AC ,这时BE =AB -AC ,如果连接EM ,在△
BME 中,显然有MB -ME <BE .这表明只要证明ME =MC ,则结论成立.充分利用角平
分线的对称性,截长补短是关键.
(4).在角的平分线上取一点向角的两边作垂线段.
1、如图所示,已知E 为正方形ABCD 的边CD 的中点,点F 在BC 上,且∠DAE =∠FAE .
求证:AF =AD +CF .
(答案与解析)
证明: 作ME ⊥AF 于M ,连接EF .
∵ 四边形ABCD 为正方形,∴ ∠C =∠D =∠EMA =90°.
又∵ ∠DAE =∠FAE ,∴ AE 为∠FAD 的平分线,∴ ME =DE .
在Rt △AME 与Rt △ADE 中,()()AE AE DE ME =??=
?公用边,
已证,
∴ Rt △AME ≌Rt △ADE(HL).∴ AD =AM(全等三角形对应边相等).
又∵ E 为CD 中点,∴ DE =EC .∴ ME =EC .
在Rt △EMF 与Rt △ECF 中,()(ME CE EF EF =??=?已证,
公用边),
∴ Rt △EMF ≌Rt △ECF(HL).∴ MF =FC(全等三角形对应边相等).
由图可知:AF =AM +MF ,∴ AF =AD +FC(等量代换).
(点评)与角平分线有关的辅助线: 在角两边截取相等的线段,构造全等三角形;在角的平
分线上取一点向角的两边作垂线段. 四边形ABCD为正方形,则∠D=90°.而∠DAE
=∠FAE说明AE为∠FAD的平分线,按常规过角平分线上的点作出到角两边的距离,而E到AD的距离已有,只需作E到AF的距离EM即可,由角平分线性质可知ME=
DE.AE=AE.Rt△AME与Rt△ADE全等有AD=AM.而题中要证AF=AD+CF.根据图
知AF=AM+MF.故只需证MF=FC即可.从而把证AF=AD+CF转化为证两条线段相
等的问题.
2、如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,
且AE垂直BD的延长线于E,
1
2
AE BD
,求证:BD是∠ABC的平分线.
(答案与解析)
证明:延长AE和BC,交于点F,
∵AC⊥BC,BE⊥AE,∠ADE=∠BDC(对顶角相等),∴∠EAD+∠ADE=∠CBD+∠BDC.即∠EAD=∠CBD.
在Rt△ACF和Rt△BCD中.
所以Rt△ACF≌Rt△BCD(ASA).
则AF=BD(全等三角形对应边相等).
∵AE=BD,∴AE=AF,即AE=EF.
在Rt△BEA和Rt△BEF中,
则Rt△BEA≌Rt△BEF(SAS).
所以∠ABE=∠FBE(全等三角形对应角相等),即BD是∠ABC的平分线.
(点评)如果由题目已知无法直接得到三角形全等,不妨试着添加辅助线构造出三角形全等的条件,使问题得以解决.平时练习中多积累一些辅助线的添加方法.
类型三、全等三角形动态型问题
解决动态几何问题时要善于抓住以下几点:
(1)变化前的结论及说理过程对变化后的结论及说理过程起着至关重要的作用;
(2)图形在变化过程中,哪些关系发生了变化,哪些关系没有发生变化;原来的线段
之间、角之间的位置与数量关系是否还存在是解题的关键;
(3)几种变化图形之间,证明思路存在内在联系,都可模仿与借鉴原有的结论与过程,
其结论有时变化,有时不发生变化
1、已知:在△ABC中,∠BAC=90°,AB=AC,点D为射线BC上一动点,连结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)当点D在线段BC上时(与点B不重合),如图1,
求证:CF=BD
(2)当点D运动到线段BC的延长线上时,如图2,
第(1)问中的结论是否仍然成立,并说明理由.
(答案)证明:(1)∵正方形ADEF ∴AD=AF,∠DAF=90°
∴∠DAF-∠DAC=∠BAC-∠DAC,即∠BAD=∠CAF
在△ABD和△ACF中,
AB AC
BAD CAF
AD AF
=
?
?
∠=∠
?
?=
?
∴△ABD≌△ACF(SAS)∴BD=CF
(2)当点D运动到线段BC的延长线上时,仍有BD=CF
此时∠DAF+∠DAC=∠BAC+∠DAC,即∠BAD=∠CAF
在△ABD和△ACF中,
AB AC
BAD CAF
AD AF
=
?
?
∠=∠
?
?=
?
∴△ABD≌△ACF(SAS)∴BD=CF
2、如图(1),△ABC中,BC=AC,△CDE中,CE=CD,现把两个三角形的C点重合,且使∠BCA =∠ECD,连接BE,AD.求证:BE=AD.若将△DEC绕点C旋转至图(2),(3)所示的情况时,其余条件不变,BE与AD还相等吗?为什么?
(答案)证明:∵∠BCA=∠ECD,∴∠BCA-∠ECA=∠ECD-∠ECA,即∠BCE=∠ACD 在△ADC与△BEC中ACD=BCE
AC BC
CD CE
=
?
?
∠∠
?
?=
?
∴△ADC≌△BEC(SAS) ∴BE=AD.
若将△DEC绕点C旋转至图(2),(3)所示的情况时,其余条件不变,BE与AD还相等,因为还是可以通过SAS证明△ADC≌△BEC.
全等三角形证明经典题(含答案) 1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADCBD=DC ∴△ACD ≌△BDE ∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE ∵AB=4即 4-2<2AD <4+21<AD <3∴AD=2 2. 已知:D 是AB 中点,∠ACB=90°,求证:12 CD AB 延长CD 与P ,使D 为CP 中点。连接AP,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB 3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 4. 5. 证明:连接BF 和EF ∵BC=ED,CF=DF,∠BCF=∠EDF ∴三角形BCF 全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF 连接BE 在三 角形BEF 中,BF=EF ∴∠EBF=∠BEF 。 ∵∠ABC=∠AED 。∴∠ABE=∠AEB 。∴AB=AE 。在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴三角形ABF 和三角形AEF 全等。∴∠BAF=∠ EAF(∠1=∠2)。 6. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC A D B C
过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGD DE =DC ∠FDE =∠GDC (对顶角)∴△EFD ≌△CGD EF =CG ∠CGD =∠EFD 又EF ∥AB ∴∠EFD =∠1∠1=∠2 ∴∠CGD =∠2∴△AGC 为等腰三角形,AC =CG 又EF =CG ∴EF =AC 7. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠ C 证明:延长AB 取点E ,使AE =AC ,连接DE ∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD ∴△AED ≌△ACD (SAS ) ∴∠E =∠C ∵AC =AB+BD ∴AE =AB+BD ∵AE =AB+BE ∴BD =BE ∴∠BDE =∠E ∵∠ABC =∠E+∠BDE ∴∠ABC =2∠E ∴∠ABC =2∠C 8. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF ∵CE ⊥AB ∴∠CEB =∠CEF =90° ∵EB =EF ,CE =CE ,∴△CEB ≌△CEF ∴∠B =∠CFE ∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC ∴△ADC ≌△AFC (SAS ) ∴AD =AF ∴AE =AF +FE =AD +BE 9. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。求证:BC=AB+DC 。 在BC 上截取BF=AB ,连接EF ∵BE 平分∠ABC ∴∠ABE=∠FBE 又∵BE=BE ∴⊿ABE ≌⊿FBE (SAS ) ∴∠A=∠BFE ∵AB//CD ∴∠A+∠D=180o ∵∠BFE+∠CFE=180o ∴∠D=∠CFE 又∵∠DCE=∠FCECE 平分∠BCDCE=CE ∴⊿DCE ≌⊿FCE (AAS )∴CD=CF ∴BC=BF+CF=AB+CD 10. 已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C AB ‖ED ,得:∠EAB+∠AED=∠BDE+∠ABD=180度, ∵∠EAB=∠BDE , B A C D F 2 1 E D C B A F E A
一、填空题(每小题4分,共32分). 1.已知:///ABC A B C ??≌,/A A ∠=∠,/B B ∠=∠,70C ∠=?,15AB cm =,则/ C ∠=_________,//A B =__________. 2.如图1,在ABC ?中,AB=AC ,AD ⊥BC 于D 点,E 、F 分别为DB 、DC 的中点,则图中共有全等三 角形_______对. 图1 图2 图3 3. 已知△ABC ≌△A ′B ′C ′,若△ABC 的面积为10 cm 2,则△A ′B ′C ′的面积为______ c m 2,若△A ′B ′C ′的周长为16 cm ,则△ABC 的周长为________cm . 4. 如图2所示,∠1=∠2,要使△ABD ≌△ACD ,需添加的一个条件是________________(只添一个条件即可). 5.如图3所示,点F 、C 在线段BE 上,且∠1=∠2,BC =EF ,若要使△ABC ≌△DEF ,则还需补充一个条件________,依据是________________. 6.三角形两外角平分线和第三个角的内角平分线_____一点,且该点在三角形______部. 7.如图4,两平面镜α、β的夹角 θ,入射光线AO 平行于β,入射到α上,经两 次反射后的出射光线CB 平行于α,则角θ等于________. 8.如图5,直线AE ∥BD ,点C 在BD 上,若AE =4,BD =8,△ABD 的面积为16,则ACE △ 的面积为 ______. 二、选择题(每小题4分,共24分) 9.如图6,AE =AF ,AB =AC ,E C 与BF 交于点O ,∠A =600,∠B =250,则∠E O B 的度数为( ) A 、600 B 、700 C 、750 D 、850 10.△ABC ≌△DEF ,且△ABC 的周长为100 cm ,A 、B 分别与D 、E 对应,且AB =35 cm ,DF =30 cm ,则EF 的长为( ) A .35 cm B .30 cm C .45 cm D .55 cm 11.图7是一个由四根木条钉成的框架,拉动其中两根木条后,它的形状将会改变,若固定其形状,下列有四种加固木条的方法,不能固定形状的是钉在________两点上的木条.( ) A .A 、F B . C 、E C .C 、A D . E 、F 12.要测量河两岸相对的两点A 、B 的距离,先在AB 的垂线BF 上取两点C 、D ,使CD=?BC ,再定出BF 的垂线DE ,使A 、C 、E 在一条直线上,可以证明△EDC ?≌△ABC ,?得到ED=AB ,因此测得ED 的长就是AB 的长(如图8),判定△EDC ≌△ABC 的理由是( ) N A M C B 图7 图8 图9 图10
1、.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N. 求证:∠OAB=∠OBA 证明: ∵OM平分∠POQ ∴∠POM=∠QOM ∵MA⊥OP,MB⊥OQ ∴∠MAO=∠MBO=90 ∵OM=OM ∴△AOM≌△BOM(AAS) ∴OA=OB ∵ON=ON ∴△AON≌△BON(SAS) ∴∠OAB=∠OBA,∠ONA=∠ONB ∵∠ONA+∠ONB=180 ∴∠ONA=∠ONB=90 ∴OM⊥AB 2、如图,在△ABC中,BD=DC,∠1=∠2,求证:AD⊥BC. 解:延长AD至BC于点E, ∵BD=DC∴△BDC是等腰三角形 ∴∠DBC=∠DCB 又∵∠1=∠2∴∠DBC+∠1=∠DCB+∠2 即∠ABC=∠ACB ∴△ABC是等腰三角形 ∴AB=AC 在△ABD和△ACD中 {AB=AC ∠1=∠2 BD=DC ∴△ABD和△ACD是全等三角形(边角边) ∴∠BAD=∠CAD ∴AE是△ABC的中垂线 ∴AE⊥BC ∴AD⊥BC
3、如图:AE、BC交于点M,F点在AM上,BE∥CF,BE=CF。求证:AM是△ABC的中线。 M F E C B A 证明: ∵BE‖CF ∴∠E=∠CFM,∠EBM=∠FCM ∵BE=CF ∴△BEM≌△CFM ∴BM=CM ∴AM是△ABC的中线. 4、10分)AB=AC,DB=DC,F是AD的延长线上的一点。求证:BF=CF F D C B A 在△ABD与△ACD中AB=AC BD=DC AD=AD ∴△ABD≌△ACD ∴∠ADB=∠ADC ∴∠BDF=∠FDC 在△BDF与△FDC中
七年级数学下册《全等三角形》专题练习 1、已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C(做AB=AE交AC于E点) 6、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE(做AD=AF交AB于F点) 8. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。求 证:BC=AB+DC。 C D B A
9、已知:AB 知:如图所示,AB = AD ,BC =DC ,E 、F 分别是DC 、BC 的中点,求证: AE =AF 。 35.在△ABC 中,?=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ?≌CEB ?;②BE AD DE +=; (2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗若成立,请给出证明;若不成立,说明理由. A B C D D C B A F E P E D C B A D C B A M F E C B A F E D C B A F D C B F E D C B A D B C A F E
46. 如图, AB=12, CA⊥AB于A, DB⊥AB于B, 且AC=4m, P点从B向A运动, 每分钟走1m, Q 点从B向D运动, 每分钟走2m,P、Q两点同时出发, 运动几分钟后△CAP≌△PQB 试说明理由. 47、如图(1), 已知△ABC中, ∠BAC=900, AB=AC, AE是过A的一条直线, 且B、C在A、E的异侧, BD⊥AE于D, CE⊥AE于E. (图1) (图2) (图3) (1)试说明: BD=DE+CE. (2) 若直线AE绕A点旋转到图(2)位置时(BD
全等三角形证明经典50题(含答案) 1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 延长AD 到E,使DE=AD, 则三角形ADC 全等于三角形EBD 即BE=AC=2 在三角形ABE 中,AB-BE 4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴⊿ADC≌⊿GDE (AAS )∴EG=AC∵EF//AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=E G ∴EF=AC 5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C 证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C 6. 已知:AC 平分∠BAD ,CE ⊥AB , ∠B+∠D=180°,求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE⊥AB 所以∠CEB=∠CEF=90° 因为EB =EF ,CE =CE , 所以△CEB≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE+∠CFA=180° 所以∠D=∠CFA 因为AC 平分∠BAD 所以∠DAC=∠FAC 又因为AC =AC 所以△ADC≌△AFC(SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE 12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。求证:BC=AB+DC 。 证明:在BC 上截取BF=BA,连接EF.∠ABE=∠FBE,BE=BE,则⊿ABE≌ΔFBE(SAS),∠EFB=∠A;AB 平行于CD, 则:∠A+∠D=180°;又∠EFB+∠EFC=180°,则∠EFC=∠D;又∠FCE=∠DCE,CE=CE,故⊿FCE≌ΔDCE(AAS),FC=CD.所以,BC=BF+FC=AB+CD. 13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F= C D B D E A B A C D F 2 1 E B C 全等三角形难题题型归类及解析 一、角平分线型 角平分线是轴对称图形,所以我们要充分的利用它的轴对称性, 常作的辅助线是:一利用截取一条线段构造全等三角形,二是经过平 分线上一点作两边的垂线 。另外掌握两个常用的结论:角平分 线与平行线构成等腰三角形,角平分线与垂线构成等腰三角 形。 1. 如图,在ΔABC 中,D 是边 BC 上一点,AD 平分∠BAC ,在 AB 上截取 AE=AC , 连结 DE ,已知 DE=2cm ,BD=3cm ,求线段 BC 的长。 A E D 2. 已知:如图所示,BD 为∠ABC 的平分线,AB=BC ,点 P 在 BD 上,PM⊥AD 于 M , ?PN⊥CD 于 N ,判断 PM 与 PN 的关系. A M D P N C B 3. 已知:如图 E 在△ABC 的边 AC 上,且∠AEB=∠ABC 。 (1) 求证:∠ABE=∠C ; (2) 若∠BAE 的平分线 AF 交 BE 于 F ,FD∥BC 交 AC 于 D ,设 AB=5,AC=8,求 DC 的长。 . 2 5、如图所示,已知∠1=∠2,EF⊥AD于P,交BC延长线于M,求证:2∠M=(∠ACB-∠B) A 12 E P B F D C M 6、如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E. 1 (1)若BD平分∠ABC,求证CE=BD; (2)若D为AC上一动点,∠AED如何变化,若变化,求它的变化范围; 若不变,求出它的度数,并说明理由。 C D E B A 8、如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB, 求证:AC=AE+CD. 二、中点型 由中点应产生以下联想: 1、想到中线,倍长中线 全等三角形题型总结 题型一、一线三垂直 1、如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E,(1)求证:BD=AE。 (2)若将MN绕点A旋转,使MN与BC相交于点O,其他条件都不变,BD与AE边相等吗?为什么?(3)BD、CE与DE有何关系? 2、如图,两根旗杆间相距12m,某人从点B沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆AC的高为3m,此人的运动速度为1m/s,求这个人运动了多长时间. 27、王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以 放进一个等腰直角三角板(AC=BC, ∠ABC=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵 木墙之间的距离. 题型二、角平分线与全等 1、如图所示,四边形ABCD中AB=AD,CA平分∠BCD,AE⊥BC,AF⊥CD,图中有无和△ABE全等的三角形?请说明理由。 2.如图,OC是∠AOB的角平分线,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F是OC上除点P、O外的一点,连接DF,EF,则DF与EF的关系如何?证明你的结论. 图 题型三、旋转与全等 1、如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG,(1)观察猜想BE与DC之间的大小关系,并证明你的结论。(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说出旋转过程,若不存在,说明理由。 B A C D E 2、图17,△ABC 和△ADE 都是等腰直角三角形,CE 与BD 相交于点M ,BD 交AC 于点N . 证明:(1)BD =CE ; (2)BD ⊥CE . 图17 3、如图,ABC ?为等边三角形,D 为边BA 延长线上一点,连接CD ,以CD 为一边作等边三角形 CDE ?,连接AE . (1)求证:CBD ?≌CAE ?. (2)判断AE 与BC 的位置关系,并说明理由. 4、如图,AD 是△ABC 的高,E 为AC 上一点,BE 交AD 于F ,具有BF=AC ,FD=CD ,试探究BE 与AC 的位置关 系. A B D C E F 全等三角形证明经典50题(含答案) 1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 延长AD 到E,使DE=AD, 则三角形ADC 全等于三角形EBD 即BE=AC=2 在三角形ABE 中,AB-BE 4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS ) ∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC 5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C 证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB , AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C 6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°, 求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF , CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE 12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。求证:BC=AB+DC 。 证明:在BC 上截取BF=BA,连接EF.∠ABE=∠FBE,BE=BE,则 ⊿ABE ≌ΔFBE(SAS),∠EFB=∠A;AB 平行于CD,则:∠A+∠D=180°;又∠EFB+∠EFC=180°,则∠EFC=∠D;又∠FCE=∠DCE,CE=CE,故⊿FCE ≌ΔDCE(AAS),FC=CD.所以,BC=BF+FC=AB+CD. 13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C AB//ED,AE//BD 推出AE=BD, C D B D C B A F E A B A C D F 2 1 E 全等三角形的证明 全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等. 寻找对应边和对应角,常用到以下方法: (1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边. (2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角. (3)有公共边的,公共边常是对应边. (4)有公共角的,公共角常是对应角. (5)有对顶角的,对顶角常是对应角. (6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角). 要想正确地表示两个三角形全等,找出对应的元素是关键. 全等三角形的判定方法: (1)边角边定理(SAS):两边和它们的夹角对应相等的两个三角形全等. (2)角边角定理(ASA):两角和它们的夹边对应相等的两个三角形全等. (3)边边边定理(SSS):三边对应相等的两个三角形全等. (4)角角边定理(AAS):两个角和其中一个角的对边对应相等的两个三角形全等. (5)斜边、直角边定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.全等三角形的应用:运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线. 拓展关键点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系.而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础. 专题1、常见辅助线的做法 典型例题 找全等三角形的方法: (1)可以从结论出发,寻找要证明的相等的两条线段(或两个角)分别在哪两个可能全等的三角形中; (2)可以从已知条件出发,看已知条件可以确定哪两个三角形全等; (3)可从条件和结论综合考虑,看它们能确定哪两个三角形全等; (4)若上述方法均不可行,可考虑添加辅助线,构造全等三角形。 三角形中常见辅助线的作法: ①延长中线构造全等三角形; ②利用翻折,构造全等三角形; ③引平行线构造全等三角形; ④作连线构造等腰三角形。 常见辅助线的作法有以下几种: 全等三角形_探究题_(各种题型非常全) 探究题讲练 类型1.如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=() A.330° B.315° C.310° D.320° 2.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是() A.50 B.62 C.65 D.68 3.如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(4,4)处,两直角边与坐标轴交于点A和点B。 (1)求OA+OB的值; (2)将直角三角形绕点P逆时针旋转,两直角边与坐标轴交于点A和点B,求OA-OB的值; 类型2.线段间的数量关系 基础练习 1.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证: ①△ADC≌△CEB;②DE=AD+BE; (2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE; (3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明. 2.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠ D=30°,点E落在AB上,DE所在直线交AC所在直线于点F. (1)求证:AF+EF=DE; (2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立; (3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由. 3.如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l,边EF 与边AC重合,且EF=FP. (1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想; (3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由. 全等三角形证明经典50题(含答案) 1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 2. 已知:D 是AB 中点,∠ACB=90°,求证:12 CD AB 延长CD 与P ,使D 为CP 中点。连接AP ,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90 ∴平行四边形ACBP 为矩形 A D B C ∴AB=CP=1/2AB 3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。 ∵ ∠ABC=∠AED 。 ∴ ∠ABE=∠AEB 。 ∴ AB=AE 。 在三角形ABF 和三角形AEF 中 AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。 ∴ ∠BAF=∠EAF (∠1=∠2)。 4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ,可得,∠EFD =CGD DE =DC ∠FDE =∠GDC (对顶角) B A C D F 2 1 E 第十二章 全等三角形 第Ⅰ卷(选择题 共30 分) 一、选择题(每小题3分,共30分) 1.下列说法正确的是( ) A.形状相同的两个三角形全等 B.面积相等的两个三角形全等 C.完全重合的两个三角形全等 D.所有的等边三角形全等 2. 如图所示,a,b,c 分别表示△ABC 的三边长,则下面与△ABC 一定全等的三角形是( ) 3.如图所示,已知△ABE ≌△ACD ,∠1=∠2,∠B=∠C , 下列不正确的等式是( ) A.AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE 4. 在△ABC 和△A /B /C /中,AB=A /B /,∠B=∠B /,补充条件后 仍不一定能保证△ABC ≌△A /B /C /,则补充的这个条件是 ( ) A .BC= B / C / B .∠A=∠A / C .AC=A /C / D .∠C=∠C / 5.如图所示,点B 、C 、E 在同一条直线上,△ABC 与△CDE 都是等边三角形,则下列结论不一定成立的是( ) A.△ACE ≌△BCD B.△BGC ≌△AFC C.△DCG ≌△ECF D.△ADB ≌△CEA 6. 要测量河两岸相对的两点A,B 的距离,先在AB 的垂 线BF 上取两点C,D ,使CD=BC ,再作出BF 的垂线DE , 使A,C,E 在一条直线上(如图所示),可以说明 △EDC ≌△ABC ,得ED=AB ,因此测得ED 的长就是AB 的长,判定△EDC ≌△ABC 最恰当的理由是( ) A.边角边 B.角边角 C.边边边 D.边边角 7.已知:如图所示,AC=CD ,∠B=∠E=90°,AC ⊥CD ,则不 正确的结论是( ) A .∠A 与∠D 互为余角 B .∠A=∠2 C .△ABC ≌△CE D D .∠1=∠2 8. 在△ABC 和△FED 中,已知∠C=∠D ,∠B=∠E ,要判定 这两个三角形全等,还需要条件( ) 第3题图 第5题图 第7题图 第2题图 第6题图 A B C D 全等三角形练习题及答案 1、下列判定直角三角形全等的方法,不正确的是() A、两条直角边对应相等。 B、斜边和一锐角对应相等。 C、斜边和一条直角边对应相等。 D、两锐角相等。 2、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是() A.∠A B.∠B C.∠C D.∠B或∠C 3、下列各条件中,不能作出唯一三角形的是() A.已知两边和夹角 B.已知两角和夹边 C.已知两边和其中一边的对 角 D.已知三边 4、在△ABC与△DEF中,已知AB=DE;∠A=∠D;再加一个条件,却不能判断 △ABC与△DEF全等的 是(). A. BC=EF B.AC=DF C.∠B=∠E D.∠C=∠F 5、使两个直角三角形全等的条件是() A.一锐角对应相等B.两锐角对应相等 C.一条边对应相等D.两条直角边对应相等 6、在△ABC和△A'B'C'中有①AB=A'B',②BC=B'C',③AC=A'C',④∠A=∠A', ⑤∠B=∠B',⑥∠C=∠C',则下列各组条件中不能保证△ABC≌△A'B'C'的是() A、①②③ B、①②⑤ C、①②④ D、②⑤⑥ 7、如图,已知∠1=∠2,欲得到△ABD≌△ACD,还须从下列条件中补选一个,错误的选法是 () A、∠ADB=∠ADC B、∠B=∠C C、DB=DC D、AB=AC 8、如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠BAC的度数为 A. 40° B. 80° C.120° D. 不能确定 9、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=600,∠B=250,则∠EOB的度数为() A.600 B.700C.750D.850 10、如图,已知AB=DC,AD=BC,E.F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( ) A. 150° B.40° C.80° D. 90° 11、①两角及一边对应相等②两边及其夹角对应相等③两边及一边所对的角对应相等④两角及其夹边对应相等,以上条件能判断两个三角形全等的是( ) A.①③ B.②④ C.②③④ D.①②④ 12、下列条件中,不能判定两个三角形全等的是() A.三条边对应相等 B.两边和一角对应相等 C.两角及其一角的对边对应相等 D.两角和它们的夹边对应相等 13、如图,已知,,下列条件中不能判定⊿≌⊿的是() (A)(B) (C)(D)∥ 14、如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠B=30°, 则∠D的度数为(). 初中数学全等三角形常见题目型训练基础 测试卷 初中数学全等三角形常见题型训练基础测试卷 一、单选题(共4道,每道25分) 1.如图,在AB、AC上各取一点D、E,使得AE=AD,连接CD、BE相交于点O,再连接AO.若∠CAO=∠BAO,则图中全等三角形共有() A.3对 B.4对 C.5对 D.6对 2.如图,已知点E在△ABC的外部,点D在BC边上,DE交AC于F,若 ∠1=∠2=∠3,AC=AE。求证:△ABC≌△ADE. 证明:∵∠1=∠2=∠3 ∴∠1+∠DAC=∠2+∠DAC 即∠BAC=∠DAE 又∵∠3=∠B+ ,∠2=∠B+ ∴∠E=∠C 在△ABC和△ADE中 ∴ ①∠DAC,②∠E,③∠C,④,⑤,⑥△ABC≌△ADE(ASA),⑦△ABC≌△ADE(AAS), 以上空缺处依次填写正确的顺序为() A.①②⑤⑦ B.②③⑤⑦ C.①③④⑥ D.②③④⑥ 3.如图,四边形ABCD为正方形,∠ABE=∠DCE=90°,AB=BC=CD=AD,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,∠ABF=∠CBF,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由. 解:垂直.理由如下: 在△ABF与△CBF中 ∴ ∴∠BAF=∠BCF 在Rt△ABE和Rt△DCE中 ∴ ∴∠BAE=∠CDE ∴∠BCF=∠CDE ∵∠CDE+∠DEC=90° ∴∠BCF+∠DEC=90° ∴DE⊥CF ①,②,③,④ ,⑤Rt△ABE≌Rt△DCE(HL),⑥△ABE≌△DCE(SAS),⑦△ABF≌△CBF(SAS),⑧△ABF≌△CBF(SSS), 以上空缺处依次填写正确的顺序 为() A.①⑦④⑥ B.②⑧③⑤ C.①⑦③⑤ D.②⑧④⑥ 4.如图,四边形ABCD中,AB=CD,BC=AD.求证:∠A=∠C. 证明:如图,_________________ 在△ABD和△CDB中 ________________ ∴________________ ∴∠A=∠C(全等三角形对应角相等) ①作直线BD,②连接BD,③作射线 BD,④,⑤,⑥△ABD≌△CDB(SSS),⑦△ABD≌△BCD(SSS),⑧△ABD≌△CDB(SAS), 以上空缺处依次填写正确的顺 序为() 1、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE 2、已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC 3、如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC . 4.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N . 求证:∠OAB =∠OBA 5.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线 交AP 于D .求证:AD +BC =AB . P E D C B A F A E D C B 6.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F , 若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF (2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立 请给予证明;若不成立请说明理由. 7.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积 相等的三角形.(直接写出结果,不要求证明): 8.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线 垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE . O E D C B A F E D C B A 全等三角形经典题型题带答案 ————————————————————————————————作者:————————————————————————————————日期: 全等三角形证明经典50题(含答案) 1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 延长AD 到E,使DE=AD, 则三角形ADC 全等于三角形EBD 即BE=AC=2 在三角形ABE 中,AB-BE 4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC 5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C 证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C 6. 已知:AC 平分∠BAD ,CE ⊥ AB ,∠B+∠D=180°,求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE 12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。求证:BC=AB+DC 。 证明:在BC 上截取BF=BA,连接EF.∠ABE=∠FBE,BE=BE,则⊿ABE ≌ΔFBE(SAS),∠EFB=∠A;AB 平行于CD,则:∠A+∠D=180°;又∠EFB+∠EFC=180°,则∠EFC=∠D;又∠FCE=∠DCE,CE=CE,故⊿FCE ≌ΔDCE(AAS),FC=CD.所以,BC=BF+FC=AB+CD. C D B A B A C D F 2 1 E 全等三角形难题题型归类及解析 一、角平分线型 角平分线是轴对称图形,所以我们要充分的利用它的轴对称性,常作的辅助线是:一利用截取一条线段构造全等三角形,二是经过平分线上一点作两边的垂线。另外掌握两个常用的结论:角平分线与平行线构成等腰三角形,角平分线与垂线构成等腰三角形。 如图,在ΔABC 中,D 是边BC 上一点,AD 平分∠BAC ,在AB 上截取AE=AC ,连结DE ,已知DE=2cm ,BD=3cm ,求线段BC 的长。 已知:如图所示,BD 为∠ABC 的平分线,AB=BC ,点P 在BD 上,PM ⊥AD 于M ,?PN ⊥CD 于N ,判断PM 与PN 的关系. 已知:如图E 在△ABC 的边AC 上,且∠AEB=∠ABC 。 求证:∠ABE=∠C ; 若∠BAE 的平分线AF 交BE 于F ,FD ∥BC 交AC 于D ,设AB=5,AC=8,求DC 的长。 . 5、如图所示,已知∠1=∠2,EF ⊥AD 于P ,交BC 延长线于M ,求证:2∠M=(∠ACB-∠B ) 2 1P F M D B A C E A B C D E P D A C M N 6、如图,已知在△ABC 中,∠BAC 为直角,AB=AC ,D 为AC 上一点,CE ⊥BD 于E . 若BD 平分∠ABC ,求证CE= 1 2 BD ; 若D 为AC 上一动点,∠AED 如何变化,若变化,求它的变化范围;若不变,求出它的度数,并说明理由。 如图,在△ABC 中,∠ABC=60°,AD 、CE 分别平 分 ∠BAC 、∠ACB , 求证:AC=AE+CD . 二、中点型 由中点应产生以下联想: 1、想到中线,倍长中线 利用中心对称图形构造8字型全等三角形 3、在直角三角形中联想直角三角形斜边上的中线 4、三角形的中位线 2、已知:如图,ABC △中,45ABC ∠=°, CD AB ⊥于D ,BE 平分ABC ∠,且BE AC ⊥于E ,与CD 相交于点F H ,是BC 边的中点,连结DH 与BE 相交于点G . (1)求证:BF AC =; (2)求证:1 2 CE BF = E D C B全等三角形题型归类与解析
八年级数学上册 《全等三角形常考题型总结》
全等三角形经典题型50题含答案
专题研究:全等三角形证明方法归纳及典型例题
全等三角形_探究题_(各种题型非常全)教学内容
全等三角形证明经典50题(含答案)
全等三角形练习题(很经典)
全等三角形练习题及答案26384
最新初中数学全等三角形常见题目型训练基础测试卷
全等三角形证明经典50题(含答案)
全等三角形经典题型题带标准答案
全等三角形题型归类及解析