04第四章 图论方法建模2
- 格式:pdf
- 大小:290.11 KB
- 文档页数:11


![[高等教育]图论方法建模](https://uimg.taocdn.com/6af62872e45c3b3567ec8bd7.webp)


§9.2 循环比赛的排名问题问题:n 支球队参加循环比赛,两两交锋,一场决胜,不容平局,“0、1”打分。
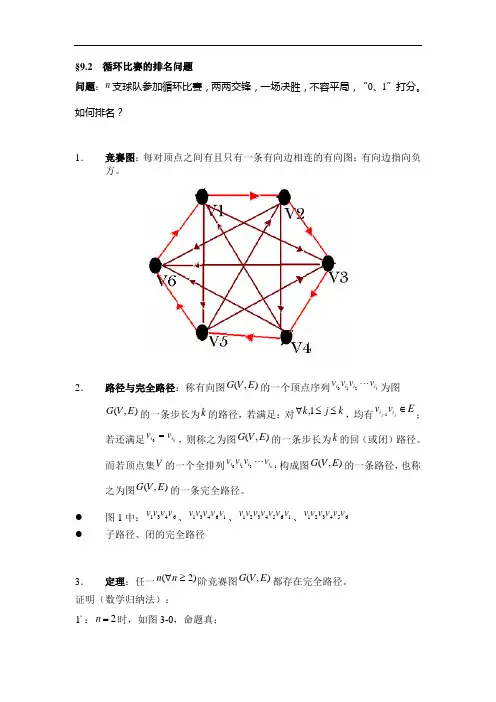
如何排名?1.竞赛图:每对顶点之间有且只有一条有向边相连的有向图;有向边指向负方。
2.路径与完全路径:称有向图),(E V G 的一个顶点序列ki i i i v v v v 210为图),(E V G 的一条步长为k 的路径,若满足:对k j k ≤≤∀1,,均有E v v j j i i ∈-1;若还满足ki i v v =0,则称之为图),(E V G 的一条步长为k 的回(或闭)路径。
而若顶点集V 的一个全排列1210-n i i i i v v v v 构成图),(E V G 的一条路径,也称之为图),(E V G 的一条完全路径。
● 图1中:6431v v v v 、16431v v v v v 、1654321v v v v v v v 、654321v v v v v v ●子路径、闭的完全路径3.定理:任一)2(≥∀n n 阶竞赛图),(E V G 都存在完全路径。
证明(数学归纳法):1:2=n 时,如图3-0,命题真;2:设k n =时命题真;3:当1+=k n 时,设{}121,,,+=k k v v v v V 为顶点集,记{}k v v v V ,,21~=,~G 为图),(E V G 关于{}k v v v V ,,21~=的生成子图;由归纳假设2,在~G 中存在完全路径,不失一般性,设k k v v v v 121...-为~G 中的一条完全路径,考虑顶点1+k v 与{}k v v v V ,,21~=的邻接关系,有如下三种情形:图3-1:k k k v v v v v 1211...-+为G 中的一条完全路径;图3-2:1121...+-k k k v v v v v 为G 中的一条完全路径图3-3:k k i k i v v v v v v v 11121......-+-为G 中的一条完全路径。



数学建模中的图论算法及其应用研究引言:数学建模是指利用数学方法和技巧对实际问题进行分析、抽象、描述、求解和预测的一种研究方法。
图论作为数学建模中的重要工具之一,被广泛应用于各个领域,如网络分析、交通规划、社交网络等。
本文将介绍数学建模中常用的图论算法,并探讨它们在实际问题中的应用。
一、图论基础知识1.1 图的概念图是由一些点和连接这些点的边组成的集合。
点表示图中的实体或对象,边表示实体之间的关系。
图包含了很多重要的信息,例如节点的度、连通性等。
1.2 图的表示方法图可以用邻接矩阵或邻接表来表示。
邻接矩阵是一个二维矩阵,其中的元素表示节点之间是否相连。
邻接表是一个由链表构成的数组,数组的每个元素表示一个节点,每个节点的链表存储了与该节点相连的节点列表。
二、图的遍历算法2.1 深度优先搜索(DFS)深度优先搜索是一种用于图的遍历的算法。
从一个节点出发,递归地访问它的相邻节点,直到所有可达的节点都被访问过为止。
DFS可以用于寻找连通分量、路径搜索等问题。
2.2 广度优先搜索(BFS)广度优先搜索是另一种图的遍历算法。
从一个节点出发,依次访问它的相邻节点,然后再依次访问相邻节点的相邻节点。
BFS可以用于寻找最短路径、网络分析等问题。
三、最短路径算法3.1 Dijkstra算法Dijkstra算法用于寻找图中两个节点之间的最短路径。
它基于贪心策略,从起点开始逐步扩展最短路径,直到到达终点或无法扩展为止。
Dijkstra算法在交通网络规划、电力网络优化等领域有广泛应用。
3.2 Floyd-Warshall算法Floyd-Warshall算法用于寻找图中所有节点之间的最短路径。
它通过动态规划的思想,逐步更新每对节点之间的最短路径。
Floyd-Warshall算法在地理信息系统、通信网络等领域有重要应用。
四、最小生成树算法4.1 Prim算法Prim算法用于寻找连通图的最小生成树。
它从一个起始节点开始,逐步选择与当前生成树距离最近的节点,并将其加入最小生成树中。

![[高等教育]图论方法建模](https://uimg.taocdn.com/07356f8cdd3383c4bb4cd27f.webp)
数学建模中的图论方法一、引言我们知道,数学建模竞赛中有问题A和问题B。
一般而言,问题A是连续系统中的问题,问题B是离散系统中的问题。
由于我们在大学数学教育内容中,连续系统方面的知识的比例较大,而离散数学比例较小。
因此很多人有这样的感觉,A题入手快,而B题不好下手。
另外,在有限元素的离散系统中,相应的数学模型又可以划分为两类,一类是存在有效算法的所谓P类问题,即多项式时间内可以解决的问题。
但是这类问题在MCM中非常少见,事实上,由于竞赛是开卷的,参考相关文献,使用现成的算法解决一个P类问题,不能显示参赛者的建模及解决实际问题能力之大小;还有一类所谓的NP问题,这种问题每一个都尚未建立有效的算法,也许真的就不可能有有效算法来解决。
命题往往以这种NPC问题为数学背景,找一个具体的实际模型来考验参赛者。
这样增加了建立数学模型的难度。
但是这也并不是说无法求解。
一般来说,由于问题是具体的实例,我们可以找到特殊的解法,或者可以给出一个近似解。
图论作为离散数学的一个重要分支,在工程技术、自然科学和经济管理中的许多方面都能提供有力的数学模型来解决实际问题,所以吸引了很多研究人员去研究图论中的方法和算法。
应该说,我们对图论中的经典例子或多或少还是有一些了解的,比如,哥尼斯堡七桥问题、中国邮递员问题、四色定理等等。
图论方法已经成为数学模型中的重要方法。
许多难题由于归结为图论问题被巧妙地解决。
而且,从历年的数学建模竞赛看,出现图论模型的频率极大,比如:AMCM90B-扫雪问题;AMCM91B-寻找最优Steiner树;AMCM92B-紧急修复系统的研制(最小生成树)AMCM94B-计算机传输数据的最小时间(边染色问题)CMCM93B-足球队排名(特征向量法)CMCM94B-锁具装箱问题(最大独立顶点集、最小覆盖等用来证明最优性)CMCM98B-灾情巡视路线(最优回路)等等。
这里面都直接或是间接用到图论方面的知识。
要说明的是,这里图论只是解决问题的一种方法,而不是唯一的方法。
第四章 图论方法建模20 第四章 图论方法建模图论是离散数学的重要分支,是研究离散问题的重要手段,已经建立起来了一些重要的理论和算法,虽然这些理论还不系统、不完备,但是能解决许多的实际问题。
不系统就没有太强的连贯性,这就使得学习起来较为方便,可以随意挑选适宜的内容去学习。
如果将要解决的实际问题归结为图论中的某些概念或某些算法,就可以利用图论中已有的理论,这样就可以较快的解决问题。
在国内外的大学生数学建模竞赛中,利用图论知识去建立数学模型的机会还是很多的。
限于时间与篇幅,我们在本章先学习一些图论知识,愿意深入学习的可以参阅有关的资料。
然后学习一个较为完整的数学建模例子。
§4.1 有关的图论知识——图、算法与矩阵一.图的定义例1.城市之间的运输通路问题A 城与B 城间有通路,为2公里,B 城与C 城间有通路,为1公里,C 城与D 城间有通路,为5公里,D 城与F 城间有通路,为3公里,F 城与A 城间有通路,为7公里,B 城与F 城间有通路,为6公里。
问A 城到D 城的最短路程为多少?用这么长的一段话来表述,听起来太累,想起来也不清楚。
若换一种方式,用下面的图4.1来描述该问题,看起来就清楚多了。
C图4.1由此我们引进图的定义。
定义1:称}),(),({G G E G V G ψ=为一个图,其中φ≠)(G V 叫做顶点集合,E(G)第四章 图论方法建模 21叫做边集合,φ=)()(G E G V I ,而G ψ是关联函数,使G的每条边对应于G的无序顶点对。
若,而,使得)(G E e ∈)(,G V v u ∈uv e G =)(ψ,则称与u 、相关联。
顶点和称为的端点,此时也称和相邻。
e v u v e u v 一个图常常简记为G=(V,E )或G (V,E ),这是因为边集E 中的任一 元素总是和某二顶点相连接的,所以V 、E 确定了,就可以了。
上述例子的图即为:G(V,E),其中V={A,B,C,D,F },E={e 1,e 2,e 3,e 4,e 5,e 6},e 1=AB, e 2=BC, e 3=CD, e 4=DF, e 5=FA, e 6=BF 。
说明:①这里用图表述城市间的运输通路问题很清楚,说明对这类问题,用图来表述是恰当的,“图”是一个强有力的表述工具。
②数学里有“图论”这门学科,一个问题用图表达后,可用图论的知识、算法等来解决此问题。
关于图论方面的知识可参阅有关的书籍、资料。
③若A为一集合,其元素个数记为:|A|。
如上例中的顶点集合和边集的元素个数分别为:|V|=5,|E|=6。
例2.哥尼斯堡(königsberg )七桥问题1736年以前,哥尼斯堡市民热中于一有趣的游戏,在如下图4.2所示的该市桥河图中,从A,B,C,D四块陆地某一处出发,通过每座桥恰好一次,再回到出发地,是否可能?1736年,欧拉(Euler )发表了图论的第一篇论文,证明了七桥问题无解.欧拉就是把A,B,C,D四陆地抽象成为四个点,桥用连接两点的线段表示,于是就得到一个图G(V,E)。
, },,,{D C B A V =},,,,,,{7654321e e e e e e e E =, 这里,e 1=AD, e 2=BD, e 3=CD, e 4=BC, e5=BC, e 6=AB, e 7=AB 。
定义2:图G(V , E)中顶点的度数是指顶点所连的边数。
图G 的度数为图G 中各顶点度数中的最大者。
记为或V v ∈)(v d v Δ)(G Δ。
说明:①七桥问题可归结为一笔画问题。
②关于一笔画问题有如下的结论:若图中每个顶点的度数都为偶数,则可从某点画完每条边,且回到起点。
第四章 图论方法建模22 若图中顶点的度数为奇数的顶点仅仅有两个,则可从此二点中的一个起始,画完每条边到达另一顶点(即不能回到起始点)。
③七桥问题的图中4个顶点的度数为奇数,由上面的结论知,不可能从出发点走完每条边恰好一次,又回到出发点。
定义3:一个图中任意两顶点之间至多有一边,则称之为简单图。
定义4:若图G(V ,E)中边有头尾之分,即E uv ∈vu uv ≠,则称之为有向图。
以后说“图”皆指无向图,要指有向图应特别说明。
并且若无特别说明,我们所说的图皆指简单图。
每对顶点都相邻的图称为完全图。
定理:对于简单图,有:),(E V G ∑∈=)(||2)(G V v E v d 。
二.最短路问题及其算法定义5:在G 中, 其中,...2110k k e v e v e v w =)(G E e i ∈,k i ≤≤1;)(G V v i ∈,;与、关联,称是从到的一条途径,也记为或。
若途径中的边,,……,互不相同,称为迹。
若的顶点,,…,也互不相同,则称为路。
k i ≤≤0i e 1−i v i v w 0v k v ),(0k v v w ),(0k v v 1e 2e k e w w 0v 1v k v w 上述例1中问题的一般提法为:给定连接若干城市的铁路网,寻找两个指定城市间的最短路。
这个问题用图论的语言来描述就是:已知图及每条边的权,对于任意指定的二点、,寻找路,使得),(E V G )(e w 0v )(0G V u ∈),(00u v P )}({)),((min 00P w u v P w P Ω∈=其中是从到的所有路的集合,是路Ω0v 0u )(P w P 上的各边权之和。
解决这一问题可用下面的Dijkstra 算法:(1):令;,;0)(0=v l ∞=)(v l 0v v ≠}{00v S =;0=i ;(2):对每个,用i S v ∉)}()(),(min{v v w v l v l i i +代替,计算)(v l )}({min v l iS v ∉,并把达到这个最小值的一个顶点记为,置1+i v }{11++=i i i v S S U 。
(3):若1−=V i ,则停止。
若1−<V i ,则用1+i 代替,并转入第二步。
i 说明:①当算法结束时,从到的距离(最短路的长度)由标号的终值给出。
即算法求出了至其它所有顶点的最短路的长度。
0v v )(v l 0v ②Dijkstra 算法仅确定了从到所有其它顶点的距离,而并未给出实际最短路。
实际最短路可以很容易确定。
0v ③若只是想计算某指定两点、的最短路(或最短距离)也较为容易求出。
0v 0u第四章 图论方法建模 23三.对集和二部图例3.人员分派问题:工作人员x 1,x 2,……,x n 去做n 项工作y 1,y 2,……,y n ,每人适合做其中一项或几项工作,问能否每人都能被分派一项适合的工作?如果不能,最多几人可以有适合的工作?作为一个简单的例子,我们设n=4,将4个人用4个点表示,将4项工作也用4个点表示,若有某人x i适合作某项工作y j ,则用边连接起来。
这样可以得到一个图如下:定义5:二部图(偶图)是指一个图G(V ,E),V=X ∪Y ,X ∩Y=∅,,X 中无相邻顶点,Y 中亦无相邻顶点。
0||||≠•Y X 定义6:若,)(G E M ⊆M e e j i ∈∀,,与无公共顶点(i e j e j i ≠),则称M 为图G 的对集(或称为匹配)。
M 中的一条边的两个端点叫做在对集中相配;M 中的边的端点叫做被M 许配;若图G 中每个端点皆被M 许配时,M 称为完备对集。
若G 中无使的对集M’,则称M 为最大对集。
|||'|M M >说明:①人员分派问题的图是二部图。
②若人员分派问题的图有完备对集,则可以为每人分派一项适合的工作。
③最多有几个人可以有适合的工作,就是人员分派图中最大对集M 的边数,即|M |。
四.求最大对集的算法定义7:若G 中有一条路,其边交替地在对集M 内外出现,则称此路为M 的交错路,交错路之起止顶点都未被M 许配时,此交错路称为可增广路。
注:若把可增广路上在M 外的边纳入对集,把M 内的边从对集中删除,则被许配的顶点数增加2,对集中的边增加一个。
关于一般图求最大对集的算法,Edmonds 在1965年提出了一种算法。
关于偶图求最大对集的算法有多种。
这里介绍一种偶图求完备对集的算法――匈牙利算法。
设G 为二分图,,求此图的完备对集的匈牙利算法如下:(0):从G 中任意取定一个初始对集M 。
(1):若M 把X 中的顶点都许配,止。
M 即为完备对集;否则取X 中未被M 许配的一顶点u ,记S={u},T=∅。
第四章 图论方法建模24 (2):若N(S)=T ,止。
无完备对集;否则取y ∈N(S)-T 。
(3):若y 是被M 许配的,设yz ∈M ,S ←S ∪{z},T ←T ∪{y},转(2)。
否则,取可增广路P(u,y),令M ←M ΔE(P),转(1)。
说明:①算法的要点是把已有的对集通过可增广路逐次增广以至得到完备对集。
②N(S)={y | y 与S 中的某点相邻}③M ΔE(P)是将可增广路P 中的在M 外的边纳入对集,把M 内的边从对集中删除,该运算结果仍为对集。
五.独立数与色数例4.化学制品的存放问题一家公司制造n 种化学制品,C 1,C 2,……,C n ,其中某些制品是互不相容的,如果它们互相接触则会引起爆炸。
作为一种预防措施,该公司希望把它的仓库分成若干隔间,以便使不相容的药品存放在不同的隔间里。
试问,这个仓库至少应分成几个隔间?为了方便,设n=6,这6种化学制品C 1,C 2,……,C 6分别用6个点代表,它们之间互不相容的制品用一条边连接起来,这样就得到一个图如下所示:定义8:若,I 中任意二顶点不相邻,则称I 为图G 的一个独立集。
,不是独立集,则称I 为极大独立集。
顶点数最多的独立集叫做最大独立集,其顶点数记成)(G V I ⊆I G V u −∈∀)(}{u I ∪)(G α,称为图G 的独立数。
定义9:把图G 的顶点都染上颜色,且使相邻顶点异色,又使所用的颜色数最少,称这个颜色数为G 的顶点色数,记成)(G χ。
定理:1)(+Δ≤G χ,(其中为图G 的度数)。
Δ说明:①每个隔间里存放的化学制品集合即为独立集。
②极大独立集和最大独立集是不同的。
③仓库至少应分成几个隔间就化为求一个图的顶点色数)(G χ,而)(G χ的求法是较为困难的。
虽然也有些算法可求,但都不是十分有效。
六.关联矩阵与邻接矩阵一个图存放在计算机里的方式很多,但一般是以矩阵的方式来存储的。
第四章 图论方法建模 25定义10:设图G(V, E),,},...,,{21γv v v V =},......,,{21εe e e E =,称矩阵()γγ×=ij a G A )(为图G 的邻接矩阵,其中)(G V =γ, ⎪⎩⎪⎨⎧∉∈=).(,0);(,1G E v v G E v v a j i j i ij 称矩阵()εγ×=ij b G B )(为图G 的关联矩阵,其中)(G V =γ,|)(|G E =ε,。