
前饋式類神經網路
1前言
前饋式類神經網路是第一個也是最簡單的類神經網路,它是由多層的神經元所組成,其訊息傳遞的方式是從輸入層經由隱藏層往輸出層的方向傳送,每一層神經元只會接受上層神經元所傳送過來的輸出值,不同於循環式網路(Recurrent network)。
2神經元
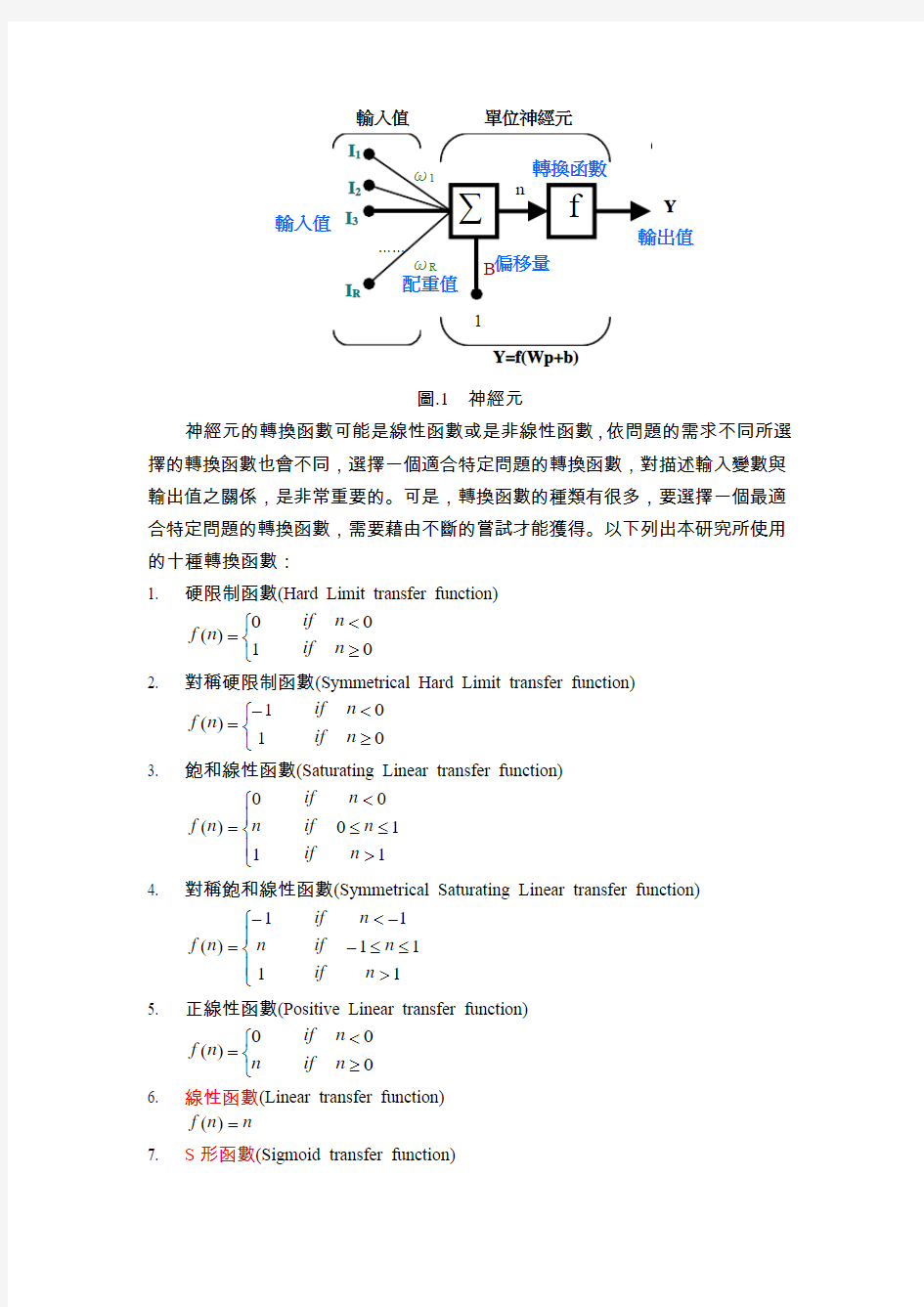
類神經網路最基本單位的是神經元(如圖1),神經元主要負責對資料的處理行為。在類神經網路中的某個神經元,可能接收一個到數個不等的輸入變數,變數的多寡取決於傳送到該神經元的輸入值個數。神經元接收輸入變數(I)後,視輸入變數的重要性,給予一個改變比重的參數,這些參數稱為配重值(Weight, ω),神經元會將所有輸入變數經由配重值的加權後累加,然後再與神經元中的偏移量(Bias, B)相加,會產生一個淨值(n),這個淨值將經由轉換函數的轉換,轉換出來的數值當成該神經元的輸出值。神經元的輸出值可以傳送到一個以上的神經元當作該神經元的輸入變數,或是當成網路的輸出值,一切依網路結構的情況而定。雖然,每個神經元可以同時接收一至多個不等的輸入變數,卻只有一個輸出值。神經元的計算公式如式(1)、(2)所示,
∑=
+?
=
R
j
j
j
B I
n
1
ω(1)
)
(n
f
Y=(2)式中R為神經元輸入變數的個數,I1,I2,?,I R為神經元的輸入變數,ω1,ω2,?,ωR為神經元各個輸入變數的配重值,B為該神經元的偏移量,)
(?
f為神經元的轉換函數。
1
Y
輸入值單位神經元
Y=f(Wp+b)
圖.1神經元
神經元的轉換函數可能是線性函數或是非線性函數,依問題的需求不同所選擇的轉換函數也會不同,選擇一個適合特定問題的轉換函數,對描述輸入變數與輸出值之關係,是非常重要的。可是,轉換函數的種類有很多,要選擇一個最適合特定問題的轉換函數,需要藉由不斷的嘗試才能獲得。以下列出本研究所使用的十種轉換函數:
1. 硬限制函數(Hard Limit transfer function)
?
?
?
≥
<
=
1
)
(
n
if
n
if
n
f
2. 對稱硬限制函數(Symmetrical Hard Limit transfer function)
?
?
?
≥
<
-
=
1
1
)
(
n
if
n
if
n
f
3. 飽和線性函數(Saturating Linear transfer function)
?
?
?
?
?
>
≤
≤
<
=
1
1
1
)
(
n
if
n
if
n
n
if
n
f
4. 對稱飽和線性函數(Symmetrical Saturating Linear transfer function)
?
?
?
?
?
>
≤
≤
-
-
<
-
=
1
1
1
1
1
1
)
(
n
if
n
if
n
n
if
n
f
5. 正線性函數(Positive Linear transfer function)
?
?
?
≥
<
=
)
(
n
if
n
n
if
n
f
6. 線性函數(Linear transfer function)
n
n
f=
)
(
7. S形函數(Sigmoid transfer function)
n
e n
f -+=
11
)( 8. 雙曲正切函數(Hyperbolic Tangent transfer function)
n
n n
n e e e e n f --+-=)(
9. 三角基函數(Triangular basis transfer function)
?????????>≤<-=<≤-+-<=101010
101110
)(n if n if n n if n if n n if n f 10. 高斯函數(Gaussian transfer function)
2
2
)(n e n f -=
3 網路組織架構
前饋式類神經網路結構如圖12所示,數個接收相同輸入變數的神經元並聯組成網路的基礎結構 ? 層,再由數個層串聯組成一個前饋式類神經網路。同一層的神經元接收前一層所有神經元的輸出,並將輸出送至下一層做為下一層每個神經元的輸入變數。依各層的特質又可以區分為輸入層、輸出層和隱藏層三種。
1. 輸入層:輸入層每個神經元只接受一個輸入變數作為其輸入值,並將輸出送
至下一層的每個神經元,所以輸入層神經元的個數等於輸入變數的個數。輸入層有兩種類型,第一種輸入層中的神經元具有配重值與偏移量,且具有轉換函數;第二種輸入層中的神經元只有接收輸入變數的功能,輸出值便是輸入變數,不具有運算的功能,本研究採用第二種類型的輸入層。一般若採用第二種類型的輸入層,不將此層當成一層。
2. 輸出層:輸出層每個神經元的輸出值便是網路的輸出值,所以輸出層神經元
的個數等於網路的輸出值個數。
3. 隱藏層:介於輸入層與輸出層之間的層便是隱藏層,隱藏層的層數可以是
零,也可以很多層,不過最常見的為一層,隱藏層神經元的個數也沒有一定,使用者視資料的複雜度調整隱藏層的層數與該隱藏層神經元的個數。
輸入層 隱藏層1 隱藏層k 輸出層
圖12 前饋式類神經網路結構
前饋式類神經網路是類神經網路最常見到的網路結構(如圖12),這種網路結構神經元間的資料傳遞方向與整個網路資料傳遞的方向相同,每一層的神經元只會接受前一層所有的神經元傳送過來的輸入變數,並經過處理後得到一個新輸出值,也就是說,第一層隱藏層只會接收來自輸入層的輸入變數,而第二層隱藏層只會接收來自第一層隱藏層的輸入變數,依此類推。使用前饋式類神經網路,一定會有輸入層與輸出層。一個非常簡單的問題可以沒有隱藏層,但是,類神經網路要具備處理複雜數據的能力,必須藉助隱藏層的使用,甚至於使用多層隱藏層。
通常不同層有不同的神經元個數和轉換函數。同一層各神經元的轉換函數通常是相同的,也就是說,同一層的神經元有相同的輸入變數與轉換函數,但因為每個神經元內有不同的配重值和偏移量,導致同一層的神經元雖然接收相同的輸入變數,但輸出值卻大不相同。也有可能同一層各神經元有不同的轉換函數,但本研究所開發的程式只提供同一層各個神經元使用相同的轉換函數之功能。
4 資料處理
類神經網路可能具有很多層的網路結構,每一層中又有數個神經元,每一個神經元又有數個網路參數值與輸入變數與輸出值,所以必須對每個參數值、輸入變數與輸出值做一個區別,使每個符號更容易被辨別其所代表的意義。在此用上標來表示其所在的層數,用下標來表示其所在的神經元,輸入變數m j I 代表第m
層的神經元接收來自第m-1層第j 個神經元所傳送過來的輸入變數,1-m j O 代表第m-1層第j 個神經元之輸出值,也就是說1-=m j m j O I 。m j I 所相對應的配重值為m j i ,ω,
其代表意義為第m 層第i 個神經元接收上一層第j 個神經元的輸出值,該神經元的偏移量為m i B 。
舉一個例子(如圖3)來介紹前饋式類神經網路的輸出值與輸入變數之間的關係式,來說明整個類神經網路的計算過程。從圖中的輸入層與輸出層神經元個
數可知,此網路結構會從外界接收一個輸入變數,經過類神經網路的處理後,而得到一個輸出值,而其輸出值與輸入變數間的關係可表示成式(3)的通式。
)(X f Y overall =
(3)
Y
輸入層
隱藏層
輸出層
圖13 一層隱藏層的前饋式網路
首先,本研究認為輸入層中的神經元只有接收輸入變數的功能,而其輸出值就是輸入變數,不具有運算的功能,所以輸入層的輸出值為X 。將輸出值X 傳送到隱藏層各神經元內,當作隱藏層神經元的輸入變數,接著,經由隱藏層神經
元的處理後,隱藏層各神經元的輸出值分別為)(1111,11B X f +?ω、)(1
211,21B X f +?ω與)(1311,31B X f +?ω,其中)(1?f 代表隱藏層的轉換函數。再將隱藏層各神經元的輸
出值傳送到輸出層,當成輸出層神經元的輸入變數,在經由輸出層神經元的處理後,便可得到一個網路輸出值,其值為
])()()([211311,3123,11211,2122,11111,1121,12B B X f B X f B X f f Y ++??++??++??=ωωωωωω
(4)
在式(2-4)中,[]?2f 代表輸出層神經元的轉換函數。
上述的運算過程中,假如網路輸出值與目標值的誤差過大,可依據學習法則來調整各配重值與偏移量,使得網路輸出值與目標值的誤差可以達到要求。
f (n )
-1.0
-0.5
0.0
0.5
1.0-0.2
0.00.20.40.60.8
1.01.2
n 圖2.2 硬限制函數
f (n )
-1.0
-0.5
0.0
0.5
1.0-1.2
-0.8-0.40.0
0.4
0.8
1.2
n 圖2.3 對稱硬限制函數
f (n )
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2-0.2
0.00.20.40.60.8
1.0
1.2
N
圖2.4 飽和線性函數
f (n )
-1.2
-0.6
0.0
0.6
1.2-1.2
-0.8-0.40.00.4
0.8
1.2
n
圖2.5 對稱飽和線性函數
f (n )
-0.4
0.0
0.4
0.8
1.2-0.2
0.00.20.40.60.8
1.0
1.2
n 圖2.6 正線性函數
f (n )
-1.0
-0.5
0.0
0.5
1.0-1.0
-0.5
0.0
0.5
1.0
n 圖2.7 線性函數
f (n )
-6.0
-3.0
0.0
3.0
6.0-0.2
0.00.20.40.60.8
1.0
1.2
n 圖2.8 S 形函數
f (n )
-4.0
-2.0
0.0
2.0
4.0-1.2
-0.8-0.40.00.4
0.8
1.2
n
圖2.9 雙曲正切函數
f (n )
-1.6
-0.8
0.0
0.8
1.6-0.2
0.00.20.40.60.8
1.0
1.2
n
圖2.10 三角基函數
f (n )
-4.0
-2.0
0.0
2.0
4.0-0.2
0.00.20.40.60.8
1.0
1.2
n 圖2.11 高斯函數
前馈神经网络 前馈神经网络的结构一般包含输入层、输出层、及隐含层,隐含层可以是一层或多层。各神经元只接收前一层的输出作为自己的输入,并且将其输出给下一层,整个网络中没有反馈。每一个神经元都可以有任意多个输入,但只允许有一个输出。图1选择只含一个隐含层的前馈神经网络。其原理框图如图1所示。 图中,只有前向输出,各层神经元之间的连接用权值表示。设输入层有M 个输入信号,其中任一输入信号用i ()M i ,2,1 =表示;隐含层有N 个神经元,任一隐含层神经元用j ()N j ,2,1 =表示;输入层与隐含层间的连接权值为()n w ij , ()N j M i ,2,1;,2,1 ==;隐含层与输出层的连接权值为()n w j 。假定隐含层神 经元的输入为()n u j ,输出为()n v j ;输出层神经元的输入为()n o ,网络总输出为 ()n x ~。则此神经网络的状态方程可表示为: ()()()∑+-==M i ij j i n y n w n u 11 ()()[] ()()?? ? ???∑+-===M i ij j j i n y n w f n u f n v 11 ()()()∑==N j j j n v n w n o 1 ()()[]()()?? ????==∑=N j j j n v n w f n o f n x 1~ 图1 三层前馈神经网络结构图 输入层 隐含层 输出层 (y n (1y n -(1y n M -+
式中,()?f 表示隐含层、输出层的输入和输出之间的传递函数,也称为激励函数。 定义代价函数为瞬时均方误差: ()()()()[] ()()()2 12 2~?? ? ????? ????????-=-==∑=N j j j n v n w f n d n x n d n e n J 式中,()n d 为训练信号。 递归神经网络 对角递归神经网络 图2为典型的对角递归神经网络,它具有三层结构,分别为输入层,隐层和输出层,在隐层的权值叠加中,引入了输入的前一时刻的输出作为反馈控制信号。选用这种网络的优点是结构简单,易于实现,可以直观的体现反馈神经网络的结构模式和工作方式。 设输入层与隐层间的连接权值为()n w h ij ()k j m i ,2,1;,,1,0==,隐层与输 出层之间的权值为()n w o j ,递归层的权值为()n w d j 。设输入层的输入为()i n y -, 隐层的输入为()n u j ,输出为()n I j ,输出层的输入为()n v ,输出层的输出为()n x ~,则对角递归神经网络的状态方程为 ()()()()()10-+-=∑=n I n w i n y n w n u j d j m i h ij j 输入层 输出层 隐层 图2 对角递归神经网络的结构 ()y n ()1y n - ()1y n m -+ ()y n m - mj d
多层前馈神经网络 5 多层前馈网络及BP算法 多层前馈网络的反向传播 (BP)学习算法,简称BP算法,是有导师的学习,它是梯度下降法在多层前馈网中的应用。 (a) 网络结构 yu 见下图,、是网络的输入、输出向量,神经元用节点表示,网络由输入层、隐层和输出层节点组成,隐层可一层,也可多层(图中是单隐层),前层至后层节点通过权联接。由于用BP学习算法,所以常称BP神经网络。 I:y:x:每个神经元(节点)的输入;每个神经元(节点)的输出;神经元j w:jji的第个输入。神经元到神经元的连接权 ij ,,y,f(x,,)节点的作用函数:, 为阈值(可设置一个偏置节点代替) 1,f可为线性函数,一般取为Sigmoid函数 , 为很小的数,如0.1 ,x/,1,e (b) BP学习算法 ? 已知网络的输入/输出样本,即导师信号。 ? BP学习算法由正向传播和反向传播组成: ? 正向传播是输入信号从输入层经隐层,传向输出层,若输出层得到了期望
的输出,则学习算法结束;否则,转至反向传播。 ? 反向传播是将误差(样本输出与网络输出之差)按原联接通路反向计算, 由梯度下降法调整各层节点的权值和阈值,使误差减小。 BP学习算法步骤如下: W(0)(1) 设置初始权值,它是较小的随机非零值。 (2) 给定输入/输出样本对,计算网络的输出。 ,,u,u,u,...,u设第p组样本输入: p1p2pnp ,,d,d,d,...,d,p,1,2,..,L 输出: p1p2pmp ypi节点在第组样本输入时,输出为 : ip ,, ,,y(t),fx(t),fw(t)I ----(1式) ,,,ipipijjpj,, Ijpi式中,是在第组样本输入时,节点的第个输入。 jp 1f(,)f(x)s取可微的型作用函数式 = -------(2式) ,x1,e可由输入层隐层至输出层,求得网络输出层节点的输出。 J(1) 计算网络的目标函数 ELp设为在第组样本输入时,网络的目标函数,取范数,则 p2 111222E(t),||d,y(t)||,[d,y(t)],e(t)--------(3式) ,,pppkpkpkp2222kk y(t)pkt式中,是在第组样本输入时,经次权值调整后网络的输出:是p k输出层第个节点。 E(t)J(t),网络的总目标函数: = ----------(4式) p p 作为对网络学习状况的评价。 (2) 判别 J(t),若 ? -------(5式)
第一节、神经网络基本原理 1. 人工神经元( Artificial Neuron )模型 人工神经元是神经网络的基本元素,其原理可以用下图表示: 图1. 人工神经元模型 图中x1~xn是从其他神经元传来的输入信号,wij表示表示从神经元j 到神经元i的连接权值,θ表示一个阈值( threshold ),或称为偏置( bias )。则神经元i的输出与输入的关系表示为: 图中yi表示神经元i的输出,函数f称为激活函数( Activation Function )或转移函数( Transfer Function ) ,net称为净激活(net activation)。若将阈值看成是神经元i的一个输入x0的权重wi0,则上面的式子可以简化为:
若用X表示输入向量,用W表示权重向量,即: X = [ x0 , x1 , x2 , ....... , xn ] 则神经元的输出可以表示为向量相乘的形式: 若神经元的净激活net为正,称该神经元处于激活状态或兴奋状态(fire),若净激活net为负,则称神经元处于抑制状态。 图1中的这种“阈值加权和”的神经元模型称为M-P模型 ( McCulloch-Pitts Model ),也称为神经网络的一个处理单元( PE, Processing Element )。 2. 常用激活函数 激活函数的选择是构建神经网络过程中的重要环节,下面简要介绍常用的激活函数。 (1) 线性函数( Liner Function ) (2) 斜面函数( Ramp Function ) (3) 阈值函数( Threshold Function )
图2 . 阈值函数图像 以上3个激活函数都是线性函数,下面介绍两个常用的非线性激活函数。 (4) S形函数( Sigmoid Function ) 该函数的导函数: (5) 双极S形函数
第三章常用神经网络 3.1前馈型人工神经网络 前馈神经网络是神经网络中的一种典型分层结构,信息从输入层进入网络后逐层向前传递至 输出层。根据前馈网络中神经元转移函数、隐层数以及权值调整规则的不同,可以形成具有各种功 能特点的神经网络。 例如,如果转移函数采用线性阈值函数或符号函数且只有一个输出层(无隐层),或有一个以上的隐层,则分别称为单层感知器和多层感知器;如果转移函数采用非线性连续有界函数且只有一个输出层(无隐层),或有一个以上的隐层,则分别称为单层BP网络和多层BP网络。 3.1.1 线性阈值单元组成的前馈网络 这类前馈网络的转移函数采用线性阈值函数或符号函数。 1.单层感知器 1958年,美国心理学家Frank Rosenblat提出一种具有单层计算单元的神经网络,称为Perception,即感知器。感知器是模拟人的视觉接受环境信息,并由神经冲动进行信息传递。感知器研究中首次提出了自组织、自学习的思想,而且对所能解决的问题存在着收敛算法,并能从数学上严格证明,因而对神经网络的研究起了重要推动作用。单层感知器的结构与功能都非常简单,以 单层感知器(图3-1 神经元基本模型(即MP 基本模型。 1) 图3-1 为第j(j=1,2,…m x n)T,通过一个阈值函数f( 从数学观点来说, 等于0时,输出为1 神经元的连接权值w ji 当输入为X,对于j n i i ji j x w s=∑ =1其输出为:
2 )(1 j n i i ji j x w f y θ+=∑= (3-1) 转移函数f (?)是阈值函数(即单位阶跃函数),故: ??? ??? ? <+≥+=∑∑==0 ,00,11 1j n i i ji j n i i ji j x w x w y θθ (3-2) 通过转移函数,其输出只有两个状态,“1”或“0”,所以,它实际上是输入模式的分类器,即可以辨识输入模式属两类中的那一类。 当单层感知器模型只有1个输出结点时,称为简单感知器,其实就是MP 模型。 对于输出结点为的简单感知器,若输入向量的维数n=2,则向量X 用两维平面上的一个点来表示。设被观察的模式只有A 、B 两类,则: (3-3) A 、 B 两类分别属于集合R 1 (A ∈R 1)、R 2(B ∈R 2),且R 1与R 2是 线性可分的,如图3-2所示。 利用简单感知器的计算式(3-3)可以实现逻辑代数中的一些运算: (1)当取w 1=w 2=1, θ=-1.5时, 完成逻辑“与”的运算功 能,即 x 1∧x 2; (2)当取w 1=w 2=1, θ=-0.5时,完成逻辑“或”的运算功能, 即x 1∨x 2; (3)当取w 1= -1,w 2=0, θ= 1时,完成逻辑“非”的运算功能, 即x 。 若x 1与x 2分别取布尔值,逻辑运算列入表3-1中。 表3-1 逻辑运算表 若净输入为零,便得到一条线性的模式判别函数: ?? ?→→=++=+=∑ =类类 B A x w x w f x w f y i i i 01)()(2 12211θθ图3-2 线性可分两维模式
前饋式類神經網路 1前言 前饋式類神經網路是第一個也是最簡單的類神經網路,它是由多層的神經元所組成,其訊息傳遞的方式是從輸入層經由隱藏層往輸出層的方向傳送,每一層神經元只會接受上層神經元所傳送過來的輸出值,不同於循環式網路(Recurrent network)。 2神經元 類神經網路最基本單位的是神經元(如圖1),神經元主要負責對資料的處理行為。在類神經網路中的某個神經元,可能接收一個到數個不等的輸入變數,變數的多寡取決於傳送到該神經元的輸入值個數。神經元接收輸入變數(I)後,視輸入變數的重要性,給予一個改變比重的參數,這些參數稱為配重值(Weight, ω),神經元會將所有輸入變數經由配重值的加權後累加,然後再與神經元中的偏移量(Bias, B)相加,會產生一個淨值(n),這個淨值將經由轉換函數的轉換,轉換出來的數值當成該神經元的輸出值。神經元的輸出值可以傳送到一個以上的神經元當作該神經元的輸入變數,或是當成網路的輸出值,一切依網路結構的情況而定。雖然,每個神經元可以同時接收一至多個不等的輸入變數,卻只有一個輸出值。神經元的計算公式如式(1)、(2)所示, ∑= +? = R j j j B I n 1 ω(1) ) (n f Y=(2)式中R為神經元輸入變數的個數,I1,I2,?,I R為神經元的輸入變數,ω1,ω2,?,ωR為神經元各個輸入變數的配重值,B為該神經元的偏移量,) (? f為神經元的轉換函數。
1 Y 輸入值單位神經元 Y=f(Wp+b) 圖.1神經元 神經元的轉換函數可能是線性函數或是非線性函數,依問題的需求不同所選擇的轉換函數也會不同,選擇一個適合特定問題的轉換函數,對描述輸入變數與輸出值之關係,是非常重要的。可是,轉換函數的種類有很多,要選擇一個最適合特定問題的轉換函數,需要藉由不斷的嘗試才能獲得。以下列出本研究所使用的十種轉換函數: 1. 硬限制函數(Hard Limit transfer function) ? ? ? ≥ < = 1 ) ( n if n if n f 2. 對稱硬限制函數(Symmetrical Hard Limit transfer function) ? ? ? ≥ < - = 1 1 ) ( n if n if n f 3. 飽和線性函數(Saturating Linear transfer function) ? ? ? ? ? > ≤ ≤ < = 1 1 1 ) ( n if n if n n if n f 4. 對稱飽和線性函數(Symmetrical Saturating Linear transfer function) ? ? ? ? ? > ≤ ≤ - - < - = 1 1 1 1 1 1 ) ( n if n if n n if n f 5. 正線性函數(Positive Linear transfer function) ? ? ? ≥ < = ) ( n if n n if n f 6. 線性函數(Linear transfer function) n n f= ) ( 7. S形函數(Sigmoid transfer function)
5 多层前馈网络及BP 算法 多层前馈网络的反向传播 (BP )学习算法,简称BP 算法,是有导师的学习,它是梯度下降法在多层前馈网中的应用。 (a ) 网络结构 见下图,u 、 y 是网络的输入、输出向量,神经元用节点表示,网络由 输入层、隐层和输出层节点组成,隐层可一层,也可多层(图中是单隐层),前层至后层节点通过权联接。由于用BP 学习算法,所以常称BP 神经网络。 :x 每个神经元(节点)的输入;:y 每个神经元(节点)的输出;:j I 神经元 的第 j 个输入。:ij w 神经元j 到神经元i 的连接权 节点的作用函数:)(θ-=x f y , θ 为阈值(可设置一个偏置节点代替θ) f 可为线性函数,一般取为Sigmoid 函数 ξ /11x e -+, ξ为很小的数,如0.1 (b ) BP 学习算法 ? 已知网络的输入/输出样本,即导师信号。 ? BP 学习算法由正向传播和反向传播组成: ? 正向传播是输入信号从输入层经隐层,传向输出层,若输出层得到了期望的输出,则学习算法结束;否则,转至反向传播。 ? 反向传播是将误差(样本输出与网络输出之差)按原联接通路反向计算,由梯度下降法调整各层节点的权值和阈值,使误差减小。 BP 学习算法步骤如下: (1) 设置初始权值)0(W ,它是较小的随机非零值。
(2) 给定输入/输出样本对,计算网络的输出。 设第p 组样本输入:()np p p p u u u u ,...,,21= 输出:()L p d d d d m p p p p ,..,2,1,,...,,21== 节点i 在第 p 组样本输入时,输出为 ip y : ()?? ? ???==∑j jp ij ip ip I t w f t x f t y )()()( ----(1式) 式中,jp I 是在第 p 组样本输入时,节点 i 的第j 个输入。 )(?f 取可微的s 型作用函数式 )(x f = x e -+11 -------(2式) 可由输入层隐层至输出层,求得网络输出层节点的输出。 (1) 计算网络的目标函数 J 设p E 为在第 p 组样本输入时,网络的目标函数,取2L 范数,则 ∑∑=-=-= k kp k kp kp p p p t e t y d t y d t E )(21)]([21||)(||21)(2 222--------(3式) 式中, )(t y p 是在第p 组样本输入时,经t 次权值调整后网络的输出:k 是 输出层第k 个节点。 网络的总目标函数: )(t J =∑p p t E )( ----------(4式) 作为对网络学习状况的评价。 (2) 判别 若 )(t J ≤ε -------(5式) 算法结束;否则,至步骤(4)。式中,ε是预先确定的,0>ε. (3) 反向传播计算 由输出层,依据 J ,按梯度下降法反向计算,可逐层调整权值。 由式() k k k k k a a J a a ??-=+η1,取步长为常值,可得到神经元j 到神经元i 的
第三章径向基函数网络 (44) 3.1 径向基函数(Redial Basis Function,RBF) (44) 3.2 径向基函数参数的选取 (46) c的选取 (46) 3.2.1 基函数中心 p 3.2.2权系数 的确定 (47) 3.3 高斯条函数 (48)
)(1 )(p h P p p λx g ?∑==第三章 径向基函数网络 径向基函数网络利用具有局部隆起的所谓径向基函数来做逼近或分类问题。它可以看作是一种前馈网络,所处理的信息在工作过程中逐层向前流动。虽然它也可以像BP 网络那样利用训练样本作有教师学习,但是其更典型更常用的学习方法则与BP 网络有所不同,综合利用了有教师学习和无教师学习两种方法。对于某些问题,径向基函数网络可能比BP 网络精度更高。 3.1 径向基函数(Redial Basis Function ,RBF ) [Powell 1985]提出了多变量插值的径向基函数方法。稍后[Broomhead 1988]成功地将径向基函数用于模式识别。径向基函数可以写成 ||)1 (||)(∑=-= P p p c x p x g ?λ (3.1.1) 其中N R x ∈表示模式向量;N P p p R c ?=1 }{ 是基函数中心;j λ是权系数;?是选定的非线性基函数。(3.1.1)可以看作是一个神经网络,输入层有N 个单元,输入模式向量x 由此进入网络。隐层有P 个单元,第p 个单元的输入为||||p p c x h -=,输出为)(p h ?。输出层1个单元, 输出为 。 假设给定了一组训练样本11},{R R y x N J j j j ??=。当j y 只取有限个值(例如,取0,1或±1)时,可以认为是分类问题;而当j y 可取任意实数时,视为逼近问题。网络学习(或训练)的任务就是利用训练样本来确定输入层到隐层的权向量p c 和隐层到输出层的权系数p λ,使得 J j y x g j j ,,1 ,)( == (3.1.2) 为此,当P J =时,可以简单地令 P p x c p p ,,1 , == (3.1.3) 这时(3.1.2)成为关于{}p λ的线性方程组,其系数矩阵通常可逆,因此有唯一解(参见[MC])。在实践中更多的情况是P J >。这时, (3.1.2)一般无解, 只能求近似解。我们将在下一节详细讨论这种情况。 常用的非线性基函数有以下几种: 1) 高斯基函数 确定了}{p c 后,可以选取如下的高斯基函数来构造径向基函数: )()(1x x g P p p p ∑==?λ (3.1.4a) 式中
第一章概论 1.神经元的基本结构:处理单元(兴奋、抑制)、连接(输入、输出) 2.神经元模型-激励函数:硬极限激励函数、线性激励函数、对数-S形激励函数 3.人工神经网络的定义:由大量处理单元互联组成的非线性、自适应、分布式并行信息处 理系统。依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的,是一种基于统计的学习方法。 4.神经网络:神经元模型(激励函数)+网络结构+学习算法 5.神经网络的分类:(了解) 拓扑结构:前馈神经网络、递归(反馈)神经网络 按连续性:连续性、离散型 按学习方式:有监督学习、无监督学习 网络应用:自组织神经网络、联想记忆神经网络 6.神经网络分类 前馈神经网络:感知机、自适应线性元、多层感知机、深度学习网络 自组织神经网络(无监督学习):自组织映射网络(SOM)、自适应谐振理论(ART)、径向基函数网络(RBF) 递归网络模型(简单反馈):hopfield网络 7.神经网络的特点: 数量巨大(含有大量极其简单的处理单元); 计算简单(每一个计算单元的处理简单); 高度复杂的互连。 8.神经网络的特点:
非线性:大多数系统都是非线性的自适应:时变系统、非平稳随机过程分布式:并行计算、大规模并行表示
第二章前馈神经网络(感知机+自适用线性元+BP算法) 2.1感知机 1.感知机的特点:(针对之前神经运算模型的改进) 权值和偏置值能够解析确定,也能学习 二值、多值、连续模型都可以处理 对于线性可分问题,学习步数存在上限 2.感知机组成:一个具有线性组合功能的累加器+硬极限函数激励 3.感知机局限: 对于线性可分问题、学习过程一定收敛; 线性不可分问题:判定边界对震荡不休; 传输函数不可导 4.学习规模:初始化权值;计算输出值;调节权值以及偏置值;迭代完所有样本;判断结 束条件 5.输入向量归一化:很大或很小的输入向量都会导致感知机训练时间大幅度增加,因此对 输入向量归一化(除以向量的模) 6.学习率算法:加一个学习率系数 7.口袋算法:针对线性不可分问题,保留最佳的权值 主要区别在权值更新步骤:若当前权值能将训练样本正确分类,且能够正确分类的训练样本数量大于口袋中权值向量能够正确分类的训练样本数量,则以现权值向量代替原权值向量,并更新口袋中权值向量能够正确分类的样本个数。 若分类错误,则进行常规权值更新
第三章 前馈型神经网络模型 3.1 感知器(Perception ) 感知器(Perception )是由美国学者F.Rosenblatt 于1957年提出的一个具有单层计算单元的神经网络。它在识别印刷体字符方面表现出了良好的性能,引起人们很多兴趣。后来许多改进型的感知器在文字识别、语音识别等应用领域取得了进展,使得早期的神经网络的研究达到了高潮。 感知器的输入可以是非离散量,它的权向量不仅是非离散量,而且可以学习调整。感知器是一个线性阈值单元组成的网络,可以对输入样本进行分类,而且多层感知器,在某些样本点上对函数进行逼近,虽然在分类和逼近的精度上都不及非线性单元组成的网络,但是可以对其他网络的分析提供依据。 3.1.1 单层感知器 一、单层感知器网络 图为一单层感知器神经网络,输入向量为X=(X 1,X 2,…,X n ),输出向量为Y=(Y 1,Y 2,…,Y n )。最简单的感知器仅有一个神经元。 1 122i n n 感知器的输入向量为X ∈R n , 权值向量为W ∈R n ,单元的输出为为Y ∈{1,-1}。其中: ∑==-=-=n i T T i i W X f XW f W X f Y 1 '')()()(θθ (3.1.1) 其中,X ˊ= (X ,-1),W ˊ= (W ,θ)。 ???<-≥==0 '',10 '',1)''sgn(T T T W X W X W X y (3.1.2) 与M-P 模型不同的是,权值W 可以通过学习训练而加以改变。 二、单层感知器的学习算法
令W n+1=θ, X n+1=-1, 则, )( 1 1 ∑+== n i i i W X f y (3.1.3) 具体算法如下: ①初始化 给W i (0)各赋一个较小的随机非零值。这里W i (t)为t 时刻第i 个输入的权值(1≤i ≤n ),W n+1(t)为t 时刻的阈值。 ②输入样本 X=(X 1,X 2,…,X n ,T),T 称为教师信号,在两类样本分类中,如果X ∈A 类,则T=1;如果X ∈B 类,则T=-1。 ③计算实际输出 ))(()(1 1t W X f t Y n i i i ∑+== (3.1.4) ④修正权值 W i (t+1)= W i (t)+η(T-Y(t))X i i=(1,2,…,n,n+1) (3.1.5) 其中,0<η≤1用于控制修正速度,通常η不能太大,会影响W i (t)的稳定,也不能太小,会使W i (t)的收敛速度太慢。 ⑤转到②直到W 对一切样本均稳定不变为止。 用单层感知器可实现部分逻辑函数,如: X 1∧X 2: Y=1·X 1+1·X 2-2 即W 1=W 2=1,θ=2 X 1∨X 2: Y=1·X 1+1·X 2-0.5 即W 1=W 2=1,θ=0.5 : Y=(-1)·X 1+0.5 即W 1=-1,θ=-0.5 三、单层感知器的局限性 1969年Minsky 和Papert 出版了《Perception 》一书,他们从数学上分析了单层感知器为代表的人工神经网络系统的功能和局限性,指出单层感知器仅能解决一阶谓词逻辑和线性分类问题,不能解决高阶谓词和非线性分类问题。为解决高阶谓词和非线性分类问题,必须引入含有隐层单元的多层感知器。书中举出了异或(XOR)问题不能使用单层感知器来解决。异或逻辑为2121X X X X - -- -∨,假定单层感知器能实现异或逻辑,那么, θ-+=2211X W X W Y ,要求: 表 3.1 - -X
神经网络简介 神经网络简介: 人工神经网络是以工程技术手段来模拟人脑神经元网络的结构和特征的系统。利用人工神经网络可以构成各种不同拓扑结构的神经网络,他是生物神经网络的一种模拟和近似。神经网络的主要连接形式主要有前馈型和反馈型神经网络。常用的前馈型有感知器神经网络、BP 神经网络,常用的反馈型有Hopfield 网络。这里介绍BP (Back Propagation )神经网络,即误差反向传播算法。 原理: BP (Back Propagation )网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。BP 神经网络模型拓扑结构包括输入层(input )、隐层(hide layer)和输出层(output layer),其中隐层可以是一层也可以是多层。 图:三层神经网络结构图(一个隐层) 任何从输入到输出的连续映射函数都可以用一个三层的非线性网络实现 BP 算法由数据流的前向计算(正向传播)和误差信号的反向传播两个过程构成。正向传播时,传播方向为输入层→隐层→输出层,每层神经元的状态只影响下一层神经元。若在输出层得不到期望的输出,则转向误差信号的反向传播流程。通过这两个过程的交替进行,在权向量空间执行误差函数梯度下降策略,动态迭代搜索一组权向量,使网络误差函数达到最小值,从而完成信息提取和记忆过程。 单个神经元的计算: 设12,...ni x x x 分别代表来自神经元1,2...ni 的输入; 12,...i i ini w w w 则分别表示神经
元1,2...ni 与下一层第j 个神经元的连接强度,即权值;j b 为阈值;()f ?为传递函数;j y 为第j 个神经元的输出。若记001,j j x w b ==,于是节点j 的净输入j S 可表示为:0*ni j ij i i S w x ==∑;净输入j S 通过激活函数()f ?后,便得到第j 个神经元的 输出:0 ()(*),ni j j ij i i y f S f w x ===∑ 激活函数: 激活函数()f ?是单调上升可微函数,除输出层激活函数外,其他层激活函数必须是有界函数,必有一最大值。 BP 网络常用的激活函数有多种。 Log-sigmoid 型:1 (),,0()11x f x x f x e α-= -∞<<+∞<<+,'()()(1())f x f x f x α=- tan-sigmod 型:2()1,,1()11x f x x f x e α-=--∞<<+∞-<<+,2(1()) '()2 f x f x α-= 线性激活函数purelin 函数:y x =,输入与输出值可取任意值。 BP 网络通常有一个或多个隐层,该层中的神经元均采用sigmoid 型传递函数,输出层的神经元可以采用线性传递函数,也可用S 形函数。 正向传播:
第4章 多层感知器 多层感知器有三个突出的特点: 1. 网络中的每个神经元包括一个非线性激活 函数, 非线性是光滑的(每一点都可微分), 如为logistic 函数: 2. 网络包括一个或多个神经元的隐层; 3. 网络显示了一种高程度的互联; 基于此网络行为的缺陷。 1.由于非线性分布式的存在和网络的高度互连接使得多层感知器的理论分析难于进行。 2.隐层的使用使得学习过程变得更不可捉摸。 反向传播算法的发展是神经网络发展史上的一个里程碑. 4. 2预备知识 网络中有两种信号: 1. 函数信号。 2. 误差信号。 多层感知器每一个隐层或输出层的神经元被设计用来进行两种计算: 1.函数信号的计算 2.梯度向量估计计算 需要使用的符号: 1.符号i 、j 、k 是指网络中不同的神经元; 2.在迭代(时间步)n ,网络的第n 个训练模式 (例子)呈现给网络; 3.符号E(n)指第n 次迭代的瞬间误差平方和 或误差能量的瞬间和。 4.号e j (n)指的是第n 次迭代神经元j 的输出 误差信号; 5.符号d j (n)指的是关于j 的期望响应; ) exp(11 j j v y -+=
6.符号y j(n)指的是第n次迭代神经元j的输出函数信号; 7.w ji(n)指突触权值,该权值是第n次迭代时从神经元i输出连接到神经元j输入。 该权值在n时的校正量为Δw ji(n); 8.n次迭代的神经元j的诱导局部域用v j(n) 表示; 9.激活函数表示为)(?j?; 10.阈值由一个突触的权值w j0=b j表示,这个突触与一个等于+1的固定输入相连;11.输入向量的第i个元素用x i(n)表示;12.输出向量的第k个元素用o k(n)表示;13.学习率参数记为η; m表示多层感知器的第l层的大小14.符号 l (也就是节点的数目),l=0,1,…,L,而L就是网络的“深度”。因此m0是输入层的大小, m l是第l隐层的大小,m L是输出层的大小。也使用m L=M。 4. 3反向传播算法 1. 函数信号的计算 输入信号x, 第一个隐层的神经元的诱导局部域 v1 =W1x, 第一个隐层的神经元的输出 y1=?(v1) 同理 第l个隐层的神经元的诱导局部域 v l =W l y l-1, 第l个隐层地神经元的输出 y l=?(v l) 输出层的神经元的诱导局部域 v L =W L y l, 输出层的神经元的实际输出
3.4几种典型的神经网络 神经网络除了前向型网络外,还有反馈型、随机型和自组织竞争型等类型,本节主要介绍这三种神经网络,以及多神经网络集成。 3.4.1 反馈型神经网络 反馈型神经网络又称为递归网络或回归网络,它是一种反馈动力学系统,比前向神经网络具有更强的计算能力。其中Hopfield 神经网络是其典型代表,也是得到最充分研究和应用的神经网络之一,它是由美国物理学家J.J.Hopfield 于1982年首先提出的,主要用于模拟生物神经网络的记忆机理。由于网络的运行是一个非线性的动力系统,所以比较复杂。因此Hopfield 为这类网络引入了一种稳定过程,即提出了神经网络能量函数(也称李雅普诺夫函数)的概念,使网络的运行稳定判断有了可靠而简便的依据。 Hopfield 神经网络已在联想记忆和优化计算中得到成功应用,并拓宽了神经网络的应用范围。另外,Hopfield 网络还有一个显著的优点,就是它与电子电路存在明显的对应关系,使得该网络易于理解和便于实现。 Hopfield 网络有离散型[1](DHNN )和连续型[2](CHNN )两种实用形式。离散型Hopfield 网络的结构比较简单,在实际工程中的应用比较广泛,因此本节重点介绍离散型Hopfield 网络,并作仿真分析。 1、离散Hopfield 神经网络模型 离散Hopfield 神经网络是一种单层反馈型非线性网络,每一个结点的输出均反馈到其他结点的输入,其工作原理如图3.4.1所示。 设有n 个神经元,()n v v v V ,,,21L 为神经网络的状态矢量,i v 为第i 个神经元的输出,输出取值为0 或者为1的二值状态。对任一神经元n v v v i ,,,,21L 为第i 个神经元的输入,它们对该神经元的影响程度用连接权in i i w w w ,,,21L 表示i θ为其阈值,则有: 图3.4.1 离散Hopfield 神经网络的工作原理图 ?? ?>>=0 1i i i Net Net v (3.4.1) 式中,∑≠=?= n i j j i j ij i v w Net ,1θ,称为单元i 的状态。 Hopfield 网络是对称网络,故ji ij w w =。当0=ii w 时,称为无自反馈的离散Hopfield 网络;反之,称为有自反馈的离散Hopfield 网络。 Hopfield 网络有两种工作方式: (1)异步方式:在任一时刻t ,只有某一个神经元按式(3.4.1)发生变化,而其余1?n 神经元的状态保持不变。 (2)同步方式:在任一时刻t ,有部分神经元按式(3.4.1)变化(部分同步)或所有神经元按式(3.4.1)变化(全并行方式)。 反馈神经网络的一个重要特点就是它具有稳定状态。 定义3.4.1 若神经网络从t = 0的任意一个初始状态)0(V 开始,存在一个有限的时刻,从该时刻后,神经网络状态不再发生变化,即: ()0)(>Δ=Δ+t t V t t V (3.4.2) 则称网络是稳定的。 Hopfield 神经网络是多个神经元相互结合的网络,它有两个最基本的最重要的约束条件: (1)神经元之间的相互结合强度是对称的,即ji ij w w =; (2)各神经元之间状态完全动态地异步变化。 基于这两个约束条件,我们来考察一下网络的状态变化规律,并给出计算机仿真。
基于构造型前馈神经网络的函数逼近与应用众所周知,人工神经网络具有很好的函数逼近能力,但传统的学习型神经网络存在许多缺陷,如对初始权重非常敏感,极易收敛于局部极小;往往停滞于误差梯度曲面的平坦区,收敛缓慢甚至不能收敛;过拟合与过训练;网络隐含节点数不确定等。针对此,本文主要研究近年来发展起来的单隐层构造型前馈神经网络的函数逼近能力及其在EEG信号预测、长株潭地区环境数据预测和股市数据挖掘中的应用,以及构造型前馈神经网络与学习型前馈神经网络在上述领域的应用比较。 首先,在B. Llanas和F.J.Sainz的工作的启发下,将前馈神经网络的激活函数换成Gaussian函数,得到构造岭函数型Gaussian前馈神经网络,证明了具有单隐层n+1个神经元的神经网络,能精确插值n+1个样本,然后,根据样本值构造出Gaussian型前馈神经网络的内部和外部权值,证明了它能以任意精度近似地插值这些样本,并给出了其误差的上界。进一步,证明了这种构造型Gaussian型前馈神经网络能以任意精度一致逼近闭区间上的任意连续函数,并给出了其误差的上界。 同时将上述结论推广到了多维的情况。并通过数值实验,验证了上述结论的正确性和有效性。 由于上述造岭函数型Gaussian前馈神经网络在推广到多维的情况时的复杂性和具体操作上的困难性。将构造岭函数型Gaussian前馈神经网络的激活函数换成径向基函数(RBF),得到构造型前馈RBF神经网络。 针对这种径向基函数型前馈单隐层神经网络,根据样本值直接构造出多维(包含一维)情况下的内部和外部权值,并给出了相应的形状参数,证明了它能以
任意精度近似地插值这些样本,并给出了其误差的上界。进一步,证明了这种构造型RBF前馈单隐层神经网络能以任意精度一致逼近闭区间上的任意连续函数,并给出了其误差的上界。 通过数值实验,验证了上述结论的正确性和有效性。进一步,将前馈神经网络的激活函数换成小波函数,得到小波前馈神经网络,证明了这种具有n+1单隐层个神经元的神经网络,能精确插值n+1个样本,同样根据样本值构造它的内部和外部权值,证明了这种构造型小波前馈神经网络能以任意精度近似地插值这些样本。 进一步,证明了它能以任意精度一致逼近闭区间上的任意连续函数。同时将上述结论推广到了多维的情况。 并通过数值实验,验证了上述结论的正确性和有效性。对于多维情况,采用比以前更简洁、更有效的构造方法,得到另一种构造型前馈小波径向基神经网络,同样证明了这种具有n+1单隐层个神经元的小波径向基神经网络,能精确插值 n+1个多维样本,进一步,证明了它能以任意精度一致逼近闭区域上任意多维连续函数。 并通过Matlab编程和数值实验,验证了这种网络操作上更简洁,收敛速度更快。将上述小波径向基神经网络推广到L2(R)RBF神经网络,对于多维数据与连续函数,证明了与小波神经网络同样的结论。 并和CRBF网络、BP网络、ELM、SVM比较起来,通过8个实验进一步验证了L2RNNs具有更快的收敛速度和更好的泛化性能。将上述构造型sigmoid神经网络应用到EEG信号预测、并和学习型BP神经网络的预测方法和结果作对比,在样本数量不至于出现灾难维的情况下,构造型sigmoid神经网络体现出了明显的优
神经网络考试重点 1、熵和信息的关系、性质,什么叫熵,条件熵、联合熵、互信息之间的关系,K-L 散度的定义(K-L 极小等于极大似然估计)。第十章 答:熵H(X):表示每一个消息所携带的信息的平均量。在H(X)中X 不是H(X)的变量,而是一个随机变量的标记。 条件熵:给定Y 时X 的条件熵为H(X|Y)=H(X,Y)—H(Y) 具有性质:0<=H(X|Y)<=H(X) 条件熵H(X|Y)表示在观测到系统输出Y 后,对X 保留的不确定性度量。 H(X,Y)是X 和Y 的联合熵,由 ∑∑∈∈=X Y y ),(log ),(-Y H(X,x y x p y x p ) 定义,其中,p(x,y)是离散随机变量X 和Y 的联合概率质量函数,而x 和y 表示它们各自的字母表。 互信息:I(X;Y)=H(X)—H(X|Y)= ∑∑∈∈? ?? ? ? ?X Y y )()(),(log ),(x y p x p y x p y x p 熵是互信息的一个特例。 熵H(X)表示在没有观测系统输出前我们对系统输入的不确定性,条件熵H(X|Y)表示在观测到系统输出后对系统的不确定性,差H(X)—H(X|Y)表示观察到系统输出之后我们对系统输入的不确定性的减少。 信息的属性: (1)X 和Y 的互信息具有对称性:I(X;Y)=I(Y;X) (2)X 和Y 的互信息总是非负的:0Y)I(X;≥ (3)X 和Y 的互信息也可以用Y 的熵表示为:I(X;Y)=H(Y)—H(Y|X) 定义 )(X f x 和)(X g x 的K-L 散度为: dx X g X f X f g D x x x x f x ? ∞∞ -??? ? ??=)()(log )( I(X;Y)=Y X f f |D Y X,f 总的来说,X 和Y 之间的互信息等于联合概率密度函数 ),(,y x f Y X 以及概率密度函数)(X f x 和 )(Y f y 的乘积的K-L 散度。 2、ICA 原理,推导过程、数学模型、降维。简述PCA 原理(第一个成分如何得来,第一、二个成分关系),推导过程(方差最大)。ICA 与PCA 的差异。 答:ICA 的原理: 无噪声信号模型为: X=As , 其中,A 为信号混合矩阵,x 是N 维观测信号向量,s 是M (N>M) 维原始信号向量。 X=kA. s/k 信号S 放大 k 倍与A 的相应列缩小k 倍的结果相同,从而决定了ICA 得到的信号存在强