下载文档原格式
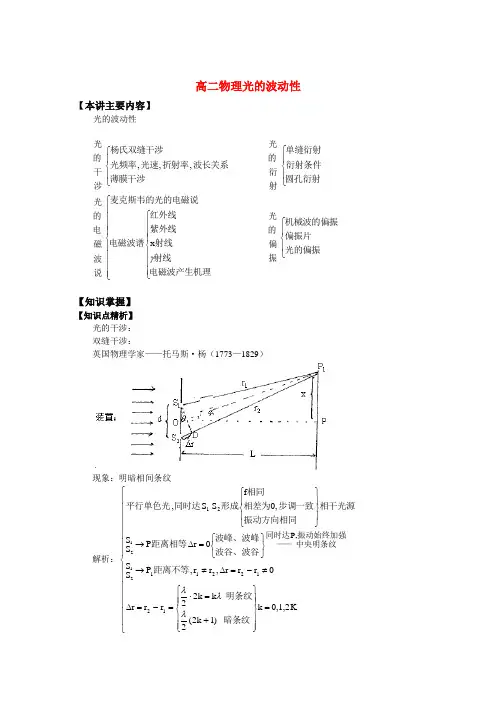
高二物理光的波动性【本讲主要内容】光的波动性 涉干的光⎪⎩⎪⎨⎧薄膜干涉波长关系折射率光速光频率杨氏双缝干涉,,,射衍的光⎪⎩⎪⎨⎧圆孔衍射衍射条件单缝衍射说波磁电的光⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧电磁波产生机理射线射线紫外线红外线电磁波谱麦克斯韦的光的电磁说γx振偏的光⎪⎩⎪⎨⎧光的偏振偏振片机械波的偏振【知识掌握】【知识点精析】 光的干涉：双缝干涉：英国物理学家——托马斯·杨（1773—1829）现象：明暗相间条纹解析：⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧+=⋅=-=∆≠-=∆≠→⎭⎬⎫⎩⎨⎧=∆→⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧ 0,1,2k )1k 2(2k k 22r r r 0r r r ,r r ,P S S 0r P S S 0,f S S ,1212211211212,P 暗条纹明条纹距离不等波谷、波谷波峰、波峰距离相等相干光源振动方向相同步调一致相差为相同形成同时达平行单色光振动始终加强同时达中央明条纹——λλλ相邻两明纹或相邻两暗纹间距离：⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧∴∆⋅=∆⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧=+-++⋅=∆-=∆+==-+=∆-=∆⋅==∆==⋅=⋅=⋅=∆∴≈∴⊥⊥⊥∴<<=-=∆++出现彩色条纹不同不同不同不同色光纹都适用无论相邻明纹或相邻暗暗纹明纹很小且很小上取点在x d L x d L )1k 2(2d L ]1)1k (2[2d L x x x x )1k 2(2d L x :d L k d L )1k (d L x x x x k d L k 22d L x :r d L x L x dtg d tg d sin d r ,OP O S ,OP D S P S D S ,d L d D S r r r D P S k1k k k 1k k 11112121212λνλλλλλλλλλλϕθθϕθ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧===⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧↑→↓∴⎪⎩⎪⎨⎧↑↓→=↑→=↓→⎪⎩⎪⎨⎧==不同不同不同不变光在不同介质中同紫红不同紫红不同紫红不同紫红不同波长不同速度相同光在真空中不同不同不同色光在同一介质中n v n C v n v v n v C n v v C Cv n ,v ,,λνλννλννλνλνλνννν薄膜干涉：演示：⎪⎩⎪⎨⎧−−→−明暗彩色花纹——薄膜单色黄光形成薄膜——铁丝圈蘸肥皂水。
波动光学【知识点】 一、光的干涉 1、 光波定义 光波是某一波段的电磁波，是电磁量E 和H 的空间的传播． 2、 光的干涉定义 满足一定条件的两束（或多束）光波相遇时，在光波重叠区域内，某些点合光强大于分光强之和，在另一些点合光强小于分光强之和，因而合成光波的光强在空间形成强弱相间的稳定分布，称为光的干涉现象，光波的这种叠加称为相干叠加，合成光波的光强在空间形成强弱相间的稳定分布称为干涉条纹，其中强度极大值的分布称为明条纹，强度极小值的分布称为暗条纹． 3、 相干条件表述 两束光波发生相干的条件是：频率相同，振动方向几乎相同，在相遇点处有恒定的相位差． 4、 光程差与相位差定义 两列光波传播到相遇处的光程之差称为光程差；两列光波传播到相遇处的相位之差称为相位差． 5、 双光束干涉强度公式表述 在满足三个相干条件时，两相干光叠加干涉场中各点的光强为12I I I ϕ=++∆ 式中，相位差122()πϕϕϕδλ∆=--保持恒定，若120I I I ==，则2002(1cos )4cos 2I I I ϕϕ∆=+∆= 6、 杨氏双缝干涉实验实验装置与现象 如图1所示，狭缝光源S 位于对称轴线上，照明相距为a 的两个狭缝1S 和2S ，在距针孔为D 的垂轴平面上观察干涉图样，装置放置在空气(1)n =中，结构满足,,sin tan d D D x θθ≈．在近轴区内，屏幕上的是平行、等间距的明暗相间的直条纹，屏幕上P 点的光程差δ为 21sin xr r d d Dδθ=-≈≈ 相应明暗纹条件是(21)2k x d D k λδλ⎧⎪==⎨+⎪⎩，干涉加强，，干涉减弱， 干涉条纹的位置是0,1,2,(21)2D k dx k D k d λλ⎧⎪⎪==±±⎨⎪+⎪⎩，明纹中心位置，，暗纹中心位置，式中，整数k 称为干涉级数，用以区别不同的条纹． 7、 薄膜干涉实验装置 如图2所示，扩展单色光源照射到薄膜上反射光干涉的情况，光源发出的任一单条光线经薄膜上下两个面反射后，形成两条光线○1、○2，在实验室中可用透镜将它们会聚在焦平面处的屏上进行观察，在膜的上下两个表面反射的两束光线○1和○2的光程差为22λδ=21S S图1图 23n二、光的衍射 1、光的衍射现象定义 一束平行光通过一狭缝K ，在其后的屏幕上将呈现光斑，若狭缝的宽度比波度大得多时，屏幕E 上的光斑和狭缝完全一致，如图3（a ）所示，这时可成光沿直线传播的；若缝宽与光波波长可以相比拟时，在屏幕E 上的光斑亮度虽然降低，但光斑范围反而增大，如图3（b ）所示的明暗相间的条纹，这就是光的衍射现象，称偏离原来方向传播的光为衍射光．2、惠更斯-菲涅耳原理表述 任何时刻波面上的每一点都可以作为子波的波源，从同一波面上各点发出的子波在空间相遇时，可以相互叠加产生干涉． 3、菲涅耳衍射与夫琅禾费衍射定义 光源到障碍物，或障碍物到屏的距离为有限远，这类衍射称为菲涅尔衍射；光源到障碍物，以及障碍物到屏的距离都是无限远，这时入射光和衍射光均可视为平行光，这类衍射称为夫琅禾费衍射．三、光的偏振 1、光的偏振性定义 光波是电磁波，其电矢量称为光矢量，在垂直于传播方向的平面内，光矢量E 可能具有的振动状态(矢量端点的轨迹)，称为光的偏振态．光矢量的振动方向与光传播方向所组成的平面称为振动面． 2、偏振光定义 振动方向具有一定规则的光波，称为偏振光。
高中物理光的波动性知识点总结参考高中物理光的波动性知识点总结参考一. 教学内容：光的波动性二. 要点扫描：（一）光的干涉1. 产生相干光源的方法（必须保证r相同）。
⑴利用激光；⑵将一束光分为两束。
2. 双缝干涉的定量分析如图所示，缝屏间距L远大于双缝间距d，O点与双缝S1和S2等间距，则当双缝中发出光同时射到O点附近的P点时，两束光波的路程差为δ＝r2－r1。
条纹间距△x＝λ。
上述条纹间距表达式提供了一种测量光波长的方法。
结论：由同一光源发出的光经两狭缝后形成两列光波叠加产生。
当这两列光波到达某点的路程差为波长的整数倍时，即kδ＝∝d。
由于膜上各处厚度不同，故各处两列反射波的路程差不等。
若：ΔT＝2d＝nλ（n＝1，2，?）则出现明纹。
ΔT＝2d＝（2n－1）λ/2 （n＝1，2，?）则出现暗纹。
应注意：干涉条纹出现在被照射面。
薄膜干涉应用（1）透镜增透膜：透镜增透膜的厚度应是透射光在薄膜中波长的1／4倍。
使薄膜前后两面的反射光的光程差为波长的一半，（ΔT＝2d＝λ，得d＝λ），故反射光叠加后减弱，从能量的角度分析E入＝E反＋E透＋E吸。
在介质膜吸收能量不变的前提下，若E 反＝0，则E透最大。
增强透射光的强度。
（2）“用干涉法检查平面”：如图所示，两板之间形成一层空气膜，用单色光从上向下照射，如果被检测平面是光滑的，得到的干涉图样必是等间距的。
如果某处凸起来，则对应明纹（或暗纹）提前出现，如图甲所示；如果某处凹下，则对应条纹延后出现，如图乙所示。
（注：“提前”与“延后”不是指在时间上，而是指由左向右的顺序位置上。
）4. 光的波长、波速和频率的关系V＝λf。
光在不同介质中传播时，其频率f不变，其波长λ与光在介质中的波速V成正比。
色光的颜色由频率决定，频率不变则色光的颜色也不变。
（二）光的衍射。
1. 光的衍射现象是光离开直线路径而绕到障碍物阴影里的现象。
2. 泊松亮斑：当光照到不透光的极小圆板上时，在圆板的阴影中心出现的亮斑。
第二讲 物 理 光 学§2.1 光的波动性2.1.1光的电磁理论19世纪60年代，美国物理学家麦克斯韦发展了电磁理论，指出光是一种电磁波，使波动说发展到了相当完美的地步。
2.1.2光的干涉1、干涉现象是波动的特性凡有强弱按一定分布的干涉花样出现的现象，都可作为该现象具有波动本性的最可靠最有力的实验证据。
2、光的相干迭加两列波的迭加问题可以归结为讨论空间任一点电磁振动的力迭加，所以，合振动平均强度为)cos(212212221ϕϕ-++=A A A A I其中1A 、2A 为振幅，1ϕ、2ϕ为振动初相位。
⎪⎩⎪⎨⎧=-=+=-==-12121212)(,2,1,0,)12(,2,1,0,2A A j j j j 为其他值且ϕϕπϕϕπϕϕ2cos4)()(1222221221ϕϕ-=-=+=A I A A I A A I 干涉相消干涉相加3、光的干涉 (1)双缝干涉在暗室里，托马斯·杨利用壁上的小孔得到一束阳光。
在这束光里，在垂直光束方向里放置了两条靠得很近的狭缝的黑屏，在屏在那边再放一块白屏，如图2-1-1所示，阳光图2-1-1于是得到了与缝平行的彩色条纹；如果在双缝前放一块滤光片，就得到明暗相同的条纹。
A 、B 为双缝，相距为d ，M 为白屏与双缝相距为l ，DO 为AB 的中垂线。
屏上距离O 为x 的一点P 到双缝的距离，222222)2(,)2(d x l PB d x l PA ++=-+=dx PA PB PA PB 2)()(=+⋅-由于d 、x 均远小于l ，因此PB+PA=2l ，所以P 点到A 、B 的光程差为：x l dPA PB =-=δ若A 、B 是同位相光源，当δ为波长的整数倍时，两列波波峰与波峰或波谷与波谷相遇，P 为加强点（亮点）；当δ为半波长的奇数倍时，两列波波峰与波谷相遇，P 为减弱点（暗点）。
因此，白屏上干涉明条纹对应位置为)2,1,0( =⋅⋅±=k d l k x λ暗条纹对应位置为)2,1,0()21( =⋅-±=k l dk x λ。
第二讲 物 理 光 学§2.1 光的波动性2.1.1光的电磁理论19世纪60年代，美国物理学家麦克斯韦发展了电磁理论，指出光是一种电磁波，使波动说发展到了相当完美的地步。
2.1.2光的干涉1、干涉现象是波动的特性凡有强弱按一定分布的干涉花样出现的现象，都可作为该现象具有波动本性的最可靠最有力的实验证据。
2、光的相干迭加两列波的迭加问题可以归结为讨论空间任一点电磁振动的力迭加，所以，合振动平均强度为)cos(212212221ϕϕ-++=A A A A I其中1A 、2A 为振幅，1ϕ、2ϕ为振动初相位。
⎪⎩⎪⎨⎧=-=+=-==-12121212)(,2,1,0,)12(,2,1,0,2A A j j j j 为其他值且ϕϕπϕϕπϕϕ 2cos4)()(1222221221ϕϕ-=-=+=A I A A I A A I 干涉相消干涉相加3、光的干涉 (1)双缝干涉在暗室里，托马斯·杨利用壁上的小孔得到一束阳光。
在这束光里，在垂直光束方向里放置了两条靠得很近的狭缝的黑屏，在屏在那边再放一块白屏，如图2-1-1所示，于是得到了与缝平行的彩色条纹；如果在双缝前放一块滤光片，就得到明暗相同的条纹。
A 、B 为双缝，相距为d ，M 为白屏与双缝相距为l ，DO 为AB 的中垂线。
屏上距离O 为x 的一点P 到双缝的距离，阳光图2-1-1222222)2(,)2(d x l PB d x l PA ++=-+=dx PA PB PA PB 2)()(=+⋅-由于d 、x 均远小于l ，因此PB+PA=2l ，所以P 点到A 、B 的光程差为：x l dPA PB =-=δ若A 、B 是同位相光源，当δ为波长的整数倍时，两列波波峰与波峰或波谷与波谷相遇，P 为加强点（亮点）；当δ为半波长的奇数倍时，两列波波峰与波谷相遇，P 为减弱点（暗点）。
因此，白屏上干涉明条纹对应位置为)2,1,0( =⋅⋅±=k d l k x λ暗条纹对应位置为)2,1,0()21( =⋅-±=k l d k x λ。
其中k =0的明条纹为中央明条纹，称为零级明条纹；k =1，2…时，分别为中央明条纹两侧的第1条、第2条…明（或暗）条纹，称为一级、二级…明（或暗）条纹。
相邻两明（或暗）条纹间的距离λd lx =∆。
该式表明，双缝干涉所得到干涉条纹间的距离是均匀的，在d 、l 一定的条件下，所用的光波波长越长，其干涉条纹间距离越宽。
x l d ∆=λ可用来测定光波的波长。
(2)类双缝干涉双缝干涉实验说明，把一个光源变成“两相干光源”即可实现光的干涉。
类似装置还有①菲涅耳双面镜：如图2-1-2所示，夹角α很小的两个平面镜构成一个双面镜（图中α已经被夸大了）。
点光源S 经双面镜生成的像1S 和2S 就是两个相干光源。
②埃洛镜如图2-1-3所示，一个与平面镜L 距离d 很小（数量级0.1mm ）的点光源S ，它的一部分光线图2-1-3图2-1-2掠入射到平面镜，其反射光线与未经反射的光线叠加在屏上产生干涉条纹。
因此S 和S '就是相干光源。
但应当注意，光线从光疏介质射入光密介质，反射光与入射光相位差π，即发生“并波损失”，因此计算光程差时，反身光应有2λ的附加光程差。
③双棱镜如图2-1-4所示，波长nm 8.632=λ的平行激光束垂直入射到双棱镜上，双棱镜的顶角033'''=α，宽度w=4.0cm ，折射率n=1.5．问：当幕与双棱镜的距离分别为多大时，在幕上观察到的干涉条纹的总数最少和最多？最多时能看到几条干涉条纹？平行光垂直入射，经双棱镜上、下两半折射后，成为两束倾角均为θ的相干平行光。
当幕与双棱镜的距离等于或大于0L 时，两束光在幕上的重叠区域为零，干涉条纹数为零，最少，当幕与双棱镜的距离为L 时，两束光在幕上的重叠区域最大，为L ∆，干涉条纹数最多。
利用折射定律求出倾角θ，再利用干涉条纹间距的公式及几何关系，即可求解．αθ)1(-=n式中α是双棱镜顶角，θ是入射的平行光束经双棱镜上、下两半折射后，射出的两束平行光的倾角。
如图2-1-5所示，相当于杨氏光涉，d »D,λd Dx =∆，而D dtg 2sin =≈θθ条纹间距mman x 62.0)1(2sin 2=-==∆λθλS 1 S 2d 图2-1-5图2-1-4可见干涉条纹的间距与幕的位置无关。
当幕与双棱镜的距离大于等于0L 时，重叠区域为零，条纹总数为零m n W W L 3.39)1(220=-==αθ当屏与双棱镜相距为L 时，重叠区域最大，条纹总数最多m L L 65.1920==相应的两束光的重叠区域为mm L n n L L L 98.9)1()1(220=-=-==∆ααθ．其中的干涉条纹总数16=∆∆=∆x LN 条。
④对切双透镜如图2-1-6所示，过光心将透镜对切，拉开一小段距离，中间加挡光板（图a ）；或错开一段距离（图b ）；或两片切口各磨去一些再胶合（图c ）。
置于透镜原主轴上的各点光源或平行于主光轴的平行光线，经过对切透镜折射后，在叠加区也可以发生干涉。
(3)薄膜干涉当透明薄膜的厚度与光波波长可以相比时，入射薄膜表面的光线薄满前后两个表面反射的光线发生干涉。
①等倾干涉条纹如图2-1-7所示，光线a 入射到厚度为h ，折1 2图2-1-7（a ）（b ）（a ）图2-1-6射率为1n 的薄膜的上表面，其反射光线是1a ，折射光线是b ；光线b 在下表面发生反射和折射，反射线图是1b ，折射线是1c ；光线1b 再经过上、下表面的反射和折射，依次得到2b 、2a 、2c 等光线。
其中之一两束光叠加，1a 、2a 两束光叠加都能产生干涉现象。
a 、b 光线的光程差AD n CB AC n 12)(-+=δi htg n hn sin 2cos 212⋅⋅-⋅=γγ=in n h h n h n 22122222sin 2cos 2)sin 1(cos 2⋅-==-⋅γγγ如果i =0，则上式化简为h n 22=δ。
由于光线在界面上发生反射时可能出现“半波损失”，因此可能还必须有“附加光程差”，2λδ='是否需要增加此项，应当根据界面两侧的介质的折射率来决定。
当321n n n >>时，反射线1a 、1b 都是从光密介质到光疏介质，没有“半波损失”，对于1a 、2a ，不需增加δ'；但反射线2b 是从光疏介质到光密介质，有“半波损失”，因此对于1c 、2c ，需要增加δ'。
当321n n n <<时，反射线1a 、1b 都有“半波损失”，对于1a 、2a 仍然不需要增加δ'；而反射线2b 没有“半波损失”，对于1c 、2c 仍然必须增加δ'。
同理，当321n n n >>或321n n n <<时，对于1a 、2a 需要增加δ'；对于1c 、2c 不需要增加δ'。
在发生薄膜干涉时，如果总光程等于波长的整数倍时，增强干涉；如果总光程差等于半波长的奇数倍时，削弱干涉。
入射角i 越小，光程差δδ'+越小，干涉级也越低。
在等倾环纹中，半径越大的圆环对应的i 也越大，所以中心处的干涉级最高，越向外的圆环纹干涉级越低。
此外，从中央外各相邻明或相邻暗环间的距离也不相同。
中央的环纹间的距离较大，环纹较稀疏，越向外，环纹间的距离越小，环纹越密集。
②等厚干涉条纹当一束平行光入射到厚度不均匀的透明介质薄膜上，在薄膜表面上也可以产生干涉现象。
由于薄膜上下表面的不平行，从上表面反射的光线1b 和从下面表反射并透出上表面的光线1a 也不平行，如图2-1-8所示，两光线1a 和1b 的光程差的精确计算比较困难，但在膜很薄的情况下，A 点和B 点距离很近，因而可认为AC 近似等于BC ，并在这一区域的薄膜的厚度可看作相等设为h ，其光程差近似为δδ'+⋅-='+i n n h r h n 221222sin 2cos 2当i 保持不变时，光程差仅与膜的厚度有关，凡厚度相同的地方，光程差相同，从而对应同一条干涉条纹，将此类干涉条纹称为等厚干涉条纹。
当i 很小时，光程差公式可简化为δ'+h n 22。
③劈尖膜如图2-1-9所示，两块平面玻璃片，一端互相叠合，另一端夹一薄纸片（为了便于说明问题和易于作图，图中纸片的厚度特别予以放大），这时，在两玻璃片之间形成的空气薄膜称为空气劈尖。
两玻璃片的交线称为棱边，在平行于棱边的线上，劈尖的厚道度是相等的。
当平行单色光垂直（0=i ）入射于这样的两玻璃片时，在空气劈尖（12=n ）的上下两表面所引起的反射光线将形成相干光。
如图1-2-9所示，劈尖在C 点处的厚度为h ，在劈尖上下表面反射的两光线之间的光程差是22λ+h 。
由于从空气劈尖的上表面（即玻璃与空气分界面）和从空气劈尖的图2-1-9下表面（即空气与玻璃分界面）反射的情况不同，所以在式中仍有附加的半波长光程差。
由此λλk h =+223,2,1=k ……明纹2)12(22λλ⋅+=+k h 3,2,1=k ……暗纹干涉条纹为平行于劈尖棱边的直线条纹。
每一明、暗条纹都与一定的k 做相当，也就是与劈尖的一定厚度h 相当。
任何两个相邻的明纹或暗纹之间的距离l 由下式决定：221)1(21sin 1λλλθ=-+=-=+k k h h l k k式中θ为劈尖的夹角。
显然，干涉条纹是等间距的，而且θ愈小，干涉条纹愈疏；θ愈大，干涉条纹愈密。
如果劈尖的夹角θ相当大，干涉条纹就将密得无法分开。
因此，干涉条纹只能在很尖的劈尖上看到。
④牛顿环在一块光平的玻璃片B 上，放曲率半径R 很大的平凸透镜A ，在A 、B 之间形成一劈尖形空气薄层。
当平行光束垂直地射向平凸透镜时，可以观察到在透镜表面出现一组干涉条纹，这些干涉条纹是以接触点O 为中心的同心圆环，称为牛顿环。
牛顿环是由透镜下表面反射的光和平面玻璃上表面反射的光发生干涉而形成的，这也是一种等厚条纹。
明暗条纹处所对应的空气层厚度h 应该满足：明环 3,2,1,22==+k k h λλ2)12(22λλ⋅+=+k h暗环 3,2,1=k从图2-1-10中的直角三角形得22222)(h Rh h R R r -=--=图2-1-10因R»h ，所以2h <<2Rh ，得R r h 22=上式说明h 与r 的平方成正比，所以离开中心愈远，光程差增加愈快，所看到的牛顿环也变得愈来愈密。
由以上两式，可求得在反射光中的明环和暗环的半径分别为：明环 3,2,1,2)12(=⋅-=k R k r λ暗环 2,1,0,=⋅⋅=k R k r λ随着级数k 的增大。
