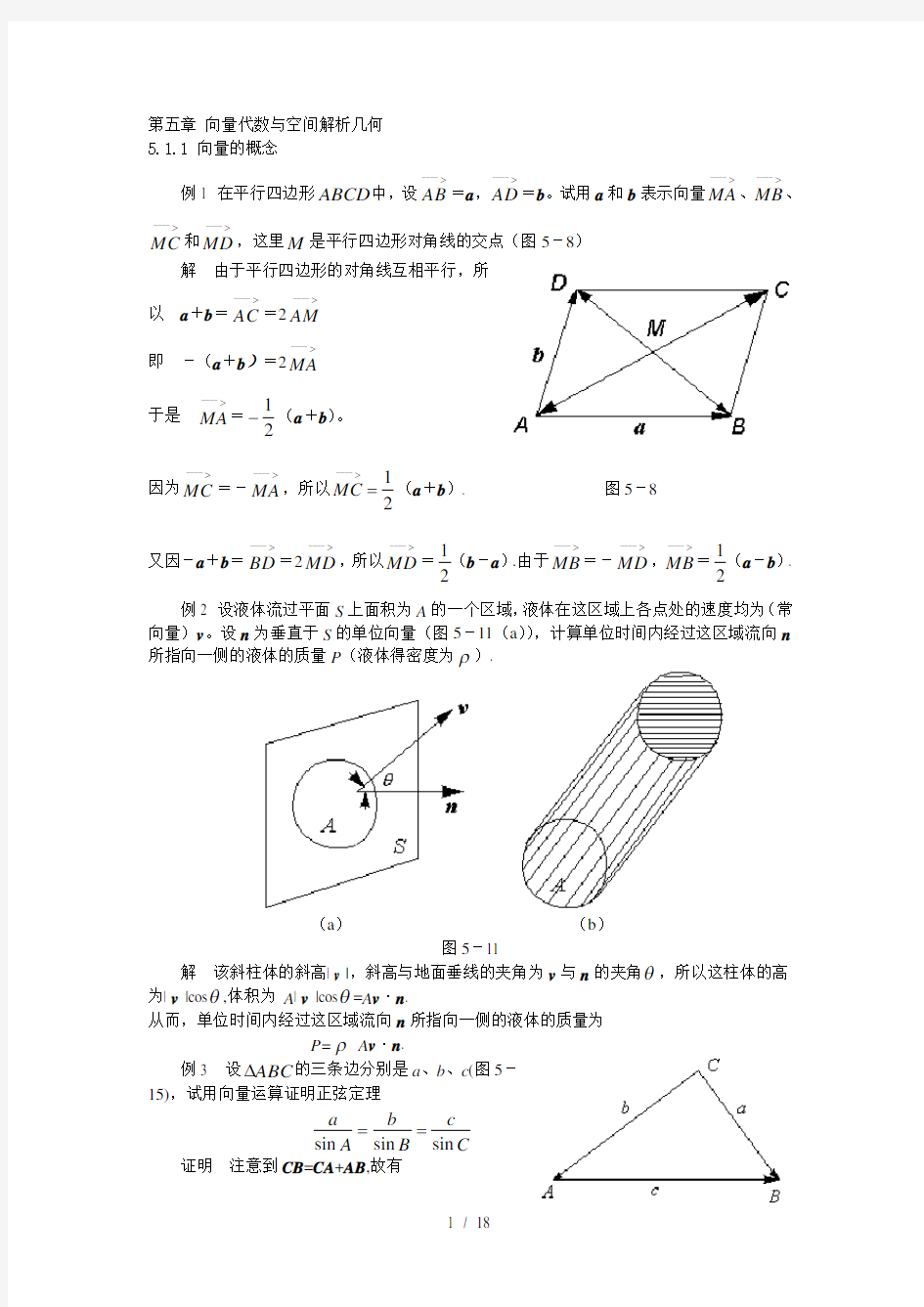

第五章 向量代数与空间解析几何 5.1.1 向量的概念
例1 在平行四边形ABCD 中,设>
____
AB =a ,>
____
AD =b 。试用a 和b 表示向量>
____
MA 、>
____
MB 、
>
____
MC 和>
____
MD ,这里M 是平行四边形对角线的交点(图5-8)
解 由于平行四边形的对角线互相平行,所
以 a +b =>
____
AC =2>
____
AM
即 -(a +b )=2>
____
MA
于是 >
____
MA =2
1
-
(a +b )。 因为>
____
MC =->
____
MA ,所以2
1
____
=
>
MC (a +b ).
图5-8
又因-a +b =>
____
BD =2>
____
MD ,所以>
____
MD =21(b -a ).由于>____
MB =->____
MD ,>____
MB =2
1
(a -b ).
例2 设液体流过平面S 上面积为A 的一个区域,液体在这区域上各点处的速度均为(常
向量)v 。设n 为垂直于S 的单位向量(图5-11(a )),计算单位时间内经过这区域流向n 所指向一侧的液体的质量P (液体得密度为ρ).
(a ) (b ) 图5-11
解 该斜柱体的斜高| v |,斜高与地面垂线的夹角为v 与n 的夹角θ,所以这柱体的高为| v |cos θ,体积为 A | v |cos θ=A v ·n .
从而,单位时间内经过这区域流向n 所指向一侧的液体的质量为
P=ρ A v ·n . 例3 设ABC ?的三条边分别是a 、b 、c (图5-15),试用向量运算证明正弦定理
C
c
B b A a sin sin sin ==
证明 注意到CB =CA +AB ,故有
CB ?CA =(CA+AB) ?CA =CA ?CA+AB ?CA =AB ?CA =AB ?(CB+BA) =AB ?CB 图5-15
于是得到 CB ?CA =AB ?CA =AB ?CB 从而 |CB ?CA |=|AB ?CA | =|AB ?CB | 即 ab sin C =cb sin A =ca sin B 所以
C
c
B b A a sin sin sin =
= 5.2 点的坐标与向量的坐标
例1 已知点A (4,1,7)、B (-3,5,0),在y 轴上求一点M ,使得|MA |=|MB |. 解 因为点在y 轴上,故设其坐标为)0,,0(y M ,则由两点间的距离公式,有
222222)00()5()03()07()1()04(-+-+--=-+-+-y y
解得4-=y ,故所求点为)0,4,0(-M
例2 求证以)3,2,5()2,1,7()1,3,4(321M M M 、、三点为顶点的三角形是一个等腰三角
形. 解 因为
6
)31()23()54(||6)23()12()75(||14
)12()31()47(||222213222232222221=-+-+-==-+-+-==-+-+-=M M M M M M 所以||||1332M M M M =,即△321M M M 为等腰三角形.
5.2.2 向量运算的坐标表示
例3 设有点),,(1111z y x M ,),,(2222z y x M ,求向量21M M 的坐标表示式。
解 由于1221OM OM M M -=,而),,(1111z y x OM =,),,(2222z y x OM =,于是
),,(),,(),,(12121211122212z z y y x x z y x z y x OM OM ---=-=-
即 ),,(12121221z z y y x x M M ---=
例4 已知两点A (4,0,5)和B (7,1,3),求与>
____
AB 方向相同的单位向量e .
解 因为
>
____
AB =>
____
OB –>
____
OA =(7,1,3)-(4,0,5)=(3,1,–2)
,
所以 >
____
AB =14)2(13222=-++,
于是
e )2,1,3(14
1
|
|-=
=
→
-→
-AB AB .
例5 求解以向量为未知元的线性方程组?
??=-=-b y x a
y x 2335 其中a =(2,1,2),b =(-1,1,-2).
解 解此方程组得x=2a –3b , y =3a –5b
以a ,b 代入,即得 x =2(2,1,2)–3(–1,1,–2)=(7,–1,10) y =3(2,1,2)–5(–1,1,–2)=(11,–2,16).
例6 已知两点A ),,(111z y x 和B ),,(222z y x 以及实数1-≠λ,在直线AB 上求点M ,使
>
____
AM λ=>
____
MB .
解 如图7-13所示.由于
>
____
AM =>
____
OM –>
____
OA ,>
____
MB =>
____
OB –>
____
OM ,
因此 >
____
OM –>
____
OA λ=(>
____
OB –>
____
OM )
,
从而
>
____
OM λ+=
11
(>____
OA λ+>
____
OB ).
以>
____
OA 、>
____
OB 的坐标(即点A 、点B 的坐标)代入
图7-13
>
____
OM ???
??++++++=λλλλλ
λ1,1,1212121z z y y x x 本例中的点M 称为定比分点,特别地当1=λ时,得线段AB 的中点为
??
?
??+++2,2,2212121z z y y x x M .
例7 已知两点)2,2,2(1M 和)0,3,1(2M ,计算向量>
____
21M M 的模、方向余弦和方向角.
解 >
____
21M M =(1–2, 3–2,0–2)
=(–1, 1,–2);
|>
____
21M M |=2
2
2
)2(1)1(-++-
=24211==
++;
2
2
cos ,21cos ,21cos -==-=γβα;
4
3,3,32π
γπβπα=
==
. 例8 已知三点M ( 1, 1, 1)、A ( 2, 2, 1)和B ( 2, 1, 2), 求∠AMB .
解 作向量→MA ,→MB ,则∠AMB 为向量→MA 与→MB 的夹角. 这时→
MA =( 1, 1, 0),
→
MB =( 1, 0, 1),从而
→MA ?→
MB =1?1+1?0+0?1=1;
|→
MA |=2011222=
++;
→
MB =2101222=++.
从而
cos ∠AMB =
2
1
221|
|||==?→→→
→MB MA MB
MA , 由此得 ∠AMB =
3
π.
例9 设立方体得一条对角线为OM ,一条棱为OA ,且|OA|=a ,求→
OA 在方向OM 上的
投影→
→OA prj OM
.
解 如图5-21所示,记∠MOA =?,有
3
1
||||cos ==
OM OA ?,
于是
→→OA prj O M
=→OA 3
cos a
=?.
图5-21
例10 设a =(2,1,-1),b =(1,-1,2),计算a ?b.
解
a ?
b =k j i k
j i
352
1
111
2
--=--. 例11 已知三角形ABC 的顶点分别是A (1,2,3)、B (3,4,5)、和C (2,4,7),求三角形ABC 的面积.
解 由向量积对于,可知三角形ABC 的面积
||2
1
sin ||||2
1→→→
→?=∠=?AC AB A AC AB S ABC
由于||→AB =(2,2,2), ||→
AC =(1,2,4),因此
,-AC AB k j i k
j i
264
21222+==?→
→4
于是
.142)6(42
1264|21222
=+-+=+=
?k j i -S ABC 例12 设刚体以等角速度ω绕l 轴旋转,计算刚体上一点M 的线速度.
解 刚体绕l 轴旋转时,我们可以用在l 轴上的一个向量ω表示角速度,它的大小等于角速度的大小,它的方向由右手规则定出:即以右手握住l 轴,当右手的四个手指的转向与刚体的
旋转方向一致时,大拇指的指向就是ω的方向(图5-22). 图5-22
设点M 到旋转轴l 轴上任取一点O 做向量r =→
OM ,并以θ表示ω与r 的夹角,那么 a =| r |sin θ.
设线速度为v ,那么由物理学上线速度与角速度的关系可知,v 的大小为
| v |=|ω| a =|ω|| r |sin θ;
v 的方向垂直于通过点M 的与l 轴的平面,即v 垂直于ω与r ;又v 的指向是使ω、r 、v 符合右手规则,因此有v =ω?r .
例13 已知不在一平面上的四点:A (111,,z y x )、B (222,,z y x )、C (333,,z y x )、 D (444,,z y x ). 求四面体ABCD 的体积.
解 由立体几何知道,四面体的体积T V 等于以向量→AB 、→AC 和→
AD 为棱的平行六面
体的体积的六分之一. 因而
T V =.|][|6
1→
→→AD AC AB
由于
→
AB =),,(121212z z y y x x ---, →
AC =),,(131313z z y y x x ---,
→
AD =),,(141414z z y y x x ---
所以
T V =1
41
41
413131
31212126
1
z z y y x x z z y y x x z z y y x x ---------± 上式中符号的选择必须和行列式的符号一致. 5.3 空间的平面与直线 5.3.1 平面
例1 已知空间两点)1,2,1(1-M 和)2,1,3(2-M ,求经过点1M 且与直线21M M 垂直的平
面方程。 解 显然21M M 就是平面的一个法向量
)3,3,2()12,21,13(21-=+---=M M
由点法式方程可得所求平面的方程为
0)1(3)2(3)1(2=++---z y x
即
07332=++-z y x
例2 求过三点1M (2,-1,4)、2M (-1,3,-2)和3M (0,2,3)的平面的方程。
解 先找出这平面的法线向量n . 由于向量n 与向量→21M M 、→31M M 都垂直,而→
21M M =(-3,4,-6),→
31M M =(-2,3,-1),所以可取它们的向量积为n :
n =→21M M ?→
31M M =1
32643
----k
j i =14i +9j -k ,
根据平面的点法式方程(1),得所求平面的方程为
14(x -2)+9(y +1)-(z -4)=0,
即 14x +9y -z -15=0.
例3 设一平面与x ,y ,z 轴的交点依次为P (a ,0,0)、Q (0,b ,0)、R (0,0,c )三点(图5-24),求这平面的方程(其中a ≠0,b ≠0,c ≠0). 解 设所求的平面的方程为
Ax+By+C z+D =0.
因P (a ,0,0)、Q (0,b ,0)、R (0,0,c )三点都在平面上,所以点P 、Q 、R 的坐标都满足方程(2);即有
??
?
??=+=+=+,0,0,
0D cC D bB D aA
得c
D C b D B a D A -=-=-
=,,. 以此代入(2)并除以D (D ≠0),便得所求的平面方程为
图5-24 1=++c
z
b y a x
(5)
方程(5)叫做平面的截距式方程,而a 、b 、c 依次叫做平面在x 、y 、z 轴上的截距. 例4 因平面通过z 轴及点(1,2,-3)的平面方程。 解 因平面通过z 轴,故可设其方程为 Ax +By =0 又因(1,2,-3)点在平面上,将其坐标代入方程,则有 A +2B =0,即A =-2B 故所求平面方程为-2Bx +By =0,即2x -y =0 例5 设平面π的方程为3x -2y +z +5=0,求经过坐标原点且与π平行的平面方程。 解 显然所求平面与平面π有相同的法向量n =(3,-2,1),又所求平面经过原点,故它的方程为 3x -2y +z =0
5.2.3 空间直线
例6 求经过两点),,(1111z y x M 和),,(2222z y x M 的直线方程。
解 该直线的方向向量可取n =),,(12121221z z y y x x M M ---=。由点法式方程立即得
到所求直线的方程
1
21
121121z z z z y y y y x x x x --=--=--
该方程称为直线的两点式方程。 例7 用直线的对称式方程及参数式方程表示直线
??
?=++-=+++.
0432,
01z y x z y x (4)
解 易得(1,0,-2)为直线上的一点。直线的方向向量为两平面的法线向量的向量积,从而
s ==-3
1211
1
k
j i
4i – j - 3k .
因此,所给直线的对称式方程为 3
2
141-+=-=-z y x 令
3
2
141-+=-=-z y x =t , 得所给直线的参数方程为
??
?
??--=-=+=.32,
,41t z t y t x 5.3.3 点、平面、直线的位置关系
1. 点到平面的距离
例8 求两个平行平面122:1+-=y x z π,03244:2=+--z y x π之间的距离。
解 在平面1π上任取一点)1,0,0(M ,则两平面间的距离d 就是点M 到2π的距离,于是
d =
6
1)2()4(431204042
22=
-+-++?-?-? 2. 点到直线的距离
例9 求点)3,2,1(M 到直线L :5
322z
y x =--=
-的距离
解 由直线方程知点)0,2,2(0M 在L 上,且L 的方向向量s=(1,-3,5)。从而
)3,0,1(0-=M M
k j i k
j i
s M M 3895
31
30
1
0++=--=?
代入(11),得点M 到L 的距离为
|||
|10s s M M d ?==
5
22
5
)3(1389222222=+-+++ 3. 两平面之间的夹角
例10 一平面通过两点)1,1,1(1M 和)1,1,0(2-M 且垂直于平面x+y+z =0,求它的方程.
解 设所求平面的一个法线向量为 n =(A ,B ,C ).
因→
21M M =(-1,0,-2)在所求平面上,它必与n 垂直,所以有
-A -2C =0 (7)
又因所求的平面垂直于已知平面x+y+z=0,所以又有 A+B+C=0. (8) 由(7)、(8)得到 A=-2C , B =C . 由点法式,平面方程为A (x -1)+B (y -1)+C (z -1)=0.将A=-2C ,B =C 代入上式,并约去C (C ≠0),便得
-2(x -1)+(y -1)+(z -1)=0或2x -y -z =0.
这就是所求的平面方程. 4.两直线的夹角
例11 求直线1L :
13411+=-=-z y x 和2L :1
222-=
-+=z
y x 的夹角. 解 直线1L 的方向向量s 1=(1,-4,1),2L 的方向向量s 2=(2,-2,-1).设直线1L 和2L 的夹角为?,那么由公式(5)有
cos ?=2
1
)1()2(21)4(1|)1(1)2()4(21|2
22222=
-+-+?+-+-?+-?-+?,故?4π=.
5. 直线与平面的夹角
例12 求过点(1,-2,4)且与平面2x -3y +z -4=0垂直的直线方程。 解 因为直线垂直于平面,所以平面的法线向量即为直线的方向向量,从而所求直线的方程为
1
4
3221-=
-+=-z y x . 6.平面束
例13
求直线?
??=++-=--+01,
01z y x z y x
在平面x+y+z =0上的投影直线的方程.
解 过直线??
?=++-=--+0
1,
01z y x z y x 的平面束的方程为
0)1()1(=++-+--+z y x z y x λ
即
0)1()1()1()1(=+-++-+-++λλλλz y x ,
(14)
其中λ为待定系数。这平面与平面x+y+z =0垂直的条件是
01)1(1)1(1)1(=?+-+?-+?+λλλ,
即 1-=λ.
代入(14)式,得投影平面的方程为
0222=--z y
即
01=--z y .
所以投影直线的方程为
?
?
?=++=--.0,
01z y x z y 7.杂例
例14 求与两平面x -4z =3和2x -y -5z =1的交线平行且过点(-3,2,5)得直线方程
解 因为所求直线与两平面的交线平行,所以其方向向量s 一定同时垂直于两平面的法
向量n 1、n 2,所以可以取
s =n 1?n 25
1240
1
---k
j i
=-(4i+3j +k ),
因此所求直线方程为
1
5
3243-=
-=+z y x .
例15 求直线2
4
1312-=
-=-z y x 与平面2x +y +z -6=0的交点. 解 所给直线的参数方程为x=2+t ,y=3+t ,z=4+2t ,
代入平面方程中,得 2(2+t )+(3+t )+(4+2t )-6=0. 得t =-1,代入参数方程得交点为 x=1,y =2,z =2. 例16 求过点(2,1,3)且与直线
1
2131-=
-=+z
y x 垂直相交的直线的方程.
过点(2,1,3)且垂直于已知直线的平面方程为
3(x -2)+2(y -1)-(z -3)=0
(9) 已知直线的参数方程为x =-1+3t ,y =1+2t ,z =-t .
(10)
将(10)代入(9)求得73=
t ,从而求得直线与平面的交点为??
?
??-73,713,72.
以点(2,1,3)为起点,点???
?
?-73,713,
72为终点的向量 )4,1,2(76373,1713,272--=??
?
??----
这就是所求直线的方向向量,故所求直线的方程为
.4
3
1122-=--=-z y x
5.4 曲面与曲线
5.4.1 曲面、曲线的方程
例1 建立球心在点)(0000,z ,y x M 、半径为R 的球面的方程.
解 设M (x ,y ,z )是球面上的任一点(图5-31),那么 |M M 0|=R .
向量代数与空间解析几何-期末复习题-高等数学下册-(上海电机学院)
第七章 空间解析几何 一、选择题 1. 在空间直角坐标系中,点(1,-2,3)在[ D ] A. 第一卦限 B. 第二卦限 C. 第三卦限 D. 第四卦限 2.方程2 222 =+y x 在空间解析几何中表示的图形为 [ C ] A. 椭圆 B. 圆 C. 椭圆柱面 D. 圆柱面 3.直线3 1 2141:1+=+=-z y x l 与?? ?=-++=-+-0 20 1:2z y x y x l ,的夹角是 [ C ] A. 4 π B. 3 π C. 2 π D. 0 4. 在空间直角坐标系中,点(1,2,3)关于xoy 平面的对称点是[ D ] A. (-1,2,3) B. (1,-2,3) C. (-1,-2,3) D. (1,2,-3)
5.将xoz 坐标面上的抛物线x z 42 =绕z 轴旋转一 周,所得旋转曲面方程是[B ] A. ) (42y x z += B. 2 2 2 4y x z +±= C. x z y 422 =+ D. x z y 422 ±=+ 6.平面2x-2y+z+6=0与xoy 平面夹角的余弦是 [B ] A. 13 - B. 13 C. 23 - D. 23 7. 在空间直角坐标系中,点(1,2,3)关于yoz 平面的对称点是[ A ] A. (-1,2,3) B. (1,-2,3) C. (-1,-2,3) D. (1,2,-3) 8.方程 222 22 x y z a b +=表示的是 [ B ] A.椭圆抛物面 B.椭圆锥面 C. 椭球面 D. 球面 9. 已知 a ?={0, 3, 4}, b ?={2, 1, -2},则 = b proj a ?ρ[ C ]
第七章空间解析几何 第一节作业 一、选择题(单选): 1. 点M(2,-3,1)关于xoy平面的对称点是: (A)( -2,3,1 );( B)( -2,-3,-1 );(C)( 2,-3,-1 );( D)( -2,-3,1 ) 答:() 2. 点M(4,-3,5)到x轴距离为: (A).. 42—(—3)2—52; (B) 3)2—52; (cr. 4252; (D) : 4252. 答:() 、在yoz面上求与A(3,1,2),B(4,-2,-2) 和C(0,5,1)等距离的点。 第二节作业 设u a b c, v a b 2c.试用a, b, c表示2u 3v. 第三节作业 一、选择题(单选): 已知两点M'2,2,?一2)和M2(1,3,0),则MM2的三个方向余弦为: 1 1 V 2 1 1 <2 1 1 42 1 1 V2 (A) , , ; (B) , , ; (C) —, , . (D) —,,. 2 2 2 2 2 2 2 2 2 2 2 2 答:() 二、试解下列各题: 1. 一向量的终点为B( 2,-1,7),它在x轴,y轴,z轴上的投影依次为4, -4,4,求这向量的起点A的坐标。
2. 设m 3i 5 j 3k, n 2i j 4k, p 5i j 4k 求向量 a 4m 3n p 在x 轴 上的投影及在y 轴上的分向量. 3. 求平行于向量a 6,7, 6的单位向量 第四节作业 一、选择题(单选): 1. 向量a 在b 上的投影为: 答:() 2. 设a 与b 为非零向量,则a b 0是: (A )a//b 的充要条件; (B )a b 的充要条件; (C ) a b 的充要条件; (D ) a //b 的必要但不充分条件 答:() 3.向量a,b,c 两两垂直,w —1- — a 1, b —1- J )2, C 3,则s a b c 的长度 为 (A)1 2 3 6; 2 2 2 (B)1 2 3 14; (C)J12 22 32 ; (D) J1 2 3 勺6. 答:() (A) (B) -a a b (D)
第五章 向量代数与空间解析几何 5.1向量 既有大小又有方向的量 表示:→ -AB 或a (几何表示)向量的大小称为向量的模,记作||AB 、|a |、||a 1. 方向余弦:? ?? ? ??=||,||,||)cos ,cos ,(cos r r r z y x γβα r =(x ,y ,z ),| r |=2 22z y x ++ 2. 单位向量 )cos ,cos ,(cos γβα=→ ο a 模为1的向量。 3. 模 → →→ ?=++=a a z y x a 2 22|| 4. 向量加法(减法) ),,(212121z z y y x x b a ±±±=±→ → 5. a ·b =| a |·| b |cos θ212121z z y y x x ++= a ⊥ b ?a ·b =0(a ·b =b ·a ) 6. 叉积、外积 |a ?b | =| a || b |sin θ= z y x z y x b b b a a a k j i a // b ?a ?b =0.( a ?b= - b ?a ) ? 2 1 2121z z y y x x == 7. 数乘:),,(kz ky kx ka a k ==→ → 例1 1||,2||==→ → b a ,→a 与→ b 夹角为3 π ,求||→ →+b a 。 解 22 ||cos ||||2||2)()(||→ →→→ →→→→→→→→→→→ →++=?+?+?=+?+=+b b a a b b b a a a b a b a b a θ 713 cos 12222=+???+= π 例2 设2)(=??c b a ,求)()]()[(a c c b b a +?+?+。 解 根据向量的运算法则 )()]()[(a c c b b a +?+?+
《空间解析几何2》教学大纲 课程编号:12307229 学时:22 学分:1.5 课程类别:限制性选修课 面向对象:小学教育专业本科学生 课程英语译名:Interspace Analytic Geometry(2) 一、课程的任务和目的 任务:本课程要求学生熟练掌握解析几何的基本知识和基本理论,正确地理解和使用向量代数知识,并解决一些实际问题。深刻理解坐标观念和曲线(面)与方程相对应的观念,熟练掌握讨论空间直线、平面、曲线、曲面的基本方法,训练学生的空间想象能力和运算能力。 目的:通过本课程的学习,使学生掌握《空间解析几何》的基本知识、基本思想及基本方法,培养学生的抽象思维能力及空间想象力,培养学生用代数方法处理几何问题的能力,提高学生从几何直观分析问题和和解决问题的能力。为学习《高等代数》及《数学分析》及后继课程打下坚实基础,为日后胜任小学教学工作而作好准备。 二、课程教学内容与要求 (一)平面与空间直线(14学时) 1.教学内容与要求:本章要求学生熟练掌握平面与空间直线的各种形式的方程,能判别空间有关点、直线与平面的位置关系,能熟练计算它们之间的距离与交角。 2.教学重点:根据条件求解平面和空间直线的方程,及点、直线、平面之间的位置关系 3.教学难点:求解平面和空间直线的方程。 4. 教学内容: (1)平面的方程(2课时):掌握空间平面的几种求法(点位式、三点式、点法式、一般式)。 (2)平面与点及两个平面的相关位置(2课时):掌握平面与点的位置关系及判定方法;掌握空间两个平面的位置关系及判定方法。 (3)空间直线的方程(2课时):掌握空间直线的几种求法(点向式、两点式、参数式、一般式、射影式)。 (5)直线与平面的相关位置(2课时):掌握空间直线与平面的位置关系及判定方法。 (6)空间两直线的相关位置(2课时):掌握空间两直线的位置关系及判定方法。 (7)空间直线与点的相关位置(2课时):掌握直线与点的位置关系及判定方法。 (8)平面束(2课时):掌握平面束的定义(有轴平面束和平行平面束),并能根据题意求平面束的方程。
《空间解析几何》课程教学大纲 一课程说明 1.课程基本情况 课程名称:空间解析几何 英文名称:Analytic geometry 课程编号:2411207 开课专业:数学与应用数学 开课学期:第1学期 学分/周学时:3/3 课程类型:专业基础课 2.课程性质(本课程在该专业的地位作用) 本课程是数学与应用数学及信息与计算机科学专业的一门专业基础课,是初等数学通向高等数学的桥梁,是高等数学的基石,线性代数,数学分析,微分方程,微分几何,高等几何等课程的学习都离不开空间解析几何的基本知识及研究方法。空间解析几何是用代数的方法研究几何图形的一门学科,是从初等数学进入高等数学的转折点,是沟通几何形式与数学关系的一座桥梁。 3.本课程的教学目的和任务 通过本课程的学习,学生在掌握解析几何的基本概念的基础上,树立起空间观念。使学生受到几何直观及逻辑推理等方面的训练,扩大知识领域,培养空间想象能力以及运用向量法与坐标法计算几何问题和证明几何问题的能力,并且能用解析方法研究几何问题和对解析表达式给予几何解释,为进一步学习其它课程打下基础;另一方面加深对中学几何理论与方法的理解,从而获得在比较高的观点下处理几何问题的能力,借助解析几何所具有的较强的直观效果提高学生认识事物的能力。 4.本课程与相关课程的关系、教材体系特点及具体要求
本课程的教学,要求学生熟练掌握用代数的方法在空间直角坐标系下,研究平面、空间直线、柱面、锥面、旋转曲面和二次曲面等几何图形的性质,能对坐标化方法运用自如,从而达到数与形的统一。了解二次曲线的一般理论和二次曲面的一般理论。以培养学生掌握解析几何的基础知识为主,着力培养学生运用解析几何的思想和方法解决实际问题的能力,以及娴熟的矢量代数的计算能力和推理、演绎的逻辑思维能力,为后续课程的学习打下良好的基础。 5.教学时数及课时分配 二教材及主要参考书 1.李养成,《空间解析几何》,科学出版社。 2.吴光磊、田畴编,《解析几何简明教程》,高等教育出版社。 3.丘维声,《解析几何》,北京大学出版社。 4.南开大学《空间解析几何引论》编写组编,《空间解析几何引论》,高教出版社。 5.吕林根许子道等编《解析几何》(第三版),高等教育出版社出版 三教学方法和教学手段说明 1.启发式教学,课堂教学与课后练习相结合。 2.可考虑运用多媒体教学软件辅助教学。
空间解析几何与矢量代数小练习 一 填空题 5’x9=45分 1、 平行于向量)6,7,6(-=a 的单位向量为______________. 2、 设已知两点)2,0,3()1,2,4(21M M 和,计算向量21M M 的模_________________, 方向余弦_________________和方向角_________________ 3、以点(1,3,-2)为球心,且通过坐标原点的球面方程为__________________. 4、方程0242222=++-++z y x z y x 表示______________曲面. 5、方程22x y z +=表示______________曲面. 6、222x y z +=表示______________曲面. 7、 在空间解析几何中2x y =表示______________图形. 二 计算题 11’x5=55分 1、求过点(3,0,-1)且与平面3x-7y+5z-12=0平行的平面方程. 2、求平行于x 轴且过两点(4,0,-2)和(5,1,7)的平面方程. 3、求过点(1,2,3)且平行于直线 5 1132-=-=z y x 的直线方程. 4、求过点(2,0,-3)且与直线? ??=+-+=-+-012530742z y x z y x 垂直的平面方
5、已知:k i OA 3+=,k j OB 3+=,求OAB ?的面积。 参考答案 一 填空题 1、? ?????-±116,117,116 2、21M M =2,21cos ,22cos ,21cos ==- =γβα,3,43,32πγπβπα=== 3、14)2()3()1(222=++-+-z y x 4、以(1,-2,-1)为球心,半径为6的球面 5、旋转抛物面 6、 圆锥面 7、 抛物柱面 二 计算题 1、04573=-+-z y x 2、029=--z y 3、5 31221-=-=-z y x 4、065111416=---z y x 5 219== ?S
第七章 空间解析几何参考答案 第七章 空间解析几何 一、选择题 1. 在空间直角坐标系中,点( 1,- 2,3)在 [ D ] A. 第一卦限 B. 第二卦限 C. 第三卦限 D. 第四卦限 2. 方程 2 x 2 y 2 2 在空间解析几何中表示的图形为 [ C ] A. 椭圆 B. 圆 C. 椭圆柱面 D. 圆柱面 3. 直线 l 1 x 1 y 1 z 1 x y 1 0 : 2 3 与 l 2 : x y z 2 ,的夹角是 [ C ] 4 A. 4 B. 3 C. D. 0 2 4. 在空间直角坐标系中,点( 1, 2,3 )关于 xoy 平面的对称点是 [ D ] A. (-1,2,3) B. (1,-2,3) C. (-1,-2,3) D. (1,2,-3) 5. 将 xoz 坐标面上的抛物线 z 2 4 x 绕 z 轴旋转一周,所得旋转曲面方程是[B ] A. z 2 4 ( x y ) B. z 2 4 x 2 y 2 C. y 2 z 2 4 x D. y 2 z 2 4 x 6. 平面 2x-2y+z+6=0 与 xoy 平面夹角的余弦是 [B ] A. 1 B. 1 C. 2 2 3 3 3 D. 3 7. 在空间直角坐标系中,点( 1, 2,3 )关于 yoz 平面的对称点是 [ A ] A. (-1,2,3) B. (1,-2,3) C. (-1,-2,3) D. (1,2,-3) 2 2 8. 方程 x y z 2 表示的是 [ B ] a 2 b 2 A. 椭圆抛物面 B. 椭圆锥面 C. 椭球面 D. 球面 9. 已知 a ={0, 3, 4}, b ={2, 1, -2},则 proj a b [ C ] A. 3B. 1 C. -1 D. 1 3 10.已知 a , b 为不共线向量,则以下各式成立的是 D A. a 2 b 2 (a b ) 2 B. a 2 b 2 ( a b ) 2 C. (a b) 2 (a b )2 D. ( a b ) 2 ( a b ) 2 a 2 b 2
空间向量练习 一、选择题(共15小题,每小题4.0分,共60分) 1.已知平面α的一个法向量是(2,-1,1),α∥β,则下列向量可作为平面β的一个法向量的是() A. (4,2,-2) B. (2,0,4) C. (2,-1,-5) D. (4,-2,2) 2.如图,过边长为1的正方形ABCD的顶点A作线段EA⊥平面AC,若EA=1, 则平面ADE与平面BCE所成的二面角的大小是() A. 120° B. 45° C. 150° D. 60° 3.已知=(1,2,3),=(2,1,2),=(1,1,2),点Q在直线OP上运动,则当 ·取得最小值时,点Q的坐标为() A. B. C. D. 4.将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论: ①AC⊥BD;②△ACD是等边三角形;③AB与平面BCD所成的角为60°;④AB与CD所成的角为60°.其中错误的结论是() A.① B.② C.③ D.④ 5.如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点 E,F分别是棱AB,BB1的中点,则直线EF和BC1的夹角是() A. 45° B. 60° C. 90° D. 120° 6.已知在空间四面体O-ABC中,点M在线段OA上,且OM=2MA,点N为BC中点, 设=a,=b,=c,则等于() A.a+b- c B.-a+b+ c C.a-b+ c D.a+b-c 7.已知在棱长为2的正方体ABCD-A1B1C1D1中,E是DC的中点,建立如图所示的空 间直角坐标系,则AB1与D1E所成角的余弦值为() A. B. C.- D.- 8.如图所示,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱CC1,BC,A1B1上的点, 若∠B1MN=90°,则∠PMN的大小() A.等于90° B.小于90° C.大于90° D.不确定 9.如图,S是正三角形ABC所在平面外一点,M,N分别是AB和SC的中点,SA=SB= SC,且∠ASB=∠BSC=∠CSA=90°,则异面直线SM与BN所成角的余弦值为() A.- B. C.- D. 10.已知平面α内两向量a=(1,1,1),b=(0,2,-1)且c=ma+nb+(4,-4,1).若c为平
高等数学空间解析几何 练习 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
向量代数与空间解析几何 第一部分 向量代数___线性运算 [内容要点]: 1. 向量的概念. 2. 向量的线性运算. 3. 向量的坐标,利用坐标作向量的线性运算. [本部分习题] 1. 指出下列各点所在的坐标轴、坐标面或哪个卦限. (2,3,5);(0,4,3);(0,3,0)A B C --- 2. 求点(1,3,2)--关于点(1,2,1)-的对称点坐标. 3. 求点(4,3,5)M --到各坐标轴的距离. 4. 一向量的起点为(1,4,2)A -,终点为(1,5,0)B -,求AB →在x 轴、y 轴、z 轴上的投影,并求||AB →。 5. 已知两点1M 和2(3,0,2)M ,计算向量12M M ??→的模、方向余弦和方向角. 6. 已知{3,5,4},{6,1,2},{0,3,4},a b c →→→==-=--求234a b c →→→-+及其单位向量. 7.设358,247,54,a i j k b i j k c i j k →→→→→→→→→→→→=++=--=--求向量43l a b c →→→→ =+-在x 轴上的投影以及在y 轴上的分向量.
第二部分 向量代数___向量的“积” [内容要点]: 1.向量的数量积、向量积的概念、坐标表示式及其运算规律。 2.向量的混合积的概念、坐标表示式及其几何意义。 3.向量垂直、平行、共面的条件. [本部分习题] 1. 设{3,1,2},{1,2,1},a b →→ =--=-求: (1);(2);(3)cos(,);(4)Pr ;(5)Pr .a b a b a b a b j b j a →→→→→→→→?? 2. 设{2,3,1},{1,1,3},{1,2,0},a b c →→→=-=-=-求: (1)();(2)();(3)();a b c a b c a b c →→→→→→→→→?????? 3. 112233a b a b a b ≥++ 其中,(1,2,3)i i a b i =均为实数,并指出等号成立的条件. 4.设{3,5,2},{2,1,9},a b →→=-=试求λ的值,使得: (1)a b λ→→+与z 轴垂直; (2)a b λ→→+与a →垂直,并证明此时||a b λ→→+取最大值。 5.已知||3,||36,||72,a b a b →→→→==?=求a b →→ ?。 6.判断向量,,a b c →→→是否共面。 (1){3,2,5},{1,1,2},{9,7,16};a b c →→→===- (2){1,2,3},{3,3,1},{1,7,5};a b c →→→=-==-
空间解析几何与矢量代数小练习 一填空题 5 ’x9=45 分 1、平行于向量a(6,7, 6) 的单位向量为______________. 2、设已知两点M1( 4, 2 ,1)和 M 2 (3,0,2) ,计算向量M1M2的模_________________,方向余弦 _________________和方向角 _________________ 3、以点 (1,3,-2) 为球心,且通过坐标原点的球面方程为__________________. 4、方程x2 y 2 z 2 2x 4 y 2z 0 表示______________曲面. 5、方程x2 y2 z 表示______________曲面. 6、x2 y2 z2 表示 ______________曲面 . 7、在空间解析几何中y x2 表示 ______________图形 . 二计算题11 ’x5=55 分 1、求过点 (3,0,-1)且与平面3x-7y+5z-12=0平行的平面方程. 2、求平行于x 轴且过两点 (4,0,-2)和(5,1,7)的平面方程. 3、求过点 (1,2,3) 且平行于直线x y 3 z 1 的直线方程 . 2 1 5 4、求过点 (2,0,-3) x 2 y 4z 7 0 且与直线 5 y 2z 1 垂直的平面方3x 0 5、已知:OA i 3k ,OB j 3k ,求OAB 的面积。 1
参考答案 一 填空题 1、 6 , 7 , 6 11 11 11 2、 M 1 M 2 =2, cos 1 ,cos 2 ,cos 1 , 2 , 3 , 2 2 2 3 4 3 3、 ( x 1) 2 ( y 3) 2 ( z 2) 2 14 4、以 (1,-2,-1) 为球心 , 半径为 6 的球面 5、旋转抛物面 6、 圆锥面 7、 抛物柱面 二 计算题 1、 3x 7y 5 z 4 0 2 、 9 y z 2 0 3、 x 1 y 2 z 3 4 、 16x 14y 11z 65 0 2 1 5 5 S 1 OA OB 19 2 2 2
第三节 曲面及其方程 [教学目的]掌握曲面方程、旋转曲面、柱面、二次曲面方程概念,了解空间常用二次曲面的标准方程,会用“截痕法”画出其简图 [教学重点]曲面方程、旋转曲面、柱面、二次曲面方程 [教学难点]空间想象能力和曲面图形的描绘 [教学过程] 一、问题的提出 在日常生活中,我们经常遇到各种曲面,例如反光镜的镜面、管道的外表面以及锥面等等。那这些曲 面相应的方程是什么呢,怎样才能准确地画出准确的图形呢? 二、曲面方程的概念 (一)曲面方程的基本概念 在一般情况下,如果曲面S 与三元方程 (,,)0F x y z = (1) 有下述关系: (1) 曲面S 上任一点的坐标都满足方程(1); (2) 不在曲面S 上的点的坐标都不满足方程(1) 那么方程(1)就叫做曲面S 的方程,而曲面S 就叫做方程(1)的图形。 象在平面解析几何中把平面曲线当作动点轨迹一样,在空间解析几何中,我们常把曲面看作一个动点按照某个规律运动而成的轨迹。 (二)建立几个常见的曲面方程 例1 若球心在点0000(,,)M x y z ,半径为R ,求该球面方程。 解:设(,,)M x y z 是球面上任一点,那么 0M M R = 又 0M M = 故 2222000()()()x x y y z z R -+-+-= (2) 这就是球面上的点的坐标所满足的方程,而不在球面上的点的坐标都不满足该方程,所以该方程就是以
0000(,,)M x y z 为球心,R 为半径的球面方程。 如果球心在原点,那么0000x y z ===,从而球面方程为 2222x y z R ++= 将(2)式展开得 222222 0000002220x y z x x y y z z x y z R ++---+++-= 所以,球面方程具有下列两个特点: (1) 它是,,x y z 之间的二次方程,且方程中缺,,xy yz zx 项; (2) 2 2 2 ,,x y z 的系数相同且不为零。 (三)曲面研究的两个基本问题 以上表明作为点的几何轨迹的曲面可以用它的点的坐标间的方程来表示,反之,变量,,x y z 间的方程通常表示一个曲面。因此在空间解析几何中关于曲面的研究,有下面两个基本问题。 (1) 已知一曲面作为点的几何轨迹时,建立曲面方程。 (2) 已知坐标,,x y z 间的一个方程时,研究这方程所表示的曲面形状。 例2 方程2 2 2 40x y z x y ++-+=表示怎样的曲面? 解:配方,得 222117 (2)()24x y z -+++= 所以所给方程为球面,球心为1(2,,0) 2-,半径为2。 三、旋转曲面 (一)旋转曲面的定义 一条平面曲线绕该平面上一条定直线旋转一周所形成的曲面。旋转曲线和定直线依次叫做旋转曲面的母线和轴。 (二)旋转曲面的方程 设在y z O 坐标面上有一条已知曲线C ,它的方程为(,)0f y z =,曲线C 绕z 轴旋转一周,得到一个以z 轴为轴的旋转曲面
2013专转本高数空间向量复习资料(同方)
第七章 矢量与空间解析几何 本章主要知识点 ● 矢量运算 ● 平面 ● 直线方程 ● 主要的几个立体图形及方法 一、矢量运算 着重掌握矢量的内积、叉积运算,并深刻理解这两种运算在研究线线、线面、面面之间位置关系时的作用;掌握以矢量为主要线索来建立直线和平面方程的方法和实质。 1.矢量的内积 (1)?Skip Record If...?,其中?Skip Record If...?为?Skip Record If...?的夹角 (2)若?Skip Record If...?, ?Skip Record If...? 且?Skip Record If...? (3)?Skip Record If...? (?Skip Record If...?为非零矢量) 例7.1.?Skip Record If...?,求?Skip Record If...?。 解:?Skip Record If...?。 例7.2.如果?Skip Record If...?,且?Skip Record If...?,求?Skip Record If...?。 解:?Skip Record If...? 得:?Skip Record If...? 得:?Skip Record If...?。 2.矢量的叉积?Skip Record If...? 如图所示,如果?Skip Record If...?不平行于 ?Skip Record If...?,则?Skip Record If...?同时垂直 与?Skip Record If...?又垂直于?Skip Record If...?, 或者等价地,?Skip Record If...?垂直于由?Skip ??Ski p
第七章 空间解析几何与向量代数 §7.1 空间直角坐标系 §7.2 向量及其加减法、向量与数的乘法 一、判断题。 1. 点(-1,-2,-3)是在第八卦限。 ( ) 2. 任何向量都有确定的方向。 ( ) 3. 任二向量, =.则=同向。 ( ) 4. 若二向量, + ,则,同向。 ( ) 5. 若二向量b a ,满足关系b a ??-=a ?+b ? ,则b a ,反向。 ( ) 6. 若 +=+,则 = ( ) 7. 向 量 ,满 足 = ,则 ,同向。 ( ) 二、填空题。 1. 点(2,1,-3)关于坐标原点对称的点是 2. 点(4,3,-5)在 坐标面上的投影点是M (0,3,-5) 3. 点(5,-3,2)关于 的对称点是M (5,-3,-2)。 4. 设向量与有共同的始点,则与,共面且平分与的夹角的向量为 5. 已知向量a 与b 方向相反,且|2|a b =,则b 由a 表示为b = 。 6.设,有共同的始点,则以,为邻边的平行四边形的两条对角线的向量分别为 。 三、选择题。 1.点(4,-3,5)到oy 轴的距离为 (A )2225)3(4+-+ (B ) 225)3(+- (C )22)3(4-+ (D )2254+ 2.已知梯形OABC 、CB // OA 且 2 1 a ,OC = b ,则AB = (A ) 2 1 - (B )21- (C )-21 (D )21- 3.设有非零向量,,若a ⊥ b ,则必有
(A+(B+- (C+<-(D+>- 三、试证明以三点A(4,1,9)、B(10,-1,6)、C(2,4,3)为顶点的三角形为等腰直 角三角形。 四、在yoz平面上求与三个已知点A(3,1,2)、B(4,-2,-2)、C(0,5,1)等距离的 点D。 六、用向量方法证明:三角形两边中点的连线平行与第三边,且长度为第三边的一半。
例1 已知长方体ABCD -A 1B 1C 1D 1中,棱长AB =BC =3,BB 1=4,连结B 1C ,过B 点作B 1C 的垂线交CC 1于点E ,交B 1C 于点F . (1)求证:A 1C ⊥平面EBD ; (2)设A 1C ∩平面EBD =K ,求线段A 1K 的长; (3)求A 1B 与平面BDE 所成角的大小. 解法1:(1)证BE C A ⊥1,BD C A ⊥1,可得A 1C ⊥平面EBD . (2)在平面1BC 中用平几知识可求得4 9 = CE ,在对角面1AC 中,设AC 与BD 交于点O ,可求得22CE OC OE +=4173=,由面积法得34 34 9=CK , 2 121AA AC C A +=34=,34 342511= -=CK C A K A . (3)∵A 1C ⊥平面B DE ,∴∠A 1BK 就是所求的直线A 1B 与平面BDE 所成的角. ∴BK A 1sin ∠B A K A 11= 34345= ,∴直线A 1B 与平面BDE 所成的角为34 34 5arcsin . 解法2:(1)以D 为原点,DA 、DC 、DD 1所在直线分别为x 轴,y 轴, z 轴建立空间直角坐标系D-xyz ,则D (0,0,0),A (3,0,0),C (0,3,0),B (3,3,0),A 1(3,0,4),D 1(0,0,4),C 1(0,3,4), B 1(3,3,4). 设E (0,3,z ),则∵BE ⊥B 1C ,∴BE ·C B 1=0,BE =(-3,0,z ),B 1=(-3,0,-4), ∴·B 1C=(-3,0,z )·(-3,0,-4)=9-4z=0,∴z=49 , ∴E(0,3,4 9), ∴A 1·=-3×3+3×3=0,A 1·=3×3-4×4 9=0, ∴A 1⊥,A 1⊥,∴A 1⊥DB ,A 1C ⊥DE , ∴A 1C ⊥平面BDE . (2)DK =m +n =m (3,3,0)+n (0,3,49)=(3m ,3m +3n ,4 9n ), ∴K (3m ,3m +3n ,49n ),∴A 1=(3m -3,3m +3n ,4 9n-4), A 1⊥?A 1·=(3m -3,3m +3n , 4 9 n -4)·(3,3,0)=0, A B C D 1 A 1 B 1 C 1 D E F
高等数学期末复习 第八章 向量代数与空间解析几何 一、容要求 1、了解空间直角坐标系,会求点在坐标面、坐标轴上的投影点的坐标 2、掌握向量与三个坐标面夹角余弦关系 3、会运用定义和运算性质求向量数量积 4、会运用定义和运算性质求向量的向量积 5、掌握向量数积和向量积的定义形式 6、掌握向量模的定义与向量数量积关系 7、掌握向量的方向余弦概念 8、掌握向量的平行概念 9、掌握向量的垂直概念 10、能识别如下空间曲面图形方程:柱面,球面、锥面,椭球面、抛物面,旋转曲面,双曲 面 11、掌握空间平面截距式方程概念,会化平面方程为截距式方程和求截距 12、会求过三点的平面方程,先确定平面法向量 13、会用点法式求平面方程,通常先确定平面法向量 14、会求过一点,方向向量已知的直线对称式方程,通常先确定直线方向向量 15、会用直线与平面平行、垂直的方向向量法向量关系确定方程中的参数 16、掌握直线对称式方程标准形式,能写出直线方向向量 二、例题习题 1、点)2,4,1(-P 在yoz 面上的投影点为( ); (容要求1) A. )2,4,1(-Q B. )2,0,1(-Q C. )0,4,1(-Q D. )2,4,0(Q 解:yoz 面不含x ,所以x 分量变为0,故选D 2、设向量a 与三个坐标面zox yoz xoy ,,的夹角分别为321,,θθθ(2 ,,0321π θθθ≤ ≤),则 =++322212cos cos cos θθθ( ) (A) 0 (B) 1 (C) 2 (D); 3 解:由作图计算可知,222 123cos cos cos 2θθθ++=,所以选C 。(容要求2) 3、设向量a 与三个坐标面zox yoz xoy ,,的夹角分别为321,,θθθ(2 ,,0321π θθθ≤ ≤),则 =++322212cos cos cos θθθ ; 解:222 123cos cos cos 2θθθ++=,所以填2。(容要求2) 4、向量)3,1,1(-=a ,)2,1,3(-=b ,则=?b a ( ); A. 0 B. 1 C. 2 D. )2,11,5(---
第七章 空间解析几何 一、选择题 1. 在空间直角坐标系中,点(1,-2,3)在[ D ] A. 第一卦限 B. 第二卦限 C. 第三卦限 D. 第四卦限 2.方程2222=+y x 在空间解析几何中表示的图形为[ C ] A. 椭圆 B. 圆 C. 椭圆柱面 D. 圆柱面 3.直线3 12 14 1: 1+=+=-z y x l 与?? ?=-++=-+-0 201:2z y x y x l ,的夹角是 [ C ] A. 4 π B. 3 π C. 2 π D. 0 4. 在空间直角坐标系中,点(1,2,3)关于xoy 平面的对称点是[ D ] A. (-1,2,3) B. (1,-2,3) C. (-1,-2,3) D. (1,2,-3) 5.将xoz 坐标面上的抛物线x z 42=绕z 轴旋转一周,所得旋转曲面方程是[B ] A. )(42y x z += B. 2224y x z +±= C. x z y 422=+ D. x z y 422±=+ 6.平面2x-2y+z+6=0与xoy 平面夹角的余弦是[B ] A. 13 - B. 13 C. 23 - D. 23 7. 在空间直角坐标系中,点(1,2,3)关于yoz 平面的对称点是[ A ] A. (-1,2,3) B. (1,-2,3) C. (-1,-2,3) D. (1,2,-3) 8.方程 222 2 2 x y z a b + =表示的是 [ B ] A.椭圆抛物面 B.椭圆锥面 C. 椭球面 D. 球面 9. 已知a ={0, 3, 4}, b ={2, 1, -2},则=b proj a [ C ] A. 3 B.3 1- C. -1 D.1 10.已知,a b 为不共线向量,则以下各式成立的是 D A. 2 2 2 ()a b a b =? B. 2 2 2 ()a b a b ?=? C. 2 2 ()()a b a b ?=? D. 2 2 2 2 ()()a b a b a b ?+?=
第八章练习题 (一)填空题 1. 直线 2 2111z y x =+=--与z 轴夹角的余弦是 . 2. 设直线 x y z -= += 1 1 1 2 5 在平面x +2y -z +k =0上,则 k =______. 3. 球面x 2-2x +y 2+y +z 2=0的球心是______. 4. 点(-1,-2,-1)到平面0522=-++z y x 的距离d= . 5. 方程22y x z +=表示的二次曲面是 . (二)选择题 1.同时与向量a ={2,1,4}和z 轴垂直的向量是 ( ) A . {-2,1,0} B . {1,-2,0} C . {2,1,0} D. {1,2,0} 2.若一直线的方向向量为{2,3,3},则此直线与z 轴的夹角是( )。 A . 0 B . 3 π C . 2 π D. 4 π 3. 设向量k j b k,j a 2 3 213-=+-=,那么( )。 A .a b ⊥ B . a ∥b 且a b ,同向 C . a ∥b 且a b ,反向 D. a 与b 既不平行,也不垂直 4.与向量a ={1,0,-1} 垂直的单位向量是( ) A .{-1,0,1} B . {1,0,1} C . { 2 1, 0,2 1} D.{1/2, 0,1/2} 5.方程y +z =0 的图形是( )的平面. A .平行于坐标面yz B .平行于y 轴 C .过x 轴 D.平行于z 轴 6.过点(1,2,1)M -且与平面010352=-+-z y x 平行的平面方程式是-------( ) A. 2(1)5(2)3(1)0x y z ---+-=; B. 253110x y z +++= C. 253110x y z -++=; D. 253110x y z ---= (三)计算题 1.求过点(1,1,1)且平行于直线???=--=-+0 2223z x z y x 与 11122z y x =-+=-的平面方程.
第五章 向量代数与空间解析几何 向量 既有大小又有方向的量 表示:→ -AB 或a (几何表示)向量的大小称为向量的模,记作||AB 、|a |、||a 1. 方向余弦:??? ? ??=||,||,||)cos ,cos ,(cos r r r z y x γβα r =(x ,y ,z ),| r |=2 22z y x ++ 2. 单位向量 )cos ,cos ,(cos γβα=→ a 模为1的向量。 3. 模 → →→ ?=++= a a z y x a 2 22|| 4. 向量加法(减法) ),,(212121z z y y x x b a ±±±=±→ → 5. a ·b =| a |·| b |cos θ212121z z y y x x ++= a ⊥ b ?a ·b =0(a ·b =b ·a ) 6. 叉积、外积 |a ?b | =| a || b |sin θ= z y x z y x b b b a a a k j i a ?? a ?b= - b ?a ) ? 2 1 2121z z y y x x == 7. 数乘:),,(kz ky kx ka a k ==→ → 例1 1||,2||==→ → b a ,→a 与→ b 夹角为3 π ,求||→ →+b a 。 解 22 ||cos ||||2||2)()(||→ →→→ →→→→→→→→→→→ →++=?+?+?=+?+=+b b a a b b b a a a b a b a b a θ 713 cos 12222=+???+= π 例2 设2)(=??c b a ,求)()]()[(a c c b b a +?+?+。
第七章 空间解析几何及向量代数 第一节 空间直角坐标系 教学目的:将学生的思维由平面引导到空间,使学生明 确学习空间解析几何的意义和目的。 教学重点:1.空间直角坐标系的概念 2.空间两点间的距离公式 教学难点:空间思想的建立 教学内容: 一、空间直角坐标系 1.将数轴(一维)、平面直角坐标系(二维)进一步推广建立空间直角坐标系(三维)如图7-1,其符合右手规则。即以右手握住z 轴,当右手的四个手指从正向x 轴以2 角度转向正向y 轴时,大拇指的指向就是z 轴的正向。
2. 间直角坐标系共有八个卦限,各轴名称分别为:x 轴、y 轴、z 轴,坐标面分别为xoy 面、yoz 面、zox 面。坐标面以及卦限的划分如图7-2所示。图7-1右手规则演示 图7-2空间直角坐标系图 图7-3空间两点21M M 的距离图3.空间点),,(z y x M 的坐标表示方法。通 过坐标把空间的点及一个有序数组一一对应起来。 注意:特殊点的表示 a)在原点、坐标轴、坐标面上的点; b)关于坐标轴、坐标面、原点对称点的表示法。4.空间两点间的距离。 若),,(1111z y x M 、),,(2222z y x M 为空间任意两点, 则21M M 的距离(见图7-3),利用直角三角形 勾股定理为: 222212221 22 12NM pN p M NM N M M M d ++=+== 而 121x x P M -= 12y y PN -=
1 22z z NM -= 所以 21221221221)()()(z z y y x x M M d -+-+-== 特殊地:若两点分别为),,(z y x M ,)0,0,0(o 222z y x oM d ++== 例1:求证以)1,3,4(1M 、)2,1,7(2M 、)3,2,5(3M 三点为顶点的三角形是一个等腰三角形。 证明: 14)21()13()74(2222 21=-+-+-=M M 6)23()12()75(222232=-+-+-=M M 6)13()32()45(222213=-+-+-=M M 由于 1332M M M M =,原结论成立。 例2:设P 在x 轴上,它到)3,2,0(1P 的距离为到点)1,1,0(2-P 的距离的两倍,求点P 的坐标。 解:因为P 在x 轴上,设P 点坐标为)0,0,(x ()11 3222221+=++=x x PP ()211222 22+=+-+=x x PP 212PP PP = 221122+=+∴x x 1±=?x
向量代数与空间解析几何 第一部分 向量代数___线性运算 [内容要点]: 1. 向量的概念. 2. 向量的线性运算. 3. 向量的坐标,利用坐标作向量的线性运算. [本部分习题] 1. 指出下列各点所在的坐标轴、坐标面或哪个卦限. (2,3,5);(0,4,3);(0,3,0)A B C --- 2. 求点(1,3,2)--关于点(1,2,1)-的对称点坐标. 3. 求点(4,3,5)M --到各坐标轴的距离. 4. 一向量的起点为(1,4,2)A -,终点为(1,5,0)B -,求AB →在x 轴、y 轴、z 轴上的投影,并求||AB →。 5. 已知两点1M 和2(3,0,2)M ,计算向量12M M ??→的模、方向余弦和方向角. 6. 已知{3,5,4},{6,1,2},{0,3,4},a b c →→→==-=--求234a b c →→→ -+及其单位向量. 7.设358,247,54,a i j k b i j k c i j k →→→→→→→→→→→→=++=--=--求向量43l a b c →→→→=+-在x 轴上的投影以及在y 轴上的分向量. 第二部分 向量代数___向量的“积” [内容要点]: 1.向量的数量积、向量积的概念、坐标表示式及其运算
规律。 2.向量的混合积的概念、坐标表示式及其几何意义。 3.向量垂直、平行、共面的条件. [本部分习题] 1. 设{3,1,2},{1,2,1},a b →→=--=-求: (1);(2);(3)cos(,);(4)Pr ;(5)Pr .a b a b a b a b j b j a →→→→→→→→ ?? 2. 设{2,3,1},{1,1,3},{1,2,0},a b c →→→=-=-=-求: (1)();(2)();(3)(a b c a b c a b c →→→→→→→→→?????? 3. 112233a b a b a b ++ 其中,(1,2,3)i i a b i =均为实数,并指出等号成立的条件. 4.设{3,5,2},{2,1,9},a b →→=-=试求λ的值,使得: (1)a b λ→→+与z 轴垂直; (2)a b λ→→+与a →垂直,并证明此时||a b λ→→ +取最大值。 5.已知||3,||36,||72,a b a b →→→→==?=求a b →→?。 6. 判断向量,,a b c →→→是否共面。 (1){3,2,5},{1,1,2},{9,7,16};a b c →→→ ===- (2){1,2,3},{3,3,1},{1,7,5};a b c →→→=-==- (3){1,1,2},{2,4,5},{3,9,8};a b c →→→=-== 第三部分 空间解析几何 [内容要点]: