lecture6-06

Lecture06 受控电源及分压分流电路
例
+
US _
求电流i1 R1 R3
R1 +
i1
R2
ri1
+
US _
i1
ri1/R3
R2//R3
_
R2 R3 R R1 R2 R3
+
US _ 注:
i1
R
+
(R2//R3)ri1/R3 _
Ri1 ( R2 // R3 )ri1 / R3 U S
图1－6-3
广东海洋大学 信息学院 徐国保
Lecture06 受控电源及分压分流电路
广东海洋大学
信息学院
徐国保
Lecture06 受控电源及分压分流电路
例1.6.2.含CCCS电路如图,求Us并计算受控源功率
I1 6Ω + US – + I2 Vf + 0.98I1 – 5Ω 4.9V 0.1 – Ω
Lecture06 受控电源及分压分流电路
lecture_06 受控电源及分压分流电路

内 容 提 纲
1受控电源
（cha.1-7,cha.1-8）
重点难点 含受控电源的电阻电 路分析 分压分流电路的分析
2分压电路
3分流电路
Next: cha.1-10,cha.2-1
作业：1-23，1-28
广东海洋大学 信息学院 徐国保
US i1 R ( R2 // R3 )r / R3
广东海洋大学
受控源和独立源一样可以进行电 源转换；转换过程中注意不要丢 失控制量。
信息学院 徐国保
Lecture06 受控电源及分压分流电路

Flux of energy
Dissipating eddies
Energy Cascade (after Richardson, 1922)
ANSYS, Inc. Proprietary © 2009 ANSYS, Inc. All rights reserved.
6-4
April 28, 2009 Inventory #002600
Turbulence Modeling
Introduction to Turbulence Modeling
Training Manual
• Characterization of Turbulent Flows • From Navier-Stokes Equations to Reynolds-Averaged Navier-Stokes (RANS) Models • Reynolds Stress Tensor and the Closure Problem • Turbulence Kinetic Energy (k) Equation • Eddy Viscosity Models (EVM) • Reynolds Stress Model • Near-wall Treatments Options and Mesh Requirement • Inlet Boundary Conditions • Summary: Turbulence Modeling Guidelines • Appendix
• Very sensitive to (or dependent on) initial conditions.
ANSYS, Inc. Proprietary © 2009 ANSYS, Inc. All rights reserved.

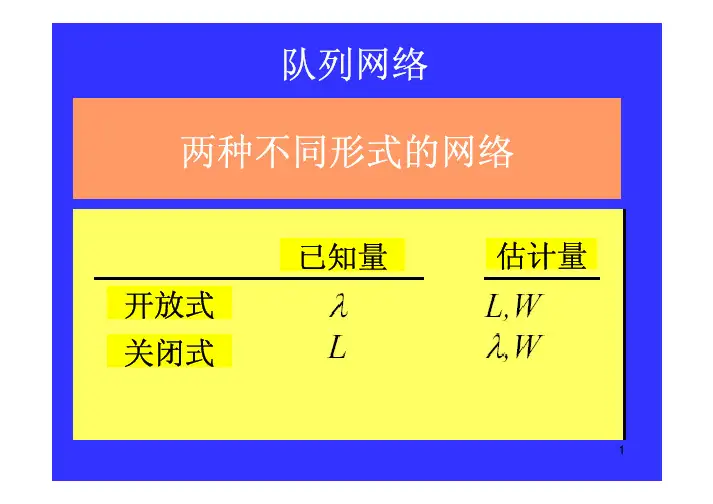
队列网络两种不同形式的网络已知量估计量开放式关闭式12•因特网流量•急诊室（Denardo ）•美食广场•飞机场（抵达、检票、安检、护照、控制、通道、登机）•有一系列生产系统，但没有物料控制的工厂.例子开放式网络3人例子开放式网络美食广场入口人Sbarro 比萨TCBY 冷冻酸乳酪麦当劳餐桌出口人和盘子4•通过保持恒定数量的项目来进行物料控制的工厂（CONWIP ）•有限个固定设备的工厂例子封闭式网络杰克逊网络队列网络经常被建模成杰克逊网络。

•易于计算性能（系统容量、系统中平均时间、平均队列长度）。

•易于理解•易于进行设计优化•对大规模的系统有效…5杰克逊网络•…但也有其不足之处。

要求存储区必须是足够大的（例如：大到从不出现堵塞）67开放式杰克逊网络ii K i i µα==提供单一服务的站点站点的服务率--指数分布站点的到达率--泊松分布01()1()r Ki ij r j P i j P P P i ===−=∑ij P 顾客离开站点到下一站点顾客在离开站点后退出系统:12,P 0i >i0注释、从概率角度讲,顾客被不能辨别、顾客的行程是无记忆的3、在每一个站点都遵守先到先服务(FCFS)的原则4、至少对于一个有例子89开放式杰克逊网络的解决方案i i λ=站点的有效到达率在孤立情况下站i 内平均等待时间流量方程（流入量＝流出量）令稳态概率站点i 内处于稳态的顾客数量生产形式解决方案（行向量）是单一M/M/1队列中n 项的概率(1)nρρ−10注释1）杰克逊猜想并验证了站点的流出量＝站点的流入量2）每一站点的输入看上去像服从泊松分布，但如果路径中有反馈，则这种输入就不服从泊松分布3）在没有顾客插队的情况下，系统中平均等待时间＝在孤立状态下在各站点平均等待时间之和4）生产形式解决方案适于处理提供多种服务的站点(...)i k n n (...)i k n n，有：12封闭式杰克逊网络（续）生产形式解决方案这里，校正常数是1kijij i ii iλλρλλρµ===∑i 流量方程只能被解释成一个比例常数通过体现出相关性令13Buzen 算法第一步：定义一个辅助方程第二步：设计一个关于以及在j 上的代数和的递归关系条件k X j =11{0:...}(,)()*()Ki Ki i i X X XN n i i iC K N f X f X πρ=≥++===∑改变了符号目标：Buzen算法（续）第三步：初始化没有顾客时一个节点顾客第四步：填充k×N矩阵站从左上角开始,从上至下填写，15封闭式网络简单的FMS 模型另外转换站装载/卸载转换站Otherwise16生产率为：并且在这种情况下C(M , N )很容易计算封闭式网络简单的FMS 模型。

Introduction to British Educational System
General classification of British Educational System

Compulsory education Further education Higher education

Core subjects: English, Math, Science

Foundation subjects:
Design &Technology, Information and Communication Technology(ICT), History, Geography, Music, Art, Physical Education, A modern foreign language （usually French )
Introduction to British Educational System
Five stages
1st : nursery school(3-4) 2nd :Primary school(5-11) 3rd :Secondary school (11-16) 5-16 years old (compulsory education) 义务教育 16-18 中学高级班(或大学预科) 4th :18岁大学3-4(医科5) for BA/BScs;1-2 MA/MScs;PhD(35) 5th : further education : 青年和成年人的职业教育( 不含正 规的大学
Introduction to British Educational System
Text A Going to school :British Style

McGraw-Hill/Irwin
Copyright © 2001 by The
5-5
Purchasing Power Parity
• Absolute Purchasing Power Parity • Relative Purchasing Power Parity
McGraw-Hill/Irwin
McGraw-Hill/Irwin
Copyright © 2001 by The
5-4
Purchasing Power Parity
• The theory of purchasing power parity(PPP) is based on the The law of one price. • The law of one price states that one basket of goods should cost the same regardless of the currency in which it is sold.
McGraw-Hill/Irwin
Copyright © 2001 by The
5-10
Purchasing Power Parity
The US dollar appreciates against sterling by about 12%. A basket of goods costing USD 15,450 in the USA has a sterling cost of 15,450/1.32= £11,500and thus PPP maintained.
Value of £ $1.60 $1.55 S: Supply of £ equilibrium exchange rate D: Demand for £ Quantity of £ Copyright © 2001 by The

• 杭州的春天，淡妆浓抹，无不相宜。Sunny or rainy, Hangzhou looks its best in spring. • 两位作家来湖州，为书市注入了新的活力。 • Their arrival also poured energy into the book market. / Their arrival also made the book market brisk. • 科学是永恒的，艺术是永恒的。Science is long as art is!
• 这里山峦交错，峡谷相连，江水汹涌。 • The valley is full of multi-peaked mountains, joined canyons and turbulent waters. • 这里气候温和，四季分明，雨量充沛，日 照充足。
• The place enjoys a temperate climate with well-marked seasons, plenty of rainfall and sunshine. • 基本建设要遵循合理布局、优化结构、重 点突出的原则。 • The principle of a rational distribution, an optimized structure and a priority order should be followed in capital construction.
• 3.学校而无书籍，就不能称为真正的学校。 • 分析：“称为”还是解为“视为”较妥， 当然句子应该译成一个更为紧凑的简单句。 • A school without books cannot be considered a true school. • 试比较：without books, a school cannot be named a true school.

O2 S
O CH3
base
SO3 CH3 SO2Ar
SO2Ar
(2) Which pathway dominates?
Me
Scope of Lecture Baeyer-Villiger rearrangements dioxirane and peracid epoxidations geometric constraints in SN2 reactions Baldwin's Rules stereoelectronic effects on reactivity
E. Kwan, D.A. Evans
Lecture 6: Stereoelectronic Effects on Reactivity
Chem 106
The Endocyclic Restriction Test It has been estimated that a deviation of 17° away from linearity is allowed in this degenerate exchange, which is exocyclic in two five-membered rings, but endocyclic in one eight-membered ring:
OSAr OSAr
Cyclizations are classified as favored or disfavored, rather than allowed or disallowed; the "rules" merely suggest whether a particular reaction would be facile or not.

lecture的意思用法大全lecture的意思n. 演讲,训斥，教训vi. 作演讲vt. 给…作演讲,教训(通常是长篇大论的)变形：过去式: lectured; 现在分词：lecturing; 过去分词：lectured;lecture用法lecture可以用作名词lecture主要指教育性或学术性“演讲”,引申可指“冗长的训斥或谴责”。

lecture是可数名词,其后接介词on或about ,意为“关于…的演讲”“就…做演讲”“因…训斥或谴责某人”。

lecture作“讲演,讲课”解时,是不及物动词。

说“讲授某课程”时常与介词on连用,说“在某地讲演”时常与介词at〔in〕连用。

lecture用作名词的用法例句She ran over her notes before giving the lecture.她讲课前把讲稿匆匆看了一遍。

His lecture covered various aspects of language.他的讲课涉及到语言诸方面的问题。

They could not follow the lecture.他们听不懂这次演讲。

lecture可以用作动词lecture作“讲演,讲课”解时,是不及物动词。

说“讲授某课程”时常与介词on连用,说“在某地讲演”时常与介词at〔in〕连用。

lecture也可用作及物动词,意思是“向…讲演,给…讲课”,接名词或代词作宾语。

lecture还可作“责备”“教训”“训斥”解,用作及物动词,接名词或代词作宾语。

“因…而受到训斥”可说lecture sb for n./v -ing。

lecture用作动词的用法例句It was a shame for me to be lectured in front of the whole class.当着整个班级的面被训斥了一顿，真让我感到羞辱。

He lectured to his students on modern writers.他给学生们讲了关于现代作家的一课。

9;
Galilean velocity transformation equation
Inertial frames of reference S' is moving at a velocity u with respect to another inertial frames of reference S.
2-3-2 Galilean principle of relativity
Galileo’s observation and understanding of the motion suffered two limitations: • within the realm of mechanics • the mechanical motions at very low speed: v « 299,792,458 meters per second Both of these two factors have greatly influenced Galileo’ s view of space and time and hence his concept of the principle of relativity.
The rigorous expression of the velocity transformation
dr dR dr ′ dR dr ′ dt ′ dt ′ v= = + = + ⋅ = u + v′ dt dt dt dt dt ′ dt dt
Galileo’s velocity transformation demands dt/dt’= 1, or
∆t = ∆t′
The central idea of Galileo’s concept of time: The time is absolute, the time interval is not rested upon the choice of the frame of reference.

lecture的用法和短语例句lecture有讲课;演讲;训话等意思，那么你知道lecture的用法吗?下面店铺为大家带来有关lecture的用法和短语例句，供大家参考学习!lecture的用法：lecture的用法1：lecture主要指教育性或学术性“演讲”,引申可指“冗长的训斥或谴责”。

lecture的用法2：lecture是可数名词,其后接介词on或about ,意为“关于…的演讲”“就…做演讲”“因…训斥或谴责某人”。

lecture的用法3：lecture作“讲演,讲课”解时,是不及物动词。

说“讲授某课程”时常与介词on连用,说“在某地讲演”时常与介词at〔in〕连用。

lecture的用法4：lecture也可用作及物动词,意思是“向…讲演,给…讲课”,接名词或代词作宾语。

lecture的用法5：lecture还可作“责备”“教训”“训斥”解,用作及物动词,接名词或代词作宾语。

“因…而受到训斥”可说lecture sb for n./v -ing。

lecture的常用短语：用作动词 (v.)lecture about〔on〕 (v.+prep.)lecture at (v.+prep.)lecture for (v.+prep.)lecture的用法例句：1. Chuck would lecture me, telling me to get a haircut.查克就会数落我，让我去理一下发。

2. Within this lecture I cannot pretend to deal adequately with dreams.在这一次讲座中，我不敢自诩能对梦境作透彻的分析。

3. Our captain gave us a stern lecture on safety.船长就安全问题严厉地训斥了我们一顿。

4. We picked up our conference materials and filed into the lecture hall.我们领了会议材料后鱼贯进入讲演厅。

6.3 Cohesion in English texts
❖cohesion
❖衔接
❖ Means of cohesion (衔接）:
a. Lexically
(repetition, synonymy, hyponymy--reiteration)
antonymy,
b. Grammatically
Discuss
❖P. 90 No. 1 ❖a. What does “it” refer to? ❖ MONEY ❖b. What is omitted in the sentence? ❖“WORK HARD” is omitted after
“DOESN’T”.
6.4 Turn taking in Engliile the next speaker may opt to interrupt in order to seize the floor, he or she can wait to be nominated by the current speaker, or take the hints from him such as a long pause, a gesture, a gaze, etc.
❖For endophoric reference, further distinction is attempted between anaphoric reference and cataphoric reference. The former involves a relation between a preceding referential expression or an antecedent and the current pronominal item (as in “John loves Jane.

OO R1 OH R2 R1
Reagents
O R2 R1 O R2
a2 a
d2
OH
Example 1
CH2COOH
4
OH
O
+ CH2(COOEt)2
1,4-Difunctionalised Compounds - Strategy 3 Reagents
O R1 O R2 R1 O
d1
R2 R1 O
HO R1 OH R2 R1 R2 R1 R2 HO OH O O
Example
FGI O R O
R OH O OH HO COOH R
HO R
O R
1,4-Difunctionalised Compounds - Strategy 5 - Allylation FGI
CHO COOEt COOEtOa3with nitrile or nitro derivative
Lecture 6 Two Group Disconnections
1,4-Difunctionalised Compounds Difunctionalised
1,4-Difunctionalised Compounds - Strategy 3 Nitrile
or
R1 OH
R2
Reagents
O R2 R1 X R2
a2
d2
OO
Example: Precursor of antibiotic methylenomycin
methylenomycin
O O COOH
O
O
1
O
O
O
1,4-diCO
O Br COOEt
COOEt

lecture6译文（1）WuxiWuxi is a small city in Jiangsu Province of the South, situated between Nanjing and Shanghai. As early as 6,000 years ago, there had been a primitive tribe settled here. Today' s Wuxi began to be built in the second century B.C. At that time tin ore was excavated from Xishan southwest of the city. After the discovery of tin, people started to call this place"Youxi". As time passed by, the tin mine ran out and "Youxi" was changed to "Wuxi". Wuxi is a small city in South China' s Jiangsu Province, located mid-way between Nanjing and Shanghai. Established as early as 6,000 years ago by a primitive clan tribe, the present city was first built in the second century B.C. when tin was mined from a hill in the southwest named Xishan. After tin was discovered there, the place began to be called Youxi, literally "has tin", and with the passage of time, the tin was mined out and the name was changed to Wuxi, meaning "no tin".Wuxi faces the Taihu Lake in the south and leans against the Huishan Mountain in the west, both of which are the major local scenic spots. Besides, the old Jing-Hang Grand Canal and the Jing-Hu Railway pass through here. Wuxi is bordered by Taihu Lake on the south, and Huishan Hill in the west. They are the major scenic spots there. In addition, the ancient Grand Canal from Beijing to Hangzhou was dug to run through the city, as was the Beijing-Shanghai Railway.As one of the five large freshwater lakes in China, the T aihu Lake has a water area of 36,000 square hectares, with about 100 small islands and 72 mountain peaks along its shore. Several thousand years ago, here used to be a shallow water bend. Lateron the Changjiang Delta gradually expanded and connected with the dikes and dams in the gulf, thus forming an interior lake and turning the original isles into mountain peaks. With its misty water, the Taihu Lake is surrounded by grotesque peaks. This nature-made scenery of lakes and mountains is so beautiful that one simply cannot take them all in. The Taihu Lake is one of the five largest freshwater lakes in China. Covering a water area of 36,000 hectares, it has scores of islets and 72 peaks along its banks. Thousands of years ago, the lake was a shallow bay. Later the gradually expanding Yangtse Delta linked with the dykes in the bay and turned it into an inland lake and the original islets into the peaks along the water. The mist-covered surface of the water and surrounding peaks make Taihu a splendid natural landscape of mountains and lakes.The part of the Grand Canal in Wuxi is 40 kilometres long, of which 14.6 kilometres is in the urban area. With a history of over 2,400 years, this green chain of water is still running merrily, with many places of historic interest and scenic beauty along its bank. The cutting of this canal dated back to the 5th century B.C. and its full length is 1,794 kilometres. Like the 10-thousand-li Great Wall, it is also the symbol of China's ancient civilization. The Wuxi section of the Grand Canal is 40 kilometres long, with 14.6 kilometres in the city area. With a history of more than 2,400 years, this green belt of water still flows pleasantly with many scenic spots and historical sites on both banks. The Grand Canal was first dug in the 5th century B.C. and is 1,794 kilometres. Like the Great Wall, this project is a symbol of ancient Chinese civilization.The Canal is both narrow and deep in Wuxi, and along the two banks there are rows of old-style dwelling houses with greentiles and white walls. The canal at Wuxi is narrow and deep, and row upon row of old residential buildings with white walls and black tiles stand along both sides.Every year there are many tourist activities in Wuxi and from 8th to 14th this October, there will be a "Wuxi Taihu International Fishing Competition, "which can be entered for by both individuals and groups, professionals and amateurs. Wuxi arranges many tourist programmes each year and during the coming October 8--14, there is a"Wuxi Taihu International Angling T ournament". Catering to both professionals and amateurs, the contest can either be entered in group or singles.译文二WuxiWuxi is a small city in South China' s Jiangsu Province, located mid-way between Nanjing and Shanghai. Established as early as 6,000 years ago by a primitive clan tribe, the present city was first built in the second century B.C. when tin was mined from a hill in the southwest named Xishan. After tin was discovered there, the place began to be called Youxi, literally "has tin", and with the passage of time, the tin was mined out and the name was changed to Wuxi, meaning"no tin".Wuxi is bordered by Taihu Lake on the south, and Huishan Hill in the west. They are the major scenic spots there. In addition, the ancient Grand Canal from Beijing to Hangzhou was dug to run through the city, as was the Beijing-Shanghai Railway.The Taihu Lake is one of the five largest freshwater lakes in China. Covering a water area of 36,000 hectares, it has scores of islets and 72 peaks along its banks. Thousands of years ago, the lake was a shallow bay. Later the gradually expanding Yangtse Delta linked with the dykes in the bay and turned it into an inlandlake and the original islets into the peaks along the water. The mist-covered surface of the water and surrounding peaks make Taihu a splendid natural landscape of mountains and lakes.The Wuxi section of the Grand Canal is 40 kilometres long, with 14.6 kilometres in the city area. With a history of more than 2,400 years, this green belt of water still flows pleasantly with many scenic spots and historical sites on both banks. The Grand Canal was first dug in the 5th century B.C. and is 1,794 kilometres. Like the Great Wall, this project is a symbol of ancient Chinese civilization.The canal at Wuxi is narrow and deep, and row upon row of old residential buildings with white walls and black tiles stand along both sides.Wuxi arranges many tourist programmes each year and during the coming October 8--14, there is a"Wuxi Taihu International Angling Tournament". Catering to both professionals and amateurs, the contest can either be entered in group or singles.第六讲主语的确定汉语：意合语言，重意念，轻形式英语：行合语言，重形式，讲逻辑如何确立主语？一、补充主语汉语句子中主语旺旺不突出，很多句子为无主句。

To characterize fully the data needs of the prospective database users. method: questionaire, chatting, Result: requirements of database users
Database Design phases---step2
The needs of the users play a central role in the design process.
We focus on the design of the database schema in this chapter.
Database Design phases---step1
Chooses a data model and translate those requirements into a conceptual schema. method: E-R model or E-R diagram Result: E-R diagram
Database Design phases---step3
E-R model consists of:
Entity sets Relationship sets Attributes constraints

Entity sets
A database can be modeled as: a collection of entities, relationship among entities.
Incompleteness, eg:
student(student_id, select_course, grade) What happened when you insert a student who didn’t

2. The Legend of the Sleep Hollow
• Source: The story is based on a German folktale. • Setting: The story is set about 1790 in the Dutch settlement of Tarry Town, New York, in a secluded hollow called Sleepy Hollow. • Story and plot: It tells the story of Ichabod Crane, a lean, lanky, and extremely superstitious schoolmaster from Connecticut, who competes with Abraham "Brom Bones" Van Brunt, the town rowdy, for the hand of 18-year-old Katrina Van Tassel, the daughter and sole child of a wealthy farmer, Baltus Van Tassel.
1. Rip Van Winkle
• • German recourse It is the fantasy tale about a man who somehow stepped outside the main stream of life. Rip Van Winkle is a simple, good-natured and hen-pecked man. The story reveals, to some extent, the conservative attitude of its author:

Lecture 6 The Present
By Tian Ying
Teaching Contents
Elements of Fiction Video Watching Reading Questions Meet the Author Text Reading Interpretation and Discussion Homework Assignment
2. 八十大寿，毕竟非同一般，不管怎么说你又活了 十年，或者说熬了十年，是活还是熬，全在于你 怎么看了
3. The old lady was sure of that. (para.9)
Interpretation and Discussion
Read the details about the cheque, and what can you infer from these? 1. The cheque fluttered to the floor like a bird with a broken wing. 2. Her present, her lovely present.
Interpretation and Discussion
Read the details about the old lady, and what can you infer from these? 1. After all eighty was a special birthday, another decade lived or endured just as you choose to look at.
A. B. C. D.
Reading Questions
The old lady got up early to wait for her _____ from her daughter A. Birthday present B. A mail C. money D. Phone call

Lecture 6. Early Buddhist Art in ChinaContent1.Devotion belief of Maitreya2.Sinicization in early Chinese Buddhist Art2.1.Sinicization policy in the Northern Wei2.2.Yungang Grottoes2.3.Longmen Grottoes◎E-Resources :1. Timeline and Maps of China :/chinaciv/timeline.htm2. Timeline of Chinese History and Dynasties [Asia for Educators]/tps/1000bce.htm3. Database for Buddhist Cave Temples in Chinahttp://dsr.nii.ac.jp/china-caves/index.html.en4. Chinese Symbols and Art Motifs/chinese-symbols.html5. How to identify a Buddhist images :/002F/index.htm◎Readings :[Maitreya]Jaini, Padmanabh S. “Stages in the Bodhisattva Career of the Tathāgata Maitreya.” In Maitreya, the Future Buddha. Edited by Alan Sponberg and Helen Hardacre, 54–90. New York: Cambridge University Press, 1988.Kim, Inchang.The future Buddha Maitreya : an iconological study,New Delhi : D.K. Printworld, 1997, [294.342113 K49]Kitagawa, Joseph M. “The Many Faces of Maitreya: A Historian of Religions’ Reflections.” In Maitreya, the Future Buddha. Edited by Alan Sponberg and Helen Hardacre, 7–22. New York: Cambridge University Press, 1988.Lancaster, Lewis. “Maitreya.” In The Encyclopedia of Religion. 2d rev. edition. V ol.8. Edited by Lindsay Jones, Mircea Eliade, and Charles J. Adams. Detroit: Macmillan Reference USA, 2005.[Sinicization]ALEXANDER C. SOPER, IMPERIAL CA VE-CHAPELS OF THE NORTHERN DYNASTIES: DONORS, BENEFICIARIES, DATES , Artibus Asiae, V ol. 28, No.4 (1966), pp. 241-270ARPUTHARANI SENGUPTA, CULTURAL SYNTHESIS IN THE BUDDHIST ART OF CHINA, E-resources : http://ignca.nic.in/ks_41026.htmKatherine R. Tsiang, Changing Patterns of Divinity and Reform in the Late Northern Wei, The Art Bulletin, V ol. 84, No. 2, Jun., 2002 .Liu, Hongshi. "Early Chinese Buddhist stone carvings." Chinese Literature 4 (April 1982): 130-135.Rhie, Marylin M. "Late Sui Buddhist sculpture: a chronology and regional analysis." Archives of Asian Art 35 (1982): 27-54.Caswell, James O. Written and Unwritten: A New History of the Buddhist Caves at Yungang. Vancouver: University of British Columbia Press, 1988.Caswell, James D. "The 'Thousand-Buddha' pattern in caves XIX and XVI atYun-kang," Ars Orientalis 10 (1975):35-54.Chen, C.M. Buddha's statues in the Yunkang caves. Berkeley: [the author], 1977. Gabain, A. Annemarie von. "Types of arhats on a series of wall paintings from Turfan," Memoirs of the Research Department of the Toyo Bunko 33 (1975):161-9.Huntington, John C. "The iconography and iconology of the 'Tan Yao' caves at Yungang." Oriental Art 32:2 (Summer 1986): 142-160.Knauer, Elfriede Regina. The fifth century A.D. Buddhist cave temples at Yun-kang, North China: a look at their western connections." Expedition 25:4 (Summer 1983): 27-46.★James C. Y. Watt, Art and History in China from the Third to the Eighth Century, in China : Dawn of a Golden Age, 200-750 AD, New York : Metropolitan Museum of Art ; New Haven : Yale University Press, c2004. [LB 709.21 C5 W ]★Leidy, Denise Patry, The art of Buddhism : an introduction to its history and meaning, Boston : Shambhala, 2008. Chap.3, [704.948943 L52 a]Soper, Alexander C. Literary evidence for early Buddhist art in China. Ascona, Switzerland: Artibus Asiae Publishers, 1959.WU, HUNG, BUDDHIST ELEMENTS IN EARLY CHINESE ART (2nd and 3rd Centuries), Artibus Asiae, V ol. 47, No. 3/4 (1986), pp. 263-303+305-352"Stone Sculptures of the Northern Wei Dynasty." Arts of Asia 25:5 (1995):134.【E-resources】Video from web :Yungang Grottoes/program/newsupdate/20100930/104106.shtml※Glossary of Chinese Art/china/glossary.htmlGao gu you si miao高古游絲描Archaic floating gossamer threadsAo-tu painting technique凹凸畫法in the Western Regions‘ convex-concave technique 凹凸畫法is used, first creating an ink outline and then applying color shading to show a three dimension of pictureBao yi bo dai褒衣博帶: Confucian-style loose robe with a broad sashXiu gu qing xiang秀骨清像: graceful and elegant lookSome famous artists in the 3-6 century1.Dai Kui 戴逵, (326－396)2.Gu Kaizhi顧愷之, (344－405)3.Cao Zhongda曹仲達, (active in Northern Qi dynasty, ca.550-577)4.Zhang Sengyao張僧繇. (502-549)5.Lu Tanwei 陸探微(?-485)Basic Terms in Chinese PAINTINGS and CALLIGRAPHY Formats:hanging scrolls: vertically proportioned for hanging on wallshandscrolls: h orizontal scrolls viewed section by section (right to left) on a table fan: oval with a handle or folded and set in a frame; can be removed from holder and mounted in an albumalbum: paintings mounted on individual leaves in book-like form Materials:silk: smooth, fine fabric made from cocoons of silkworms in China since Neolithic timespaper: made in China since at least the Han dynasty of a variety of fibrous materials, such as mulberry bark and hempbrush: used in China since Neolithic times and made with a pointed tip and in many sizes of a variety of materials, such as rabbit, goat, and weasel hairink: made of pine soot or lampblack combined with glue and pressed into cakes or sticks in dried form, which must be ground with water for usecolor pigments: water-based and derived primarily from plants and minerals◎Key Images : (The images are collected from public domain and used only for education purpose only.)◎Iconography of Maitreya◎◎◎◎◎◎◎◎◎◎◎Sinicization in the Northern WeiYungang Grottoes (雲崗石窟)The Buddhist statues (cave 20) Yungang Grottoes in Datong, Shanxi Province. Yungang Grottoes (雲崗石窟)(cave 16, Yungang Grottoes) Bao yi bo dai褒衣博帶: Confucian-style loose robe with a broad sashYungang Caves, Datong, Shanxi Province Cave 9, AntechamberNorth Wall, Top of DoorNorthern Wei, Late 5th Century Sandstone, Photograph taken in 1982 Huntington Archive Image Scan # C7193Buddha, Yungang Cave 5,Longmen Cave 19, Fengxian Temple, at Longmen,Tang (early 670's CE, 672 CE - 675 CE) Material: grey limestone , Dimensions: H - ca. 55.00 ftCopyright Holder: Huntington, John C. and Susan L.Guyang Grotto 古陽洞Northern Wei Dynasty 493-534 AD; the oldest cave at Longmen(Binyang cave, Longmen grottoes, 龍門石窟賓陽中洞Luoyang, Henan province)Longmen Grottoes, Fengxian Tample, 奉先寺, Tang dynasty.Binyang Cave, Longmen 龍門賓陽洞Gong Xian County Grottoes 鞏縣石窟is in the Northern Wei Dynasty another great treasure house of Buddhist art besides the Longmen Grottoes. It is located in Luoyang northeast about 55 km（500-503AD）.Northern Wei :Buddha's monk's robe covering both shoulders, with thin underrobe and knotted cross-tie (a loose gown with wide girdle褒衣博帶),flowing in patterned folds over his throne;。