flexible_factorial_design_specification_Glascher_Gitelman(2008)

fractional factorial conjoint
我们要了解fractional factorial conjoint的含义。

首先，我们需要了解什么是fractional factorial design和conjoint analysis。

Fractional factorial design是一种实验设计方法，用于在有限的资源下进行多因素实验。

Conjoint analysis是一种统计方法，用于研究产品或服务的不同属性如何影响消费者对产品的整体评价。

当我们结合这两种方法时，我们得到fractional factorial conjoint。

这种方法允许我们同时考虑多个因素及其交互作用，并确定哪些因素对产品的整体评价有显著影响。

为了更好地理解fractional factorial conjoint，我们可以考虑一个简单的例子：
假设我们正在测试两种不同品牌的手机，每种手机都有三个属性：价格、屏幕大小和电池寿命。

使用fractional factorial conjoint，我们可以设计实验来同时测试所有可能的属性组合，并确定哪些属性组合对消费者的购买决策有最大影响。

总结：Fractional factorial conjoint是一种结合了fractional factorial design和conjoint analysis的方法，用于在有限的资源下研究多个因素及其交互作用对产品整体评价的影响。

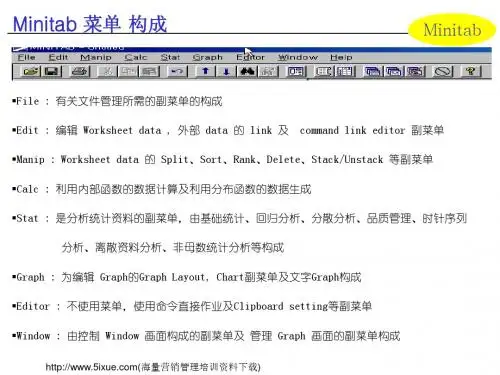
六西格玛培训—改进阶段模块部分因子设计Patrick ZhaoI&CIM Deployment Champion部分因子设计介绍创建部分因子设计分析部分因子设计其他部分因子（筛选）设计部分因子设计介绍创建部分因子设计分析部分因子设计其他部分因子（筛选）设计以因子水平的仅执行全因子确定了重要因特殊的响应曲使产品或过程试验设计类型全因子部分因子响应曲面混料田口试验目的全部组合度量响应的设计。

设计中的部分设计。

子后进行模型改进。

面试验，主要研究产品的多种成分组成。

在操作环境中更加稳定试验设计。

因子个数≤4≥5≤3 3 ~ 5≥7试验设计路线图部分因子设计•在分析初期对大量潜在因子做筛选，确定少量关键因子。

全因子设计•针对部分关键因子，全面分析各因子之间的交互作用。

响应曲面设计•对模型进行更深入分析，识别模型中的弯曲现象。

为了节省资源，一般采用其中两种设计就已经足够分析。

优点：大量减少试验组合数。

•对于一个2水平，6因子的试验设计，采用全因子和部分因子的试验组合数如下：全因子部分因子26=6412∗26=32 14∗26=16 18∗26=8缺点：只分析关键的因子效应，忽略部分交互效应。

•对于一个2水平，3因子的试验设计，采用全因子和部分因子在分析因子效应时的区别如下：全因子部分因子•主效应与两因子交互作用混杂，三因子交•所有效应均能被分析。

互作用不能被分析。

混杂•混杂发生于部分因子设计中，原因是设计中不包括因子水平的所有组合。

例如，如果因子A 与3 因子交互作用BCD 相混杂，则A 的估计效应是A 的效应与BCD 的效应的合计。

您无法确定显著效应是因为A、因为BCD，还是因为两者的组合。

•办公室上班族为了健康，办了健身卡，每周请私人教练2次进行锻炼。

•与此同时，开始控制饮食，每天科学摄入合理的卡路里。

•3个月后，身体状态感觉良好，体脂率下降3%。

此时，我们无法得知，到底是锻炼还是控制饮食对降低体脂率更有帮助，也无法得知这两种措施的影响程度分别有多少。

常用实验设计方法（三）六.析因设计（f a c t o r i a l d e s i g n）◆析因设计是一种多因素试验设计。

◆可将两个或多个因素的各个水平进行排列组合，交叉分组进行全面实验。

◆总的实验方案(组合)是各因素水平的乘积。

例如：2×2析因设计（两个因素，每个因素均为2个水平，常可写成22析因设计）A因素（A1、A2）和B因素（B1、B2）共4种实验方案或组合（A1B1、A1B2、A2B1、A2B2）3×3析因设计（两个因素，每个因素均为3个水平，常可写成23析因设计）A因素（A1、A2、A3）和B因素（B1、B2、B3）共9种组合（A1B1、A1B2、A1B3、A2B1、A2B2A2B3、A3B1、A3B2A3B3）2×3×3析因设计（三个因素，一个因素为2个水平，余均为3个水平）共18种组合1.特点①研究的因素个数m≥2，各因素的水平数≥2；②各因素在实验中同时实施且所处的地位基本平等。

③每个因素水平相互组合的实验方案，至少进行2次及以上独立重复实验。

④因素间存在交互效应。

例如，一级（两个因素间）或二级交互（三个因素间）效应。

⑤统计学分析时，各因素及交互项所用误差项是相同的。

◆优点：⏹可分析各因素的主效应(m a i n e f f e c t s)（某因素各水平间的平均效应差异）⏹因素间的交互效应(i n t e r a c t i o n)(一个因素的水平改变会影响另一个因素的效应)⏹寻找最优方案或最佳组合⏹可允许数据缺失（完全随机分配情况下）◆缺点：⏹当因素较多或水平数较多时，所需实验次数过多。

⏹一般来说，因素数最好不要多于6个，水平数亦不要过多，一般为2或3个。

2.析因设计的类型➢可采用完全随机分配方法或随机区组的析因设计。

➢可安排两因素或多因素实验⑴2×2析因设计结果见下表：分析：设计类型？如何制定设计方案？如何进行统计学分析？①设计类型两个因素：甲药（不用、用），乙药（不用、用），交叉全面组合，各实验方案独立重复3次，为2×2析因设计。

Factorial experimentIn statistics, a full factorial experiment is an experiment whose design consists of two or more factors, each with discrete possible values or "levels", and whose experimental units take on all possible combinations of these levels across all such factors. A full factorial design may also be called a fully crossed design. Such an experiment allows studying the effect of each factor on the response variable, as well as the effects of interactions between factors on the response variable.For the vast majority of factorial experiments, each factor has only two levels. For example, with two factors each taking two levels, a factorial experiment would have four treatment combinations in total, and is usually called a 2×2 factorial design.If the number of combinations in a full factorial design is too high to be logistically feasible, a fractional factorial design may be done, in which some of the possible combinations (usually at least half) are omitted.HistoryFactorial designs were used in the 19th century by John Bennet Lawes and Joseph Henry Gilbert of the Rothamsted Experimental Station.[1]Ronald Fisher argued in 1926 that "complex" designs (such as factorial designs) were more efficient than studying one factor at a time.[2] Fisher wrote,"No aphorism is more frequently repeated in connection with field trials, than that we must ask Nature few questions, or, ideally, one question, at a time. The writer is convinced that this view is wholly mistaken." Nature, he suggests, will best respond to a logical and carefully thought out questionnaire". A factorial design allows the effect of several factors and even interactions between them to be determined with the same number of trials as are necessary to determine any one of the effects by itself with the same degree of accuracy.Frank Yates made significant contributions, particularly in the analysis of designs, by the Yates analysis.The term "factorial" may not have been used in print before 1935, when Fisher used it in his book The Design of Experiments. [3]ExampleThe simplest factorial experiment contains two levels for each of two factors. Suppose an engineer wishes to study the total power used by each of two different motors, A and B, running at each of two different speeds, 2000 or 3000 RPM. The factorial experiment would consist of four experimental units: motor A at 2000 RPM, motor B at 2000 RPM, motor A at 3000 RPM, and motor B at 3000 RPM. Each combination of a single level selected from every factor is present once.This experiment is an example of a 22 (or 2x2) factorial experiment, so named because it considers two levels (the base) for each of two factors (the power or superscript), or #levels#factors, producing 22=4 factorial points.Designs can involve many independent variables. As a furtherexample, the effects of three input variables can be evaluated in eightexperimental conditions shown as the corners of a cube.This can be conducted with or without replication, depending on itsintended purpose and available resources. It will provide the effects ofthe three independent variables on the dependent variable and possibleinteractions.2×2 factorial experimentA B(1) − −a +−b − +ab ++To save space, the points in a two-level factorial experiment are often abbreviated with strings of plus and minus signs. The strings have as many symbols as factors, and their values dictate the level of each factor: conventionally, for the first (or low) level, and for the second (or high) level. The points in this experiment can thus berepresented as , , , and .The factorial points can also be abbreviated by (1), a, b, and ab, where the presence of a letter indicates that the specified factor is at its high (or second) level and the absence of a letter indicates that the specified factor is at its low (or first) level (for example, "a" indicates that factor A is on its high setting, while all other factors are at their low (or first) setting). (1) is used to indicate that all factors are at their lowest (or first) values.ImplementationFor more than two factors, a 2k factorial experiment can be usually recursively designed from a 2k-1 factorial experiment by replicating the 2k-1 experiment, assigning the first replicate to the first (or low) level of the new factor, and the second replicate to the second (or high) level. This framework can be generalized to, e.g., designing three replicates for three level factors, etc.A factorial experiment allows for estimation of experimental error in two ways. The experiment can be replicated, or the sparsity-of-effects principle can often be exploited. Replication is more common for small experiments and is a very reliable way of assessing experimental error. When the number of factors is large (typically more than about 5 factors, but this does vary by application), replication of the design can become operationally difficult. In these cases, it is common to only run a single replicate of the design, and to assume that factor interactions of more than a certain order (say, between three or more factors) are negligible. Under this assumption, estimates of such high order interactions are estimates of an exact zero, thus really an estimate of experimental error.When there are many factors, many experimental runs will be necessary, even without replication. For example, experimenting with 10 factors at two levels each produces 210=1024 combinations. At some point this becomes infeasible due to high cost or insufficient resources. In this case, fractional factorial designs may be used.As with any statistical experiment, the experimental runs in a factorial experiment should be randomized to reduce the impact that bias could have on the experimental results. In practice, this can be a large operational challenge. Factorial experiments can be used when there are more than two levels of each factor. However, the number of experimental runs required for three-level (or more) factorial designs will be considerably greater than for their two-level counterparts. Factorial designs are therefore less attractive if a researcher wishes to consider more than two levels.A factorial experiment can be analyzed using ANOVA or regression analysis . It is relatively easy to estimate the main effect for a factor. To compute the main effect of a factor "A", subtract the average response of all experimental runs for which A was at its low (or first) level from the average response of all experimental runs for which A was at its high (or second) level.Other useful exploratory analysis tools for factorial experiments include main effects plots, interaction plots, and a normal probability plot of the estimated effects.When the factors are continuous, two-level factorial designs assume that the effects are linear. If a quadratic effect is expected for a factor, a more complicated experiment should be used, such as a central composite design. Optimization of factors that could have quadratic effects is the primary goal of response surface methodology.Notes[1]Frank Yates and Kenneth Mather (1963). "Ronald Aylmer Fisher" (.au/coll/special//fisher/fisherbiog.pdf). Biographical Memoirs of Fellows of the Royal Society of London9: 91–120. .[2]Ronald Fisher (1926). "The Arrangement of Field Experiments" (.au/coll/special//fisher/48.pdf).Journal of the Ministry of Agriculture of Great Britain33: 503–513. .[3]/f.htmlReferences•Box, G.E., Hunter,W.G., Hunter, J.S., Statistics for Experimenters: Design, Innovation, and Discovery, 2nd Edition, Wiley, 2005, ISBN 0471718130Article Sources and Contributors4 Article Sources and ContributorsFactorial experiment Source: /w/index.php?oldid=430074649 Contributors: AS, AbsolutDan, AdmiralHood, Alansohn, Baccyak4H, Btyner, Chris Bainbridge, Chris the speller, DanielCD, DanielPenfield, Darkildor, Eric Kvaalen, Euyyn, Fbriere, Giftlite, Intgr, IrisKawling, Jayen466, John Bessa, Kiefer.Wolfowitz, Michael Hardy, Mira, NatusRoma, Nesbit,Nicoguaro, Qwfp, RichardF, Rlsheehan, Rouenpucelle, Rsolimeno, Shanes, Statwizard, Zvika, 21 anonymous editsImage Sources, Licenses and ContributorsFile:Factorial Design.svg Source: /w/index.php?title=File:Factorial_Design.svg License: Public Domain Contributors: NicoguaroLicenseCreative Commons Attribution-Share Alike 3.0 Unported/licenses/by-sa/3.0/。

1Full Factorial Design of Experiments 全因子实验设计2Module Objectives 模块目标该模块学习后, 学员将学习:•Generated a full factorial design 产生全因子设计•Created and analyzed designs in MINITAB ™用MINITAB 创立和分析实验•Looked for factor interactions 寻找因子交互作用•Evaluated residuals 残差评估•Set factors for process optimization 设立因子水平让过程最优3Select the DOE Design 选择实验设计The selected design should align with the objectives of the experiment and resource commitment选择的设计应与实验目标和资源相符合•OFAT (One Factor at a Time) •2k-n Fractional Factorial Designs •2k Full Factorial•2k Full Factorial (center points)•Full Factorial (with or without replication)•RSM (response surface method)4复杂的设计需要更多的知识与成本Experimental Design Considerations实验设计考虑实验设计类型实验目标RSM 响应表面设计Optimize最优化Model建模解析度III全因子设计解析度V 部分因子设计2k 全因子Screen区分少多P I V ’s少多知识少多成本(6-15)(2-5)5Why Learn About Full Factorial DOE?为什么学习全因子DOEA Full Factorial Design of Experiment will 全因子设计将•Provide the most response information about 提供响应信息包括•Factor main effects 因子主效应•Factor interactions 交互效应•When validated, allow process to be optimized 当验证后, 能让过程达到最优6What is a Full Factorial DOE什么是全因子DOEA full factorial DOE is a planned set of tests on the response variable(s) (KPOVs) with one or more inputs (factors) (PIVs) with all combinations of levels evaluated全因子DOE 是用1个或多个因子(KPIV)的所有组合水平来评估响应变量(KPOV)的一组计划好的测试.•ANOVA will show which factors are significant ANOVA 将显示什么因子是显著的.•Regression analysis will provide the coefficients for the prediction equations (for the case where all factors have 2 levels)回归分析将提供预测公式的系数( 如所有因子2个水平)•Mean 均值•Standard deviation 标准差•Residual analysis will show the fit of the model 残差分析将显示模型的符合性7DOE TerminologyDOE 术语•Response 响应(Y, KPOV): the process output linked to the customer CTQ 与客户CTQ 相关的过程输出•Factor 因子(X, PIV): uncontrolled or controlled variable whose influence is being studied 被研究的非受控或受控变量•Factor Level 因子水平: setting of a factor (+, -, 1, -1, hi, low, alpha, numeric)一个因子的设置•Treatment Combination 处理组合(run 运行): setting of all factors to obtain a response 所有因子的设置以得到一个响应值•Replicate 复制: number of times a treatment combination is run (usually randomized)一个处理组合随机运行的次数•Inference Space 推断空间: operating range of factors under study 被研究因子的操作范围•MINITAB Design Matrix MINITAB 设计矩阵:a table with all the runs listed with the Factor Levels for each factor identified. In MINITAB it will also include Run Order and Standard Order Columns. The response is recorded against these runs 所有列出的运行在每一个因子的所有因子水平下的表格. 在MINITAB 软件中它包括运行顺序和标准顺序栏目. 响应值记录在这些运行后.•Fit 符合值: predicted value of the response variable, given a specificcombination of factor settings 响应变量的预测值, 已知一个特定的因子组合下•Residual 残差: the difference between a fitted (predicted) value and an actual experimental value 预测值与实际实验数据之差8Full Factorial DOE Objectives全因子DOE 目标•Learning the most from as few runs as possible.. 用尽可能少的运行来了解更多•Identifying which factors affect mean, variation, both, or have no effect 识别哪些因子影响均值, 方差, 都影响或都无影响•Optimizing the factor levels for desired response 最优化因子水平以得到需要的响应值•Validating the results through confirmation 通过确认来验证结果9Factorial Combinations 因子组合10Is testing all combinations possible,reasonable and practical?测试所有的组合可能吗?合理吗?可行吗?Combinations of Factors and Levels (1)因子和水平组合(1)•We have a process whose output Y is suspected of being influenced by three inputs A, B and C. The SOP ranges on the inputs are 过程输出Y 可能被3个输入因子A B C 影响. 输入的范围是: •A 15 through 25, in increments of 1从15 –25, 增量为1•B 200 through 300, in increments of 2从200 –300, 增量为2•C 1 or 21 或2•A DOE is planned to test all combinations 我们将设计一个实验来测试所有的因子组合11为做好实验我们必须对影响变量做假设Combinations of Factors and Levels (2)•Setting up a matrix for the factors at all possible process setting levels will produce a really large number of tests.设立一个包括所有可能设置水平的因子矩阵将产生一个相当大数量的实验.•The possible levels for each factor are 每个因子可能的水平包括•A =11•B =51•C =2•How many combinations are there?共有多少组合?•2 x 51 x 11 = ?A B C 152001162001172001182001192001202001212001222001232001242001252001152021162021172021 (22300223300224300225)300212The design becomes much more manageable!实验更好管理了!Factors at Selected Levels选择因子水平•The team decides, from process knowledge, that the test conditions of interest within the operating range of the factors (inference space) is as shown below.团队决定, 从过程知识中得知, 在因子操作范围( 推断空间)选择的测试条件如下:•A 15, 20, and 25•B 200, 225, 250, 275, and 300•C 1 and 2Tool Bar Menu > Stat > DOE > Factorial > Create Factorial Design2. 去掉Randomize runs(为教学用)3. 点OK 2. 输入每个因子的水平值, 因子水平间用空白搁开(不用逗号)3. 点OKStep 74 X 3 X 2 设计的标准顺序The StdOrder Column 显示运行如果设计没有随机化的运行顺序The RunOrder column 显示设计随机运行时的运行顺序注意: 当我们创建实验时, 因为我们没有勾Randomize 栏, StdOrder和RunOrder 是相同的.点OK不点randomize第1组复制Replicate第2组复制Response Y would be placed in C6响应变量值放在C6栏Step 4随机复制Response Y would be placed in C643Issues When Testing for Normality (1)正态测试(1)Test the Right Data 测试正确的数据Remember, the assumption in ANOVA is that the residuals are normal –therefore we test them, not the data记住, ANOVA 假设是残差是正态分布的-因此我们测试残差而不是数据Sample Size 样本大小•直方图需要大样本(推荐50个以上)•概率图不需要这样大的样本量•正态测试至少要25个样本, 但最好50以上•作为中心极限定理的结论, 当样本量大于20时, 大多数假设测试对非正态都稳健正态性测试总是比其他假设正态性的统计测试需要更多数据.44Issues When Testing for Normality (2)正态测试(2)Nature of Non-Normality 非正态本质•严重偏态数据比非正态对称数据更值得关注•严重偏态数据更容易用”转换”成正态数据•Log, Box-Cox Power Transformation, Square Root, Arcsine, etc.非参数替换-不适用于全因子,除非只有两个因子的特例•大多数非参数测试需要对称数据, 对严重偏态数据与参数测试一样敏感•所有非参数测试比相对应的参数测试效力差很多, 除非样本量很大(这种情况下参数测试非常稳健)如果数据严重偏态, 最好将其转换为正态而不是用非参数测试来替换45Steps for Testing Normality Assumption正态假设测试的步骤•Step 1: Test the right data (residuals) 测试正确的数据(残差)•Step 2: Graphical methods 图象化方法•Histogram of residuals 残差直方图•Normal probability plot of residuals 残差正态概率图•Step 3: Statistical tests 统计测试•Anderson-Darling test (preferred) 推荐•Chi-Square goodness of fit test 卡方符合性测试如果可能尽量用图象化工具46Graphical Methods for Checking Normality (1)正态测试的图象化方法(1)109876543212010Right Skewed F r e q u e n c yP-Value: 0.004A-Squared: 1.177Anderson-Darling Normality TestN: 100StDev: 2.30456Average: 4.38216108642.999.99.95.80.50.20.05.01.001P r o b a b i l i t yRight SkewedNormal Probability PlotUse a histogram and probability plot together 同时使用直方图和概率图•Histogram for visualizing shape 直方图显示形状•Probability plot for precision 概率图显示精确性右偏分布数据低段出现低迷–左尾太多数据47Graphical Methods for Checking Normality (2)2019181716151413121110105Fat Tails F r e q u e n c yP-Value: 0.043A-Squared: 0.772Anderson-Darling Normality TestN: 100StDev: 2.81680Average: 14.9555201510.999.99.95.80.50.20.05.01.001P r o b a b i l i t yFat TailsNormal Probability Plot 两端出现低迷肥尾分布Use a histogram and probability plot together 同时使用直方图和概率图•Histogram for visualizing shape 直方图显示形状•Probability plot for precision 概率图显示精确性48Statistical Tests for Checking Normality正态性检验P-Value: 0.043A-Squared: 0.772Anderson-Darling Normality TestN: 100StDev: 2.81680Average: 14.9555201510.999.99.95.80.50.20.05.01.001P r o b a b i l i t yFat TailsNormal Probability PlotGraph > Probability Plot…49Equal Variances 等变差•统计建模技术(ANOVA 和回归等)假设残差有相等的变差•不等的变差影响P 值和效力计算-导致效力降低和P 值比实际小•大多数统计测试技术对不等变差十分稳健,特别是当样本数量相等和近似相等时(对ANOVA, 意味着每个因子的每个水平的运行次数, 或2个或多个因子的每个水平下的运行次数是相同的)•转换将能纠正该问题50Issues When Testing for Equal Variances等变差测试Sample Sizes 样本量•当组的大小相等或接近相等时, 成组数据测试(ANOVA)对不等变差是十分稳健的Non-Parametric Alternatives 非参数测试替换•不适用全因子,除非2因子特例•除非样本量十分大, 所有参数测试都没有相对应的参数测试有效力. •大多数非参数测试需要分布有相同的形状, 即对不等变差同样敏感If the variance increases as the mean increases, it is better to try a transformation than a non-parametric alternative!!如果变差随均值增加而增加, 最好用转换而不用非参数替换51Steps for Testing Equal Variance Assumption等变差假设测试步骤•Step 1: Test the right data (residuals) 测试正确的数据或残差•Step 2: Define the right test 定义正确的测试•Equal variances for all residuals (one group of data)所有残差组的变差相等•Step 3: Graphical methods 图象方法•Residuals vs. fits•Step 4: Statistical tests 统计测试•F test for 2 variances F 测试2变差•Bartlett’s and Levene’s tests for > 2 variancesBartlett’s and Levene’s 测试超过2变差如果可能尽量用图形方法52Testing Assumptions for Residuals残差假设测试-101012345678ResidualF r e q u e n c yHistogram of Residuals10203040-20-1001020Observation NumberR e s i d u a lI Chart of ResidualsM ean=-3.2E -15UC L=17.63LCL=-17.63708090-15-10-50510FitR e s i d u a lResiduals vs. Fits-2-112-15-10-50510Normal Plot of ResidualsNormal Score R e s i d u a l正态性检验独立性检验等变差检验本例中均符合假设图形检验三个假设53The Importance of Orthogonal Designs正交设计的重要性当因子间相关性为0时, 因子在数学上独立•Only the response is a function of the factors 只有响应变量是因子的公式•A factor is not a function of another factor 一个因子不是另一个因子的公式当因子独立且实验设计完全平衡时, 因子正交•Each level of a factor appears the same number of times 因子每水平出现相同次数正交设计很重要, 因为: •设计中每项都能从其他项中独立地测试•从模型中去处一项不影响其他剩余项•正交设计保证因子是独立的•正交设计让不等变差分析更稳健54Types of Orthogonal Designs正交设计类型•Full factorial experiments 全因子•2-level full factorial experiments 2水平全因子•2-level fractional factorial experiments 2水平部分因子•Plackett-Burman and Taguchi arrays Plackett-Burman 和田口设计•Some response surface experiments 一些响应表面设计使用正交设计以确保因子们是独立地因为设计是平衡地, 正交设计也让不等变差的分析更稳健Tool Bar Menu > Stat > DOE > Factorial >Create Factorial点Design 按钮Click OK Click OK, then OK againStat > DOE > Factorial > Analyze Factorial Design点OK,再点OK Stat > DOE > Factorial > Factorial Plots67Draw Conclusions (11)28321516120130140Wheel SizeAir PressureM e a nInteraction Plot - Data Means for Stop Dist当Air Pressure = 32 和Wheel Size = 15 的响应均值.交互作用不显著. 注意: 两条线平行的.Air Pressure 保持在28 psi 时的Wheel Size 的主效应图.Air Pressure 保持在32 psi 时的Wheel Size 的主效应图.交互作用图-停止距离的数据均值68Steps to Conduct a Full Factorial Experiment 实施全因子实验设计的步骤步骤•Step 1: 描述实际问题和实验目标•Step 2: 描述因子和水平值•Step 3: 决定适当的样本大小, 给定α and β 风险•Step 4: 用MINITAB 创建一个实验设计. 实验设计表上的运行应随机.•Step 5: 实施实验•Step 6: 全模型实验分析•Step 7: 简化模型•评估ANOVA 表, 消除P 值大于0.05的项.•先消除最高阶项, 再到更低项, 最后是主效应项.•一次消除一项Terms should be removed one at a time.•不应消除包含在高阶项中的任何项, 以保证层级的完整.•最终模型中只包括那些P 显著的项•Step 8: 检查是否违反假设•分析简化模型的残差以确保我们具有适当的模型•Step 9: Determine optimal settings by graphically analyzing remaining terms 用图形分析决定保留项的最优设置•Interactions (using interaction plot) 交互图•Look at the highest order interactions first.先看最高级别交互.•一旦最高级别交互作用能解释后, 继续分析更低级别的交互•Main Effects (using main effects plot)主效应图•主效应图用来决定未经交互作用图决定的因子设置•Step 10: 计算每项的能解释的变差比例(epsilon square)•Step 11: 重复实验优化条件以验证结果•Step 12: 最终报告Steps to Conduct a Full Factorial Experiment71Full Factorial Example (1)全因子例子你负责一个项目, 检查一个呼叫中心的来电. 其中一个事项是电话保留时间总和. 显然你希望该时间能越短越好, 并且能尽可能一致..你将设计一个实验来确定是否不同的承包商和不同的电话系统,对保留时间有任何影响.有3个承包商: HiTech OnTimeAcme3个电话系统:PBXContractPhoneCo72Full Factorial Example (2)Step 1: 陈述实际问题和实验目标:确定什么影响保留时间, 发现最好的组合来减少保留时间Step 2: 陈述因子和水平设置:因子水平Vendor:HiTech OnTime Acme Phone System:PBXContractPhoneCoStep 3:确定适当样本量, 给定α and β risks 已经决定要有4个复制.为教学起见,我们未随机化runsStep 5: 实验实施要点:运行实验和收集数据前, 必须确保因子和响应变量的测量系统是可靠的. (MSA)打开文件: W3 CallCenter.mtw利用我们学习的技术进行分析:模型选择/简化/模型因子设置分析/假设检验产生残差图方法Note: This method generateseach graph separately.Enter the fits and residuals you stored…Title is totally optionalPhone System 占47%2)选择一般全模型4)点OK to 选择defaults, 点OK againTo get the 2-way interaction for CNC fill in as shown, repeat for mill. After both plots are made,模块回顾Module ObjectivesBy the end of this module, the participant will:学习到:•Generate a full factorial design•Create and analyze designs in MINITAB™•Look for factor interactions•Evaluate residuals•Set factors for process optimization103。

DX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06Multifactor RSM Tutorial (Part 1 – The Basics)Response Surface Design and AnalysisThis tutorial shows the use of Design-Expert® software for response surface methodology (RSM). This class of designs is aimed at process optimization. A case study provides a real-life feel to the exercise. Due to the specific nature of the case study, a number of features that could be helpful to you for RSM will not be exercised in this tutorial. Many of these features are used in the General One Factor, RSM One Factor or Two-Level Factorial tutorials. If you have not completed all of these tutorials, consider doing so before starting in on this one. We will presume that you can handle the statistical aspects of RSM. For a good primer on the subject, see RSM Simplified (Anderson and Whitcomb, Productivity, Inc., New York). You will find overviews on RSM and how it’s done via Design-Expert in the online Help system. To gain a working knowledge of RSM, we recommend you attend our Response Surface Methods for Process Optimization workshop. Call Stat-Ease or visit our website, , for a schedule. The case study in this tutorial involves production of a chemical. The two most important responses, designated by the letter “y”, are: • • y1 - Conversion (% of reactants converted to product) y2 - Activity.The experimenter chose three process factors to study. Their names and levels can be seen in the following table.FactorA – Time B - Temperature C - CatalystUnitsminutes degrees C percentLow Level (-1)40 80 2High Level (+1)50 90 3Factors for response surface study You will study the chemical process with a standard RSM design called a central composite design (CCD). It’s well suited for fitting a quadratic surface, which usually works well for process optimization. The three-factor layout for the CCD is pictured below. It is composed of a core factorial that forms a cube with sides that are two coded units in length (from -1 to +1 as noted in the table above). The stars represent axial points. How far out from the cube these should go is a matter for much discussion between statisticians? They designate this distance “alpha” – measured in terms of coded factor levels. As you will see Design-Expert offers a variety of options for alpha.Design-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 1Central Composite Design for three factors Assume that the experiments will be conducted over a two-day period, in two blocks: 1. Twelve runs: composed of eight factorial points, plus four center points. 2. Eight runs: composed of six axial (star) points, plus two more center points.Design the ExperimentStart the program by finding and double clicking the Design-Expert software icon. Take the quickest route to initiating a new design by clicking the blank-sheet icon on the left of the toolbar. The other route is via File, New Design (or associated Alt keys).Main menu and tool bar Click on the Response Surface folder tab to show the designs available for RSM.Response surface design tab The default selection is the Central Composite design, which will be used for this case study. Click on the down arrow in the Numeric Factors entry box and Select 3. Ignore the option of including categoric factors in your designs (leave at default of 0).2 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06To see alternative RSM designs for three factors, click on the choices for BoxBehnken (17 runs) and Miscellaneous designs, where you find the 3-Level Factorial option (32 runs, including 5 center points). Now go back and re-select the Central Composite design. Before entering the factors and ranges, click the Options at the bottom of the CCD screen. Notice that it defaults to a Rotatable design with the axial (star) points set at 1.68719 coded units from the center – a conventional choice for the CCD. For Center points increase the number to the normal default of 6 and press the Tab key.Default CCD option for alpha set so design will be rotatable Many of the options are statistical in nature, but one that produces less extreme factor ranges is the “Practical” value for alpha. This is computed by taking the fourth root of the number of factors (in this case 3¼ or 1.31607). See RSM Simplified Chapter 8 “Everything You Should Know About CCDs (but dare not ask!)” for details on this practical versus other levels suggested for alpha in CCDs – the most popular of which may be the “Face Centered” (alpha equal one). Press OK to accept the rotatable value. Using the information provided in the table on page 1 of this tutorial (or on the screen capture below), type in the details for factor Name (A, B, C), Units and levels for low (-1) and high (+1), by tabbing or clicking to each cell and entering the details given in the introduction to this case study.Completed factor formDesign-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 3You’ve now specified the cubical portion of the CCD. As you did this, Design-Expert calculated the coded distance “alpha” for placement on the star points in the central composite design. Alternatively, by clicking an option further down this screen, you could have entered values for alpha levels and let the software figure out the rest. This would be helpful if you wanted to avoid going out of operating constraints. Now go back to the bottom of the central composite design form. Leave the Type at its default value of Full (the other option is a “small” CCD, which we do not recommend unless you must cut the number of runs to the bare minimum). You will need two blocks for this design, one for each day, so click on the Blocks field and select 2.Selecting the number of blocks Notice that the software displays how this CCD will be laid out in the two blocks. Click on the Continue button to reach the second page of the “wizard” for building a response surface design. You now have the option of identifying Block Names. Enter Day 1 and Day 2 as shown below.Block names Press Continue to enter Responses. Select 2 from the pull down list. Then enter the response Name and Units for each response as shown below.Completed response form At any time in the design-building phase, you can return to the previous page by pressing the Back button. Then you can revise your selections. Press the Continue button to get the design layout (your run order may differ due to randomization).4 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06Design layout (only partially shown, your run order may differ due to randomization) Design-Expert offers many ways to modify the design and how it’s laid out on-screen. Preceding tutorials, especially in Part 2 for the General One Factor, delved into this in detail, so go back and look this over if you haven’t already. Click the Tips button for a refresher.Save the Data to a FileNow that you’ve invested some time into your design, it would be prudent to save your work. Click on the File menu item and select Save As.Save As selection You can then specify the File name (we suggest tut-RSM) to Save as type *.dx7” in the Data folder for Design-Expert (or wherever you want to Save in).Design-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 5File Save As dialog boxEnter the Response Data – Create Simple Scatter PlotsAssume that the experiment is now completed. Obviously at this stage the responses must be entered into Design-Expert. We see no benefit to making you type all the numbers, particularly with the potential confusion due to differences in randomized run orders. Use the File, Open Design menu and select RSM.dx7 from the Design-Expert program Data directory. Click on Open to load the data. Let’s examine the data, which came in with the file you opened (no need to type it in!). Move your cursor to the top of the Std column and perform a right-click to bring up a menu from which you should select Sort by Standard Order (this could also be done via the View menu).Sorting by Standard (Std) Order Next go to the Block column and do a right click. Choose Display Point Type.6 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06Displaying the Point Type (Notice that we widened the column so that you can see how some points are labeled “Fact” for factorial and others “Center” for center point, etc. Do this by placing your mouse cursor over the border and, when it changes to a double-arrow [↔], drag it where you want. Some times this does not work the first time, but do not be discouraged: It will probably work the second time. What a drag!) Before doing the analysis, it might be interesting to take a look at some simple plots. Click on the Graph Columns node which branches from the design ‘root’ at the upper left of your screen. You should now see a scatter plot with factor A:Time on the X-axis is set at and the response of Conversion on the Y-axis. It will be much more productive to see the impact of the control factors on response surface graphics to be produced later. For now it would be most useful to produce a plot showing the impact of blocks, because this will be literally blocked out in the analysis. On the floating Graph Columns tool click on the X Axis downlist symbol and select Block.Design-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 7Graph Columns feature for design layout The graph shows a slight correlation (0.152) of conversion by block. Change the Y Axis to Activity to see how it’s affected by the day-to-day blocking (not much!).Changing response (resulting graph not shown) Finally, to see how the responses correlate with each other, change the X Axis to Conversion.Plotting one response versus the other (resulting graph not shown) Feel free to make other scatter plots. Notice that you can also color the by selected factors, including run (the default). However, do not get carried away with this, because it will be much more productive to do statistical analysis first before drawing any conclusions.8 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06Analyze the ResultsYou will now start analyzing the responses numerically. Under the Analysis branch click the node labeled Conversion. A new set of buttons appears at the top of your screen. They are arranged from left to right in the order needed to complete the analysis. What could be simpler?Begin analysis of Conversion Design-Expert provides a full array of response transformations via the Transform option. Click Tips for details. For now, accept the default transformation selection of None. Click on the Fit Summary button next. At this point Design-Expert fits linear, twofactor interaction (2FI), quadratic and cubic polynomials to the response. To move around the display, use the side and/or bottom scroll bars. You will first see the identification of the response, immediately followed in this case by a warning: “The Cubic Model is Aliased.” Do not be alarmed. By design, the central composite matrix provides too few unique design points to determine all of the terms in the cubic model. It’s set up only for the quadratic model (or some subset). Next you will see several extremely useful summary tables for model selection. Each of these tables will be discussed briefly below. The table of “Sequential Model Sum of Squares” (technically “Type I”) shows how terms of increasing complexity contribute to the total model. The model hierarchy is described below: • • “Linear vs Block”: the significance of adding the linear terms to the mean and blocks, “2FI vs Linear”: the significance of adding the two factor interaction terms to the mean, block and linear terms already in the model,Design-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 9•“Quadratic vs 2FI”: the significance of adding the quadratic (squared) terms to the mean, block, linear and two factor interaction terms already in the model, “Cubic vs Quadratic”: the significance of the cubic terms beyond all other terms.•Sequential Model Sum of Squares For each source of terms (linear, etc.), examine the probability (“Prob > F”) to see if it falls below 0.05 (or whatever statistical significance level you choose). So far, the quadratic model looks best – these terms are significant, but adding the cubic order terms will not significantly improve the fit. (Even if they were significant, the cubic terms would be aliased, so they wouldn’t be useful for modeling purposes.) Scroll down to the next table for lack of fit tests on the various model orders.Summary Table: Lack of Fit Tests The “Lack of Fit Tests” table compares the residual error to the “Pure Error” from replicated design points. If there is significant lack of fit, as shown by a low probability value (“Prob>F”), then be careful about using the model as a response predictor. In this10 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06case, the linear model definitely can be ruled out, because its Prob > F falls below 0.05. The quadratic model, identified earlier as the likely model, does not show significant lack of fit. Remember that the cubic model is aliased, so it should not be chosen. Scroll down to the last table in the Fit Summary report, which provides “Model Summary Statistics” for the ‘bottom line’ on comparing the options.Summary Table: Model Summary Statistics The quadratic model comes out best: It exhibits low standard deviation (“Std. Dev.”), high “R-Squared” values and a low “PRESS.” The program automatically underlines at least one “Suggested” model. Always confirm this suggestion by looking at these tables. Check Tips for more information about the procedure for choosing model(s). Design-Expert now allows you to select a model for an in-depth statistical study. Click on the Model button at the top of the screen next to see the terms in the model.Model resultsDesign-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 11The program defaults to the “Suggested” model from the Fit Summary screen. If you want, you can choose an alternate model from the Process Order pull-down list. (Be sure to do this in the rare cases when Design-Expert suggests more than one model.)The options for process order At this stage you could press the Add Term button and insert higher degree terms with integer powers, such as quartic (4th degree). However, for this case study, we’ll leave the selection at Quadratic. You could now manually reduce the model by clicking off insignificant effects. For example, you will see in a moment that several terms in this case are marginally significant at best. Design-Expert also provides several automatic reduction algorithms as alternatives to the “Manual” method: “Backward,” “Forward” and “Stepwise.” Click the down arrow on the Selection list box to use these. Click on the ANOVA button to produce the analysis of variance for the selected model. The ANOVA table is available in two views. By default it will add text providing brief explanations and guidelines to the reported statistics. To turn this off, choose View, Annotated ANOVA. Notice that this toggles off the check mark (√).Statistics for selected model: ANOVA table12 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06The ANOVA in this case confirms the adequacy of the quadratic model (the Model Prob>F is less than 0.05.) You can also see probability values for each individual term in the model. You may want to consider removing terms with probability values greater than 0.10. Use process knowledge to guide your decisions. Next, see that Design-Expert presents various statistics to augment the ANOVA – most notably various R-Squared values. These look very good.Post-ANOVA statistics Scroll down to bring the following details on model coefficients to your screen. The mean effect shift for each block is listed here too. (Under certain circumstances the display may be adversely affected when scrolled. To rectify this problem, maximize the screen by clicking the icon at upper right of Windows.)Coefficients for the quadratic model Again scroll down to bring the next section to your screen: the predictive models in terms of coded versus actual factors (shown side-by-side below). Block terms are left out. These terms can be used to re-create the results of this experiment, but they cannot be used for modeling future responses.Design-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 13Final equation: coded versus actual You cannot edit any of the ANOVA outputs. However, you can copy and paste the data to your favorite Windows word processor or spreadsheet.Diagnose the Statistical Properties of the ModelThe diagnostic details provided by Design-Expert can best be digested by viewing plots the come with a click on the Diagnostics button. The most important diagnostic, the normal probability plot of the residuals, comes up by default.Normal probability plot of the residuals14 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06The data points should be approximately linear. A non-linear pattern (look for an Sshaped curve) indicates non-normality in the error term, which may be corrected by a transformation. There are no signs of any problems in our data. At the left of the screen you see the Diagnostics Tool palette. First of all, notice that residuals will be studentized unless you uncheck the first box on the floating tool palette (not advised). This counteracts varying leverages due to location of design points. For example, the center points carry little weight in the fit and thus exhibit low leverage. Each button on the palette represents a different diagnostics graph. Check out the other graphs if you like. Explanations for most of these graphs were covered in prior Tutorials. In this case, none of the graphs indicate any cause for alarm. Now click the option for Influence. Here’s where you find the find plots for externally studentized residuals (better known as “outlier t”) and other plots that may be helpful for finding problem points in the design. Also, from here you can click Report to bring up a detailed case-by-case diagnostic statistics, many of which have already been shown graphically. (In previous versions of Design-Expert, this report appeared under ANOVA.)Diagnostics report The note below the table (“Predicted values include block corrections.”) alerts you that any shift from block 1 to block 2 will be included for purposes of residual diagnostics. (Recall that block corrections did not appear in the predictive equations shown in the ANOVA report.) Also note that one value of DFFITS is flagged. As we discussed in the General One-Factor Tutorial (Part 2 – Advanced Features), this statistic stands for difference in fits. It measures the change in each predicted value that occurs when that response is deleted. To see what program Help says about DFFFITs, right-click the number.Design-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 15Accessing context-sensitive Help Given that only this one diagnostic is flagged, it probably is not a cause for alarm. Press X to close out the screen tip provided by the program’s Help system.Examine Model GraphsThe diagnosis of residuals reveals no statistical problems, so you will now generate the response surface plots. Click on the Model Graphs button. The 2D contour plot of factors A versus B comes up by default in graduated color shading.Response surface contour plot Note that Design-Expert will display any actual point included in the design space shown. In this case you see a plot of conversion as a function of time and temperature at a mid-level slice of catalyst. This slice includes six center points as indicated by the dot at the middle of the contour plot. By replicating center points, you get a very good power of prediction at the middle of your experimental region. The Factors Tool comes along with the default plot. Move this floating tool as needed by clicking on the top blue border and dragging it. The tool controls which factor(s) are16 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06plotted on the graph. The Gauges view is the default. Each factor listed will either have an axis label, indicating that it is currently shown on the graph, or a red slider bar, which allows you to choose specific settings for the factors that are not currently plotted. The red slider bars will default to the midpoint levels of the factors not currently assigned to axes. You can change a factor level by dragging the red slider bars or by right clicking on a factor name to make it active (it becomes highlighted) and then typing the desired level in the numeric space near the bottom of the tool palette. Click on the C:Catalyst toolbar to see its value. Don’t worry if it shifts a bit – we will instruct you on how to reset it in a moment.Factors tool with factor C highlighted and value displayed Click down on the red bar with your mouse and push it to the right.Slide bar for C pushed right to higher value As indicated by the color key on the left, the surface becomes ‘hot’ at higher response levels, yellow in the ’80’s and red above 90 for conversion. To enable a handy tool for reading coordinates off contour plots, go to View, Show Crosshairs Window.Design-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 17Showing crosshairs window Now move your mouse over the contour plot and notice that Design-Expert generates the predicted response for specific values of the factors that correspond to that point. If you place the crosshair over an actual point, for example – the one at the upper left corner of the graph now on screen, you also get that observed value (in this case: 66).Prediction at coordinates of 40 and 90 where an actual run was performed Now press the Default button to put factor C back at its midpoint. Then switch to the Sheet View by clicking on the Sheet button.Factors tool – Sheet view18 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06In the columns labeled Axis and Value you can change the axes settings or type in specific values for factors. Return to the default view by clicking on the Gauges button. At the bottom of the Factors Tool is a pull-down list from which you can also select the factors to plot. Only the terms that are in the model are included in this list. If you select a single factor (such as A) the graph will change to a One Factor Plot. From this view, if you now choose a two-factor interaction term (such as AC) the plot will become the interaction graph of that pair. The only way to get back to a contour graph is to use the menu item View, Contour.Perturbation PlotWouldn’t it be handy to see all your factors on one response plot? You can do this with the perturbation plot, which provides silhouette views of the response surface. The real benefit from this plot is for selecting axes and constants in contour and 3D plots. Use the View, Perturbation menu item to select it.The Perturbation plot with factor A clicked to highlight it For response surface designs the perturbation plot shows how the response changes as each factor moves from the chosen reference point, with all other factors held constant at the reference value. Design-Expert sets the reference point default at the middle of the design space (the coded zero level of each factor). Click on the curve for factor A to see it better. (The software will highlight it with a different color.) In this case, you can see that factor A (time) produces a relatively small effect as it changes from the reference point. Therefore, because you can only plot contours for two factors at a time, it makes sense to choose B and C, and slice on A.Design-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 19Contour Plot: RevisitedLet’s look at the contour plot of factors B and C. Return to the contour plots via the View, Contour selection.Back to Contour view In the Factors Tool right click on the Catalyst bar palette. Then select X1 axis by left clicking on it.Making factor C the x1-axis You now see a catalyst versus temperature plot of conversion, with time held as a constant at its midpoint. The colors are neat, but what if you must print the graphs in black and white? That can be easily fixed by right-clicking over the graph and selecting Graph Preferences.Graph preferences Click the Graphs 2 tab and change the Contour graph shading to Std Error shading.20 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06Changing contour graph shading Press OK to see the effect on your plot. Change factor A:time by dragging the slider left. See how it affects the shape of the contours. Also, notice how the plot darkens as you approach the extreme. You’re getting into areas of extrapolation. Be careful out there!Contour plot with standard error shading (shows up when A set at lowest level) Put the slider back at its center point by pressing the Default button. As you’ve no doubt observed by now, Design-Expert contour plots are highly interactive. For example, move your mouse over the center point. Notice that it turns into a crosshair ( ) and the prediction appears in the Crosshairs Window along with the X1-X2 coordinate. (If you do not see crosshairs, go to View, Show Crosshairs Window.) For more statistical detail, such as the very useful individual prediction interval (PI), can be found by pressing the Full button.Design-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 21Crosshairs Window set to Full display of statistics Watch what happens to the numbers as you mouse the cross-hairs around the plot. We hope you are sitting down because it may make you dizzy! Perhaps it may be best if you press the Small button before passing out and falling on to the floor. Design-Expert draws five contour levels by default. They range from the minimum response to the maximum response. Click on a contour to highlight it. You can move the contours by dragging them to new values. (Place the mouse cursor on the contour and hold down the left button while moving the mouse.) Give this a try – it’s fun! Also you can add new contours via a right mouse click. Find a vacant region on the plot and check it out: Right-click and select Add contour. Then drag the contour around (it will become highlighted). You may get two contours from one click, such as those with the same response value shown below. (This pattern is indicative of a shallow valley, which will become apparent when we get to the 3D view later.)Adding contours To get more precise contour levels for your final report, you could right-click each one and enter the desired value.22 • Multifactor RSM Tutorial – Part 1Design-Expert 7 User’s GuideDX7-04C-MultifactorRSM-P1.doc Rev. 4/12/06Setting a contour value Check this out if you like. But we recommend another approach: right click in the drawing or label area of the graph and choose Graph Preferences. Then choose Contours. Now select the Incremental option and fill in the Start at 66, Step at 3 and Levels at 8. Also, under Format choose 0.0 to display whole numbers (no decimals). Your screen should now match that shown below.Contours dialog box: Incremental option Press OK to get a good-looking contour plot.Design-Expert 7 User’s GuideMultifactor RSM Tutorial – Part 1 • 23。