实验报告
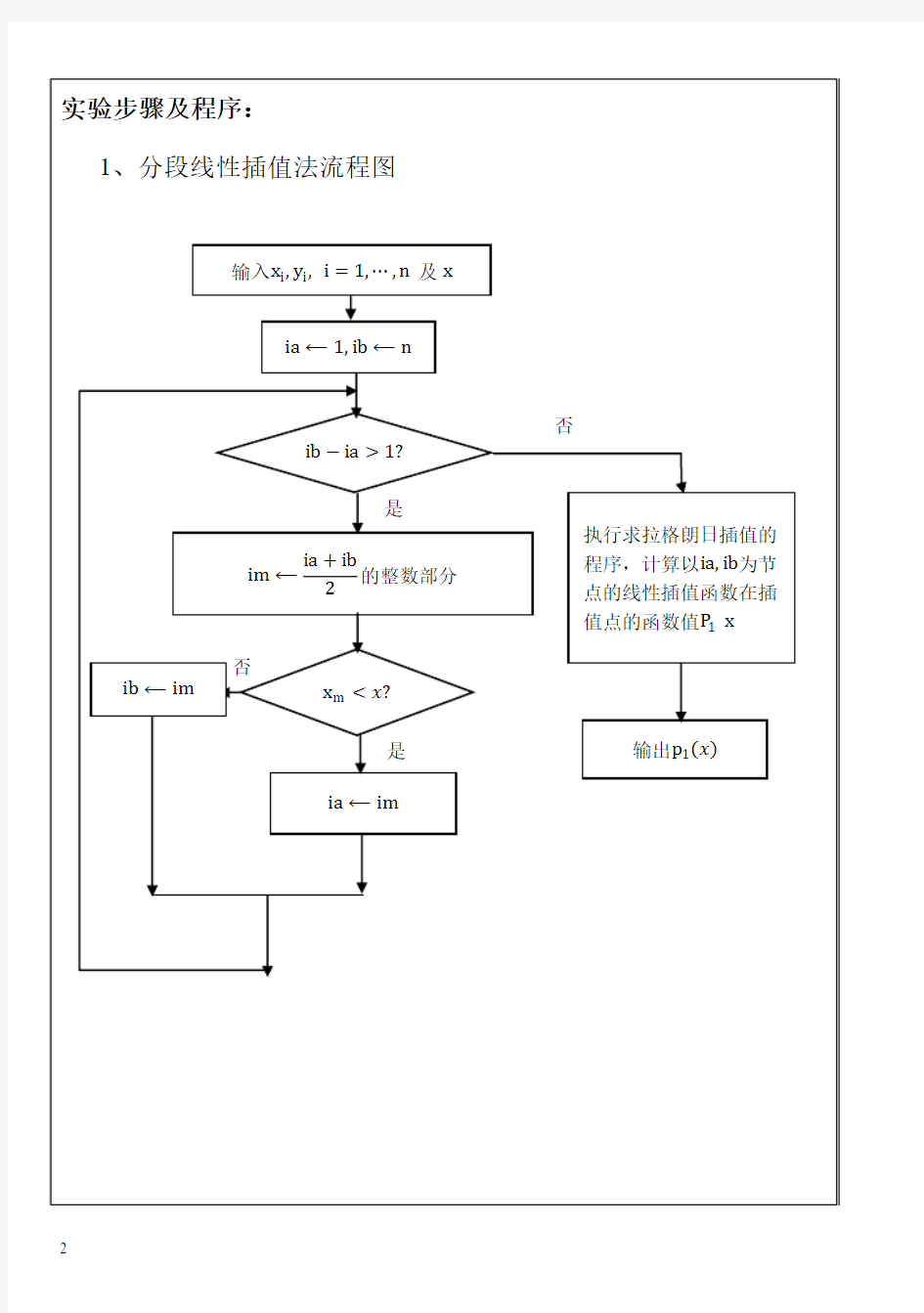
《数值分析》实验报告 实验序号:实验五 实验名称: 分段线性插值法 1、 实验目的: 随着插值节点的增加,插值多项式的插值多项式的次数也增加,而对于高次的插值容易 带来剧烈的震荡,带来数值的不稳定(Runge 现象)。为了既要增加插值的节点,减小插值 的区间,以便更好的逼近插值函数,又要不增加插值多项式的次数以减少误差,可采用分段 线性插值。 2、 实验内容: 求一个函数?(x )用来近似函数f (x ),用分段线性插值的方法来求解近似函数?(x ) 并画出近似函数图像及原函数图像。 设在区间[a,b]上,给定n+1个插值节点b x x x x a n =<<<<=...210和相应的函数 值n y y y ,...,,10,求一个插值函数)(x ?,满足以下条件: (1) ),...,2,1,0()(n j y x j j ==?; (2) )(x ?在每一个小区间[1,+j j x x ]上是线性函数。 对于给定函数11-,2511)(2≤≤+= x x x f 。在区间[]11-,上画出f (x )和分段线性插值函数)(x ?的函数图像。 1. 分段线性插值的算法思想: 分段线性插值需要在每个插值节点上构造分段线性插值基函数)(x l j ,然后再 作它们的线性组合。分段线性插值基函数的特点是在对应的插值节点上函数值取 1,其它节点上函数值取0。插值基函数如下:
?????≤≤--=其它 ,0,)(101010x x x x x x x x l ???????????≤<--≤≤--=+++---其它 ,0,,)(11 1111j j j j j j j j j j j x x x x x x x x x x x x x x x l ?? ???≤≤--=---其它 ,0,)(111n n n n n n x x x x x x x x l 设在节点a ≤x0 《数值分析》实验报告 实验序号:实验五 实验名称: 分段线性插值法 1、 实验目的: 随着插值节点的增加,插值多项式的插值多项式的次数也增加,而对于高次的插值容易带来剧烈的震荡,带来数值的不稳定(Runge 现象)。为了既要增加插值的节点,减小插值的区间,以便更好的逼近插值函数,又要不增加插值多项式的次数以减少误差,可采用分段线性插值。 2、 实验内容: 求一个函数?(x )用来近似函数f (x ),用分段线性插值的方法来求解近似函数?(x )并画出近似函数图像及原函数图像。 设在区间[a,b]上,给定n+1个插值节点b x x x x a n =<<<<=...210和相应的函数值n y y y ,...,,10,求一个插值函数)(x ?,满足以下条件: (1) ),...,2,1,0()(n j y x j j ==?; (2) )(x ?在每一个小区间[1,+j j x x ]上是线性函数。 对于给定函数11-,2511)(2≤≤+= x x x f 。在区间[]11-,上画出f (x )和分段线性插值函数)(x ?的函数图像。 1. 分段线性插值的算法思想: 分段线性插值需要在每个插值节点上构造分段线性插值基函数)(x l j ,然后再 作它们的线性组合。分段线性插值基函数的特点是在对应的插值节点上函数值取 1,其它节点上函数值取0。插值基函数如下: 设在节点a ≤x0 一、填空题: 1. 满足()a a f x x =,()b b f x x =,()c c f x x =的拉格朗日插值余项为 。 答:()() ()()()3! a b c f R x x x x x x x ξ'''=--- 2.已知函数()f x 的函数值()()()()()0,2,3,5,6f f f f f ,以及均差如下 ()()()()()00,0,24,0,2,35,0,2,3,51,0,2,3,5,60f f f f f ===== 那么由这些数据构造的牛顿插值多项式的最高次幂的系数是 答: 1 二、选择题 1. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足( ) A .()00l x =0,()110l x = B . ()00l x =0,()111l x = C .()00l x =1,()110l x = D . ()00l x =1,()111l x = 答:D 2.. 已知等距节点的插值型求积公式 ()()35 2 k k k f x dx A f x =≈∑?,那么3 k k A ==∑( ) A .1 B. 2 C. 3 D. 4 答:C 3.过点(x 0,y 0), (x 1,y 1),…,(x 5,y 5)的插值多项式P(x)是( )次的多项式。 (A). 6 (B).5 (C).4 (D).3. 答:B 三、证明题 1. 设 f (x) = (x-1) (x-2) .证明对任意的x 有: f [1, 2, x)]= 1 证明:f [1, 2] = [f (1) – f (2)]/ (1 – 2) = [0 – 0]/ (-1) = 0, 对任意的x 有 F[2, x] = [f (2) – f (x)]/ (2 – x) = [0 – (x-1) (x-2)]/ (2 – x) = (x-1), 所以 f [1, 2, x] = [f (1, 2) - f (2, x)]/ (1 – x) = [0 - (x-1)]/ (1 – x) = 1 2.设 在 上具有二阶连续导数,且 ,求证: MATLAB三次样条插值之三弯矩法 首先说这个程序并不完善,为了实现通用(1,2,…,n)格式解题,以及为调用追赶法程序,没有针对节点数在三个以下的情况进行分类讨论。希望能有朋友给出更好的方法。 首先,通过函数 sanwanj得到方程的系数矩阵,即追赶法方程的四个向量参数,接下来调用 追赶法(在intersanwj函数中),得到三次样条分段函数系数因子,然后进行多项式合并得 到分段函数的解析式,程序最后部分通过判断输入值的区间自动选择对应的分段函数并计算改 点的值。附:追赶法程序 chase %%%%%%%%%%%%%% function [newv,w,newu,newd]=sanwj(x,y,x0,y0,y1a,y1b) % 三弯矩样条插值 % 将插值点分两次输入,x0 y0 单独输入 % 边值条件a的二阶导数 y1a 和b的二阶导数 y1b,这里建议将y1a和y1b换成y2a和 y2b,以便于和三转角代码相区别 n=length(x);m=length(y); if m~=n error('x or y 输入有误,再来'); end v=ones(n-1,1);u=ones(n-1,1);d=zeros(n-1,1); w=2*ones(n+1); h0=x(1)-x0; h=zeros(n-1,1); for k=1:n-1 h(k)=x(k+1)-x(k); end v(1)=h0/(h0+h(1)); u(1)=1-v(1); d(1)=6*((y(2)-y(1))/h(1)-(y(1)-y0)/h0)/(h0+h(1)); % for k=2:n-1 v(k)=h(k-1)/(h(k-1)+h(k)); u(k)=1-v(k); d(k)=6*((y(k+1)-y(k))/h(k)-(y(k)-y(k-1))/h(k-1))/(h(k-1)+h(k)); end newv=[v;1]; newu=[1;u]; d0=6*((y(1)-y0)/h0-y1a)/h0; 几种常用的插值方法 数学系 信息与计算科学1班 李平 指导老师:唐振先 摘要:插值在诸如机械加工等工程技术和数据处理等科学研究中有许多直接的应用,在很多领域都要用插值的办法找出表格和中间值,插值还是数值积分微分方程数值解等数值计算的基础。本文归纳了几种常用的插值方法,并简单分析了其各自的优缺点。 关键词:任意阶多项式插值,分段多项式插值。 引言:所谓插值,通俗地说就是在若干以知的函数值之间插入一些未知函数值,而插值函数的类型最简单的选取是代数多项式。用多项式建立插值函数的方法主要用两种:一种是任意阶的插值多项式,它主要有三种基本的插值公式:单项式,拉格朗日和牛顿插值;另一种是分段多项式插值,它有Hermite 和spine 插值和分段线性插值。 一.任意阶多项式插值: 1.用单项式基本插值公式进行多项式插值: 多项式插值是求通过几个已知数据点的那个n-1阶多项式,即P n-1(X)=A 1+A 2X+…A n X n-1,它是一个单项式基本函数X 0,X 1…X n-1的集合来定义多项式,由已知n 个点(X,Y )构成的集合,可以使多项式通过没数据点,并为n 个未知系数Ai 写出n 个方程,这n 个方程组成的方程组的系数矩阵为Vandermonde 矩阵。 虽然这个过程直观易懂,但它都不是建立插值多项式最好的办法,因为Vandermonde 方程组有可能是病态的,这样会导致单项式系数不确定。另外,单项式中的各项可能在大小上有很大的差异,这就导致了多项式计算中的舍入误差。 2.拉格朗日基本插值公式进行插值: 先构造一组插值函数L i (x ) =011011()()()() ()()()() i i n i i i i i i n x x x x x x x x x x x x x x x x -+-+--------L L L L ,其中i=0,… n.容易看出n 次多项式L i (x )满足L i (x )=1,(i=j );L i (x )=0,(i ≠j ),其中 《数值分析》课程设计 题目考察分段线性插值 学生黄立健丁威程发林 指导教师郭阁阳 天津工程师范学院 课程设计任务书 数理系数学班学生黄立健丁威程发林 课程设计课题: 考察分段线性插值 一、课程设计工作日自 2009 年 6 月 22 日至 2009 年 6 月 28 日 二、同组学生:黄立健丁威程发林 三、课程设计任务要求(包括课题来源、类型、目的和意义、基本要求、完成时 间、主要参考资料等): 【来源与意义】 本课题来源于教材第二章插值法,目的是从几何意义掌握分段线性插值的思想,加深对其的理解以及掌握用计算机与Matlab解决相关问题的能力。 【基本要求】 要求自编程序;掌握编程思想,学会一门编程语言;报告要有较强的理论分析;有较强说服力的数据表或图像;对结果进行分析;给出相应结论;鼓励创新; 【参考资料】 1.数值分析,李庆扬,王能超,易大义,2001,清华大学出版社(第四版)。 2.数值方法,关治,陆金甫,2006,清华大学出版社。 3.数值分析与实验学习指导,蔡大用,2001,清华大学出版社。 4.数值分析与实验,薛毅,2005,北京工业大学出版社。 指导教师签字:教研室主任签字: 天津工程师范学院 课程设计评审表系班学生 一、 问题提出: 题目:对2 1 ()1f x x = +在【-5,5】上进行分段线性插值,取不同节点个数n ,得到不同分段线性插值函数。(要求:自编程序,报告有数据表、图像、分析、结论。) 二、 理论基础: 通过学习构造插值公式的方法,以及分析了它们的余项知道了在实际应用插值函数作近似计算时,我们总是希望插值公式余项的绝对值小一些,即使得逼近的精度良好。从插值公式余项表达式()n R x 看,似乎提高插值多项式的次数便可达到 目的,但实际上会产生一称为Runge 现象的畸形现象,如下图所示: 从上图易知:Lagrange 插值多项式只在区间【-3.63,3.63】内收敛。因此我们通过构造分段线性插值的方法(在每个小区间上采用一次Lagrange 插值)来消除Runge 现象。 下面我们构造分段线性插值函数: 易知 在每个子区间 上是一次插值多项式 分段线性插值的余项: 其中: 1[,](0,1,)i i x x i n +=()x ?11111(),i i i i i i i i i i x x x x x y y x x x x x x x ?+++++--=+≤≤--2 ()()()8Mh f x x R x ?-=≤ max ''() a x b M f x ≤≤= 摘要 本文细致的讲解了三次样条插值函数的产生及在实际中解决的问题,通过MATLAB的程序编写,可以将复杂的计算省去,直接的给出了三次样条插值的结果与实际结果间的误差,验证实际结果和理论值的一致性。避免了求解方程中的不必要计算,使求解效率得到显著的提高。 关键词插值函数三次样条插值 MATLAB 1 三次样条插值函数概论 当插值节点很多时,插值多项式的次数就会很高,这不仅增大了计算量,还会影响结果的精确度.虽然可以采用上述分段插值,但是主要缺点就是个分段接头处不光滑,插值函数的导数不连续,因此想构造这样的插值:既能分段的低次插值,又能保证接头处的光滑,就产生了三次样条插值函数. 1.1定义 设函数()f x 市区间[a,b]上的二次连续可微函数,在区间[a,b]上给处一个划分。设函数()f x 是区间[a,b]上的一个划分 011...n n a x x x x b -?=<<<<= 如果函数()S x 满足条件 (1)在每个小区间1[,]k k x x +(k=1,2,….,n )上()S x 是一个部超过m 次的多项式。 (2)在节点k x (k=1,2,….,n )处具有m-1阶的连续导数。 (3)()()(0,1,2,...) j j s x f x j n == 1.2三次样条差值函数的构造 由于三次样条插值我、函数s(x)的插值节点处的二阶导数存在,因此令各节点处的二阶导数为 ' ()(0,1,...,)k s x m k n == (1.01) 根据样条插值函数的定义,三次样条插值函数是s(x)在每一个小区间)1....,1,0](,[]1-=+n k x x k k 上市不超过三次的多项式。在每一个小区间 )1....,1,0](,[]1-=+n k x x k k 上,其二阶导数为线性函数,即 '' 11 11()k k k k k k k k x x x x s x m m x x x x ++++--=+-- (1.02) 对式(1.02)积分两次,则得到 k k k k k k k k k b x x a h x x m h x x m x s +-+-++=++)(6)(6)()(3 1 3 1 (1.03) natural cubic spine二阶导数求解 1 Natural cubic spine is The formula (3.37) in book ‘Numerical Recipes in Fortran 77’ is: (1) Where . Formula (1) can be simplified as: (2) Where: (3) Formula (2) can be written as: (4) This is a ‘m=n-2’ dimensional equation, then change the subscript. Take: , and (4) can be changed into: (5) To solve equation (5), we can get , then we can get . 三次样条插值法使用时,一般要对y均分取值。 2 The second derivative is known: , (6) When : (7) When : (8) So formula (4) can be written as: (9) Then we can solve equation (9). 3 The first derivative is known. The formula (3.35) is : (6) Where: Case 1: , (6) can be changed into: (7) And , (7) can be written as: (8) (9) Case 2: , (6) can be written as: (10) And , (10) can be written as: (11) (12) , (13) j=2: 页眉内容 《数值分析》课程设计 分段线性插值 牛彦坡陈彬冯梦雨 指导教师 天津工程师范学院 课程设计任 考察分段线性插值 、课程设计工作日自2009 年6月22 日至2009 年6月28 日 三、课程设计任务要求(包括课题来源、类型、目的和意义、基本要求、参考资 料等): 来源与意义: 本课题来源于教材第二章插值法,目的是从几何意义掌握分段线性插值的思 想,加深对其的理解以及掌握用计算机与 Matlab 解决相关问题的能力。 基本要求: 要求自编程序;掌握编程思想,学会一门编程语言;报告要有较强的理论分 析;有较强说服力的数据表或图像;对结果进行分析;给出相应结论;鼓励创新; 参考资料: 1. 数值分析,李庆扬,王能超,易大义,2001,清华大学出版社(第四版)。 2. 数值方法,关治,陆金甫,2006,清华大学出版社。 3. 数值分析与实验学习指导,蔡大用,2001,清华大学出版社。 理学 数学0702 班 学生 牛彦坡 陈彬 冯梦雨 课程设计课题: 郭阁阳 、同组学生: 牛彦坡 陈彬 冯梦雨 4. 数值分析与实验,薛毅,2005,北京工业大学出版社。 教研室主任签字: 天津工程师范学院 程设计评审表 数学0702 班 学生牛彦坡陈彬冯梦雨 设计任务完成情况及指导教 师评语 答辩情况 教研室主任: 日期: 指导教师签字: 理学 评定成绩 成绩: 指导教师签字: 日期: 主任签字: 日期: 问题提出: 考察分段线性插值: 对f(x) 丄在(-5,5)上进行分段线性插值,取不同节点个数 n ,得到不同 1 x 分段线性插值函数。(要求:自编程序,报告有数据表、图像、分析、结论。) 虽然matlab 里有直接分段线形插值的函数,但为了对分段插值算法有更明确 的理解,编写该程序是有必要的 需要解决的问题: 1、由已知数据节点编写分段线形插值函数,从而能由所编函数得到非节点的函 数值。 2、比较用不同节点数所得插值函数与真实函数的误差,从而得出节点数与插值 效果的关系 二、理论基础 所谓分段线性插值就是通过插值点用折线段连接起来逼近 f (X )。设已知节 点a=x o vx i v …vx n =b 上的函数值f o , f i ,…,f n ,求一折线函数满足: l h (x)在每个小区间[x k ,X k+1 ]上是线性函数。 则称l h (x)为分段线性插值函数。 模型一:由定义可知l h (x)在每个小区间[X k ,X k+l ]上可表示为 x x k 1 x x k I h (x) = ------- f k ------------------ f k 1 (X k x X k1) X k X k 1 X k 1 X k 模型二:首先确定间隔序列k ,使得: 第二个量是局部变量S ,其定义为: 最后一个量是一阶均差 1o l h (x) C[a,b], 2。 I h (x) f k (k 0,1, n , 3。 CENTRAL SOUTH UNIVERSITY 数值分析实验报告 三次样条插值方法的应用 一、问题背景 分段低次插值函数往往具有很好的收敛性,计算过程简单,稳定性好,并且易于在在电子计算机上实现,但其光滑性较差,对于像高速飞机的机翼形线船体放样等型值线往往要求具有二阶光滑度,即有二阶连续导数,早期工程师制图时,把富有弹性的细长木条(即所谓的样条)用压铁固定在样点上,在其他地方让他自由弯曲,然后沿木条画下曲线,称为样条曲线。样条曲线实际上是由分段三次曲线并接而成,在连接点即样点上要求二阶导数连续,从数学上加以概括就得到数学样条这一概念。下面我们讨论最常用的三次样条函数及其应用。 二、数学模型 样条函数可以给出光滑的插值曲线(面),因此在数值逼近、常微分方程和偏微分方程的数值解及科学和工程的计算中起着重要的作用。 设区间[]b ,a 上给定有关划分b x x n =<<<= 10x a ,S 为[]b ,a 上满足下面条件的函数。 ● )(b a C S ,2∈; ● S 在每个子区间[]1,+i i x x 上是三次多项式。 则称S 为关于划分的三次样条函数。常用的三次样条函数的边界条件有三种类型: ● Ⅰ型 ()()n n n f x S f x S ''0'',==。 ● Ⅱ型 ()()n n n f x S f x S ''''0'''',==,其特殊情况为()()0''''==n n x S x S 。 ● Ⅲ型 ()() 3,2,1,0,0==j x S x S n j j ,此条件称为周期样条函数。 鉴于Ⅱ型三次样条插值函数在实际应用中的重要地位,在此主要对它进行详细介绍。 三、算法及流程 按照传统的编程方法,可将公式直接转换为MATLAB 可是别的语言即可;另一种是运用矩阵运算,发挥MATLAB 在矩阵运算上的优势。两种方法都可以方便地得到结果。方法二更直观,但计算系数时要特别注意。这里计算的是方法一的程序,采用的是Ⅱ型边界条件,取名为spline2.m 。 Matlab 代码如下: function s=spline2(x0,y0,y21,y2n,x) %s=spline2(x0,y0,y21,y2n,x) %x0,y0 are existed points,x are insert points,y21,y2n are the second 摘要 用函数来表示变量间的数量关系广泛应用于各学科领域,但是在实际问题中,往往是通过实验、观测以及计算等方法,得到的是函数在一些点上的函数值。如何通过这些离散数据找到函数的一个满足精度要求且便于使用的近似表达式,是经常遇到的问题。 对于这类问题我们解决的方法为插值法,而最常用也最简单的插值方法就是多项式插值。当然用插值法得到的近似表达式必须满足插值条件即假设给定了n+1个点的自变量的值以及函数值,近似函数必须要过这n+1 (x)通个点。多项式插值,从几何角度看,就是寻求n次代数曲线y=P n 过n+1个点作为f(x)的近似。 但是随着插值节点个数的增加,高次插值多项式的近似效果并不理想。根据大量实验得出,在进行高次多项式插值时,会出现龙格现象。龙格(Runge)现象即当n趋于无穷大时,x在某一邻域内,f(x)收敛,而在这个区域外f(x)发散。 因此,为了解决这样的一个问题,我们可以通过缩小插值区间的办法达到减小误差的目的,所以本实验将针对低次分段插值多项式来做具体的讨论和学习。 关键词:龙格现象分段差值 1、实验目的 1)通过对分段线性插值算法程序的编写,提高自己编写程序的能力 2)体会分段线性插值是如何消除龙格现象的。 3)用实验报告的形式展现,提高自己在写论文方面的能力 2、算法理论 设在节点处的函数值为,i=0,1,,n。为了提高近似程度,可以考虑用分段线性插值来逼近原函数,这时的插值函数为分段函数: 在区间上的线性函数为 误差为: 易见,是平面上以点为节点的折线,有如下的特点: 1.在上为次数不超过一次的多项式; 2.; 3.; 如果,由线性插值的误差公式得到 令,则有 关于整体误差: 可以按如下方式考虑,若记则对任一都有 于是,当时,说明分段线性插值收敛于。 3、数值算例 0.5 0.7 0.9 1.1 1.3 x i y 0.4579 0.644 0.783 0.891 0.964 i 非常类似前面的三弯矩法,这里的sanzhj函数和intersanzhj作用相当于前面的sanwanj和intersanwj,追赶法程序通用,代码如下。 %%%%%%%%%%%%%%%%%%% function [newu,w,newv,d]=sanzhj(x,y,x0,y0,y1a,y1b) % 三转角样条插值 % 将插值点分两次输入,x0 y0 单独输入 % 边值条件a的一阶导数 y1a 和b的一阶导数 y1b n=length(x);m=length(y); if m~=n error('x or y 输入有误,再来'); end v=ones(n-1,1); u=ones(n-1,1); d=zeros(n-1,1); w=2*ones(n-1,1); h0=x(1)-x0; h=zeros(n-1,1); for k=1:n-1 h(k)=x(k+1)-x(k); end v(1)=h0/(h0+h(1)); u(1)=1-v(1); d(1)=3*(v(1)*(y(2)-y(1))/h(1)+u(1)*((y(1)-y0))/h0); % for k=2:n-1 v(k)=h(k-1)/(h(k-1)+h(k)); u(k)=1-v(k); d(k)=3*(v(k)*(y(k+1)-y(k))/h(k)+u(k)*(y(k)-y(k-1))/h(k-1)); end d(1)=d(1)-u(1)*y1a; d(n-1)=d(n-1)-v(n-1)*y1b; newv=v(1:n-2,:); newu=u(2:n-1,:); %%%%%%%%%%%% function intersanzhj(x,y,x0,y0,y1a,y1b) % 三转角样条插值 《数值分析》实验报告 实验序号:实验五 实验名称: 分段线性插值法 1、 实验目的: 随着插值节点的增加,插值多项式的插值多项式的次数也增加,而对于高次的插值容易带来剧烈的震荡,带来数值的不稳定(Runge 现象)。为了既要增加插值的节点,减小插值的区间,以便更好的逼近插值函数,又要不增加插值多项式的次数以减少误差,可采用分段线性插值。 2、 实验内容: 求一个函数?(x )用来近似函数f (x ),用分段线性插值的方法来求解近似函数?(x )并画出近似函数图像及原函数图像。 设在区间[a,b]上,给定n+1个插值节点b x x x x a n =<<<<=...210与相应的函数值n y y y ,...,,10,求一个插值函数)(x ?,满足以下条件: (1) ),...,2,1,0()(n j y x j j ==?; (2) )(x ?在每一个小区间[1,+j j x x ]上就是线性函数。 对于给定函数11-,2511)(2≤≤+= x x x f 。在区间[]11-,上画出f (x )与分段线性插值函数)(x ?的函数图像。 1. 分段线性插值的算法思想: 分段线性插值需要在每个插值节点上构造分段线性插值基函数)(x l j ,然后再 作它们的线性组合。分段线性插值基函数的特点就是在对应的插值节点上函数值取 1,其它节点上函数值取0。插值基函数如下: ?????≤≤--=其它 ,0,)(101010x x x x x x x x l ???????????≤<--≤≤--=+++---其它 ,0,,)(11 1111j j j j j j j j j j j x x x x x x x x x x x x x x x l ?? ???≤≤--=---其它 ,0,)(111n n n n n n x x x x x x x x l Lagrange插值: x=0:3; y=[-5,-6,-1,16]; n=length(x); syms q; for k=1:n fenmu=1; p=1; for j=1:n if(j~=k) fenmu=fenmu*(x(k)-x(j)) p=conv(p,poly(x(j))) end end c(k,:)=p*y(k)/fenmu end a=zeros(1,n); for i=1:n for j=1:n a(i)=a(i)+c(j,i) end end 输出结果: fenmu = -1 p = 1 -1 fenmu = 2 p = 1 -3 2 fenmu = -6 p = 1 -6 11 -6 c = 0.8333 -5.0000 9.1667 -5.0000 fenmu = 1 p = 1 0 fenmu = -1 p = 1 - 2 0 fenmu = 2 p = 1 -5 6 0 c = 0.8333 -5.0000 9.1667 -5.0000 -3.0000 15.0000 -18.0000 0 fenmu = 2 p = 1 0 fenmu = 2 p = 1 -1 0 fenmu = -2 p = 1 -4 3 0 c = 0.8333 -5.0000 9.1667 -5.0000 -3.0000 15.0000 -18.0000 0 0.5000 -2.0000 1.5000 0 fenmu = 3 p = 1 0 fenmu = 6 p = 1 -1 0 fenmu = 6 p = 1 -3 2 0 c = 0.8333 -5.0000 9.1667 -5.0000 -3.0000 15.0000 -18.0000 0 0.5000 -2.0000 1.5000 0 2.6667 -8.0000 5.3333 0 a = 分段线性插值法 ————————————————————————————————作者: ————————————————————————————————日期: 《数值分析》实验报告 实验序号:实验五 实验名称: 分段线性插值法 1、 实验目的: 随着插值节点的增加,插值多项式的插值多项式的次数也增加,而对于高次的插值容易带来剧烈的震荡,带来数值的不稳定(Rung e现象)。为了既要增加插值的节点,减小插值的区间,以便更好的逼近插值函数,又要不增加插值多项式的次数以减少误差,可采用分段线性插值。 2、 实验内容: 求一个函数?(x )用来近似函数f (x),用分段线性插值的方法来求解近似函数?(x )并画出近似函数图像及原函数图像。 设在区间[a,b]上,给定n +1个插值节点b x x x x a n =<<<<=...210和相应的函数值n y y y ,...,,10,求一个插值函数)(x ?,满足以下条件: (1) ),...,2,1,0()(n j y x j j ==?; (2) )(x ?在每一个小区间[1,+j j x x ]上是线性函数。 对于给定函数11-,2511)(2≤≤+= x x x f 。在区间[]11-,上画出f (x )和分段线性插值函数)(x ?的函数图像。 1. 分段线性插值的算法思想: 分段线性插值需要在每个插值节点上构造分段线性插值基函数)(x l j , 然后再作它们的线性组合。分段线性插值基函数的特点是在对应的插值节 点上函数值取 1,其它节点上函数值取0。插值基函数如下: ?????≤≤--=其它 ,0,)(101010x x x x x x x x l ???????????≤<--≤≤--=+++---其它 ,0,,)(11 1111j j j j j j j j j j j x x x x x x x x x x x x x x x l ?? ???≤≤--=---其它 ,0,)(111n n n n n n x x x x x x x x l 设在节点a≤x0<x1<…≤b=f(xi),(i=0,1,2,…,n)求折线函数L(x)满足: (1) L (x )∈C [a,b] (2) L(x[i]=y[i]) (3) L(x )在每个小区间(x[i],x[i+1])上是线性 插值函数¢(x )叫做区间[a ,b]上对数据(x[j],y[j ])(j=0,1,2,…,n)的分段区间函数。 利用一介拉格朗日函数,直接得到线性插值函数为: L(x0)=(x-x[1])/x [0]-x [1];(x [0]≤x ≤x[1]) L(x 0)=0(x[1]≤x ≤x[n]) 分段线性方程的表达式: ¢(x )=∑(j=0,..,n)y[j]*L [j](x); 3、实验代码: // LDlg .c pp : im plement ation #include "st daf x.h" #include "L.h" #in clud e "LDlg .h" #if de f _DE BU G #define new DEB UG _NE W #undef TH IS _ ch ar T HIS _FILE [] = __FI LE__; #en dif ///////////////////////////////////////////////////////////////////////////// 实验报告:牛顿差值多项式&三次样条 问题:在区间[-1,1]上分别取n=10、20用两组等距节点对龙格函数2 1()25f x x 作多项式插值及三次样条插值,对每个n 值,分别画出插值函数及()f x 的图形。 实验目的:通过编程实现牛顿插值方法和三次样条方法,加深对多项式插值的理解。应用所编程序解决实际算例。 实验要求: 1. 认真分析问题,深刻理解相关理论知识并能熟练应用; 2. 编写相关程序并进行实验; 3. 调试程序,得到最终结果; 4. 分析解释实验结果; 5. 按照要求完成实验报告。 实验原理: 详见《数值分析 第5版》第二章相关内容。 实验内容: (1)牛顿插值多项式 1.1 当n=10时: 在Matlab 下编写代码完成计算和画图。结果如下: 代码: clear all clc x1=-1:0.2:1; y1=1./(1+25.*x1.^2); n=length(x1); f=y1(:); for j=2:n for i=n:-1:j f(i)=(f(i)-f(i-1))/(x1(i)-x1(i-j+1)); end end syms F x p ; F(1)=1;p(1)=y1(1); for i=2:n F(i)=F(i-1)*(x-x1(i-1)); p(i)=f(i)*F(i); end syms P P=sum(p); P10=vpa(expand(P),5); x0=-1:0.001:1; y0=subs(P,x,x0); y2=subs(1/(1+25*x^2),x,x0); plot(x0,y0,x0,y2) grid on xlabel('x') ylabel('y') P10即我们所求的牛顿插值多项式,其结果为:P10(x)=-220.94*x^10+494.91*x^8-9.5065e-14*x^7-381.43*x^6-8.504e-14*x^5+123.36*x^4+2.0202e-1 4*x^3-16.855*x^2-6.6594e-16*x+1.0 并且这里也能得到该牛顿插值多项式的在[-1,1]上的图形,并和原函数进行对比(见Fig.1)。 Fig.1 牛顿插值多项式(n=10)函数和原函数图形 从图形中我们可以明显的观察出插值函数在两端点处发生了剧烈的波动,产生了极大的误差,即龙格现象,当n=20时,这一现象将更加明显。 1.2 当n=20时: 对n=10的代码进行修改就可以得到n=20时的代码。将“x1=-1:0.2:1;”改为“x1=-1:0.1:1;”即可。运行程序,我们得到n=20时的牛顿插值多项式,结果为:P20(x)= 260188.0*x^20 - 1.0121e6*x^18 + 2.6193e-12*x^17 + 1.6392e6*x^16 + 2.248e-11*x^15 - 1.4429e6*x^14 - 4.6331e-11*x^13 + 757299.0*x^12 + 1.7687e-11*x^11 - 245255.0*x^10 + 2.1019e-11*x^9 + 49318.0*x^8 + 3.5903e-12*x^7 - 6119.2*x^6 - 1.5935e-12*x^5 + 470.85*x^4 + 1.3597e-14*x^3 - 24.143*x^2 - 1.738e-14*x + 1.0 同样的,这里得到了该牛顿插值多项式的在[-1,1]上的图形,并和原函数进行对比(见Fig.2)。 1 问题的提出 对2 1 ()1f x x = +在(-5,5)上进行分段线性插值,取不同节点个数n ,得到不同分段线性插值函数. 虽然MATLAB 里有直接分段线性插值的函数,但为了对分段插值算法有更明确的理解,编写该程序是有必要的. 需要解决的问题: 1、 由已知数据节点编写程序,实现分段线性插值函数,从而能由所编函数得到非节点的函数值. 2、 比较用不同节点数所得插值函数与真实函数的误差,从而得出节点数与插值效果的关系. 2 理论基础 分段线性插值适用于计算简单、光滑性要求不高的插值问题,且其整体逼近 )(x f 的效果较好. 从几何意义上看,分段线性插值就是用折线近似代替曲线错误!未找到引用源。. 设在区间[a,b]上取n+1个点 .a 110b x x x x n n =<<<<=- 函数)(x f 在上述节点处的函数值为 )(y i i x f = ,,2,1,0)(n i = 于是得到n+1个点 ). , (, ), , (, , 1 1 0n n y x y x y x ) ( 连接相邻两点错误!未找到引用源。和) , ( 1 1+ +i i y x, , 2,1,0) (n i =,得一折线函数) (x ?,若满足: (1)) (x ?在[a,b]上连续; (2)错误!未找到引用源。) , ,2,1,0 (n i =; (3)) (x ?在每个小区间错误!未找到引用源。上是线性函数, 则称折线函数) (x ?为分段线性插值函数. 模型一: 由分段线性插值函数的定义可知,) (x ?在每个小区间错误!未找到引用源。上可表为 , ) ( 1 1 1 1 + + + + - - + - - = i i i i i i i i y x x x x y x x x x x ? 错误!未找到引用源。)1- , ,2,1,0 (n i =. ) (x ?是一分段函数,若用基函数表示,只需对1 , ,2,1,0- =n i 令 ? ? ? ? ? ? ? ? ? = ≤ ≤ - - = ≤ ≤ - - = + + + - - - ,其他 略去 略去 ) ( , ) ( , ) ( 1 1 1 1 1 1 n i x x x x x x x i x x x x x x x x l i i i i i i i i i i i 显然,() i l x是分段的线性连续函数,且满足 ? ? ? ≠ = = k i k i x l k i,0 ,1 ) ( 于是 ∑ = = n i i i x l y x ), ( ) (?b x a≤ ≤ 模型二: 三次样条插值C/C++程序(自己整理的) 具体推导看书<<数值分析>> code: #include freopen("threeInsert.in", "r", stdin); scanf("%d", &n); for (i = 0; i <= n; i++) scanf("%lf%lf", &x[i], &y[i]); // scanf("%lf%lf", &m[0], &m[n]); for (i = 0; i <= n - 1; i++) h[i] = x[i + 1] - x[i]; //第一种边界条件 //alph[0] = 0; alph[n] = 1; beta[0] = 2 * m[0]; beta[n] = 2 * m[n]; //第二种边界条件 alph[0] = 1; alph[n] = 0; beta[0] = 3 * (y[1] - y[0]) / h[0]; beta[n] = 3 * (y[n] - y[n - 1] / h[n - 1]); for (i = 1; i <= n - 1; i++) { alph[i] = h[i - 1] / (h[i - 1] + h[i]); beta[i] = 3 * ((1 - alph[i]) * (y[i] - y[i - 1]) / h[i - 1] + alph[i] * (y[i + 1] - y[i]) / h[i]); } a[0] = - alph[0] / 2; b[0] = beta[0] / 2; for (i = 1; i <= n; i++) { a[i] = - alph[i] / (2 + (1 - alph[i]) * a[i - 1]); b[i] = (beta[i] - (1 - alph[i]) * b[i - 1]) / (2 + (1 - alph[i]) * a[i - 1]); } m[n + 1] = 0; for (i = n; i >= 0; i--) { m[i] = a[i] * m[i + 1] + b[i]; } scanf("%lf", &xx); for (i = 0; i < n; i++) { if (xx >= x[i] && xx <= x[i + 1]) break ; } printf("%lf\n", sunc(xx, i));分段线性插值法
插值法习题及解答
MATLAB三次样条插值之三弯矩法
几种常用的插值方法
考察分段线性插值
计算方法三次样条插值课程设计
三次样条插值法
分段线性插值
三次样条插值方法的应用
分段线性插值.doc
MATLAB三次样条插值之三转角法
分段线性插值法
lagrange插值分段线性插值matlab代码
分段线性插值法
数值分析实验报告-插值、三次样条(教育教学)
分段线性插值函数的编程实现
三次样条插值的C程序(很全啊)