第五章相平衡教案

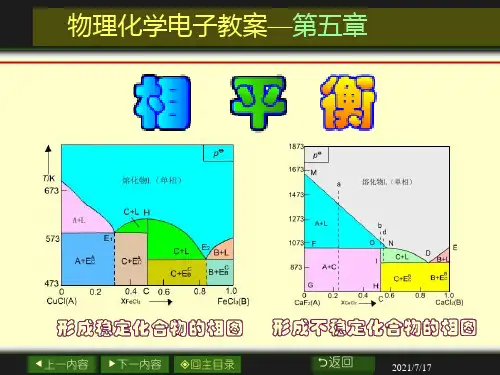
第五章多相平衡教学目的及要求1、掌握描述单组分系统相平衡规律的克—克方程。

2、明确相、组分数、自由度及相律的意义并应用于相图分析中。

3、掌握单、双组分系统典型相图的制作方法，图中点、线、面的意义及相图的应用。

教学重点1、克劳修斯—克拉佩龙方程及应用。

2、相律的应用。

3、相图分析及应用。

教学难点1、组分数的求算及相律应用。

2、相图分析及应用。

相平衡、热平衡和化学平衡是热力学在化学领域中的重要应用，也是化学热力学的主要研究对象。

相平衡研究对生产和科学研究具有重大的实际意义。

例如在化学研究和化学生产过程的分离操作中，经常会遇到各种相变化过程，如蒸发、冷凝、升华、溶解、结晶和萃取等，这些过程及到不同相之间的物质传递。

相平衡研究是选择分离方法、设计分离装置以及实现最佳操作的理论基础。

除了分离以外，相平衡及其基本理论还广泛应用于冶金、材料科学、地质矿物学、晶体生长等学科中，对这些部门的科研和生产有着重要的指导意义。

相平衡研究多相系统相变化规律，是热力学基本原理在化学领域中的重要应用。

“相律”是根据热力学原理推导出来的，以统一观点处理各种类型多相平衡的理论方法十分严谨明确。

它表明一个多相平衡系统的组分数、相数以及自由度之间的关系，可以帮助我们确定系统的平衡性质以及达平衡的必要条件。

然而，相律也有其局限性，它只能对多相平衡作定性描述。

可指明特定条件下平衡系统至多的相数以及为保持这些相数所必具的独立变量数。

但究竟是哪些相共存？哪些性质可作为独立变量以及它们之间的定量关系如何等问题，相律均无能为力。

这方面知识仍有待从实验中确定。

本章着重讨论各种相平衡系统所遵守的一个普遍规律----相律，以及各种基本类型的相图，具体分析系统的相平衡情况与温度、压力和组成等因素的关系，并举例说明其实际应用。

5－1 相律一几个概念1、相相是系统内部物理性质和化学性质完全均匀（完全相等）的一部分。

物质从一个相转移到另一个相的过程称为相变化过程，而相平衡状态就是相变化过程的极限，此时宏观上没有任何物质在相间传递。

此处“完全均匀”，是指系统中的物质在分子水平上的均匀混合的状态，此时即便是由多种物质构成的系统，但其物理性质和化学性质都达到了完全均匀的程度，用一般的仪器已分不出其界面了，形成一个均相系统。

多相系统中，相与相之间存在明显的界面，称为相界面。

越过相界面，有些性质发生突变。

例如，在373.15K的温度下，液体水和水蒸气的标准摩尔等压热容C p,m分别为75.48、34.10J·K-1·mol-1。

可见，在气—液之间相界面的两侧，水的C p,m具有不同的数值。

系统中所具有的相的总数目，称为“相数”，记作Φ，如Φ＝3、2、4等.对于相数Φ的确定，有几条原则：1、气体：系统中无论有多少种气体存在，都只有一个相，即气相。

如空气。

2、液体：由于不同种的液体的互相溶解程度不同，一个液体系统中可能存在一个（水加醇）或几个液相（水加苯、水加苯加汞）。

3、固体：系统中每一种固体，不论其数量多少，就算一个相，增加一种固体，就增加了一个相。

但同一种固体的几种同素异晶体共存时，如a-SiO2和β-SiO2的混合物中，虽然其化学组成都是SiO2，化学性质也相同，但其固态晶型不同，其物理性质各异，所以是两种不同的固相。

均匀的固态溶液被认为是一个相。

在固态溶液中粒子的分散程度和在液态溶液中是相似的，达到了分子程度的均匀混合，形成了“固溶体”。

没有气相，或讨论时不考虑气相的系统，称为“凝聚系统”。

2、组分数和物种数系统中所包含的化学物质数，称为系统的“物种数”，记作S。

注意：化学物质是指能够单独分离出来而且稳定存在的物质，其与聚集状态无关。

如水与水蒸气是同一种物种。

独立组分数K：足以确定系统中的所有各相组成所需要的最少数目的独立物种数，以K表示。

所谓独立物质是指可以单独分离出来并能够单独存在的物质。

组分数与物种数是两个不同的概念，有时二者不同。

两者之间的关系分以下几种情况来讨论：（1）无化学反应的系统：这时一般来说，组分数K 等于物种数S（2）有化学反应条件时的组分数对于每个一个独立的化学反应都应满足① 如果系统中没有化学反应发生，则平衡系统中没有化学平衡存在，这是一般来说：K=S 。

② 如果系统中有化学反应，对于每一个化学反应都应满足：0=∑B B B μν或理解为每一个化学平衡都有一个平衡常数，而平衡常数则联系了参加反应物质的浓度关系。

例如由PCl 5，PCl 3，Cl 2三种物质构成的系统，由于存在下列化学平衡：PCl 5 → PCl 3 + Cl 2虽然系统中的物种数为3，但组分数却是2，因为只要任意确定两种物质则第三种物质必然存在，其组成由平衡常数确定，并不在于起始是否放入此种物质，在这种情况下：K=S-R （独立化学平衡数）应注意系统中的化学反应并不全是独立的，例如系统中若有：(1) CO(g) + H 2O(g) ==== CO 2 + H 2(2) CO + 1/2O 2 ==== CO 2(3) H2 + 1/2O 2 ===== H 2O三个反应同时存在，但只有两个是独立的，因为（2）=（3）+（1），所以其独立平衡数是2而不是3.（3）如果除了化学平衡关系式外，系统的强度因素还要满足R ’个附加条件，则物种数S 与组分数的关系为：K= S-R-R ’（独立浓度关系数）例如在上述PCl5分解反应中，假若指定PCl3与Cl2的物质的量之比为1：1或开始时只有PCl5存在，则平衡时PCl3与Cl2的比例一定是1：1，这时就存在一浓度关系的限制条件，这时系统的组分数既不是3也不是2，而是1。

K= S-R-R’=3-1-1=1●物质之间的浓度关系只有在同一相中才能应用。

如碳酸钙的分解。

●一个系统的物种数是可以随人们考虑问题的出发点不同而不同，但在平衡系统中的组分数却是确定的。

例如对于NaCl 和水（H2O）组成的溶液，若不计它们的电离，则K＝2。

若要考虑其电离，则生成的物质共有H2O、H3O+、OH-、NaCl（固）及Na+、Cl-等六种，而此时相应地必须考虑以下两个平衡：，。

此外又存在两个独立的浓度限制条件：=C OH-，C Na+=C Cl-，故组分数仍然不变即K＝6-2-2＝2。

可见，组分数确是表征系统性质的一个客观重要参数。

3、自由度数f在不引起旧相消失和新相形成的前提下，可以在一定范围内可独立变动的强度性质，称为系统在指定条件下的"自由度"。

常用强度性质有温度、压力和物质的浓度等，用符号"f "表示。

相平衡系统的相数与温度、压力、组成有关。

例如：单组分系统：水保持液态(单相)可在一定的温度、压力范围内任意变化，要使液相不消失，同时不形成冰和水蒸气，温度T、压力P都可在一定范围内独立f ；当液态水与其蒸气平衡共存时，若要这两个相都不消失，又不变动，故2形成固相冰，系统的压力必须是所处温度T时的饱和蒸气压，因其压力与温度f=；当气液固(三相)平衡具有函数关系，所以两者之中只有一个可以独立变动1f=。

时，温度和压力均为一定值，不能变化0双组分系统：如盐水系统，影响相态的有温度T、压力p和盐的量x。

当溶液不饱和时，T、p、x 均可一定范围内改变，故自由度为3；当保持盐水溶液+盐固体两相共存时，指定温度、压力后，饱和盐水的浓度是定值，说明可以改变f=。

的变量为2个，2多组分系统：直接分析f 比较麻烦。

必须引进规律计算。

二、相律相律就是在平衡系统中，联系系统内相数、组分数、自由度数及影响物质性质的外界因素（如温度、压力、重力场、磁场、表面能等）之间关系的规律。

用数学表达式为：f＝K－Ф＋n外界因素只考虑温度和压力两个变量因素时，上式就变成：f＝K－Ф＋2 由相律f =K－Ф＋2 可以看出，当平衡系统中组分数K 已确定时，f 与Ф 存在着相互制约的关系：系统相数愈多时，自由度数愈少。

反之，相数愈少时，自由度数愈多。

然而，自由度数最少仅能为零（无变量系统），故平衡时系统相数有一最大值。

而系统最少相数为1，在此条件下自由度数最多。

因此，当外界条件及系统组分数既定时，可由相律确定应该用多少变量才足以完整地描述系统的平衡性质以及在此系统中达平衡时最多相数可能是多少。

其推导过程这里不作介绍。

三、相律使用时的注意事项(1) 相律仅适用于相平衡系统，即在系统的各相压力和温度都是同样的，且物质流动已达平衡的系统。

不使用于非平衡系统。

相律是各种相平衡系统都必须遵守的规律。

但从相律得到的结论只是定性的，它只能确定平衡系统中可以独立改变的强度性质的数目，而不能具体指出是哪些强度性质，也不能指出这些强度性质之间的函数关系，如不能得出液体的蒸气压与温度的具体关系。

相律是相图的理论基础，可利用它来分析和解释具体问题。

(2) 在组分数的计算式K=S－R－R'中，R是指独立存在的化学平衡数，若其中一个反应可由其它反应组合得到，则不是独立的。

例如在C(s)、CO(g)、CO2(g)和O2(g)组成的系统中可能存在反应：C(s)+(1/2)O2(g)=CO(g)、C(s)+O2(g)=CO2(g)、C(s)+CO2(g)=2CO(g)、CO(g)+(1/2)O2(g)=CO2(g)等，但只有两个反应是独立的即R=2，因为其中两个反应通过加减组合可得到其它反应。

(3) 在组分数的计算式K=S－R－R'中，其它浓度限制条件R'通常是反应产生的产物符合一定比例（仅对同相有效，通常指气相，固相一般不考虑）或者人为指定而引起的个数(4) 关于相数Ф的计算: 气相不管有多少物质，一般只有一个相; 液体不分层时也只有一个相，分层时一层一相; 固体物质不形成固溶体时一个固体一个相，形成固溶体时与液相类似。

若某相存在的量很少可以忽略不计时，则可不算，例如凝聚系统不考虑气相。

(5) 相律f =K－Ф＋2式中的2表示系统的温度和压力对相平衡的影响。

当温度或压力之一固定不变（即指定）时，只有一个强度量可变（压力或温度），相律计算式变为f =K－Ф+1。

当系统的状态受到有n个强度性质影响时，相律变为f =K－Ф + n。

四、相律应用举例例题1 试用相律来讨论以下反应的相平衡：HCl(g)+NH3(g) ＝NH4Cl(s) （a）以等物质的量NH3和HCl开始（b）以任意量的NH3和HCl开始分析过程：由NH 4Cl(s)、HCl(g)和NH3(g)构成的系统，系统的S=3，三种物质之间又存在化学反应NH4Cl(s)＝HCl(g)+NH3(g)所以R=1。

平衡系统内，在同一相中若干物质的浓度(或分压)之间始终存在某种数量关系，称其为浓度限制条件。

系统中这种独立的浓度限制条件数用符号R’表示。