当前位置：文档之家 › 1.1.2弧 度 制

1.1.2弧 度 制

  • 格式：ppt
  • 大小：681.00 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

课件13： 1.1.2　弧度制

课件13： 1.1.2　弧度制


跟踪训练 1.将下列角度与弧度进行互化． ①20°＝________；②－15°＝________；③－151π＝________． 解析：①20°＝20×18π0＝π9. ②－15°＝－15×18π0＝－1π2. ③－151π＝－151π×180π°＝－396°. 答案：π9 －1π2 －396°
(2)“弧度”与“角度”之间可以相互转化
已知扇形的周长为 10 cm，面积为 4 cm2，求扇形圆心 角的弧度数． 【解】 设扇形圆心角的弧度数为 θ(0<θ<2π)，弧长为 l，半径为 r，
l＋2r＝10，① 依题意有12lr＝4，②
①代入②得 r2－5r＋4＝0，解得 r1＝1，r2＝4. 当 r＝1 cm 时，l＝8 cm，此时 θ＝8 rad>2π rad(舍去)； 当 r＝4 cm 时，l＝2 cm，此时 θ＝24＝12(rad)．
自我尝试
1．判断(正确的打“√”，错误的打“×”) (1)1 弧度指的是 1 度的角．( × )
(2)弧长为 π，半径为 2 的扇形的圆心角是直角．( √ )
解析：(1)错误.1 弧度指的是长度等于半径长的弧所对的圆心角． (2)正确．若弧长为 π，半径为 2，则|α|＝π2，故其圆心角是直角．
2.85π弧度化为角度是(
c 所以当 l＝2c时，Smax＝1c62 ，此时 α＝rl＝c－2 2c＝2，
2
所以当扇形圆心角为 2 弧度时，扇形的面积有最大值1c62 .
规律方法 (1)求扇形的弧长和面积 ①记公式：弧度制下扇形的面积公式是 S＝12lr＝12αr2(其中 l 是 扇形的弧长，α 是扇形圆心角的弧度数，0＜α＜2π)． ②找关键：涉及扇形的半径、周长、弧长、圆心角、面积等的 计算问题，关键是分析题目中已知哪些量、求哪些量，然后灵 活运用弧长公式、扇形面积公式直接求解或列方程(组)求解．
1.1.2弧度制

1.1.2弧度制

MODE MODE °′″
2
°′″ SHIFT DRG 1
67
=
30
1.178097245
因此,67° 因此 °30′≈1.178 rad
换算成角度(用度数表示 例2 将3.14 rad换算成角度 用度数表示 精 换算成角度 用度数表示,精 确到0.001) 确到 解:利用计算器
MODE 3.14 MODE
练习： 已知一半径为R的扇形 的扇形， 练习： 已知一半径为 的扇形，它的周长等 于所在圆的周长， 于所在圆的周长，那么扇形的中心角是多少 弧度？合多少度？扇形的面积是多少？ 弧度？合多少度？扇形的面积是多少？ 解：周长=2πR=2R+l，所以l=2(π－1)R. 周长=2πR=2R+l，所以l=2(π－ 所以扇形的中心角是2(π－ 所以扇形的中心角是 －1) rad. 合(
l 证明:(1) :(1)由公式 =αR 证明:(1)由公式 α = 得l=α =α r
知圆心角为n 知圆心角为n°的扇形的弧长公式和面积 2 公式分别是 nπ R nπ R
l=
180
,S =
360
n°转换为弧度
1 2 S = αR 2
nπ α= 180 1 S = lR 2
利用计算器比较sin1.5和sin85°的大小 例4 利用计算器比较 和 ° 解:由计算器
角度制 在平面几何中研究角的度量，当 时是用度做单位来度量角，1°的角 是如何定义的？
1 叫做1度角,记为1 周角的 叫做1度角,记为1° 360
我们把用度做单位来度量角的制 度叫做角度制，在数学和其他许多科 学研究中还要经常用到一种度量角的 弧度制，它是如何定义呢？ 制度—弧度制 弧度制
弧度制定义 我们把等于半径长的圆弧所对的圆心 角叫做1弧度的角．
1.1.2弧度制

1.1.2弧度制


-180° 0° 180° 360°
一般地，正角的弧度数是一个正数，负角的弧度数 是一个负数，零角的弧度数是0。如果半径为r的圆 的圆心角α 所对弧的长为 l ，那么，角 的弧度数 的绝对值是 对应角的 l 弧度数 r

这里，α的正负由角α的终边的旋转方向决定 正角 零角 负角 角的弧度数 正实数 零 负实数 实数集R
180 rad
n n rad 180
(2)将弧度化为角度
2 360

180
180 1rad ( ) 57 .30 57 18'
一般地，我们只需根据
1


180
rad 0.01745 rad

180°=πrad
180 1rad 57.30
例3 利用弧度制证明下列关于扇形面积的公式：
(1)l R
其中R是半径， 是弧长， 0 2 为圆心角， l S是扇形的面积
1 2 (2) S R 2
1 (3) S lR 2
l 证明:(1)由公式 = r 得l=αR
知圆心角为n°的扇形的弧长公式和面积 2 公式分别是 n R n R
2
°′″ SHIFT DRG 1
67
=
30
1.178097245
因此,67°30′≈1.178 rad
例2 将3.14 rad换算成角度(用度数表示,精确到0.001)
解:利用计算器
MODE MODE
1
=
3.14
SHIFT DRG 2
179.909
今后用弧度表示角时，“弧度”二字或“rad”通 常略去不写，而只写该角对应的弧度数。例如， 角α =2就表示α 是2rad的角， sin 就 示 rad 的 表 角 3 3 3 的 弦 即 sin sin 60 正， 3 2
初中数学：1.1.2弧度制

初中数学：1.1.2弧度制


弧度
π
角度 270° 300° 315° 330° 360°
弧度
2π
例4. 扇形AOB中， 所对的圆心角是60º， 半径是50米，求 的长l（精确到0.1米 ）。
解：因为60º= ,所以 l=α·r= ×50≈52.5 .
答： 的长约为52.5米.
例5. 在半径为R的圆中，240º的中心角所对的
解： （1）112º30′=112.5º，
所以112º30′≈112.5×0.0175≈1.969rad. (2) 112º30′=112.5× = .
例2. 把 化成度。 解：1rad=
例3. 填写下表：
角度 0°
弧度 0
30° 45° 60° 90° 120°
角度 135° 150° 180° 210° 225° 240°
3. 弧度制与角度制相比：
(1) 弧”为单位来度量角的单位 制；1弧度≠1º；
（2）1弧度是弧长等于半径长的圆弧所对的圆 心角的大小，而1度是圆周 的所对的圆心 角的大小；
（3）弧度制是十进制，它的表示是用一个实 数表示，而角度制是六十进制；
1.1.2 弧度制
在初中几何里，我们学习过角的度量， 1度的角是怎样定义的呢？
周角的 为1度的角。
这种用1º角作单位来度量角的制度叫做 角度制 ，今天我们来学习另一种在数学和其 他学科中常用的度量角的制度——弧度制。
1. 圆心角、弧长和半径之间的关系： 角是由射线绕它的端点旋转而成的，在旋
转的过程中射线上的点必然形成一条圆弧， 不同的点所形成的圆 弧的长度是不同的， 但都对应同一个圆心角。
合
例7. 已知一半径为R的扇形，它的周长等于 所在圆的周长，那么扇形的中心角是多少弧 度？合多少度？扇形的面积是多少？
人教版数学必修4第一章1.1.2弧度制课件

人教版数学必修4第一章1.1.2弧度制课件

3.无论是以“弧度”还是以“度”为单位, 角的大小都是一个与半径大小无关的定值.
（二）弧度制的绝对值公式
完成下列表格,你能得出哪些结论？
弧AB的长 OB旋转的方向 AOB 的弧度数 AOB 的度数
r
逆时针方向
2 r 逆时针方向
r
逆时针方向
1
2r
顺时针方向
-2
顺时针方向
未旋转
0
逆时针方向
180
逆时针方向
运用新知
根据度与弧度的换算关系，下表中各特殊角对应 的弧度数分别是多少？
注意：用弧度制表示角时，“弧度”二字或 “rad”通常略去不写，而只写该角所对应的弧 度数.如α=2表示α是2rad的角.
随堂练习： 1.根据条件完成下列度和弧度的转化；
（1）把 - 35 化成弧度；
（2）把 - 弧度化成度； 2.把下列角化成 0 到 2 的角加上 2 k 的形式；
4.在半径为r的圆中，n°的圆心角所对的圆弧长 如何计算？
l 2r n nr
360 180
5. 圆心角的大小是否与圆半径的大小有关?
探究新知
（一）弧度制的概念
讨论：角除了以度为单位，还有分和秒，他们 是六十进制的，计算不方便，角的度量是否也 能用不同的单位制？（类比长度的度量单位）
新知1：弧度制的定义
3.正角的弧度数是一个正数，负角的弧度数是一 个负数，零角的弧度数是0.
4.如果半径为R的圆的圆心角 所对弧的长为l，
那么，角的弧度数的绝对值是 l.
r
5.角度制与弧度制换算 ：180°=π rad
运用新知
例1按照下列要求，把67°30′化成弧度：
（1）精确值；
（2）精确到0.001的近似值.
1.1.2弧度制

1.1.2弧度制


例6、如图，已知扇形AOB的周长是6cm，该 扇形的中心角是1弧度，求该扇形的面积。
解：设扇形的半径为r，弧长为l ，则有
2r + l = 6 r = 2 l =1 l = 2 r
A B
o
∴
扇形的面积 S =
1 rl = 2(cm)2 . 2
练习： P9（6）
例7、已知扇形AOB的圆心角为120°，半 径为6，求此扇形所含弓形面积。
l=2πr
O r
A（B）
2r 周角的弧度数为： 2 r
360°= 2π rad 180°= π rad
360°= 2π rad
180°= π rad
(1)把角度转化为弧度：
1 180 0.01745
(2)把弧度转化为角度：
180 / 1 ( ) 57 18

高一年级集体备课
§1.1.2
弧
度
制
主备人：罗瑜、唐强
复习：
任 意 角 正角：按逆时针方向旋转形成的角
负角：按顺时针方向旋转形成的角
零角：射线不做旋转时形成的角
象限角：角的终边（除端点外）在第几象限就说这个角 是第几象限角。
所有与角α终边相同的角，连同角α在内可 构成一个集合 Ｓ＝｛β｜β＝ α ＋ k· 360°，k∈Z｝ 即任一与角α终边相同的角，都可以表示成 α与整数个周角的和.
填写下列特殊角的度数和弧度数的对应表
度
弧 度
00 300 450 600 900 1200 1350 1500 1800 2700 3600
0
2 3 5
6 4 3 2 3 4 6

3 2
2
注：今后我们用弧度制表示角的时候，“弧度” 二字或者“rad”通常省略不写，而只写这个角 。 所对应的弧度数.但如果以度（ ）为 单位表 。 示角时，度（ ）不能省略.
课件6：1.1.2 弧度制

课件6：1.1.2 弧度制

答案：4 cm2
(2)已知一半径为 R 的扇形，它的周长等于所在圆的周长，那么扇形的 圆心角是多少弧度？面积是多少？
解：设扇形的弧长为 l， 由题意得 2πR＝2R＋l，所以 l＝2(π－1)R， 所以扇形的圆心角是Rl ＝2(π－1)， 扇形的面积是12Rl＝(π－1)R2.
谢谢观看！
解：如图，330°角的终边与－30°角的终边相同，
将－30°化为弧度，即－π6，而 75°＝75×1π80＝51π2，
∴终边落在阴影部分内(不包括边界)的角的集合为
θ|
2kπ－π6＜θ＜2kπ＋51π2，k∈Z.
题型三 扇形的弧长及面积公式
例 3 (1)若圆的半径变为原来的 2 倍，弧长也变为原来的 2 倍，则( )
题型二 用弧度制表示角的集合
例 2 已知角 α＝2 005°. (1)将 α 改写成 β＋2kπ(k∈Z，0≤β＜2π)的形式，并指出 α 是第几象限的角； (2)在[－5π，0)内找出与 α 终边相同的角．
解：(1)2
005°＝2
π 005×180
rad＝40316π
rad＝5×2π＋4316π
答案：(1)D (2)2
(3)如图所示，扇形 AOB 的面积是 4 cm2，它的周长是 10 cm，求扇形的 圆心角 α 的弧度数及弦 AB 的长．
解：设弧 AB 的长为 l(cm)，扇形半径为 r(cm)， 由题意得l12＋lr＝2r＝ 4，10，解得rl＝＝24，或rl＝＝81，(舍)， 故 α＝24＝12(弧度)，AB＝2×4sin 14＝8sin 14(cm)．
变式训练 3 (1)已知扇形的周长为 8 cm，圆心角为 2， 则扇形的面积为________．
解析：设扇形的半径为 r cm，弧长为 l cm，由圆心角为 2 rad， 依据弧长公式可得 l＝2r，从而扇形的周长为 l＋2r＝4r＝8， 解得 r＝2，则 l＝4. 故扇形的面积 S＝12rl＝12×2×4＝4 (cm2)．
课件1：1.1.2 弧度制

课件1：1.1.2 弧度制


把长度等于半 周角的1/360叫做1
单位规 径长的弧所对 度的角。
定
的圆心角叫做1
弧度的角。
换算关
系
360 2rad
180 rad
基本关系
1

rad 0.01745rad
180
180
1rad
57.30 5718

导出关系
弧度制与角度制的互化技巧
=
180 8

.
把
8
5
化成度。
解：1rad=
180
(
)

8 8 180

(
)
5
5

288Βιβλιοθήκη 度与角度的互化过程中，要掌握其中的原理和方法，必要时可以借助一些特殊角
来判断，会转换到别的地方。
题型三
将3.14 rad 换算成角度(用度数表示，
精确到0.001).
解:∵1=(180/π)0
弧度的角，用符号rad表示，读作弧度。这种
用弧度作为单位度量角的单位制叫做弧度制。
要点阐释
一般地，正角的弧度数是一个正数，负角的
弧度数是一个负数，零角的弧度数是0，如果
半径为r的圆的圆心角a所对弧的长为l，那么，
角a的弧度数的绝对值是 | a | = l / r
典例剖析
题型一
1．下列说法中，错误的说法是 (
180π°进行转化．
题型二
（1) 把112º30′化成弧度(精确到0.001)；
（2）把112º30′化成弧度（用π表示）。
解： （1）112º30′=112.5º，

1
0.0175
1.1.2 弧度制

1.1.2 弧度制


L=2r
O A
A
l=αr
把长度等于半径长的圆弧所对的圆心 角叫做1弧度的角。
角α的弧度数的绝对值:
|α| = — r
(其中l为以角α为圆心角时所对圆弧的长,
l
r为圆的半径. )
α的正负由角α的终边的旋转方向决定．
正角的弧度数
负角的弧度数
零角的弧度数
正数 负数
零
角的弧度数
实数集R
若弧是一个半圆，则其圆心角的弧度数是多 少？若弧是一个整圆呢？
课堂小结
1. 什么叫1弧度角? 2. 任意角的弧度的定义.
3. “角度制”与“弧度制”的联系与区别．
课后作业
1. 阅读教材P.6-P.8；
2. 教材P.9练习第1、2、3、4题； 3. 教材P.10习题1.1A组第7、8题
B组第2、3题.
一条弦的长等于半径，这条弦所对 的圆心角等于1弧度吗？为什么？
l ) 180
1
0
r

180
rad
180 rad
360 2 rad
180 o 1 rad ( ) 57.30 0 57 018 '

角度制与弧度制的互换：
180 rad
这个角的弧度数 0 180 这个角的角度数
练习：在半径不等的两个圆内，1弧度的圆心角( C A.所对弧长相等 B.所对的弦长相等 57.3R C.所对弧长等于各自半径 D.所对的弧长为
)
180
练习
1、已知扇形的周长为 8cm，面积为 4cm 2 ，求扇 形的中心角的弧度数．
4 2.半径为10的圆中, 的圆心角所对的弧长 ( ) 3 40 20 200 400 A. B. C. D. 3 3 3 3 3.若一圆弧长等于其所在圆的内接正三角形的 边长 , 则其圆心角的弧度数为( ) 2 A. B. C. 3 D .2 3 3 4.圆的半径是 6, 则15的圆心角与圆弧围成的扇 形面积是________________.
1.1.2弧度制

1.1.2弧度制


0
π π 6 4
π π 3 2
2π 3π 5π 3 4 时候，“弧度” 二字或者“rad”通常省略不写，而只写这个角 。 所对应的弧度数.但如果以度（ ）为 单位表 。 示角时，度（ ）不能省略.
1 例1:利用弧度制证明扇形面积公式 S = lR 2
其中是l扇形弧长，R是圆的半径。
π rad=0.01745 rad 1°= 180
课堂练习
1、－300°化为弧度是（ Ｂ ）
Ａ. - 4π
3
Ｂ．- 5π
3
Ｃ．- 7π
4
Ｄ．- 7π
6
2、计算
tan1.5

解： 1.5rad = 57.30按 1.5 = 85.95 = 85 57'
所以 tan1.5 = tan 85 57 ' = 14.12
周角的弧度数是2π，而在角度制 下的度数是360。 ∴ 360°= 2πrad； 180°= πrad.
π 1= rad ≈ 0.01745rad 180
°
180°= πrad
180 ° 1rad = （ ）≈ 57.30° π
角 度 弧 度
0

30 45 60 90 120 135 150 270 360 180
3 、不论是以“弧度”还是以“度”为单位 的角的大小都是一个与圆的半径大小无关的 定值．
一般地，我们规定：
正角的弧度数是正数。 负角的弧度数是负数。
零角的弧度数是0。
弧度数的绝对值公式 角的弧度数的绝对值
l （l为弧长，r为半径） r
l |α|= r
r r
其中 : 1、l是以角α作为圆心角时所对弧的长，r是半径； 2、正角的弧度数是一个正数，负角的弧度数是 一个负数，零角的弧度数是0； 2 πr 3、圆心角θ为周角时，l = 2πr，则θ = = 2 π； r πr 4、圆心角θ为半角时，l = πr，则θ = = π。 r
1.1.2弧度制

1.1.2弧度制


二、弧度制
我们规定，长度等于半径的弧所 对的圆心角叫做1弧度的角；
B
l r
设弧AB的长为 l ，
l 若 l r ，则∠AOB= = 1 弧度 r
1弧度
O
r
A
l 若l=2r，则∠AOB= = 2 弧度 r l 若l= 3 r，则∠AOB= =3弧度 r
B r O
2弧度
l=2r
l=3r
3rad
角度制与弧度制的比较
①弧度制是以“弧度”为单位度量角的制度， 角度制是以“度”为单位度量角的制度； ②1弧度是等于半径长的圆弧所对的圆心角的大 1 小，而 1 是圆的 360 所对的圆心角的大小； ③不论是以“弧度”还是以“度”为单位的角的 大小都是一个与半径大小无关的定值．
例2：请用弧度制表示下列角度的范围。
1 3 67 30' rad 67 rad 180 2 8


3 （2）、把 —π 弧度化成度。 5
3 3 rad 180 108 解： 5 5
特殊角的弧度
角 o 0 度 弧 度 角 o o o 135 150 180 度 弧 度 30
o
45
o
60
o
90
o
120
•任意角（旋转成角）
•正角、负角、零角
•象限角
•终边相同的角
1.1.2 弧度制 （第一课时）
一、知识再现 1、角度制的定义 • 初中所学的角度制是怎样规定角的度量的? •规定周角的1/360为1度的角，这种用度做单位 来度量角的制度叫角度制。
90°
60°
2、弧长公式
nπR l= ——— 180
o
270
o

1.1.2弧度制


弧度的概念
思考：在平面几何中，1°的角是怎样定义的？
将圆周分成360等份，每一段圆弧所对的圆心 角就是1°的角.
即：规定把周角的
1 360 作为1度的角，
用度做单位来度量角的制度叫做角度制．
弧度制定义：
把长度等于半径长的弧所对的圆心角叫做１弧度的角。 用弧度来度量角的单位制叫做弧度制． rad 符号： 读作：弧度。
π ∴ 1°= —— rad ≈ 0．01745 rad 180
周角的弧度数是2π 角度制下的度数是360° ∴ 360°= 2π rad； 180°= π rad.
180 1 rad =（——）°≈ 57．30°= 57°18′ π
常规写法 ① 用弧度数表示角时，常常把弧度数
写成多少的形式，不必写成小数．
练习：将弧度转化为角度，角度转化为弧度
7 （ 1） = 15 ° （2） =－157° 30 ′； 8 12
13 （ 3） = 390 ° （4）36°= 6 5
7π （6）37°30′= （5）－105°= 12
5π 24
练习：与角－1825º 的终边相同，且绝对值最
5 － 25º 小的角的度数是＿＿＿，即＿＿＿弧度。 36
随堂练习
1、 直径为20cm的圆中，求下列各圆
4π 心所对的弧长⑴ 3
⑵ 165o
解： r = 10cm
4π 40π （1）l = α ×r = ´ 10 = (cm) 3 3
π 11π （2） 165 = ´ 165(rad) = rad 180 12
o
11π 55π 所以l = ´ 10 = (cm) 12 6
② 弧度与角度不能混用．
特殊角的弧度数

1.1.2弧度制


9.已知扇形的周长为20 cm，当扇形的中心角为多
大时，它有最大面积，最大面积是多少?
本节课到此结束！
1号骰子
2号骰子
1
2
3
4
5
6
1 2
（ 1， ） （ 1， 5） （ 1， 6） （ 1， 1） （ 1， 2） （ 1， 3） （1 ， 44 ） 2， ） （2，4）（2，5） （2，6） （2，1） （2，2）（（ 2， 33 ） 3， ） （ 3， 3） （ 3， 4） （ 3， 5） （ 3， 6） （3，1）（（ 3， 22 ） （ 4， 1） ） （4，2） （4，3） （4，4）（4，5） （4，6） （ 4， 1
o o

（2）把112º30′化成弧度（用π 表示）。
8 （ 3） 把 化成度。 5
5 解： . 8
解： 288 。
o
例2
用弧度制表示
（ 1 ）终边在x轴上的角的集合
（2）终边在 y轴上的角的集合
4、圆的弧长公式及扇形面积公式
由︱α︱= l
l r
得 r
O
α
=︱ α ︱ r
l
S
=— l r 2
n i 1 i
i
i
2 x i
i
2 ( x x ) i i 1
n

i 1 n
i i
2 2 x nx i i 1
, a y bx
量数也不同。
3、弧度与角度的换算
若l=2 π r，
l 则∠AOB= = 2π rad r
此角为周角 即为360°
l=2 π r
O r A(B)
360°= 2π rad
180°= π rad

1.1.2弧 度 制(1)1


0

4
3
2

23
例1. 按照下列要求，把67 °30 化成弧度： （1）精确值； （2）精确到0.001的近似值。
例2. 将3.14 rad换算成角度（用度数 表示，精确到0.001).
例3.利用弧度制来推导扇形的公式：
(1)S

1 2
R 2;
(2)S
1 2lR.l OS弧度制
弧度制的定义:用弧度做单位来度量
角的制度叫做 弧度制
1.定义：把长度等于半径长的弧所对的圆 心角叫做1弧度的角.用符号rad表示。
正角
2.正角的弧负度角数 负角的弧零度角数
零角的任弧意度角数的集合
正数
负数 正数 0 负数
实数集R 零
3.任一已知角α的弧度数的绝对值
|α| = —lr
其中l为以角α作为圆心角时所对圆弧的 长,r为圆的半径.
正角
正实数
零角 负角
零 负实数
4.
l = |α| r (弧长计算公式)
5.角度制与弧度制的换算:
360º= 2π rad, 180º= π rad
1º=
π
180
rad
0.01745rad
1rad = ( 180) º 57.3º =57º 18′
π
6 .特殊角的度数与弧度数的对应表:
0º 30º 45º 60º 90º 180º 270º
R
由弧度的定义可知：
圆心角AOB的弧度数等于它所对的弧的长与半径
定
长的比的绝对值。
B
义
的 合 理
B
l=r
1弧l=度r
1弧度
OO
A rr
A

1.1.2弧度制


o
例2 把3.14 rad化成角度（用度表示， rad化成角度（用度表示， 精确到0.001） 精确到0.001）
例3利用弧度制证明下列关于扇形的公式 （1） l = α R
1 2 (2) S = α R 2 (3) 1 S = lR 2
利用计算器比较sin sin1 例 4 ． 利用计算器比较 sin1.5 和 sin 85 o的 大小
2.角度制与弧度制的换算： 角度制与弧度制的换算： 角度制与弧度制的换算 360°=2π 360°=2π rad
,
180° 180°=π rad
1 =
0
π
180 o 180 o o 1rad = ≈ 57.30 = 57 18' π
rad ≈ 0.01745rad
按照下列要求， 例1 按照下列要求，把 67 30' 化成弧度 精确值；（ ；（2 精确到0.001 0.001的近似 （1）精确值；（2）精确到0.001的近似 值。
1 周角的 为1度的角 度的角 360
π =180° ° 换算关系
1rad=
180 ≈ 57 .30 ° = 57°18′， ° ， π π rad=0.01745 rad 1°= ° 180
°
2r
r
1rad
r r
2rad
r
3r
3rad
l
α rad

r
r
探究： 探究：
=2π ⑴平角、周角的弧度数，（平角=π rad、周角=2π rad） 平角、周角的弧度数，（平角= rad、周角=2 rad） ，（平角
⑵正角的弧度数是正数，负角的弧度数是负数， 正角的弧度数是正数，负角的弧度数是负数， 零角的弧度数是0 零角的弧度数是0

1.1.2弧度制 教案

1.1.2弧度制教案1. 1.2 弧度制【教学目标】①了解弧度制，能进行弧度与角度的换算.②认识弧长公式，能进行简单应用. 对弧长公式只要求了解，会进行简单应用，不必在应用方面加深.③了解角的集合与实数集建立了一一对应关系，培养学生学会用函数的观点分析、解决问题.【教学重难点】重点：了解弧度制，并能进行弧度与角度的换算.难点：弧度的概念及其与角度的关系.【教学过程】（一）复习引入.复习初中学习过的知识：角的度量、圆心角的度数与弧的度数及弧长的关系提出问题：①初中的角是如何度量的？度量单位是什么？② 1°的角是如何定义的？弧长公式是什么？一些特殊角的度数与弧度数的互相转化,请补充完整30° 90° 120° 150° 270°0 4π 3π43π π π2 例1、把下列各角从度化为弧度：(1)0252 （2）0/1115 (3) 030 (4)'3067︒解：(1) π57 （2）π0625.0 (3) π61(4) π375.0变式练习：把下列各角从度化为弧度：(1)22 º30′ （2）—210º (3)1200º解：(1) π81（2）π67- (3) π320例2、把下列各角从弧度化为度：（1）35π (2) 3.5 (3) 2 (4)4π 解：（1）108 º (2)200.5 º (3)114.6 º (4)45 º变式练习：把下列各角从弧度化为度：（1）12π （2）—34π（3）103π解：（1）15 º （2）-240 º （3）54 º 弧度数表示弧长与半径的比,是一个实数,这样在角集合与实数集之间就建立了一个一一对应关系. 正角 正实弧度下的弧长公式和扇形面积公式 弧长公式：||l r α=⋅因为||l r α=（其中l 表示α所对的弧长），所以，弧长公式为．||l r α=⋅ 扇形面积公式：．说明：以上公式中的α必须为弧度单位． 例3、知扇形的周长为8cm ，圆心角α为2rad ，，求该扇形的面积。

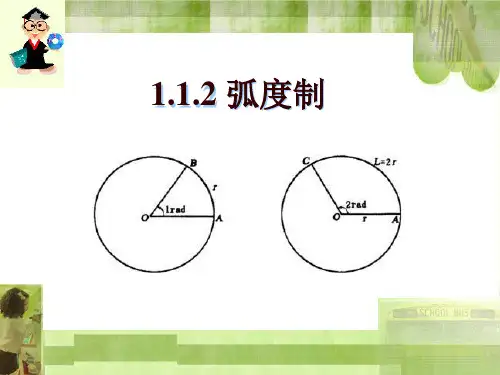
1.1.2弧度制

1.1.2弧度制教学重点弧度的概念．弧长公式及扇形的面积公式的推导与证明．教学难点“角度制”与“弧度制”的区别与联系．规定把周角的{ EMBED Equation.3 |3601作为1度的角,用度做单位来度量角的制度叫做角度制我们规定,长度等于半径的弧所对的圆心角叫做1弧度的角；用弧度来度量角的单位制叫做弧度制．在弧度制下, 1弧度记做1rad ．在实际运算中，常常将rad单位省略3．思考：（1）一定大小的圆心角所对应的弧长与半径的比值是否是确定的？与圆的半径大小有关吗？弧度制的性质：①半圆所对的圆心角为 ②整圆所对的圆心角为③正角的弧度数是一个正数． ④负角的弧度数是一个负数．⑤零角的弧度数是零． ⑥角α的弧度数的绝对值|α|=4．角度与弧度之间的转换：①将角度化为弧度：②将弧度化为角度； ；；．5．常规写法：① 用弧度数表示角时,常常把弧度数写成多少π 的形式, 不必写成小数． ② 弧度与角度不能混用． 6．特殊角的弧度角度 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°弧度0 7．弧长公式|α|=弧长等于弧所对应的圆心角(的弧度数)的绝对值与半径的积例1．把67°30＇化成弧度．例2．把化成度．例3．计算：； (2)sin例4．将下列各角化成0到2π的角加上2kπ（k∈Z）的形式：；．例5．将下列各角化成2kπ + α(k∈Z,0≤α＜2π)的形式,并确定其所在的象限．；．R lO证法一:∵圆的面积为,∴圆心角为1rad的扇形面积为,又扇形弧长为l,半径为R,∴扇形的圆心角大小为rad, ∴扇形面积．证法二:设圆心角的度数为n，则在角度制下的扇形面积公式为，又此时弧长，∴．可看出弧度制与角度制下的扇形面积公式可以互化，而弧度制下的扇形面积公式显然要简洁得多．随堂练习一、选择题1．的值是（）．A．B．C．D．2．一条弦长等于半径的，则此弦所对圆心角（）．A．等于弧度B．等于弧度C．等于弧度D．以上都不对3．把化为的形式是（）．A．B．C．D．4．扇形的周长是16，圆心角是2弧度，则扇形面积是（）．A．B．C．16 D．32二、填空题1．度；弧度．2．半径为2的圆中，长为2的弧所对的圆周角的弧度数为__________，度数为____________．3．3弧度的角的终边在第_____________象限，7弧度的角的终边在第_____________象限．4．扇形的圆心角为，半径为，则弧长为____________．5．若的圆心角所对的弧长为，则此圆的半径为______________．三、解答题1．在半径为的圆中，扇形的周长等于半圆的弧长，那么扇形的圆心角是多少度？扇形的面积是多少？2．在直径为的滑轮上有一条弦，其长为，且为弦的中点，滑轮以每秒5弧度的角速度旋转，则经过后，点转过的弧长是多少？3．扇形的面积为，它的周长为，求扇形圆心角的弧度数4．一扇形周长是，扇形的圆心角为多少弧度时，这个扇形的面积最大？最大面积是多少？参考答案：一、选择题1．B 2．D 3．D 4．C二、填空题1．36，2．，3．二、一4．5．三、解答题1．，2．3．，4．圆心角为2弧度时，最大值为．。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(1)l = α R; 1 2 (2)S = α R ; 2 1 (3)S = lR. 2
O R
S
l
随堂练习
1、下列诸命题中，真命题是（ ） 、下列诸命题中， 命题是（ A、一弧度是一度的圆心角所对的弧 、 B、一弧度是长度为半径的弧 、 C、一弧度是长度等于半径长的弧所对的 、 圆心角 D、一弧度是一度的弧与一度的角之和 、
3、把下列各角从度化成弧度 、
(1) − 210°
3 (1) π 10
(2)22°30′
4、把下列各角从弧度化成度 、
(2) −
π
12
5.填表： 填表： 填表
表1： ：
度 0º 30 45 60 90 120 135 150 180 270 360 º º º º º º º º º º
弧度数 0
π
180
rad ≈ 0.01745rad
°
换算关系
180° = πrad
基本关系
180 1rad = ≈ 57.30° = 57°18′ π 导出关系
2、下列诸命题中，假命题是（ ） 、下列诸命题中， 命题是（ A、“度”与“弧度”是度量角的两种不同的 、 弧度” 度量单位 的
1 B、一度的角是周角的 、 ，一弧度的角是周角 1 360
2π
180 C、根据弧度的定义， °一定等于 、根据弧度的定义，
π
弧度
D、不论是用角度制还是用弧度制度量角，它们 、不论是用角度制还是用弧度制度量角， 与圆的半径长短有关
角度制
′′) 度(60进制,1°=60,1′=60′′ 进 ,1°=60,1′=60′′
把长度等于半径长 周角的 周角的1/360叫做 度的 叫做1度的 叫做 单位规定 的弧所对的圆心角 角。 叫做1弧度的角 弧度的角。 叫做 弧度的角。 弧长公式
l=αr
360° = 2πrad
1° =
l=
nπ ⋅ r 180
正角 正数 负数 0
角的制度叫做 弧度制
2.正角的弧度数 正角的弧度数 负角
零角 负角的弧度数 任意角的集合 零角的弧度数
正数 负数 零
实数集R 实数集
3.任一已知角 的弧度数的绝对值 任一已知角α的弧度数的绝对值 任一已知角
|α| = r 其中l为以角 其中 为以角α作为圆心角时所对圆弧的
为圆的半径. 长,r为圆的半径 为圆的半径
6 .特殊角的度数与弧度数的对应表 特殊角的度数与弧度数的对应表: 特殊角的度数与弧度数的对应表
度 0o 30o 45o 60o 90o 120o 135o 150o 180o 弧 度
0
π
6
πቤተ መጻሕፍቲ ባይዱ
4
π
π
3
2
2 π 3
3 π 4
5 π 6
π
7.弧长公式 : (1) l =| α | ⋅r (弧度制) 即 : 弧长等于弧所对的圆心角(的弧度数)的绝对 值与半径的积. nπ r (2) l= (角度制) 180
π
6
π
4
π
3
π
2
2π 3 2π 3
3π 4 3π 4
5π 6
π
3π 2
2π
表2： ：
弧度数 度
5π 6
7π 6
π
12
5π − − 5 2
π
4π − 3
150º 210º 15º 120º 135º -36º -450º -240º
小结： 小结：
弧度制
度量单位 弧度(10进制) 弧度(10进制) (10进制
πrad = 180°
2πrad = 360°
°
1rad = 180 ≈ 57.30° = 57°18′ π
3 化成度。 例2、把 — π rad ,-2.1 rad 化成度。 、 5 解： 3 π rad = 3 × 180 ° = 108 °
5
5
− 2 .1rad ≈ − 2 .1 × 57 .30 ° = − 120 .33 °
l —
4.
l = |α| r
(弧长计算公式 弧长计算公式) 弧长计算公式
5.角度制与弧度制的换算 角度制与弧度制的换算: 角度制与弧度制的换算
1、把角度换成弧度： 、把角度换成弧度：
360° = 2πrad
[总结 总结] 总结
（1）仅出现度的，可以 ）仅出现度的， 直接乘以
π
180° = πrad π rad ≈ 0.01745 rad 1° =
按照下列要求， 化成弧度： 例1. 按照下列要求，把67 °30′化成弧度： （1）精确值； ）精确值； （2）精确到0.001的近似值。 ）精确到 的近似值。 的近似值
换算成角度（ 例2. 将3.14 rad换算成角度（用度数 换算成角度 表示，精确到0.001). 表示，精确到
利用弧度制来推导扇形的公式： 例3.利用弧度制来推导扇形的公式： 利用弧度制来推导扇形的公式
π
2
个
rad
的形式， π 的形式，如不作特 殊说明不必将π 写成小 数。
1 π 1 3 rad × (67 ) = π rad 67°30′ = (67 )° = 2 180 2 8
2、把弧度换成角度： 把弧度换成角度：
[总结 总结] 总结
π 者常可用来 180º 代 换； 不 带 π
带 者 可用 其 弧 度 数 乘 以57.30º 来 求近 似 值。
弧度制
复习回顾 1、初中几何研究过角的度量，10的角是如何定 义？角度制呢？
1 答 : 规定把周角的 作为1度的角; 而把用度做单位 360 来度量角的制度叫做角度制.
2、什么叫圆心角？什么叫做圆周角？
A A
O
B
C
O
B
弧度制的定义: 弧度制的定义 用弧度做单位来度量
1.定义：把长度等于半径长的弧所对的圆 弧度的角.用符号 表示。 心角叫做1弧度的角 用符号 弧度的角 用符号rad表示。 表示
180
90º 67º30 化成弧度。 30′ 例1、把 90 , 67 30′ 化成弧度。
解：
180
rad ，
约简即可； 约简即可；出现分秒的应 先化为度 然后再换算。 先化为度，然后再换算。 （2）用弧度作单位时， ）用弧度作单位时， 常常把弧度数写成多少 常常把弧度数写成多少
90° =
π
180
rad × 90 =