下载文档原格式
大学物理第四版下册课后题答案习题1111-1．直角三角形ABC 的A 点上，有电荷C 108.191-⨯=q ，B 点上有电荷C 108.492-⨯-=q ，试求C 点的电场强度(设0.04m BC =，0.03m AC =)。
解：1q 在C 点产生的场强：11204ACq E irπε=， 2q 在C 点产生的场强：22204BCq E j r πε=，∴C 点的电场强度：4412 2.710 1.810E E E i j =+=⨯+⨯；C 点的合场强：22412 3.2410VE E E m =+=⨯，方向如图： 1.8arctan33.73342'2.7α===。
11-2．用细的塑料棒弯成半径为cm 50的圆环，两端间空隙为cm 2，电量为C 1012.39-⨯的正电荷均匀分布在棒上，求圆心处电场强度的大小和方向。
解：∵棒长为2 3.12l r d m π=-=， ∴电荷线密度：911.010q C m l λ--==⨯⋅可利用补偿法，若有一均匀带电闭合线圈，则圆心处的合场强为0，有一段空隙，则圆心处场强等于闭合线圈产生电场再减去m d 02.0=长的带电棒在该点产生的场强，即所求问题转化为求缺口处带负电荷的塑料棒在O 点产生的场强。
解法1：利用微元积分：21cos 4O x Rd dE Rλθθπε=⋅，∴2000cos 2sin 2444O dE d R R R ααλλλθθααπεπεπε-==⋅≈⋅=⎰10.72V m -=⋅；解法2：直接利用点电荷场强公式：由于d r <<，该小段可看成点电荷：112.010q d C λ-'==⨯， 则圆心处场强：1191220 2.0109.0100.724(0.5)O q E V m R πε--'⨯==⨯⨯=⋅。
方向由圆心指向缝隙处。
11-3．将一“无限长”带电细线弯成图示形状，设电荷均匀分布，电荷线密度为λ，四分之一圆弧AB 的半径为R ，试求圆αi2cm O R x αα心O 点的场强。
大学物理第四版课后习题答案
《大学物理第四版课后习题答案：探索自然规律的奥秘》
在大学物理第四版课后习题答案中，我们不仅可以找到对各种物理问题的解答，更可以感受到探索自然规律的乐趣和奥秘。
物理作为自然科学的一门重要学科，通过研究物质和能量的运动规律，揭示了世界的奥秘，为人类社会的发展进步
做出了巨大贡献。
在课后习题答案中，我们可以看到许多经典物理问题的解答，比如力学、热学、电磁学等各个领域的问题都有详细的解析。
这些问题不仅考察了我们对物理知
识的理解和掌握，更重要的是让我们通过解题的过程，深入思考自然规律的本
质和规律的应用。
通过这些问题，我们可以更加深入地理解物理学的基本原理，培养我们的逻辑思维能力和问题解决能力。
除了习题答案，大学物理第四版还提供了丰富的案例分析和实验设计，让我们
更加直观地感受物理规律的应用和实验方法的设计。
这些案例和实验不仅可以
帮助我们更好地理解物理理论，还可以培养我们的实践能力和创新思维，为我
们今后的科学研究和工程实践打下坚实的基础。
通过学习大学物理第四版课后习题答案，我们可以更加深入地了解物理学的世界，感受到自然规律的奥秘和美妙。
希望广大学生能够在学习物理的过程中，
不仅能够掌握知识，更能够培养批判性思维和创新能力，为未来的科学研究和
社会发展做出更大的贡献。
习题 11-1．已知质点位矢随时间变化的函数形式为(cos sin )r =R ωt i ωt j + 其中ω为常量．求：（1）质点的轨道；(2)速度和速率。
解：(1) 由(cos sin )r =R ωt i ωt j +，知：cos x R t ω= ，sin y R t ω=消去t 可得轨道方程：222x y R +=∴质点的轨道为圆心在（0，0）处，半径为R 的圆；（2）由d rv dt=，有速度：sin Rcos v R t i t j ωωωω=-+ 而vv =，有速率：1222[(sin )(cos )]v R t R t R ωωωωω=-+=。
1-2．已知质点位矢随时间变化的函数形式为24(32)r t i t j =++，式中r 的单位为m ，t 的单位为s 。
求：（1）质点的轨道；（2）从0=t到1=t 秒的位移；（3）0=t 和1=t 秒两时刻的速度。
解：（1）由24(32)r t i t j =++，可知24x t = ，32y t =+消去t 得轨道方程为：x =2(3)y -，∴质点的轨道为抛物线。
（2）由d rv dt=，有速度：82v t i j =+从0=t到1=t 秒的位移为：11(82)42r v d t t i j d t i j ∆==+=+⎰⎰（3）0=t和1=t 秒两时刻的速度为：(0)2v j =，(1)82v i j =+ 。
1-3．已知质点位矢随时间变化的函数形式为22r t i t j =+，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。
解：(1)由d r v dt =，有：22v t i j =+，d va dt=，有：2a i =； （2）而vv =，有速率：12222[(2)2]21v t t =+=+∴t dv a dt ==222t n a a a =+有： n a ==1-4．一升降机以加速度上升，在上升过程中有一螺钉从天花板上松落，升降机的天花板与底板相距为d ，求螺钉从天花板落到底板上所需的时间。
习 题1-1. 已知质点位矢随时间变化的函数形式为)ωt sin ωt (cos j i +=R r其中ω为常量．求：（1）质点的轨道；(2)速度和速率。
解：1） 由)ωt sin ωt (cos j i +=R r 知 t cos R x ω= t sin R y ω=消去t 可得轨道方程 222R y x =+2） j rv t Rcos sin ωωt ωR ωdtd +-==i R ωt ωR ωt ωR ωv =+-=2122])c o s ()s i n [(1-2. 已知质点位矢随时间变化的函数形式为j i r )t 23(t 42++=，式中r 的单位为m ，t 的单位为s .求：（1）质点的轨道；（2）从0=t 到1=t 秒的位移；（3）0=t 和1=t 秒两时刻的速度。
解：1）由j i r )t 23(t 42++=可知2t 4x =t 23y +=消去t 得轨道方程为：2)3y (x -=2）j i rv 2t 8dtd +==j i j i v r 24)dt 2t 8(dt 11+=+==⎰⎰Δ3） j v 2(0)= j i v 28(1)+=1-3. 已知质点位矢随时间变化的函数形式为j i r t t 22+=，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。
解：1）j i rv 2t 2dt d +== i va 2dtd ==2）212212)1t (2]4)t 2[(v +=+= 1t t 2dtdv a 2t +==n a ==1-4. 一升降机以加速度a 上升，在上升过程中有一螺钉从天花板上松落，升降机的天花板与底板相距为d ，求螺钉从天花板落到底板上所需的时间。
解：以地面为参照系，坐标如图，升降机与螺丝的运动方程分别为20121at t v y += （1） 图 1-420221gt t v h y -+= （2）21y y = （3） 解之t =初速度0v 水平抛出，求：1-5. 一质量为m 的小球在高度h 处以（1）小球的运动方程；（2）小球在落地之前的轨迹方程； （3）落地前瞬时小球的t d d r ，t d d v ，tv d d . 解：（1） t v x 0= 式（1）2gt 21h y -= 式（2）j i r )gt 21-h (t v (t)20+=（2）联立式（1）、式（2）得 22v 2gx h y -=（3）j i rgt -v t d d 0= 而 落地所用时间 gh 2t = 所以j i r 2gh -v t d d 0= j v g td d -= 2202y 2x )gt (v v v v -+=+=212220[()]g t dvdt v gt ==+1-6. 路灯距地面的高度为1h ，一身高为2h 的人在路灯下以匀速1v 沿直线行走。
第十六章相对论题16.1：设'S 系以速率v = 0.60c 相对于S 系沿'xx 轴运动，且在t ='t = 0时，0'==x x 。
（1）若有一事件，在 S 系中发生于t = 2.0×10－7 s ，x = 50 m 处，该事件在 'S 系中发生于何时刻？（2）如有另一事件发生于 S 系中 t = 3.0×10－7 s ，x = 10 m 处，在 S ′系中测得这两个事件的时间间隔为多少？题16.1解：（1）由洛伦兹变换可得S ′系的观察者测得第一事件发生的时刻为s 1025.1/1'7221211-⨯=--=c v x c v t t（2）同理，第二个事件发生的时刻为s 105.3/1'7222222-⨯=--=c v x c v t t所以，在S ′系中两事件的时间间隔为s 1025.2'''721-⨯=-=∆t t t题16.2：设有两个参考系S 和S ′，它们的原点在t = 0和t ′ = 0时重合在一起。
有一事件，在 S ′系中发生在 t ′ = 8.0×10-8 s ，x ′ = 60 m ，y ′ = 0，z ′ = 0处，若S ′系相对于S 系以速率v = 0.6c 沿xx ′轴运动，问该事件在S 系中的时空坐标各为多少？题16.2解：由洛伦兹逆变换得该事件在S 系的时空坐标分别为m 93/1''22=-+=c v vt x x 0'==y y0'==z zs 105.2/1''7222-⨯=-+=c v x c v t t题16.3：一列火车长 0.30 km （火车上观察者测得），以 100 km/h 的速度行驶，地面上观察者发现有两个闪电同时击中火车的前后两端。
问火车上的观察者测得两闪电击中火车前后两端的时间间隔为多少？题16.3解：设地面为S 系，火车为S ′系，把闪电击中火车前后端视为两个事件（即两组不同的时空坐标）。
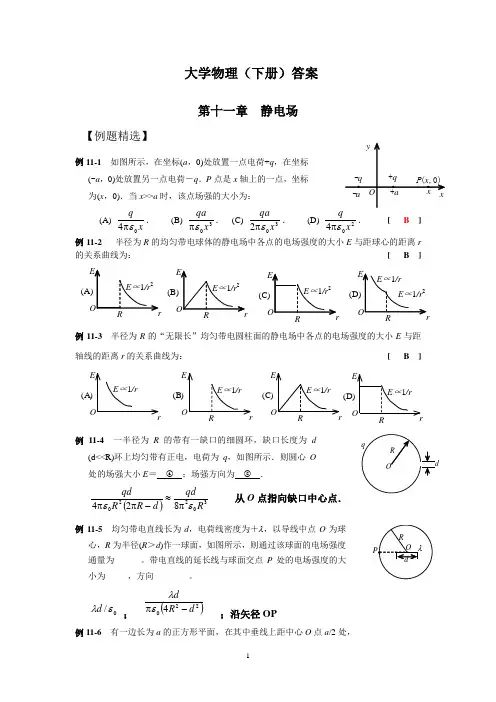
大学物理（下册）答案第十一章 静电场【例题精选】例11-1 如图所示，在坐标(a ，0)处放置一点电荷+q ，在坐标(-a ，0)处放置另一点电荷－q ．P 点是x 轴上的一点，坐标为(x ，0)．当x >>a 时，该点场强的大小为：(A)x q 04επ． (B) 30x qa επ． (C) 302x qa επ． (D) 204x qεπ． [ B ]例11-2半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r的关系曲线为：[ B ]例11-3 半径为R 的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为：[ B ]例11-4一半径为R 的带有一缺口的细圆环，缺口长度为 d (d<<R)环上均匀带有正电，电荷为q ，如图所示．则圆心O 处的场强大小E ＝ ；场强方向为 ．()30220824Rqdd R R qd εεπ≈-ππ 从O 点指向缺口中心点． 例11-5 均匀带电直线长为d ，电荷线密度为＋λ，以导线中点O 为球心，R 为半径(R ＞d )作一球面，如图所示，则通过该球面的电场强度通量为______。
带电直线的延长线与球面交点P 处的电场强度的大小为_____，方向________。
0/ελd ； ()2204d R d-πελ ；沿矢径OP例11-6 有一边长为a 的正方形平面，在其中垂线上距中心O 点a /2处，EO r(A) E ∝1/r有一电荷为q 的正点电荷，如图，则通过该平面的电场强度通量为 (A)03εq ． (B) 04επq (C) 03επq ． (D) 06εq [ D ] 例11-7 两块“无限大”的均匀带电平行平板，其电荷面密度分别 为σ( σ＞0)及－2 σ，如图所示。
试写出各区域的电场强度E 。
Ⅰ区E 的大小__________________，方向____________。
大学物理第四版下册答案【篇一：大学物理(上海交通大学)课后习题答案(第四版)】已知质点位矢随时间变化的函数形式为其中?为常量．求：（1）质点的轨道；(2)速度和速率。
消去t可得轨道方程x?y?r 2）v?222dr1-2. 已知质点位矢随时间变化的函数形式为r?4ti?(3?2t)j，式中r的单位为m，t的单位为s.求：（1）质点的轨道；（2）从t?0到t?1秒的位移；（3）t?0和t?1秒两时刻的速度。
解：1）由r?4ti?(3?2t)j可知22x?4t2 y?3?2t消去t得轨道方程为：x?(y?3) 2）v?2dr?8ti?2j dt113）v(0)?2jv(1)?8i?2j1-3. 已知质点位矢随时间变化的函数形式为r?ti?2tj，式中r的单位为2（1）任一时刻的速度和加速度；（2）任一时刻的切向加速m，t的单位为s.求：度和法向加速度。
解：1）v?dr?2ti?2j dta?dv?2i dt22）v?[(2t)?4]?2(t2?1)at?dv?dt2tt?12an??1-4. 一升降机以加速度a上升，在上升过程中有一螺钉从天花板上松落，升降机的天花板与底板相距为d，求螺钉从天花板落到底板上所需的时间。
解：以地面为参照系，坐标如图，升降机与螺丝的运动方程分别为 12at（1）图 21y2?h?v0t?gt2 （2）2y1?v0t?1-4y1?y2 （3）解之t?1-5. 一质量为m的小球在高度h处以水平抛出，求：（1）小球的运动方程；（2）小球在落地之前的轨迹方程；（3）落地前瞬时小球的初速度v0drdvdv，，. dtdtdt解：（1） x?v0t 式（1）1y?h?gt2 式（2）21r(t)?v0ti?(h-gt2)j2gx2（2）联立式（1）、式（2）得 y?h?22v0（3）dr?v0i-gtj而落地所用时间t?dt2h g所以drdv?v0i-2ghj??gj dtdt22v?v2v0?(?gt)2 x?vy?g2tdv??[v2?(gt)2]01-6. 路灯距地面的高度为h1，一身高为h2的人在路灯下以匀速v1沿直线行走。
习题11-1．已知质点位矢随时间变化的函数形式为(cos sin )r =R ωt i ωt j + 其中ω为常量．求：（1）质点的轨道；(2)速度和速率。
解：(1)由(cos sin )r =R ωt i ωt j +，知：cos x R t ω=，sin y R t ω=消去t 可得轨道方程：222x y R +=∴质点的轨道为圆心在（0，0）处，半径为R 的圆； （2而v v =，有速率：cos )]v t R ωω==。
1-2．已知质点位矢随时间变化的函数形式为2(32)i t j ++，式中r 的单位为m ，t 0=t 和1=t 解：（消去t 3)，∴质点的轨道为抛物线。
（2d r，有速度：82v t i j =+ 从0=t 秒的位移为：1100(82)42r v d t t i j d t i j ∆==+=+⎰⎰（3）和秒两时刻的速度为：1-3．已知质点位矢随时间变化的函数形式为22r t i t j =+，式中r 的单位为，t ）任一时刻的速度和加速度；（2）任一时刻的切向加速度和 解：由d r v dt =，有：22v t i =+d （2）而v v =，有速率：2[(2)2]21v t t =+=+dtt 1-4a 机的天花板与底板相距为d ，求螺钉从天花板落到底板上所需的时间。
解法一：以地面为参照系，坐标如图，设同一时间内螺钉下落的距离为1y ，升降机上升的高度为2y ，运动方程分别为21012y v t gt =-（1）22012y v t at =+（2）12y y d +=（3）2（注意到1y 为负值，有11y y =-）联立求解，有：t ='g g a =+，利用21'2d g t =，有：t ==1-5．一质量为m h 0v 水平抛出，求：解：（）如图，可建立平抛运动学方程： 0x v t =21()t i h g t j +-；（2）联立上面两式，消去t 得小球轨迹方程：2y v =-；（30r v i g t j =-， 即：0v v i g t j -，g j d t=- 在落地瞬时，有：2ht =，∴02d r v i gh j =- 又∵v 12g gh g t dv==1-6∴112x =两边对时间求导有：11212d x h d x d t h h d t =-，考虑到：21d x v d t=， 知人影中头的速度：21112d x hv v d t h h ==-影（常数）。
习题11-1．已知质点位矢随时间变化的函数形式为(cos sin )r =R ωt i ωt j + 其中ω为常量．求：（1）质点的轨道；(2)速度和速率。
解：(1) 由(cos sin )r =R ωt i ωt j +，知：cos x R t ω= ，sin y R t ω=消去t 可得轨道方程：222x y R +=∴质点的轨道为圆心在（0，0）处，半径为R 的圆；（2）由d rv dt =，有速度：sin Rcos v R t i t j ωωωω=-+而v v =，有速率：1222[(sin )(cos )]v R t R t R ωωωωω=-+=。
1-2．已知质点位矢随时间变化的函数形式为24(32)r t i t j =++，式中r 的单位为m ，t 的单位为s 。
求：（1）质点的轨道；（2）从0=t 到1=t 秒的位移；（3）0=t 和1=t 秒两时刻的速度。
解：（1）由24(32)r t i t j =++，可知24x t = ，32y t =+消去t 得轨道方程为：x =2(3)y -，∴质点的轨道为抛物线。
（2）由d rv dt =，有速度：82v t i j =+从0=t 到1=t 秒的位移为：11(82)42r v d t t i j d t i j ∆==+=+⎰⎰（3）0=t 和1=t 秒两时刻的速度为：(0)2v j =，(1)82v i j =+ 。
1-3．已知质点位矢随时间变化的函数形式为22r t i t j =+，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。
解：(1)由d r v dt =，有：22v t i j =+，d va dt =，有：2a i =；（2）而v v =，有速率：12222[(2)2]21v t t =+=+∴t dv a dt==，利用222t n a a a =+有： n a ==1-4．一升降机以加速度a 上升，在上升过程中有一螺钉从天花板上松落，升降机的天花板与底板相距为d ，求螺钉从天花板落到底板上所需的时间。
习题1111-1．直角三角形ABC的A点上，有电荷C108.191-⨯=q，B点上有电荷C108.492-⨯-=q，试求C点的电场强度(设0.04mB C=，0.03mA C=)。
解：1q在C点产生的场强：1124A CqE irπε=，2q在C点产生的场强：2224B CqE jrπε=，∴C点的电场强度：44122.710 1.810E E E i j=+=⨯+⨯；C点的合场强：43.2410VEm==⨯，方向如图：1.8arctan33.73342'2.7α===。
11-2．用细的塑料棒弯成半径为cm50的圆环，两端间空隙为cm2，电量为C1012.39-⨯和方向。
解：∵棒长为2 3.12l r d mπ=-=，∴电荷线密度：911.010qC mlλ--==⨯⋅可利用补偿法，若有一均匀带电闭合线圈，则圆心处的合场强为0，有一段空隙，则圆心处场强等于闭合线圈产生电场再减去md02.0=长的带电棒在该点产生的场强，即所求问题转化为求缺口处带负电荷的塑料棒在O点产生的场强。
解法1：利用微元积分：21cos4O xR ddERλθθπε=⋅，∴2000cos2sin2444OdE dR R Rααλλλθθααπεπεπε-==⋅≈⋅=⎰10.72V m-=⋅；解法2：直接利用点电荷场强公式：由于d r<<，该小段可看成点电荷：112.010q d Cλ-'==⨯，则圆心处场强：1191222.0109.0100.724(0.5)OqE V mRπε--'⨯==⨯⨯=⋅。
方向由圆心指向缝隙处。
11-3．将一“无限长”带电细线弯成图示形状，设电荷均匀分布，电荷线密度为λ，四分之一圆弧AB的半径为R，试求圆ix心O 点的场强。
解：以O 为坐标原点建立xOy 坐标，如图所示。
①对于半无限长导线A ∞在O 点的场强：有：00(cos cos )42(sin sin )42A x A yE R E R λπππελπππε=-=-⎧⎪⎪⎨⎪⎪⎩②对于半无限长导线B ∞在O 点的场强：有：00(sin sin )42(cos cos )42B x B yE R E R λπππελπππε=-=-⎧⎪⎪⎨⎪⎪⎩③对于AB圆弧在O 点的场强：有：2000200cos (sinsin )442sin (coscos )442AB x AB y E d RRE d RRππλλπθθππεπελλπθθππεπε==-=⎧⎪⎪⎨⎪⎪=--⎩⎰⎰∴总场强：04O x E Rλπε=，04O y E Rλπε=，得：0()4O E i j Rλπε=+ 。
或写成场强：0E ==45 。
11-4．一个半径为R 的均匀带电半圆形环，均匀地带有电荷，电荷的线密度为λ，求环心处O 点的场强E 。
解：电荷元dq 产生的场为：204d q d E Rπε=；根据对称性有：0yd E=⎰，则：20sin sin 4xR d E dEd E R πλθθθπε===⎰⎰⎰02Rλπε=，方向沿x 轴正向。
即：02E iR λπε=。
11-5．带电细线弯成半径为R 的半圆形，电荷线密度为0sin λλϕ=，式中0λ为一常数，ϕ为半径R 与x 轴 所成的夹角，如图所示．试求环心O 处的电场强度。
解：如图，0200sin 44d d ldE RRλϕϕλπεπε==，λxyEcos sin x y dE dE dE dE ϕϕ==⎧⎪⎨⎪⎩考虑到对称性，有：0=xE ；∴200000sin (1cos 2)sin 4428yd d E d EdE RRR ππλϕϕλλϕϕϕπεπεε-=====⎰⎰⎰⎰， 方向沿y 轴负向。
11-6．一半径为R 的半球面，均匀地带有电荷，电荷面密度为σ，求球心O 处的电场强度。
解：如图，把球面分割成许多球面环带，环带宽为d l R d θ=，所带电荷：2dq r d l πσ=。
利用例11-3结论，有：332220024()4x dqr x d ld E x r σππεπε⋅==+∴322202cos sin 4[(sin )(cos )]R R Rd dE R R σπθθθπεθθ⋅⋅⋅=+，化简计算得：20001sin 2224E d πσσθθεε==⎰，∴04E σε= 。
11-7．图示一厚度为d 的“无限大”均匀带电平板，电荷体密度为ρ。
求板内、外的场强分布，并画出场强随坐标x 变化的图线，即x E -图线(设原点在带电平板的中央平面上，Ox 轴垂直于平板)。
解：在平板内作一个被平板的中间面垂直平分的闭合圆柱面1S 为高斯面，当2d x ≤时，由12S E dS E S ⋅=⋅∆⎰和2q x S ρ=∆∑，有：0x E ρε=；当2d x >时，由22S E dS E S⋅=⋅∆⎰和2q d S ρ=∆∑，有：02dE ρε=。
图像见右。
11-8．在点电荷q 的电场中，取一半径为R 的圆形平面(如图所示)，平面到q 的距离为d ，试计算通过该平面的E 的通量.解：通过圆平面的电通量与通过与A 为圆心、AB 为半径、圆的平面 为周界的球冠面的电通量相同。
x【先推导球冠的面积：如图，令球面的半径为r ，有球冠面一条微元同心圆带面积为：2sin dSr rd πθθ=⋅ ∴球冠面的面积：200cos 2sin 2cos d rS r rd r θθπθθπθ==⋅=⎰22(1)d r rπ=-】∵球面面积为：24S rπ=球面，通过闭合球面的电通量为：qεΦ=闭合球面，由：S S Φ=Φ球冠球面球面球冠，∴1(1)(122d qq r εεΦ=-⋅=-球冠。
11-9．在半径为R 的“无限长”直圆柱体内均匀带电，电荷体密度为ρ，求圆柱体内、外的场强分布，并作E ~r 关系曲线。
解：由高斯定律01iSS E dS qε⋅=∑⎰⎰内，考虑以圆柱体轴为中轴，半径为r ，长为l 的高斯面。
（1）当r R <时，22r l r l E ρππε⋅=，有2E rρε=；（2）当r R >时，22R l r l E ρππε⋅=，则：E =即：020()2()2rr R E R r R r ρερε⎧<⎪⎪=⎨⎪>⎪⎩；图见右。
11-10．半径为1R 和2R （21R R <）的两无限长同轴圆柱面，单位长度分别带有电量λ和λ-，试求：（1）1R r <；（2）21R r R <<；（3）2R r >处各点的场强。
解：利用高斯定律：1iSS E dS qε⋅=∑⎰⎰内。
（1）1r R <时，高斯面内不包括电荷，所以：10E =； （2）12R r R <<时，利用高斯定律及对称性，有：202l r l E λπε=，则：202E rλπε=；Oθr（3）2r R >时，利用高斯定律及对称性，有：320rlE π=，则：30E =；即：112020ˆ20E r R E rR r R r E r R E λπε⎧=<⎪⎪=<<⎨⎪⎪==>⎩。
11-11．一球体内均匀分布着电荷体密度为ρ的正电荷，若保持电荷分布不变,在该球体中挖去半径为r 的一个小球体，球心为O '，两球心间距离d O O ='，如图所示。
求：（1）在球形空腔内，球心O '处的电场强度0E ；（2）在球体内P 点处的电场强度E ，设O '、O 、P 三点在同一直径上，且dOP=。
解：利用补偿法，可将其看成是带有电荷体密度为ρ的大球和带有电荷体密度为ρ-的小球的合成。
（1）以O 为圆心，过O '点作一个半径为d 的高斯面，根据高斯定理有： 13043S E d S d ρπε⋅=⋅⎰ ⇒003d E ρε=，方向从O 指向O '；（2）过P 点以O 为圆心，作一个半径为d 的高斯面。
根据高斯定理有：13043S E d S d ρπε⋅=⋅⎰ ⇒103P d E ρε=，方向从O 指向P ，过P 点以O '为圆心，作一个半径为d 2的高斯面。
根据高斯定理有：23043S E d S r ρπε⋅=-⋅⎰⇒32203P r E d ρε=-，∴1232()34P P rE E E d dρε=+=-，方向从O 指向P 。
11-12．设真空中静电场E的分布为E c x i = ，式中c 为常量，求空间电荷的分布。
有：0S E d S c x S⋅=⋅∆⎰⎰由高斯定理：1SS E d S qε⋅=∑⎰⎰内，设空间电荷的密度为()x ρ，有：0000()x x Sd x c x S ρε∆⋅∆=⎰∴000()x x x d x cd xρε=⎰⎰，可见()x ρ为常数⇒0c ρε=。
11-13．如图所示，一锥顶角为θ的圆台，上下底面半径分别为1R 和2R ，在它的侧面上均匀带电，电荷面密度为σ，求顶点O 的电势．(以无穷远处为电势零点)解：以顶点为原点，沿轴线方向竖直向下为x 轴，在侧面上取环面元，如图示，易知，环面圆半径为：t a n2r x θ=，环面圆宽：cos2d x d l θ=22tan2cos2d xdS r d l x θππθ=⋅=⋅⋅，利用带电量为q 的圆环在垂直环轴线上0x 处电势的表达式：14U πε=环有：02tan2cos1tan 422d x x dU d xθσπθσθπεε⋅⋅==⋅，考虑到圆台上底的坐标为：11cot2x R θ=，22cot2x R θ=，∴U =21tan22x x d x σθε⋅⎰21cot 2cot2tan22R R d x θθσθε=⋅⎰210()2R R σε-=。
11-14．电荷量Q 均匀分布在半径为R 的球体内，试求：离球心r 处（r R <）P 点的电势。
解：利用高斯定律：1SS E dS qε⋅=∑⎰⎰内（1）r R <时，32304Qrr E Rπε=⋅内；有：304Q r E R πε=内（2）r R >时，24Qr E πε=外；有：204Q E rπε=外；xcos2dx θ离球心r 处（r R <）的电势：R rrRU E d r E d r∞=⋅+⋅⎰⎰外内，即：320044R r rRQ r Q U d r d r Rrπεπε∞=⋅+⋅⎰⎰2300388Q Q rRRπεπε=-。
11-15．图示为一个均匀带电的球壳，其电荷体密度为ρ，球壳内表面半径为1R ，外表面半径为2R ．设无穷远处为电势零点，求空腔内任一点的电势。
解：当1r R <时，因高斯面内不包围电荷，有：1E=，当12R r R <<时，有：203132031323)(4)(34rR r rR r E ερπεπρ-=-=，当2r R >时，有：20313220313233)(4)(34rR R rR R E ερπεπρ-=-=，以无穷远处为电势零点，有：21223R R R U E d r E d r ∞=⋅+⋅⎰⎰⎰⎰∞-+-=2R dr rR R dr rR r R R 203132203133)(3)(21ερερ)(221220R R -=ερ。
