
练习6.7
1.有两个煤厂A,B,每月进煤不少于60t,100t,它们担负供应三个居
民区的用煤任务,这三个居民区每月用煤量分别为45t,75t和45t.A 厂离这三个居民区的距离分别为10km,5km,6km,B厂离这三个居民区的距离分别为4km,8km,15km.问这两个煤厂如何分配供煤量能使总运输量(t.km)最小。
解:设甲对三个居民区的供煤量分别为:x1,x2,x3,乙对三个居民区的供煤量分别为x4,x5,x6.由已知有:
y=10x1+5x2+6x3+4x4+8x5+15x6
-x1-x2-x3<=-60,
-x4-x5-x6<=-100,
x1+x4=45,x2+x5=75,x3+x6=40,
X1>=0,x2>=0,x3>=0,x4>=0,x5>=0,x6>=0.
输入命令:
> c=[10 5 6 4 8 15];A=[-1 -1 -1 0 0 0;0 0 0 -1 -1 -1;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];
>> b=[-60;-100;0;0;0;0];Aeq=[1 0 0 1 0 0;0 1 0 0 1 0;0 0 1 0 0 1;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];
>> beq=[45 75 40 0 0 0];
>> lb=ones(6,1);
>> [x,fval]=linprog(c,A,b,Aeq,beq,lb)
Optimization terminated.
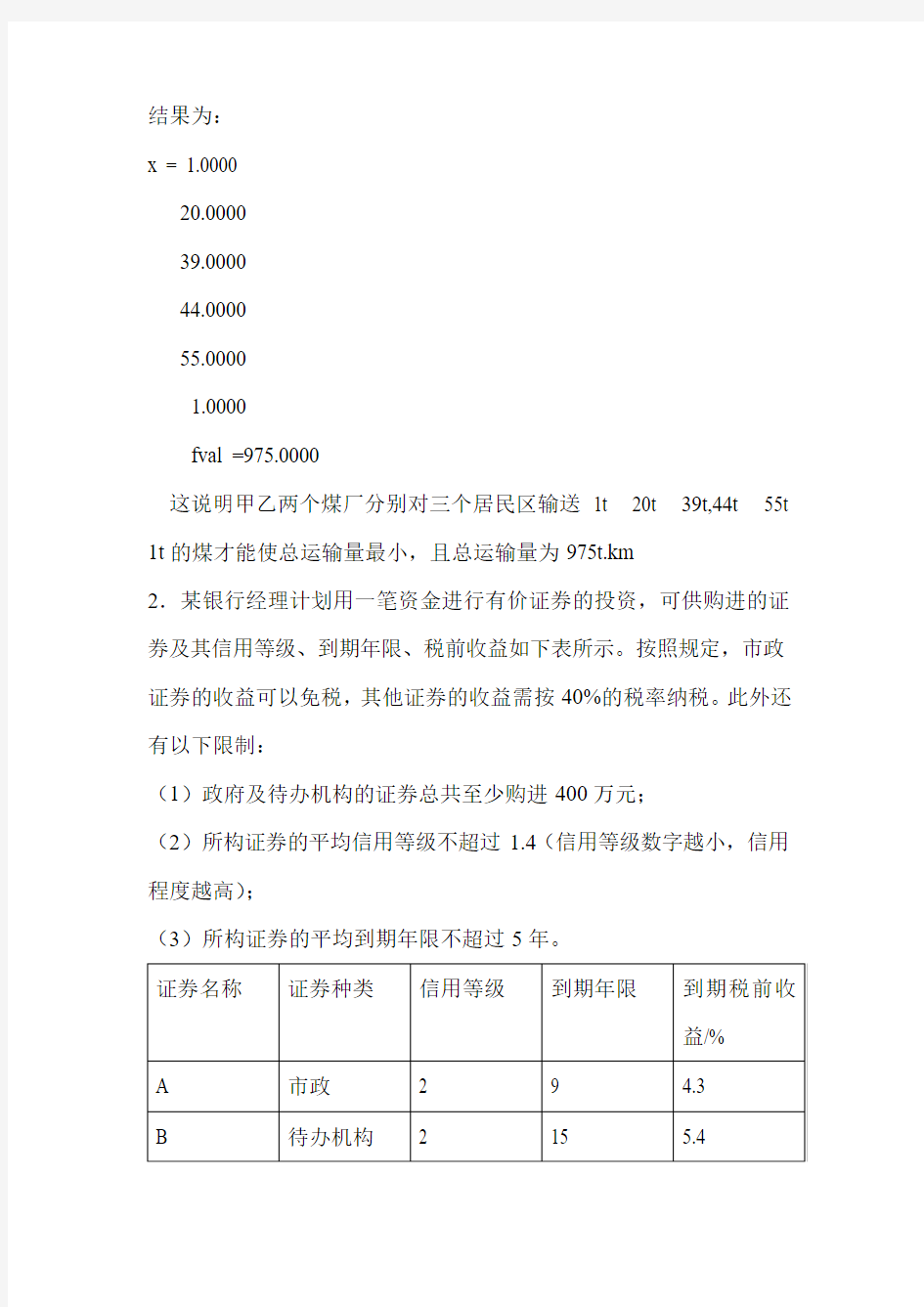
结果为:
x = 1.0000
20.0000
39.0000
44.0000
55.0000
1.0000
fval =975.0000
这说明甲乙两个煤厂分别对三个居民区输送1t 20t 39t,44t 55t 1t的煤才能使总运输量最小,且总运输量为975t.km
2.某银行经理计划用一笔资金进行有价证券的投资,可供购进的证券及其信用等级、到期年限、税前收益如下表所示。按照规定,市政证券的收益可以免税,其他证券的收益需按40%的税率纳税。此外还有以下限制:
(1)政府及待办机构的证券总共至少购进400万元;
(2)所构证券的平均信用等级不超过1.4(信用等级数字越小,信用程度越高);
(3)所构证券的平均到期年限不超过5年。
问:(1)若经理有1000万元资金,应如何投资?
(2)如果能以2.75%的利率借到不超过100万元的资金,该不该借?如何投资?
(3)在1000万元资金的情况下,若证券A的税前收益增加为4.5%,投资应否改变?若证券C的税前收益减少为4.8%,投资应否改变?解:(1)设A、B、C、D、E证券分别购进x1,x2,x3,x4,x5(单位:万元),则有:
目标函数f=0.043x1+0.0216x2+0.02x3+0.0176x4+0.045x5
s.t. –x2-x3-x4<=-400,
2x1+2x2+x3+x4+5x5<=7,
9x1+15x2+4x3+x4+x5<=25,
X1+x2+x3+x4+x5<=1000,
0<=x1,0<=x2,0<=x3,0<=x4,0<=x5.
输入命令:
>> c=[-0.043 -0.0216 -0.02 -0.0176 -0.045];
>> A=[0 -1 -1 -1 0;2 2 1 1 5;9 15 4 3 2;1 1 1 1 1];
>> b=[-400;7;25;10000];
>> Aeq=[];beq=[];
>> lb=zeros(5,1);ub=[];
>> [x,fval]=linprog(c,A,b,Aeq,beq,lb,ub)
结果为:
x = 0.0001
0.0005
0.0000
481.1525
0.0000
fval = -8.4683
所以对A、B、C、D、E证券应分别购进0.0001万元、0.0005万元、0.0000万元、481.1525万元、0.0000万元才能是所得利益最大。(2)设A、B、C、D、E证券分别购进x1,x2,x3,x4,x5(单位:万元),则有:
目标函数f=(0.043x1+0.0216x2+0.02x3+0.0176x4+0.045x5)*0.0275 s.t. 2x1+2x2+x3+x4+5x5<=7,
9x1+15x2+4x3+x4+x5<=25,
X1+x2+x3+x4+x5<=100,
0<=x1,0<=x2,0<=x3,0<=x4,0<=x5.
输入命令:
>> A=[2 2 1 1 5;9 15 4 3 2];
>> b=[7;25];
>> Aeq=[];beq=[];
>> lb=zeros(5,1);
>> ub=[];
>> [x,fval]=linprog(c,A,b,Aeq,beq,lb,ub)
Optimization terminated.
结果为:
x =
1.0e-008 *
0.4324
0.7401
0.0453
0.2629
0.4695
fval =1.6841e-011
所以对A、B、C、D、E证券应该分别购进1.0e-008 *0.4324万元、1.0e-008 * 0.7401万元、1.0e-008 * 0.0453万元、1.0e-008 *0.2629
万元、1.0e-008 *0.4695,才能使所得利益最大。
(3)设A、B、C、D、E证券分别购进x1,x2,x3,x4,x5(单位:万元)①目标函数f1=0.045x1+0.0216x2+0.02x3+0.0176x4+0.045x5
s.t. –x2-x3-x4<=-400,
2x1+2x2+x3+x4+5x5<=7,
9x1+15x2+4x3+x4+x5<=25,
0<=x1,0<=x2,0<=x3,0<=x4,0<=x5.
输入命令:
>> c=[-0.045 -0.0216 -0.02 -0.0176 -0.045];
>> A=[0 0 -1 -1 -1;2 2 1 1 5;9 15 4 3 2;1 1 1 1 1;0 0 0 0 0];
>> b=[7;25;1000;0;0];
>> Aeq=[];beq=[];
>> lb=zeros(5,1);ub=[];
>> [x,fval]=linprog(c,A,b,Aeq,beq,lb,ub)
Optimization terminated.
x =1.0e-010 *
0.0250
0.0018
0.0263
0.0276
0.1106
fval =-7.1543e-013
由(1)知f=8.4683万元>f1=7.1543e+013万元,所以,当证券A的税前收益增加为4.5%时,不应该改变投资。
②目标函数f2=0.045x1+0.0216x2+0.0192x3+0.0176x4+0.045x5
s.t. –x2-x3-x4<=-400,
9x1+15x2+4x3+x4+x5<=25,
X1+x2+x3+x4+x5<=1000,
0<=x1,0<=x2,0<=x3,0<=x4,0<=x5.
输入命令:
>> c=[-0.043 -0.0216 -0.0192 -0.0176 -0.045];
>> A=[0 0 -1 -1 -1;2 2 1 1 5;9 15 4 3 2;1 1 1 1 1;0 0 0 0 0]; >> b=[7;25;1000;0;0];
>> Aeq=[];beq=[];
>> lb=zeros(5,1);ub=[];
>> [x,fval]=linprog(c,A,b,Aeq,beq,lb,ub)
Optimization terminated.
结果为:
x =
1.0e-010 *
0.0250
0.0018
0.0265
0.0278
0.1104
fval =
-7.0816e-013
由(1)知f=8.4683万元>7.0816e+013万元,所以当证券C的税前收益减少为4.8%时,不应该改变投资。
3.某厂向用户提供发电机,合同规定第一、第二、第三季度分别交货40台、60台、80台,每季度的生产费用为f(x)=ax+bx^2,其中x是该季度生产发动机的台数。若交货后有剩余,可用于下季度,但需支付存储费,每台每季度c元。已知工厂每季度最大生产能力为100台,第一季度开始时无2存货。设a=50,b=0.22,c=4,问工厂应如何安排生产计划才能既满足合同要求又使总费用最低?
解:设第一、第二、第三季度分别生产x1、x2、x3台发动机,则:f=50x1+0.22x1^2+50x2+0.22x2^2+x3+0.22x3^2+8(x1-40)+4(x2-60)
=0.22x1^2+0.22x2^2+0.22x3^2+58x1+54x2+50x3-560
s.t. x1-40+x2>=60,
x1-40+x2-60+x3=80,
40<=x1<=100,
0<=x2<=100,
0<=x3<=100.
标准形式:
s.t. –x1-x2<=-100,
x1+x2+x3=180,
40<=x1<=100,
0<=x2<=100,
0<=x3<=100.
输入命令:
>> c=[58 54 50];
>> H=[0.22 0 0;0 0.22 0;0 0 0.22];
>> A=[-1 -1 0];
>> b=[-100];
>> Aeq=[1 1 1];
>> beq=[180];
>> lb=[40;0;0];
>> ub=[100;100;100];
>> [x,fval]=quadprog(H,c,A,b,Aeq,beq,lb,ub)
Warning: Large-scale method does not currently solve this problem formulation,
switching to medium-scale method.
> In quadprog at 236
Optimization terminated.
结果为:
x = 41.8182
60.0000
78.1818
fval =
1.0835e+004
所以工厂应该在第一、第二、第三季度分别生产42台、60台、78台发动机,才能既满足合同要求又使总费用最低。
练习6.8
1.一电路由三个电阻R1,R2,R3并联,再与电阻R4串联而成。记
Rk上的电流为Ik,电压为Vk,在下列情况下确定Rk,使电路总功率最小(k=1,2,3,4).
I1=4,I2=6.I3=8,2<=Vk<=100
解:目标函数f=18v1+18v2
s.t. 2<=v1<=100
2<=v2<=100
输入命令:
>> c=[18 18];
>> A=[];b=[];
>> Aeq=[];beq=[];
>> lb=[2;2];ub=[100;100];
>> [x,fval]=linprog(c,A,b,Aeq,beq,lb,ub)
Optimization terminated.
结果为:
x =
2.0000
2.0000
fval =
72.0000
2.某厂生产容积为1L的圆柱形铁罐,请根据以下情景分别设计下料方案。
(1)现有2m长、1m宽的铁皮两张,一张用来冲压上盖和下底,一张用来切割铁罐侧面长方形。问如何下料,可使生产的铁罐尽可能多?此时,铁罐的地面直径和高各是多少?
(2)如果工厂大规模生产铁罐,铁罐的上盖和下底以及侧面都从2m 长、1m宽的铁皮冲压或切割出来(为方便加工,圆料和方料不在同一张铁皮上混合下料),问如何下料,可使生产的铁罐尽可能多?此时,铁罐的地面直径和高各是多少?
解:
练习6.10
1.给定数据表如下:
分别就下列端点条件求三次样条插值S(x),并作图。
(1)S’(0.25)=1,S’(0.53)=0.6868.(2)S’’(0.25)=S’’(0.53)=0. 解:(1)输入命令:
>> t=[0.25 0.30 0.39 0.45 0.53];
>> V=[0.5000 0.5477 0.6245 0.6708 0.7280];
>> pp=spline(t,V)
结果为:
pp =
form: 'pp'
breaks: [0.2500 0.3000 0.3900 0.4500 0.5300]
coefs: [4x4 double]
pieces: 4
order: 4
dim: 1
输入命令:
>> plot(t,V)
结果为:
0.25
0.30.350.40.450.50.550.6
0.50.55
0.6
0.65
0.7
0.75
(2)输入命令:
>> t=[0.25 0.30 0.39 0.45 0.53];
>> V=[0.5000 0.5477 0.6245 0.6708 0.7280]; >> pp=csape(t,V ,'variational') 结果为: pp =
form: 'pp'
breaks: [0.2500 0.3000 0.3900 0.4500 0.5300] coefs: [4x4 double] pieces: 4 order: 4
dim: 1 输入命令: >> plot(t,V) 结果为:
0.25
0.30.350.40.450.50.550.6
0.50.55
0.6
0.65
0.7
0.75
2.领导视察大学城,坐车从大学城边界上某处出发,沿边界行驶了15min45s ,然后作90度做拐弯沿直线边界直奔起点。下表给出了汽车在钱15 min45s 行驶过程中每个2min 左右的记录数据。
请根据数据提供的数据,(1)估计汽车绕大学城行驶的总路程;(2)估计大学城的占地面积;(3)确定该汽车的行驶路线的函数表达式。解:(1)输入命令:
>> t1=0;t2=2;t3=4;t4=6;t5=8;t6=10;t7=12;t8=14;t9=15.75;
>>
v1=0;v2=0.67;v3=0.85;v4=0.97;v5=1.07;v6=1.15;v7=1.22;v8=1.29;v9=1 .34;
>> s=ti*v1+t2*v2+t3*v3+t4*v4+t5*v5+t6*v6+t7*v7+t8*v8+t9*v9
结果为:
s =
84.4250 84.4250 84.4250 84.4250 84.4250 84.4250 84.4250 84.4250 84.4250
输入命令:
>> sum=84.4250+ 84.4250+84.4250 +84.4250+84.4250 +84.4250 +84.4250 +84.4250 +84.4250
结果为:
sum =759.8250
所以汽车绕大学城形式的总路程估计为759.8250km^2
(2)
(3)输入命令:
>> t=[0 2 4 6 8 10 12 14 15.75];
>> v=[0 0.67 0.85 0.97 1.07 1.15 1.22 1.29 1.34];
>> a=[0 91 144 189 229 266 300 333 360];
>> pp=spline(t,v,a)
结果为:
pp =
1.0e+004 *
0 -0.0210 -0.1000 -0.2427 -0.4485 -0.7206 -1.0518 -1.4576 -1.8583
练习6.11
1,。假定某天的气温变化记录如下表,试找出这一天的气温变化规律。
解:输入命令:
>> t=0:1:24;
>> T=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];
>> p=polyfit(t,T,2)
结果为:
p =
-0.0936 2.5943 8.4157
输入命令:
>> T=poly2sym(p)
结果为:
T=-2519/26910*t^2+58177/22425*t+24616/2925
所以这一天的气温变化规律为:
T=-2519/26910*t^2+58177/22425*t+24616/2925
2.用电压v=10v的电池给电容器充电,电容器上时刻t的电压u(t)=v-(v-vo)exp(-t/r),其中v0是电容器的初始电压,r是充电常数,试由下面一组t,v数据确定vo和r.
解:先编写M-文件fun.m
function f=fun(c,t)
t=[0.5 1 2 3 4 5 7 9]
v=[6.36 6.48 7.26 8.22 8.66 8.99 9.43 9.63]
f=v-(v-c(1))*exp(-t/c(2))
输入命令:
>> c0=[0.2 0.05 0.05];
>> [c,fval]=lsqnonlin('fun',c0);
结果为:
t = 0.5000 1.0000 2.0000 3.0000 4.0000 5.0000 7.0000 9.0000
v = 6.3600 6.4800 7.2600 8.2200 8.6600 8.9900 9.4300 9.6300
练习6.4
1.试在以下列弧表矩阵表示的无向图中找一条从1到8点的最短路。解:>> G=[1 2 7;1 3 8;1 4 2;1 7 4;2 3 1;2 5 2;2 8 3;3 4 4;3 5 2;3 6 7;4 6 3;4 7 6;5 6 5;5 8 1;6 7 4;6 8 3;7 8 6];
>> if G=(1,1)==0
??? if G=(1,1)==0
|
Error: The expression to the left of the equals sign is not a valid target for an assignment.
>> if G(1,1)==0
A=G;
n-size(A,1);A1=A;A1(A1==inf)=0;
M=sum(sum(A1));A1(A1==0)=M;A=A1-M*eye(n);
break
else
e=G
n=max([e(:,3);
m=size(e,1);
??? m=size(e,1);
|
Error: The expression to the left of the equals sign is not a valid target for an assignment.
>> n=max([e(:,1);e(:,2)]);
>> m=size(e,1);
>> M=sum(e(:,3));
>> A=M*ones(n,n);
>> for k=1:m
>> A(e(k,1),e(k,2))=e(k,3);
>> if 0pt=0
A(e(k,1),e(k,2))=e(k,3);
end
>> end
2.一个农夫带了一条狗、三只鸡和一袋米准备过河,过河的船太小,
农夫一次只能带一条沟,或三只鸡,或一袋米上船。在无人看守时,狗会咬鸡,鸡会吃米。问农夫有没有办法把随身带的狗、鸡米安全过河。
解:农夫第一次过河时带三只鸡过去,然后农夫一个人回来;第二次过河时带着一袋米过去,回来时带着三只鸡回来;第三次过河时带着一条狗过去,然后一个人回来;第四次过河时带着三只鸡过去。这样就可以安全过河了。
数学软件与数学实验作业 一.《数学软件》练习题(任选12题,其中19-24题至少选2题): 3.对下列各式进行因式分解. (1). syms x y >> factor(x^5-x^3) (2). syms x y >> factor(x^4-y^4) (3). syms x >> factor(16-x^4) (4). syms x >> factor(x^3-6*x^2+11*x-6) (5). syms x y >> factor((x+y)^2-10*(x+y)+25) (6). syms x y >> factor(x^2/4+x*y+y^2) (7). syms x y a b >> factor(3*a*x+4*b*y+4*a*y+3*b*x) (8). syms x >> factor(x^4+4*x^3-19*x^2-46*x+120) 5.解下列方程或方程组. (1).solve('(y-3)^2-(y+3)^3=9*y*(1-2*y)') (2). solve('3*x^2+5*(2*x+1)') (3). solve('a*b*x^2+(a^4+b^4)*x+a^3*b^3','x') (4). solve('x^2-(2*m+1)*x+m^2+m','x') (5). [x,y]=solve('4*x^2-9*y^2=15','2*x-3*y=15') 6.计算极限. (1). syms x f=(exp(x)-exp(-x))/sin(x); limit(f,x,0) (2) syms x >> f=(x/(x-1)-1/log(x)); >> limit(f,x,1) (3). syms x >> f=(1-cos(x))/x^2; >> limit(f,x,0)
数学实验 期末上机考核 学号201519030102 姓名曹欣辉年级专业2015级水产养殖学 学号201519030103 姓名陈妙珊年级专业2015级水产养殖学 学号201519030104 姓名杜日臻年级专业2015级水产养殖学 学号姓名年级专业 学号姓名年级专业
注意事项: 1、考核方式:以组(3~4人)为单位,请于指定时间内开卷完成所布置的任务,地点为实验 室机房或课室。 2、发题时间为6月25号早上8:30,请到如下邮箱提取题目,账号:nongkeshuxue@https://www.doczj.com/doc/2c14831154.html,, 密码:shuxueshiyan。 3、关于试卷提交时间: (1)电子版提交时间于6月26晚上12:00前,发送本班任课老师给定的email地址,任课老师以收到信件的时间为准,提交文件的同学可通过收到任课老师回复的邮件接收函作为提交信息。 (2)纸质版提交时间于6月27日早上11:30前,由学委收齐后交与任课老师。 4、每小组同学可以使用无生命的数据或材料:如计算机、软件、参考文献、网络、图书等。 5、除小组成员内相互讨论,队伍成员不可以向老师及其他人员寻求帮助。任何从非小组成员 内得到的帮助都是被严格禁止的,这包括通过邮件,电话交谈,聊天,网络聊天等其他交流工具得到的他人的帮助。 6、每位同学需在承诺书上签字,如无签字,可视为放弃该科目考试,并且一经发现抄袭作弊 等行为,将取消该组所有同学的答卷分数。 7、每组同学完成答题后,请组内同学根据所作贡献协商讨论后进行评价打分,每组同学贡献 值总分为100。 8、请在下列表中有学生姓名的地方填上相应的名字。 组内同学互评后贡献值表:注:贡献值≤100 学生姓名曹欣辉陈妙珊杜日臻张照明 贡献值 老师评分表: 题号 1 2 3 4 5 7 总分得分 签名 学生成绩: 学生姓名 成绩 注:表中每位学生成绩得分计算公式如下: 该学生贡献分 卷面总分 该组最高贡献分
练习2﹒1 画出下列常见曲线的图形(其中a=1,b=2,c=3)。 1. 立方抛物线y = 解: x=-4:0.1:4; y=x.^(1/3); plot(x,y) -4 -3-2-101234 0.20.40.60.811.21.4 1.6 2.高斯曲线2 x y e -= 解: fplot('exp(-x^2)',[-4,4])
-4 -3 -2 -1 1 2 3 4 00.10.20.30.40.50.60.70.80.9 1 3、笛卡儿曲线23 3 2 2 33,(3)11at at x y x y axy t t = = +=++ 解:ezplot('x^3+y^3-3*x*y',[-4,4])
-4 -3-2-1 01234 -4-3-2-10123 4x y x 3+y 3-3 x y = 0 或:t=-4:0.1:4; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)
-1.5 -1-0.500.51 1.5 00.5 1 1.5 2 2.5 3 4、蔓叶线233 2 2 2 ,()11at at x x y y t t a x = = = ++- 解:t=-4:0.1:4; x=t.^2./(1+t.^2); y=t.^3,/(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)
00.10.20.30.40.50.60.70.80.91 -4 -3-2-10123 4 或: ezplot('y .^2-x.^3/(1-x)',[-4,4])
《数学建模与数学实验》本科教学日历 数学建模部分 开设课程课程名称数学建模课程编号0701107 施教单位理学院 课内学时 总课时36 课程性质公共基础讲授课时28 修读要求选修实践课时8 选用教材教材名称数学建模教程出版社名称高等教育出版社 出版时间 及版次 2011年出版,第一版印刷时间2011年 其他情况 教学安排 班次授课对象及人数任教教员(指导教员)姓名及职称数学建模A 各专业本科学员 吴孟达教授 段晓君教授 毛紫阳讲师 王丹讲师 数学建模B 各专业本科学员 吴孟达教授 段晓君教授 毛紫阳讲师 王丹讲师 课次节 次 授课内容 教学 方法 采用现代化教学手段(课时) 多媒体电教双语网络实验 1 1 (1)什么是数学建模?数学建模的一般概念 (2)几个数学建模问题 讲授 1 2 (1)数学建模的一般步骤 (2)敏感问题调查案例 讲授 1 2 3 (1)行走步长问题 (2)雨中行走淋雨量最小问题 (3)道路是越多越通畅吗? 讲授 1 4 (1)有奖销售的抽奖策略问题 (2)“非诚勿扰”女生最佳选择问题 (3)网络文章流行度预测和招聘匹配 讲授 1 3 5 (1)线性规划模型基本概念 (2)整数规划模型 (3)0-1规划模型 讲授 1 6 (1)非线性规划 (2)多目标规划 讲授 1 4 7 (1)最短路算法 (2)最小生成树算法 讲授 1 8 (1)最大流算法 (2)PageRank算法 讲授 1 5 9 规划模型上机实践实践 1
课次节 次 授课内容 教学 方法 采用现代化教学手段(课时) 多媒体电教双语网络实验10 图论模型上机实践实践 1 6 11 (1)博弈模型基本概念 (2)Nash平衡和Pareto最优 (3)博弈论案例 讲授 1 12 (1)贝叶斯纳什均衡 (2)拍卖模型 讲授 1 7 13 社会选择理论中的选举问题数学模型-阿罗不可能定理讲授 1 14 越野长袍团体赛排名规则公平性问题讲授 1 8 15 军事作战模型-Lanchester作战模型讲授 1 16 自动化车床管理模型讲授 1 9 17 (1)“边际效应”基本概念 (2)实物交换模型,最佳消费模型、报童售报问题 讲授 1 18 (1)价格弹性模型 (2)合作效益的Shapley值分配模型 讲授 1 10 19 (1)聚类分析基本概念 (2)常用聚类算法 讲授 1 20 (1)方差分析基本概念 (2)单因素方差分析 (3)双因素方差分析 讲授 1 11 21 (1)主成分分析基本概念 (2)因子分析 讲授 1 22 (1)一元回归分析 (2)多元回归分析 (3)多元回归模型的检验与优化 讲授 1 12 23 聚类分析和方差分析上机实践实践 1 24 主成分分析和多元回归分析上机实践实践 1 13 25 (1)遗传算法基本思想 (2)算法步骤 讲授 1 26 遗传算法计算实例讲授 1 14 27 (1)模拟退火算法基本思想 (2)算法步骤 讲授 1 28 模拟退火算法计算实例讲授 1 15 29 (1)蚁群算法基本思想 (2)算法步骤 讲授 1 30 (1)数学建模中的计算机仿真 (2)不可召回的秘书招聘问题 (3)车灯光源优化设计 (4)生命游戏 讲授 1 16 31 遗传算法上机实践实践 1 32 模拟退火算法上机实践实践 1
清华大学2002至2003学年第二学期数学实验期末考试试题A 数学实验试题 2003.6.22 上午 (A卷;90分钟) 一. 某两个地区上半年6个月的降雨量数据如下(单位:mm): 月份123456 地区A259946337054 地区B105030204530 在90%的置信水平下,给出A地区的月降雨量的置信区 间: 在90%的置信水平下,A地区的月降雨量是否不小于70(mm)? 在90%的置信水平下,A、B地区的月降雨量是否相同? A地区某条河流上半年6个月对应的径流量数据如下(单位:m3):110,184,145,122,165,143。该河流的径流量y与当地的降雨量x的线性回归方程为;若当地降雨量为55mm,该河流的径流量的预测区间为(置信水平取90%)。 答案:(程序略) (1) [32.35,76.65] (2) 是 (3) 否 (4) y=91.12+0.9857x (5) [130.9,159.7] 二.(10分) (1)(每空1分)给定矩阵,如果在可行域上考虑线性函数,其中,那么的最小值是,最小点为;最大值是,最大点为。 (每空2分)给定矩阵,,考虑二次规划问题,其最优解为,(2) 最优值为,在最优点处起作用约束 为 。 答案:(1)最小值为11/5,最大值为7/2,最小点为(0,2/5,9/5),最大点为(1/2,0,3/2)。 (2)最优解为(2.5556,1.4444),最优值为–1.0778e+001,其作用约束为。 三.(10分)对线性方程组:,其中A=,b= (3分)当时,用高斯—赛德尔迭代法求解。取初值为,写出迭代第4步的结果=____________________。 (4分)当时,用Jacobi 迭代法求解是否收敛?__________ , 理由是_________________________________________________ 。 (3分)求最大的c, 使得对任意的,用高斯—赛德尔迭代法求解一定收敛,则c应为__________。 答案:(1)x = [ -1.0566 1.0771 2.9897]
数学实验报告实验题目:赛车车道路况分析问题 小组成员: 填写日期2012 年 4 月20 日
一.问题概述 赛车道路况分析问题 现要举行一场山地自行车赛,为了了解环行赛道的路况,现对一选手比赛情况进行监测,该选手从A地出发向东到B,再经C、D回到A地(如下图)。现从选手出发开始计时,每隔15min观测其位置,所得相应各点坐标如下表(假设其体力是均衡分配的): 由D→C→B各点的位置坐标(单位:km) 假设:1. 车道几乎是在平原上,但有三种路况(根据平均速度v(km/h)大致区分): 平整沙土路(v>30)、坑洼碎石路(10 2.估计车道的长度和所围区域的面积; 3.分析车道上相关路段的路面状况(用不同颜色或不同线型标记出来); 4.对参加比赛选手提出合理建议. 二.问题分析 1.模拟比赛车道的曲线:因为赛道散点分布不规则,我们需要用光滑曲线来近 似模拟赛道。由于数据点较多,为了避免龙格现象,应采用三次样条插值法来对曲线进行模拟(spline命令)。全程曲线为环路,我们需要对上下两部分分别 模拟,设模拟出的曲线为P:。 2.把A到B点的曲线分成若干小段: 赛道的路程L:取dL=,对模拟出的整条曲线求线积分,即 所围区域的面积:用上下部分曲线的差值对求定积分,即 3.用样条插值法模拟出比赛车道曲线后,根据曲线分别计算出原数据中每两点 ()间的路程,即求线积分 由于每两点间时间间隔相同且已知(15min),故可求出每段路程的平均速度 易知即为的积分中值 将此速度近似作为两点间中点时刻的速度,然后再次采用样条插值法,模拟出全过程的图像。而根据求出的与之间的关系,再次采用样条插值法,即可模拟出全过程的图像 4. 由赛道曲线可求出赛道上任一点到点的路程 同时图像也可以求出赛道上任一点到点的路程 数学建模与数学实验课程总结与练习内容总结 第一章 1.简述数学建模的一般步骤。 2.简述数学建模的分类方法。 3.简述数学模型与建模过程的特点。 第二章 4.抢渡长江模型的前3问。 5.补充的输油管道优化设计。 6.非线性方程(组)求近似根方法。 第三章 7.层次结构模型的构造。 8.成对比较矩阵的一致性分析。 第五章 9.曲线拟合法与最小二乘法。 10 分段插值法。 第六章 11 指数模型及LOGISTIC模型的求解与性质。 12.VOLTERRA模型在相平面上求解及周期平均值。 13 差分方程(组)的平衡点及稳定性。 14 一阶差分方程求解。 15 养老保险模型。 16 金融公司支付基金的流动。 17 LESLLIE 模型。 18 泛函极值的欧拉方法。 19 最短路问题的邻接矩阵。 20 最优化问题的一般数学描述。 21 马尔科夫过程的平衡点。 22 零件的预防性更换。 练习集锦 1. 在层次分析法建模中,我们介绍了成对比较矩阵概念,已知矩阵P 是成对比较矩阵 31/52a b P c d e f ?? ??=?????? ,(1)确定矩阵P 的未知元素。 (2)求 P 模最大特征值。 (3)分析矩阵P 的一致性是否可以接受(随机一致性指标RI取0.58)。 2. 在层次分析法建模中,我们介绍了成对比较矩阵概念,已知矩阵P 是三阶成对比较矩阵 322P ? ???=?????? ,(1)将矩阵P 元素补全。 (2)求P 模最 大特征值。 (3)分析矩阵P 的一致性是否可以接受。 3.考虑下表数据 (1)用曲改直的思想确定经验公式形式。 (2)用最小二乘法确定经验公式系数。 4.. 考虑微分方程 (0.2)0.0001(0.4)0.00001dx x xy dt dy y xy dt εε?=--????=-++?? (1)在像平面上解此微分方程组。(2)计算0ε=时的周期平均值。(3)计算0.1ε=时,y 的周期平均值占总量的周期平均值的比例增加了多少? 5考虑种群增长模型 '()(1/1000),(0)200x t kx x x =-= (1)求种群量增长最快的时刻。(2)根据下表数据估计参数k 值。 6. 布均匀,若环保部门及时发现并从某时刻起切断污染源,并更新湖水(此处更新指用新鲜水替换污染水),设湖水更新速率是 3 (m r s 单位:)。 (1) 试建立湖中污染物浓度随时间下降的数学模型? 求出污染物浓度降为控制前的5%所需要的时间。 7. 假如保险公司请你帮他们设计一个险种:35岁起保,每月交费400元,60岁开始领取养老金,每月养老金标准为3600元,请估算该保险费月利率为多少(保留到小数点后5位)? 8. 某校共有学生40000人,平时均在学生食堂就餐。该校共有,,A B C 3 个学生食堂。经过近一年的统计观测发现:A 食堂分别有10%,25%的学生经常去B ,C 食堂就餐,B 食堂经常分别有15%,25%的同学去 一. 1. 1/e 2. 3 3.1 4.e3 5. ∞ 6. 0 7.∞ 8.0 9.1/2 10.0 11.e2c12.不存在13. 1/12 Matlab实验过程: 1.1/exp(1) syms n; f=(1-1/n)^n; limit(f,n,inf) ans = 1/exp(1) 2.3 syms n; f=(n^3+3^n)^(1/n); limit(f,n,inf) ans = 3 3. 1 syms n; f=(1+sin(2*n))/(1-cos(4*n)); limit(f,n,pi/4) ans = 1 4.e^3 syms x; f=(1+cos(x))^(3*sec(x)); limit(f,x,pi/2) ans = exp(3) 5.inf syms x; f=(x^2)*exp(1/(x^2)); limit(f,x,0) ans = Inf 6.0 syms x; f=(x^2-2*x+1)/(x^3-x); limit(f,x,1) ans = 7.inf syms x; f=((2/pi)*atan(x))^x; limit(f,x,+inf) ans = Inf 8.0 syms x y; f=(1-cos(x^2+y^2))/((x^2+y^2)*exp(x^2+y^2)); limit(limit(f,x,0),y,0) ans = 9.1/2 syms x; f=(1-cos(x))/(x*sin(x)); limit(f,x,0) ans = 1/2 10.0 syms x; f=atan(x)/(2*x); limit(f,x,inf) ans = 11.exp(2*c) syms c; f=sym('((x+c)/(x-c))^x'); limit(f,'x',inf) ans = exp(2*c) 12.极限不存在 syms x; f=cos(1/x); limit(f,x,0) ans = limit(cos(1/x), x = 0) 13.1/12 syms x; f=1/(x*log(x)^2)-1/(x-1)^2; limit(f,x,1) ans = 1/12 二.观察函数logbx,当b=1/2,1/3,1/4和b=2,3,4时函数的变化特点,总结logbx的图形特点。 数学建模与数学实验试卷及答案 二、本题10分(写出程序和结果) 蚌埠学院2010—2011学年第二学期 2,x在 [-5 ,5] 区间内的最小值,并作图加以验证。求函数yxe,,,3《数学建模与数学实验》补考试卷答案 f1=inline('x.^2 +exp(-x)-3') 注意事项:1、适用班级:09数学与应用数学本科1,2班 2、本试卷共1页,附答题纸1页。满分100分。 x=fmin(f1,-5,5) 3、考查时间100分钟。 y=f1(x) 4、考查方式:开卷 fplot(f1,[-5,5]) 一、填空:(每空4分,共60分) x = 0.3517,y== -2.1728 123111,,,,, ,,,,三、本题15分(写出程序和结果) 1. 已知,,则A的秩为 3 ,A的特征值为 A,612B,234,,,, ,,,,,215531,,,,,360000xx,,,12,max2.5fxx,,求解:, stxx..250000,,,1212-1.9766 4.4883 + 0.7734i 4.4883 - 0.7734i ,若令 A([1,3],:)= B([2,3],:),则,x,150001,A(2,:)= 6 1 2 ; 解: xxx,,,22,123,model: 2. 的解为 1.25 ,0.25 0.5 ; xxx,,,521,123max=2.5*x1+x2; ,242xxx,,,123,3*x1+x2<=60000; 装订线内不要答题 2*x1+x2<=50000; 3. 将1234521 分解成质因数乘积的命令为_factor(sym(‘1234521’)), 2014-2015学年第一学期数学实验上机试卷 一、上机操作题 1. 画出以下函数图形(要求写出程序和结果): ⑴ 3411()2 1 x x x f x x x ?++≥=? +>求 ⑵22(sin )(1cos )x a t t d y y a t dx =-??=-? 求 ⑶ 2cos (sin )'x y x y =求 ⑷22 2''02 1 (,),x y x y x y u u x y e u u x +==?=?求及 结果:⑴ ⑵ ⑶ ⑷ 4. 计算下列积分(要求写出程序和计算结果): ⑴ 211ln 11x dx x x +--? ⑵2220sec 2tan x dx x π+? (3) 2,02}x x ≤≤≤?? 2其中D={(x,y):y (4) 2221 L dl x y z ++?其中L 为空间螺旋线cos ,sin ,(02,0)x a t y a t z bt t b π===≤≤> . (5) 222()S x y z dS ++?? 其中S 是球2222x y z az ++=. (6) 22S x dydz y dzdx +?? 其中S 为球面2222()()()x a y b z c R -+-+-=的外侧. 结果:⑴ ⑵ ⑶ ⑷ ⑸ ⑹ 5. 判断以下级数的敛散性: ⑴ 1()21n n n n +∞ =+∑ ⑵ 12n n n x n +∞ =∑ 结果:⑴ ⑵ 6. 用两种以上的方法求解下列方程组: 1234234 1242342344331733 x x x x x x x x x x x x x -+-=??-+=-?? ++=??-++=-? 结果: 二、写出解题的思想,计算过程和程序,结果及分析等内容. ⑴在某化学反应里,由实验得到生成物的浓度y 与时间t 有如下关系,求浓度与时间的关系的拟合函数.(30分) ⑵某公司刊登广告:“现有一栋住宅楼,每套只需自备七万元,其余由公司贷款,贷款可分期偿还,每月只需800元,十年还清。”现在的问题是如果一次性付清该付多少(即该房屋的实际价格是多少)?如果贷款,买房人实际借了多少钱?(假设月利率为1%)(40分) 数学实验 期 末 作 业 学号: 班级: 姓名: 1. 求函数x x y 2sin 3=的5阶导数。 2. 使用sparse 命令描述? ? ???? ? ? ??30001 020******* 01020 10003。 3. 求解边值问题 1)0(,0)0(,34,43==+-=+=g f g f dx dg g f dx df 。 4. 建立函数1 2sin )(3-=x x f x 的M-文件,并计算)2(f 和)10(f 。 5. 计算二重积分dy dx x y ??211 0][。 6. 已知数列满足2,11 01=+= +a ka a k k ,求5a ,并要求最后结果分别以小数点后两位和有理数这两种数据显示格式输出。 7. 大约在1500年前,《孙子算经》中就记载了这个有趣的问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”请根据你的思路编程求解。 8. 绘制以下方程所表示的图形。 (1)x x y -=23 2 (2)y z cos =绕z 轴的旋转曲面 (3))40(,) 2sin(sin )]2cos(4[cos )]2cos(4[π< 10.根据中华人民共和国个人所得税法规定:公民的个人工资、薪金应依法缴纳个人所得税。所得税计算办法为:在每个人的月收入中超过2000元以上的部分应该纳税,这部分收入称为应纳税所得额。应纳税所得额实行分段累计税率,按下列税率表计算: 个人所得税税率表: 等级全月应纳税所得额税率(%) 1 不超过500元的部分 5 2 超过500元,不到2000元的部分10 3 超过2000元,不到5000元的部分15 4 超过5000元,不到20000元的部分20 5 超过20000元,不到40000元的部分25 6 超过40000元,不到60000元的部分30 7 超过60000元,不到80000元的部分35 8 超过80000元,不到100000元的部分40 9 超过100000元的部分45 若某人的工资是x元,试建立税款y与收入x之间的M-文件,并要求程序运行时可以告知操作者“please input the number of your wage”。 P59 4.学校共1002名学生,237人住在A 宿舍,333人住在B 宿舍,432人住在C 宿舍。学生要组织一个10人的委员会,使用Q 值法分配各宿舍的委员数。 解:设P 表示人数,N 表示要分配的总席位数。i 表示各个宿舍(分别取A,B,C ),i p 表示i 宿舍现有住宿人数,i n 表示i 宿舍分配到的委员席位。 首先,我们先按比例分配委员席位。 A 宿舍为:A n = 365.21002 10237=? B 宿舍为:B n =323.31002 10333=? C 宿舍为:C n =311.4100210432=? 现已分完9人,剩1人用Q 值法分配。 5.93613 22372 =?=A Q 7.92404 33332 =?=B Q 2.93315 44322 =?=C Q 经比较可得,最后一席位应分给A 宿舍。 所以,总的席位分配应为:A 宿舍3个席位,B 宿舍3个席位,C 宿舍4个席位。 商人们怎样安全过河 由上题可求:4个商人,4个随从安全过河的方案。 解:用最多乘两人的船,无法安全过河。所以需要改乘最多三人乘坐的船。 如图所示,图中实线表示为从开始的岸边到河对岸,虚线表示从河对岸回来。商人只需要按照图中的步骤走,即可安全渡河。总共需要9步。 P60 液体在水平等直径的管内流动,设两点的压强差ΔP 与下列变量有关:管径d,ρ,v,l,μ,管壁粗糙度Δ,试求ΔP 的表达式 解:物理量之间的关系写为为()?=?,,,,,μρ?l v d p 。 各个物理量的量纲分别为 []32-=?MT L p ,[]L d =,[]M L 3-=ρ,[]1-=LT v ,[]L l =,[]11--=MT L μ,Δ是一个无量纲量。 ???? ??????-----=?0310100011110010021113173A 其中0=Ay 解得 ()T y 00012111---=, ()T y 00101102--=, ()T y 01003103--=, ()T y 10000004= 所以 l v d 2111---=ρπ,μρπ112--=v ,p v ?=--313ρπ,?=4π 因为()0,,,,,,=??p l v d f μρ与()0,,,4321=ππππF 是等价的,所以ΔP 的表达式为: ()213,ππψρv p =? 实验十三回归分析 电61 张俊翔2016010891 13.5 (1)首先对于所给数据,分别画出y关于三个因素x1、x2、x3的散点图如下:犯罪率y关于年收入低于5000美元家庭的百分比x1: 犯罪率y关于失业率x2: 犯罪率y关于人口总数x3: 由上图可以看出,y关于x1、x2应该有线性关系,而与x3无明显的相关性。 由此选取y关于x1、x2、x3的线性模型进行拟合。即 Y=β0+β1*x1+β2*x2+β3*x3 首先选取x1、x2作拟合,程序如下: n=20; X=[ones(n,1),x1',x2']; [b,bint,r,rint,s]=regress(y',X); b,bint,s 三者比较可知,最好的模型是只选择x1、x2的情况,此时决定系数最大,剩余方差最小,而且不存在系数的置信区间包含零的情况。 β3的置信区间包含零点,说明x3对y几乎没有什么影响,因此包含3个自变量的模型并没有比只含x1、x2的模型好。 因此选择最终模型是只含x1、x2的模型。 表达式为y=-34.0725+1.2239*x1+4.3989*x2 (3)对最终模型用rcoplot命令观察残差,可得下面的图形: 可见剩余方差和决定系数都有了明显的改进。此时的残差图如下: 这时不再有异常数据点,表达式为:y=-35.7095+1.6023*x1+3.3926*x2 13.10 首先假设风险偏好度对人寿保险额没有二次效应,两个自变量对人寿保险额也没有交互效应,来看已经确定的影响因素的系数: 由于已知经理的年均收入和人寿保险额之间存在着二次关系,而风险偏好度对人寿保险额有线性效应,因此模型为: Y=β0+β1*x1+β2*x2+β3*x1^2 程序如下(数据输入略): n=18; xx1=x1.^2; xx2=x2.^2; xx=x1.*x2; X=[ones(n,1),x1',x2',xx1']; [b,bint,r,rint,s]=regress(y',X); b,bint,s rcoplot(r,rint) 《数学实验》报告 实验名称Matlab三维曲面绘图 学院东凌经济管理学院 专业班级 姓名 学号 2016年3月 一、【实验目的】 1.了解并掌握Matlab三维曲面绘图; 2.进一步掌握绘图程序格式和意义; 3.初步掌握meshgrid, mesh, surf, colordef, colormap, light等使用。 二、【实验任务】 79-7 79-9 三、【实验程序】 79-7 t1=-3:0.1:3; [x1,y1]=meshgrid(t1); z1=x1.^2+y1.^2; subplot(1,2,1);colordef white;light('position',[20,20,5]);colormap(pin k); mesh(x1,y1,z1),title('x^2+3.*y^2'); subplot(1,2,2);colordef white;light('position',[20,20,5]);colormap(pin k); surf(x1,y1,z1),title('x^2+3.*y^2') 79-9 t=-2:0.1:2; [x,y]=meshgrid(t); z1=5-x.^2-y.^2; subplot(1,3,1),mesh(x,y,z1),title('抛物面') z2=3*ones(size(x)); subplot(1,3,2),mesh(x,y,z2),title('平面') r0=abs(z1-z2)<=0.2; zz=r0.*z2;yy=r0.*y;xx=r0.*x; subplot(1,3,3),plot3(xx,yy,zz,'x'),title('交线') 四、【实验结果】 79-1 10级信息《数学建模与数学实验(实践)》任务书 一、设计目的 通过《数学建模与数学实验(实践)》实践环节,掌握本门课程的众多数学建模方法和原理,并通过编写C语言或matlab程序,掌握各种基本算法在计算机中的具体表达方法,并逐一了解它们的优劣、稳定性以及收敛性。在熟练掌握C 语言或matlab语言编程的基础上,编写算法和稳定性均佳、通用性强、可读性好,输入输出方便的程序,以解决实际中的一些科学计算问题。 二、设计教学内容 1线性规划(掌握线性规划的模型、算法以及Matlab 实现)。整数线性规划(掌握整数线性规划形式和解法)。 2微分方程建模(掌握根据规律建立微分方程模型及解法;微分方程模型的Matlab 实现)。 3最短路问题(掌握最短路问题及算法,了解利用最短路问题解决实际问题)。 行遍性问题(了解行遍性问题,掌握其TSP算法)。 4回归分析(掌握一元线性回归和多元线性回归,掌握回归的Matlab实现)。 5计算机模拟(掌握Monte-carlo方法、了解随机数的产生;能够用Monte-carlo 解决实际问题)。 6插值与拟合(了解数据拟合基本原理,掌握用利用Matlab工具箱解决曲线拟合问题)。 三、设计时间 2012—2013学年第1学期:第16周共计一周 目录 一、10级信息《数学建模与数学实验(实践)》任务书 (1) 二、饭店餐桌的布局问题 (3) 摘要 (3) 问题重述 (3) 模型假设 (3) 模型分析 (4) 模型的建立和求解 (4) 模型推广 (9) 参考文献 (9) 三、白酒配比销售问题 (10) 摘要 (10) 问题重述 (11) 问题分析 (12) 模型假设 (12) 符号及变量说明 (12) 模型的建立与求解 (13) 模型的检验 (18) 模型的评价与推广 (19) 附录 (21) 饭店餐桌的布局问题 摘要 饭店餐桌的布局对于一个饭店有着很重要的作用。本文讨论的就是饭店餐桌的布局问题,根据实际需求及规定建立模型,同时考虑餐桌的类型及规格,尤其是餐桌的摆放技巧,保证使饭店能容纳的人数达到最大。根据所需餐桌的数量 数学实验试题 2003.6.22 上午 班级姓名学号得分 说明: (1)第一、二、三题的答案直接填在试题纸上; (2)第四题将数学模型、简要解题过程和结果写在试题纸上;卷面空间不够时,可写在背面; (3)考试时间为90分钟。 一.(10分,每空2分)(计算结果小数点后保留4位有效数字) 地区的月降雨量的置信区间: (2)在90%的置信水平下,A地区的月降雨量是否不小于70(mm)? (3)在90%的置信水平下,A、B地区的月降雨量是否相同? (4)A地区某条河流上半年6个月对应的径流量数据如下(单位:m3):110,184,145,122,165,143。该河流的径流量y与当地的降雨量x的线性回归方程为;若当地降雨量为55mm,该河流的径流量的预测区间为(置信水平取90%)。 二.(10分) (1)(每空1分)给定矩阵,如果在可行域上考虑线性函数,其中,那么的最小值是,最小点为;最大值是,最大点为。 (2)(每空2分)给定矩阵,,考虑二次规划问题,其最优解 为,最优值为,在最优点处起作用约束为。 三.(10分)对线性方程组:,其中A=,b= (1)(3分)当时,用高斯—赛德尔迭代法求解。取初值为, 写出迭代第4步的结果=____________________。 (2)(4分)当时,用Jacobi 迭代法求解是否收敛?__________ , 理由是_________________________________________________ 。 (3)(3分)求最大的c, 使得对任意的,用高斯—赛德尔迭代法求解一 定收敛,则c应为__________。 四.(20分)一个二级火箭的总重量为2800公斤。第一级火箭的重量为1000公斤,其中燃料为800公斤。第一级火箭燃料燃烧完毕后自动脱落,第二级火箭立即继续燃烧。第二级火箭中的燃料为600公斤。假设火箭垂直向上发射,两级火箭中的燃料同质,燃烧率为15公斤/秒,产生的推力为30000牛顿。火箭上升时空气阻力正比于速度的平方,比例系数为0.4公斤/米。 (1)建立第一级火箭燃烧时火箭运行的数学模型,并求第一级火箭脱落时的高度、速度和加速度; (2)建立第二级火箭燃烧时火箭运行的数学模型,并求火箭所有燃料燃烧完毕瞬间的高度、速度、和加速度。 (提示:牛顿第二定律f=ma,其中f为力,m为质量,a为加速度。重力加速度9.8米/平方秒。) 数学实验作业一 对以下问题,编写M文件: (1)用起泡法对10个数由小到大排序. 即将相邻两个数比较,将小的调到前头. 解: 代码如下: zuoye1 clear all;clc; a=[7 2 1 0 9 4 5 -3 8 6]; n=length(a); for ii=1:n-1 if a(ii+1)>=a(ii) t1=a(ii); a(ii)=a(ii+1); a(ii+1)=t1; end for jj=1:n-1 if a(jj+1)>=a(jj) t2=a(jj); a(jj)=a(jj+1); a(jj+1)=t2; end end end a 运行结果显示如下: a = 9 8 7 6 5 4 2 1 0 -3 (2)有一个 矩阵,编程求出其最大值及其所处的位置. 解: 代码如下:zuoye2.m clear; clc; a=[1 2 3 4 5 3 4 5 6 9 6 7 8 8 0 1 2 4 5 6] max=-1; flage1=0; flage2=0 for i=1:4 for j=1:5 if (a(i,j)>max) t=max; max=a(i ,j); a(i,j)=t; flage1=i; flage2=j ; end end end max flage1 flage2 运行结果显示如下: a = 1 2 3 4 5 3 4 5 6 9 6 7 8 8 0 1 2 4 5 6 flage2 = max = 45′ 9 flage1 = 2 flage2 = 5 结果: (3)编程求∑=20 1 !n n 。 解: 代码如下:zuoye3.m clear; clc; sum=0; for i=2:11 sum=sum+gamma(i); end sum 电子科技大学二零零八到二零零九学年第二学期期末考试《数学实验》课程考试题A卷(120分钟) 考试形式:闭卷考试日期:2009年7月8日 一、单项选择题(20分) 1、三阶幻方又称为九宫图,提取三阶幻方矩阵对角元并构造对角阵用( ) (A) diag(magic(3)); (B) diag(magic); (C) diag(diag(magic(3))); (D) diag(diag(magic))。 2、MATLAB命令P=pascal(3)将创建三阶帕斯卡矩阵,max(P)的计算结果是( ) (A) 1 2 3 (B) 1 2 1 (C) 3 6 10 (D) 1 3 6 3、命令J=*1;1;1+**1,2,3+;A=j+j’-1将创建矩阵( ) (A) 123 234 345 ?? ?? ?? ?? ?? ; (B) 234 345 456 ?? ?? ?? ?? ?? (C) 123 123 123 ?? ?? ?? ?? ?? (D) 111 222 333 ?? ?? ?? ?? ?? 4、data=rand(1000,2);x=data(:,1);y=data(:,2);II=find(y 成都信息工程大学 《数学建模与数学实验》上机实验报告 专业信息与计算科学班级姓名学号 实验日期成绩等级教师评阅日期 [问题描述] 下表给出了某一海域以码为单位的直角坐标Oxy 上一点(x,y)(水面一点)以英尺为单位的水深z,水深数据是在低潮时测得的,船的吃水深为5英尺,问在矩形区域(75,200)x (-50,150)里那些地方船要避免进入。 [模型] 设水面一点的坐标为(x,y,z),用基点和插值函数在矩形区域(75,200)*(-50,150)内做二维插值、三次插值,然后在作出等高线图。 [求解方法] 使用matlab求解: M文件:water.m x=[129 140 103.5 88 185.5 195 105.5 157.5 107.5 77 81 162 162 117.5]; y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5]; z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9]; cx = 75:0.5:200; cy = -50:0.5:150; [cx,cy]=meshgrid(cx,cy); 作出曲面图: 代码如下: >> water >> cz=griddata(x,y,z,cx,cy,'cubic'); >> meshz(cx,cy,cz) >> xlabel('X'),ylabel('Y'),zlabel('Z') >> 作出等高线图: 代码如下: >> water >> cz=griddata(x,y,z,cx,cy,'cubic'); >> figure(2) >> contour(cx,cy,cz,[-5,-5],'r') >> hold on >> plot(x,y,'*') >> xlabel('X'),ylabel('Y') [结果]数学建模与数学实验习题
北理工数学实验作业
数学建模与数学实验试卷及答案
数学实验期末考试上机考试
山东建筑大学数学实验期末作业matlab
数学建模与数学实验课后习题答案
数学实验 作业10
最新版北京科技大学第三次数学实验报告
《数学建模与数学实验》课程论文
大学数学实验—期末考试试题6
数学实验作业一
电子科技大学《数学实验》2008-2009学年期末试题(含答案)
《数学建模与数学实验》上机实验报告