
一、反比例函数真题与模拟题分类汇编(难题易错题)
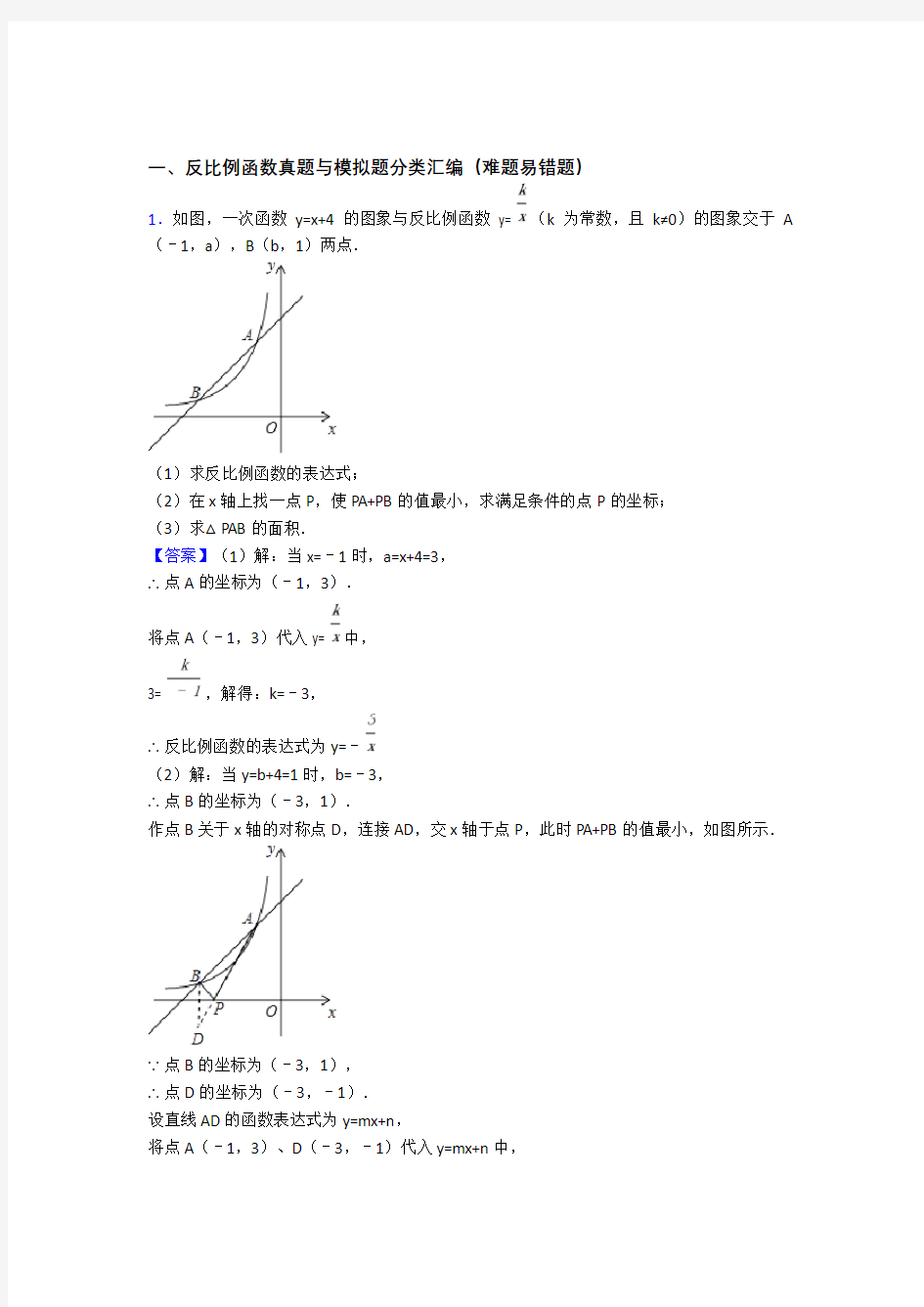
1.如图,一次函数y=x+4的图象与反比例函数y= (k为常数,且k≠0)的图象交于A (﹣1,a),B(b,1)两点.
(1)求反比例函数的表达式;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;
(3)求△PAB的面积.
【答案】(1)解:当x=﹣1时,a=x+4=3,
∴点A的坐标为(﹣1,3).
将点A(﹣1,3)代入y= 中,
3= ,解得:k=﹣3,
∴反比例函数的表达式为y=﹣
(2)解:当y=b+4=1时,b=﹣3,
∴点B的坐标为(﹣3,1).
作点B关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB的值最小,如图所示.
∵点B的坐标为(﹣3,1),
∴点D的坐标为(﹣3,﹣1).
设直线AD的函数表达式为y=mx+n,
将点A(﹣1,3)、D(﹣3,﹣1)代入y=mx+n中,
,解得:,
∴直线AD的函数表达式为y=2x+5.
当y=2x+5=0时,x=﹣,
∴点P的坐标为(﹣,0)
(3)解:S△PAB=S△ABD﹣S△BDP= ×2×2﹣ ×2× =
【解析】【分析】(1)由一次函数图象上点的坐标特征可求出点A的坐标,根据点A的坐标利用待定系数法,即可求出反比例函数的表达式;(2)利用一次函数图象上点的坐标特征可求出点B的坐标,作点B关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB的值最小,由点B的坐标可得出点D的坐标,根据点A、D的坐标利用待定系数法,即可求出直线AB的函数表达式,再由一次函数图象上点的坐标特征即可求出点P的坐标;(3)根据三角形的面积公式结合S△PAB=S△ABD﹣S△BDP,即可得出结论.
2.如图直角坐标系中,矩形ABCD的边BC在x轴上,点B,D的坐标分别为B(1,0),D(3,3).
(1)点C的坐标________;
(2)若反比例函数y= (k≠0)的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接EF,在直线AB上找一点P,
使得S△PEF= S△CEF,求点P的坐标.
【答案】(1)(3,0)
(2)解:∵AB=CD=3,OB=1,
∴A的坐标为(1,3),又C(3,0),
设直线AC的解析式为y=ax+b,
则,解得:,
∴直线AC的解析式为y=﹣ x+ .
∵点E(2,m)在直线AC上,
∴m=﹣ ×2+ = ,
∴点E(2,).
∵反比例函数y= 的图象经过点E,
∴k=2× =3,
∴反比例函数的解析式为y=
(3)解:延长FC至M,使CM= CF,连接EM,则S△EFM= S△EFC, M(3,﹣0.5).
在y= 中,当x=3时,y=1,
∴F(3,1).
过点M作直线MP∥EF交直线AB于P,则S△PEF=S△MEF.
设直线EF的解析式为y=a'x+b',
∴,解得,
∴y=﹣ x+ .
设直线PM的解析式为y=﹣ x+c,
代入M(3,﹣0.5),得:c=1,
∴y=﹣ x+1.
当x=1时,y=0.5,
∴点P(1,0.5).
同理可得点P(1,3.5).
∴点P坐标为(1,0.5)或(1,3.5).
【解析】【解答】解:(1)∵D(3,3),
∴OC=3,
∴C(3,0).
故答案为(3,0);
【分析】(1)由D的横坐标为3,得到线段OC=3,即可确定出C的坐标;(2)由矩形的对边相等,得到AB=CD,由D的纵坐标确定出CD的长,即为AB的长,再由B的坐标确定出OB的长,再由A为第一象限角,确定出A的坐标,由A与C的坐标确定出直线AC的解析式,将E坐标代入直线AC解析式中,求出m的值,确定出E的坐标,代入反比例解
析式中求出k的值,即可确定出反比例解析式;(3)延长FC至M,使CM=CF,连接
EM,则S△EFM=S△EFC, M(3,﹣0.5).求出F(3,1),过点M作直线MP∥EF交直线AB于P,利用平行线间的距离处处相等得到高相等,再利用同底等高得到S△PEF=S△MEF.此时直线EF与直线PM的斜率相同,由F的横坐标与C横坐标相同求出F 的横坐标,代入反比例解析式中,确定出F坐标,由E与F坐标确定出直线EF斜率,即为直线PM的斜率,再由M坐标,确定出直线PM解析式,由P横坐标与B横坐标相同,将B横坐标代入直线PM解析式中求出y的值,即为P的纵坐标,进而确定出此时P的坐标.
3.平面直角坐标系xOy中,已知函数y1= (x>0)与y2=﹣(x<0)的图象如图所示,
点A、B是函数y1= (x>0)图象上的两点,点P是y2=﹣(x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(1)求△APQ的面积;
(2)若△APQ是等腰直角三角形,求点Q的坐标;
(3)若△OAB是以AB为底的等腰三角形,求mn的值.
【答案】(1)解:过点P、A、Q分别作PM x轴交x轴于点M,PN x轴交x轴于点N,QR AP轴交AP轴于点R,则四边形APMN、四边形PMQR、四边形ARQN是矩形,如图所示:
∵点A的横坐标为m,且在函数上,AP∥x轴,且点P在函数上,
∴点A(m, ),点P(-m, ),
∴MN=m-(-m)=2m,PM= ,
∴S矩形PMNA=2m╳ =8,
∵四边形PMQR、四边形ARQN是矩形,
∴S△PQM=S△PRQ, S△ANQ=S△ARQ,
∴S△APQ=S△PRQ+ S△ARQ= S矩形PMNA=4
(2)解:当PQ x轴时,则PQ=,,AP=2m,
∵PQ=AP
∴2m= ,
∴m=
∴ ,
当PQ=AQ时,则
(3)解:∵△OAB是以AB为底的等腰三角形,
∴OA=OB,
∵A(m, ),B(n, ),
∴
∴mn=4.
【解析】【分析】(1)过点P、A、Q分别作PM ⊥ x轴交x轴于点M,PN ⊥ x轴交x轴于点N,QR ⊥ AP轴交AP轴于点R,则四边形APMN、四边形PMQR、四边形ARQN是矩形,根据点A的横坐标为m,利用函数解析式表示出点A的坐标和点P的坐标,最后用三角形的面积公式即可得出结论。
(2)分情况讨论:当PQ=AP和当PQ=AQ时,利用等腰直角三角形和AP∥x轴,建立方程求解即可;
(3)利用等腰三角形的两腰相等建立方程,即可得出结论。
4.如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折现”)
(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y= 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
【答案】(1)解:如图1,新函数的性质:1.函数的最小值为0;2.函数图象的对称轴为直线x=3.
由题意得,点A的坐标为(-3,0),分两种情况:
①当x-3时,y=x+3;
②当x<-3时,设函数解析式为y=kx+b,
在直线y=x+3中,当x=-4时,y=-1,
则点(-4,-1)关于x轴的对称点为(-4,1),
把点(-4,1),(-3,0),代入y=kx+b中,
得:,
解得:,
∴y=-x-3.
综上,新函数的解析式为y=.
(2)解:如图2,
①∵点C(1,a)在直线y=x+3上,
∴a=4,
∵点C(1,4)在反比例函数y=上,
∴k=4,
∴反比例函数的解析式为y=.
∵点D是线段AC上一动点,
∴设点D的坐标为(m,m+3),且-3 ∵DP∥x轴,且点P在双曲线上, ∴点P的坐标为(,m+3), ∴PD=-m, ∴S△PAD=(-m)(m+3)=m2-m+2=(m+)2+, ∵a=<0, ∴当m=时,S有最大值,最大值为, 又∵-3<<1, ∴△PAD的面积的最大值为. ②在点D的运动的过程中,四边形PAEC不能为平行四边形,理由如下: 当点D为AC的中点时,其坐标为(-1,2),此时点P的坐标为(2,2),点E的坐标为(-5,2), ∵DP=3,DE=4, ∴EP与AC不能互相平分, ∴四边形PAEC不能为平行四边形. 【解析】【分析】(1)根据一次函数的性质,结合函数图象写出新函数的两条性质;利用待定系数法求新函数解析式,注意分两种情况讨论;(2)①先求出点C的坐标,再利用待定系数法求出反比例函数解析式,设出点D的坐标,进而得到点P的坐标,再根据三角形的面积公式得出函数解析式,利用二次函数的性质求解即可;②先求出A的中点D的坐标,再计算DP、DE的长度,如果对角线互相平分,则能成为平行四边形,如若对角线不互相平分,则不能成为平行四边形. 5.如图,一次函数y=kx+b(k≠0)与反比例函数y= (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C. (1)求一次函数与反比例函数的解析式; (2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值; (3)求△ABC的面积. 【答案】(1)解:∵反比例函数经过点D(﹣2,﹣1), ∴把点D代入y= (m≠0), ∴﹣1= , ∴m=2, ∴反比例函数的解析式为:y= , ∵点A(1,a)在反比例函数上, ∴把A代入y= ,得到a= =2, ∴A(1,2), ∵一次函数经过A(1,2)、D(﹣2,﹣1), ∴把A、D代入y=kx+b (k≠0),得到:,解得:, ∴一次函数的解析式为:y=x+1 (2)解:如图:当﹣2<x<0或x>1时,一次函数的值大于反比例函数的值 (3)解:过点A作AE⊥x轴交x轴于点E, ∵直线l⊥x轴,N(3,0),∴设B(3,p),C(3,q), ∵点B在一次函数上,∴p=3+1=4, ∵点C在反比例函数上,∴q= , ∴S△ABC= BC?EN= ×(4﹣)×(3﹣1)= . 【解析】【分析】由反比例函数经过点D(-2,-1),即可求得反比例函数的解析式;然后求得点A的坐标,再利用待定系数法求得一次函数的解析式; 结合图象求解即可求得x在什么范围内,一次函数的值大于反比例函数的值; 首先过点A作AE⊥x轴交x轴于点E,由直线l与x轴垂直于点N(3,0),可求得点E,B,C的坐标,继而求得答案. 6.如图,在矩形OABC中,OA=6,OC=4,F是AB上的一个动点(F不与A,B重合),过 点F的反比例函数的图象与BC边交于点E. (1)当F为AB的中点时,求该函数的解析式; (2)当k为何值时,△EFA的面积最大,最大面积是多少? 【答案】(1)解:∵在矩形OABC中,OA=6,OC=4,∴B(6,4), ∵F为AB的中点,∴F(6,2), 又∵点F在反比例函数(k>0)的图象上,∴k=12, ∴该函数的解析式为y= (x>0) (2)解:由题意知E,F两点坐标分别为E(,4),F(6,), ∴, = = = = , ∴当k=12时,S有最大值.S最大=3 【解析】【分析】)当F为AB的中点时,点F的坐标为(3,1),由此代入求得函数解析式即可;根据图中的点的坐标表示出三角形的面积,得到关于k的二次函数,利用二次函数求出最值即可. 7.如图,一次函数的图象与反比例函数的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点). (1)利用图中条件,求反比例函数的解析式和m的值; (2)求△DOC的面积. (3)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由. 【答案】(1)解:将C(1,4)代入反比例函数解析式可得:k=4,则反比例函数解析式为: , 将D(4,m)代入反比例函数解析式可得:m=1 (2)解:根据点C和点D的坐标得出一次函数的解析式为:y=-x+5 则点A的坐标为(0,5),点B的坐标为(5,0) ∴S△DOC=5×5÷2-5×1÷2-5×1÷2=7.5 (3)解:双曲线上存在点P(2,2),使得S△POC=S△POD,理由如下: ∵C点坐标为:(1,4),D点坐标为:(4,1), ∴OD=OC=, ∴当点P在∠COD的平分线上时,∠COP=∠POD,又OP=OP, ∴△POC≌△POD, ∴S△POC=S△POD. ∵C点坐标为:(1,4),D点坐标为:(4,1), 可得∠COB=∠DOA, 又∵这个点是∠COD的平分线与双曲线的y=交点, ∴∠BOP=∠POA, ∴P点横纵坐标坐标相等, 即xy=4,x2=4, ∴x=±2, ∵x>0, ∴x=2,y=2, 故P点坐标为(2,2),使得△POC和△POD的面积相等 利用点CD关于直线y=x对称,P(2,2)或P(?2,?2). 答:存在,P(2,2)或P(-2,-2) 【解析】【分析】(1)观察图像,根据点C的坐标可求出函数解析式及m的值。 (2)利用待定系数法,由点D、C的坐标求出直线CD的函数解析式,再求出直线CD与两坐标轴的交点A、B的坐标,然后利用S△DOC=S△AOB-S△BOC-S△AOD,利用三角形的面积公式计算可解答。 (3)双曲线上存在点P,使得S△POC=S△POD,这个点就是∠COD的平分线与双曲线的y=交点,易证△POC≌△POD,则S△POC=S△POD,可得出点P点横纵坐标坐标相等,利用反比例函数解析式,建立关于x的方程,就可得出点P的坐标,利用对称性,可得出点P的另一个坐标,即可得出答案。 8.在平面直角坐标系xOy中,对于双曲线y= (m>0)和双曲线y= (n>0),如果m=2n,则称双曲线y= (m>0)和双曲线y= (n>0)为“倍半双曲线”,双曲线y= (m>0)是双曲线y= (n>0)的“倍双曲线”,双曲线y= (n>0)是双曲线y= (m>0)的“半双曲线”, (1)请你写出双曲线y= 的“倍双曲线”是________;双曲线y= 的“半双曲线”是________; (2)如图1,在平面直角坐标系xOy中,已知点A是双曲线y= 在第一象限内任意一点,过点A与y轴平行的直线交双曲线y= 的“半双曲线”于点B,求△AOB的面积; (3)如图2,已知点M是双曲线y= (k>0)在第一象限内任意一点,过点M与y轴 平行的直线交双曲线y= 的“半双曲线”于点N,过点M与x轴平行的直线交双曲线y= 的“半双曲线”于点P,若△MNP的面积记为S△MNP,且1≤S△MNP≤2,求k的取值范围. 【答案】(1)y= ;y= (2)解:如图1, ∵双曲线y= 的“半双曲线”是y= , ∴△AOD的面积为2,△BOD的面积为1, ∴△AOB的面积为1 (3)解:解法一:如图2, 依题意可知双曲线的“半双曲线”为, 设点M的横坐标为m,则点M坐标为(m,),点N坐标为(m,),∴CM= ,CN= . ∴MN= ﹣ = . 同理PM=m﹣ = . ∴S△PMN= MN?PM= ∵1≤S△PMN≤2, ∴1≤ ≤2. ∴4≤k≤8, 解法二:如图3, 依题意可知双曲线的“半双曲线”为, 设点M的横坐标为m,则点M坐标为(m,),点N坐标为(m,),∴点N为MC的中点,同理点P为MD的中点. 连接OM, ∵, ∴△PMN∽△OCM. ∴. ∵S△OCM=k, ∴S△PMN= . ∵1≤S△PMN≤2, ∴1≤ ≤2. ∴4≤k≤8. 【解析】【解答】解:(1)由“倍双曲线”的定义 ∴双曲线y= ,的“倍双曲线”是y= ; 双曲线y= 的“半双曲线”是y= . 故答案为y= ,y= ; 【分析】(1)直接利用“倍双曲线”的定义即可;(2)利用双曲线的性质即可;(3)先利用双曲线上的点设出M的横坐标,进而表示出M,N的坐标;方法一、用三角形的面积公式建立不等式即可得出结论;方法二、利用相似三角形的性质得出△PMN的面积,进而建立不等式即可得出结论. 9.如图,在平面直角坐标系中,直线AB与x轴交于点B、与y轴交于点A,与反比例函数y= 的图象在第二象限交于C,CE⊥x轴,垂足为点E,tan∠ABO= ,OB=4,OE=2. (1)求反比例函数的解析式; (2)若点D是反比例函数图象在第四象限内的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO,求点D的坐标. (3)若动点D在反比例函数图象的第四象限上运动,当线段DC与线段DB之差达到最大时,求点D的坐标. 【答案】(1)解:∵tan∠ABO= , ∴ = ,且OB=4, ∴OA=2, ∵CE⊥x轴,即CE∥AO, ∴△AOB∽△CEB, ∴ = ,即 = ,解得CE=3, ∴C(﹣2,3), ∴m=﹣2×3=﹣6, ∴反比例函数解析式为y=﹣ (2)解:设D(x,﹣), ∵D在第四象限, ∴DF=x,OF= , ∴S△DFO= DF?OF= x× =3, 由(1)可知OA=2, ∴AF=x+ , ∴S△BAF= AF?OB= (x+ )×4=2(x+ ), ∵S△BAF=4S△DFO, ∴2(x+ )=4×3,解得x=3+ 或x=3﹣, 当x=3+ 时,﹣的值为3﹣, 当x=3﹣时,﹣的值为3+ , ∵D在第四象限, ∴x=3﹣不合题意,舍去, ∴D(3+ ,3﹣) (3)解:∵D在第四象限, ∴在△BCD中,由三角形三边关系可知CD﹣CB≤BC,即当B、C、D三点共线时,其差最大, 设直线AB解析式为y=kx+b, 由题意可得,解得, ∴直线AB解析式为y=﹣ x+2, 联立直线AB和反比例函数解析式可得,解得或 (舍去), ∴D(6,﹣1), 即当线段DC与线段DB之差达到最大时求点D的坐标为(6,﹣1) 【解析】【分析】(1)由条件可求得OA,由△AOB∽△CEB可求得CE,则可求得C点坐标,代入反比例函数解析式可求得m的值,可求得反比例函数解析式;(2)设出D的坐标,从而可分别表示出△BAF和△DFO的面积,由条件可列出方程,从而可求得D点坐标;(3)在△BCD中,由三角形三边关系可知CD﹣CB≤BC,当B、C、D三点共线时,其差最大,联立直线BC与反比例函数解析式可求得D点坐标. 10.如图,在菱形ABCD中,, ,点E是边BC的中点,连接DE,AE. (1)求DE的长; (2)点F为边CD上的一点,连接AF,交DE于点G,连接EF,若 , ①求证:△△; ②求DF的长. 【答案】(1)解:连结BD (2)解:① ② 【解析】【分析】(1)连结BD ,根据菱形的性质及等边三角形的判定方法首先判定出△CDB是等边三角形,根据等边三角形的性质得出DE⊥BC,CE=2,然后利用勾股定理算出DE的长; (2)①首先判断出△AGD∽△EGF,根据相似三角形对应边成比例得出,又∠AGE=∠DGF,故△AGE∽△DGF; ②根据相似三角形的性质及含30°直角三角形的边之间的关系及勾股定理得出EF的长,然后过点E作EH⊥DC于点H,在Rt△ECH中,利用勾股定理算出FH的长,从而根据线段的和差即可算出答案. 11.已知抛物线与轴的两个交点间的距离为2. (1)若此抛物线的对称轴为直线,请判断点(3,3)是否在此抛物线上? (2)若此抛物线的顶点为(S,t),请证明; (3)当时,求的取值范围 【答案】(1)解:抛物线的对称轴为直线,且抛物线与轴的两个交点间的距离为2,可得抛物线与轴的两个交点为(0,0)和(2,0), 所以抛物线的解析式为与 当时, 所以点(3,3)在此抛物线上 . (2)解:抛物线的顶点为,则对称轴为直线,且抛物线与轴的两个交点间的距离为2, 可得抛物线与轴的两个交点为(,,0)和(,0) 所以抛物线的解析式为与 由得 所以; (3)解:由(2)知即整理得 由对称轴为直线,且二次项系数 可知当时,b的随a的增大而增大 当a=10时,得 当a=20时,得 所以当时, 【解析】【分析】(1)根据已知条件得出两个交点坐标,利用待定系数法求出解析式,然后验证点(3,3)是否在这条抛物线上即可;(2)先确定对称轴为直线,再得出与x 轴的两交点坐标为(,0)和(,0),再利用待定系数法求出解析式的顶点 式可得解;(3)把t=-1代入顶点坐标公式,得到二次函数解析式,根据函数的增减性分别计算a=10和20时b的值从而得解. 12.已知,抛物线的图象经过点,. (1)求这个抛物线的解析式; (2)如图1,是抛物线对称轴上一点,连接,,试求出当的值最小时点的坐标; (3)如图2,是线段上的一点,过点作轴,与抛物线交于点,若直线把分成面积之比为的两部分,请求出点的坐标. 【答案】(1)解:将,的坐标分别代入. 得 解这个方程组,得, 所以,抛物线的解析式为 (2)解:如图1,由于点、关于轴对称,所以连接,直线与轴的交点即为所求的点, 由,令,得, 解得,, 点的坐标为, 又, 易得直线的解析式为:. 当时,, 点坐标 (3)解:设点的坐标为, 所以所在的直线方程为.那么,与直线的交点坐标为,