第一部分:微积分部分
I 。一元函数微积分部分
§1 曲线的渐近线
函数曲线的渐近线对于作那些可以延伸到无穷远的函数的图形,把握图形的变化趋势具有重要的作用,曲线的渐近线分为:垂直,水平,斜渐近线(水平渐近线是其特殊情况),我们先给出它们的统一定义,然后分别给出计算方法。
关于函数的渐近线一般教科书通常只给出水平及垂直渐近线的求法,但曲线的斜渐近线通常也是研究生考试的必考内容,这里给出了斜渐近线的一般定义及求法
一。渐近线的统一定义:
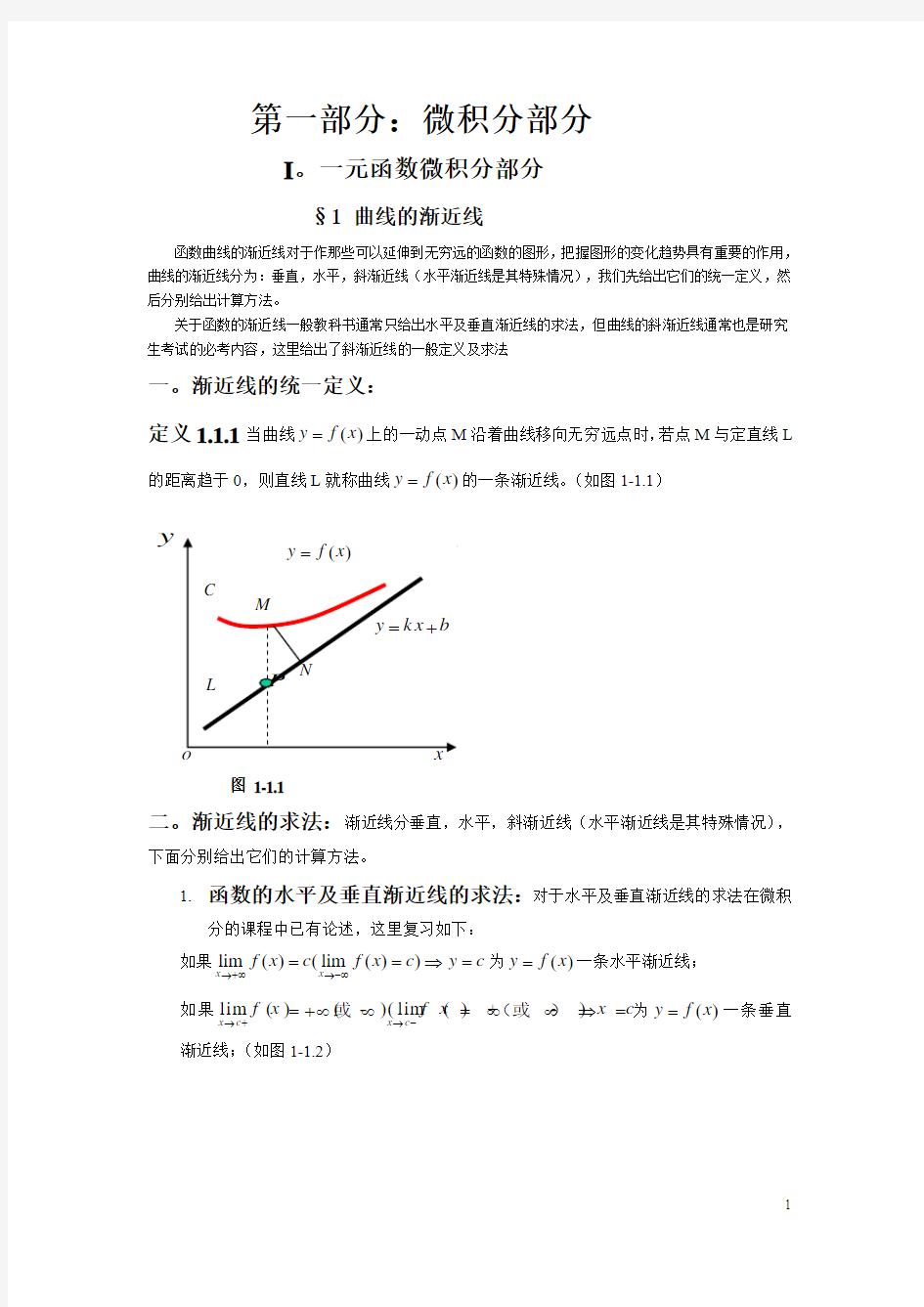
定义1.1.1当曲线()y f x =上的一动点M 沿着曲线移向无穷远点时,若点M 与定直线L
的距离趋于0,则直线L 就称曲线()y f x =的一条渐近线。(如图1-1.1)
图 1-1.1
二。渐近线的求法:渐近线分垂直,水平,斜渐近线(水平渐近线是其特殊情况),
下面分别给出它们的计算方法。
1.
函数的水平及垂直渐近线的求法:对于水平及垂直渐近线的求法在微积
分的课程中已有论述,这里复习如下:
如果lim ()(lim ())x x f x c f x c y c →+∞
→-∞
==?=为()y f x =一条水平渐近线;
如果lim ()(-)(lim ()+-)x c x c f x f x x c →+
→-
=+∞∞=∞∞?=或
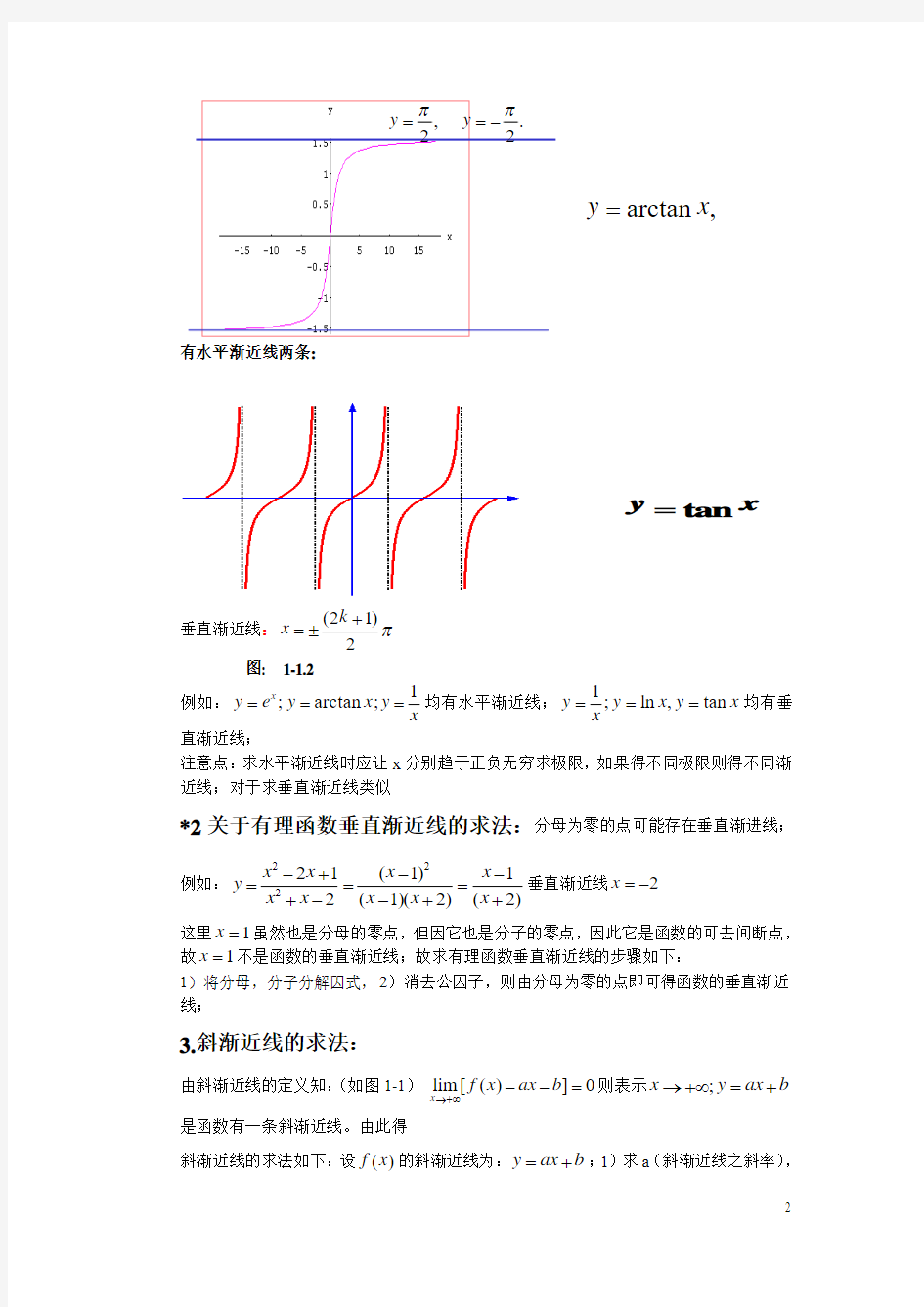
(或)为()y f x =一条垂直渐近线;(如图1-1.2)
y
有水平渐近线两条:
垂直渐近线:(21)
2
k x π+=± 图: 1-1.2
例如:1;arctan ;x
y e y x y x ===
均有水平渐近线;1
;ln ,tan y y x y x x
===均有垂直渐近线;
注意点:求水平渐近线时应让x 分别趋于正负无穷求极限,如果得不同极限则得不同渐近线;对于求垂直渐近线类似
*2关于有理函数垂直渐近线的求法:分母为零的点可能存在垂直渐进线;
例如:22221(1)1
2(1)(2)(2)
x x x x y x x x x x -+--===
+--++垂直渐近线2x =- 这里1x =虽然也是分母的零点,但因它也是分子的零点,因此它是函数的可去间断点,故1x =不是函数的垂直渐近线;故求有理函数垂直渐近线的步骤如下:
1)将分母,分子分解因式,2)消去公因子,则由分母为零的点即可得函数的垂直渐近线;
3.斜渐近线的求法:
由斜渐近线的定义知:(如图1-1) lim [()]0x f x ax b →+∞
--=则表示;x y ax b
→+∞=+是函数有一条斜渐近线。由此得
斜渐近线的求法如下:设()f x 的斜渐近线为:y ax b =+;1)求a (斜渐近线之斜率),
arctan ,
y x =,.
2
2
y y π
π
=
=-
tan y x
=
因()lim [()]0lim
()()lim lim lim 0lim x x x x x x f x ax b
f x ax b x f x ax b f x a x x x x →+∞→+∞→+∞→+∞→+∞→+∞----=?=--=?= (1.1.1)
2)求出a 后再由lim [()]x f x ax b →+∞
-= (1.1.2)
(斜渐近线之截距)即可求出一条斜渐近线, 注:1). 如果 ()
lim x f x x
→+∞
不存在或为无穷大,则表示这时无斜渐近线。 2).如果()
lim
0x f x x
→+∞
=,lim [()]lim ()x x f x ax f x b →+∞→+∞-==有水平渐近线y=b ,故在求
斜渐近线时顺便可求出水平渐近线。
3)和求垂直,水平渐近线类似,求斜渐近线时也应分别就;x x →+∞→-∞分别讨论。
4.例题:
例1.1.1 求1
)
3)(2(2)(-+-=
x x x x f 的渐近线.
解 易见函数)(x f 的定义域为).,1()1,(+∞-∞ ,)(lim 1
-∞=+→x f x ,)(lim 1
+∞=-
→x f x 1=∴x 是曲线的垂直渐近线.
又x
x f x )
(lim
∞
→ )1()3)(2(2lim -+-=∞→x x x x x ,2= ???
???--+-∞→x x x x x 21)3)(2(2lim 1)1(2)3)(2(2lim
---+-=∞
→x x x x x x ,4= 42+=∴x y 是曲线的一条斜渐近线.,无水平渐近线(为什么)
三。考研真题:
1.曲线 的斜渐近线的方程为—
2.曲线 的斜渐近线的方程为—
*3曲线
的斜渐近线的方程为—
4 的水平渐近线为—— *5. 的渐近线的条数为——
A 0; B. 1; C. 2; D. 3
1
(21)y x e =-2
21
x y x =+32
)y =52cos x y x x +=-1ln(1)x
y e x =++
答案与提示:1). Y=2x+1(无垂直渐近线);2) (垂直:12
x =-
) 3) (垂直:x=0)
( 3)的提示:计算y-ax=b 时既可用罗比达法则,也可采取折分的方法)
4) 垂直:设a 为满足5x-2cosx=0的点 ,则垂直渐近线为:x=a
* 5)D ,提示;
有一条垂直渐近线;x=0;一条水平渐近线;y=0(x →-∞); 一条斜渐近线:y=x (x →+∞)
§2. 定积分的应用
定积分是求某种总量的数学模型,它在几何学、物理学、经济学、社会学等方面都有着广泛的应用,显示了它的巨大魅力. 也正是这些广泛的应用,推动着积分学的不断发展和完善. 因此,在学习的过程中,我们不仅要掌握计算某些实际问题的公式,更重要的还在于深刻领会用定积分解决实际问题的基本思想和方法——微元法,不断积累和提高数学的应用能力.
一.定积分的元素法:在应用学科中广泛采用的将所求量
U (总量)表示为定积分的
方法——微元法,1.元素法的步骤: 元素法的主要步骤如下:
1)由分割写出微元 根据具体问题,选取一个积分变量,例如x 为积分变量,并确定它的变化区间【a ,b 】,任取【a ,b 】的区间微元【x ,x+dx 】求出相应于这个区间微元上部分量△U 的近似值,即求出所求总量U 的一个区间微元,并将其表示为: 2)、由微元写出积分 根据 写出表示总量U 的定积分
应用微元法解决实际问题时,应注意如下两点:
1) 所求总量U 关于区间【a ,b 】应具有可加性,即如果把区间【a ,b 】分成许多部分区间, 则相应地U 分成许多部分量, 而总量U 等于所有部分量△U 之和. 这一要求是由定积分概念本身所决定的;
2)使用微元法的关键是正确给出部分量△U 的近似表达式 即使得
在通常情况下,要检验 是否为dx 的高阶无
穷小并非易事,因此,在实际应用要注意 的合理性.
2.定积分的意义
1).定积分 可看作一个“高级”的加法—即求和与取极限;即将“微元”在区间[a,b]上进行“累积”
这就是“元素法”的思想,因此在用元素法计算定积分时关键在于找准“元素”及“累积”的区间[a,b]
2)这种加法是建立在“平行”意义上的,如果是非平行意义,例如非平行力,则要进行“平行
1124y x =-3
2
y x =+1
5
y =()dU f x dx
=()dU f x dx =()b b
a a U dU f x dx
==??
()f x dx ()f x dx dU U =≈?()U f x dx ?-()dU f x dx =()b a
f x dx ?
化”处理。
3).要注意定积分的应用是有范围的:其总量必须与某直线段(区间)有关,否则便不能用定积分处理。
3.元素法的应用 1)几何应用
平面图形面积;体积(旋转体体积,平行截面积已知体积),
2)物理应用:(功;水压力;引力等)
二。利用定积分计算体积
1. 旋转体的体积: 1)绕x 轴旋转
体积微元dx x f dV 2)]([π=, 旋转体的体积.)]([2?=b
a dx x f V π (1.1.3)
2)绕y 轴旋转
体积微元2
[()]dV y dy π?=旋转体的体积2[()].d
c
V y dy π
?=?
(1.1.4)
2.平行截面面积为已知的立体的体积
体积微元,)(dx x A dV = 所求立体的体积 .)(?=b
a dx x A V (1.1.5)
注:绕y 轴旋转还可用所谓的“柱壳法”:设由函数y=f(x),直线:x=a ,x=b ,x 轴围成的曲边梯形绕y 轴旋转:取区间微元:【x ,x+dx 】其对应的以dx 为底,f(x)为高的矩形绕 Y 轴旋转的体积微元为dv=2()xf x dx π,故绕y 轴旋转的体积为:
2()b
y a
V xf x dx π=? (1.1.6)
图1-1.3
例1.1..2.求sin ,(0)y x x π=≤≤x 轴所围曲边梯形绕y 轴旋转的旋转体体积
解1.如应用公式(1.2。1)则化成两个曲边梯形绕y 轴旋转体积之差12V V -(运算麻烦)
2.应用公式(1.2.4)20
2()2sin 2y V xf x dx x xdx π
π
πππ===?
?
例1.1.3.计算摆线(sin ),(1cos )x a t t y a t =-=-相应于02t π≤≤的一拱,直线y=0所围
成的图形绕x ,y 轴旋转所得旋转体体积。
解:方法1.绕y 轴旋转:222233
2
10
()()6a
a
y V x y dy x y dy a πππ=
-=??(运算麻烦) 方法2.应用公式(1.2.4)得223330
22(sin )(1cos )(sin )6a y V xydx a t t t d t t a ππ
π
ππ==---=?
?
三。 物理应用:
1.功:由定积分的引入可知,沿x 轴方向作用于物体上连续变化的力()y x ?=使物体从点
x a =移动到点x b =时,它所作的功为
()d b
a
W x x ?=
?. (功元素()dw x dx ?=)
注:具体计算作功一类的问题时,不可死套公式,而应具体分析用元素法求解。
例1.1.4 把一个带q +电量的点电荷放在r 轴上坐标原点处,它产生一个电场,这个电场对周围的电荷有作用力. 由物理学知道, 如果一个单位正电荷放在这个电场中距离原点为r
的地方, 那么电场对它的作用力的大小为).(2
是常数k r q
k F = 当这个单位正电荷 在电场中从 a r =处沿r 轴移动到b r =处时, 计算电场力F 对它所作
的功.
解 取r 为积分变量,],,[b a r ∈任取一小区间],,[dr r r +功微元:,2
dr r kq
dW =
所求功为 .1112??
? ??-=??????-==?
b a kq r kq dr r kq W b
a b
a
如果要考虑将单位电荷从点a 移到无穷远处.12a kq r kq dr r kq W a
a
=???
???-==
+∞
∞
+?
例 1.1.5 在底面积为S 的圆柱形容器中盛有一定量的气体. 在等温条件下, 由于气体的膨
胀, 把容器中的一个活塞(面积为S )从点a 处推移到b 处. 计算在移动过程中, 气体压力所作的功.(如图1-1.4)
解 如图,活塞的位置可用坐标x 表示. 由物理学知道,一定量的气体在等温条件下,压强
p 与体积V 的乘积是常数,k 即k pV = 或.V k p =
因为,xS V = 所以.xS
k p =故作用在活塞上的力.x
k
S xS k S p F =?=
?=在气体膨胀过程中,体积V 是变的,因而x 也是变的,所以作用在活塞上的力也是变的.取x 为积分变量,它 的变化区间为].,[b a 设],[dx x x +为
],[b a 上任一小区间. 当活塞从x 移动到dx x +时,变力F 所作的功近似于,dx x
k
即功微元
为.dx x k dW =于是所求的功为 .ln ][ln a b
k x k dx x k W b
a
b a ===?
图1-1。4
例1.1.7 如图1-1.5一圆柱形蓄水池高为5米, 底半径为3米, 池内盛满了水. 问要把池内的水全部吸出, 需作多少功?
解 建立如下坐标系,取x 为积分变量,],5,0[∈x 取任一小区间],,[dx x x + 这一薄层水的重力为,38.92dx ?π
功微元 ,2.88dx x dW ??=π所求功346222.882.885
25
≈???
???=??=?x dx x W ππ(千焦)
图1-1.5
例1.1.8 如图1-1.6 设有一直径为20m 的半球形水池, 池内贮满水, 若要把水抽尽, 问至少作多少功.
解: 选取区间微元],,[dx x x +相应该微元上的一层水的体
x x x y V ?-=?≈?)100(22ππ(3m ), 抽出这层水需作的功为
22(100)(100)W g x x x g x x x ρππρ?≈-??=-?(焦)其中1000=ρ( kg/3m )是水的密度,
)/(8.92s m g =是重力加速度. 故微元.)100(2dx x x g dW -=πρ
所求功为
1010
2240
(100)(100)104
W g x x dx g x x dx g
πρ
πρπρ=-=-=???
710693.72500?≈=g πρ(焦).
x
x x
+?
图1-1.6 2.水压力
由物理学知道,在水深为h 处的压强为gh p ρ=,这里
ρ
是水的密度.如果有
一面积为A 的平板水平地放置在水深为h 处,那么,平板一侧所受的水压力为A p P ?=. 如果平板垂直放置在水中,由于水深不同的点处压强p 不相等,平板一侧所受的水压力就不能直接使用此公式,而采用“微元法”思想.
例1.1.9 一个横放着的圆柱形水桶, 桶内盛有半桶水, 设桶的底半径为R 水的比重为,γ 计算桶的一端面上所受的压力.(图1-1.7)
图1-1.7(1) 图1-1.7(2)
解 在桶一端面建立如图坐标系,取x 为积分变量,],,0[R x ∈取任一小区间
],,[dx x x +小矩形片上各处压强近似相等x p γ=小矩形片的压力微元为
,222dx x R x dP -=γ端面上所受的压力 )
(2220
220
22x R d x R dx x R x P R
R ---=-=?
?γγ
.32)(3230
322R x R R
γγ=???
???--=
例1.1.10 将直角边各为a 及2a 的直角三角形薄板垂直地浸入水中,斜边朝下,直角边的边长与水面平行,且该边到水面的距离恰等于该边的边长,求薄板所受的侧压力.(图1-1.8) 解:取任一小区间],,[dx x x +面积微元
,)(2dx x a -压力微元,)(2)2(dx x a a x dP -??+=γ
所求压力
3(2)2()7.3
a
P x a a x dx
a γγ=+??-=?
图1-1.8
3.引力
由物理学知道,质量分别为12,m m 相距为r 的两个质点间的引力的大小为12
2
,km m F r
=
其中k 为引力系数,引力的方向沿着两质点的连线方向.
如果要计算一根细棒对一个质点的引力,那么,由于细棒上各点与该质点的距离是变化的,且各点对该质点的引力方向也是变化的,就不能用此公式计算.
例1.1.11假设有一长度为 l 线密度为ρ的均匀细棒,在其中垂线上距棒a 单位处有一质量为m 的质点M ,试计算该棒对质点M 的引力. (图1-1.9) 解 如图 建立如下坐标系,取y 为积分变量
,2,2??
?
???-∈l l y 任取一微元],,[dy y y +
小段与质点的距离为,22y a r +=
小段对质点的引力,2
2y a dy
m k
F +≈?ρ
水平方向的分力微元,)
(2
322y a dy
am k
dF x +-=ρ,)
4(2)
(2
12222
2
322l a a l km y a dy am k
F l l x +-=
+-=?-ρρ
由对称性,在铅直方向分力为 .0=y F
图1-1.9
*例1.1.12 计算半径为a , 密度为,μ均质的圆形薄板以怎样的引力吸引质量为m 的质点P . 此质点位于通过薄板中心Q 且垂直于薄板平面的垂直直线上, 最短距离PQ 等于b .(如图1-1.10)
解 .由于薄板均质均质且关于两坐标轴对称,P 在圆心的中垂线上
,显然引力在水平方向的分力为0,在垂直方向的分力指向y 轴的正向,所求的引力F 看成分布在区间],0[a 上.选取区间微元],,[dx x x +对于以x 为内半径的圆环,其质量
,2xdx m πμ≈?对质点P 的引力在y 轴上的分力
222232
cos 22.(y x bx
F km dx km dx b x b x θμπμπ?≈=++)
即相应于微元],[dx x x +的引力微元 从而
22320221.(a
y bx F km dx km b x μπμπ??
== +?
?
) 即所求引力F 的大小,y F 方向指向y 轴的正向.
图1-1.10
四。考研真题:
1.设曲线2
(0,0)y ax a x =>≥,与2
1y x =-交与点A ,过坐标原点O 与A 的直线与曲线围成一平面图形,问a 为何值时该图形绕x 轴旋转一周所得旋转体体积最大?最大体积是多少?
解:当0x ≥时,由2
2
11y ax
a x y a y x
?=??==?+=-?? 直线OA 的方程为:
y =
所求旋转体体积为:222245
2
272
max 2()(0)
115
(1)
(4)
0415(1)a x a V a x dx a a a dV a a a da
a V ππ=-=>++-==?=+=
2.位于曲线(0)x y xe x -=≤<∞下方,x 轴的上方的无界图形的面积是
解:0
1x s xe dx +∞
-=
=?
3.设1D 是由抛物线2
2y x =,和直线x=a ,x=2和y=0所围成的平面区域,2D 是由抛物线
22y x =,和直线x=a ,和y=0所围成的平面区域,其中0 (1)试求1D 绕x 轴旋转所成的旋转体体积1V 及2D 绕y 轴旋转所成的旋转体体积2V (2)试问a 为何值时,12V V +取得最大值,试求此最大值。 解:(1)2 2 2522 224120 4(32)(2),252 a a a y V x dx V a a dy a πππππ-== =?-=?? (2) 54312max 4 (32)4(1)05 1291,5 V V V a a V a a a V πππ'=+= -+?=-=?== 4.过坐标原点作曲线y=lnx 的切线,该切线与曲线y=lnx 及x 轴所成平面图形D (1)求D 的面积;(2)D 绕直线:x=e 旋转一周所成旋转体体积。 解:(1)设切点为0x 则切线方程为:000 1 ln ()y x x x x =+ -,因切线过原点,有:01e x e x =?方程:y=,D 的面积:1 ()12y e A e ey dy =-=-? (2)可视为切线,x 轴,及x=e 所围三角形绕x=e 旋转的圆锥体体积1V 与曲线y=lnx ,x 轴,及x=e 所围图形绕直线:x=e 的体积2V 之差。 222120 1()(5123)36y V V V e e e dy e e π π ππ=-=--=-+? 5..某闸门的形状与大小如图1-1.11所示:其中直线l 为对称轴,闸门的上部为矩形ABCD , 下部由二次抛物线与线段AB 所围成,当水面与闸门的上端相平时,欲使闸门矩形部分承受的水压力与闸门下部承受的水压力之比为5:4,闸门矩形部分的高h 应为多少m (米)。 解:抛物线方程:21x h y =+-,闸门矩形部分承受水压力: 2 102h p gxdx gh ρρ==? 闸门下部分承受水压1 212 24()315h h p g h ρρ+==+? 由题意:12:5:4p p =即得:h=2 图1-1.11 6.某建筑工程打地基时,需用气锤将桩打进土层,气锤每次击打都将克服土层对桩的阻力作功,设桩的阻力大小与桩被打进地下的深度成正比,(比例系数为k (k>0))气锤第一次击打将桩打进地下am (米),根据设计方案要求气锤每次击打桩时所做的功与前一次击打桩时所做的功之比为常数r (0 1) 气锤击打三次后,可将桩打进地下多少米? 2) 若打击次数不限,气锤至多能将桩打进地下多深? 解:1)设第n 次击打后,桩被打进地下n x ,第n 次击打时气锤所做的功为:n W (n=1,2,3,。。。),由题意当桩被打进地下深为x 时,土层对桩所得功为:kx ,所以: 1 2 1 222211220111 ,() 222x x x W kxdx kx ka W kxdx k x a =====-?? 由 2 22122(1)W rW x r a x =?=+?= 同理可得:3x =。 2) 设 1 212 111 11 ((1)) 2 lim n n n x n n n n n x n n n x k W kxdx x r r a rW r W x x + - ++ ++ →∞ = ==-+++=== ?==?= ? *7.为清除井底的污泥用缆绳将抓斗放入井底抓起污泥后提出井口,已知井深30m抓斗自重400N缆绳每米重50N,抓斗抓起的污泥重2000N,提升速度为3m/s,在提升的过程中, 污泥以20N/s的速度从抓斗缝隙中漏掉。现将抓起污泥的抓斗提升至井口,问克服重力需作多少焦尔的功?(说明:①1N×1m=1J;②抓斗的高度及位于井口上方的缆绳的长度忽略不计) 分析:所求共应分为三部分:①克服抓斗自身重力做功是常力作功;②克服缆绳重量作功,因缆绳随提升高度增加重量减少,故是变力作功③克服污泥重量作功,因污泥也是随提升高度增加重量减少(漏掉)也是变力作功。 解: 方法1.从井底起作向上的x轴,做的功为 123 W W W W =++它们分别表示克服抓斗重力功, 缆绳功,污泥功,其中: 1 4003012000 W J =?= 将抓斗从x提升到x+dx处提升缆绳需作的功元素为: 30 22 50(30)50(30)22500 dW x dx W x dx J =?-?=?-= ? 在【t,t+dt】时间间隔内提升污泥所需作的功元素为: 3 3(200020) dW t dt =- 将污泥从井底提升至井口所需时间为:30/3=10(s)故所做的功为: 10 3(200020)57000 t dt J -= ?故总功为: 123 12000250005700091500 W W W W J =++=++= *方法2.在时间段【t,t+dt】用微元法分析得: 10 [400(200020)50(303)]330(39017) 30(39017)91500 W dW t t dt t dt W t dt J ?≈=+-+-?=- =-= ? §3:广义积分敛散性的判别法 判定一个广义积分的收敛性,是一个重要的问题. 当被积函数的原函数求不出来,或者求原函数的计算过于复杂时,利用广义积分的定义来判断它的收敛性就不适用了. 因此,我们需要其它方法来判断广义积分的收敛性. 一。无穷限广义积分的审敛法: 定理1.1(比较审敛原理):设(),()f x g x 在区间[,);(0)a a +∞>上连续,, 1)如果:0()g(),()f x x a x ≤≤≤<+∞且 ()a g x dx +∞ ?收敛,则()a f x dx +∞ ? 收敛; 2)如果:0g()(),()x f x a x ≤≤≤<+∞且 ()a g x dx +∞ ?发散,()a f x dx +∞ ? 发散; 注:1.可将广义积分比较原理与级数相应比较法对比,其是类似的; 2.可通俗的说:大积分收敛,则小积分收敛;反之,小积分发散,则大积分发散。 推论1.设()f x 在区间[,);(0)a a +∞>上连续,且()0f x ≥ 1) 如果存在常数M>0,及p>1,使得:(),()p M f x a x x ≤ ≤<+∞ (1.1.7) 则 ()a f x dx +∞ ? 收敛; 2)如果存在常数N>0,使得:(),()N f x a x x ≥ ≤<+∞ (1.1.8) 则 ()a f x dx +∞ ? 发散; 推论2(极限形式)设()f x 在区间[,);(0)a a +∞>上连续,且()0f x ≥则 1)当lim (),(1)p x x f x p →+∞ > (1.1.9) 存在时 ()a f x dx +∞ ? 收敛; 2)当lim (),(1)x xf x p →+∞ > (1.1.10) 存在或为无穷大时, ()a f x dx +∞ ? 发散; 定义1.1.2:绝对收敛:如果积分()a f x dx +∞ ? 收敛,则称级数 ()a f x dx +∞ ? 绝对收敛 定理1.2:绝对收敛级数必收敛 例1.1.13 判别广义积分 ? +∞ +1 3 4 1 x dx 的敛散性. 解 因为,1 11 1 03 /44 3 4x x x = < +< 这里4 1,3 p =>故由推论1知,题设广义积分收敛. 例1.1.14 判别广义积分 ? ∞ ++1 2 2 /31dx x x 的敛散性. 解 因为 ,1lim 1lim 2 222/3+∞=+=++∞→∞→x x x x x x x x 故根据推论2知,题设广义积分发散. 例1.1.15 判别广义积分 dx x e x ? ∞ +-+1 1的敛散性. 解 因为当1≥x 时,,1 1x x e x >+- 故由推论1知,题设广义积分发散 . 例1.1.16 判别广义积分? +∞1arctan dx x x 的敛散性. 解 因为,2 arctan lim arctan lim π ==+∞→+∞→x x x x x x 故根据推论2知,题设广义积分发散 . 例1.1.17 判别广义积分? +∞ -0 sin bxdx e ax 的收敛性,其中b a ,都是常数,且.0>a 解 ,s i n ax ax e bx e --≤而 dx e ax ? +∞ -0 收敛 . ∴dx bx e ax |sin |0 -+∞ ?收敛,故题设广义积分收敛 . 例1.1.18 判别广义积分 ? +∞ a dx x x 2 3 sin )0(>a .的收敛性 解 由于,1|sin |223x x x ≤而dx x a ?+∞21收敛,故dx x x a |sin |23∞+?收敛,即dx x x a ? +∞ 23 sin 绝对收敛 因而收敛。 二。无界函数的广义积分审敛法 定理1.3:(比较原理)设函数(),()f x g x 在区间(,]a b 上连续,, 1)如果:当x 充分靠近点a 时有0()g(),f x x ≤≤且 ()a g x dx +∞ ?收敛,则()a f x dx +∞ ? 收敛; 2)如果:当x 充分靠近点a 时有0()g(),f x x ≤≤且,且 ()a f x dx +∞ ? 发散则 ()a g x dx +∞ ?发散 (即大的收敛则小的也收敛,反之小的发散则大的也发散) 取(),(0)() p c g x c x a = >- 推论3设()f x 在区间(,]a b 上连续,且0 ()0,lim ()x a f x f x →+≥=+∞ 1)如果存在常数M>0,及1q <,使得:(),()()q M f x a x b x a ≤ <≤- (1.1.11) 则 ()a f x dx +∞ ? 收敛; 2) 如果存在常数N>0,及1q ≥,使得(),()()q N f x a x b x a ≥ <≤- (1.1.12) 则 ()a f x dx +∞ ? 发散 推论4.(极限形式)设()f x 在区间(,]a b 上连续,且0 ()0,lim ()x a f x f x →+≥=+∞ 1) 如果存在常数0 lim ()()q x a x a f x →+- (1.1.13) 存在,则广义积分 ()a f x dx +∞ ? 收敛 2)如果存在常数1q ≥,使得: lim ()()0(lim ()()=+)q q x a x a x a f x d x a f x →+→+-=>-∞或 (1.1.14) 存在,则广义积分 ()a f x dx +∞ ? 发散 例1.1.19 判别广义积分 ? 3 1ln x dx 的收敛性. 解 被积函数在点1=x 的右邻域内无界.又由洛必达法则知 1 111 lim(1)lim 1,1 ln x x x x x + +→→-== 故根据推论4知,题设广义积分发散. 例1.1.20 判别广义积分 ? 1 1 sin dx x x 的收敛性. 解: 因为 ,11 sin x x x ≤而? 1 x dx 收敛,根据比较审敛原理知, 广义积分 dx x x ? 1 1 sin 收敛,从而题设广义积分也收敛. 例1.1.21 判别广义积分 ? -20 cos 1π dx x x m 的收敛性. 解 由于0=x 是m x x x f cos 1)(-=的瑕点,且 ),0(1 2121~cos 122→=--x x x x x x m m m 所以,当,12<-m 即3 三。考研真题: 1.求 2 ln e dx x x +∞ ? 解一: 221 lim lim (1)1ln ln ln b b b e e dx dx x x x x b +∞ →+∞→+∞==-=? ?; 解二: 211ln ln e e dx x x x +∞ +∞ =-=? 2 . 2 +∞ =? 解: 222 22 (/3)2 arctan(/3)/3(9)31(/3)3tdt d t t t t t π+∞ +∞ = ==++? ? 3. 32 解: 222,01 ,13/2x x x x x x x x ?-≤≤?-=?-<≤??原式 =3 1 2 1 /22)π+=+ 4. 设m ,n 均为正整数,,则反常积分 的收敛性为( ) (A )仅与m 的值有关;(B )仅与n 的值有关 (C )与m ,n 的值都有关;(D )与m ,n 的值都无关 解:瑕点:X=0与x=1 对于: 分1)n>1,2)n=1,m=1,2; 3)n=1,m>2讨论,知 对任意的m ,n 均收敛; 对于 当 0 (罗比达)故知 对任意的m ,n 均收敛 故无论 对于任意的m ,n 均收敛,故选(D ) 10 1 2112 00I I =+=+1I 21()((),(0)m n x f x x x x -+--==→1 lim ()(1)0p x f x x - →-=2I 2I 1I 1I 2I (3)反证法 这种证法是从反面考虑问题。先假设在已知条件成立的情况下,要证的结论不成立,而后从已知条件出发,运用基本概念和基本定理,通过逻辑推理导出矛盾(或与已知条件矛盾;或与某一已知概念、公式、公理、定理等矛盾;或自相矛盾等),这样则否定假设,从而肯定原结论正确。 例如,证明不是的多项式. 事实上,利用反证法,设是的多项式,不妨记此多项式为次多项式,即,则有 于是次多项式有无穷多个不同实根,这与次多项式最多只有个不同实根相矛盾,由此证明了不是的多项式. 又如,证明不存在(为自然数). 事实上,利用反证法,假设存在且设,则有 又因为 所以有 故 这与产生矛盾,因此不存在. (2)分析法 这种方法基本思路是逆着想。先假设结论正确,运用已有的定义、定理、公式、性质,从后向前一步一步地分析,直至推出已知条件,即由结论找需知,再找需知,……,直至已知。这种“执果溯因”的方法,叫做分析法。 分析法是探求证题途径的重要方法之一。它的优点在于思考过程比较自然,目的明确,较为容易找到证明的思路,但缺点是分析的过程叙述起来往往比较繁琐,因而过程多在草稿纸上进行,不正式写出。在实际解题时,特别对于一些较难的问题,常常先用分析法寻找解题的途径,然后再用综合法叙述解题过程,这种方法也可叫做分析综合法。 例如,设在时连续,且;而在时有单调递增导数,试证在时是单调递增的。 事实上,欲证为单调递增,只需证明就行了,而由于 因此就归结为证明. 利用拉格朗日中值定理及已知条件,有 单调递增 因此在时是单调递增的. 又如,用极限定义证明一数列或函数有已知极限时,多采用分析综合法证明。比如证明,其方法如下: ,欲使不等式成立, 由 所以只需,即成立. 取,于是当时,就有,从而保证了希望的不等式成立. 综合以上分析,就有 ,当时,,根据极限定义,有 一 单项选择题(每小题3分,共15分) 1.设lim ()x a f x k →=,那么点x =a 是f (x )的( ). ①连续点 ②可去间断点 ③跳跃间断点 ④以上结论都不对 2.设f (x )在点x =a 处可导,那么0()(2)lim h f a h f a h h →+--=( ). ①3()f a ' ②2()f a ' ③()f a ' ④ 1()3f a ' 3.设函数f (x )的定义域为[-1,1],则复合函数f (sinx )的定义域为( ). ①(-1,1) ②,22ππ??-??? ? ③(0,+∞) ④(-∞,+∞) 4.设2()()lim 1() x a f x f a x a →-=-,那么f (x )在a 处( ). ①导数存在,但()0f a '≠ ②取得极大值 ③取得极小值 ④导数不存在 5.已知0lim ()0x x f x →=及( ),则0 lim ()()0x x f x g x →=. ①g (x )为任意函数时 ②当g (x )为有界函数时 ③仅当0lim ()0x x g x →=时 ④仅当0 lim ()x x g x →存在时 二 填空题(每小题5分,共15分) 1.sin lim sin x x x x x →∞-=+____________. 2.31lim(1)x x x +→∞+=____________. 3.()f x =那么左导数(0)f -'=____________,右导数(0)f +'=____________. 三 计算题(1-4题各5分,5-6题各10分,共40分) 1.111lim()ln 1 x x x →-- 2.t t x e y te ?=?=?,求22d y dx 3.ln(y x =,求dy 和22d y dx . 4.由方程0x y e xy +-=确定隐函数y =f (x ) ,求dy dx . 5.设111 1,11n n n x x x x --==++,求lim n x x →∞. 一元函数微积分学在物理学上的应用速度、加速度、功、引力、压力、形心、质心 用导数描述某些物理量1.速度是路程对时间的导数.加速度是速度对时间的导数。????(t),内转过的角度则物体在时刻?2.设物体绕定轴旋转,在时间间隔t0,t的???(t).(t)?角速度3.当物体的温度高于周围介质的温度时,物体就不断冷却,若物体的温度T与时间?(t).Tt 的冷却速度为t的函数关系为T=T(t),则物体在时刻??段干的质量为m?m(x),0点算起,则杆在点0,x x处的3.一根杆从一端??(x).(x)=m线密度是??这段 时间内通过导线横截面的电量为Q?Q(t4.一根导线在),0,t则导线?(t).t的电流强度 I(t)=Q在时刻5.某单位质量的物体从某确定的温度升高到温度T时所需的热量为 q(T),?(T).时的比热C(T)=q则物体在温度T???(t).t时刻的功率为w?w(t),6. 某力在0,t 则时间内作的功w例1 . 设有长为12cm的非均匀杆AB,AM部分的质量与动点M到端点A的距离x的平 方52成正比,杆的全部质量为360g,则杆的质量的表达式m(x)?x,杆在任一点2 ?(x)=5x M处的线密度 5522??(x)m?x)?x5,x(x)=(m(x)=kx解:?,令x?12,m360得k?,所以m22 ?dx)F(?wx)(xF a b所作的功到b变力沿直线运动从a变力作功: 例2(1)(功1.)一圆柱形的注水桶高为5m,底圆半径为3m,桶内盛满了水,试问要把桶内的水全部吸出需作多少功?解:作x轴如图所示取深度x为积分变量,它的变化区间为[0,5]相应于[0,上任一小区间5][x,x?dx]的一薄层水的高度为dx,因此如x的单位为m,2??dxkN,这薄层水的重力为9.8把这层水吸出桶外需作的功近似为 ?3?dx?x88dw??2525????3462(kJ?8dx?w?所求的功为?882x?82?)20. 例2(2)(功2)设有一半径为.R,长度为l的圆柱体平放在深度为2R的水池中,???1))(圆柱体的侧面与水面相切,设圆柱体的比重为(,现将圆柱体从水中移出水面,问需作多少功?解:分析:依题意就是把圆柱体的中心轴移至x?2R处,计算位于[x,x?1]上的体积微元移至[2R?x,2R?x?dx]时所作的微元功。由于在水面上方与下方所受力不同,所以应分开计算,注意到介于x与x?dx之间的体积微元为2222dx(长?宽lR??x2R高?x)dx?l?2它在水面下方需移动R?x,上方需移动R?x RR 2222????dxx?R?x2)R?xdx?l)R(w?2l(?1)?(Rx?R?RR 理学院 School of Sciences 微积分基本定理的证明 Proof of the fundamental theorem of calculus 学生姓名:张智 学生学号:201001164 所在班级:数学101 所在专业:数学与应用数学 指导老师:杨志林 摘要 微积分学这门学科在数学发展中的地位是十分重要的,自十七世纪以来,微积分不断完善成为一门学科。而微积分基本定理的则是微积分中最重要的定理,它的建立标志着微积分的完成,成为数学发展史的一个里程碑。因此就有了研究微积分基本定理的必要性。本文从十七世纪到二十世纪以来的科学家如巴罗、牛顿、莱布尼兹、柯西、黎曼、勒贝格等人对微积分基本定理的发展所作出的贡献展开论述。并论述了定理在微积分学理论发展中的应用。如换元公式、分部积分公式、Taylor中值定理的积分证明、连续函数的零点定理的证明,建立了微分中值定理与积分中值定理的联系,在一元函数和多元函数上的推广等等。最后给出定理的几个证明方法。 关键词:微积分基本定理,发展史,定理的应用,定理的证明 ABSTRACT Calculus the subject in the position of the development of mathematics is very important,since seventeenth Century,calculus constantly improved as a discipline.While the fundamental theorem of calculus is the most important theorems in calculus,which establishment marks the complete of the calculus, become a milepost of the development history of mathematics. So it is necessary to study the fundamental theorem of calculus. In this paper,since seventeenth Century to twentieth Century,launches the elaboration from scientists such as Barrow, Newton, Leibniz, Cauchy, Riemann, Lebesgue and others on made the contribution to the development of the fundamental theorem of calculus. And discusses the application of theorem in the development of the calculus theory.Such as the transform formula, integral formula of integration by parts, proof of the Taylor mean value theorem of continuous function, the zero point theorem proof, established the differential mean value theorem and the integral mean value theorem in contact,a unary function and multivariate function on the promotion and so on.Finally gave several proofs of the theorem. Keywords:Fundamental Theorem of Calculus,phylogeny,Application,Proof 微积分中10大经典问题 最初的想法来自大一,当时想效仿100个初等数学问题,整理出100个经典的 高等数学问题(这里高等数学按广义理解)。可惜的是3年多过去了,整理出 的问题不足半百。再用经典这把尺子一量,又扣去了一半。 这里入选原则是必须配得起“经典”二字。知识范围要求不超过大二数学系水平, 尽量限制在实数范围内,避免与课本内容重复。排名不分先后。 1)开普勒定律与万有引力定律互推。绝对经典的问题,是数学在实际应用中的光辉 典范,其对奠定数学科学女皇的地位起着重要作用。大家不妨试试,用不着太多的专业知识,不过很有挑战性。重温下牛顿当年曾经做过的事,找找当牛人的感觉吧,这个问题是锻炼数学能力的好题! 2)最速降线问题。该问题是变分法中的经典问题,不少科普书上也有该问题。答案 是摆线(又称悬轮线),关于摆线还有不少奇妙的性质,如等时性。其解答一般变分书上均有。本问题的数学模型不难建立,即寻找某个函数,它使得某个积分取最小值。这个问题往深层次发展将进入泛函领域,什么是泛函呢?不好说,一个通俗的解释是“函数的函数”,即“定义域”不是区间,而是“一堆”函数。最速降线问题通过引 入光的折射定律可以直接化为常微分方程,大大简化了求解过程。不过变分法是对这类问题的一般方法,尤其在力学中应用甚广。 3)曲线长度和曲面面积问题。一条封闭曲线,所围面积是有限的,但其周长却可以 是无限的,比如02年高中数学联赛第14题就是这样一条著名曲线-----雪花曲线。 如果限制曲线是可微的,通过引入内折线并定义其上确界为曲线长度。但把这个方法搬到曲面上却出了问题,即不能用曲面的内折面的上确界来定义曲面面积。德国数学家H.A.Schwarz举出一个反例,说明即使像直圆柱面这样的简单的曲面,也可以具有面积任意大的内接折面。 4)处处连续处处不可导的函数。长久以来,人们一直以为连续函数除了有限个或可数无穷个点外是可导的。但是,魏尔斯特拉斯给出了一个函数表达式,该函数处处连续却处处不可导。这个例子是用函数级数形式给出的,后来不少人仿照这种构造方式给出了许多连续不可导的函数。现在教材中举的一般是范德瓦尔登构造的比较简单的例子。至于魏尔斯特拉斯那个例子,可以在齐民友的《重温微积分》中找到证明。其实上面那个雪花曲线也是一条处处连续处处不可导的曲线。 微积分期末试卷 选择题(6×2) cos sin 1.()2 ,()()22 ()()B ()()D x x f x g x f x g x f x g x C π ==1设在区间(0,)内( )。 A是增函数,是减函数是减函数,是增函数二者都是增函数二者都是减函数 2x 1 n n n n 20cos sin 1n A X (1) B X sin 21C X (1) x n e x x n a D a π→-=--== >、x 时,与相比是( ) A高阶无穷小 B低阶无穷小 C等价无穷小 D同阶但不等价无价小 3、x=0是函数y=(1-sinx)的( ) A连续点 B可去间断点 C跳跃间断点 D无穷型间断点4、下列数列有极限并且极限为1的选项为( )n 1 X cos n = 2 00000001() 5"()() ()()0''( )<0 D ''()'()0 6x f x X X o B X o C X X X X y xe =<===、若在处取得最大值,则必有( )Af 'f 'f '且f f 不存在或f 、曲线( ) A仅有水平渐近线 B仅有铅直渐近线 C既有铅直又有水平渐近线 D既有铅直渐近线 1~6 DDBDBD 一、填空题 1d 12lim 2,,x d x ax b a b →++=x x2 21 1、( )= x+1 、求过点(2,0)的一条直线,使它与曲线y= 相切。这条直线方程为: x 2 3、函数y=的反函数及其定义域与值域分别是: 2+14、y拐点为:x5、若则的值分别为: x+2x-3 1 In 1x + ; 2 322y x x =-; 3 2 log ,(0,1),1x y R x =-; 4(0,0) 5解:原式=11 (1)() 1m lim lim 2 (1)(3) 3 4 77,6 x x x x m x m x x x m b a →→-+++== =-++∴=∴=-= 二、判断题 1、 无穷多个无穷小的和是无穷小( ) 2、 0 sin lim x x x →-∞+∞在区间(,)是连续函数() 3、 0f"(x )=0一定为f(x)的拐点() 4、 若f(X)在0x 处取得极值,则必有f(x)在0x 处连续不可导( ) 5、 设 函数f(x)在 [] 0,1上二阶可导且 ' ()0A ' B ' (f x f f C f f <===-令(),则必有 1~5 FFFFT 三、计算题 1用洛必达法则求极限2 1 2 lim x x x e → 解:原式=2 2 2 1 1 1 3 3 2 (2)lim lim lim 12x x x x x x e e x e x x --→→→-===+∞- 2 若3 4 ()(10),''(0)f x x f =+求 解:3 3 2 2 3 3 3 3 2 3 2 2 3 3 4 3 2 '()4(10)312(10) ''()24(10)123(10)324(10)108(10)''()0 f x x x x x f x x x x x x x x x x f x =+?=+=?++??+?=?+++∴= 3 2 4 lim (cos )x x x →求极限 第九讲 一元微积分的应用 §1 函数单调增减性的判别 定理:设函数()f x 在(),a b 内恒有()'0f x >(()'0f x <),则()f x 在(),a b 内是单调增 的(或单调减的),记为: (或 )。 注意:个别点处()'0f x =不影响()f x 的单调性。 例:3'2,3,0y x y x x ===时'0y =,但是3y x = 应用: 一.判别单调性: 例1:设函数()f x 在[]0,a 0a ≥连续,()0f x =。在()0,a 内可导,()'f x 单调增, 令()()f x F x x =。证明:在()F x 在()0,a 内单增。 证明:()()() ()'00f x f x f xf x ξξ=- <<= 拉氏定理 ()()()()()()()()' ' ' ''' ' 2 2 f x xf x f x xf x xf f x f F x x x x x ξξ---??==== ≥???? ( ()' f x 单调增,0x >) ; 故在()F x 在()0,a 内单增。 二.求单调区间 例2:设()() 1 10x f x dt x ?= > ? ? ,求()f x 的单减区间。 解:()' 1f x =()' 0f x =1x ?=; ∴当()0,1x ∈时,()' 0f x <,所以()f x 单调减; 当()1,x ∈∞时,()' 0f x >,所以()f x 单调增; ∴()f x 的单减区间为:()0,1或者(]0,1。 三.证明不等式 例3:证明:1x >时,() ()2 2 1ln 1x x x ->- 证明:令:()() ()2 2 1ln 1F x x x x =---,则: 微积分期末试卷 一、选择题(6×2) cos sin 1.()2,()()22 ()()B ()()D x x f x g x f x g x f x g x C π ==1设在区间(0,)内( )。 A是增函数,是减函数是减函数,是增函数二者都是增函数二者都是减函数 2x 1 n n n n 20cos sin 1n A X (1) B X sin 21C X (1) x n e x x n a D a π →-=--==>、x 时,与相比是( ) A高阶无穷小 B低阶无穷小 C等价无穷小 D同阶但不等价无价小3、x=0是函数y=(1-sinx)的( ) A连续点 B可去间断点 C跳跃间断点 D无穷型间断点4、下列数列有极限并且极限为1的选项为( )n 1 X cos n = 2 00000001 () 5"()() ()()0''( )<0 D ''()'()06x f x X X o B X o C X X X X y xe =<===、若在处取得最大值,则必有( )Af 'f 'f '且f f 不存在或f 、曲线( ) A仅有水平渐近线 B仅有铅直渐近线C既有铅直又有水平渐近线 D既有铅直渐近线 二、填空题 1 d 1 2lim 2,,x d x ax b a b →++=xx2 211、( )=x+1 、求过点(2,0)的一条直线,使它与曲线y=相切。这条直线方程为: x 2 3、函数y=的反函数及其定义域与值域分别是: 2+1 x5、若则的值分别为: x+2x-3 三、判断题 1、 无穷多个无穷小的和是无穷小( ) 2、 0sin lim x x x →-∞+∞在区间(,)是连续函数() 3、 0f"(x )=0一定为f(x)的拐点() 4、 若f(X)在0x 处取得极值,则必有f(x)在0x 处连续不可导( ) 5、 设 函 数 f (x) 在 [] 0,1上二阶可导且 '()0A '0B '(1),(1)(0),A>B>C( )f x f f C f f <===-令(),则必有 四、计算题 1用洛必达法则求极限2 1 2 lim x x x e → 2 若34()(10),''(0)f x x f =+求 3 2 4 lim(cos )x x x →求极限 4 (3y x =-求 5 3tan xdx ? 五、证明题。 1、 证明方程3 10x x +-=有且仅有一正实根。 2、arcsin arccos 1x 12 x x π +=-≤≤证明() 六、应用题 1、 描绘下列函数的图形 21y x x =+ 第四章一元函数微积分的应用 内容提要:一元函数微分学的应用很广:导数与切线的关系直接从导数的定义上就可以得到,它也进一步反应了微分学的基本思想:“以曲代直”;导数与单调性的关系是中值定理的推论,它不但可以帮助我们很方便地计算函数的单调区间,还是我们证明很多不等式的重要思路;函数的极值点与拐点是重要的考点,考生需要理解并掌握它们的定义和判别定理,它们也都可以通过函数的单调性来理解。一元函数微分学的应用在考试中出现的频率很高,但总体难度不大,只要记住相应的定理和计算公式即可。 定积分的应用分为几何应用和物理应用两部分。几何应用包括通过定积分计算平面图形的面积、平面曲线的弧长、旋转体的体积和侧面积;物理应用主要是通过定积分计算一些物理量:变力做的功,液体的静压力,平面图形的质心或形心等。定积分的应用的理论基础是定积分的定义,它的基本思想是微元法,微元法可以概括为分割、近似、求和、取极限,其中近分割和近似是这四步的关键。考生复习时应该掌握常见的几何量和物理量的计算公式,同时还要深入理解微元法的思想,对主要公式要掌握其推导过程。 第一节导数的应用 Ⅰ考点精讲 1.导数与切线 设函数可导,则曲线在任意一点的切线斜率等于该点的导数值。也就是说,曲线在处的切线方程可表示为,该点的法线方程可表示为。 2.单调性定理:设函数在上连续,在上可导。 (1)如果在上有,那么函数在上单调递增。 (2)如果在上有,那么函数在上单调递减。 (单调性定理也是中值定理的推论,考生可以尝试自行推导) 3.函数极值点及其判定方法 1).极值点 设函数在点的某领域内有定义,如果对任意的,有 ,则称是函数的一个极大值(或极小值)。2).极值点的判别定理 a.(必要条件)设函数在处可导,并在处取得极值,那么。(罗尔定理 的推论) b.(第一充分条件)设函数在处连续,并在的某去心邻域内可导。 ⅰ)若时,而时,则在处取得极大值; ⅱ)若时,而时,则在处取得极小值; ⅲ)若时,符号保持不变,则则在处没有极值; c.(第二充分条件)设函数在处存在二阶导数且,那么 ⅰ)若则在处取得极小值; ⅱ)若则在处取得极大值。 4.函数的凹凸性 1)凹函数与凸函数的定义 定义(定积分) 设函数f (x )是定义在闭区间[a ,b ]上的连续函数,用n + 1个分点 a = x 0 < x 1 < x 2 < … < x n – 1 < x n = b 把闭区间[a ,b ]划分成n 个小区间 [x 0,x 1],[x 1,x 2],…,[x i – 1,x i ],…,[x n – 1,x n ] 记各小区间[x i – 1,x i ](i = 1,2,…,n )的长度为Δx i = x i - x i – 1,在各小区间[x i – 1,x i ]内任取一点ξi ,取函数值f (ξi )与小区间长度Δx i 的乘积f (ξi )Δx i ,作和式 n n i i n i i i x f x f x f x f x f Δ)(Δ)(Δ)(Δ)(Δ)(22111ξξξξξ+++++=∑= 称为函数f (x )在区间[a ,b ]上的积分和。记各小区间的最大长度为d = max{Δx i },如果对于区间 [a ,b ]任意的划分和点ξi 在[x i – 1,x i ]上的任意取法,当d → 0时,积分和的极限存在,则称此极限为函数f (x )在区间[a ,b ]上的定积分,简称积分,记为 ∑?=→=n i i i d b a x x f x x f 10Δ)(lim d )( 其中?为积分号,[a , b ]称为积分区间,f (x )称为被积函数,x 称为积分变量,a 称为积分下限,b 称为积分上限。如果函数f (x )在区间[a ,b ]上的积分存在,则称f (x )在[a ,b ]上可积。 上述定义中的积分限要求a < b ,实际上这个限制可以解除,补充两条规定: (1)当a = b 时,规定0d )(=?a a x x f ; (2)当a > b 时,规定??-=a b b a x x f x x f d )(d )(。 可以看出,这两条规定是合理的,其中第一条规定也可以根据第二条推出。 定理1(可积的必要条件) 如果函数f (x )在闭区间[a ,b ]上的可积,则f (x )在[a ,b ]上有界。 定理2(可积的充分条件) 1.如果函数f (x )在闭区间[a ,b ]上的连续,则f (x )在[a ,b ]上可积。 2.如果函数f (x )在闭区间[a ,b ]上的单调,则f (x )在[a ,b ]上可积。 3.如果在闭区间[a ,b ]内除去有限个不连续点外,函数f (x )有界,则f (x )在[a ,b ]上可积。 引理(微分中值定理) 设函数f (x )在闭区间[a ,b ]内连续,在开区间(a ,b )内可导,则至少存在一点ξ∈(a ,b ),成立等式 f (b ) ? f (a ) = f'(ξ)(b ? a ) 以上结论称为微分中值定理,等式称为微分中值公式。 设函数f (x )在闭区间[a ,b ]内连续,则可以证明f (x )在[a ,b ]上可积,于是存在新的函数F (x ),成立微分关系F'(x ) = f (x )或d F (x ) = f (x )d x ,则称F (x )为f (x )的一个原函数。试利用微分中值定理和定积分的定义证明微积分基本公式 )()()(d )(a F b F x F x x f b a b a -==? 这个公式又称为牛顿-莱布尼茨公式。 证明: 大一微积分期末试卷及 答案 Company number:【0089WT-8898YT-W8CCB-BUUT-202108】 微积分期末试卷 选择题(6×2) 1~6 DDBDBD 一、 填空题 1 In 1x + ; 2 322y x x =-; 3 2 log ,(0,1),1x y R x =-; 4(0,0) 5解:原式=11(1)()1m lim lim 2(1)(3)3477,6 x x x x m x m x x x m b a →→-+++===-++∴=∴=-= 二、 判断题 1、无穷多个无穷小的和是无穷小( ) 2、若f(X)在0x 处取得极值,则必有f(x)在0x 处连续不可导( ) 3、设函数f(x)在[]0,1上二阶可导且 '()0A '0B '(1),(1)(0),A>B>C( )f x f f C f f <===-令(),则必有 1~5 FFFFT 三、 计算题 1用洛必达法则求极限21 20 lim x x x e → 解:原式=22211 1 33 0002(2)lim lim lim 12x x x x x x e e x e x x --→→→-===+∞- 2 若34()(10),''(0)f x x f =+求 解: 3 24 lim(cos )x x x →求极限 4 (3y x =-求 5 3tan xdx ? 6arctan x xdx ?求 四、 证明题。 1、证明方程310x x +-=有且仅有一正实根。 证明:设3()1f x x x =+- 2、arcsin arccos 1x 12 x x π +=-≤≤证明() 五、 应用题 1、描绘下列函数的图形 3. 4.补充点7179(2,).(,).(1,2).(2,)2222 --- 50 lim (),()0x f x f x x →=∞∴=有铅直渐近线 6如图所示: 2.讨论函数22()f x x Inx =-的单调区间并求极值 由上表可知f(x)的单调递减区间为(,1)(0,1)-∞-和 单调递增区间为(1,0)1-+∞和(,) 且f(x)的极小值为f(-1)=f(1)=1 一元微积分在经济上的运用 近几年来,我国的经济学界和经济部门越来越意识到用数学方法来解决经济问题的重要性,正在探索经济问题中应用数学的规律。鹤壁职业技术学院李兰军老师在《商场现代化》2008年10月(下旬刊)上作了概率统计在经济问题中的应用研究。实践证明,一元微积分也是对经济和经济管理问题进行量的研究的有效工具。本文将利用一元微积分方法解决一些经济问题,分析生产量、成本与利润和需求量(销售量)、价格与收益的关系,研究怎样确定或变动产品的生产量、销售量,以及商品的价格。 一、微分在经济学中的应用 由微分的定义知,当很小时,有近似公式,而所以,这个公式可用来计算函数在某一点附近的函数值的近似值。 例1设某国的国民经济消费模型为。其中:y为总消费(单位:十亿元);x为可支配收入(单位:十亿元)。当x=100.05时,问总消费是多少? 解令因为相对于较小,可用上面的近似公式来求值。 由此可以通过统计可支配收入来预测总消费是多少,以便确定产品的生产量。 二、最值在经济学中的应用 在经济分析中,经常遇到利润最大,成本最低等问题 1.最大利润问题 利润是衡量企业经济效益的一个主要指标。在一定的设备条件,如何安排生产才能获得最大利润,这是企业管理中的现实问题。 例2某厂生产某种产品,其固定成本为3万元,每生产一百件产品,成本增加2万元。其总收入R(单位:万元)是产量q(单位:百件)的函数,,求达到最大利润时的产量。 解由题意,成本函数为,于是,利润函数 , 令,得(百件).又,所以当时,函数取得极大值,因为这里极值点是惟一的,所以极大值又是最大值,即产量为300件时取得最大利润。 2.最小成本问题 例3 已知某个企业的成本函数为:, 其中C——成本(单位:千元)q——产量(单位:t).求平均可变成本y(单位:千元/t)的最小值。 解平均可变成本,令,得。 又,所以时,y取得极小值,由于因为这里极值点是惟一的,所以极小值又是最小值。(千元/t), 即产量为4.5t时平均可变成本取得最小值9750元/t. 导数概念在经济学中有两个重要的应用——边际分析和弹性分析。 1.边际分析 边际概念是经济学中的一个重要概念,一般指经济函数的变化率。当经济函数的自变量改变很小时,经济函数的边际函数是指它的导函数。利用导数研究经济变量的边际变化的方法,称为边际分析方法。 例4设某产品的需求函数为q=100-5p,求边际收益函数,以及q=20,50和70时的边际收益。 解收入函数为R(q)=pq,式中的销售价格p需要从需求函数中反解出来,即, 于是收入函数为,边际收入函数为, 牛顿—莱布尼茨公式 前言 此证明主要是献给那些无论如何,竭斯底里都想知道自已手上这条无与伦比公式背后的秘密的高中生。 公式的证明首先是从定积分的基本性质和相关定理的证明开始,然后给出积分上限函数的定义,最后总揽全局,得出结论。证明过程会尽可能地保持严密,也许你会不太习惯,会觉得多佘,不过在一些条件上如函数f(x),我们是默认可积的。 所有证明过程都是为后续的证明做铺掂的,都是从最低层最简单开始的,所以你绝对,注意,请注意,你是绝对能看懂的,对于寻求真理的人,你值得看懂! (Ps :如果你不太有耐心,我建议你别看了,因为这只会让你吐出垃圾两个字) 定积分性质的证明 首先给出定积分的定义: 设函数f(x)在区间[a,b]上连续,我们在区间[a,b]上插入n-1个点分成n 个区间[a,x 1],[x 1,x 2]…[x n ,x n-1],其中x 0=a ,x n =b ,第i 个小区间?x i = x i -x i-1(i=1,2…n)。 由它的几何意义,我们是用无数个小矩形的面积相加去模拟它的面积,因此任一个小矩形的面积可表示为?S i =f(εi ) ?x i ,为此定积分可以归结为一个和式的极 限 即: 性质1:证明?b a c dx = C(b-a),其中C 为常数. 几何上这就是矩形的面积 性质2:F(x)和G(x)为函数z(x)的两个原函数,证明F(x)=G(x)+C,C 为常数. 设K(x)=F(x)-G(x) 定义域为K 1021110()lim ()lim (...)lim ()()n b i i n n a n n i n n f x dx f x c x x x x x x c x x c b a ε-→∞→∞=→∞=?=-+-++-=-=-∑?0()()() ()()()()()0()()()lim 0x F x G x z x K x F x G x z x z x K x x K x K x x ?→''=='''∴=-=-=+?-'∴==?Q 1()lim ()n b a n i i i f x dx f x ε→∞==?∑ ? 1、已知22 (,)f x y x y x +=-,则=),(y x f _____________. 2、已知,则= ?∞ +--dx e x x 21 ___________. π =? ∞ +∞ --dx e x 2 3、函数 22 (,)1f x y x xy y y =++-+在__________点取得极值. 4、已知y y x x y x f arctan )arctan (),(++=,则=')0,1(x f ________. 5、以x e x C C y 321)(+=(21,C C 为任意常数)为通解的微分方程是 ____________________. 6 知dx e x p ?∞ +- 0 )1(与 ? -e p x x dx 1 1ln 均收敛,则常数p 的取值范围是( c ). (A) 1p > (B) 1p < (C) 12p << (D) 2p > 7 数 ?? ?? ?=+≠++=0 ,0 0 ,4),(222 22 2y x y x y x x y x f 在原点间断, 是因为该函数( b ). (A) 在原点无定义 (B) 在原点二重极限不存在 (C) 在原点有二重极限,但无定义(D) 在原点二重极限存在,但不等于函数值 8 、若2 211 x y I +≤= ?? ,2 2 212x y I ≤+≤= ?? , 2 2 324x y I ≤+≤= ?? ,则下列关 系式成立的是( a). (A) 123I I I >> (B) 213I I I >> (C) 123I I I << (D) 213I I I << 9、方程x e x y y y 3)1(596+=+'-''具有特解( d ). (A) b ax y += (B) x e b ax y 3)(+= (C) x e bx ax y 32)(+= (D) x e bx ax y 323)(+= 10、设∑∞ =12n n a 收敛,则∑∞ =-1) 1(n n n a ( d ). (A) 绝对收敛 (B) 条件收敛 (C) 发散 (D) 不定 一、填空题(每小题3分,共15分) 1、2(1)1x y y -+. 2 3、) 32 ,31(-. 4、1. 5、"6'0y y y -+=. 11、求由2 3x y =,4=x ,0=y 所围图形绕y 轴旋转的旋转体的体积.解: 32 y x =的函数为 《微积分基本定理》(说课稿) 一、教材分析 1、教材的地位及作用 我所选用的教材是科学出版社出版的高等教育“十一五”规划教材《经济数学基础》,由宋劲松老师主编。微积分基本定理是第四章第二节内容,本节内容共设计两个课时,这节课的主要内容是微积分基本公式的导出以及用它求定积分。 本节课是学生学习了不定积分和定积分这两个概念后的继续,它不仅揭示了不定积分和定积分之间的内在联系,同时也提供计算定积分的一种有效方法,为后面的学习奠定了基础。因此它在教材中处于极其重要的地位,起到了承上启下的作用,不仅如此,它甚至给微积分学的发展带来了深远的影响,是微积分学中最重要最辉煌的成果。 二、教学目标及重点、难点 1、教学目标 根据学生的认知结构特征以及教材内容的特点,依据新课程标准要求,确定本节课的教学目标如下: (1)知识与技能目标:通过本节的学习,使学生了解变上限的定积分的定义及相关定理,掌握牛顿—莱布尼兹公式,通过例题及练习,使学生在增加对牛顿—莱布尼兹公式感性认识的基础上,熟练掌握求定积分的方法,从而能够熟练计算定积分. (2)能力目标:本节所讲数学知识主要是为学生学习专业课做准备。要逐步培养学生具有比较熟练的基本运算能力、提高综合运用所学知识分析和解决实际问题的能力。 (3)德育目标:通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩证唯物主义观点,提高理性思维能力。 2、教学重点、难点 根据教材内容特点及教学目标的要求确定本节重点为通过探究变上限定积分与原函数的关系,使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分. 根据学生的年龄结构特征和心理认知特点确定本节难点:了解微积分基本定理的含义. ——以学生现有的知识水平对于微积分基本定理的严密证明是存在着一定难度的,而突破难点的关键在于让学生主动去探索,体会微积分基本公式的导出以及利用它来计算简单的定积分,这样才能从真正意义上把握该定理的含义,提高学生的能力,体现学生的主体地位. 三、教法和学法 1、教法: 素质教育理论明确要求:教师是主导,学生是主体,只有教师在教学过程中注重引导,才能充分发挥学生的主观能动性,有利于学生创造性思维的培养和能力的提高,根据本节的教学内容及教学目标和学生的认识规律,我采用类比、启发、引导、探索式相结合的方法,启发、引导学生积极思考本节课所遇到的问题,引导学生联想旧知识来解决和探索新知识,从而使学生产生浓厚的学习兴趣和求知欲,体现了学生的主体地位。 2、学法: 微积分期末测试题及答 案 Document number:NOCG-YUNOO-BUYTT-UU986-1986UT 一 单项选择题(每小题3分,共15分) 1.设lim ()x a f x k →=,那么点x =a 是f (x )的( ). ①连续点 ②可去间断点 ③跳跃间断点 ④以上结论都不对 2.设f (x )在点x =a 处可导,那么0()(2)lim h f a h f a h h →+--=( ). ①3()f a ' ②2()f a ' ③()f a ' ④1()3f a ' 3.设函数f (x )的定义域为[-1,1],则复合函数f (sinx )的定义域为( ). ①(-1,1) ②,22ππ??-???? ③(0,+∞) ④(-∞,+∞) 4.设2 ()()lim 1()x a f x f a x a →-=-,那么f (x )在a 处( ). ①导数存在,但()0f a '≠ ②取得极大值 ③取得极小值 ④导数不存在 5.已知0lim ()0x x f x →=及( ),则0 lim ()()0x x f x g x →=. ①g (x )为任意函数时 ②当g (x )为有界函数时 ③仅当0lim ()0x x g x →=时 ④仅当0 lim ()x x g x →存在时 二 填空题(每小题5分,共15分) sin lim sin x x x x x →∞-=+. 31lim(1)x x x +→∞+=. 3.()f x =那么左导数(0)f -'=____________,右导数(0)f +'=____________. 三 计算题(1-4题各5分,5-6题各10分,共40分) 1.111lim()ln 1 x x x →-- 2.t t x e y te ?=?=? ,求22d y dx 3.ln(y x =,求dy 和22d y dx . 4.由方程0x y e xy +-=确定隐函数y =f (x ) ,求 dy dx . 5.设111 1,11n n n x x x x --==+ +,求lim n x x →∞. 【最新整理,下载后即可编辑】 第五章 一元微积分的应用 5.1 函数图象的几何性质 一 基本概念 定义1 极值点与极值: (1)极大值点(极小值点):函数()y f x =在0x 的某邻域内有定义,若0()x U x ?∈有 0()()f x f x <(0()()f x f x >), 则称0x 为()f x 的极大值点(极小值点);函数值0()f x 为()f x 的极大值(极小值). (2)极大值点和极小值点统称为极值点;极大值和极小值统称为极值. 定义2 凸凹函数: 函数()f x 在I 上有定义,若对任意的12,x x I ∈,有 1212()() ( )22 x x f x f x f ++<12 12()()()22x x f x f x f ++??> ? ?? (1) 则称()f x 在区间I 上是凹函数(凸函数). 公式(1)可以改写为: 1212()()() f x x f x f x αβαβ+<+1212()()() f x x f x f x αβαβ+>+ (2) 其中,(0,1)αβ∈,且1αβ+=. 定义3 拐点: 如果函数()f x 在点0x 的左右邻域的凸凹性不同,则称点00(,())x f x 是函数()f x 的拐点; 定义4 渐近线: 若曲线()y f x =上的点M ,沿曲线无限远离原点时,它与定直线L 的距离趋于零,则称直线L 就是曲线()y f x =的渐近线。 注1 极值点和最值点的区别和联系: (1)极值点未必是最值点,最值点也未必是极值点; (2)最值点若是在区间内部,最值点就是极值点; (3)若函数在定义域区间内仅有唯一极值点,则此极值点就是最值点. 注2 拐点是曲线上的点00(,())x f x ,并非是数轴上的点0x x =. 二 基本方法 1 求极值点 有两类点可能成为极值点:导数等于0的点和导数不存在的点(仅仅可能是极值点). 判断上述两类点是否为极值点的具体方法: (1)几何方法:若0x 的左右邻域的单调性不同,则0x 是极值点,0()f x 是极值; 在0x 的左邻域00(,)x x δ-上,()0f x '>;在0x 的右邻域00(,)x x δ+上,()0f x '<,0x 为极大值点. 在0x 的左邻域00(,)x x δ-上,()0f x '<;在0x 的右邻域00(,)x x δ+上,()0f x '>,0x 为极小值点. (2)代数方法:求0x 的导数,若0()f x '=(1)00()()0n f x f x -''===,而()0()0n f x ≠,则 (a) 如果n 是偶数,0x 是极值点,若()0()0n f x >,0x 是极小值点,若()0()0n f x <,0x 是极大值点; (b) 如果n 是奇数,0x 不是极值点. 2 求函数()y f x = 的单调区间 (1)求函数()f x 的定义域; (2)在定义域内求出一阶导函数()f x '等于零的点和一阶导函数不存在的点; (3)用上述两类点将定义域分成若干区间,并判断导函数()f x '在每个区间的符号,从而得到单调区间. 3 求函数()y f x = 在区间[,]a b 或(,)a b 上的最值: 具体方法:求函数()f x 在闭区间[,]a b 上一阶导函数等于0点和一阶导函数不存在的点:令12,,,n x x x ,则函数()y f x =在[,]a b 的高等数学证明方法
微积分期末测试题及复习资料
一元函数微积分学在物理学上的应用1
微积分基本定理的证明
微积分中10大经典问题
大一微积分期末试卷及答案
一元微积分的应用
大一微积分期末试题附答案
第四章 一元函数微积分的应用
证明微积分基本公式
大一微积分期末试卷及答案
一元微积分在经济上的运用
牛顿-莱布尼茨公式的详细证明
微积分下册期末试卷及答案[1]
微积分基本定理说课稿
微积分期末测试题及答案
第五章 一元函数微积分的应用(完整资料).doc