变温大气压强与海拔高度关系公式推导

海拔与大气密度和温度间的换算关系Revised by Hanlin on 10 January 2021海拔高度与大气密度和温度间的换算关系1、根据大气压力和空气密度计算公式，以及空气湿度经验公式，可得出大气压、空气密度、湿度与海拔高度的关系。

注：标准状态下大气压力为1，相对空气密度为1，绝对湿度为11g/m3。

从表中可以看出，海拔高度每升高1000m，相对大气压力大约降低12%，空气密度降低约10%，绝对湿度随海拔高度的升高而降低。

绝对湿度是指每单位容积的气体所含水分的重量，用mg/L或g/m3表示；相对湿度是指绝对湿度与该温度饱和状态水蒸气含量之比用百分数表达。

2、空气温度与海拔高度的关系在无热源、无遮护的情况下，空气温度随海拔高度的增高而降低。

一般研究所采集的温度与海拔高度的关系：从表中可以看出：空气温度在一般情况下，海拔高度每升高1000m，最高温度会降低5℃，平均温度也会降低5℃。

大气密度（atmosphericdensity）单位容积的大气质量。

空气密度在标准状况（0℃（273k），101KPa）下为1.293g·L-1。

空气的密度大小与气温等因素有关，我们一般采用的空气密度是指在0摄氏度、绝对标准指标下，密度为1.297千克每立方米(1.297kg/m3).大气压力随海拔高度而变化,由经验公式P=P0（1-0.02257h）5.256（kPa）式中h一海拔高度（km）.用上面公式,算出压力,然后根据密度=P*29/(8314*T),其中P的单位是帕,T的单位是K,通常也就是273.15+t不同温度下干空气算公式:空气密度=1.293(实际压力/标准物理大气压)*(273/实际绝对温度),绝对温度=+273通常情况下,即30摄氏度时,取1.165KG/M3-60摄氏度时,取1.65KG/M3。

变温大气压强与海拔高度关系公式推导首先，理想气体状态方程为：PV=nRT其中，P表示气体的压强，V表示气体的体积，n表示气体的物质的量，R表示气体常数，T表示气体的温度。

假设在其中一地点，大气温度T1与压强P1之间的关系为：P1=kT1其中，k是一个常量。

我们假设在其中一高度上，大气温度由T1变为T2，压强由P1变为P2、根据理想气体状态方程：P1V1=nRT1P2V2=nRT2由于物质的量n和气体常数R的数值不会发生变化，可以将上述两个方程进行除法运算，得到：P1V1/P2V2=T1/T2假设V1和V2分别表示海拔高度为h1和h2时单位质量气体的体积，且两者之间的变化与压强和温度的变化成正比。

即：V1/V2=mP2/P1其中，m是一个常量。

将上述两个等式联立，得到：P1V1/P2V2=T1/T2mP2/P1=V1/V2整理以上两个等式，可以得到：T2/T1=P2/P1V1/V2=mP2/P1将海拔高度h1和h2分别表示为海拔h1和h2时单位质量气体所占体积的比值，即：V1/V2=h1/h2将以上两个等式代入前两个等式中，可以得到：T2/T1=P2/P1h1/h2=mP2/P1由于压强和海拔高度之间的变化符合以下方程：P = P0 e^(-Mgh/RT)其中，P0表示海平面上的大气压强，M表示空气的摩尔质量，g表示重力加速度，R表示气体常数，T表示温度，h表示海拔高度。

现在我们可以将P1和P2分别表示为海拔h1和h2时的大气压强，代入上述方程中：P1 = P0 e^(-Mgh1/RT1)P2 = P0 e^(-Mgh2/RT2)将上述两个等式带入之前推导得到的关系中：T2/T1=P2/P1h1/h2=mP2/P1可以得到：T2 / T1 = e^(-Mgh2/RT2) / e^(-Mgh1/RT1)h1 / h2 = m e^(-Mgh2/RT2) / e^(-Mgh1/RT1)通过进一步化简与推导，可以得到变温大气压强与海拔高度之间的关系公式。

气压随高度的变化公式
气压随高度的变化公式是指随着海拔的增加，大气压力如何变化的数学表达式。

根据国际标准大气模型和理想气体状态方程，可以得到以下气压随高度变化的公式：P = P0 * e^(-h/H)
其中，P表示某一高度处的气压，P0表示参考高度处的气压，h表示所在高度
与参考高度之间的垂直高度差，H表示大气压力尺度高度。

这个公式是基于理想气体的假设，并且在国际标准大气模型的前提下得出。

根
据这个公式，我们可以观察到以下规律：
1. 高度增加，气压逐渐减小：随着海拔的增加，气压会逐渐减小，因为上方的
空气重量减小。

2. 气压变化非线性：气压随高度的变化不是线性的，而是呈指数减小。

这意味
着在低海拔地区，气压的变化较为缓慢，而在高海拔地区，气压的变化速度会更快。

3. 气压随高度变化的速率与气温有关：根据理想气体状态方程，气压的变化与
温度有关。

一般情况下，随着高度的增加，气温下降。

因此，气压随高度变化的速率也会受到气温变化的影响。

这个气压随高度变化的公式在气象学和航空航天工程等领域具有广泛的应用。

通过了解气压随高度变化的规律，可以帮助我们理解大气环境的变化，进行气象预测和天气预报等工作。

同时，在航空航天工程中，了解海拔对气压的影响也对设计和操作飞行器具有重要意义。

大气压力与海拔高度转换一个地方气压值经常有变化→其上空大气柱中空气质量的多少→大气柱厚度和密度改变的反映：大气柱厚度和密度与空气质量应该是成正比关系任何地方的气压值总是随着海拔高度的增加而递减。

据实测，在地面层中，高度每升100m，气压平均降低12.7hPa，在高层则小于此数值。

确定空气密度大小与气压随高度变化的定量关系，一般是应用静力学方程和压高方程。

1、静力学方程假使大气相对于地面处于静止状态，则某一点的气压值等于该点单位面积上所承受空气柱的重量。

公式是：h≈8000（1+t/273）/P（m/hPa）其中h是气压高度差，t是摄氏温标，P是气压从公式可以看出①在同一气压下，气柱的温度越高，密度越小，气压随高度递减越慢，单位气压高度差越大。

②在同一温度下，气压值越大的地方，空气密度越大，气压随高度递减越快，单位高度差越小。

通常，大气处于静力平衡状态，当气层不太厚和要求精度不太高时，这公式可粗略估算气压与高度的定量关系。

如果研究的气层高度变化范围很大，气柱中上下层温度、密度变化显著时，该公式就不适合用了，这时候可以用压高方程。

2、压高方程为了精确地获得气压与高度的对应关系，通常将静力学方程从气层底部到顶部进行积分，即得出压高方程，然后再将之替换简化为：Z2-Z1=18400（1+t/273）log( P1/P2)式中P1、P2分别是高度Z2、Z1的气压值，t是摄氏温标从公式可以看出①气压随高度增加按指数规律递减②高度越高，气压减小得越慢这公式是将大气当成干空气处理的，但当空气中水汽含量较多时，就必须用虚温代替式中的气温。

大气密度与海拔高度和温度间的换算1、根据大气压力和空气密度计算公式，以及空气湿度经验公式，可得出大气压、空气密度、湿度与海拔高度的关系。

从表中可以看出，海拔高度每升高1 000 m，相对大气压力大约降低12%，空气密度降低约10%，绝对湿度随海拔高度的升高而降低。

2、空气温度与海拔高度的关系在无热源、无遮护的情况下，空气温度随海拔高度的增高而降低。

气压和海拔的换算公式嘿，咱们来聊聊气压和海拔的换算公式这事儿。

咱先从一个小事儿说起哈。

有一回，我跟几个朋友一块儿去爬山。

那山啊，可高可高啦。

我们一路爬呀爬，越往上走，就感觉呼吸越费劲。

这时候，我就想到了气压和海拔的关系。

咱都知道，随着海拔的升高，气压是会逐渐降低的。

那这降低的规律是啥呢？这就得说到换算公式啦。

一般来说，气压和海拔的换算公式可以简单表示为：P = P0 × (1 -H/44300)^5.255 。

这里面的 P 就是咱们要求的海拔 H 处的气压，P0 呢，是海平面的标准大气压，大概是 101325 帕斯卡。

你看啊，这个公式里，每一个数都有它的作用。

就比如说那个44300 ，它代表着一个特定的数值，和大气的性质啥的都有关系。

还有那个 5.255 ，也不是随便来的，是经过好多科学家研究、测量得出来的。

咱再回到爬山那事儿。

当我们爬到半山腰的时候，我就琢磨着，按照这个公式，这地方的气压得是多少呢？然后我就掏出手机，查了查海平面的大气压数值，再大概估计了一下咱们所处的海拔高度，就开始算起来。

算出来的结果还真和我当时身体的感觉挺对得上的，感觉特别神奇。

这公式在实际生活中的用处可大了去啦。

比如说飞机飞行的时候，飞行员就得知道不同高度的气压，这样才能保证飞行的安全和稳定。

还有气象学家，他们通过测量气压来预测天气变化，这可都离不开气压和海拔的换算公式呢。

另外啊，要是你喜欢搞一些户外探险活动，比如登山、高原徒步啥的，了解这个公式也能帮你更好地准备装备，提前知道可能会遇到的身体反应。

再往深了说，研究气压和海拔的关系，对于我们理解地球的大气环流、气候变化等等这些大问题也特别重要。

总之，气压和海拔的换算公式虽然看起来有点复杂，但只要咱多琢磨琢磨，多联系实际生活中的例子，就能发现它其实挺有意思，也挺有用的。

下次当你再去到高海拔的地方，或者看到飞机在天上飞的时候，说不定就会想起这个公式，然后心里就更明白是咋回事啦！。

大气压力与海拔高度怎么转换标准大气压强Po= Pa= cmHg= mmHgPo=1.01325×10^5 Pa=76cmHg=760mmHg一个地方气压值经常有变化→其上空大气柱中空气质量的多少→大气柱厚度和密度改变的反映：大气柱厚度和密度与空气质量应该是成正比关系任何地方的气压值总是随着海拔高度的增加而递减。

据实测，在地面层中，高度每升100m，气压平均降低12.7hPa，在高层则小于此数值。

确定空气密度大小与气压随高度变化的定量关系，一般是应用静力学方程和压高方程。

1、静力学方程假使大气相对于地面处于静止状态，则某一点的气压值等于该点单位面积上所承受空气柱的重量。

公式是：h≈8000（1+t/273）/P（m/hPa）其中h是气压高度差，t是摄氏温标，P是气压从公式可以看出①在同一气压下，气柱的温度越高，密度越小，气压随高度递减越慢，单位气压高度差越大。

②在同一温度下，气压值越大的地方，空气密度越大，气压随高度递减越快，单位高度差越小。

通常，大气处于静力平衡状态，当气层不太厚和要求精度不太高时，这公式可粗略估算气压与高度的定量关系。

如果研究的气层高度变化范围很大，气柱中上下层温度、密度变化显著时，该公式就不适合用了，这时候可以用压高方程。

2、压高方程为了精确地获得气压与高度的对应关系，通常将静力学方程从气层底部到顶部进行积分，即得出压高方程，然后再将之替换简化为：Z2-Z1=18400（1+t/273）log( P1/P2)式中P1、P2分别是高度Z2、Z1的气压值，t是摄氏温标从公式可以看出①气压随高度增加按指数规律递减②高度越高，气压减小得越慢这公式是将大气当成干空气处理的，但当空气中水汽含量较多时，就必须用虚温代替式中的气温。

大气密度与海拔高度和温度间的换算1、根据大气压力和空气密度计算公式，以及空气湿度经验公式，可得出大气压、空气密度、注：标准状态下大气压力为1，相对空气密度为1，绝对湿度为11 g/m3。

大气压和海拔的换算公式咱们先来说说大气压和海拔这一对“欢喜冤家”。

不知道大家有没有这样的体验，当咱们去爬山的时候，越往高处走，是不是感觉呼吸会变得有点儿困难？这其实就和大气压与海拔的关系有关系啦。

大气压呀，简单来说就是空气对我们的压力。

而海拔呢，就是我们所处位置距离海平面的高度。

这两者之间可是有着神秘的换算公式哦。

大气压和海拔的换算公式是：大气压（hPa）= 1013.25 × [1 - (海拔÷44330)^(1/7)] 。

这个公式看起来有点复杂，别着急，咱们慢慢理解。

就拿我之前去西藏旅游的经历来说吧。

我一路欣赏着美丽的风景，可当到达比较高的地方时，我明显感觉到身体有些不舒服。

后来我才知道，那是因为海拔升高了，大气压变小了。

在平原地区，大气压一般在1013 百帕左右，咱们感觉挺舒服的。

可到了海拔3000 米的地方，大气压就下降到了大概 700 百帕。

想象一下，就好像有一只无形的手，随着海拔的升高，一点点地把压在我们身上的空气给抽走了。

这导致我们呼吸的空气变得稀薄，氧气也不够用了。

在日常生活中，这个换算公式也有不少用处呢。

比如说气象部门可以通过这个公式来预测天气变化。

因为大气压的变化和天气可是密切相关的。

对于航空领域来说，这个公式更是至关重要。

飞行员们得清楚地知道不同海拔高度的大气压情况，才能保证飞行的安全。

再比如，登山爱好者们也需要了解这个公式。

知道了大气压随着海拔的变化规律，就能提前做好准备，应对可能出现的高原反应。

总之，大气压和海拔的换算公式虽然看起来有点头疼，但只要咱们多结合实际去理解，就会发现它其实挺有趣，也很有用。

不管是探索大自然，还是保障我们的生活和工作，它都默默地发挥着重要的作用。

所以呀，别小看这个公式，它就像是一个隐藏在背后的小魔法师，悄悄地影响着我们周围的世界。

下次当您再去到不同高度的地方，说不定就会想起这个神奇的公式呢！。

海拔与气压的关系
通常情况下，海拔与温度的关系是海拔越高，温度越低。

因为对流层大气的主要直接
热源是地面，离地面越远，得到的地面辐射越少，温度也就越低.每上升米，温度下降0.6摄氏度。

温度与海拔的关系式为：t=20-(6*h)。

每升高1km，温度下降6℃，则1千米高处，温度是20-6=14℃；2千米高处，温度是20-6×2=8℃；所以，高度h(km)的高处，温度t=20-6h。

任一地的将近地面大气（对流层），温度均随其海拔高度的增高而减少——因为温度
的热源就是地面。

一般来说：温度也是随高度增加而递减；越高越冷。

同一水平面上，气压与温度呈负
相关；同一水平面上，相对较热的地方是低压，相对较冷的地方是高压。

也有例外的，比
如副极地地区因为冷暖气流相遇，气流抬升，反而形成低压，而副高所在地区由于高空气
压堆积，导致气流下沉，反而在热的地方形成了高压，这都是动力原因形成的。

气压与海拔
任意地的气压值均随海拔高度的升高而降低——气压是作用在单位面积上的大气压力，在数值上等于单位面积上的垂直空气柱所受到的重力。

海拔就是指地面某个地点或者地理事物高于或者高于海平面的垂直距离，就是海拔高
度的缩写，例如海拔越高的地方，空气越浑浊，气压也越高，这个地方水的沸点就减少了。

高海拔地带，如果需要烹饪食物，由于气压较低，所以需要使用高压锅等器具来进行
烹饪，不然会出现水烧不开、食物煮不熟等情况。

0度等温线高度计算公式等温线高度的计算公式主要是根据大气的垂直温度变化关系来推导得出的。

根据热力学第一定律和理想气体状态方程，可以推导出等温线高度计算公式。

首先我们需要了解一些相关的基本概念和公式：1.大气压强的变化与高度的关系：大气压强随着高度的增加而逐渐减小，可以近似地用指数函数关系来表示：P=P0*e^(-h/h0)其中，P是高度为h处的大气压强，P0是参考气压（通常取地表气压），h是高度，h0是压度尺度高度。

2.大气温度的变化与高度的关系：大气温度随着高度的增加而逐渐减小，一般假设大气是按照一个温度梯度降低的。

dT/dh = -α其中，dT/dh表示单位高度上的温度变化率，α是温度梯度（通常取正值）。

3.等温线的定义：等温线是指大气中其中一特定温度的水平面。

在等温线上，大气中每层的压强P1、P2与相应高度h1、h2之间的关系可以表示为：P1/P2=(T1/T2)^(κ/α)其中，T1、T2分别是高度h1、h2处的温度，κ是理想气体的比热容比（通常取值为1.4，即大气近似为二氧化碳）。

4.压强的高度变化关系：根据大气压强的变化与高度的关系公式，可以将等温线上的两个压强P1、P2之间的关系转化为对应的高度h1、h2之间的关系，得到：h1 - h2 = log(P1/P2) * h0综上所述，我们可以得到等温线高度计算公式：h1 - h2 = log(T1/T2) * (κ * h0 / α)这个公式可以用来计算两个等温线上对应温度的高度差。

通过这个公式，我们可以研究大气层结、温度分布等大气的特性。

需要注意的是，上述公式是一个简化的模型，实际情况中，大气的温度梯度和压强变化并不是严格按照上述模型进行，受到多种因素的影响而呈现复杂的变化。

因此，具体的高度计算还需要考虑更多的因素和实际情况。

海拔高度与大气密度和温度间的换算关系
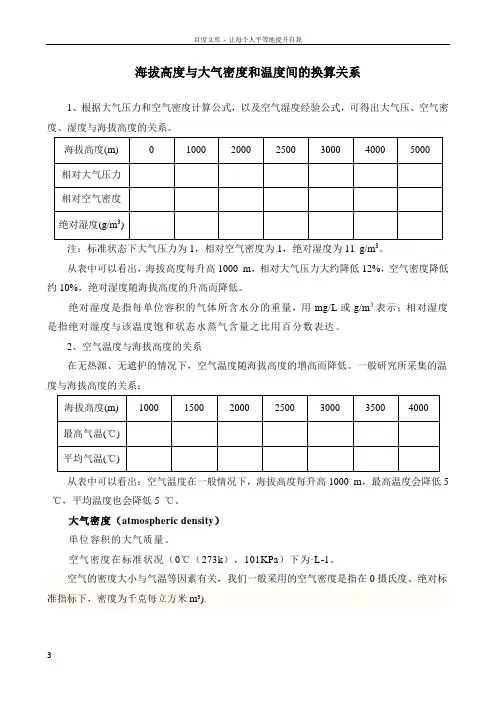
1、根据大气压力和空气密度计算公式，以及空气湿度经验公式，可得出大气压、空气密度、湿度与海拔高度的关系。

注：标准状态下大气压力为1，相对空气密度为1，绝对湿度为11 g/m3。

从表中可以看出，海拔高度每升高1000 m，相对大气压力大约降低12%，空气密度降低约10%，绝对湿度随海拔高度的升高而降低。

绝对湿度是指每单位容积的气体所含水分的重量，用mg/L或g/m3表示；相对湿度是指绝对湿度与该温度饱和状态水蒸气含量之比用百分数表达。

2、空气温度与海拔高度的关系
在无热源、无遮护的情况下，空气温度随海拔高度的增高而降低。

一般研究所采集的温度与海拔高度的关系：
从表中可以看出：空气温度在一般情况下，海拔高度每升高1000 m，最高温度会降低5℃，平均温度也会降低5 ℃。

大气密度（atmospheric density）
单位容积的大气质量。

空气密度在标准状况（0℃（273k），101KPa）下为·L-1。

空气的密度大小与气温等因素有关，我们一般采用的空气密度是指在0摄氏度、绝对标准指标下，密度为千克每立方米m³).
大气压力随海拔高度而变化,由经验公式P=P0（）（kPa）式中h一海拔高度（km）. 用上面公式,算出压力,然后根据密度= P *29/(8314*T),其中P的单位是帕,T的单位是K,通常也就是+t
不同温度下干空气算公式:
空气密度=(实际压力/标准物理大气压) *(273/实际绝对温度),绝对温度= + 273通常情况下,
即30摄氏度时,取M3
-60摄氏度时,取M3。

一个地方气压值经常有变化→其上空大气柱中空气质量的多少→大气柱厚度和密度改变的反映：大气柱厚度和密度与空气质量应该是成正比关系任何地方的气压值总是随着海拔高度的增加而递减。

据实测，在地面层中，高度每升100m，气压平均降低12.7hPa，在高层则小于此数值。

确定空气密度大小与气压随高度变化的定量关系，一般是应用静力学方程和压高方程。

1、静力学方程具体太长，我简单说明下：假使大气相对于地面处于静止状态，则某一点的气压值等于该点单位面积上所承受空气柱的重量。

公式是：h≈8000（1+t/273）/P（m/hPa）其中h是气压高度差，t是摄氏温标，P是气压从公式可以看出①在同一气压下，气柱的温度越高，密度越小，气压随高度递减越慢，单位气压高度差越大。

②在同一温度下，气压值越大的地方，空气密度越大，气压随高度递减越快，单位高度差越小。

通常，大气处于静力平衡状态，当气层不太厚和要求精度不太高时，这公式可粗略估算气压与高度的定量关系。

如果研究的气层高度变化范围很大，气柱中上下层温度、密度变化显著时，该公式就不适合用了，这时候可以用压高方程。

2、压高方程为了精确地获得气压与高度的对应关系，通常将静力学方程从气层底部到顶部进行积分，即得出压高方程，然后再将之替换简化为：Z2-Z1=18400（1+t/273）log( P1/P2)式中P1、P2分别是高度Z2、Z1的气压值，t是摄氏温标从公式可以看出①气压随高度增加按指数规律递减②高度越高，气压减小得越慢这公式是将大气当成干空气处理的，但当空气中水汽含量较多时，就必须用虚温代替式中的气温。

这就不详细再说了，太复杂了，你应该也不需要用到这么复杂的公式吧！呵呵，我没看清楚你的真正题意，给你一个相关的链接，可能比较准确。

大气压力与海拔高度关系表大气压力与海拔高度关系表（1mmHg=133.32Pa）大气压力（mmHg）海拔高度（m）PO2(mmHg)768760752745737730728714707699 692 684 676 669 661 654 646 638-84 085 170 256 343 431 519 608 698 789 880 9721066116012541350 1447160159157154151146138135 155.6152.4149.5147.7144.5142.8141.3139.7136.5133.3631623616608600593585570 562 555 547 5401544 1643 1743 1843 1945 2047 2151 2256 2362 2469 2577 2687 2797 2908 3020 313233603472358436953806131.8130.2128.6127125.4123.8122.3120.6119117.5116114112.7 111109108106105103 101.6100983916 403096.8 95。

海拔与气压的换算公式
咱们来聊聊海拔与气压的换算公式这事儿。

不知道您有没有过这样的经历，就是去爬山的时候，越往高处走，感觉呼吸越困难，甚至会有点头晕目眩。

这其实就和海拔与气压的关系有关啦。

咱们先来说说什么是气压。

简单来讲，气压就是空气对物体表面的压力。

在海平面附近，气压通常比较高，这时候咱们呼吸起来也相对轻松。

可一旦海拔升高，气压就会逐渐降低。

那海拔与气压到底是怎么换算的呢？这就有个公式啦，叫“气压随高度变化的经验公式”。

这个公式大概是这样的：P = P0 × (1 -
h/44300)^5.255 。

这里面的 P 就是要求的海拔 h 处的气压，P0 是海平面的气压，一般取 101325 帕斯卡。

比如说，您想知道在海拔 2000 米的地方气压是多少，那就把 h = 2000 米代入这个公式去算算。

算出来的结果，就能大概知道那个高度的气压情况啦。

我记得有一次去旅游，去了一个海拔挺高的山区。

当时就明显感觉到自己的身体有些不对劲，走几步路就气喘吁吁的。

后来一查资料，才明白原来是因为气压变低了，空气变得稀薄，氧气含量也少了，身体一时没适应过来。

这个换算公式在很多领域都有用处呢。

像是气象学，能帮助预测天气变化；在航空领域，能保证飞机的飞行安全；还有在登山活动中，能让登山者提前做好准备，应对可能出现的高原反应。

总之，了解海拔与气压的换算公式，不仅能让咱们更好地理解自然现象，还能在实际生活中派上用场。

下次您要是去高海拔的地方，就可以根据这个公式提前心里有个底，做好充足的准备，让旅程更加愉快和安全！。

标准大气的高度和气温、气压的关系
工作中经常用到大气资料，总结如下
这里所说的标准大气指国际民航组织采用的“1964，ICAO标准大气”。

在海拔32公里以下，它与“1976，.标准大气”相同。

近地面（32公里以下）大气气温的变化为：
---地面：气温的℃，气压P=
---地面至海拔11公里的气温变化率：–℃/公里
在11公里的界面上：
气温为–℃气压P=
海拔11—20公里的气温变化率：℃/公里
海拔20—32公里的气温变化率：+公里
更详细的数据可以参考《北半球标准大气(-2~80公里)》给出的大气参数。

气压的国际单位制是帕斯卡（或简称帕，符号是Pa），泛指是气体对某一点施加的流体静力压强，来源是大气层中空气的引力，即为单位面积上的大气压力。

在一般气象学中人们用千帕斯卡（KPa）、或使用百帕（hPa）作为单位。

测量气压的仪器叫气压表。

其它的常用单位分别是：巴（bar，1bar=100,000帕）和厘米水银柱（或称厘米汞柱）。

在海平面的平均气压约为千帕斯卡（76厘米水银柱），这个值也被称为标准大气压。

另外，在化学计算中，气压的国际单位是“atm”。

一个标准大气压即是1atm。

1个标准大气压等于101325帕，巴，或者76厘米水银柱。

大气压会随着高度的提升而下降，其关系为每提高12米，大气压下降1mm-Hg（1毫米水银柱），或者每上升9米，大气压降低100Pa。

下图给出了的大气温度、密度、压力分布图。

从图中可以看出温度在0-11km 成线性关系，压力和温度在0-3km(甚至5km)都成线性关系。

v1.0 可编辑可修改。

大气压海拔换算
大气压海拔换算
大气压海拔换算
由于大气压随着海拔高度的增加而逐渐下降，因此可以通过大气压值来推算出当前的海拔高度。

一般来说，海拔与大气压的换算关系如下：
海拔（m）= 44330 × [1 - （大气压/kPa）^（1/5.255）] 需要注意的是，这个公式只适用于标准大气条件下，即海平面上的大气压为101.325 kPa。

在实际应用中，由于大气压的变化和地理位置的不同，可能会有一定的误差。

除了用公式进行计算外，还可以使用一些常见的工具来进行海拔的测量，比如高度计、气压计等。

不过，无论采用何种方法进行海拔的测量，正确的数据处理和分析都是非常重要的，这样才能得到准确的结果。

- 1 -。

海拔与气压之间存在一定的关系，通常海拔越高，气压越低。

这是因为随着海拔的升高，空气的密度和压力逐渐减小。

具体的换算关系可以根据气象学公式进行计算。

一般来说，海拔每升高300米，气压会降低10hPa（百帕）。

因此，如果我们知道某地的海拔高度，就可以大致计算出该地的气压值。

例如，如果某地的海拔高度为1000米，那么该地的大气压强约为850hPa（（根据海平面处的大气压强为1013hPa计算得出）。

需要注意的是，这种换算方法是一种近似计算，实际的气压值可能会受到其他因素的影响，例如温度、湿度等。

因此，如果需要更精确的气压值，最好使用专业的气象仪器进行测量。

变温大气压强与海拔高度关系网上关于已知压强、温度求海拔高度的算法、公式的资料，有些是偏向于工程快速计算的，一般只给出了经验公式或部分代码；有些是在热力学基础上推导但仅仅停留在公式阶段。

不同计算方法之间，公式与公式差别也比较大，有的只给出压强与海拔高度的转化公式，有的加了温度修正，还有的直接给出表格供查询，由于没有对所应用的场合、计算精度加以说明，导致照抄归搬过来用后，实际计算出来的海拔高度与真值相差甚远，已经失去了实际意义。

下面针对气压、温度与海拔之间的关系及计算从理论到工程实践详细加以说明，作者才疏学浅，如有披露，还望各位网友加以斧正。

空气作为流体，我们对它进行静力学分析，先假设一定空间的空气作为不可压缩模型，在重力场中，有：空气的静力学模型1)上端面所受总压力为A p F 11=，方向向下2)下端面所受总压力为：A p F 22=，方向向上3)液体重力为：)(21z z gA G -=ρ4）液体处于静止时，上述三力合力为0，即A p 2-A p 1-)(21z z gA -ρ=0即1122z gp z g p +=+ρρ (1)整理为：)(1212z z g p p --=-ρ (2)上面的模型其实是把空气看成一个块状的，认为这一小段空间中压强不变，但其实空气气压是随高度渐变的，为了精确地获得气压与高度的对应关系，通常将静力学方程从气层底部到顶部进行积分，即得出压高方程⎰⎰-=-2121z z p p dz g dp ρ.....................(3)式中：m-气体质量M-气体分子量29R--常数8.51T--热力学温度(t+273.15)由理想气态方程RT Mm pV =..........................(4)即RT MVm p =(3)式左右同除p (m/MV)RT，有⎰⎰-=-2121z z p p dz RT V m Mg dp ρ.....................(5)又RT pM V m ==ρ，代入(5),有⎰⎰-=-2121z z p p dz RT Mg p dp .....................(6)即)(ln 1212z z RTMg p p --=-.....................(7)(7)式是大家都熟悉的气压方程了，但是从上面推导可以看出对于(7)式的应用有几点要注意：a)气压方程没考虑气温的变化，它的推导是建立在高空同温层上的b)公式中有4个变量，要选择一对气压和高度坐标为参考点。

变温大气压强与海拔高度关系公式推导bwdqy有些网上朋友提问关于大气压与海拔高度的关系、公式及推导。

回答各有所长，为了互相交流、互补，特写本文。

提到大气压与高度关系，自然想到相关的等温气压方程，网上朋友也多次提到它，下面就从它的推导过程说起。

一、等温气压方程推导理想气体状态方程式 nRT pV = 将M m n =代入上式得 RT MmpV = 式中：m —气体质量；M —气体分子量（或摩尔质量）。

将上式引入气体密度ρ的定义式中得RT pMV m ==ρ 在流体中，压强随高度的变化率是 g dhdpρ-=将ρ式代入上式得 RT gM p dh dp ⋅⋅-= 或dh RTg M p dp ⋅⋅-= 上式（T 为衡量）积分后得 )h (h RTg M p p ln 1212-⋅-= 这就是众所周知的“气压方程”。

二、等温气压方程分析现在从解决我们的问题角度考虑，对这个气压方程进行分析，它有以下几个特点： （1）气压方程没考虑气温的影响，因为它是用于高空同温层的公式。

而我们关心的是同温层以下温度有变化的区间，所以该式不能直接使用，必须加以温度校正。

（2）气压方程采取定积分形式，出现四个变量，用起来不方便。

平常只需要含有气压和高度两个变量的公式，因此应该预先定位，而且对于我们的问题也有条件预先定位。

（3）推导该式使用气压和高度的微小变化量列出方程，以求得非直线函数，方法合理可以采纳。

（4）推导该式基于液体压强计算公式h g p ⋅⋅ρ=，用于气体时因密度随气压而变，需要代入经过气压校正的密度。

该推导为了用气压校正密度，从nRT pV =、M m n =和Vm=ρ三式开始，导出了用分子量和气压共同计算密度的式子（前面的ρ式），终于把密度和气压联系到一起了，但是同时也把计算压强的起点从密度转移到了分子量。

而空气是一种混合物没有现成的分子量，反倒是密度容易被测定，数据较为原始，并能用它计算出(平均)分子量，现在又要从分子量算回密度，显得有些反复。