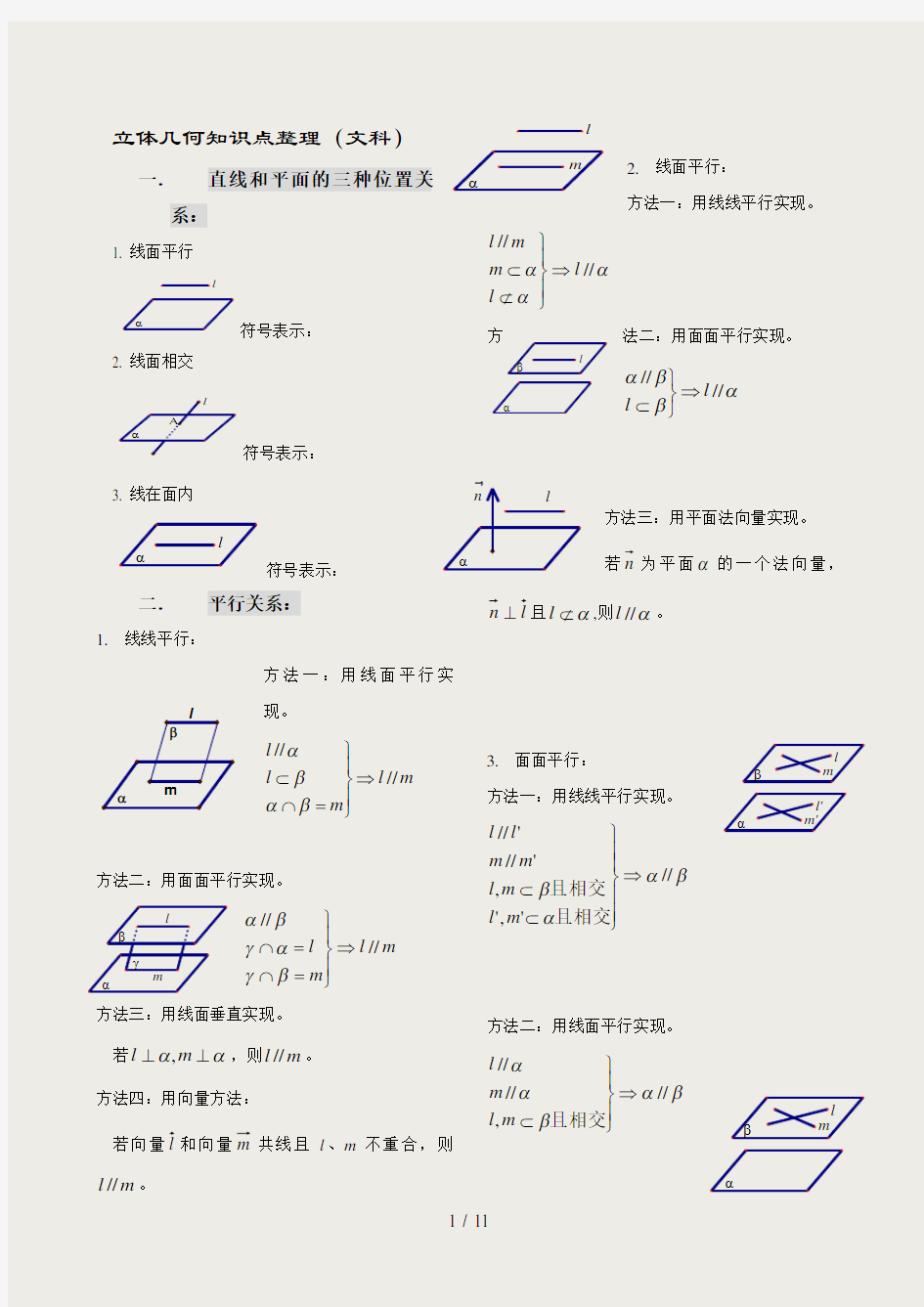

γm
βα
l
l
α
β立体几何知识点整理(文科)
一.
直线和平面的三种位置关
系:
1. 线面平行
α
l
符号表示:
2. 线面相交
α
A
l
符号表示:
3. 线在面内
α
l
符号表示:
二. 平行关系:
1. 线线平行:
方法一:用线面平行实
现。
m l m l l ////???
?
??=??βαβ
α
方法二:用面面平行实现。
m l m l ////???
?
??
=?=?βγαγβα 方法三:用线面垂直实现。 若αα⊥⊥m l ,,则m l //。 方法四:用向量方法:
若向量l 和向量m 共线且l 、m 不重合,则
m l //。
2. 线面平行:
方法一:用线线平行实现。
ααα////l l m m l ???
?
??
?? 方
法二:用面面平行实现。
αββα////l l ??
??
?
方法三:用平面法向量实现。
若n 为平面α的一个法向量,
l n ⊥且α?l ,则α//l 。
3. 面面平行:
方法一:用线线平行实现。
β
ααβ//',','
//'//?????
???
??且相交且相交m l m l m m l l
方法二:用线面平行实现。
βαβαα
//,////???
?
??
?且相交m l m l
m
l
α
n
α
l
m'l'l
α
βm m
β
α
l
l m
β
α
三.垂直关系: 1. 线面垂直:
方法一:用线线垂直实现。
αα⊥????
?
???
?=?⊥⊥l AB AC A AB AC AB l AC
l ,
方法二:用面面垂直实现。
αββαβα⊥???
?
??
?⊥=?⊥l l m l m ,
2. 面面垂直:
方法一:用线面垂直实现。
βαβα⊥??
??
?⊥l l
方法二:计算所成二面角为直角。 3. 线线垂直:
方法一:用线面垂直实现。
m l m l ⊥??
??
?⊥αα
方法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥?
?
⊥?⊥????
方法三:用向量方法:
若向量l 和向量m 的数量积为0,则m l ⊥。
三. 夹角问题。
(一) 异面直线所成的角: (1) 范围:]90,0(?? (2)求法: 方法一:定义法。
步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。(常用到余弦定理) 余弦定理:
ab
c
b a 2cos 2
22-+=θ
(计算结果可能是其补角) 方法二:向量法。转化为向量的夹角
(计算结果可能是其补角): AC
AB AC AB ??=
θcos
(二) 线面角
(1)定义:直线l 上任取一点P (交点除外),作PO ⊥α于O,连结AO ,则AO 为斜线PA 在面α内的射影,PAO ∠(图中θ)为直线l 与面α所成的角。
A
B
C αl
l
β
α
m
l
β
α
m α
l θ
c b
a
A
B
C
θn A
O
θ
P αl
A
O
P
α
A
O
θ
P
α
(2)范围:]90,0[??
当?=0θ时,α?l 或α//l 当?=90θ时,α⊥l (3)求法: 方法一:定义法。
步骤1:作出线面角,并证明。 步骤2:解三角形,求出线面角。
(三) 二面角及其平面角
(1)定义:在棱l 上取一点P ,两个半平面内分别作l 的垂线(射线)m 、n ,则射线m 和n 的夹角θ为二面角α—l —β的平面角。
n m l
β
α
P
θ
(2)范围:]180,0[?? (3)求法: 方法一:定义法。
步骤1:作出二面角的平面角(三垂线定理),并证明。
步骤2:解三角形,求出二面角的平面角。 方法二:截面法。
步骤1:如图,若平面POA 同时垂直于平面
βα和,则交线(射线)AP 和AO 的夹角就是二面
角。
步骤2:解三角形,求出二面角。
θA
O
P α
β
方法三:坐标法(计算结果可能与二面角互补)。
θ
n 1n 2
步骤一:计算121212
cos n n n n n n ?=?
步骤二:判断θ与12n n 的关系,可能相等或者互补。
四.
距离问题。
1.点面距。
方法一:几何法。
O
A
P
α
步骤1:过点P 作PO ⊥α于O ,线段PO 即为所求。
步骤2:计算线段PO 的长度。(直接解三角形;等体积法和等面积法;换点法)
2.线面距、面面距均可转化为点面距。 3.异面直线之间的距离 方法一:转化为线面距离。
n
m
α
如图,m 和n 为两条异面直线,α?n 且
α//m ,则异面直线m 和n 之间的距离可转化为
直线m 与平面α之间的距离。 方法二:直接计算公垂线段的长度。 方法三:公式法。
d c
b
a
θm'
D
C
B A
m
n
如图,AD 是异面直线m 和n 的公垂线段,
'//m m ,则异面直线m 和n 之间的距离为: θ
cos 2222ab b a c d ±--=
五. 空间向量
(一) 空间向量基本定理
若向量c b a ,,为空间中不共面的三个向量,则对空间中任意一个向量p ,都存在唯一的有序实数对
z y x 、、,使得c z b y a x p ++=。
(二) 三点共线,四点共面问题 1. A ,B ,C 三点共线?
OA xOB yOC =+,且1x y +=
当2
1
=
=y x 时,A 是线段BC 的 A ,B ,C 三点共线?AC AB λ= 2. A ,B ,C ,D 四点共面?
OA xOB yOC zOD =++,且1x y z ++=
当1
3
x y z ===
时,A 是△BCD 的 A ,B ,C ,D 四点共面?AD y AC x AB += (三)空间向量的坐标运算
1. 已知空间中A 、B 两点的坐标分别为:
111(,,)A x y z ,222(,,)B x y z 则:
AB = ;=B A d ,AB =
A
B
C D
1
A
1
C
1
B
2. 若空间中的向量111(,,)a x y z =,),,(222z y x b = 则a b += a b -=
a b ?= cos a b =
六.常见几何体的特征及运算 (一) 长方体
1. 长方体的对角线相等且互相平分。
2. 若长方体的一条对角线与相邻的三条棱所成的角分别为αβγ、、,则2
2
2
cos cos cos αβγ=++
β
γ
αα
βγ
若长方体的一条对角线与相邻的三个面所成的角分别为αβγ、、,则2
2
2
cos cos cos αβγ=++ 3.若长方体的长宽高分别为a 、b 、c ,则体对角线长为 ,表面积为 ,体积为 。 (二) 正棱锥:底面是正多边形且顶点在底面的射影在底面中心。 (三) 正棱柱:底面是正多边形的直棱柱。
(四) 正多面体:每个面有相同边数的正多边形,且每个顶点为端点有相同棱数的凸多面体。 (只有五种正多面体)
(五) 棱锥的性质:平行于底面的的截面与底面相似,且面积比等于顶点到截面的距离与棱锥的高的平方
比。
正棱锥的性质:各侧棱相等,各侧面都是全等的等腰三角形。 (六) 体积:=棱柱V =棱锥V (七) 球
1.定义:到定点的距离等于定长的点的集合叫球面。
2. 设球半径为R ,小圆的半径为r ,小圆圆心为O 1,球心O 到小圆的距离为d ,则它们三者之间的数量关系是 。
3. 球面距离:经过球面上两点的大圆在这两点间的一段劣弧的长度。
4.球的表面积公式: 体积公式:
高考题典例
考点1 点到平面的距离
例1如图,正三棱柱111ABC A B C -的所有棱长都为2,D 为1CC 中点.(Ⅰ)求证:1AB ⊥平面1A BD ;(Ⅱ)求二面角1A A D B --的大小;(Ⅲ)求点C 到平面1A BD 的距离.
解答过程(Ⅰ)取BC 中点O ,连结AO .
ABC △为正三角形,AO BC ∴⊥.
正三棱柱111ABC A B C -中,平面ABC ⊥平面11BCC B ,
AO ∴⊥平面11BCC B .连结1B O ,在正方形11BB C C 中,O D ,分
别
为
1BC CC ,的中点, 1B O BD ∴⊥, 1AB BD ∴⊥.
在正方形11ABB A 中,11AB A B ⊥, 1AB ∴⊥平面1A BD .
(Ⅱ)设1AB 与1A B 交于点G ,在平面1A BD 中,作
1GF A D
⊥于
F ,连结AF ,由(Ⅰ)得1AB ⊥平面1A BD .
1AF A D ∴⊥, AFG ∴∠为二面角1A A D B --的平面角.
在1AA D △中,由等面积法可求得455
AF =,
又1122AG AB ==, 210sin 4
455AG AFG AF ∴===∠.
所以二面角1A A D B --的大小为10arcsin 4
.
(Ⅲ)1A BD △中,1115226A BD BD A D A B S ===∴=△,,,1BCD S =△.在正三棱柱中,1A 到平面11BCC B 的距离为3.设点C 到平面1A BD 的距离为d .由1
1
A BCD C A BD V V --=,得11133
3BCD
A BD S S d =△△,
1322
BCD A BD S d S ∴==
△△.
∴点C 到平面1A BD 的距离为22
.
A
B
C D
1
A
1
C
1
B
O F
考点2 异面直线的距离
例2 已知三棱锥ABC S -,底面是边长为24的正三角形,棱SC 的长为2,且垂直于底面.D E 、分别为AB BC 、的中点,求CD 与SE 间的距离.
解答过程: 如图所示,取BD 的中点F ,连结EF ,SF ,CF ,
EF ∴为BCD ?的中位线,EF ∴∥CD CD ∴,∥面
SEF ,CD ∴到平面SEF 的距离即为两异面直线间的距离.又
线面之间的距离可转化为线CD 上一点C 到平面SEF
的距离,设其为h ,由题意知,24=BC ,D 、E 、F 分别是AB 、BC 、BD 的中点,
2,2,62
1
,62=====∴SC DF CD EF CD 3
3222621312131=????=????=
∴-SC DF EF V CEF S 在Rt SCE ?中,3222=+=CE SC SE
在Rt SCF ?中,30224422=++=+=CF SC SF
又3,6=∴=
?SEF S EF 由于h S V V SEF CEF S SEF C ??==?--3
1
,即332331=
??h ,解得332=h 故CD 与SE 间的距离为
3
3
2. 考点3 直线到平面的距离
例3. 如图,在棱长为2的正方体1AC 中,G 是1AA 的中点,求BD 到平面11D GB 的距离. 思路启迪:把线面距离转化为点面距离,再用点到平面距离的方法求解. 解答过程:解析一BD ∥平面11D GB ,
BD ∴上任意一点到平面11D GB 的距离皆为所求,以下求
点O 平面11D GB 的距离,
1111C A D B ⊥ ,A A D B 111⊥,⊥∴11D B 平面11ACC A ,
又?11D B 平面11D GB ∴平面1111D GB ACC A ⊥,两个平面的交线是G O 1,
B
A
C
D
O
G
H 1
A 1
C 1D
1
B 1O
作G O OH 1⊥于H ,则有⊥OH 平面11D GB ,即OH 是O 点到平面11D GB 的距离. 在OG O 1?中,2222
1
2111=??=??=?AO O O S OG O . 又3
6
2,23212111=∴=??=??=
?OH OH G O OH S OG O . 即BD 到平面11D GB 的距离等于3
6
2. 解析二 BD ∥平面11D GB ,
BD ∴上任意一点到平面11D GB 的距离皆为所求,以下求点B 平面11D GB 的距离.
设点B 到平面11D GB 的距离为h ,将它视为三棱锥11D GB B -的高,则
,由于632221
,111111=??=
=?--D GB GBB D D GB B S V V 3
4
222213111=
????=-GBB D V ,
,3
6
26
4=
=
∴h 即BD 到平面11D GB 的距离等于
3
6
2. 小结:当直线与平面平行时,直线上的每一点到平面的距离都相等,都是线面距离.所以求线面距离关键是选准恰当的点,转化为点面距离.本例解析一是根据选出的点直接作出距离;解析二是等体积法求出点面距离.
考点4 异面直线所成的角
例4如图,在Rt AOB △中,π6
OAB ∠=,斜边4AB =.Rt AOC △可以通过Rt AOB △以直线AO 为轴旋转
得到,且二面角B AO C --的直二面角.D 是AB 的中点. (I )求证:平面COD ⊥平面AOB ;
(II )求异面直线AO 与CD 所成角的大小. 解答过程:(I )由题意,CO AO ⊥,BO AO ⊥,
BOC ∴∠是二面角B AO C --是直二面角,
CO BO ∴⊥,又AO BO O =,CO ∴⊥平面AOB ,
又CO ?平面COD .∴平面COD ⊥平面AOB .
(II )作DE OB ⊥,垂足为E ,连结CE (如图),则DE AO ∥,
O
C
A
D
B
E
A
D
z
CDE ∴∠是异面直线AO 与CD 所成的角.
在Rt COE △中,2CO BO ==,112
OE BO ==,225CE CO OE ∴=+=.
又132DE AO ==.∴在Rt CDE △中,515tan 33
CE CDE DE ===.
∴异面直线AO 与CD 所成角的大小为15arctan 3
.
小结: 求异面直线所成的角常常先作出所成角的平面图形,作法有:①平移法:在异面直线中的一条直线上选择“特殊点”,作另一条直线的平行线,如解析一,或利用中位线,如解析二;②补形法:把空间图形补成熟悉的几何体,其目的在于容易发现两条异面直线间的关系,如解析三.一般来说,平移法是最常用的,应作为求异面直线所成的角的首选方法.同时要特别注意异面直线所成的角的范围:??
? ??2,
0π.
考点5 直线和平面所成的角
例5. 四棱锥S ABCD -中,底面ABCD 为平行四边形,侧面SBC ⊥底面ABCD .已知45ABC =∠,
2AB =,22BC =,3SA SB ==.
(Ⅰ)证明SA BC ⊥;(Ⅱ)求直线SD 与平面SAB 所成角的大小.
解答过程:(Ⅰ)作SO BC ⊥,垂足为O ,连结AO ,由侧面
SBC ⊥
底面ABCD ,得SO ⊥底面ABCD . 因为SA SB =,所以AO BO =,
又45ABC =∠,故AOB △为等腰直角三角形,
AO BO ⊥,由三垂线定理,得SA BC ⊥.
(Ⅱ)由(Ⅰ)知SA BC ⊥,依题设AD BC ∥, 故SA AD ⊥,由22AD BC ==,3SA =
,
2AO =,得 1SO =,11SD =. SAB △的面积2
2
11122
2S AB
SA AB ??
=-= ???
.
连结DB ,得DAB △的面积21
sin13522
S AB AD =
= 设D 到平面SAB 的距离为h ,由于D SAB S ABD V V --=,得12113
3
h S SO S =,解得2h =. 设SD 与平面SAB 所成角为α,则222sin 1111h SD α===.
所以,直线SD 与平面SBC 所成的我为22arcsin 11
.
D
B
C
A
S
O
D
B
C
A
S
小结:求直线与平面所成的角时,应注意的问题是(1)先判断直线和平面的位置关系;(2)当直线和平面斜交时,常用以下步骤:①构造——作出斜线与射影所成的角,②证明——论证作出的角为所求的角,③计算——常用解三角形的方法求角,④结论——点明直线和平面所成的角的值. 考点6 二面角
例6.如图,已知直二面角PQ αβ--,A PQ ∈,B α∈,C β∈,CA CB =,
45BAP ∠=,直线CA 和平面α所成的角为30.(I )证明BC PQ ⊥
(II )求二面角B AC P --的大小.
过程指引:(I )在平面β内过点C 作CO PQ ⊥于点O ,连结OB . 因为αβ⊥,PQ α
β=,所以CO α⊥,
又因为CA CB =,所以OA OB =.
而45BAO ∠=,所以45ABO ∠=,90AOB ∠=, 从而BO PQ ⊥,又CO PQ ⊥,
所以PQ ⊥平面OBC .因为BC ?平面OBC ,故PQ BC ⊥. (II )由(I )知,BO PQ ⊥,又αβ⊥,PQ α
β=,
BO α?,所以BO β⊥.过点O 作OH AC ⊥于点H ,连结BH ,由三垂线定理知,BH AC ⊥.故BHO ∠是二面角B AC P --的平面角.
由(I )知,CO α⊥,所以CAO ∠是CA 和平面α所成的角,则30CAO ∠=,
不妨设2AC =,则3AO =,3sin 302
OH AO ==
. 在Rt OAB △中,45ABO BAO ∠=∠=,所以3BO AO ==,于是在Rt BOH △中,
3
tan 232
BO
BHO OH
∠=
==.故二面角B AC P --的大小为arctan 2. 小结:本题是一个无棱二面角的求解问题.解法一是确定二面角的棱,进而找出二面角的平面角.无棱二面角棱的确定有以下三种途径:①由二面角两个面内的两条相交直线确定棱,②由二面角两个平面内的两条平行直线找出棱,③补形构造几何体发现棱;解法二则是利用平面向量计算的方法,这也是解决无棱
A
B
C
Q
α
β P A
B C
Q
α
β P O H
二面角的一种常用方法,即当二面角的平面角不易作出时,可由平面向量计算的方法求出二面角的大小. 考点7 利用空间向量求空间距离和角
例7. 如图,已知1111ABCD A B C D -是棱长为3的正方体, 点E 在1AA 上,点F 在1CC 上,且11AE FC ==. (1)求证:1E B F D ,,,四点共面;
(2)若点G 在BC 上,2
3
BG =,点M 在1BB 上,
GM BF ⊥,垂足为H ,求证:EM ⊥平面11BCC B ;
(3)用θ表示截面1EBFD 和侧面11BCC B 所成的锐二面角的大小,求tan θ. 过程指引:(1)如图,在1DD 上取点N ,使1DN =,连结EN ,
CN ,则1AE DN ==,12CF ND ==.
因为AE DN ∥,1ND CF ∥,所以四边形ADNE ,1CFD N 都为平行四
边形.从而EN AD ∥
,1FD CN ∥. 又因为AD BC ∥
,所以EN BC ∥,故四边形BCNE 是平行四边形,由此推知CN BE ∥,从而1FD BE ∥.因此,1E B F D ,,,四点共面. (2)如图,GM BF ⊥,又BM BC ⊥,所以BGM CFB =∠∠,
tan tan BM BG BGM BG CFB ==∠∠23
132
BC BG
CF ==?=. 因为AE BM ∥
,所以ABME 为平行四边形,从而AB EM ∥. 又AB ⊥平面11BCC B ,所以EM ⊥平面11BCC B .
(3)如图,连结EH .因为MH BF ⊥,EM BF ⊥,所以BF ⊥平面EMH ,得EH BF ⊥.于是
EHM ∠是所求的二面角的平面角,即EHM θ=∠.
因为MBH CFB =∠∠,所以sin sin MH BM MBH BM CFB ==∠∠
22
22
33113
32BC BM
BC CF ==?
=
++, tan 13EM MH θ==.
C
B
A
G H
M
D
E
F
1
B
1
A
1
D
1
C
C
B
A
G H
M
D
E
F 1
B
1
A
1
D
1
C
N