Model checking probabilistic pushdown automata
- 格式:pdf
- 大小:205.00 KB
- 文档页数:10

负载均衡MLB方案验证与建议配置参数1.背景描述随着LTE业务的不断的发展,热点区域、高业务量区域、景区突发高用户数区域等相继出现。
针对容量不足问题,小区扩容、站点新建等措施不断开展,而通过监控现网KPI指标发现,同覆盖小区间的容量差异问题日益严重,一个因资源耗尽而无法使用正常业务,另一个却因空闲而资源浪费。
移动性负载均衡功能作为业务分担的有效策略,在早期版本中已实现落地。
由最开始的PRB利用率触发方式,到现在的仅用户数触发和PRB与用户数联合触发方式等多种策略方案,为解决业务分担不均问题,提供了的有力的解决方案。
MLB方案在实际落地过程中,室分同覆盖场景的优化效果相对明显,但针对宏站同覆盖场景,却收效甚微。
为研究问题原因,解决宏站同覆盖业务分担不均问题,针对MLB方案涉及的相关参数进行充分验证,指导后续优化并推广应用。
2.方案概述2.1. 基本流程MLB流程整体分为三个阶段如下:第一步:本区监测负载水平,当负载超过算法触发门限时,触发MLB算法,交互邻区负载信息,作为算法输入。
第二步:筛选可以作为MLB的目标邻区和执行UE第三步:基于切换或者重选完成MLB动作。
2.2. 适用场景异频负载均衡的主要适用场景包括如下几类:•同站同覆盖场景•同站大小覆盖场景•同站交叠覆盖场景•异站交叠覆盖场景•宏微站交叠覆盖场景3.实际问题3.1. 异频策略当前温州现网总体的FD频段策略如下:1)D频段重选优先级高于F频段2)F频段异频启测A2门限普遍为-82dBm,D频段为-96dBm该策略的主要目的为F频段作为连续覆盖层,D频段作为容量层,用户在共覆盖区域优先主流D频段小区。
由此,当区域用户集中增加时,D频段小区容易吸收过多用户,而F频段小区因启测门限过高而驻留能力偏弱,导致出现一个过忙一个过闲的现象。
3.2. MLB当前策略针对如上异频策略,前期工作也已经采取了相关负载均衡的优化,但实际效果远没有达到预期。
前期的主要策略如下:1、打开异频负载均衡开关,选择仅用户数触发方式2、开启连接态用户负载均衡,未开启空闲态用户负载均衡3、自定义调整用户数(异频负载均衡用户数门限+负载均衡用户数偏置)触发门限,一般选取同覆盖区域每小区平均用户数为触发门限4、其他参数保持默认状态采用如上方式进行优化后,产生负载均衡效果的小区较少,未能实现充分利用无线资源的预期。

principles of model checkingModel checking is a formal verification technique used to check whether a model of a system meets a desired property or specification. The principles of model checking include:1. Formal specification: The desired property or behavior of the system is formally specified using a temporal logic language, such as linear temporal logic (LTL) or computational tree logic (CTL). This specification serves as the basis for model checking.2. Finite-state model: The system is modeled as a finite-state model, which consists of a set of states and transitions between states. This model captures the behavior of the system's components and their interactions.3. State space exploration: The state space of the model is systematically explored to check whether the desired property holds for all possible system executions. This involves generating and evaluating the possible execution paths of the system.4. Verification algorithm: A verification algorithm is used to traverse the state space and check the specified property at each state. Model checking algorithms, such as depth-first search or breadth-first search, are typically used for this purpose.5. Counterexample generation: If the desired property does not hold, the model checking process can generate a counterexample, which is a specific sequence of system states and transitions that violates the property. This provides insights into the specific causes of the violation and helps in debugging and refinement.6. Scalability: Model checking can be applied to both small-scale and large-scale systems. To handle complex systems, various techniques such as abstraction, symmetry reduction, and partial order reduction are used to reduce the size of the state space and make the verification process more efficient.7. Automation: Model checking is largely an automated process, where computer tools are used to systematically explore the state space and check the specified property. This helps in reducing human error and makes the verification process more reproducible and reliable.8. Soundness and completeness: Model checking aims to provide sound and complete results. Soundness means that if the model checker reports that the property holds, then it indeed holds in all possible executions of the system. Completeness means that if the property does not hold, the model checker will eventually find a counterexample.By following these principles, model checking provides a systematic and rigorous approach to verify the correctness of system models, which has applications in various domains such as software engineering, hardware design, and protocol verification.。

一:介绍1. 范围2. 概况3. 参考文件二:RADIO FREQUENCY无线电频率测试1. 介绍2. 测试环境3. 测试项目3.1 Output power输出功率3.2 Power Control 功率控制3.3 Initial Carrier Frequency 最初的载波频率3.4 Carrier Frequency Drift 载波频率漂移3.5 Modulation Characteristic 调制特性3.6 Single Slot Sensitivity单插槽的敏感性3.7 Multi Slots Sensitivity 多槽灵敏度3.8 Maximum Input Level最大输入标准三:蓝牙耳机功能测试1. 耗电量静态及工作电流/待机电流2. 充电、充电连接、显示3. 频率调整4. 配对5. 音频连接6. 仿真音频7. 兼容性8. 通话距离9. 外观结构四:附件功能测试1. 火牛高压2. 火牛输出电压3. SPK功能4. MIC功能五:运行条件一:介绍1. 范围此文件概括说明所有蓝牙产品的初步测试计划2. 概况3.1~3.8项目主要描述射频测试,三项主要描述耳机实际使用功能测试,四项主要描述耳机附件的功能测试3. 参考文件[1]Bluetooth: Specification of the Bluetooth System, Volume 2: Core(Controller v1.2 )蓝牙:蓝牙系统的规范,卷2:核心(控制器v1.2)[2]Bluetooth: Specification of the Bluetooth System, Volume 3: Core (Hostv1.2 )[3]Bluetooth: Specification of the Bluetooth System, Volume 2: Core(Controller v2.0)[4]Bluetooth: Specification of the Bluetooth System, Volume 3: Core (Host v2.0)[5]Bluetooth: Headset Profile (v1.1) 蓝牙:耳机概要(v1.1[6]Bluetooth: Core System Package : RF Test Suite Structure (TSS) /TestPurpose(TP) (v2.0)蓝牙:核心系统方案:射频测试套件结构(TSS)/测试目的(TP)(v2.0)[7]Bluetooth: Core System Package : Baseband Test Suite Structure (TSS) /TestPurpose(TP) (v2.0) 蓝牙:核心系统方案:基带测试套件结构(TSS)/测试目的(TP)(v2.0)[8]Bluetooth: Core System Package : LM Test Suite Structure (TSS) /TestPurpose(TP) (v2.0)蓝牙:核心系统方案:LM测试套件结构(TSS)/测试目的(TP)(v2.0)[9]Bluetooth: Core System Package : General Access Profile Test SuiteStructure (TSS) /Test Purpose(TP) (v2.0) 蓝牙:核心系统方案:通用访问配置文件测试套件结构(TSS)/测试目的(TP)(v2.0[10]Bluetooth: Headset Profile Specification 1.1 Test Suite Structure (TSS)/Test Purpose(TP)牙:耳机概要文件规范1.1测试套件结构(TSS)/测试目的(TP)[11]CSR: BlueCore2-Audio Datasheet企业社会责任:BlueCore2-Audio数据表TP是可靠性测试二:RADIO FREQUENCY TEST射频测试1. 介绍这一个测试是确定蓝牙耳机的射频 (发射器和接收器) 基本功能是否符合或超过蓝牙标准要求2. 测试环境Bluetooth Tester-- Anritsu MT8852A/MT8852B or other 蓝牙测试仪,特制MT8852A / MT8852B或其他DUT(Device Under Test)- Linnking Bluetooth DUT(测试设备)——Linnking蓝牙3. 测试项目3.1 Output power 输出功率DUT 初始设置:DUT用loop back测试模式使用跳频测试程序及标准MT8850A 传输一个标准的数据包(DH5 , DH1,DH3 或Longest )给DUT. 此DUT 环向后将数据传送给Bluetooth tester ,MT8850A 测量其功率. 这一个测试在跳时运行,而且测试被重复。

multilingual processing system 多语讯息处理系统multilingual translation 多语翻译multimedia 多媒体multi-media communication 多媒体通讯multiple inheritance 多重继承multistate logic 多态逻辑mutation 语音转换mutual exclusion 互斥mutual information 相互讯息nativist position 语法天生假说natural language 自然语言natural language processing (nlp) 自然语言处理natural language understanding 自然语言理解negation 否定negative sentence 否定句neologism 新词语nested structure 崁套结构network 网络neural network 类神经网络neurolinguistics 神经语言学neutralization 中立化n-gram n-连词n-gram modeling n-连词模型nlp (natural language processing) 自然语言处理node 节点nominalization 名物化nonce 暂用的non-finite 非限定non-finite clause 非限定式子句non-monotonic reasoning 非单调推理normal distribution 常态分布noun 名词noun phrase 名词组np (noun phrase) completeness 名词组完全性object 宾语{语言学}/对象{信息科学}object oriented programming 对象导向程序设计[面向对向的程序设计]official language 官方语言one-place predicate 一元述语on-line dictionary 线上查询词典 [联机词点]onomatopoeia 拟声词onset 节首音ontogeny 个体发生ontology 本体论open set 开放集operand 操作数 [操作对象]optimization 最佳化 [最优化]overgeneralization 过度概化overgeneration 过度衍生paradigmatic relation 聚合关系paralanguage 附语言parallel construction 并列结构parallel corpus 平行语料库parallel distributed processing (pdp) 平行分布处理paraphrase 转述 [释意;意译;同意互训]parole 言语parser 剖析器 [句法剖析程序]parsing 剖析part of speech (pos) 词类particle 语助词part-of relation part-of 关系part-of-speech tagging 词类标注pattern recognition 型样识别p-c (predicate-complement) insertion 述补中插pdp (parallel distributed processing) 平行分布处理perception 知觉perceptron 感觉器 [感知器]perceptual strategy 感知策略performative 行为句periphrasis 用独立词表达perlocutionary 语效性的permutation 移位petri net grammar petri 网语法philology 语文学phone 语音phoneme 音素phonemic analysis 因素分析phonemic stratum 音素层phonetics 语音学phonogram 音标phonology 声韵学 [音位学;广义语音学] phonotactics 音位排列理论phrasal verb 词组动词 [短语动词]phrase 词组 [短语]phrase marker 词组标记 [短语标记]pitch 音调pitch contour 调形变化pivot grammar 枢轴语法pivotal construction 承轴结构plausibility function 可能性函数pm (phrase marker) 词组标记 [短语标记] polysemy 多义性pos-tagging 词类标记postposition 方位词pp (preposition phrase) attachment 介词依附pragmatics 语用学precedence grammar 优先级语法precision 精确度predicate 述词predicate calculus 述词计算predicate logic 述词逻辑 [谓词逻辑]predicate-argument structure 述词论元结构prefix 前缀premodification 前置修饰preposition 介词prescriptive linguistics 规定语言学 [规范语言学] presentative sentence 引介句presupposition 前提principle of compositionality 语意合成性原理privative 二元对立的probabilistic parser 概率句法剖析程序problem solving 解决问题program 程序programming language 程序设计语言 [程序设计语言] proofreading system 校对系统proper name 专有名词prosody 节律prototype 原型pseudo-cleft sentence 准分裂句psycholinguistics 心理语言学punctuation 标点符号pushdown automata 下推自动机pushdown transducer 下推转换器qualification 后置修饰quantification 量化quantifier 范域词quantitative linguistics 计量语言学question answering system 问答系统queue 队列radical 字根 [词干;词根;部首;偏旁]radix of tuple 元组数基random access 随机存取rationalism 理性论rationalist (position) 理性论立场 [唯理论观点]reading laboratory 阅读实验室real time 实时real time control 实时控制 [实时控制]recursive transition network 递归转移网络reduplication 重叠词 [重复]reference 指涉referent 指称对象referential indices 指针referring expression 指涉词 [指示短语]register 缓存器[寄存器]{信息科学}/调高{语音学}/语言的场合层级{社会语言学}regular language 正规语言 [正则语言]relational database 关系型数据库 [关系数据库]relative clause 关系子句relaxation method 松弛法relevance 相关性restricted logic grammar 受限逻辑语法resumptive pronouns 复指代词retroactive inhibition 逆抑制rewriting rule 重写规则rheme 述位rhetorical structure 修辞结构rhetorics 修辞学robust 强健性robust processing 强健性处理robustness 强健性schema 基朴school grammar 教学语法scope 范域 [作用域;范围]script 脚本search mechanism 检索机制search space 检索空间searching route 检索路径 [搜索路径]second order predicate 二阶述词segmentation 分词segmentation marker 分段标志selectional restriction 选择限制semantic field 语意场semantic frame 语意架构semantic network 语意网络semantic representation 语意表征 [语义表示] semantic representation language 语意表征语言semantic restriction 语意限制semantic structure 语意结构semantics 语意学sememe 意素semiotics 符号学sender 发送者sensorimotor stage 感觉运动期sensory information 感官讯息 [感觉信息]sentence 句子sentence generator 句子产生器 [句子生成程序]sentence pattern 句型separation of homonyms 同音词区分sequence 序列serial order learning 顺序学习serial verb construction 连动结构set oriented semantic network 集合导向型语意网络 [面向集合型语意网络]sgml (standard generalized markup language) 结构化通用标记语言shift-reduce parsing 替换简化式剖析short term memory 短程记忆sign 信号signal processing technology 信号处理技术simple word 单纯词situation 情境situation semantics 情境语意学situational type 情境类型social context 社会环境sociolinguistics 社会语言学software engineering 软件工程 [软件工程]sort 排序speaker-independent speech recognition 非特定语者语音识别spectrum 频谱speech 口语speech act assignment 言语行为指定speech continuum 言语连续体speech disorder 语言失序 [言语缺失]speech recognition 语音辨识speech retrieval 语音检索speech situation 言谈情境 [言语情境]speech synthesis 语音合成speech translation system 语音翻译系统speech understanding system 语音理解系统spreading activation model 扩散激发模型standard deviation 标准差standard generalized markup language 标准通用标示语言start-bound complement 接头词state of affairs algebra 事态代数state transition diagram 状态转移图statement kernel 句核static attribute list 静态属性表statistical analysis 统计分析statistical linguistics 统计语言学statistical significance 统计意义stem 词干stimulus-response theory 刺激反应理论stochastic approach to parsing 概率式句法剖析 [句法剖析的随机方法]stop 爆破音stratificational grammar 阶层语法 [层级语法]string 字符串[串;字符串]string manipulation language 字符串操作语言string matching 字符串匹配 [字符串]structural ambiguity 结构歧义structural linguistics 结构语言学structural relation 结构关系structural transfer 结构转换structuralism 结构主义structure 结构structure sharing representation 结构共享表征subcategorization 次类划分 [下位范畴化] subjunctive 假设的sublanguage 子语言subordinate 从属关系subordinate clause 从属子句 [从句;子句] subordination 从属substitution rule 代换规则 [置换规则] substrate 底层语言suffix 后缀superordinate 上位的superstratum 上层语言suppletion 异型[不规则词型变化] suprasegmental 超音段的syllabification 音节划分syllable 音节syllable structure constraint 音节结构限制symbolization and verbalization 符号化与字句化synchronic 同步的synonym 同义词syntactic category 句法类别syntactic constituent 句法成分syntactic rule 语法规律 [句法规则]syntactic semantics 句法语意学syntagm 句段syntagmatic 组合关系 [结构段的;组合的] syntax 句法systemic grammar 系统语法tag 标记target language 目标语言 [目标语言]task sharing 课题分享 [任务共享] tautology 套套逻辑 [恒真式;重言式;同义反复] taxonomical hierarchy 分类阶层 [分类层次] telescopic compound 套装合并template 模板temporal inference 循序推理 [时序推理] temporal logic 时间逻辑 [时序逻辑] temporal marker 时貌标记tense 时态terminology 术语text 文本text analyzing 文本分析text coherence 文本一致性text generation 文本生成 [篇章生成]text linguistics 文本语言学text planning 文本规划text proofreading 文本校对text retrieval 文本检索text structure 文本结构 [篇章结构]text summarization 文本自动摘要 [篇章摘要] text understanding 文本理解text-to-speech 文本转语音thematic role 题旨角色thematic structure 题旨结构theorem 定理thesaurus 同义词辞典theta role 题旨角色theta-grid 题旨网格token 实类 [标记项]tone 音调tone language 音调语言tone sandhi 连调变换top-down 由上而下 [自顶向下]topic 主题topicalization 主题化 [话题化]trace 痕迹trace theory 痕迹理论training 训练transaction 异动 [处理单位]transcription 转写 [抄写;速记翻译]transducer 转换器transfer 转移transfer approach 转换方法transfer framework 转换框架transformation 变形 [转换]transformational grammar 变形语法 [转换语法] transitional state term set 转移状态项集合transitivity 及物性translation 翻译translation equivalence 翻译等值性translation memory 翻译记忆transparency 透明性tree 树状结构 [树]tree adjoining grammar 树形加接语法 [树连接语法] treebank 树图数据库[语法关系树库]trigram 三连词t-score t-数turing machine 杜林机 [图灵机]turing test 杜林测试 [图灵试验]type 类型type/token node 标记类型/实类节点type-feature structure 类型特征结构typology 类型学ultimate constituent 终端成分unbounded dependency 无界限依存underlying form 基底型式underlying structure 基底结构unification 连并 [合一]unification-based grammar 连并为本的语法 [基于合一的语法] universal grammar 普遍性语法universal instantiation 普遍例式universal quantifier 全称范域词unknown word 未知词 [未定义词]unrestricted grammar 非限制型语法usage flag 使用旗标user interface 使用者界面 [用户界面]valence grammar 结合价语法valence theory 结合价理论valency 结合价variance 变异数 [方差]verb 动词verb phrase 动词组 [动词短语]verb resultative compound 动补复合词verbal association 词语联想verbal phrase 动词组verbal production 言语生成vernacular 本地话v-o construction (verb-object) 动宾结构vocabulary 字汇vocabulary entry 词条vocal track 声道vocative 呼格voice recognition 声音辨识 [语音识别]vowel 元音vowel harmony 元音和谐 [元音和谐]waveform 波形weak verb 弱化动词whorfian hypothesis whorfian 假说word 词word frequency 词频word frequency distribution 词频分布word order 词序word segmentation 分词word segmentation standard for chinese 中文分词规范word segmentation unit 分词单位 [切词单位]word set 词集working memory 工作记忆 [工作存储区]world knowledge 世界知识writing system 书写系统x-bar theory x标杠理论 ["x"阶理论]zipf's law 利夫规律 [齐普夫定律]。

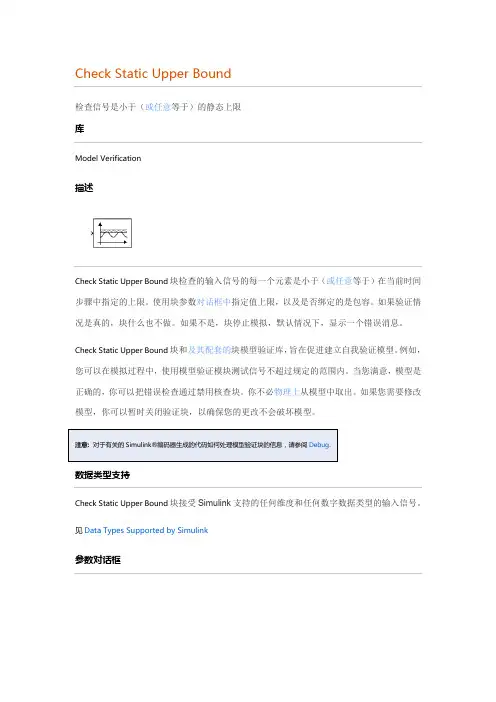
Check Static Upper Bound检查信号是小于(或任意等于)的静态上限库Model Verification描述Check Static Upper Bound块检查的输入信号的每一个元素是小于(或任意等于)在当前时间步骤中指定的上限。
使用块参数对话框中指定值上限,以及是否绑定的是包容。
如果验证情况是真的,块什么也不做。
如果不是,块停止模拟,默认情况下,显示一个错误消息。
Check Static Upper Bound块和及其配套的块模型验证库,旨在促进建立自我验证模型。
例如,您可以在模拟过程中,使用模型验证模块测试信号不超过规定的范围内。
当您满意,模型是正确的,你可以把错误检查通过禁用核查块。
你不必物理上从模型中取出。
如果您需要修改模型,你可以暂时关闭验证块,以确保您的更改不会破坏模型。
Check Static Upper Bound块接受Simulink支持的任何维度和任何数字数据类型的输入信号。
见Data Types Supported by SimulinkUpper bound指定振幅的范围内,输入信号可以具有上限。
Inclusive boundary选中此复选框,使得有效的输入幅度的范围包括上限。
Enable assertion清除此复选框禁用Check Static Upper Bound块,即,使模型表现得好像该块是不存在的。
Model Verification block enabling设置Debugging下在Data Validity诊断窗格中的配置参数对话框中,允许您启用或禁用所有模型验证块模型中,包括Check Static Upper Bound块,此选项的设置无关。
Simulation callback when assertion fails指定一个MATLAB®的表达式,以计算时诊断失败。
由于表达式求值在MATLAB工作空间,定义该工作区中表达式中使用的所有变量。

checknode参数
`checknode` 是 Hyperledger Fabric 中的一个命令行参数,用于
检查一个节点的状态和运行情况。
该参数有以下几个选项:
- `--channelconfig`: 指定通道配置文件的路径,用于检查节点
是否正确配置了指定通道的信息。
- `--profile`: 指定节点的配置文件的名称,用于检查节点是否
正确配置了指定配置的信息。
- `--mspPath`: 指定包含节点的 MSP(成员服务提供者)相关
文件的路径,用于检查节点是否正确配置了指定MSP 的信息。
- `--configPath`: 指定节点的配置文件的路径,用于检查节点是
否正确配置了指定配置的信息。
- `--ledgerconfig`: 指定账本配置文件的路径,用于检查节点是
否正确配置了指定账本的信息。
- `--cafile`: 指定可信的 CA(证书颁发机构)的证书文件的路径,用于检查节点是否正确配置了指定 CA 的信息。
- `--tls`: 启用 TLS(传输层安全)连接,用于检查节点是否正
确配置了 TLS 相关的信息。
以上是一些常见的 `checknode` 参数选项,根据具体使用场景可能还会有其他选项。


push based model 和 pull based
model
推模型(Push Model)和拉模型(Pull Model)是两种不同的数据传输和通信模型,它们在数据传递和信息交流方面有一些重要区别:
- 推模型(Push Model):在推模型中,数据或信息由数据生产者直接推送给数据消费者。
数据的推送是基于事件或时间触发的,当新数据可用时,数据生产者将数据主动发送给消费者。
推模型通常用于实时通信和事件驱动的系统中,其中数据的产生和传递是及时的,数据消费者需要立即获得新数据。
例子包括聊天应用程序、实时数据流处理系统、服务器推送等。
- 拉模型(Pull Model):在拉模型中,数据消费者主动请求数据或信息,从数据生产者那里拉取所需的数据。
数据的请求是由数据消费者启动的,它们定期或根据需要向数据生产者发送请求以获取数据。
拉模型通常用于批处理或定期数据获取的场景中,其中数据的产生和传递不需要实时性。
例子包括Web页面加载、API调用、数据仓库ETL(提取、转换、加载)作业等。
需要注意的是,有时候推模型和拉模型可以结合使用,以满足不同的需求。
例如,在实时监控系统中,数据可以通过推模型进行实时传输,同时也可以提供历史数据的拉取接口供用户查询。
选择适当的模型取决于特定应用的需求和性能要求。

西博思执行器主菜单(1) close direction [clockwise] 关方向[顺时针]*(2) closing speed [28 rpm] 关速度(3) opening speed [28 rpm] 开速度(4) em. Speed(cl.) [14 rpm] 关紧急速度(5) em. Speed(op.) [14 rpm] 开紧急速度(6) cut-off mode cl. [torque-dependent] 关末端位置的关断模式:力矩关断模式(7) cut-off mode op. [toravel-dependent] 开末端位置的关断模式:行程关断模式(8) max. cl. torque [87 Nm] 关最大转矩(9) max. op. torque [87 Nm] 开最大转矩(10) retry torq block [0] 过力矩故障后重试次数(11) rise time [0.5s] 上升时间(12) dc-brake [0] 直流制动(13) mot. temp. warn [135℃ max 155℃] 电机过热报警(14) mot. temp prot [on] 电机过热报警保护[启用](15) motor neating [off] 电机加热[关闭](16) endpos adjust 调整末端位置*(17) rec. torque graph 记录力矩曲线(18) endpos. range cl. [0% to 2%] 关末端位置范围(19) endpos. range op. [98% to 100%] 开末端位置范围(20) setpoint input [rising 4~20mA] 模拟量给定值输入信号类型[上升 4~20mA]*(21) binary inputs [NO] 开关量输入信号类型[常开接点](22) emergency input [NO] 开关量输入信号紧急的类型[常开接点](23) remote control [poscnty currImp] 远端控制类型[位置控制模拟量给定](24) remote recommect [hon-active] 远程控制选择[不起作用](25) open circ.ben [keep position] 开路特性[保持原位](26) close tightly [Yes] 关紧(27) emergency pos [0] 紧急位置(28) inter. cont. CLOSE [0% to 2%] 关位中间接点动作范围(29) inter. cont. OPEN [0% to 100%] 开位中间接点动作范围(30) act. val. output [pos, rising, 4mA] 实际值输出(31) binary output [tot, opened] 开关量输出1[全开](32) binary output [tot, closed] 开关量输出2[全关](33) binary output [TL-OPEN] 开关量输出3[开方向力矩关](34) binary output [TL-CLOSE] 开关量输出4[关方向力矩关](35) binary output [fault] 开关量输5[故障](36) binary output [local] 开关量输6[就地](37) binary output [blinker] 开关量输7[闪烁](38) binary output [MotTemp warn] 开关量输8[电机过热报警](39) maintenance [confiming] 维护[确认](40) maintenance per [↓↑E] 维护间隔(41) actuat. Tag 1-10 [-↑↑↑↑↑] 执行机构标签1—10个字母(42) actuat. Tag 11-20 [-↑↑↑↑↑] 执行机构标签11—20个字母(43) enable poscnty [enabled] 启用位置控制器功能(44) customer variant [0] 用户特殊软件代码(45) enable sp. setp. [disabled] 启用外部速度给定值[禁止](46) enable n. curve. [disabled] 启用速度曲线功能[禁止](47) en. Prop/split [disabled] 启用比例/给定拆开功能[禁止](48) ←return t menu 返回。
ap autosar中的坑英语1. Pitfall -安全问题2. Misconfiguration -配置错误3. Incompatibility -不兼容4. Ambiguity -歧义5. Overlapping -重叠6. Deadlock -死锁7. Race condition -竞争条件8. Memory leak -内存泄漏9. Stack overflow -栈溢出10. Infinite loop -无限循环11. Null pointer exception -空指针异常12. Data corruption -数据损坏13. Timing issue -时序问题14. Kernel panic -内核崩溃15. Resource exhaustion -资源耗尽16. Non-deterministic behavior -非确定性行为17. Bus contention -总线冲突18. Buffer overflow -缓冲区溢出19. Denial of Service (DoS) -拒绝服务攻击20. Input validation -输入验证21. Code injection -代码注入22. Side channel attack -侧信道攻击23. Backdoor -后门24. Man-in-the-middle attack -中间人攻击25. Security vulnerability -安全漏洞1. The system encountered a pitfall due to a software bug.系统由于软件漏洞而遭遇到一个安全问题。
2. The misconfiguration of network settings resulted in a communication failure.网络设置的配置错误导致了通讯故障。
3. The new software version is incompatible with the previous hardware version.新软件版本与之前的硬件版本不兼容。
时序违例(Temporal Violation)通常指的是在有时间限制的任务或流程中,某些操作未能按时完成的情况。
针对时序违例的优化方法可以包括以下几个方面:1. 流程优化:分析整个流程,识别瓶颈和关键节点,对流程进行优化和调整,以缩短整体的处理时间。
这可能涉及重新设计流程、简化步骤、优化资源配置等。
2. 任务调度优化:通过合理的任务调度算法,对任务进行合理的分配和调度,以尽量减少任务之间的等待时间和耗时,从而提高整体的处理效率。
3. 资源管理优化:合理管理和配置资源,包括人力、物力和财力等,在需要的地方增加资源投入,以确保任务得到及时处理。
这可能涉及到人员培训、设备更新、资源调配等方面。
4. 技术手段优化:利用现代技术手段,如自动化、智能化、数据分析等技术,来提高处理效率和准确性,从而减少时序违例的发生。
5. 风险管理:建立风险管理机制,及时识别潜在的时序违例风险点,采取相应的风险控制措施,以降低时序违例的概率和影响。
6. 数据分析和预测:通过对历史数据的分析和建模,可以预测未来可能出现时序违例的情况,从而提前采取措施来避免或减轻时序违例的发生。
当涉及到具体的时序违例优化时,可以考虑以下具体方法:1. 流程分析和重新设计:对整个流程进行详细分析,找出存在的瓶颈和不必要的步骤。
通过重新设计流程,去除冗余步骤,简化操作流程,以加快处理速度。
例如,可以通过并行处理、异步操作等方式来减少等待时间。
2. 并行处理和任务调度:将可以并行处理的任务进行分解,并合理安排任务的执行顺序。
通过并行处理和合理的任务调度算法,最大限度地减少任务之间的等待时间和耗时。
可以利用线程池、任务队列等机制来实现任务的并行处理和调度。
3. 资源优化和平衡:合理管理和配置资源,确保在关键时刻有足够的资源可用。
可以通过资源监控和负载均衡等手段,及时调整资源分配,避免资源瓶颈引起的时序违例。
同时,还可以考虑资源的预留和优先级设置,以保证重要任务的优先处理。
suboption would go past end of
option
"Suboption would go past end of option" 是一个错误消息,通常在编程或设置选项时出现。
它表示在某个选项中,你尝试设置一个子选项,但该子选项的值超过了选项的有效范围。
这种错误通常发生在以下情况:
1. 选项值的限制:某些选项可能只允许特定范围内的值,如果你尝试设置一个超出范围的值,就会出现这个错误。
2. 缓冲区溢出:在一些情况下,选项可能有一个固定的缓冲区大小,如果你输入的子选项值超过了缓冲区的大小,也会导致这个错误。
解决方法:
1. 检查选项的文档或说明,了解该选项允许的有效范围,并确保你输入的值在这个范围内。
2. 如果是缓冲区溢出的问题,尝试缩短子选项的值,或者考虑使用其他方式来传递或处理该值。
3. 如果你不确定如何解决问题,可以查看相关的文档、向开发者或技术支持团队咨询,以获取更具体的指导和帮助。
请提供更多的上下文或具体的情况,以便我能够给出更准确的建议和帮助。
dcdc带载输入正常,输出拉低英文回答:DC-DC Converter: Input Normal, Output Low Under Load. Possible Causes:Output short circuit.Inductor saturation.Excessive load current.Damaged feedback circuit.Faulty switching device.Troubleshooting Steps:1. Check for any obvious shorts or damage to theoutput circuit.2. Measure the output voltage with a load connected.3. Increase the load current gradually until the output voltage drops. If the drop occurs significantlybelow the expected level, the inductor may be saturated.4. Use an oscilloscope to verify the switching waveform. A deformed waveform or excessive ripple may indicate a damaged switching device or feedback circuit.5. Check the components in the feedback circuit, such as resistors and capacitors, for any abnormalities.Remedial Actions:Repair or replace any damaged components in the output circuit.If the inductor is saturated, consider using a larger inductor or reducing the load current.Replace the switching device or feedback circuit components as necessary.Additional Considerations:Check the input voltage to ensure it is within the operating range of the DC-DC converter.Verify that the load is compatible with the output voltage and current of the converter.中文回答:DC-DC 转换器,输入正常,输出负载低。
DC综合check_design问题总结如下图所示,当我们DC综合之后查看check_design报告,出现的一些warning以及解决方法进行总结如下。
1.LINT-2: drive by pin xxx has no loads常用在检查输出端口。
当综合之后出现这种类型的warning时,说明你的代码中在实例化某个模块的时候输出端口未连接负载,或者你只把该信号的某几bit连接到了该模块的端口上,这种警告的出现是比较常见的,比如上图所示:这表明在代码中send_check_bus_addr 是一个11bit的输入信号,它的第6~10bit没有连接到该模块的端口上,即:这样的警告虽然对DC综合的结果没有太大的影响,但是必须按照代码规范的要求,把未连接负载的部分信号重新以NC(Not Connect)为后缀来命名。
2.LINT-28: xxx is not connected to any nets常用在检查输入端口。
DC综合如果出现这样的warning,就说明你的这个信号的某些bit的悬空的,对于总线的输入数据信号bus_data_i是一个32bit的信号,但是当前模块中只用到了低20bit,而高12bit是没有连接到任何信号上面去的,那么DC就会给出这样的警告。
这种警告的消除方法就是:在你的该模块中你用到了某个信号的多少bit,那么你在顶层调用该模块的时候只把你用到的该信号对应的那些bit连进来,这样就不会出现这样的警告。
另外需要说明的是,有些时候我们为了代码的简洁性,必须要把某个信号完全连到该模块,那么这个时候造成这种warning我们是可以接受的。
还有一种可能就是有些时候你的设计需要发生变化,比如某个信号要去掉却忘记把该信号的端口连接给删掉,这样就会导致这个信号的所有bit都是没有连接到任何信号,这样的情况就是必须进行修改的,否则会对DC的综合造成不必要的影响。
3.LINT-29: input port xxx is connected directly to output port用在检查输入端口。
Model Checking Probabilistic Pushdown AutomataJavier EsparzaInstitute for Formal Methods in Computer Science,University of Stuttgart,Universit¨a t str.38,70569Stuttgart,Germany.Anton´ın Kuˇc eraFaculty of Informatics,Masaryk University, Botanick´a68a,60200Brno,Czech Republic.czRichard MayrDepartment of Computer Science,Albert-Ludwigs-University FreiburgGeorges-Koehler-Allee51,D-79110Freiburg,Germany.AbstractWe consider the model checking problem for probabilisticpushdown automata(pPDA)and properties expressible invarious probabilistic logics.We start with properties thatcan be formulated as instances of a generalized randomwalk problem.We prove that both qualitative and quantita-tive model checking for this class of properties and pPDA isdecidable.Then we show that model checking for the qual-itative fragment of the logic PCTL and pPDA is also decid-able.Moreover,we develop an error-tolerant model check-ing algorithm for general PCTL and the subclass of state-less pPDA.Finally,we consider the class of properties de-finable by deterministic B¨u chi automata,and show that bothqualitative and quantitative model checking for pPDA is de-cidable.1.IntroductionProbabilistic systems can be used for modeling systemsthat exhibit uncertainty,such as communication protocolsover unreliable channels,randomized distributed systems,or fault-tolerant systems.Finite-state models of such sys-tems often use variants of probabilistic automata whose1This is a standard notation adopted in concurrency theory.The sub-and various probabilistic logics.We start with a class of Figure1.Bernoulli random walk as a pBPAclass of stateless PDA corresponds to a natural subclass of ACP known as Basic Process Algebra[6].erties expressible in PCTL is strictly larger).In Section4.1, we give a model checking algorithm for the qualitative frag-ment of PCTL and pPDA processes.For general PCTL for-mulae and pBPA processes,an error tolerant model check-ing algorithm is developed in Section4.2.The question whether this result can be extended to pPDA is left open.Finally,in Section5we prove that both qualitative and quantitative model checking for the class of properties de-finable by deterministic B¨u chi automata is decidable for pPDA.Again,this is done without computing the probabil-ity explicitly,but rational lower and upper approximations can be computed up to an arbitrarily small given error.Due to the lack of space,some proofs have been omitted. These can be found in a full version of this paper[14]. 2.Preliminary DefinitionsDefinition2.1.A(fully)probabilistic transition system is a triple where is afinite or countably infinite set of states,is a transition relation, and is a function which to each transition of assigns its probability so that for every we have.(The sum above can be if it is empty,i.e.,if does not have any outgoing transitions.)In the rest of this paper we also write instead of.A path in is afinite or infinite se-quence of states such that for every.We also use to denote the state of(by writing we implicitly impose the condition that the length of is at least).A run is a maximal path, i.e.,a path which cannot be prolonged.The sets of allfinite paths and all runs of are denoted and,respec-tively2.Similarly,the sets of allfinite paths and runs that start in a given are denoted and, respectively.Each determines a basic cylinder which consists of all runs that start with.To everywe associate the probabilistic space where is the-field generated by all basic cylinders where starts with,and is the unique probability function such thatwhere and for every(if,we put).We say that setsand are-equivalent iff.The Logic PCTLPCTL,the probabilistic extension of CTL,was defined by Hansson&Jonsson in[17].Let be acountably infinite set of atomic propositions.The syntax of PCTL3is given by the following abstract syntax equation: Here ranges over,,and. Let be a probabilistic transition system. For all,all,and all,letand for alland for allObviously,Let be a valuation.The denotation of a PCTL formula over w.r.t.,denoted,is defined inductively as follows:As usual,we write instead of.The qualitative fragment of PCTL is obtained by restrict-ing the allowed operator/number combinations to‘’and ‘’,which will be also written as‘’and‘’,resp. (Observe that‘’,‘’are definable from‘’,‘’, and negation;for example,.)Probabilistic PDADefinition 2.2.A probabilistic pushdown automaton (pPDA)is a tuple where is afi-nite set of control states,is afinite stack alphabet,is afinite transition relation(we write instead of),and is a func-tion which to each transition assigns its proba-bility so that for all and we have that.A pBPA is a pPDA with just one control state.Formally, a pBPA is understood as a triple where.In the rest of this paper we adopt a more intuitive nota-tion,writing instead of.if for some,then there issuch that;for each we have iff. Moreover,if is regular,then is also reg-ular.For the rest of this section,let be(fixed) simple sets,and let be the sets as-sociated to in the sense of Definition3.1.To simplify our notation,we adopt the following conventions:For each,let.Observe that if is simple,then so is.For all and,we use to ab-breviate,and to abbreviate.The next lemma says how to computefrom thefinite fam-ily of all,probabilities.Lemma3.3.For each wherewe have that equals towherewhere andwith the convention that empty sum equals to and empty product equals to.Now we show that the probabilities,form the least solution of an effectively constructible system of equations.This can be seen as a generalization of a simi-lar result forfinite-state systems[17,11].In thefinite-state case,the equations are linear and can be further modified so that they have a unique solution(which is then computable, e.g.,by Gauss elimination).In the case of pPDA,the equa-tions are not linear and cannot be generally solved by ana-lytical methods.The question whether the equations can be further modified so that they have a unique solution is left open;we just note that the method used forfinite-state sys-tems is insufficient(this is demonstrated by Example3.5). Let be a set of “variables”.Let us consider the system of recursive equa-tions constructed as follows:if,then for each;other-wise,we putif,then;if,then ;otherwise we putFor given,,and we use and to denote the component of which corresponds to the variable and,respectively. The above defined system of equations determines a unique operator where is the tu-ple of values obtained by evaluating the right-hand sides of the equations where all and are substituted with and,respectively.Theorem3.4.The operator has the leastfixed-point. Moreover,for all and we have thatand.Example3.5.Let us consider the pBPA system of Fig.1, and let,.Then we obtain the following system of equations(since has only one control state, we write and instead of and, resp.):As the least solution we obtain the probabilities ,,,, ,.By applying Lemma3.3we further obtain that,e.g.,.In Example3.5,the least solution of the constructed sys-tem of equations could be computed explicitly.This is gen-erally impossible,but certain properties of the least solution are still decidable.For our purposes,it suffices to consider the class of properties defined in the next theorem. Theorem3.6.Letand,where is the set of all rational constants. Let be expressions built over using‘’and ‘’,and let.It is decidable whether. Proof.We show that,due to Theorem3.4,is ef-fectively expressible as a closed formula of. Hence,the theorem follows from the decidability offirst-order arithmetic of reals[25].For all and,let,, ,and befirst order variables,and letand be the vectors of all,,and, variables,respectively.Let us consider the formula constructed as follows:Observe that the conditions andare expressible only using multiplication,summation,and equality.The expressions and are ob-tained from and by substituting all andwith and,respectively.It follows immedi-ately that iff holds.An immediate consequence of Theorem3.6is the fol-lowing:Theorem 3.7.Let,,and.It is decidable whether.Moreover,there effectively exist ratio-nal numbers such thatand.Proof.We can assume w.l.o.g.that for some .Note that iffby Lemma3.3.Hence,we can apply Theorem3.6.The numbers are computable,e.g.,by the algorithm of Fig.2.4.Model Checking PCTL for pPDA Processes 4.1.Qualitative Fragment of PCTLFor the rest of this section wefix a pPDA.Lemma4.1.Let be a simple set.The setsandare effectively regular.Proof.Immediate.Lemma4.2.Let be simple sets.The setis effectively regu-lar.Proof.Let for all ,.For each we define the set inductively as follows:andUsing Lemma3.3,we can easily check that.To see that the set is effectively regular,for each we construct afinite automaton such that.A-automaton recognizing the setcan then be constructed using standard algorithms of au-tomata theory(in particular,note that regular languages are effectively closed under reverse).The states of are all subsets of,is the initial state,is the input alpha-bet,final states are those where for everywe have that(in particular,note that is afinal state),and transition function is given by iff for ev-ery we have that and.Note that for each. The definition of is effective due to Theorem3.6.It is straightforward to check that.Lemma4.3.Let be simple sets.The setis effectively regu-lar.Proof.Let for all ,.For each we define the set inductively as follows:andThe factfollows immediately from Lemma3.3.The set is effectively regular,which can be shown by constructing a finite automaton recognizing the set.This construction and the rest of the argument are very similar to the ones of the proof of Lemma4.2.There-fore,they are not given explicitly.Theorem4.4.Let be a qualitative pCTL formula and a regular valuation.The set is effectively regular.Proof.By induction on the structure of.The cases when and follow immediately.For Boolean connectives we use the fact that regular sets are closed under complement and intersection.The other cases arecovered by Lemma4.1,4.2,and4.3(here we also need Lemma3.2).4.2.Model Checking PCTL for pBPA ProcessesIn this section we provide an error tolerant model check-ing algorithm for PCTL formulae and pBPA processes. Since it is not so obvious what is meant by error tolerance in the context of PCTL model checking,this notion is de-fined formally.Let be a probabilistic transition sys-tem and.For every negation-free PCTL for-mula and valuation we define the denotation of over w.r.t.with error tolerance,denoted,in the same way as.The only exception is whereif,thenif,thenNote that for every negation-free formula we have that.Negations can be“pushed inside”to atomic propositions using dual connectives(note that,e.g., is equivalent to),and for regular val-uations we can further replace every with a fresh propo-sition where is the complement of.Hence,we can assume w.l.o.g.that is negation-free.An error tolerant PCTL model checking algorithm is an algorithm which,for each PCTL formula,valuation, ,and,outputs YES/NO so thatif,then the answer is YES;if the answer is YES,then.For the rest of this section,let usfix a pBPA.Since has just one(or“none”)control state ,we write and instead of and,re-spectively.Lemma4.5.Let be a simple set,,and.The setis effectively regular.Proof.Immediate.The following lemma presents the crucial part of the al-gorithm.This is the place where we need the assumption that is stateless.Lemma4.6.Let be simple sets.For all and there effectively exist-automata and such that for all we have thatif(or),then(or,respectively.)if(or),then(or,respectively.) Theorem 4.7.There is an error-tolerant PCTL model checking algorithm for pBPA processes.Proof.The proof is similar to the one of Theorem4.4,us-ing Lemma4.5and4.6instead of Lemma4.1,4.2,and4.3. Note that Lemma3.2is applicable also to pBPA(the sys-tem constructed in Lemma3.2has the same set of con-trol states as the original system).5.Model Checking Deterministic B¨uchi Au-tomata SpecificationsDefinition5.1.A deterministic B¨u chi automaton is a tuple,where is afinite alphabet,is afinite set of states,is a(total)transition function(we write instead of),is the initial state,and is a set of accepting states.A run of is an infinite sequence of states such that for every there is such that.A run is accepting if for infinitely many indices.For the rest of this section,wefix a pPDA.Definition5.2.Given a configuration of,we call the head and the tail of.The set of all heads of is also denoted by.We consider specifications given by deterministic B¨u chi automata having as their alphabet.It is well known that every LTL formula whose atomic propositions are in-terpreted over simple sets can be encoded into a nondeter-ministic B¨u chi automaton having as alphabet.Deter-ministic B¨u chi automata can encode the fragment of LTL that can also be expressed in the alternation-free modal-calculus[21].Our results can be extended to atomic propo-sitions interpreted over arbitrary regular sets of configura-tions using the same technique as in[15].Definition5.3.The product of and is a probabilistic pushdown automaton where and are determined as follows:iff and are transitions of and,respec-tively.Notice that every(finite or infinite)path in corre-sponds to a unique path in obtained by projecting the control state of every configuration of the path onto itsfirst component,yielding the configuration.Con-versely,for each path in(starting in some)and each there is exactly one path in starting in be-cause is deterministic.Definition5.4.A configuration of is accepting if.A run in is accepting if it visits accepting configurations infinitely often.A run in is accepting if its corresponding run in is accepting.The probability that a configuration of satisfies the specification is defined asis accepting.We solve the following two problems for a given config-uration of:(a)Given and,do we have?(b)Given,compute rationals such thatand.Forfinite-state automata,the problem can be solved as follows(see[11]).Let be afinite-state automaton.Since the product automaton isfinite,it can be transformed into afinite Markov chain by just‘copying’the proba-bilities of the system[11].It is then possible to reduce prob-lems(a),(b)to the problem of computing the probability of hitting a bottom strongly connected component of which contains a state of the form,where is accepting.In our case,the product automaton is again a pPDA, and so its associated probabilistic transition system is infi-nite.The key to our solution for(a)and(b)is the construc-tion of a newfinite Markov chain that plays the rˆo le of in the case offinite automata.5.1.The Markov chainA B¨u chi pPDA is a tuple, where all elements except for are defined as for pPDA and is a set of accepting states.A configuration of is accepting if.A run of is accepting if it visits accepting configurations infinitely often.For all and,the probabil-ity that a run is accepting is denoted by .Obviously,the model checking problems(a),(b)of the previous section can be reduced to the following problems about a given configuration of a B¨u chi pPDA(where ):(A)Given and,do we have?(B)Given,compute rationals such thatand.For the rest of this section,wefix a B¨u chi pPDA.Definition5.5.Let be an infinite run in.For each we define the minimum of,de-noted,inductively as follows:,where is the least number such that for each.,where. Here is the suffix of that starts with. We say thatflashes at if either and is accepting,or and visits an accept-ing configuration between and(where is not included).Sometimes we abuse language and use to de-note not only a configuration,but the particular occurrence of the configuration that corresponds to the minimum. For all and all we define a ran-dom variable over as follows:The possi-ble values of are all pairs of the form,where and is a booleanflag;there is also a special value.For a given,is de-termined as follows:if isfinite then;if conditions(1)–(3)below are satisfied,then;(1)is infinite;(2)the head of is;(3)flashes at.if conditions(1)and(2)above are satisfied and condition (3)is not satisfied,thenNotice that the random variables are well defined,because they assign to each run exactly one value.Lemma5.6.For all,,and, the probability of exists(i.e.,the set of all which satisfy this condition is-measurable).Moreover,for every rational constant there is an effectively constructible formula of which holds if and only if.The following lemma proves the Markov property.In fact,it follows immediatelly from the construction used in the proof of Lemma5.6.Lemma5.7.The conditional probability of on the hypothesis is equal to the probability of conditioned on,assuming that the probability ofis non-zero.For each control state we define aflag,which is equal either to or depending on whether or not,respectively.Another consequence of Lemma5.6is the following:Lemma 5.8.The conditional probability ofon the hypothesisis equal to the conditional probability ofon the hypothesis,assuming that.Now we can define thefinite Markov chain.Definition5.9.Let be afinite-state Markov chain where the set of states isand transition probabilities are defined as follows:,,,.One can readily check that is indeed a Markov chain,i.e.,for every state of we have that the sum of probabilities of all outgoing transitions of is equal to one.A trajectory in is an infinite sequenceof states of where for ev-ery.To every run of we associate its foot-print,which is an infinite sequence of states of de-fined as follows:if isfinite,then for every we have;if is infinite,then for every we have,where is the head of,and iffflashes at.We say that a given is good if the footprint of is a trajectory in.Our next lemma reveals that al-most all runs are good.Lemma5.10.Let.We have thatis good.It follows directly from the definition of that if both and are states of,then they have the “same”outgoing arcs(i.e.,iff,where).In particular,this means that ifor belongs to some strongly connected com-ponent of,then all of the outgoing arcs of and lead to.Hence,the following definition is correct:Definition5.11.We say that a given is recur-rent if there is a bottom strongly connected componentof such that for some.Each recurrent head is either accepting or rejecting,de-pending on whether contains a state of the formor not,respectively.We say that a run of hits a head if there is some such that the head of is. The next lemma says that an infinite run eventually hits a re-current head.Lemma5.12.Let.The conditional probabil-ity that hits a recurrent head on the hypoth-esis that is infinite is equal to one.So,an infinite run eventually hits a recurrent head.Now we prove that if this head is accepting/rejecting,then the run will be accepting/rejecting with probability one. Lemma5.13.Let be an accepting/rejecting head.The conditional probability that is accept-ing/rejecting on the hypothesis that thefirst recurrent head hit by is accepting/rejecting is equal to one.Lemma5.14.(cf.Proposition4.1.5of[11])Let .is equal to the probability that a trajec-tory from in hits a state of the form where is an accepting head(this is equivalent to saying that the trajectory hits a bottom strongly connected component of which contains a state of the form). Theorem5.15.Let be a B¨u chi pPDA.Given a head,,and, we can decide if.Further,for each we can compute rationals such thatand.Proof.Similarly as in Theorem3.6,we compute a closed formula of such that iff holds.Then,the rationals can be computed by a simple binary search similarly as in Fig.2.Due to Lemma5.14we know that,where is the set of all states of,and consists of all states of the form where is an accepting head.This means that there is a system of recur-sive equations such that appears in the tuple of values which form the least solution of the system(we can assume that is,e.g.,thefirst element of this tu-ple).Since isfinite,these equations are linear and by using the results of[17,11]we can even assume that there is a unique solution.The only problem is that numeric co-efficients in this system of equations are the probabilities of transitions in which cannot be precisely computed. This can be overcome as follows:we construct the men-tioned system of linear equations where we replace each co-efficient with a freshfirst-order variable;let be the tupleof all variables which correspond to the coefficients.Now we can effectively construct the formulawhere says that the tuple of variables is a solu-tion of the constructed system of linear equations.Note that is not closed because the variables of(which appear in the subformula)are free.Due to Lemma5.6, for each of these coefficients there effectively exists a for-mula of which says that a given coefficient is equal to the probability of the corresponding transition in (we just“translate”the definition of given in Def-inition5.9into,using the formulae provided by Lemma5.6).Let by a conjunction of all these formu-lae.The formula is constructed as follows:Obviously,iff holds.We conclude this section by trying to explain why our re-sults cannot be directly extended to nondeterministic B¨u chi automata.First of all,notice that we cannot assign proba-bilities to the transitions of in a meaningful way,be-cause a transition of should‘split’into sev-eral transitions of.In the case of afinite automaton, this problem can be solved by working with the product of and,where is the result of applying the deter-minization construction to.Let denote this product. In[11],a definition of recurrence is provided,which char-acterizes the states of that,loosely speaking,re-turn to with probability1in terms of topological prop-erties of the probabilistic transition system.It is then possible to compute the accepting recurrent states.Unfortunately,this construction does not seem to gener-alize to the case of pushdown automata.The problem is that the B¨u chi pPDA has infinitely many states,and so it must be replaced by the chain.However,inwe cannot directly‘observe’the points at which a run hits an accepting state;we can only observe the points at which a run hits a minimum.While we can use to com-pute the recurrent minima,i.e.,the heads to which one can return with probability1at a minimum,at the moment we do not know how to compute the accepting recurrent min-ima,i.e.,the recurrent minima that not only return,but also visit an accepting configuration along the way.More pre-cisely,we know how to decide for a given head if the runs starting at it will almost surely hit some head out of a set and visit some accept-ing configuration along the way.We can also decide if some head will hit with probability one.How-ever,since we do not know whether or not,this in-formation is not sufficient to decide if is an accepting recurrent minimum.6.ConclusionsWe have provided model checking algorithms for pushdown automata against PCTL specifications,and against linear-time specifications represented as determinis-tic B¨u chi automata.Contrary to the case offinite automata, qualitative properties(i.e.,whether a property holds with probability0or1),depend on the exact probabilities of the transitions.There are many possibilities for future work.An obvi-ous question is what is the complexity of the obtained al-gorithms.Since the formulae offirst order arithmetic which are constructed in our algorithms have afixed alternation depth,we can apply a powerful result of Grigoriev[16] which says that the validity of such formulae is decidable in single exponential time.From this we can easily derive the time complexity of some of our algorithms(for example, the qualitative/quantitative random walk problem of Sec-tion3is decidable in exponential time).Since the complex-ity issues were not the main priority of our work,the effi-ciency of our algorithms can be improved even by relatively straightforward optimizations.Moreover,there is a lot of space for advanced numerical algorithms which might be used to compute the required probabilities with enough pre-cision.An obvious question about linear-time specifications is whether our procedure can be improved to deal with nonde-terministic B¨u chi automata.Another possibility is to con-sider LTL specifications and try to generalize the technique of[11],which modifies the probabilistic transition systems step-by-step and at the same time simplifies the formula,un-til it becomes a propositional formula.7.AcknowledgmentsThe authors would like to thank Stefan Schwoon for many helpful insights.References[1]P.A.Abdulla,C.Baier,S.P.Iyer,and B.Jonsson.Reason-ing about probabilistic channel systems.In Proceedings of CONCUR2000,vol.1877of Lecture Notes in Computer Sci-ence,pp.320–330.Springer,2000.[2]P.A.Abdulla and A.Rabinovich.Verification of probabilis-tic systems with faulty communication.In Proceedings of FoSSaCS2003,vol.2620of Lecture Notes in Computer Sci-ence,pp.39–53.Springer,2003.[3] A.Abney,D.McAllester,and F.Pereira.Relating probabilis-tic grammars and automata.In Proceedings of ACP’99,pp.542–549,1999.[4]R.Alur,K.Etessami,and M.Yannakakis.Analysis of re-cursive state machines.In Proceedings of CAV2001,vol.2102of Lecture Notes in Computer Science,pp.207–220.Springer,2001.[5] A.Aziz,V.Singhal, F.Balarin,R.Brayton,andA.Sangiovanni-Vincentelli.It usually works:The tempo-ral logic of stochastic systems.In Proceedings of CAV’95, vol.939of Lecture Notes in Computer Science,pp.155–165.Springer,1995.[6]J.C.M.Baeten and W.P.Weijland.Process Algebra.No.18in Cambridge Tracts in Theoretical Computer Science.Cam-bridge University Press,1990.[7] C.Baier and B.Engelen.Establishing qualitative propertiesfor probabilistic lossy channel systems:an algorithmic ap-proach.In Proceedings of5th International AMAST Work-shop on Real-Time and Probabilistic Systems(ARTS’99), vol.1601of Lecture Notes in Computer Science,pp.34–52.Springer,1999.[8]N.Bertrand and Ph.Schnoebelen.Model checking lossychannel systems is probably decidable.In Proceedings of FoSSaCS2003,vol.2620of Lecture Notes in Computer Sci-ence,pp.120–135.Springer,2003.[9]O.Burkart and B.Steffen.Model checking the full modalmu-calculus for infinite sequential processes.In Proceed-ings of ICALP’97,vol.1256of Lecture Notes in Computer Science,pp.419–429.Springer,1997.[10] C.Courcoubetis and M.Yannakakis.Verifying temporalproperties offinite-state probabilistic programs.In Proceed-ings of29th Annual Symposium on Foundations of Computer Science,pp.338–345.IEEE Computer Society Press,1988.[11] C.Courcoubetis and M.Yannakakis.The complexity ofprobabilistic verification.Journal of the Association for Computing Machinery,42(4):857–907,1995.[12]J.M.Couvreur,N.Saheb,and G.Sutre.An optimal automataapproach to LTL model checking of probabilistic systems.In Proceedings of LPAR2003,vol.2850of Lecture Notes in Computer Science,pp.361–375.Springer,2003.[13]J.Esparza,D.Hansel,P.Rossmanith,and S.Schwoon.Ef-ficient algorithms for model checking pushdown systems.In Proceedings of CAV2000,vol.1855of Lecture Notes in Computer Science,pp.232–247.Springer,2000.[14]J.Esparza,A.Kuˇc era,and R.Mayr.Model checking prob-abilistic pushdown automata.Technical Report FIMU-RS-2004-03,Faculty of Informatics,Masaryk University,2004.[15]J.Esparza,A.Kuˇc era,and S.Schwoon.Model-checkingLTL with regular valuations for pushdown r-mation and Computation,186(2):355–376,2003.[16] plexity of deciding Tarski algebra.Jour-nal of Symbolic Computation,5(1–2):65–108,1988. [17]H.Hansson and B.Jonsson.A logic for reasoning abouttime and reliability.Formal Aspects of Computing,6:512–535,1994.[18]S.Hart and M.Sharir.Probabilistic temporal logic forfiniteand bounded models.In Proceedings of POPL’84,pp.1–13.ACM Press,1984.[19]M.Huth and M.Z.Kwiatkowska.Quantitative analysis andmodel checking.In Proceedings of LICS’97,pp.111–122.IEEE Computer Society Press,1997.[20]S.P.Iyer and M.Narasimha.Probabilistic lossy channel sys-tems.In Proceedings of TAPSOFT’97,vol.1214of Lecture Notes in Computer Science,pp.667–681.Springer,1997.[21]O.Kupferman and M.Y.Vardi.Freedom,weakness,and de-terminism:From linear-time to branching-time.In Proceed-ings of LICS’98,pp.81–92.IEEE Computer Society Press, 1998.[22] D.Lehman and S.Shelah.Reasoning with time and chance.Information and Control,53:165–198,1982.[23]I.Macarie and M.Ogihara.Properties of probabilistic push-down automata.Theoretical Computer Science,207:117–130,1998.[24] A.Rabinovich.Quantitative analysis of probabilistic lossychannel systems.In Proceedings of ICALP2003,vol.2719of Lecture Notes in Computer Science,pp.1008–1021.Springer,2003.[25] A.Tarski.A Decision Method for Elementary Algebra andGeometry.Univ.of California Press,Berkeley,1951. [26]M.Vardi.Automatic verification of probabilistic concurrentfinite-state programs.In Proceedings of26th Annual Sym-posium on Foundations of Computer Science,pp.327–338.IEEE Computer Society Press,1985.[27]I.Walukiewicz.Pushdown processes:Games and model-rmation and Computation,164(2):234–263, 2001.。