中考数学 圆的综合综合试题附详细答案

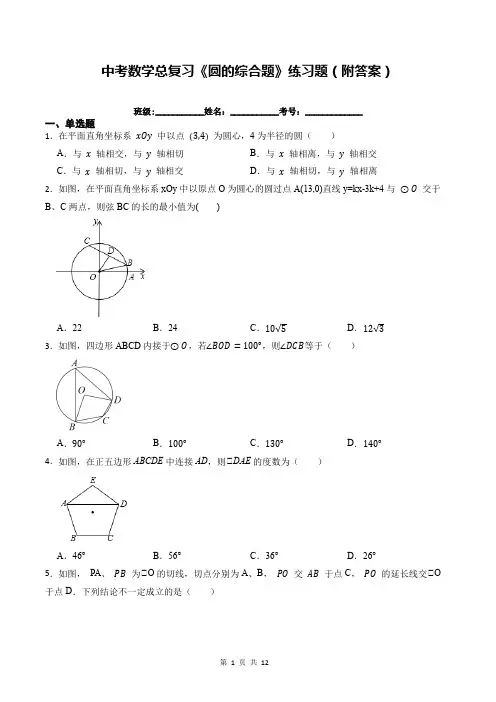
中考数学总复习《圆的综合题》练习题（附答案）班级:___________姓名：___________考号：_____________一、单选题1．在平面直角坐标系xOy中以点(3,4)为圆心，4为半径的圆（）A．与x轴相交，与y轴相切B．与x轴相离，与y轴相交C．与x轴相切，与y轴相交D．与x轴相切，与y轴相离2．如图，在平面直角坐标系xOy中以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与⊙O交于B、C两点，则弦BC的长的最小值为()A．22B．24C．10√5D．12√33．如图，四边形ABCD内接于⊙O，若∠BOD=100°，则∠DCB等于（）A．90°B．100°C．130°D．140°4．如图，在正五边形ABCDE中连接AD，则∠DAE的度数为（）A．46°B．56°C．36°D．26°5．如图，PA、PB为∠O的切线，切点分别为A、B，PO交AB于点C，PO的延长线交∠O 于点D．下列结论不一定成立的是（）A．△BPA为等腰三角形B．AB与PD相互垂直平分C．点A，B都在以PO为直径的圆上D．PC为△BPA的边AB上的中线6．如图，四边形ABCD内接于半径为6的∠O中连接AC，若AB＝CD，∠ACB＝45°，∠ACD＝12∠BAC，则BC的长度为（）A．6 √3B．6 √2C．9 √3D．9 √27．如图，点A，B，D，C是∠O上的四个点，连结AB，CD并延长，相交于点E，若∠BOD=20°，∠AOC=90°，则∠E的度数为()A．30°B．35°C．45°D．55°8．∠ABC中∠C=Rt∠，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB，BC分别交于点E，D，则AE的长为()A．95B．125C．185D．3659．如图，AB为∠O的直径，点C在∠O上，若∠B=60°，则∠A等于（）A．80°B．50°C．40°D．30°10．两个圆的半径分别是2cm和7cm，圆心距是5cm，则这两个圆的位置关系是() A．外离B．内切C．相交D．外切11．已知正三角形的边长为12，则这个正三角形外接圆的半径是()A．B．C．D．12．一个扇形的弧长为4π，半径长为4，则该扇形的面积为（）A．4πB．6πC．8πD．12π二、填空题13．在Rt∠ABC中∠C=90°，AB=5，BC=4，求内切圆半径14．如图，∠C过原点，且与两坐标轴分别交于点A，点B，点A的坐标为（0，3），M是第三象限内弧OB上一点，∠BMO=120°，则∠C的半径为．15．一个立体图形的三视图如图所示，根据图中数据求得这个立体图形的侧面积为.16．一个半径为5cm的球形容器内装有水，若水面所在圆的直径为8cm，则容器内水的高度为cm.17．如图，在直角坐标系中以点P为圆心的圆弧与x轴交于A，B两点，已知P（4，2）和A（2，0），则点B的坐标是．18．下面是“作一个30°角”的尺规作图过程．已知：平面内一点A．求作：∠A，使得∠A=30°．作法：如图①作射线AB；②在射线AB取一点O，以O为圆心，OA为半径作圆，与射线AB相交于点C；③以C为圆心，OC C为半径作弧，与⊙O交于点D，作射线AD．则∠DAB即为所求的角．请回答：该尺规作图的依据是．三、综合题19．如图，在△ABC中AC=BC=BD，点O在AC边上，OC为⊙O的半径，AB是⊙O 的切线，切点为点D，OC=2，OA=2√2．（1）求证：BC是⊙O的切线；（2）求阴影部分的面积．20．如图，△ABC内接于⊙O，CD是直径，∠CBG=∠BAC，CD与AB相交于点E，过点E作EF⊥BC，垂足为F，过点O作OH⊥AC，垂足为H，连接BD、OA．（1）求证：直线BG与⊙O相切；（2）若BEOD=54，求EFAC的值．21．如图，四边形ABCD 内接于∠O，BD是∠O的直径，过点A作∠O的切线AE交CD的延长线于点E，DA平分∠BDE．（1）求证：AE∠CD；（2）已知AE=4cm，CD=6cm，求∠O的半径．22．如图，∠O是∠ABC的外接圆，BC为∠O的直径，点E为∠ABC的内心，连接AE并延长交∠O 于D点，连接BD并延长至F，使得BD=DF，连接CF、BE．（1）求证：DB=DE；（2）求证：直线CF为∠O的切线．23．公元前5世纪，古希腊哲学家阿那克萨哥拉因“亵渎神灵罪”而被投人监狱，在狱中他对方铁窗和圆月亮产生了兴趣．他不断变换观察的位置，一会儿看见圆比正方形大，一会儿看见正方形比圆大，于是伟大的古希腊尺规作图几何三大问题之--的化圆为方问题诞生了：作一个正方形，使它的面积等于已知圆的面积（1）设有一个半径为√3的圆，则这个圆的周长为，面积为，作化圆为方得到的正方形的边长为(计算结果保留π)（2）由于对尺规作图的限制(只能有限次地使用没有刻度的直尺和圆规进行作图)，包括化圆为方在内的几何三大问题都已被证明是不可能的．但若不受标尺的限制，化圆为方并非难事。

初中圆综合试题及答案一、选择题（每题2分，共10分）1. 圆的周长公式是（）。

A. C = πdB. C = 2πrC. C = πr^2D. C = 2πd2. 圆的面积公式是（）。

A. A = πr^2B. A = 2πrC. A = πd^2D. A = πd3. 圆的直径是半径的（）倍。

A. 1B. 2C. 3D. 44. 圆的半径增加1倍，面积增加（）倍。

A. 1B. 2C. 4D. 85. 圆的半径为r，直径为d，周长为C，下列关系式正确的是（）。

A. C = 2πrB. d = 2rC. C = πdD. A和B都正确二、填空题（每题2分，共10分）1. 圆的周长公式是C = 2πr，其中r代表圆的______。

2. 圆的面积公式是A = πr^2，其中r代表圆的______。

3. 圆的直径是半径的______倍。

4. 如果圆的半径为3厘米，那么它的周长是______厘米。

5. 圆的半径增加1倍，面积增加到原来的______倍。

三、解答题（每题10分，共20分）1. 已知圆的半径为5厘米，求该圆的周长和面积。

2. 一个圆的周长为25.12厘米，求该圆的半径。

四、证明题（每题15分，共30分）1. 证明圆的周长和直径的比值是一个常数。

2. 证明圆的面积与半径的平方成正比。

答案：一、选择题1. B2. A3. B4. C5. D二、填空题1. 半径2. 半径3. 24. 31.45. 4三、解答题1. 周长：C = 2πr = 2 × 3.14 × 5 = 31.4厘米面积：A = πr^2 = 3.14 × 5^2 = 78.5平方厘米2. 半径：r = C / (2π) = 25.12 / (2 ×3.14) = 4厘米四、证明题1. 证明：设圆的直径为d，半径为r，则d = 2r。

圆的周长C = πd = 2πr，所以C/d = 2πr / 2r = π，即圆的周长和直径的比值是一个常数π。

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，⊙M交x轴于B、C两点，交y轴于A，点M的纵坐标为2．B（﹣33，O），C（3，O）．（1）求⊙M的半径；（2）若CE⊥AB于H，交y轴于F，求证：EH=FH．（3）在（2）的条件下求AF的长．【答案】（1）4；（2）见解析;（3）4．【解析】【分析】（1）过M作MT⊥BC于T连BM，由垂径定理可求出BT的长，再由勾股定理即可求出BM的长；（2）连接AE，由圆周角定理可得出∠AEC=∠ABC，再由AAS定理得出△AEH≌△AFH，进而可得出结论；（3）先由（1）中△BMT的边长确定出∠BMT的度数，再由直角三角形的性质可求出CG 的长，由平行四边形的判定定理判断出四边形AFCG为平行四边形，进而可求出答案．【详解】（1）如图（一），过M作MT⊥BC于T连BM，∵BC是⊙O的一条弦，MT是垂直于BC的直径，∴BT=TC=123∴124；（2）如图（二），连接AE，则∠AEC=∠ABC，∵CE⊥AB，∴∠HBC+∠BCH=90°在△COF中，∵∠OFC+∠OCF=90°，∴∠HBC=∠OFC=∠AFH，在△AEH和△AFH中，∵AFH AEHAHF AHE AH AH∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEH≌△AFH（AAS），∴EH=FH；（3）由（1）易知，∠BMT=∠BAC=60°，作直径BG，连CG，则∠BGC=∠BAC=60°，∵⊙O的半径为4，∴CG=4，连AG，∵∠BCG=90°，∴CG⊥x轴，∴CG∥AF，∵∠BAG=90°，∴AG⊥AB，∵CE⊥AB，∴AG∥CE，∴四边形AFCG为平行四边形，∴AF=CG=4．【点睛】本题考查的是垂径定理、圆周角定理、直角三角形的性质及平行四边形的判定与性质，根据题意作出辅助线是解答此题的关键．2．如图1，直角梯形OABC中，BC∥OA，OA=6，BC=2，∠BAO=45°．（1）OC的长为；（2）D是OA上一点，以BD为直径作⊙M，⊙M交AB于点Q．当⊙M与y轴相切时，sin∠BOQ=；（3）如图2，动点P以每秒1个单位长度的速度，从点O沿线段OA向点A运动；同时动点D以相同的速度，从点B沿折线B﹣C﹣O向点O运动．当点P到达点A时，两点同时停止运动．过点P作直线PE∥OC，与折线O﹣B﹣A交于点E．设点P运动的时间为t （秒）．求当以B、D、E为顶点的三角形是直角三角形时点E的坐标．【答案】（1）4；（2）35；（3）点E的坐标为（1，2）、（53，103）、（4，2）．【解析】分析：（1）过点B作BH⊥OA于H，如图1（1），易证四边形OCBH是矩形，从而有OC=BH，只需在△AHB中运用三角函数求出BH即可．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2），则有OH=2，BH=4，MN⊥OC．设圆的半径为r，则MN=MB=MD=r．在Rt△BHD中运用勾股定理可求出r=2，从而得到点D与点H重合．易证△AFG∽△ADB，从而可求出AF、GF、OF、OG、OB、AB、BG．设OR=x，利用BR2=OB2﹣OR2=BG2﹣RG2可求出x，进而可求出BR．在Rt△ORB中运用三角函数就可解决问题．（3）由于△BDE的直角不确定，故需分情况讨论，可分三种情况（①∠BDE=90°，②∠BED=90°，③∠DBE=90°）讨论，然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题．详解：（1）过点B作BH⊥OA于H，如图1（1），则有∠BHA=90°=∠COA，∴OC∥BH．∵BC∥OA，∴四边形OCBH是矩形，∴OC=BH，BC=OH．∵OA=6，BC=2，∴AH=0A﹣OH=OA﹣BC=6﹣2=4．∵∠BHA=90°，∠BAO=45°，∴tan∠BAH=BHHA=1，∴BH=HA=4，∴OC=BH=4．故答案为4．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2）．由（1）得：OH=2，BH=4．∵OC与⊙M相切于N，∴MN⊥OC．设圆的半径为r，则MN=MB=MD=r．∵BC ⊥OC ，OA ⊥OC ，∴BC ∥MN ∥OA ． ∵BM =DM ，∴CN =ON ，∴MN =12（BC +OD ），∴OD =2r ﹣2，∴DH =OD OH -=24r -．在Rt △BHD 中，∵∠BHD =90°，∴BD 2=BH 2+DH 2，∴（2r ）2=42+（2r ﹣4）2． 解得：r =2，∴DH =0，即点D 与点H 重合，∴BD ⊥0A ，BD =AD ． ∵BD 是⊙M 的直径，∴∠BGD =90°，即DG ⊥AB ，∴BG =AG ． ∵GF ⊥OA ，BD ⊥OA ，∴GF ∥BD ，∴△AFG ∽△ADB ， ∴AF AD =GF BD =AG AB =12，∴AF =12AD =2，GF =12BD =2，∴OF =4，∴OG同理可得：OB AB ，∴BG =12AB ．设OR =x ，则RG x ．∵BR ⊥OG ，∴∠BRO =∠BRG =90°，∴BR 2=OB 2﹣OR 2=BG 2﹣RG 2， ∴（2﹣x 2=（）2﹣（x ）2．解得：x ，∴BR 2=OB 2﹣OR 2=（2）2=365，∴BR在Rt △ORB 中，sin ∠BOR =BR OB35．故答案为35． （3）①当∠BDE =90°时，点D 在直线PE 上，如图2．此时DP =OC =4，BD +OP =BD +CD =BC =2，BD =t ，OP =t ． 则有2t =2． 解得：t =1．则OP =CD =DB =1． ∵DE ∥OC ，∴△BDE ∽△BCO ，∴DE OC =BD BC =12，∴DE =2，∴EP =2， ∴点E 的坐标为（1，2）． ②当∠BED =90°时，如图3．∵∠DBE =OBC ，∠DEB =∠BCO =90°，∴△DBE ∽△OBC ，∴BEBC =2DB BE OB ∴，∴BE ． ∵PE ∥OC ，∴∠OEP =∠BOC ．∵∠OPE =∠BCO =90°，∴△OPE ∽△BCO ， ∴OEOB =OPBC，2t ，∴OE ．∵OE+BE=OB=255，∴t+55t=25．解得：t=53，∴OP=53，OE=55，∴PE=22OE OP-=103，∴点E的坐标为（51033，）．③当∠DBE=90°时，如图4．此时PE=PA=6﹣t，OD=OC+BC﹣t=6﹣t．则有OD=PE，EA=22PE PA+=2（6﹣t）=62﹣2?t，∴BE=BA﹣EA=42﹣（62﹣2t）=2t﹣22．∵PE∥OD，OD=PE，∠DOP=90°，∴四边形ODEP是矩形，∴DE=OP=t，DE∥OP，∴∠BED=∠BAO=45°．在Rt△DBE中，cos∠BED=BEDE=22，∴DE=2BE，∴t=22（t﹣22）=2t﹣4．解得：t=4，∴OP=4，PE=6﹣4=2，∴点E的坐标为（4，2）．综上所述：当以B、D、E为顶点的三角形是直角三角形时点E的坐标为（1，2）、（51033，）、（4，2）．点睛：本题考查了圆周角定理、切线的性质、相似三角形的判定与性质、三角函数的定义、平行线分线段成比例、矩形的判定与性质、勾股定理等知识，还考查了分类讨论的数学思想，有一定的综合性．3．如图，AB是半圆O的直径，C是的中点，D是的中点，AC与BD相交于点E.（1）求证：BD平分∠ABC；（2）求证：BE=2AD；（3）求DEBE的值.【答案】（1）答案见解析（2）BE=AF=2AD（3）21 2 -【解析】试题分析：（1）根据中点弧的性质，可得弦AD=CD，然后根据弦、弧、圆周角、圆心角的性质求解即可；（2）延长BC与AD相交于点F, 证明△BCE≌△ACF, 根据全等三角形的性质可得BE=AF=2AD；（3）连接OD,交AC于H.简要思路如下：设OH为1，则BC为2，OB=OD=2，DH=21-, 然后根据相似三角形的性质可求解.试题解析：（1）∵D是的中点∴AD=DC∴∠CBD=∠ABD∴BD平分∠ABC（2）提示：延长BC与AD相交于点F,证明△BCE≌△ACF,BE=AF=2AD（3）连接OD,交AC于H.简要思路如下：设OH为1，则BC为2，2，21, DEBE=DHBCDE BE =2124．如图，△ABC内接于⊙O，弦AD⊥BC垂足为H，∠ABC＝2∠CAD．（1）如图1，求证：AB＝BC；（2）如图2，过点B作BM⊥CD垂足为M，BM交⊙O于E,连接AE、HM，求证：AE∥HM;（3）如图3，在（2）的条件下，连接BD交AE于N，AE与BC交于点F，若NH＝25，AD＝11，求线段AB的长.【答案】（1）证明见解析；（2）证明见解析；（3）AB的长为10.【解析】分析：（1）根据题意，设∠CAD=a，然后根据直角三角形的两锐角互余的关系，推导出∠BAC=∠ACB，再根据等角对等边得证结论；（2）延长AD、BM交于点N，连接ED.根据圆周角定理得出∠N=∠DEN=∠BAN，进而根据等角对等边，得到DE=DN,BA=BN，再根据等腰三角形和直角三角形的性质，求得MH∥AE；（3）连接CE，根据（2）的结论，由三角形全等的判定与性质证得HF=HC，然后结合勾股定理求出AC2-AH2=CD2-DH2，解得CD=5,CH=4,AH=8，最后根据锐角三角函数的性质得到AB.详解：（1）证明：设∠CAD=a,则∠ABC=2a,∠C=90°-a,∠BAD=90°-2a,∴∠BAC=90°-2a+a=90°-a∴∠BAC=∠ACB.∴AB=BC(2）证明：延长AD、BM交于点N，连接ED.∵∠DEN=∠DAB,∠N=∠BCD,∠BCD=∠BAN∴∠N=∠DEN=∠BAN∴DE=DN,BA=BN又∵BH ⊥AN,DM ⊥EN ∴EM=NM,HN=HA,∴MH ∥AE （3）连接CE.∠BDA=∠BCA,∠BDM=∠BAC,由（1）知∠BCA=∠BAC ∴∠BDA=∠BDM,∴△BDM ≌△BDH, ∴DH=MH,∠MBD=∠HBD,∴BD ⊥MH 又∵MH ∥AE,∴BD ⊥EF,∴△FNB ≌△ENB, 同理可证△AFH ≌△ACH,∴HF=HC,又∵FN=NE∴NH ∥EC,EC=2NH,又∵NH=25∴EC=45∠EAC=2∠AEC=2a=∠ABC,可证弧AC=弧EC, ∴AC=EC=5 设HD=x ，AH=11-x ，∵∠ADC=2∠CAD,翻折△CHD 至△CHG,可证CG=CD=AG AH=CD+DH,CD=AH-DH=11-x-x=11-2x又∵AC 2-AH 2=CD 2-DH 2,∴(52-(11-x)2=(11-2x)2-x 2 ∴x 1=3,x 2=272(舍去)∴CD=5,CH=4,AH=8. 又∵tan2AH CHa BH DH==,∴BH=6 ∴22226810BM AH +=+= 点睛：此题主要考查了圆的综合，结合圆周角定理，勾股定理，全等三角形的判定与性质，解直角三角形的性质，综合性比较强，灵活添加辅助线，构造方程求解是解题关键.5．如图，在RtΔABC 中，∠ABC=90°，AB=CB ，以AB 为直径的⊙O 交AC 于点D ，点E 是AB 边上一点（点E 不与点A 、B 重合），DE 的延长线交⊙O 于点G ，DF ⊥DG ，且交BC 于点F.（1）求证：AE=BF ；（2）连接EF ，求证：∠FEB=∠GDA ； （3）连接GF,若AE=2，EB=4，求ΔGFD 的面积.【答案】（1）（2）见解析；（3）9【解析】分析：（1）连接BD，由三角形ABC为等腰直角三角形，求出∠A与∠C的度数，根据AB 为圆的直径，利用圆周角定理得到∠ADB为直角，即BD垂直于AC，利用直角三角形斜边上的中线等于斜边的一半，得到AD=DC=BD=12AC，进而确定出∠A=∠FBD，再利用同角的余角相等得到一对角相等，利用ASA得到三角形AED与三角形BFD全等，利用全等三角形对应边相等即可得证；（2）连接EF，BG，由三角形AED与三角形BFD全等，得到ED=FD，进而得到三角形DEF为等腰直角三角形，利用圆周角定理及等腰直角三角形性质得到一对同位角相等，利用同位角相等两直线平行，再根据平行线的性质和同弧所对的圆周角相等，即可得出结论；（3）由全等三角形对应边相等得到AE=BF=1，在直角三角形BEF中，利用勾股定理求出EF的长，利用锐角三角形函数定义求出DE的长，利用两对角相等的三角形相似得到三角形AED与三角形GEB相似，由相似得比例，求出GE的长，由GE+ED求出GD的长，根据三角形的面积公式计算即可．详解：（1）连接BD．在Rt△ABC中，∠ABC=90°，AB=BC，∴∠A=∠C=45°．∵AB为圆O的直径，∴∠ADB=90°，即BD⊥AC，∴AD=DC=BD=12AC，∠CBD=∠C=45°，∴∠A=∠FBD．∵DF⊥DG，∴∠FDG=90°，∴∠FDB+∠BDG=90°．∵∠EDA+∠BDG=90°，∴∠EDA=∠FDB．在△AED和△BFD中，A FBDAD BDEDA FDB∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AED≌△BFD（ASA），∴AE=BF；（2）连接EF，BG．∵△AED≌△BFD，∴DE=DF．∵∠EDF=90°，∴△EDF是等腰直角三角形，∴∠DEF=45°．∵∠G=∠A=45°，∴∠G=∠DEF，∴GB∥EF，∴∠FEB=∠GBA．∵∠GBA=∠GDA，∴∠FEB=∠GDA；（3）∵AE=BF，AE=2，∴BF=2．在Rt△EBF中，∠EBF=90°，∴根据勾股定理得：EF 2=EB 2+BF 2．∵EB =4，BF =2，∴EF =2242+=25．∵△DEF 为等腰直角三角形，∠EDF =90°，∴cos ∠DEF =DEEF． ∵EF =25，∴DE =25×22=10． ∵∠G =∠A ，∠GEB =∠AED ，∴△GEB ∽△AED ，∴GE AE =EBED，即GE •ED =AE •EB ，∴10•GE =8，即GE =4105，则GD =GE +ED =9105． ∴119101109222S GD DF GD DE =⨯⨯=⨯⨯=⨯⨯=．点睛：本题属于圆综合题，涉及的知识有：全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，圆周角定理，以及平行线的判定与性质，熟练掌握判定与性质是解答本题的关键．6．等腰Rt △ABC 和⊙O 如图放置，已知AB=BC=1，∠ABC=90°，⊙O 的半径为1，圆心O 与直线AB 的距离为5．（1）若△ABC 以每秒2个单位的速度向右移动，⊙O 不动，则经过多少时间△ABC 的边与圆第一次相切？（2）若两个图形同时向右移动，△ABC 的速度为每秒2个单位，⊙O 的速度为每秒1个单位，则经过多少时间△ABC 的边与圆第一次相切？（3）若两个图形同时向右移动，△ABC 的速度为每秒2个单位，⊙O 的速度为每秒1个单位，同时△ABC 的边长AB 、BC 都以每秒0.5个单位沿BA 、BC 方向增大．△ABC 的边与圆第一次相切时，点B 运动了多少距离？【答案】（1）522-；（2）52-；（3）20423-【解析】分析：（1）分析易得，第一次相切时，与斜边相切，假设此时，△ABC移至△A′B′C′处，A′C′与⊙O切于点E，连OE并延长，交B′C′于F．由切线长定理易得CC′的长，进而由三角形运动的速度可得答案；（2）设运动的时间为t秒，根据题意得：CC′=2t，DD′=t，则C′D′=CD+DD′-CC′=4+t-2t=4-t，由第（1）的结论列式得出结果；（3）求出相切的时间，进而得出B点移动的距离．详解：（1）假设第一次相切时，△ABC移至△A′B′C′处，如图1，A′C′与⊙O切于点E，连接OE并延长，交B′C′于F，设⊙O与直线l切于点D，连接OD，则OE⊥A′C′，OD⊥直线l，由切线长定理可知C′E=C′D，设C′D=x，则C′E=x，∵△ABC是等腰直角三角形，∴∠A=∠ACB=45°，∴∠A′C′B′=∠ACB=45°，∴△EFC′是等腰直角三角形，∴2x，∠OFD=45°，∴△OFD也是等腰直角三角形，∴OD=DF，∴2x+x=1，则2-1，∴CC′=BD-BC-C′D=5-1-2-1）2，∴点C运动的时间为522；则经过522秒，△ABC的边与圆第一次相切；（2）如图2，设经过t秒△ABC的边与圆第一次相切，△ABC移至△A′B′C′处，⊙O与BC 所在直线的切点D移至D′处，A′C′与⊙O 切于点E ，连OE 并延长，交B′C′于F ， ∵CC′=2t ，DD′=t ，∴C′D′=CD+DD′-CC′=4+t -2t=4-t ， 由切线长定理得C′E=C′D′=4-t ， 由（1）得：4-t=2-1， 解得：t=5-2，答：经过5-2秒△ABC 的边与圆第一次相切； （3）由（2）得CC′=（2+0.5）t=2.5t ，DD′=t ， 则C′D′=CD+DD′-CC′=4+t -2.5t=4-1.5t ， 由切线长定理得C′E=C′D′=4-1.5t ， 由（1）得：4-1.5t=2-1， 解得：t=10223-， ∴点B 运动的距离为2×10223-=20423-．点睛：本题要求学生熟练掌握圆与直线的位置关系，并结合动点问题进行综合分析，比较复杂，难度较大，考查了学生数形结合的分析能力．7．已知P 是O 的直径BA 延长线上的一个动点，∠P 的另一边交O 于点C 、D ，两点位于AB 的上方，AB ＝6，OP=m ，1sin 3P ＝，如图所示．另一个半径为6的1O 经过点C 、D ，圆心距1OO n ＝． （1）当m=6时，求线段CD 的长；（2）设圆心O 1在直线AB 上方，试用n 的代数式表示m ；（3）△POO 1在点P 的运动过程中，是否能成为以OO 1为腰的等腰三角形，如果能，试求出此时n 的值；如果不能，请说明理由．【答案】(1)CD=25;(2)m=23812n n- ;(3) n 的值为955或9155 【解析】分析：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．解Rt △POH ，得到OH 的长．由勾股定理得CH 的长，再由垂径定理即可得到结论； （2）解Rt △POH ，得到Rt 3mOH OCH ＝．在和Rt △1O CH 中，由勾股定理即可得到结论；（3）△1POO 成为等腰三角形可分以下几种情况讨论：① 当圆心1O 、O 在弦CD 异侧时，分1OP OO ＝和11O P OO ＝．②当圆心1O 、O 在弦CD 同侧时，同理可得结论． 详解：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．在Rt △1sin 63POH P PO =中，＝，，∴2OH =． ∵AB ＝6，∴3OC ＝． 由勾股定理得： 5CH = ∵OH ⊥DC ，∴225CD CH ==．（2）在Rt △1sin 3POH P PO m 中，＝，＝，∴3m OH ＝． 在Rt △OCH 中，2293m CH ⎛⎫- ⎪⎝⎭＝． 在Rt △1O CH 中，22363m CH n ⎛⎫-- ⎪⎝⎭＝．可得： 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭＝，解得23812n m n -：＝． （3）△1POO 成为等腰三角形可分以下几种情况： ① 当圆心1O 、O 在弦CD 异侧时i ）1OP OO ＝，即m n ＝，由23812n n n-＝，解得9n ：＝．即圆心距等于O 、1O 的半径的和，就有O 、1O 外切不合题意舍去．ii ）11O P OO ＝，由22233m m n m -+-（）（） n ＝， 解得：23m n ＝，即23n 23812n n-＝，解得9155n ：＝． ②当圆心1O 、O 在弦CD 同侧时，同理可得： 28132n m n-＝．∵1POO ∠是钝角，∴只能是m n =，即28132nn n-＝，解得955n ：＝． 综上所述：n 的值为955或9155． 点睛：本题是圆的综合题．考查了圆的有关性质和两圆的位置关系以及解直径三角形．解答（3）的关键是要分类讨论．8．在O 中，AB 为直径，C 为O 上一点.（Ⅰ）如图①，过点C 作O 的切线，与AB 的延长线相交于点P ，若28CAB ∠=︒，求P ∠的大小；（Ⅱ）如图②，D 为弧AC 的中点，连接OD 交AC 于点E ，连接DC 并延长，与AB 的延长线相交于点P ，若12CAB ∠=︒，求P ∠的大小. 【答案】（1）∠P ＝34°；（2）∠P ＝27° 【解析】 【分析】（1）首先连接OC ，由OA=OC ，即可求得∠A 的度数，然后由圆周角定理，求得∠POC 的度数，继而求得答案；（2）因为D 为弧AC 的中点，OD 为半径，所以OD ⊥AC ，继而求得答案．【详解】（1）连接OC，∵OA＝OC，∴∠A＝∠OCA＝28°，∴∠POC＝56°，∵CP是⊙O的切线，∴∠OCP＝90°，∴∠P＝34°；（2）∵D为弧AC的中点，OD为半径，∴OD⊥AC，∵∠CAB＝12°，∴∠AOE＝78°，∴∠DCA＝39°，∵∠P＝∠DCA﹣∠CAB，∴∠P＝27°．【点睛】本题考查切线的性质以及等腰三角形的性质．注意准确作出辅助线是解此题的关键．9．如图，△ABC中，AC＝BC＝10，cosC＝35，点P是AC边上一动点（不与点A、C重合），以PA长为半径的⊙P与边AB的另一个交点为D，过点D作DE⊥CB于点E．（1）当⊙P与边BC相切时，求⊙P的半径．（2）连接BP交DE于点F，设AP的长为x，PF的长为y，求y关于x的函数解析式，并直接写出x的取值范围．（3）在（2）的条件下，当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时，求相交所得的公共弦的长.【答案】（1）409R=;（2）25880320xy x xx=-++;（3）50105-.【解析】【分析】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，即可求解；（2）首先证明PD∥BE，则EB BFPD PF=，即：2024588x yxxxy-+--=，即可求解；（3）证明四边形PDBE为平行四边形，则AG＝EP＝BD，即：AB＝DB+AD＝AG+AD＝45，即可求解．【详解】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，解得：R＝409；（2）在△ABC中，AC＝BC＝10，cosC＝35，设AP＝PD＝x，∠A＝∠ABC＝β，过点B作BH⊥AC，则BH ＝ACsinC ＝8，同理可得：CH ＝6，HA ＝4，AB ＝45，则：tan ∠CAB ＝2， BP ＝228+(4)x -＝2880x x -+，DA ＝25x ，则BD ＝45﹣25x ， 如下图所示，PA ＝PD ，∴∠PAD ＝∠CAB ＝∠CBA ＝β，tanβ＝2，则cosβ5，sinβ5， EB ＝BDcosβ＝（525x ）5＝4﹣25x ，∴PD ∥BE ，∴EB BFPD PF=，即：2024588x y x xx -+--=，整理得：y 25xx 8x 803x 20-++（3）以EP 为直径作圆Q 如下图所示，两个圆交于点G ，则PG ＝PQ ，即两个圆的半径相等，则两圆另外一个交点为D ， GD 为相交所得的公共弦， ∵点Q 是弧GD 的中点， ∴DG ⊥EP ， ∵AG 是圆P 的直径， ∴∠GDA ＝90°， ∴EP ∥BD ，由（2）知，PD ∥BC ，∴四边形PDBE 为平行四边形， ∴AG ＝EP ＝BD ，∴AB ＝DB+AD ＝AG+AD ＝5 设圆的半径为r ，在△ADG 中，AD ＝2rcosβ5DG 5AG ＝2r ，5＝52r 51+， 则：DG 550﹣5相交所得的公共弦的长为50﹣5 【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．10．如图所示，ABC ∆内接于圆O ，CD AB ⊥于D ； （1）如图1，当AB 为直径，求证：OBC ACD ∠=∠；（2）如图2，当AB 为非直径的弦，连接OB ，则（1）的结论是否成立？若成立请证明，不成立说明由；（3）如图3，在（2）的条件下，作AE BC ⊥于E ，交CD 于点F ，连接ED ，且2AD BD ED =+，若3DE =，5OB =，求CF 的长度．【答案】（1）见解析；（2）成立；（3）145【解析】 【分析】（1）根据圆周角定理求出∠ACB=90°，求出∠ADC=90°，再根据三角形内角和定理求出即可；（2）根据圆周角定理求出∠BOC=2∠A ，求出∠OBC=90°-∠A 和∠ACD=90°-∠A 即可； （3）分别延长AE 、CD 交⊙O 于H 、K ，连接HK 、CH 、AK ，在AD 上取DG=BD ，延长CG 交AK 于M ，延长KO 交⊙O 于N ，连接CN 、AN ，求出关于a 的方程，再求出a 即可． 【详解】（1）证明：∵AB 为直径， ∴ACB 90∠=︒，∵CD AB ⊥于D ，∴ADC 90∠=︒，∴OBC A 90∠∠+=︒，A ACD 90∠∠+=︒， ∴OBC ACD ∠∠=；（2）成立， 证明：连接OC ，由圆周角定理得：BOC 2A ∠∠=， ∵OC OB =， ∴()()11OBC 180BOC 1802A 90A 22∠∠∠∠=︒-=︒-=︒-， ∵ADC 90∠=︒，∴ACD 90A ∠∠=︒-，∴OBC ACD ∠∠=；（3）分别延长AE 、CD 交⊙O 于H 、K ，连接HK 、CH 、AK ，∵AE BC ⊥，CD BA ⊥，∴AEC ADC 90∠∠==︒，∴BCD CFE 90∠∠+=︒，BAH DFA 90∠∠+=︒， ∵CFE DFA ∠∠=， ∴BCD BAH ∠∠=，∵根据圆周角定理得：BAH BCH ∠∠=， ∴BCD BAH BCH ∠∠∠==，∴由三角形内角和定理得：CHE CFE ∠∠=，∴CH CF =， ∴EH EF =， 同理DF DK =， ∵DE 3=， ∴HK 2DE 6==，在AD 上取DG BD =，延长CG 交AK 于M ，则AG AD BD 2DE 6=-==，BC GC =，∴MCK BCK BAK ∠∠∠==， ∴CMK 90∠=︒，延长KO 交⊙O 于N ，连接CN 、AN ， 则NAK 90CMK ∠∠=︒=， ∴CM //AN ， ∵NCK ADK 90∠∠==︒，∴CN //AG ，∴四边形CGAN 是平行四边形， ∴AG CN 6==， 作OT CK ⊥于T ， 则T 为CK 的中点， ∵O 为KN 的中点， ∴1OT CN 32==，∵OTC 90∠=︒，OC 5=，∴由勾股定理得：CT 4=，∴CK 2CT 8==，作直径HS ，连接KS ，∵HK 6=，HS 10=，∴由勾股定理得：KS 8=， ∴3tan HSK tan HAK 4∠∠==， ∴1tan EAB tan BCD 3∠∠==， 设BD a =，CD 3a =， ∴AD BD 2ED a 6=+=+，11DK AD a 233==+， ∵CD DK CK +=， ∴13a a 283++=， 解得：9a 5=， ∴113DK a 235=+=， ∴2614CF CK 2DK 855=-=-=． 【点睛】本题考查了垂径定理、解直角三角形、等腰三角形的性质、圆周角定理、勾股定理等知识点，能综合运用知识点进行推理是解此题的关键，综合性比较强，难度偏大．。

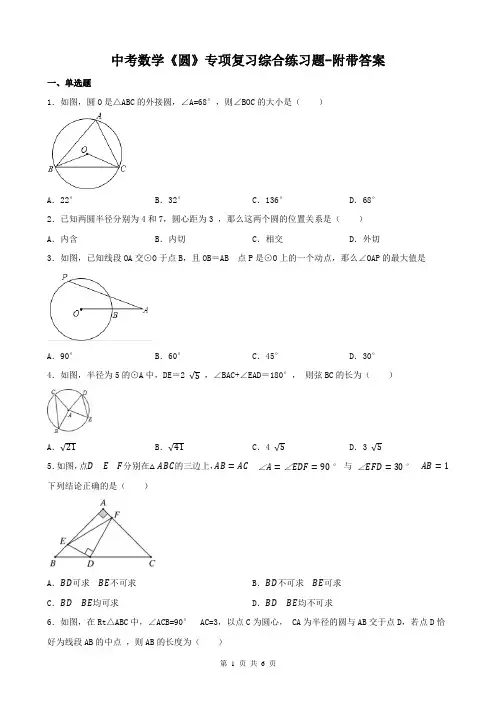
中考数学《圆》专项复习综合练习题-附带答案一、单选题1．如图，圆O是△ABC的外接圆，∠A=68°，则∠BOC的大小是（）A．22°B．32°C．136°D．68°2．已知两圆半径分别为4和7，圆心距为3 ，那么这两个圆的位置关系是（）A．内含B．内切C．相交D．外切3．如图，已知线段OA交⊙O于点B，且OB＝AB 点P是⊙O上的一个动点，那么∠OAP的最大值是A．90°B．60°C．45°D．30°4．如图，半径为5的⊙A中，DE＝2 √5，∠BAC+∠EAD＝180°，则弦BC的长为（）A．√21B．√41C．4 √5D．3 √55．如图，点D E F分别在△ABC的三边上，AB=AC∠A=∠EDF=90°与∠EFD=30°AB=1下列结论正确的是（）A．BD可求BE不可求B．BD不可求BE可求C．BD BE均可求D．BD BE均不可求6．如图，在Rt△ABC中，∠ACB=90° AC=3，以点C为圆心， CA为半径的圆与AB交于点D，若点D恰好为线段AB的中点，则AB的长度为（）B．3 C．9 D．6A．327．如图，⊙O是△ABC的外接圆，弦BD交AC于点E，AE=DE， BC=CE，过点O作OF⊥AC于点F，延长FO 交BE于点G ，若DE=6，EG=4，则AB的长为（）A．4√5B．8√3C．13 D．148．如图，把正六边形各边按同一方向延长，使延长的线段与原正六边形的边长相等，顺次连接这六条线段外端点可以得到一个新的正六边形…，重复上述过程，经过2018次后所得到的正六边形边长是原正六边形边长的（）A．（√2）2016倍B．（√3）2017倍C．（√3）2018倍D．（√2）2019倍二、填空题9．如图，PA、PB切⊙O于点A、B ，已知⊙O半径为2 且∠APB=60°，则AB= ．10．如图，矩形ABCD中，BC＝4 CD＝2 以AD为直径的半圆O与BC相切于点E，连接BD，则阴影部分的面积为.（结果保留π）11．如图，两边平行的刻度尺在圆上移动当刻度尺的一边与直径为6.5cm的圆相切时另一边与圆两个交点处的读数恰好为“2”和“8”（单位：cm）则刻度尺的宽为 cm．12．如图，两圆相交于A、B两点小圆经过大圆的圆心O 点C D分别在两圆上若∠ADB＝100°则∠ACB的度数为。

中考数学圆的综合综合题及答案一、圆的综合1．如图，⊙A过▱OBCD的三顶点O、D、C，边OB与⊙A相切于点O，边BC与⊙O相交于点H，射线OA交边CD于点E，交⊙A于点F，点P在射线OA上，且∠PCD=2∠DOF，以O为原点，OP所在的直线为x轴建立平面直角坐标系，点B的坐标为（0，﹣2）．（1）若∠BOH=30°，求点H的坐标；（2）求证：直线PC是⊙A的切线；（3）若OD=10，求⊙A的半径．【答案】（1）（132）详见解析；（3）5 3 .【解析】【分析】（1）先判断出OH=OB=2，利用三角函数求出MH，OM，即可得出结论；（2）先判断出∠PCD=∠DAE，进而判断出∠PCD=∠CAE，即可得出结论；（3）先求出OE═3，进而用勾股定理建立方程，r2-（3-r）2=1，即可得出结论．【详解】（1）解：如图，过点H作HM⊥y轴，垂足为M．∵四边形OBCD是平行四边形，∴∠B=∠ODC∵四边形OHCD是圆内接四边形∴∠OHB=∠ODC∴∠OHB=∠B∴OH=OB=2∴在Rt△OMH中，∵∠BOH=30°，∴MH=12OH=1，33∴点H的坐标为（13（2）连接AC．∵OA=AD，∴∠DOF=∠ADO∴∠DAE=2∠DOF∵∠PCD=2∠DOF ，∴∠PCD=∠DAE∵OB 与⊙O 相切于点A∴OB ⊥OF∵OB ∥CD∴CD ⊥AF∴∠DAE=∠CAE∴∠PCD=∠CAE∴∠PCA=∠PCD+∠ACE=∠CAE+∠ACE=90°∴直线PC 是⊙A 的切线；（3）解：⊙O 的半径为r ．在Rt △OED 中，DE=12CD=12OB=1，OD=10 ， ∴OE ═3∵OA=AD=r ，AE=3﹣r ．在Rt △DEA 中，根据勾股定理得，r 2﹣（3﹣r ）2=1解得r=53．【点睛】此题是圆的综合题，主要考查了平行四边形的性质，圆内接四边形的性质，勾股定理，切线的性质和判定，构造直角三角形是解本题的关键．2．在⊙O 中，点C 是AB u u u r上的一个动点(不与点A ，B 重合)，∠ACB=120°，点I 是∠ABC 的内心，CI 的延长线交⊙O 于点D ，连结AD,BD ．（1）求证：AD=BD ．（2）猜想线段AB 与DI 的数量关系，并说明理由．（3）若⊙O的半径为2，点E，F是»AB的三等分点，当点C从点E运动到点F时，求点I 随之运动形成的路径长．【答案】（1）证明见解析；（2）AB=DI，理由见解析（3）23【解析】分析：（1）根据内心的定义可得CI平分∠ACB，可得出角相等，再根据圆周角定理，可证得结论；（2）根据∠ACB=120°，∠ACD=∠BCD，可求出∠BAD的度数，再根据AD=BD，可证得△ABD是等边三角形，再根据内心的定义及三角形的外角性质，证明∠BID=∠IBD，得出ID=BD，再根据AB=BD，即可证得结论；（3）连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧，根据已知及圆周角定理、解直角三角形，可求出AD的长，再根据点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，可证得∠DAI1=∠AI1D，然后利用弧长的公式可求出点I 随之运动形成的路径长.详解：（1）证明：∵点I是∠ABC的内心∴CI平分∠ACB∴∠ACD=∠BCD∴弧AD=弧BD∴AD=BD（2）AB=DI理由：∵∠ACB=120°，∠ACD=∠BCD∴∠BCD=×120°=60°∵弧BD=弧BD∴∠DAB=∠BCD=60°∵AD=BD∴△ABD是等边三角形，∴AB=BD，∠ABD=∠C∵I是△ABC的内心∴BI平分∠ABC∴∠CBI=∠ABI∵∠BID=∠C+∠CBI，∠IBD=∠ABI+∠ABD∴∠BID=∠IBD∴ID=BD∵AB=BD∴AB=DI（3）解：如图，连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧∵∠ACB=120°，弧AD=弧BD∴∠AED=∠ACB=×120°=60°∵圆的半径为2，DE是直径∴DE=4，∠EAD=90°∴AD=sin∠AED×DE=×4=2∵点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，∴∠ADB=60°∴弧AB的度数为120°，∴弧AM、弧BF的度数都为为40°∴∠ADM=20°=∠FAB∴∠DAI1=∠FAB+∠DAB=80°∴∠AI1D=180°-∠ADM-∠DAI1=180°-20°-80°=80°∴∠DAI1=∠AI1D∴AD=I1D=2∴弧I1I2的长为：点睛：此题是一道圆的综合题，有一定的难度，熟记圆的相关性质与定理，并对圆中的弦、弧、圆心角、圆周角等进行灵活转化是解题关键，注意数形结合思想的渗透.3．如图所示，以Rt△ABC的直角边AB为直径作圆O，与斜边交于点D，E为BC边上的中点，连接DE．（1）求证：DE是⊙O的切线；（2）连接OE ，AE ，当∠CAB 为何值时，四边形AOED 是平行四边形？并在此条件下求sin ∠CAE 的值．【答案】(1)见解析;(2)1010. 【解析】 分析：（1）要证DE 是⊙O 的切线，必须证ED ⊥OD ，即∠EDB+∠ODB=90°（2）要证AOED 是平行四边形，则DE ∥AB ，D 为AC 中点，又BD ⊥AC ，所以△ABC 为等腰直角三角形，所以∠CAB=45°，再由正弦的概念求解即可．详解：（1）证明：连接O 、D 与B 、D 两点，∵△BDC 是Rt △，且E 为BC 中点，∴∠EDB=∠EBD ．（2分）又∵OD=OB 且∠EBD+∠DBO=90°，∴∠EDB+∠ODB=90°．∴DE 是⊙O 的切线．（2）解：∵∠EDO=∠B=90°，若要四边形AOED 是平行四边形，则DE ∥AB ，D 为AC 中点，又∵BD ⊥AC ，∴△ABC 为等腰直角三角形．∴∠C AB=45°．过E 作EH ⊥AC 于H ，设BC=2k ，则EH=22k ，AE=5k ， ∴sin ∠CAE=1010EH AE ．点睛：本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．4．已知：AB 是⊙0直径,C 是⊙0外一点,连接BC 交⊙0于点D ，BD=CD,连接AD 、AC ．(1)如图1,求证:∠BAD=∠CAD(2)如图2,过点C 作CF ⊥AB 于点F,交⊙0于点E,延长CF 交⊙0于点G.过点作EH ⊥AG 于点H ，交AB 于点K,求证AK=2OF ；(3)如图3,在(2)的条件下,EH 交AD 于点L,若0K=1,AC=CG,求线段AL 的长.图1 图2 图3【答案】(1)见解析(2)见解析(3)12105 【解析】试题分析：（1）由直径所对的圆周角等于90°，得到∠ADB =90°，再证明△ABD ≌△ACD 即可得到结论；（2）连接BE ．由同弧所对的圆周角相等，得到∠GAB =∠BEG ．再证△KFE ≌△BFE ，得到BF =KF =BK ．由OF =OB -BF ，AK =AB -BK ，即可得到结论． （3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．先证CM 垂直平分AG ，得到AM =GM ，∠AGC +∠GCM =90°．再证∠GAF =∠GCM =α．通过证明△AGB ≌△CMG ，得到BG =GM =12AG ．再证明∠BGC =∠MCG =α．设BF =KF =a ， 可得GF =2a ，AF =4a ． 由OK =1，得到OF =a +1，AK =2（a +1），AF = 3a +2，得到3a +2=4a ，解出a 的值，得到AF ，AB ，GF ，FC 的值．由tanα=tan ∠HAK =12HK AH =， AK =6，可以求出 AH 的长．再由1tan tan 3BAD BCF ∠=∠= ，利用公式tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD ∠+∠-∠⋅∠，得到∠GAD =45°，则AL =2AH ，即可得到结论．试题解析：解：（1）∵AB 为⊙O 的直径，∴∠ADB =90°，∴∠ADC =90°．∵BD =CD ，∠BDA =∠CDA ，AD =AD ，∴△ABD ≌△ACD ，∴∠BAD =∠CAD ．（2）连接BE ．∵BG =BG ，∴∠GAB =∠BEG ．∵CF ⊥AB ，∴∠KFE =90°．∵EH ⊥AG ，∴∠AHE =∠KFE =90°，∠AKH =∠EKF ，∴∠HAK =∠KEF =∠BEF ．∵FE =FE ，∠KFE =∠BFE =90°，∴△KFE ≌△BFE ，∴BF =KF =BK ．∵ OF =OB -BF ，AK =AB -BK ，∴AK =2OF ．（3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．∵AC =CG ， ∴点C 在AG 的垂直平分线上．∵ OA =OG ，∴点O 在AG 的垂直平分线上， ∴CM 垂直平分AG ，∴AM =GM ，∠AGC +∠GCM =90°．∵AF ⊥CG ，∴∠AGC +∠GAF =90°，∴∠GAF =∠GCM =α．∵AB 为⊙O 的直径，∴∠AGB = 90°，∴∠AGB =∠CMG =90°．∵AB =AC =CG ，∴△AGB ≌△CMG ，∴BG =GM=12AG ． 在Rt △AGB 中， 1tan tan 2GB GAB AG α∠=== ． ∵∠AMC =∠AGB = 90°，∴BG ∥CM ， ∴∠BGC =∠MCG =α．设BF =KF =a ， 1tan tan 2BF BGF GF α∠===，∴GF =2a ，1tan tan 2GF GAF AF α∠=== ，AF =4a ．∵OK =1，∴OF =a +1，AK =2OF =2（a +1），∴AF =AK +KF =a +2（a +1）=3a +2，∴3a +2=4a ，∴a =2， AK =6，∴AF =4a =8，AB =AC =CG =10，GF =2a =4，FC =CG -GF =6． ∵tanα=tan ∠HAK =12HK AH =，设KH =m ，则AH =2m ，∴AK 22(2)m m +=6，解得：m 65，∴AH =2m 125．在Rt △BFC 中，1tan 3BF BCF FC ∠== ．∵∠BAD +∠ABD =90°， ∠FBC +∠BCF =90°，∴∠BCF =∠BAD ，1tan tan 3BAD BCF ∠=∠= ，∴tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD ∠+∠-∠⋅∠=1123111123+=-⨯，∴∠GAD=45°，∴HL=AH，AL=2AH= 12105．5．已知：如图1，∠ACG=90°，AC=2，点B为CG边上的一个动点，连接AB，将△ACB沿AB边所在的直线翻折得到△ADB，过点D作DF⊥CG于点F．（1）当BC=233时，判断直线FD与以AB为直径的⊙O的位置关系，并加以证明；（2）如图2，点B在CG上向点C运动，直线FD与以AB为直径的⊙O交于D、H两点，连接AH，当∠CAB=∠BAD=∠DAH时，求BC的长．【答案】（1）直线FD与以AB为直径的⊙O相切，理由见解析；（2）22 .【解析】试题分析：（1）根据已知及切线的判定证明得，直线FD与以AB为直径的⊙O相切；（2）根据圆内接四边形的性质及直角三角形的性质进行分析，从而求得BC的长．试题解析：（1）判断：直线FD与以AB为直径的⊙O相切．证明：如图，作以AB为直径的⊙O；∵△ADB是将△ACB沿AB边所在的直线翻折得到的，∴△ADB≌△ACB，∴∠ADB=∠ACB=90°．∵O为AB的中点，连接DO，∴OD=OB=AB，∴点D在⊙O上．在Rt△ACB中，BC=，AC=2；∴tan∠CAB==，∴∠CAB=∠BAD=30°，∴∠ABC=∠ABD=60°，∴△BOD是等边三角形．∴∠BOD=60°．∴∠ABC=∠BOD，∴FC∥DO．∵DF⊥CG，∴∠ODF=∠BFD=90°，∴OD⊥FD，∴FD为⊙O的切线．（2）延长AD交CG于点E，同（1）中的方法，可证点C在⊙O上；∴四边形ADBC是圆内接四边形．∴∠FBD=∠1+∠2．同理∠FDB=∠2+∠3．∵∠1=∠2=∠3，∴∠FBD=∠FDB，又∠DFB=90°．∴EC=AC=2．设BC=x，则BD=BC=x，∵∠EDB=90°，∴EB=x．∵EB+BC=EC，∴x+x=2，解得x=2﹣2，∴BC=2﹣2．6．已知，ABC ∆内接于O e ，点P 是弧AB 的中点，连接PA 、PB ；（1）如图1，若AC BC =，求证：AB PC ⊥；（2）如图2，若PA 平分CPM ∠，求证：AB AC =；（3）在（2）的条件下，若24sin 25BPC ∠=，8AC =，求AP 的值．【答案】(1)见解析;(2)见解析5【解析】【分析】(1)由点P 是弧AB 的中点，可得出AP=BP , 通过证明APC BPC ∆≅∆ ,ACE BCE ∆≅∆可得出AEC BEC ∠=∠进而证明AB ⊥ PC.(2)由PA 是∠CPM 的角平分线，得到∠MPA=∠APC, 等量代换得到∠ABC=∠ACB, 根据等腰三角形的判定定理即可证得AB=AC.(3)过A 点作AD ⊥BC,有三线合一可知AD 平分BC,点O 在AD 上，连结OB ，则∠BOD ＝∠BAC ，根据圆周角定理可知∠BOD=∠BAC, ∠BPC=∠BAC ，由∠BOD=∠BPC 可得sin sin BD BOD BPC OB∠=∠=,设OB=25x ，根据勾股定理可算出OB 、BD 、OD 、AD 的长，再次利用勾股定理即可求得AP 的值.【详解】解：（1）∵点P 是弧AB 的中点，如图1，∴AP ＝BP ，在△APC 和△BPC 中AP BP AC BC PC PC =⎧⎪=⎨⎪=⎩，∴△APC ≌△BPC （SSS ），∴∠ACP ＝∠BCP ，在△ACE 和△BCE 中AC BC ACP BCP CE CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACE ≌△BCE （SAS ），∴∠AEC ＝∠BEC ，∵∠AEC +∠BEC ＝180°，∴∠AEC ＝90°，∴AB ⊥PC ；（2）∵PA 平分∠CPM ，∴∠MPA ＝∠APC ，∵∠APC +∠BPC +∠ACB ＝180°，∠MPA +∠APC +∠BPC ＝180°，∴∠ACB ＝∠MPA ＝∠APC ，∵∠APC ＝∠ABC ，∴∠ABC ＝∠ACB ，∴AB ＝AC ；（3）过A 点作AD ⊥BC 交BC 于D ，连结OP 交AB 于E ，如图2，由（2）得出AB ＝AC ，∴AD 平分BC ，∴点O 在AD 上，连结OB ，则∠BOD ＝∠BAC ，∵∠BPC ＝∠BAC ，∴sin sin BOD BPC ∠=∠=2425BD OB=， 设OB ＝25x ，则BD ＝24x ，∴OD ＝22OB BD -＝7x ，在Rt ABD V 中，AD ＝25x +7x ＝32x ，BD ＝24x ，∴AB ＝22AD BD +＝40x ，∵AC ＝8，∴AB ＝40x ＝8，解得：x ＝0.2，∴OB ＝5，BD ＝4.8，OD ＝1.4，AD ＝6.4，∵点P 是¶AB 的中点，∴OP 垂直平分AB ，∴AE ＝12AB ＝4，∠AEP ＝∠AEO ＝90°， 在Rt AEO ∆中，OE ＝223AO AE -=，∴PE ＝OP ﹣OE ＝5﹣3＝2，在Rt APE ∆中，AP ＝22222425PE AE +=+=．【点睛】本题是一道有关圆的综合题，考查了圆周角定理、勾股定理、等腰三角形的判定定理和三线合一，是初中数学的重点和难点，一般以压轴题形出现，难度较大.7．如图，在Rt △ABC 中，90C ∠=︒，AD 平分∠BAC ，交BC 于点D ，点O 在AB 上，⊙O 经过A 、D 两点，交AC 于点E ，交AB 于点F ．（1）求证：BC 是⊙O 的切线；（2）若⊙O 的半径是2cm ，E 是弧AD 的中点，求阴影部分的面积（结果保留π和根号）【答案】（1）证明见解析 （2）233π【解析】【分析】 （1）连接OD ，只要证明OD ∥AC 即可解决问题；（2）连接OE ，OE 交AD 于K ．只要证明△AOE 是等边三角形即可解决问题．【详解】（1）连接OD ．∵OA=OD，∴∠OAD=∠ODA．∵∠OAD=∠DAC，∴∠ODA=∠DAC，∴OD∥AC，∴∠ODB=∠C=90°，∴OD⊥BC，∴BC是⊙O的切线．（2）连接OE，OE交AD于K．∵¶¶AE DE=，∴OE⊥AD．∵∠OAK=∠EAK，AK=AK，∠AKO=∠AKE=90°，∴△AKO≌△AKE，∴AO=AE=OE，∴△AOE是等边三角形，∴∠AOE=60°，∴S阴=S扇形OAE﹣S△AOE26023360π⋅⋅=-⨯22233π=-．【点睛】本题考查了切线的判定、扇形的面积、等边三角形的判定和性质、平行线的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，属于中考常考题型．8．在平面直角坐标系中，已知点A（2，0），点B（0，），点O（0，0）．△AOB绕着O顺时针旋转，得△A'OB'，点A、B旋转后的对应点为A'，B'，记旋转角为α．（Ⅰ）如图1，A'B'恰好经过点A时，求此时旋转角α的度数，并求出点B'的坐标；（Ⅱ）如图2，若0°＜α＜90°，设直线AA'和直线BB'交于点P，求证：AA'⊥BB'；（Ⅲ）若0°＜α＜360°，求（Ⅱ）中的点P纵坐标的最小值（直接写出结果即可）．【答案】（Ⅰ）α＝60°，B'（3，）；（Ⅱ）见解析；（Ⅲ）点P纵坐标的最小值为﹣2．【解析】【分析】（Ⅰ）作辅助线,先根据点A（2,0）,点B（0,）,确定∠ABO＝30°,证明△AOA'是等边三角形,得旋转角α＝60°,证明△COB'是30°的直角三角形,可得B'的坐标;（Ⅱ）依据旋转的性质可得∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',即可得出∠OBB'＝∠OA'A＝（180°﹣α）,再根据∠BOA'＝90°+α,四边形OBPA'的内角和为360°,即可得到∠BPA'＝90°,即AA'⊥BB';（Ⅲ）作AB的中点M（1,）,连接MP,依据点P的轨迹为以点M为圆心,以MP＝AB＝2为半径的圆,即可得到当PM∥y轴时,点P纵坐标的最小值为﹣2.【详解】解：（Ⅰ）如图1，过B'作B'C⊥x轴于C,∵OA＝2,OB＝2,∠AOB＝90°,∴∠ABO＝30°,∠BAO＝60°,由旋转得：OA＝OA',∠A'＝∠BAO＝60°,∴△OAA'是等边三角形,∴α＝∠AOA'＝60°,∵OB＝OB'＝2,∠COB'＝90°﹣60°＝30°,∴B'C ＝OB’＝,∴OC＝3,∴B'（3,）,（Ⅱ）证明：如图2,∵∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',∴∠OBB'＝∠OA'A＝（180°﹣α）,∵∠BOA'＝90°+α,四边形OBPA'的内角和为360°,∴∠BPA'＝360°﹣（180°﹣α）﹣（90°+α）＝90°,即AA'⊥BB';（Ⅲ）点P纵坐标的最小值为-2．理由是：如图，作AB的中点M（1,）,连接MP,∵∠APB＝90°,∴点P的轨迹为以点M为圆心,以MP＝AB＝2为半径的圆,除去点（2,2）,∴当PM⊥x轴时,点P纵坐标的最小值为﹣2．【点睛】本题属于几何变换综合题,主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和以及圆周角定理的综合运用,解决问题的关键是判断点P的轨迹为以点M为圆心,以MP 为半径的圆．9．如图，线段BC所在的直线是以AB为直径的圆的切线，点D为圆上一点，满足BD＝BC，且点C、D位于直径AB的两侧，连接CD交圆于点E. 点F是BD上一点，连接EF，分别交AB、BD于点G、H，且EF＝BD.(1)求证：EF∥BC；(2)若EH＝4，HF＝2，求»BE的长.【答案】(1)见解析；(2) 233【解析】【分析】（1）根据EF＝BD可得»EF＝»BD，进而得到»»BE DF=，根据“在同圆或等圆中，同弧或等弧所对的圆周角相等”即可得出角相等进而可证.（2）连接DF，根据切线的性质及垂径定理求出GF、GE的长，根据“在同圆或等圆中，同弧或等弧所对的圆周角相等”及平行线求出相等的角，利用锐角三角函数求出∠BHG，进而求出∠BDE的度数，确定»BE所对的圆心角的度数，根据∠DFH＝90°确定DE为直径，代入弧长公式即可求解.【详解】(1)∵EF＝BD，∴»EF＝»BD∴»»BE DF=∴∠D＝∠DEF又BD＝BC，∴∠D＝∠C，∴∠DEF=∠CEF∥BC(2)∵AB是直径，BC为切线，∴AB⊥BC又EF∥BC，∴AB⊥EF，弧BF=弧BE,GF＝GE＝12(HF+EH)=3，HG=1DB平分∠EDF，又BF ∥CD ，∴∠FBD ＝∠FDB ＝∠BDE ＝∠BFH∴HB ＝HF ＝2∴cos ∠BHG ＝HG HB ＝12，∠BHG ＝60°. ∴∠FDB ＝∠BDE ＝30° ∴∠DFH ＝90°，DE 为直径，DE ＝43，且弧BE 所对圆心角＝60°.∴弧BE ＝16×43π＝233π【点睛】本题是圆的综合题，主要考查圆周角、切线、垂径定理、弧长公式等相关知识，掌握圆周角的有关定理，切线的性质，垂径定理及弧长公式是解题关键.10．如图，PA 切⊙O 于点A ，射线PC 交⊙O 于C 、B 两点，半径OD ⊥BC 于E ，连接BD 、DC 和OA ，DA 交BP 于点F ；（1）求证：∠ADC+∠CBD ＝12∠AOD ； （2）在不添加任何辅助线的情况下，请直接写出图中相等的线段．【答案】（1）详见解析；（2）详见解析；【解析】【分析】()1根据垂径定理得到BD CD =n n ，根据等腰三角形的性质得到()111809022ODA AOD AOD ∠=-∠=-∠o o ，即可得到结论； ()2根据垂径定理得到BE CE =，BD CD =n n ，根据等腰三角形的性质得到ADO OAD ∠=∠，根据切线的性质得到90PAO ∠=o ，求得90OAD DAP ∠+∠=o ，推出PAF PFA ∠=∠，根据等腰三角形的判定定理即可得到结论．【详解】()1证明：OD BC ⊥Q ，BD CD ∴=n n， CBD DCB ∴∠=∠，90DFE EDF ∠+∠=o Q ，90EDF DFE ∴∠=-∠o ，OD OA =Q ， ()111809022ODA AOD AOD ∴∠=-∠=-∠o o ， 190902DFE AOD ∴-∠=-∠o o ， 12DEF AOD ∴∠=∠， DFE ADC DCB ADC CBD ∠=∠+∠=∠+∠Q ，12ADC CBD AOD ∴∠+∠=∠； ()2解：OD BC ⊥Q ，BE CE ∴=，BD CD =n n， BD CD ∴=，OA OD Q =，ADO OAD ∴∠=∠，PA Q 切O e 于点A ，90PAO ∴∠=o ，90OAD DAP ∴∠+∠=o ， PFA DFE ∠=∠Q ，90PFA ADO ∴∠+∠=o ，PAF PFA ∴∠=∠，PA PF ∴=．【点睛】本题考查了切线的性质，等腰三角形的判定和性质，垂径定理，圆周角定理，正确的识别图形是解题的关键．11．在平面直角坐标系XOY 中，点P 的坐标为（x 1，y 1），点Q 的坐标为（x 2，y 2），且x 1≠x 2，若P 、Q 为某等边三角形的两个顶点，且有一边与x 轴平行（含重合），则称P 、Q 互为“向善点”．如图1为点P 、Q 互为“向善点”的示意图．已知点A 的坐标为（1，3），点B 的坐标为（m ，0）（1）在点M （﹣1，0）、S （2，0）、T （3，3A 点互为“向善点”的是_____；（2）若A 、B 互为“向善点”，求直线AB 的解析式；（3）⊙B 3⊙B 上有三个点与点A 互为“向善点”，请直接写出m 的取值范围．【答案】（1）S ，T ．（2）直线AB 的解析式为y ＝3x 或y ＝﹣3x +23；（3）当﹣2＜m ＜0或2＜m ＜4时，⊙B 上有三个点与点A 互为“向善点”．【解析】【分析】（1）根据等边三角形的性质结合“向善点”的定义，可得出点S ，T 与A 点互为“向善点”； （2）根据等边三角形的性质结合“向善点”的定义，可得出关于m 的分式方程，解之经检验后可得出点B 的坐标，根据点A ，B 的坐标，利用待定系数法即可求出直线AB 的解析式；（3）分⊙B 与直线y=3x 相切及⊙B 与直线y=-3x+23相切两种情况求出m 的值，再利用数形结合即可得出结论．【详解】（1）∵30330,3tan 60︒--===，3333tan 60︒-==， ∴点S ，T 与A 点互为“向善点”．故答案为S ，T ．（2）根据题意得：303-=， 解得：m 1＝0，m 2＝2，经检验，m 1＝0，m 2＝2均为所列分式方程的解，且符合题意，∴点B 的坐标为（0，0）或（2，0）．设直线AB 的解析式为y ＝kx +b （k ≠0），将A （1，），B （0，0）或（2，0）代入y ＝kx +b ，得：30k b b ⎧+=⎪⎨=⎪⎩320k b k b ⎧+=⎪⎨+=⎪⎩ 解得：30k b ⎧=⎪⎨=⎪⎩323k b ⎧=⎪⎨=⎪⎩， ∴直线AB 的解析式为y 3或y 33．（3）当⊙B 与直线y 3相切时，过点B 作BE ⊥直线y 3于点E ，如图2所示．∵∠BOE ＝60°，∴sin60°＝32BE OB ， ∴OB ＝2，∴m ＝﹣2或m ＝2；当⊙B 与直线y ＝﹣3x +23相切时，过点B 作BF ⊥直线y ＝﹣3x +23于点F ，如图3所示．同理，可求出m ＝0或m ＝4．综上所述：当﹣2＜m ＜0或2＜m ＜4时，⊙B 上有三个点与点A 互为“向善点”．【点睛】本题考查了等边三角形的性质、特殊角的三角函数值、待定系数法求一次函数解析式、解分式方程以及解直角三角形，解题的关键是：（1）根据等边三角形的性质结合“向善点”的定义，确定给定的点是否与A 点互为“向善点”；（2）根据点的坐标，利用待定系数法求出一次函数解析式；（3）分⊙B 与直线y=3x 相切及⊙B 与直线y=-3x+23相切两种情况考虑．12．如图，四边形为菱形，且，以为直径作，与交于点．请仅用无刻度的直尺按下列要求画图．(保留作图痕迹)(1)在如图中，过点作边上的高． (2)在如图中，过点作的切线，与交于点．【答案】(1)如图1所示．(答案不唯一),见解析；(2)如图2所示．(答案不唯一)，见解析.【解析】【分析】（1）连接AC 交圆于一点F ，连接PF 交AB 于点E,连接CE 即为所求．（2）连接OF 交BC 于Q ，连接PQ 即为所求．【详解】(1)如图1所示．(答案不唯一)(2)如图2所示．(答案不唯一)【点睛】本题考查作图-复杂作图，菱形和圆的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．13．已知四边形ABCD 是⊙O 的内接四边形，∠DAB ＝120°，BC ＝CD ，AD ＝4，AC ＝7，求AB 的长度．【答案】AB ＝3．【解析】【分析】作DE ⊥AC ，BF ⊥AC ，根据弦、弧、圆周角、圆心角的关系，求得BC CD u u u r u u u r，进而得到∠DAC ＝∠CAB ＝60°，在Rt △ADE 中，根据60°锐角三角函数值，可求得DE ＝3AE ＝2，再由Rt △DEC 中，根据勾股定理求出DC 的长，在△BFC 和△ABF 中，利用60°角的锐角三角函数值及勾股定理求出AF 的长，然后根据求出的两个结果，由AB ＝2AF ，分类讨论求出AB 的长即可.【详解】作DE ⊥AC ，BF ⊥AC ，∵BC ＝CD ，∴BC CD =u u u r u u u r ，∴∠CAB ＝∠DAC ，∵∠DAB ＝120°，∴∠DAC ＝∠CAB ＝60°，∵DE ⊥AC ，∴∠DEA ＝∠DEC ＝90°，∴sin60°＝4DE ，cos60°＝4AE ， ∴DE ＝3AE ＝2，∵AC ＝7，∴CE ＝5，∴DC ()2223537+= ∴BC 37，∵BF ⊥AC ，∴∠BFA ＝∠BFC ＝90°，∴tan60°＝BF AF，BF 2+CF 2＝BC 2， ∴BF 3，∴()2223737AF +-=， ∴AF ＝2或AF ＝32， ∵cos60°＝AF AB， ∴AB ＝2AF ，当AF ＝2时，AB ＝2AF ＝4，∴AB ＝AD ，∵DC ＝BC ，AC ＝AC ，∴△ADC ≌△ABC （SSS ），∴∠ADC ＝∠ABC ，∵ABCD 是圆内接四边形，∴∠ADC+∠ABC ＝180°，∴∠ADC ＝∠ABC ＝90°，但AC 2＝49，()222243753AD DC +=+=，AC 2≠AD 2+DC 2，∴AB ＝4（不合题意，舍去）， 当AF ＝32时，AB ＝2AF ＝3， ∴AB ＝3．【点睛】 此题主要考查了圆的相关性质和直角三角形的性质，解题关键是构造直角三角形模型，利用直角三角形的性质解题.14．我们知道，如图1，AB 是⊙O 的弦，点F 是¼AFB 的中点，过点F 作EF ⊥AB 于点E ，易得点E 是AB 的中点，即AE ＝EB ．⊙O 上一点C （AC ＞BC ），则折线ACB 称为⊙O 的一条“折弦”．（1）当点C 在弦AB 的上方时（如图2），过点F 作EF ⊥AC 于点E ，求证：点E 是“折弦ACB”的中点，即AE ＝EC+CB ．（2）当点C 在弦AB 的下方时（如图3），其他条件不变，则上述结论是否仍然成立？若成立说明理由；若不成立，那么AE 、EC 、CB 满足怎样的数量关系？直接写出，不必证明．（3）如图4，已知Rt △ABC 中，∠C ＝90°，∠BAC ＝30°，Rt △ABC 的外接圆⊙O 的半径为2，过⊙O 上一点P 作PH ⊥AC 于点H ，交AB 于点M ，当∠PAB ＝45°时，求AH 的长．【答案】（1）见解析；（2）结论AE ＝EC+CB 不成立，新结论为：CE ＝BC+AE ，见解析；（3）AH 的长为3﹣1或3+1．【解析】【分析】（1）在AC 上截取AG ＝BC ，连接FA ，FG ，FB ，FC ，证明△FAG ≌△FBC ，根据全等三角形的性质得到FG ＝FC ，根据等腰三角形的性质得到EG ＝EC ，即可证明.（2）在CA 上截取CG ＝CB ，连接FA ，FB ，FC ，证明△FCG ≌△FCB ，根据全等三角形的性质得到FG ＝FB ，得到FA ＝FG ，根据等腰三角形的性质得到AE ＝GE ，即可证明. （3）分点P 在弦AB 上方和点P 在弦AB 下方两种情况进行讨论.【详解】解：（1）如图2，在AC 上截取AG ＝BC ，连接FA ，FG ，FB ，FC ，∵点F 是¼AFB 的中点，FA ＝FB ，在△FAG 和△FBC 中，,FA FB FAG FBC AG BC =⎧⎪∠=∠⎨⎪=⎩∴△FAG ≌△FBC （SAS ），∴FG ＝FC ，∵FE ⊥AC ，∴EG ＝EC ，∴AE ＝AG+EG ＝BC+CE ；（2）结论AE ＝EC+CB 不成立，新结论为：CE ＝BC+AE ，理由：如图3，在CA 上截取CG ＝CB ，连接FA ，FB ，FC ，∵点F 是¼AFB 的中点，∴FA ＝FB ，¶¶ FAFB =, ∴∠FCG ＝∠FCB ，在△FCG 和△FCB 中，,CG CB FCG FCB FC FC =⎧⎪∠=∠⎨⎪=⎩∴△FCG ≌△FCB （SAS ），∴FG ＝FB ，∴FA ＝FG ，∵FE ⊥AC ，∴AE ＝GE ，∴CE ＝CG+GE ＝BC+AE ；（3）在Rt △ABC 中，AB ＝2OA ＝4，∠BAC ＝30°， ∴12232BC AB AC ===，， 当点P 在弦AB 上方时，如图4，在CA 上截取CG ＝CB ，连接PA ，PB ，PG ，∵∠ACB ＝90°，∴AB 为⊙O 的直径，∴∠APB ＝90°，∵∠PAB ＝45°，∴∠PBA ＝45°＝∠PAB ，∴PA ＝PB ，∠PCG ＝∠PCB ，在△PCG 和△PCB 中， ,CG CB PCG PCB PC PC =⎧⎪∠=∠⎨⎪=⎩∴△PCG ≌△PCB （SAS ），∴PG ＝PB ，∴PA ＝PG ，∵PH ⊥AC ，∴AH ＝GH ，∴AC ＝AH+GH+CG ＝2AH+BC ，∴22AH =+，∴1AH =，当点P 在弦AB 下方时，如图5， 在AC 上截取AG ＝BC ，连接PA ，PB ，PC ，PG∵∠ACB ＝90°，∴AB 为⊙O 的直径，∴∠APB ＝90°，∵∠PAB ＝45°，∴∠PBA ＝45°＝∠PAB ，∴PA ＝PB ，在△PAG 和△PBC 中，,AG BC PAG PBC PA PB =⎧⎪∠=∠⎨⎪=⎩∴△PAG ≌△PBC （SAS ），∴PG ＝PC ，∵PH ⊥AC ，∴CH ＝GH ，∴AC ＝AG+GH+CH ＝BC+2CH ，∴22CH ，=+∴1CH =，∴)11AH AC CH =-==， 即：当∠PAB ＝45°时，AH11.【点睛】考查弧，弦的关系，全等三角形的判定与性质，等腰三角形的判定与性质等，综合性比较强，注意分类讨论思想方法在解题中的应用.15．结果如此巧合!下面是小颖对一道题目的解答．题目：如图，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积．解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x．根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x．根据勾股定理，得（x+3）2+（x+4）2=（3+4）2．整理，得x2+7x=12．所以S△ABC=12 AC•BC=12（x+3）（x+4）=12（x2+7x+12）=12×（12+12）=12．小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积．这仅仅是巧合吗？请你帮她完成下面的探索．已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n．可以一般化吗？（1）若∠C=90°，求证：△ABC的面积等于mn．倒过来思考呢？（2）若AC•BC=2mn，求证∠C=90°．改变一下条件……（3）若∠C=60°，用m、n表示△ABC的面积．【答案】（1）证明见解析；（2）证明见解析；（3）S△ABC=3mn；【解析】【分析】（1）设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x，仿照例题利用勾股定理得（x＋m）2＋（x＋n）2＝（m＋n）2，再根据S△ABC＝AC×BC，即可证明S△ABC＝mn.（2）由AC•BC＝2mn，得x2＋（m＋n）x＝mn，因此AC2＋BC2＝（x＋m）2＋（x＋n）2＝AB2，利用勾股定理逆定理可得∠C＝90°.（3）过点A作AG⊥BC于点G，在Rt△ACG中，根据条件求出AG、CG，又根据BG＝BC－CG得到BG .在Rt△ABG中，根据勾股定理可得x2＋（m＋n）x＝3mn，由此S△ABC＝BC•AG＝mn.【详解】设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x，根据切线长定理，得：AE＝AD＝m、BF＝BD＝n、CF＝CE＝x，（1）如图1，在Rt△ABC中，根据勾股定理，得：（x＋m）2＋（x＋n）2＝（m＋n）2，整理，得：x2＋（m＋n）x＝mn，所以S△ABC＝AC•BC＝（x＋m）（x＋n）＝[x2＋（m＋n）x＋mn]＝（mn＋mn）＝mn;（2）由AC•BC＝2mn，得：（x＋m）（x＋n）＝2mn，整理，得：x2＋（m＋n）x＝mn，∴AC2＋BC2＝（x＋m）2＋（x＋n）2＝2[x2＋（m＋n）x]＋m2＋n2＝2mn＋m2＋n2＝（m＋n）2＝AB2，根据勾股定理逆定理可得∠C＝90°；（3）如图2，过点A作AG⊥BC于点G，在Rt△ACG中，AG＝AC•sin60°＝（x＋m），CG＝AC•cos60°＝（x＋m），∴BG＝BC﹣CG＝（x＋n）﹣（x＋m），在Rt△ABG中，根据勾股定理可得：[（x＋m）]2＋[（x＋n）﹣（x＋m）]2＝（m＋n）2，整理，得：x2＋（m＋n）x＝3mn，∴S△ABC＝BC•AG＝×（x＋n）•（x＋m）＝3x2＋（m＋n）x＋mn]＝3（3mn＋mn）3．【点睛】本题考查了圆中的计算问题、与圆有关的位置关系以及直角三角形，注意掌握方程思想与数形结合思想的应用.。

中考数学 圆的综合 综合题含详细答案一、圆的综合1．如图，已知△ABC 中，AC=BC ，以BC 为直径的⊙O 交AB 于E ，过点E 作EG ⊥AC 于G ，交BC 的延长线于F ．（1）求证：AE=BE ；（2）求证：FE 是⊙O 的切线；（3）若FE=4，FC=2，求⊙O 的半径及CG 的长．【答案】（1）详见解析；（2）详见解析；（3）.【解析】（1）证明：连接CE ，如图1所示：∵BC 是直径，∴∠BEC =90°，∴CE ⊥AB ；又∵AC =BC ，∴AE =BE ．（2）证明：连接OE ，如图2所示：∵BE =AE ，OB =OC ，∴OE 是△ABC 的中位线，∴OE ∥AC ，AC =2OE =6．又∵EG ⊥AC ，∴FE ⊥OE ，∴FE 是⊙O 的切线．（3）解：∵EF 是⊙O 的切线，∴FE 2=FC •FB ．设FC =x ，则有2FB =16，∴FB =8，∴BC =FB ﹣FC =8﹣2=6，∴OB =OC =3，即⊙O 的半径为3；∴OE =3．∵OE ∥AC ，∴△FCG ∽△FOE ，∴ ，即 ，解得：CG = ．点睛：本题利用了等腰三角形三线合一定理，三角形中位线的判定，切割线定理，以及勾股定理，还有平行线分线段成比例定理，切线的判定等知识．2．如图，在ABC V 中，90ACB ∠=o ，BAC ∠的平分线AD 交BC 于点D ，过点D 作DE AD ⊥交AB 于点E ，以AE 为直径作O e ．()1求证：BC 是O e 的切线；()2若3AC =，4BC =，求tan EDB ∠的值．【答案】（1）见解析；（2）1tan 2EDB ∠=． 【解析】【分析】 ()1连接OD ，如图，先证明OD//AC ，再利用AC BC ⊥得到OD BC ⊥，然后根据切线的判定定理得到结论；()2先利用勾股定理计算出AB 5=，设O e 的半径为r ，则OA OD r ==，OB 5r =-，再证明BDO V ∽BCA V ，利用相似比得到r ：()35r =-：5，解得15r 8=，接着利用勾股定理计算5BD 2=，则3CD 2=，利用正切定理得1tan 12∠=，然后证明1EDB ∠∠=，从而得到tan EDB ∠的值．【详解】()1证明：连接OD ，如图，AD Q 平分BAC ∠，12∴∠=∠，OA OD =Q ，23∴∠=∠，13∴∠=∠，//OD AC ∴，AC BC ⊥Q ，OD BC ∴⊥，BC ∴是O e 的切线；()2解：在Rt ACB V 中，22345AB =+=，设O e 的半径为r ，则OA OD r ==，5OB r =-，//OD AC Q ，BDO V ∴∽BCA V ，OD ∴：AC BO =：BA ，即r ：()35r =-：5，解得158r =， 158OD ∴=，258OB =， 在Rt ODB V 中，2252BD OB OD =-=， 32CD BC BD ∴=-=， 在Rt ACD V 中，312tan 132CD AC ∠===， AE Q 为直径，90ADE ∴∠=o ，90EDB ADC ∴∠+∠=o ，190ADC ∠+∠=o Q ，1EDB ∴∠=∠，1tan 2EDB ∴∠=． 【点睛】本题考查了切线的判定与性质：经过半径的外端且垂直于这条半径的直线是圆的切线；圆的切线垂直于经过切点的半径.判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”；也考查了圆周角定理和解直角三角形．3．如图，PA 、PB 是⊙O 的切线，A ，B 为切点，∠APB=60°，连接PO 并延长与⊙O 交于C 点，连接AC 、BC ．（Ⅰ）求∠ACB 的大小；（Ⅱ）若⊙O 半径为1，求四边形ACBP 的面积．【答案】（Ⅰ）60°；（Ⅱ33 【解析】分析：（Ⅰ）连接AO，根据切线的性质和切线长定理，得到OA⊥AP，OP平分∠APB，然后根据角平分线的性质和三角形的外角的性质，30°角的直角三角形的性质，得到∠ACB的度数；（Ⅱ）根据30°角的直角三角形的性质和等腰三角形的性质，结合等底同高的性质求三角形的面积即可．详解：（Ⅰ）连接OA，如图，∵PA、PB是⊙O的切线，∴OA⊥AP，OP平分∠APB，∴∠APO=12∠APB=30°，∴∠AOP=60°，∵OA=OC，∴∠OAC=∠OCA，∴∠ACO=12AOP=30°，同理可得∠BCP=30°，∴∠ACB=60°；（Ⅱ）在Rt△OPA中，∵∠APO=30°，∴33，OP=2OA=2，∴OP=2OC，而S△OPA=123∴S△AOC=12S△PAO3∴S△ACP33，∴四边形ACBP的面积=2S△ACP33．点睛：本题考查了切线的性质，解直角三角形，等腰三角形的判定，熟练掌握切线的性质是解题的关键．4．已知：AB是⊙0直径,C是⊙0外一点,连接BC交⊙0于点D，BD=CD,连接AD、AC．(1)如图1,求证:∠BAD=∠CAD(2)如图2,过点C 作CF ⊥AB 于点F,交⊙0于点E,延长CF 交⊙0于点G.过点作EH ⊥AG 于点H ，交AB 于点K,求证AK=2OF ；(3)如图3,在(2)的条件下,EH 交AD 于点L,若0K=1,AC=CG,求线段AL 的长.图1 图2 图3【答案】(1)见解析(2)见解析(3)12105 【解析】试题分析：（1）由直径所对的圆周角等于90°，得到∠ADB =90°，再证明△ABD ≌△ACD 即可得到结论；（2）连接BE ．由同弧所对的圆周角相等，得到∠GAB =∠BEG ．再证△KFE ≌△BFE ，得到BF =KF =BK ．由OF =OB -BF ，AK =AB -BK ，即可得到结论． （3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．先证CM 垂直平分AG ，得到AM =GM ，∠AGC +∠GCM =90°．再证∠GAF =∠GCM =α．通过证明△AGB ≌△CMG ，得到BG =GM =12AG ．再证明∠BGC =∠MCG =α．设BF =KF =a ， 可得GF =2a ，AF =4a ． 由OK =1，得到OF =a +1，AK =2（a +1），AF = 3a +2，得到3a +2=4a ，解出a 的值，得到AF ，AB ，GF ，FC 的值．由tanα=tan ∠HAK =12HK AH =， AK =6，可以求出 AH 的长．再由1tan tan 3BAD BCF ∠=∠= ，利用公式tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD∠+∠-∠⋅∠，得到∠GAD =45°，则AL =2AH ，即可得到结论．试题解析：解：（1）∵AB 为⊙O 的直径，∴∠ADB =90°，∴∠ADC =90°．∵BD =CD ，∠BDA =∠CDA ，AD =AD ，∴△ABD ≌△ACD ，∴∠BAD =∠CAD ．（2）连接BE ．∵BG =BG ，∴∠GAB =∠BEG ．∵CF ⊥AB ，∴∠KFE =90°．∵EH ⊥AG ，∴∠AHE =∠KFE =90°，∠AKH =∠EKF ，∴∠HAK =∠KEF =∠BEF ．∵FE =FE ，∠KFE =∠BFE =90°，∴△KFE ≌△BFE ，∴BF =KF =BK ．∵ OF =OB -BF ，AK =AB -BK ，∴AK =2OF ．（3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．∵AC =CG ， ∴点C 在AG 的垂直平分线上．∵ OA =OG ，∴点O 在AG 的垂直平分线上， ∴CM 垂直平分AG ，∴AM =GM ，∠AGC +∠GCM =90°．∵AF ⊥CG ，∴∠AGC +∠GAF =90°，∴∠GAF =∠GCM =α．∵AB 为⊙O 的直径，∴∠AGB = 90°，∴∠AGB =∠CMG =90°．∵AB =AC =CG ，∴△AGB ≌△CMG ，∴BG =GM=12AG ． 在Rt △AGB 中， 1tan tan 2GB GAB AG α∠=== ． ∵∠AMC =∠AGB = 90°，∴BG ∥CM ， ∴∠BGC =∠MCG =α．设BF =KF =a ， 1tan tan 2BF BGF GF α∠===，∴GF =2a ，1tan tan 2GF GAF AF α∠=== ，AF =4a ．∵OK =1，∴OF =a +1，AK =2OF =2（a +1），∴AF =AK +KF =a +2（a +1）=3a +2，∴3a +2=4a ，∴a =2， AK =6，∴AF =4a =8，AB =AC =CG =10，GF =2a =4，FC =CG -GF =6． ∵tanα=tan ∠HAK =12HK AH =，设KH =m ，则AH =2m ，∴AK 22(2)m m +=6，解得：m 65，∴AH =2m 125．在Rt △BFC 中，1tan 3BF BCF FC ∠== ．∵∠BAD +∠ABD =90°， ∠FBC +∠BCF =90°，∴∠BCF =∠BAD ，1tan tan 3BAD BCF ∠=∠= ，∴tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD ∠+∠-∠⋅∠=1123111123+=-⨯，∴∠GAD =45°，∴HL=AH ，AL =2AH = 12105．5．阅读下列材料：如图1，⊙O 1和⊙O 2外切于点C ，AB 是⊙O 1和⊙O 2外公切线，A 、B 为切点，求证：AC ⊥BC证明：过点C 作⊙O 1和⊙O 2的内公切线交AB 于D ，∵DA 、DC 是⊙O 1的切线∴DA=DC ．∴∠DAC=∠DCA ．同理∠DCB=∠DBC ．又∵∠DAC+∠DCA+∠DCB+∠DBC=180°，∴∠DCA+∠DCB=90°．即AC ⊥BC ．根据上述材料，解答下列问题：（1）在以上的证明过程中使用了哪些定理？请写出两个定理的名称或内容；（2）以AB 所在直线为x 轴，过点C 且垂直于AB 的直线为y 轴建立直角坐标系（如图2），已知A 、B 两点的坐标为（﹣4，0），（1，0），求经过A 、B 、C 三点的抛物线y=ax 2+bx+c 的函数解析式；（3）根据（2）中所确定的抛物线，试判断这条抛物线的顶点是否落在两圆的连心O 1O 2上，并说明理由．【答案】（1）见解析；（2）213222y x x =+- ；（3）见解析 【解析】 试题分析：（1）由切线长相等可知用了切线长定理；由三角形的内角和是180°，可知用了三角形内角和定理；（2）先根据勾股定理求出C 点坐标，再用待定系数法即可求出经过、、A B C 三点的抛物线的函数解析式；（3）过C 作两圆的公切线，交AB 于点D ，由切线长定理可求出D 点坐标，根据,C D 两点的坐标可求出过,C D 两点直线的解析式，根据过一点且互相垂直的两条直线解析式的关系可求出过两圆圆心的直线解析式，再把抛物线的顶点坐标代入直线的解析式看是否适合即可．试题解析：(1)DA 、DC 是1O e 的切线，∴DA =DC .应用的是切线长定理；180DAC DCA DCB DBC ∠+∠+∠+∠=o ，应用的是三角形内角和定理.(2)设C 点坐标为(0,y ),则222AB AC BC =+， 即()()222224141y y --=-+++，即225172y =+,解得y =2(舍去)或y =−2.故C 点坐标为(0,−2)，设经过、、A B C 三点的抛物线的函数解析式为2y ax bx c ，=++ 则164002,a b c a b c c -+=⎧⎪++=⎨⎪=-⎩ 解得12322a b c ⎧=⎪⎪⎪=⎨⎪=-⎪⎪⎩， 故所求二次函数的解析式为213 2.22y x x =+- (3)过C 作两圆的公切线CD 交AB 于D ,则AD =BD =CD ,由A (−4,0),B (1,0)可知3(,0)2D -， 设过CD 两点的直线为y =kx +b ,则 3022k b b ⎧-+=⎪⎨⎪=-⎩， 解得432k b ⎧=-⎪⎨⎪=-⎩，故此一次函数的解析式为423y x =--， ∵过12,O O 的直线必过C 点且与直线423y x =--垂直， 故过12,O O 的直线的解析式为324y x =-， 由(2)中所求抛物线的解析式可知抛物线的顶点坐标为325(,)28--，代入直线解析式得33252,428⎛⎫⨯--=-⎪⎝⎭故这条抛物线的顶点落在两圆的连心12O O上.6．如图，⊙O是△ABC的外接圆，AB是直径，过点O作OD⊥CB，垂足为点D，延长DO 交⊙O于点E，过点E作PE⊥AB，垂足为点P，作射线DP交CA的延长线于F点，连接EF，（1）求证：OD＝OP；（2）求证：FE是⊙O的切线．【答案】（1）证明见解析；（2）证明见解析．【解析】试题分析：（2）证明△POE≌△ADO可得DO=EO；（3）连接AE，BE，证出△APE≌△AFE即可得出结论．试题解析：（1）∵∠EPO=∠BDO=90°∠EOP=∠BODOE=OB∴△OPE≌△ODB∴OD="OP"（2）连接EA，EB∴∠1=∠EBC∵AB是直径∴∠AEB=∠C=90°∴∠2+∠3=90°∵∠3=∠DEB∵∠BDE=90°∴∠EBC+∠DEB=90°∴∠2=∠EBC=∠1∵∠C=90°∠BDE=90°∴CF∥OE∴∠ODP=∠AFP∵OD=OP∴∠ODP=∠OPD∵∠OPD=∠APF∴∠AFP=∠APF∴AF=AP 又AE=AE∴△APE≌△AFE∴∠AFE=∠APE=90°∴∠FED=90°∴FE是⊙O的切线考点：切线的判定．7．如图，AB为⊙O的直径，且AB＝m（m为常数），点C为»AB的中点，点D为圆上一动点，过A点作⊙O的切线交BD的延长线于点P，弦CD交AB于点E．（1）当DC⊥AB时，则DA DBDC+＝；（2）①当点D在»AB上移动时，试探究线段DA，DB，DC之间的数量关系；并说明理由；②设CD长为t，求△ADB的面积S与t的函数关系式；（3）当9220PDAC=时，求DEOA的值．【答案】（12；（2）①DA+DB2DC，②S＝12t2﹣14m2；（3）24235DEOA=.【解析】【分析】（1）首先证明当DC⊥AB时，DC也为圆的直径，且△ADB为等腰直角三角形，即可求出结果；（2）①分别过点A，B作CD的垂线，连接AC，BC，分别构造△ADM和△BDN两个等腰直角三形及△NBC和△MCA两个全等的三角形，容易证出线段DA，DB，DC之间的数量关系；②通过完全平方公式（DA+DB）2＝DA2+DB2+2DA•DB的变形及将已知条件AB＝m代入即可求出结果；（3）通过设特殊值法，设出PD的长度，再通过相似及面积法求出相关线段的长度，即可求出结果．【详解】解：（1）如图1，∵AB为⊙O的直径，∴∠ADB＝90°，∵C为»AB的中点，∴»»AC BC=，∴∠ADC＝∠BDC＝45°，∵DC⊥AB，∴∠DEA＝∠DEB＝90°，∴∠DAE＝∠DBE＝45°，∴AE＝BE，∴点E与点O重合，∴DC为⊙O的直径，∴DC＝AB，在等腰直角三角形DAB中，DA＝DB＝22AB，∴DA+DB＝2AB＝2CD，∴DA DBDC+＝2；（2）①如图2，过点A作AM⊥DC于M，过点B作BN⊥CD于N，连接AC，BC，由（1）知»»AC BC=，∴AC＝BC，∵AB为⊙O的直径，∴∠ACB＝∠BNC＝∠CMA＝90°，∴∠NBC+∠BCN＝90°，∠BCN+∠MCA＝90°，∴∠NBC＝∠MCA，在△NBC和△MCA中，BNC CMANBC MCABC CA∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△NBC≌△MCA（AAS），∴CN ＝AM ，由（1）知∠DAE ＝∠DBE ＝45°， AM ＝2DA ，DN ＝2DB ， ∴DC ＝DN+NC ＝22DB+22DA ＝22（DB+DA ）， 即DA+DB ＝2DC ；②在Rt △DAB 中， DA 2+DB 2＝AB 2＝m 2，∵（DA+DB ）2＝DA 2+DB 2+2DA•DB ， 且由①知DA+DB 2DC 2t ， ∴2t ）2＝m 2+2DA•DB ， ∴DA•DB ＝t 2﹣12m 2， ∴S △ADB ＝12DA•DB ＝12t 2﹣14m 2， ∴△ADB 的面积S 与t 的函数关系式S ＝12t 2﹣14m 2； （3）如图3，过点E 作EH ⊥AD 于H ，EG ⊥DB 于G ， 则NE ＝ME ，四边形DHEG 为正方形，由（1）知»»AC BC=， ∴AC ＝BC ，∴△ACB 为等腰直角三角形， ∴AB 2AC ， ∵92PD AC =， 设PD ＝2，则AC ＝20，AB ＝2， ∵∠DBA ＝∠DBA ，∠PAB ＝∠ADB ， ∴△ABD ∽△PBA ， ∴AB BD ADPB AB PA==， ∴20292202DB =+，∴DB ＝162， ∴AD ＝22AB DB -＝122，设NE ＝ME ＝x ， ∵S △ABD ＝12AD•BD ＝12AD•NE+12BD•ME ， ∴12×122×162＝12×122•x+12×162•x ， ∴x ＝4827， ∴DE ＝2HE ＝2x ＝967， 又∵AO ＝12AB ＝102， ∴96242735102DE OA =⨯=．【点睛】本题考查了圆的相关性质，等腰直三角形的性质，相似的性质等，还考查了面积法及特殊值法的运用，解题的关键是认清图形，抽象出各几何图形的特殊位置关系．8．如图，⊙O 的直径AB ＝8，C 为圆周上一点，AC ＝4，过点C 作⊙O 的切线l ，过点B 作l 的垂线BD ，垂足为D ，BD 与⊙O 交于点E ． （1）求∠AEC 的度数；（2）求证：四边形OBEC 是菱形．【答案】（1）30°；（2）详见解析. 【解析】 【分析】（1）易得△AOC 是等边三角形，则∠AOC ＝60°，根据圆周角定理得到∠AEC ＝30°；（2）根据切线的性质得到OC⊥l，则有OC∥BD，再根据直径所对的圆周角为直角得到∠AEB＝90°，则∠EAB＝30°，可证得AB∥CE，得到四边形OBE C为平行四边形，再由OB ＝OC，即可判断四边形OBEC是菱形．【详解】（1）解：在△AOC中，AC＝4，∵AO＝OC＝4，∴△AOC是等边三角形，∴∠AOC＝60°，∴∠AEC＝30°；（2）证明：∵OC⊥l，BD⊥l．∴OC∥BD．∴∠ABD＝∠AOC＝60°．∵AB为⊙O的直径，∴∠AEB＝90°，∴△AEB为直角三角形，∠EAB＝30°．∴∠EAB＝∠AEC．∴CE∥OB，又∵CO∥EB∴四边形OBEC为平行四边形．又∵OB＝OC＝4．∴四边形OBEC是菱形．【点睛】本题考查了切线的性质：圆的切线垂直于过切点的半径．也考查了圆周角定理及其推论以及菱形的判定方法．9．如图1，等腰直角△ABC中，∠ACB=90°，AC=BC，过点A，C的圆交AB于点D，交BC 于点E，连结DE（1）若AD=7，BD=1，分别求DE，CE的长（2）如图2，连结CD，若CE=3，△ACD的面积为10，求tan∠BCD（3）如图3，在圆上取点P使得∠PCD=∠BCD（点P与点E不重合），连结PD，且点D 是△CPF的内心①请你画出△CPF，说明画图过程并求∠CDF的度数②设PC=a，PF=b，PD=c，若（a-2c）（b-2c）=8，求△CPF的内切圆半径长．【答案】（1）DE=1，CE=32；（2）tan ∠BCD=14；（3）①135°；②2. 【解析】 【分析】（1）由A 、C 、E 、D 四点共圆对角互补为突破口求解；（2）找∠BDF 与∠ODA 为对顶角，在⊙O 中，∠COD=2∠CAD ，证明△OCD 为等腰直角三角形，从而得到∠EDC+∠ODA=45°，即可证明∠CDF=135°；（3）过点D 做DH CB ⊥于点H ，以D 为圆心，DH 为半径画圆，过点P 做D e 切线PF 交CB 的延长线于点F ，结合圆周角定理得出∠CPD=∠CAD=45°，再根据圆的内心是三角形三个内角角平分线的交点，得出∠CPF=90°，然后根据角平分线性质得出114522DCF CFD PCF PFC ∠+∠=∠+∠=︒，最后再根据三角形内角和定理即可求解；证明∠DCF+∠CFD=45°，从而证明∠CPF 是直角，再求证四边形PKDN 是正方形，最后以△PCF 面积不变性建立等量关系，结合已知（a-2c ）（b-2c ）=8，消去字母a ，b 求出c 值，即求出△CPF 的内切圆半径长为22c ． 【详解】 （1）由图可知：设BC=x ．在Rt △ABC 中，AC=BC ．由勾股定理得： AC 2+BC 2=AB 2，∵AB=AD+BD ，AD=7，BD=1， ∴x 2+x 2=82， 解得：x=2．∵⊙O 内接四边形，∠ACD=90°， ∴∠ADE=90°， ∴∠EDB=90°， ∵∠B=45°，∴△BDE 是等腰直角三形． ∴DE=DB ， 又∵DB=1， ∴DE=1， 又∵CE=BC-BE ，∴CE=42232-=． （2）如图所示：在△DCB 中过点D 作DM ⊥BE ，设BE=y ，则DM=12y ， 又∵CE=3，∴BC=3+y ， ∵S △ACB =S ACD +S DCB ，∴()1114242103y y 222⨯⨯=+⨯+⨯， 解得：y=2或y=-11（舍去）． ∴EM=1，CM=CE+ME=1+3=4， 又∵∠BCD=∠MCD ， ∴tan ∠BCD=tan ∠MCD ，在Rt △DCM 中，tan ∠MCD=DM CM =14， ∴tan ∠BCD=14． （3）①如下图所示：过点D 做DH CB ⊥于点H ，以D 为圆心，DH 为半径画圆，过点P 做D e 切线PF 交CB 的延长线于点F ．∵∠CAD=45°， ∴∠CPD=∠CAD=45°，又∵点D 是CPF ∆的内心， ∴PD 、CD 、DF 都是角平分线，∴∠FPD=∠CPD =45°，∠PCD=∠DCF ，∠PFD=∠CFD ∴∠CPF=90° ∴∠PCF+∠PFC=90°∴114522DCF CFD PCF PFC ∠+∠=∠+∠=︒ ∴∠CDF=180°-∠DCF-∠CFD F=90°+45°=135°， 即∠CDF 的度数为135°． ②如下图所示过点D 分别作DK ⊥PC ，DM ⊥CF ，DN ⊥PF 于直线PC ，CF 和PF 于点K ，M ，N 三点， 设△PCF 内切圆的半径为m ，则DN=m ， ∵点D 是△PCF 的内心， ∴DM=DN=DK ，又∵∠DCF+∠CFD+∠FDC=180°，∠FDC=45°， ∴∠DCF+∠CFD=45°，又∵DC ，DF 分别是∠PCF 和∠PFC 的角平分线， ∴∠PCF=2∠DCF ，∠PFC=2∠DFC ， ∴∠PCF+∠PFC=90°， ∴∠CPF=90°．在四边形PKDN 中，∠PND=∠NPK=∠PKD=90°， ∴四边形PKDN 是矩形， 又∵KD=ND ，∴四边形PKDN 是正方形． 又∵∠MBD=∠BDM=45°， ∠BDM=∠KDP ， ∴∠KDP=45°． ∵PC=a ，PF=b ，PD=c ， ∴PN=PK=2C 2， ∴NF=2b -，CK=2a -，又∵CK=CM ，FM=FN ，CF=CM+FM ， ∴CF=a b 2c +-， 又∵S △PCF =S △PDF +S △PDC +S △DCF ， ∴112121ab a c b c (a b 2222222=⨯+⨯++-c ）×2c 2， 化简得：ab=()22a b c c +-------（Ⅰ）， 又∵若（a-2c ）（b-2c ）=8化简得：()2ab 2c a b 2c 8-++=------（Ⅱ），将（Ⅰ）代入（Ⅱ）得：c 2=8，解得：c 22=，或c 22=-（舍去）， ∴m=22c 222=⨯=， 即△CPF 的内切圆半径长为2． 【点睛】本题考查圆的内接四边形性质，圆的内心，圆心角、圆周角，同弧（或等弧）之间的相互关系，同时也考查直角三角形，勾股定理，同角或等角的三角函数值相等和三角形的面积公式，正方形，对顶角和整式的运算等知识点；难点是作辅助线和利用等式求△CPF 的内切圆半径长．10．在中，，，，分别是边，的中点，若等腰绕点逆时针旋转，得到等腰，设旋转角为，记直线与的交点为.（1）问题发现 如图1，当时，线段的长等于_________，线段的长等于_________.（2）探究证明 如图2，当时，求证：，且.（3）问题解决 求点到所在直线的距离的最大值.（直接写出结果）【答案】（1）；；（2）详见解析；（3）【解析】（1）利用等腰直角三角形的性质结合勾股定理分别得出BD1的长和CE1的长；（2）根据旋转的性质得出，∠D1AB=∠E1AC=135°，进而求出△D1AB≌△E1AC（SAS），即可得出答案；（3）首先作PG⊥AB，交AB所在直线于点G，则D1，E1在以A为圆心，AD为半径的圆上，当BD1所在直线与⊙A相切时，直线BD1与CE1的交点P到直线AB的距离最大，此时四边形AD1PE1是正方形，进而求出PG的长．【详解】（1）解：∵∠A=90°，AC=AB=4，D，E分别是边AB，AC的中点，∴AE=AD=2，∵等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，设旋转角为α（0＜α≤180°），∴当α=90°时，AE1=2，∠E1AE=90°，∴BD1=；故答案为：；；（2）证明：由题意可知，，，∵是由绕点逆时针旋转得到，∴，，在和中，，∴，∴，.∵，∴，∴，∴，且.（3）点的运动轨迹是在的上半圆周，点的运动轨迹是在的弧段.即当与相切时，有最大值.点到所在直线的距离的最大值为.此题主要考查了几何变换以及等腰腰直角三角形的性质和勾股定理以及切线的性质等知识，根据题意得出PG的最长时P点的位置是解题关键．11．如图，△ABC中，AC＝BC＝10，cosC＝35，点P是AC边上一动点（不与点A、C重合），以PA长为半径的⊙P与边AB的另一个交点为D，过点D作DE⊥CB于点E．（1）当⊙P与边BC相切时，求⊙P的半径．（2）连接BP交DE于点F，设AP的长为x，PF的长为y，求y关于x的函数解析式，并直接写出x的取值范围．（3）在（2）的条件下，当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时，求相交所得的公共弦的长.【答案】（1）409R=;（2）25880320xy x xx=-++（3）505-【解析】【分析】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，即可求解；（2）首先证明PD∥BE，则EB BFPD PF=，即：2024588x yxxx-+--=，即可求解；（3）证明四边形PDBE为平行四边形，则AG＝EP＝BD，即：AB＝DB+AD＝AG+AD＝5【详解】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，解得：R＝409；（2）在△ABC中，AC＝BC＝10，cosC＝35，设AP＝PD＝x，∠A＝∠ABC＝β，过点B作BH⊥AC，则BH＝ACsinC＝8，同理可得：CH＝6，HA＝4，AB＝45，则：tan∠CAB＝2，BP＝228+(4)x-＝2880x x-+，DA＝25x，则BD＝45﹣25x，如下图所示，PA＝PD，∴∠PAD＝∠CAB＝∠CBA＝β，tanβ＝2，则cosβ5，sinβ5，EB ＝BDcosβ＝（45﹣25x ）×5＝4﹣25x ， ∴PD ∥BE ， ∴EB BF PD PF =，即：2024588x y x xx y -+--=， 整理得：y ＝25x x 8x 803x 20-++； （3）以EP 为直径作圆Q 如下图所示，两个圆交于点G ，则PG ＝PQ ，即两个圆的半径相等，则两圆另外一个交点为D ， GD 为相交所得的公共弦，∵点Q 是弧GD 的中点， ∴DG ⊥EP ，∵AG 是圆P 的直径，∴∠GDA ＝90°，∴EP ∥BD ，由（2）知，PD ∥BC ，∴四边形PDBE 为平行四边形，∴AG ＝EP ＝BD ，∴AB ＝DB+AD ＝AG+AD ＝5设圆的半径为r ，在△ADG 中，AD ＝2rcosβ5DG 5AG ＝2r ， 5＝52r 51+， 则：DG 550﹣5 相交所得的公共弦的长为50﹣5【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．12．如图，AB 为⊙O 的直径，BC 为⊙O 的弦，过O 点作OD ⊥BC ，交⊙O 的切线CD 于点D ，交⊙O 于点E ，连接AC 、AE ，且AE 与BC 交于点F ．（1）连接BD ，求证：BD 是⊙O 的切线；（2）若AF ：EF=2：1，求tan ∠CAF 的值．【答案】（1）证明见解析；（2）33. 【解析】【分析】 （1）根据全等三角形的性质得到∠OBD=∠OCD=90°，根据切线的判定定理即可得到结论； （2）根据已知条件得到AC ∥DE ，设OD 与BC 交于G ，根据平行线分线段成比例定理得到AC ：EG=2：1，EG=12AC ，根据三角形的中位线的性质得到OG=12AC 于是得到AC=OE ，求得∠ABC=30°，即可得到结论．【详解】证明：（1）∵OC=OB ，OD ⊥BC ，∴∠COD=∠BOD ，在△COD 与△BOD 中， OC OB COD BOD OD OD ＝＝＝⎧⎪∠∠⎨⎪⎩，∴△COD ≌△BOD ，∴∠OBD=∠OCD=90°，∴BD 是⊙O 的切线；（2）解：∵AB为⊙O的直径，AC⊥BC，∵OD⊥CB，∴AC∥DE，设OD与BC交于G，∵OE∥AC，AF：EF=2：1，∴AC：EG=2：1，即EG=12AC，∵OG∥AC，OA=OB，∴OG=12AC，∵OG+GE=12AC+12AC=AC，∴AC=OE，∴AC=12AB，∴∠ABC=30°，∴∠CAB=60°，∵¼¼CE BE=，∴∠CAF=∠EAB=12∠CAB=30°，∴tan∠CAF=tan30°=33．【点睛】本题考查了切线的判定和性质，垂径定理，全等三角形的判定与性质，三角形的中位线的性质，三角函数的定义，正确的识别图形是解题的关键．13．如图，四边形ABCD是⊙O的内接四边形，AC为直径，»»BD AD=，DE⊥BC，垂足为E．（1）判断直线ED与⊙O的位置关系，并说明理由；（2）若CE=1，AC=4，求阴影部分的面积．【答案】（1）ED 与O e 相切.理由见解析；（2）2=33S π-阴影. 【解析】【分析】 （1）连结OD ，如图，根据圆周角定理，由»»BD AD =得到∠BAD =∠ACD ，再根据圆内接四边形的性质得∠DCE =∠BAD ，所以∠ACD =∠DCE ；利用内错角相等证明OD ∥BC ，而DE ⊥BC ，则OD ⊥DE ，于是根据切线的判定定理可得DE 为⊙O 的切线；（2）作OH ⊥BC 于H ，易得四边形ODEH 为矩形，所以OD =EH =2，则CH =HE ﹣CE =1，于是有∠HOC =30°，得到∠COD =60°，然后根据扇形面积公式、等边三角形的面积公式和阴影部分的面积=S 扇形OCD ﹣S △OCD 进行计算即可．【详解】（1）直线ED 与⊙O 相切．理由如下：连结OD ，如图，∵»»BD AD =，∴∠BAD =∠ACD ．∵∠DCE =∠BAD ，∴∠ACD =∠DCE ．∵OC =OD ，∴∠OCD =∠ODC ，而∠OCD =∠DCE ，∴∠DCE =∠ODC ，∴OD ∥BC ． ∵DE ⊥BC ，∴OD ⊥DE ，∴DE 为⊙O 的切线；（2）作OH ⊥BC 于H ，则四边形ODEH 为矩形，∴OD =EH ．∵CE =1，AC =4，∴OC =OD =2，∴CH =HE ﹣CE =2﹣1=1．在Rt △OHC 中，∵OC =2，CH =1，∠OHC =90°，∠HOC =30°，∴∠COD =60°，∴阴影部分的面积=S 扇形OCD ﹣S △OCD26023360π⋅⋅=-•22 23=π3-．【点睛】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．也考查了扇形面积的计算．14．如图，AB是半圆⊙O的直径，点C是半圆⊙O上的点，连接AC，BC，点E是AC的中点，点F是射线OE上一点．（1）如图1，连接FA，FC，若∠AFC＝2∠BAC，求证：FA⊥AB；（2）如图2，过点C作CD⊥AB于点D，点G是线段CD上一点（不与点C重合），连接FA，FG，FG与AC相交于点P，且AF＝FG．①试猜想∠AFG和∠B的数量关系，并证明；②连接OG，若OE＝BD，∠GOE＝90°，⊙O的半径为2，求EP的长．【答案】（1）见解析；（2）①结论：∠GFA＝2∠ABC．理由见解析；②PE＝3．【解析】【分析】（1）证明∠OFA＝∠BAC，由∠EAO+∠EOA＝90°，推出∠OFA+∠AOE＝90°，推出∠FAO＝90°即可解决问题．（2）①结论：∠GFA＝2∠ABC．连接FC．由FC＝FG＝FA，以F为圆心FC为半径作⊙F．因为»»AG AG，推出∠GFA＝2∠ACG，再证明∠ACG＝∠ABC．②图2﹣1中，连接AG，作FH⊥AG于H．想办法证明∠GFA＝120°，求出EF，OF，OG即可解决问题．【详解】（1）证明：连接OC．∵OA＝OC，EC＝EA，∴OF⊥AC，∴FC＝FA，∴∠OFA＝∠OFC，∵∠CFA＝2∠BAC，∴∠OFA＝∠BAC，∵∠OEA＝90°，∴∠EAO+∠EOA＝90°，∴∠OFA+∠AOE＝90°，∴∠FAO＝90°，∴AF⊥AB．（2）①解：结论：∠GFA＝2∠ABC．理由：连接FC．∵OF垂直平分线段AC，∴FG＝FA，∵FG＝FA，∴FC＝FG＝FA，以F为圆心FC为半径作⊙F．∵»»，AG AG∴∠GFA＝2∠ACG，∵AB是⊙O的直径，∴∠ACB＝90°，∵CD⊥AB，∴∠ABC+∠BCA＝90°，∵∠BCD+∠ACD＝90°，∴∠ABC＝∠ACG，∴∠GFA＝2∠ABC．②如图2﹣1中，连接AG，作FH⊥AG于H．∵BD＝OE，∠CDB＝∠AEO＝90°，∠B＝∠AOE，∴△CDB≌△AEO（AAS），∴CD＝AE，∵EC＝EA，∴AC＝2CD．∴∠BAC ＝30°，∠ABC ＝60°，∴∠GFA ＝120°，∵OA ＝OB ＝2，∴OE ＝1，AE ＝，BA ＝4，BD ＝OD ＝1， ∵∠GOE ＝∠AEO ＝90°，∴OG ∥AC ， 323DG OG ∴==, 22221AG DG AD ∴=+=， ∵FG ＝FA ，FH ⊥AG ，∴AH ＝HG 21∠AFH ＝60°， ∴AF ＝27sin 603AH ︒=， 在Rt △AEF 中，EF 2213AF AE -=， ∴OF ＝OE +EF ＝43 ， ∵PE ∥OG ， ∴PE EF OG 0F=， ∴134233=， ∴PE 3． 【点睛】圆综合题，考查了垂径定理，勾股定理，圆周角定理，全等三角形的判定和性质，锐角三角函数，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题.15．如图，已知四边形ABCD 内接于⊙O ，点E 在CB 的延长线上，连结AC 、AE ，∠ACB =∠BAE =45°．（1）求证：AE 是⊙O 的切线；（2）若AB=AD ，AC =32tan ∠ADC=3，求BE 的长．【答案】（1）证明见解析；（2）52BE = 【解析】试题分析：（1）连接OA 、OB ，由圆周角定理得出∠AOB=2∠ACB=90°，由等腰直角三角形的性质得出∠OAB=∠OBA=45°，求出∠OAE=∠OAB+∠BAE=90°,即可得出结论；（2）过点A 作AF ⊥CD 于点F,由AB=AD ，得到∠ACD =∠ACB =45°，在Rt △AFC 中可求得AF ＝3，在Rt △AFD 中求得DF ＝1，所以AB ＝AD ＝10 ，CD = CF +DF =4，再证明△ABE ∽△CDA ，得出BE AB DA CD =，即可求出BE 的长度； 试题解析：（1）证明：连结OA ，OB ，∵∠ACB =45°，∴∠AOB =2∠ACB = 90°，∵OA=OB ，∴∠OAB =∠OBA =45°，∵∠BAE =45°，∴∠OAE =∠OAB +∠BAE =90°，∴OA ⊥AE ．∵点A 在⊙O 上，∴AE 是⊙O 的切线．（2）解：过点A 作AF ⊥CD 于点F ，则∠AFC =∠AFD =90°．∵AB=AD ， ∴AB u u u r =AD u u u r∴∠ACD =∠ACB =45°，在Rt △AFC 中，∵AC =32∠ACF =45°，∴AF=CF=AC ·sin ∠ACF =3，∵在Rt △AFD 中， tan ∠ADC=3AF DF=， ∴DF =1，∴22==+=，3110 AB AD且CD= CF+DF=4，∵四边形ABCD内接于⊙O，∴∠ABE=∠CDA，∵∠BAE=∠DCA，∴△ABE∽△CDA，∴BE AB=，DA CD∴10=，410∴5BE=．2。

中考数学 圆的综合综合试题附详细答案一、圆的综合1．如图，四边形OABC 是平行四边形，以O 为圆心，OA 为半径的圆交AB 于D ，延长AO 交O 于E ，连接CD ，CE ，若CE 是⊙O 的切线，解答下列问题：（1）求证：CD 是⊙O 的切线；（2）若BC=4，CD=6，求平行四边形OABC 的面积．【答案】（1）证明见解析（2）24【解析】试题分析：（1）连接OD ，求出∠EOC=∠DOC ，根据SAS 推出△EOC ≌△DOC ，推出∠ODC=∠OEC=90°，根据切线的判定推出即可；（2）根据切线长定理求出CE=CD=4，根据平行四边形性质求出OA=OD=4，根据平行四边形的面积公式=2△COD 的面积即可求解．试题解析：（1）证明：连接OD ，∵OD=OA ，∴∠ODA=∠A ，∵四边形OABC 是平行四边形，∴OC ∥AB ，∴∠EOC=∠A ，∠COD=∠ODA ，∴∠EOC=∠DOC ，在△EOC 和△DOC 中，OE OD EOC DOC OC OC =⎧⎪∠=∠⎨⎪=⎩∴△EOC ≌△DOC （SAS ），∴∠ODC=∠OEC=90°，即OD ⊥DC ，∴CD 是⊙O 的切线；（2）由（1）知CD 是圆O 的切线，∴△CDO 为直角三角形，∵S △CDO =12CD•OD ， 又∵OA=BC=OD=4，∴S△CDO=12×6×4=12，∴平行四边形OABC的面积S=2S△CDO=24．2．如图1，直角梯形OABC中，BC∥OA，OA=6，BC=2，∠BAO=45°．（1）OC的长为；（2）D是OA上一点，以BD为直径作⊙M，⊙M交AB于点Q．当⊙M与y轴相切时，sin∠BOQ=；（3）如图2，动点P以每秒1个单位长度的速度，从点O沿线段OA向点A运动；同时动点D以相同的速度，从点B沿折线B﹣C﹣O向点O运动．当点P到达点A时，两点同时停止运动．过点P作直线PE∥OC，与折线O﹣B﹣A交于点E．设点P运动的时间为t （秒）．求当以B、D、E为顶点的三角形是直角三角形时点E的坐标．【答案】（1）4；（2）35；（3）点E的坐标为（1，2）、（53，103）、（4，2）．【解析】分析：（1）过点B作BH⊥OA于H，如图1（1），易证四边形OCBH是矩形，从而有OC=BH，只需在△AHB中运用三角函数求出BH即可．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2），则有OH=2，BH=4，MN⊥OC．设圆的半径为r，则MN=MB=MD=r．在Rt△BHD中运用勾股定理可求出r=2，从而得到点D与点H重合．易证△AFG∽△ADB，从而可求出AF、GF、OF、OG、OB、AB、BG．设OR=x，利用BR2=OB2﹣OR2=BG2﹣RG2可求出x，进而可求出BR．在Rt△ORB中运用三角函数就可解决问题．（3）由于△BDE的直角不确定，故需分情况讨论，可分三种情况（①∠BDE=90°，②∠BED=90°，③∠DBE=90°）讨论，然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题．详解：（1）过点B作BH⊥OA于H，如图1（1），则有∠BHA=90°=∠COA，∴OC∥BH．∵BC∥OA，∴四边形OCBH是矩形，∴OC=BH，BC=OH．∵OA =6，BC =2，∴AH =0A ﹣OH =OA ﹣BC =6﹣2=4．∵∠BHA =90°，∠BAO =45°，∴tan ∠BAH =BH HA=1，∴BH =HA =4，∴OC =BH =4． 故答案为4． （2）过点B 作BH ⊥OA 于H ，过点G 作GF ⊥OA 于F ，过点B 作BR ⊥OG 于R ，连接MN 、DG ，如图1（2）．由（1）得：OH =2，BH =4．∵OC 与⊙M 相切于N ，∴MN ⊥OC ．设圆的半径为r ，则MN =MB =MD =r ．∵BC ⊥OC ，OA ⊥OC ，∴BC ∥MN ∥OA ．∵BM =DM ，∴CN =ON ，∴MN =12（BC +OD ），∴OD =2r ﹣2，∴DH =OD OH -=24r -．在Rt △BHD 中，∵∠BHD =90°，∴BD 2=BH 2+DH 2，∴（2r ）2=42+（2r ﹣4）2．解得：r =2，∴DH =0，即点D 与点H 重合，∴BD ⊥0A ，BD =AD ．∵BD 是⊙M 的直径，∴∠BGD =90°，即DG ⊥AB ，∴BG =AG ．∵GF ⊥OA ，BD ⊥OA ，∴GF ∥BD ，∴△AFG ∽△ADB ， ∴AF AD =GF BD =AG AB =12，∴AF =12AD =2，GF =12BD =2，∴OF =4，∴OG同理可得：OB AB ，∴BG =12AB ．设OR =x ，则RG x ．∵BR ⊥OG ，∴∠BRO =∠BRG =90°，∴BR 2=OB 2﹣OR 2=BG 2﹣RG 2，∴（2﹣x 2=（）2﹣（x ）2．解得：x =5，∴BR 2=OB 2﹣OR 2=（2﹣（5）2=365，∴BR =5．在Rt △ORB 中，sin ∠BOR =BR OB35． 故答案为35． （3）①当∠BDE =90°时，点D 在直线PE 上，如图2．此时DP =OC =4，BD +OP =BD +CD =BC =2，BD =t ，OP =t ． 则有2t =2．解得：t =1．则OP =CD =DB =1．∵DE ∥OC ，∴△BDE ∽△BCO ，∴DE OC =BD BC =12，∴DE =2，∴EP =2，∴点E的坐标为（1，2）．②当∠BED=90°时，如图3．∵∠DBE=OBC，∠DEB=∠BCO=90°，∴△DBE∽△OBC，∴BEBC =2DB BEOB∴，=25，∴BE=5t．∵PE∥OC，∴∠OEP=∠BOC．∵∠OPE=∠BCO=90°，∴△OPE∽△BCO，∴OEOB =25OPBC∴，=2t，∴OE=5t．∵OE+BE=OB=255，∴t+55t=25．解得：t=53，∴OP=53，OE=55，∴PE=22OE OP-=103，∴点E的坐标为（51033，）．③当∠DBE=90°时，如图4．此时PE=PA=6﹣t，OD=OC+BC﹣t=6﹣t．则有OD=PE，EA=22PE PA+=2（6﹣t）=62﹣2?t，∴BE=BA﹣EA=42﹣（62﹣2t）=2t﹣22．∵PE∥OD，OD=PE，∠DOP=90°，∴四边形ODEP是矩形，∴DE=OP=t，DE∥OP，∴∠BED=∠BAO=45°．在Rt△DBE中，cos∠BED=BEDE=22，∴DE=2BE，∴t=22（t﹣22）=2t﹣4．解得：t=4，∴OP=4，PE=6﹣4=2，∴点E的坐标为（4，2）．综上所述：当以B、D、E为顶点的三角形是直角三角形时点E的坐标为（1，2）、（51033，）、（4，2）．点睛：本题考查了圆周角定理、切线的性质、相似三角形的判定与性质、三角函数的定义、平行线分线段成比例、矩形的判定与性质、勾股定理等知识，还考查了分类讨论的数学思想，有一定的综合性．3．如图，已知△ABC中，AC=BC，以BC为直径的⊙O交AB于E，过点E作EG⊥AC于G，交BC的延长线于F．（1）求证：AE=BE；（2）求证：FE是⊙O的切线；（3）若FE=4，FC=2，求⊙O的半径及CG的长．【答案】（1）详见解析；（2）详见解析；（3）.【解析】（1）证明：连接CE，如图1所示：∵BC是直径，∴∠BEC=90°，∴CE⊥AB；又∵AC=BC，∴AE=BE．（2）证明：连接OE，如图2所示：∵BE=AE，OB=OC，∴OE是△ABC的中位线，∴OE∥AC，AC=2OE=6．又∵EG⊥AC，∴FE⊥OE，∴FE是⊙O的切线．（3）解：∵EF是⊙O的切线，∴FE2=FC•FB．设FC=x，则有2FB=16，∴FB=8，∴BC=FB﹣FC=8﹣2=6，∴OB=OC=3，即⊙O的半径为3；∴OE=3．∵OE∥AC，∴△FCG∽△FOE，∴，即，解得：CG=．点睛：本题利用了等腰三角形三线合一定理，三角形中位线的判定，切割线定理，以及勾股定理，还有平行线分线段成比例定理，切线的判定等知识．4．图1和图2，半圆O的直径AB=2，点P（不与点A，B重合）为半圆上一点，将图形延BP折叠，分别得到点A，O的对称点A′，O′，设∠ABP=α．（1）当α=15°时，过点A′作A′C∥AB，如图1，判断A′C与半圆O的位置关系，并说明理由．（2）如图2，当α= °时，BA′与半圆O相切．当α= °时，点O′落在上．（3）当线段BO′与半圆O只有一个公共点B时，求α的取值范围．【答案】（1）A′C与半圆O相切；理由见解析；（2）45；30；（3）0°＜α＜30°或45°≤α＜90°．【解析】试题分析：（1）过O作OD⊥A′C于点D，交A′B于点E，利用含30°角的直角三角形的性质可求得DE+OE=A′B=AB=OA，可判定A′C与半圆相切；（2）当BA′与半圆相切时，可知OB⊥A′B，则可知α=45°，当O′在上时，连接AO′，则可知BO′=AB，可求得∠O′BA=60°，可求得α=30°；（3）利用（2）可知当α=30°时，线段O′B与圆交于O′，当α=45°时交于点B，结合题意可得出满足条件的α的范围．试题解析：（1）相切，理由如下：如图1，过O作OD过O作OD⊥A′C于点D，交A′B于点E，∵α=15°，A′C∥AB，∴∠ABA′=∠CA′B=30°，∴DE=A′E，OE=BE，∴DO=DE+OE=（A′E+BE）=AB=OA，∴A′C与半圆O相切；（2）当BA′与半圆O相切时，则OB⊥BA′，∴∠OBA′=2α=90°，∴α=45°，当O′在上时，如图2，连接AO′，则可知BO′=AB，∴∠O′AB=30°，∴∠ABO′=60°，∴α=30°，（3）∵点P，A不重合，∴α＞0，由（2）可知当α增大到30°时，点O′在半圆上，∴当0°＜α＜30°时点O′在半圆内，线段BO′与半圆只有一个公共点B；当α增大到45°时BA′与半圆相切，即线段BO′与半圆只有一个公共点B．当α继续增大时，点P逐渐靠近点B，但是点P，B不重合，∴α＜90°，∴当45°≤α＜90°线段BO′与半圆只有一个公共点B．综上所述0°＜α＜30°或45°≤α＜90°．考点：圆的综合题．5．如图，AB为⊙O的直径，点E在⊙O上，过点E的切线与AB的延长线交于点D，连接BE，过点O作BE的平行线，交⊙O于点F，交切线于点C，连接AC（1）求证：AC是⊙O的切线；（2）连接EF，当∠D=°时，四边形FOBE是菱形．【答案】（1）见解析；（2）30.【解析】【分析】（1）由等角的转换证明出OCA OCE ∆∆≌，根据圆的位置关系证得AC 是⊙O 的切线. （2）根据四边形FOBE 是菱形，得到OF=OB=BF=EF ，得证OBE ∆为等边三角形，而得出60BOE ∠=︒，根据三角形内角和即可求出答案.【详解】（1）证明：∵CD 与⊙O 相切于点E ，∴OE CD ⊥，∴90CEO ∠=︒，又∵OC BE P ，∴COE OEB ∠=∠，∠OBE=∠COA∵OE=OB ，∴OEB OBE ∠=∠，∴COE COA ∠=∠，又∵OC=OC ，OA=OE ，∴OCA OCE SAS ∆∆≌（）， ∴90CAO CEO ∠=∠=︒，又∵AB 为⊙O 的直径，∴AC 为⊙O 的切线；（2）解：∵四边形FOBE 是菱形，∴OF=OB=BF=EF ，∴OE=OB=BE ，∴OBE ∆为等边三角形，∴60BOE ∠=︒，而OE CD ⊥，∴30D ∠=︒．故答案为30．【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题，熟练掌握圆的性质是本题的解题关键.6．如图，已知在△ABC 中，AB=15，AC=20，tanA=12，点P 在AB 边上，⊙P 的半径为定长.当点P 与点B 重合时，⊙P 恰好与AC 边相切；当点P 与点B 不重合时，⊙P 与AC 边相交于点M 和点N ．（1）求⊙P的半径；（2）当AP=65时，试探究△APM与△PCN是否相似，并说明理由．【答案】（1）半径为35；（2）相似，理由见解析.【解析】【分析】（1）如图，作BD⊥AC，垂足为点D，⊙P与边AC相切，则BD就是⊙P的半径，利用解直角三角形得出BD与AD的关系，再利用勾股定理可求得BD的长；（2）如图，过点P作PH⊥AC于点H，作BD⊥AC，垂足为点D，根据垂径定理得出MN=2MH，PM=PN，再利用勾股定理求出PH、AH、MH、MN的长，从而求出AM、NC的长，然后求出AMMP、PNNC的值，得出AMMP=PNNC，利用两边对应成比例且夹角相等的两三角形相似即可证明.【详解】（1）如图，作BD⊥AC，垂足为点D，∵⊙P与边AC相切，∴BD就是⊙P的半径，在Rt△ABD中，tanA= 1BD2AD =，设BD=x，则AD=2x，∴x2+(2x)2=152，解得：5∴半径为5（2）相似，理由见解析，如图，过点P作PH⊥AC于点H，作BD⊥AC，垂足为点D，∴PH垂直平分MN，∴PM=PN，在Rt△AHP中，tanA=12PHAH =，设PH=y，AH=2y，y 2+（2y ）2=（65）2 解得：y=6（取正数）， ∴PH=6，AH=12，在Rt △MPH 中，MH=()22356-=3，∴MN=2MH=6，∴AM=AH-MH=12-3=9，NC=AC-MN-AM=20-6-9=5，∴35535AM MP ==，355PN NC =， ∴AM MP =PN NC， 又∵PM=PN ，∴∠PMN=∠PNM ，∴∠AMP=∠PNC ，∴△AMP ∽△PNC.【点睛】本题考查了解直角三角形、垂径定理、相似三角形的判定与性质等，综合性较强，有一定的难度，正确添加辅助线、灵活应用相关的性质与定理是解题的关键.7．如图．在△ABC 中，∠C =90°，AC =BC ，AB =30cm ，点P 在AB 上，AP =10cm ，点E 从点P 出发沿线段PA 以2c m/s 的速度向点A 运动，同时点F 从点P 出发沿线段PB 以1c m/s 的速度向点B 运动，点E 到达点A 后立刻以原速度沿线段AB 向点B 运动，在点E 、F 运动过程中，以EF 为边作正方形EFGH ，使它与△ABC 在线段AB 的同侧，设点E 、F 运动的时间为t （s ）（0＜t ＜20）．（1）当点H 落在AC 边上时，求t 的值；（2）设正方形EFGH与△ABC重叠部分的面积为S．①试求S关于t的函数表达式；②以点C为圆心，12t为半径作⊙C，当⊙C与GH所在的直线相切时，求此时S的值．【答案】（1）t=2s或10s；（2）①S=22 2 9?(02)75050(210)240400?(1020)t tt t tt t t⎧<≤⎪⎪-+-<≤⎨⎪-+<<⎪⎩；②100cm2．【解析】试题分析：（1）如图1中，当0＜t≤5时，由题意AE=EH=EF，即10﹣2t=3t，t=2；如图2中，当5＜t＜20时，AE=HE，2t﹣10=10﹣（2t﹣10）+t，t=10；（2）分四种切线讨论a、如图3中，当0＜t≤2时，重叠部分是正方形EFGH，S=（3t）2=9t2．b、如图4中，当2＜t≤5时，重叠部分是五边形EFGMN．c、如图5中，当5＜t＜10时，重叠部分是五边形EFGMN．d、如图6中，当10＜t＜20时，重叠部分是正方形EFGH．分别计算即可；②分两种情形分别列出方程即可解决问题．试题解析：解：（1）如图1中，当0＜t≤5时，由题意得：AE=EH=EF，即10﹣2t=3t，t=2如图2中，当5＜t＜20时，AE=HE，2t﹣10=10﹣（2t﹣10）+t，t=10．综上所述：t=2s或10s时，点H落在AC边上．（2）①如图3中，当0＜t≤2时，重叠部分是正方形EFGH，S=（3t）2=9t2如图4中，当2＜t≤5时，重叠部分是五边形EFGMN，S=（3t）2﹣12（5t﹣10）2=﹣72t2+50t﹣50．如图5中，当5＜t＜10时，重叠部分是五边形EFGMN，S=（20﹣t）2﹣12（30﹣3t）2=﹣72t2+50t﹣50．如图6中，当10＜t＜20时，重叠部分是正方形EFGH，S=（20﹣t）2=t2﹣40t+400．综上所述：S=2229?(02)75050(210)240400?(1020)t tt t tt t t⎧<≤⎪⎪-+-<≤⎨⎪-+<<⎪⎩．②如图7中，当0＜t≤5时，12t+3t=15，解得：t=307，此时S=100cm2，当5＜t＜20时，12t+20﹣t=15，解得：t=10，此时S=100．综上所述：当⊙C与GH所在的直线相切时，求此时S的值为100cm2点睛：本题考查了圆综合题、正方形的性质、等腰直角三角形的性质、切线的性质等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，注意不能漏解，属于中考压轴题．8．已知：AB是⊙0直径,C是⊙0外一点,连接BC交⊙0于点D，BD=CD,连接AD、AC．(1)如图1,求证:∠BAD=∠CAD(2)如图2,过点C作CF⊥AB于点F,交⊙0于点E,延长CF交⊙0于点G.过点作EH⊥AG于点H，交AB于点K,求证AK=2OF；(3)如图3,在(2)的条件下,EH交AD于点L,若0K=1,AC=CG,求线段AL的长.图1 图2 图3 【答案】(1)见解析(2)见解析(3)12105【解析】试题分析：（1）由直径所对的圆周角等于90°，得到∠ADB =90°，再证明△ABD ≌△ACD 即可得到结论；（2）连接BE ．由同弧所对的圆周角相等，得到∠GAB =∠BEG ．再证△KFE ≌△BFE ，得到BF =KF =BK ．由OF =OB -BF ，AK =AB -BK ，即可得到结论．（3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．先证CM 垂直平分AG ，得到AM =GM ，∠AGC +∠GCM =90°．再证∠GAF =∠GCM =α．通过证明△AGB ≌△CMG ，得到BG =GM =12AG ．再证明∠BGC =∠MCG =α．设BF =KF =a ， 可得GF =2a ，AF =4a ． 由OK =1，得到OF =a +1，AK =2（a +1），AF = 3a +2，得到3a +2=4a ，解出a 的值，得到AF ，AB ，GF ，FC 的值．由tanα=tan ∠HAK =12HK AH =， AK =6，可以求出 AH 的长．再由1tan tan 3BAD BCF ∠=∠=，利用公式tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD∠+∠-∠⋅∠，得到∠GAD =45°，则AL =2AH ，即可得到结论．试题解析：解：（1）∵AB 为⊙O 的直径，∴∠ADB =90°，∴∠ADC =90°． ∵BD =CD ，∠BDA =∠CDA ，AD =AD ，∴△ABD ≌△ACD ，∴∠BAD =∠CAD ． （2）连接BE ．∵BG =BG ，∴∠GAB =∠BEG ． ∵CF ⊥AB ，∴∠KFE =90°．∵EH ⊥AG ，∴∠AHE =∠KFE =90°，∠AKH =∠EKF ，∴∠HAK =∠KEF =∠BEF ． ∵FE =FE ，∠KFE =∠BFE =90°，∴△KFE ≌△BFE ，∴BF =KF =BK ．∵ OF =OB -BF ，AK =AB -BK ，∴AK =2OF ．（3）连接CO 并延长交AG 于点M ，连接BG ．设∠GAB =α．∵AC =CG ， ∴点C 在AG 的垂直平分线上．∵ OA =OG ，∴点O 在AG 的垂直平分线上， ∴CM 垂直平分AG ，∴AM =GM ，∠AGC +∠GCM =90°． ∵AF ⊥CG ，∴∠AGC +∠GAF =90°，∴∠GAF =∠GCM =α． ∵AB 为⊙O 的直径，∴∠AGB = 90°，∴∠AGB =∠CMG =90°． ∵AB =AC =CG ，∴△AGB ≌△CMG ，∴BG =GM =12AG ．在Rt △AGB 中， 1tan tan 2GB GAB AG α∠=== ． ∵∠AMC =∠AGB = 90°，∴BG ∥CM ， ∴∠BGC =∠MCG =α． 设BF =KF =a ， 1tan tan 2BF BGF GF α∠===，∴GF =2a ，1tan tan 2GF GAF AF α∠=== ，AF =4a ．∵OK =1，∴OF =a +1，AK =2OF =2（a +1），∴AF =AK +KF =a +2（a +1）=3a +2，∴3a +2=4a ，∴a =2， AK =6，∴AF =4a =8，AB =AC =CG =10，GF =2a =4，FC =CG -GF =6． ∵tanα=tan ∠HAK =12HK AH =，设KH =m ，则AH =2m ，∴AK 22(2)m m +=6，解得：m =655，∴AH =2m 125．在Rt △BFC 中，1tan 3BF BCF FC ∠== ．∵∠BAD +∠ABD =90°， ∠FBC +∠BCF =90°，∴∠BCF =∠BAD ，1tan tan 3BAD BCF ∠=∠= ，∴tan ∠GAD =tan tan 1tan tan GAF BADGAF BAD ∠+∠-∠⋅∠=1123111123+=-⨯，∴∠GAD =45°，∴HL=AH ，AL 2AH 12109．如图1，四边形ABCD是正方形，点E是边BC上一点，点F在射线CM上,∠AEF=90°，AE=EF，过点F作射线BC的垂线，垂足为H，连接AC．(1) 试判断BE与FH的数量关系，并说明理由；(2) 求证：∠ACF=90°；(3) 连接AF，过A，E，F三点作圆，如图2. 若EC=4，∠CEF=15°，求的长.图1 图2【答案】（1）BE="FH" ；理由见解析（2）证明见解析（3）=2π【解析】试题分析：（1）由△ABE≌△EHF（SAS）即可得到BE=FH（2）由（1）可知AB=EH，而BC=AB，FH=EB，从而可知△FHC是等腰直角三角形，∠FCH 为45°，而∠ACB也为45°，从而可证明（3)由已知可知∠EAC=30°，AF是直径，设圆心为O，连接EO，过点E作EN⊥AC于点N，则可得△ECN为等腰直角三角形，从而可得EN的长，进而可得AE的长，得到半径，得到所对圆心角的度数，从而求得弧长试题解析：（1）BE=FH．理由如下：∵四边形ABCD是正方形∴∠B=90°，∵FH⊥BC ∴∠FHE=90°又∵∠AEF=90°∴∠AEB+∠HEF="90°" 且∠BAE+∠AEB=90°∴∠HEF=∠BAE ∴∠AEB=∠EFH 又∵AE=EF∴△ABE≌△EHF（SAS）∴BE=FH(2)∵△ABE≌△EHF∴BC=EH，BE=FH 又∵BE+EC=EC+CH ∴BE="CH"∴CH=FH∴∠FCH=45°，∴∠FCM=45°∵AC是正方形对角线，∴∠ACD=45°∴∠ACF=∠FCM +∠ACD =90°（3）∵AE=EF，∴△AEF是等腰直角三角形△AEF外接圆的圆心在斜边AF的中点上．设该中点为O．连结EO得∠AOE=90°过E作EN⊥AC于点NRt△ENC中，EC=4，∠ECA=45°，∴EN=NC=Rt△ENA中，EN =又∵∠EAF=45°∠CAF=∠CEF=15°（等弧对等角）∴∠EAC=30°∴AE=Rt△AFE中，AE== EF，∴AF=8AE所在的圆O半径为4，其所对的圆心角为∠AOE=90°=2π·4·（90°÷360°）=2π考点：1、正方形；2、等腰直角三角形；3、圆周角定理；4、三角函数10．如图，等边△ABC内接于⊙O，P是弧AB上任一点（点P不与A、B重合），连AP，BP，过C作CM∥BP交PA的延长线于点M，（1）求证：△PCM为等边三角形；（2）若PA＝1，PB＝2，求梯形PBCM的面积．【答案】（1）见解析；（2153 4【解析】【分析】（1）利用同弧所对的圆周角相等即可求得题目中的未知角，进而判定△PCM为等边三角形；（2）利用上题中得到的相等的角和等边三角形中相等的线段证得两三角形全等，进而利用△PCM 为等边三角形，进而求得PH 的长，利用梯形的面积公式计算梯形的面积即可． 【详解】（1）证明：作PH ⊥CM 于H ， ∵△ABC 是等边三角形， ∴∠APC=∠ABC=60°， ∠BAC=∠BPC=60°， ∵CM ∥BP ， ∴∠BPC=∠PCM=60°， ∴△PCM 为等边三角形；（2）解：∵△ABC 是等边三角形，△PCM 为等边三角形， ∴∠PCA+∠ACM=∠BCP+∠PCA ， ∴∠BCP=∠ACM ， 在△BCP 和△ACM 中，BC AC BCP ACM CP CM =⎧⎪∠=∠⎨⎪=⎩， ∴△BCP ≌△ACM （SAS ）， ∴PB=AM ，∴CM=CP=PM=PA+AM=PA+PB=1+2=3， 在Rt △PMH 中，∠MPH=30°， ∴PH=332， ∴S 梯形PBCM =12（PB+CM ）×PH=12×（2+3）×33=1534．【点睛】本题考查圆周角定理、等边三角形的判定、全等三角形的性质及梯形的面积计算方法，是一道比较复杂的几何综合题．11．如图，△ABC中，AC＝BC＝10，cosC＝35，点P是AC边上一动点（不与点A、C重合），以PA长为半径的⊙P与边AB的另一个交点为D，过点D作DE⊥CB于点E．（1）当⊙P与边BC相切时，求⊙P的半径．（2）连接BP交DE于点F，设AP的长为x，PF的长为y，求y关于x的函数解析式，并直接写出x的取值范围．（3）在（2）的条件下，当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时，求相交所得的公共弦的长.【答案】（1）409R=;（2）25880320xy x xx=-++（3）505-【解析】【分析】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，即可求解；（2）首先证明PD∥BE，则EB BFPD PF=，即：2024588x yxxx-+--=，即可求解；（3）证明四边形PDBE为平行四边形，则AG＝EP＝BD，即：AB＝DB+AD＝AG+AD＝5【详解】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，解得：R＝409；（2）在△ABC中，AC＝BC＝10，cosC＝35，设AP＝PD＝x，∠A＝∠ABC＝β，过点B作BH⊥AC，则BH＝ACsinC＝8，同理可得：CH＝6，HA＝4，AB＝45，则：tan∠CAB＝2，BP＝228+(4)x-＝2880x x-+，DA＝25x，则BD＝45﹣25x，如下图所示，PA＝PD，∴∠PAD＝∠CAB＝∠CBA＝β，tanβ＝2，则cosβ5，sinβ5，EB ＝BDcosβ＝（45﹣25x ）×5＝4﹣25x ， ∴PD ∥BE ， ∴EB BF PD PF =，即：2024588x y x xx y -+--=， 整理得：y ＝25x x 8x 803x 20-++； （3）以EP 为直径作圆Q 如下图所示，两个圆交于点G ，则PG ＝PQ ，即两个圆的半径相等，则两圆另外一个交点为D ， GD 为相交所得的公共弦，∵点Q 是弧GD 的中点， ∴DG ⊥EP ，∵AG 是圆P 的直径，∴∠GDA ＝90°，∴EP ∥BD ，由（2）知，PD ∥BC ，∴四边形PDBE 为平行四边形，∴AG ＝EP ＝BD ，∴AB ＝DB+AD ＝AG+AD ＝5设圆的半径为r ，在△ADG 中，AD ＝2rcosβ5DG 5AG ＝2r ， 5＝52r 51+， 则：DG 550﹣5 相交所得的公共弦的长为50﹣5【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．12．设C 为线段AB 的中点，四边形BCDE 是以BC 为一边的正方形，以B 为圆心，BD 长为半径的⊙B 与AB 相交于F 点，延长EB 交⊙B 于G 点，连接DG 交于AB 于Q 点，连接AD ．求证：（1）AD 是⊙B 的切线；（2）AD ＝AQ ；（3）BC 2＝CF×EG ．【答案】(1)证明见解析；（2）证明见解析；（3）证明见解析.【解析】【分析】()1连接BD ，由DC AB ⊥，C 为AB 的中点，由线段垂直平分线的性质，可得AD BD =，再根据正方形的性质，可得90ADB ∠=o ；()2由BD BG =与//CD BE ，利用等边对等角与平行线的性质，即可求得122.52G CDG BDG BCD ∠=∠=∠=∠=o ，继而求得67.5ADQ AQD ∠=∠=o ，由等角对等边，可证得AD AQ =； ()3易求得67.5GDE GDB BDE DFE ∠=∠+∠==∠o ，90DCF E ∠=∠=o ，即可证得Rt DCF V ∽Rt GED V ，根据相似三角形的对应边成比例，即可证得结论．【详解】证明：()1连接BD ，Q 四边形BCDE 是正方形，45DBA ∴∠=o ，90DCB ∠=o ，即DC AB ⊥，C Q 为AB 的中点，CD ∴是线段AB 的垂直平分线，AD BD ∴=，45DAB DBA ∴∠=∠=o ，90ADB ∴∠=o ，即BD AD ⊥，BD Q 为半径，AD ∴是B e 的切线；()2BD BG =Q ，BDG G ∴∠=∠，//CD BE Q ，CDG G ∴∠=∠，122.52G CDG BDG BCD ∴∠=∠=∠=∠=o ， 9067.5ADQ BDG ∴∠=-∠=o o ，9067.5AQB BQG G ∠=∠=-∠=o o ， ADQ AQD ∴∠=∠，AD AQ ∴=；()3连接DF ，在BDF V 中，BD BF =，BFD BDF ∴∠=∠，又45DBF ∠=o Q ，67.5BFD BDF ∴∠=∠=o ，22.5GDB ∠=o Q ，在Rt DEF V 与Rt GCD V 中，67.5GDE GDB BDE DFE ∠=∠+∠==∠o Q ，90DCF E ∠=∠=o ，Rt DCF ∴V ∽Rt GED V ，CF CD ED EG∴=， 又CD DE BC ==Q ，2BC CF EG ∴=⋅．【点睛】本题考查了相似三角形的判定与性质、切线的判定与性质、正方形的性质以及等腰三角形的判定与性质.解题的关键是注意掌握数形结合思想的应用，注意辅助线的作法．13．如图，已知AB 是⊙O 的直径，点C 、D 在⊙O 上，∠D ＝60°且AB ＝6，过O 点作OE ⊥AC ，垂足为E ．（1）求OE 的长；（2）若OE的延长线交⊙O于点F，求弦AF、AC和弧CF围成的图形（阴影部分）的面积．（结果保留π）【答案】（1）OE的长为32；（2）阴影部分的面积为3 2π【解析】（1）OE=32（2）S=32π14．如图1，⊙O的直径AB=12，P是弦BC上一动点（与点B，C不重合），∠ABC=30°，过点P作PD⊥OP交⊙O于点D．（1）如图2，当PD∥AB时，求PD的长；（2）如图3，当弧DC=弧AC时，延长AB至点E，使BE=12AB，连接DE．①求证：DE是⊙O的切线；②求PC的长．【答案】（1）6；（2）①证明见解析；33．【解析】试题分析：（1）根据题意首先得出半径长，再利用锐角三角三角函数关系得出OP，PD的长；（2）①首先得出△OBD是等边三角形，进而得出∠ODE=∠OFB=90°，求出答案即可；②首先求出CF的长，进而利用直角三角形的性质得出PF的长，进而得出答案．试题解析：（1）如图2，连接OD，∵OP⊥PD，PD∥AB，∴∠POB=90°，∵⊙O的直径AB=12，∴OB=OD=6，在Rt△POB中，∠ABC=30°，∴OP=OB•tan30°=6×=2，在Rt△POD中，PD===；（2）①如图3，连接OD，交CB于点F，连接BD，∵，∴∠DBC=∠ABC=30°，∴∠ABD=60°，∵OB=OD，∴△OBD是等边三角形，∴OD⊥FB，∵BE=AB，∴OB=BE，∴BF∥ED，∴∠ODE=∠OFB=90°，∴DE是⊙O的切线；②由①知，OD⊥BC，∴CF=FB=OB•cos30°=6×=3，在Rt△POD中，OF=DF，∴PF=DO=3（直角三角形斜边上的中线，等于斜边的一半），∴CP=CF﹣PF=3﹣3．考点：圆的综合题15．已知：如图，以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E，过点D作DF⊥BC，垂足为F．（1）求证：DF为⊙O的切线；（2）若等边三角形ABC 的边长为4，求图中阴影部分的面积．【答案】（1）见解析（2）332 23π-【解析】试题分析：（1）连接DO，要证明DF为⊙O的切线只要证明∠FDP=90°即可；（2）首先由已知可得到CD，CF的长，从而利用勾股定理可求得DF的长；再连接OE，求得CF，EF的长，从而利用S直角梯形FDOE﹣S扇形OED求得阴影部分的面积．试题解析：（1）证明：连接DO．∵△ABC是等边三角形，∴∠A=∠C=60°．∵OA=OD，∴△OAD是等边三角形．∴∠ADO=60°，∵DF⊥BC，∴∠CDF=90°﹣∠C=30°，∴∠FDO=180°﹣∠ADO﹣∠CDF=90°，∴DF为⊙O的切线；（2）∵△OAD是等边三角形，∴AD=AO=AB=2．∴CD=AC﹣AD=2．Rt△CDF中，∵∠CDF=30°，∴CF=CD=1．∴DF=，连接OE，则CE=2．∴CF=1，∴EF=1．∴S直角梯形FDOE=（EF+OD）•DF=，∴S扇形OED==，∴S阴影=S直角梯形FDOE﹣S扇形OED=﹣．【点睛】此题考查学生对切线的判定及扇形的面积等知识点的掌握情况，当已知条件中明确指出直线与圆有公共点时，常连接过该公共点的半径，证明该半径垂直于这条直线．也考查了等边三角形的性质和利用割补法计算补规则图形的面积．。

中考数学《圆的综合题》专项练习题及答案一、单选题1．如图，在一块正三角形飞镖游戏板上画一个正六边形（图中阴影部分），假设飞镖投中游戏板上的每一点是等可能的（若投中边界或没有投中游戏板，则重投1次），任意投掷飞镖1次，则飞镖投中阴影部分的概率为（）A．13B．49C．12D．232．如图，AB为⊙O的直径，弦DC垂直AB于点E，⊙DCB=30°，EB=3，则弦AC的长度为（）A．3 √3B．4√3C．5√3D．6√33．如图，AB是⊙O的弦，半径OC⊙AB于点D，且AB=6cm，OD=4cm。

则DC的长为（）A．cm B．1cm C．2cm D．5cm4．如图，四边形ABCD内接于⊙ O，AB为⊙ O的直径，∠ABD=20∘，则∠BCD的度数是（）A．90°B．100°C．110°D．120°5．如图，点A，B，C，D都在⊙O上，AC，BD相交于点E，则⊙ABD=（）A．⊙ACD B．⊙ADB C．⊙AED D．⊙ACB6．如图，在⊙O中，弦AB⊙CD，若⊙ABC=40°，则⊙BOD=（）A．20°B．40°C．50°D．80°7．下列判断结论正确的有（）（1）直径是圆中最大的弦．（2）长度相等的两条弧一定是等弧．（3）面积相等的两个圆是等圆．（4）同一条弦所对的两条弧一定是等弧．（5）圆上任意两点间的部分是圆的弦．A．1个B．2个C．3个D．4个8．已知如图，PA、PB切⊙O于A，B，MN切⊙O于C，交PB于N；若PA=7.5cm，则⊙PMN的周长是（）A．7.5cm B．10cm C．15cm D．12.5cm9．若小李同学掷出的铅球在场地航砸出一个直径为10厘米，深2厘米的小坑，则该铅球的直径为（）A．20厘米B．19.5厘米C．14.5厘米D．10厘米10．如图，如果从半径为9cm的圆形纸片剪去13圆周的一个扇形，将留下的扇形（阴影部分）围成一个圆锥（接缝处不重叠），那么这个圆锥的高为（）A．6cm B．5√3cm C．8cm D．3√5cm11．如图，△ABC内接于⊙O，∠B=65o，∠C=70o，若BC=2√2，则弧BC长为（）A．πB．√2πC．2πD．√2π12．如下图，点B，C，D在⊙O上，若⊙BCD＝130°，则⊙BOD的度数是（）A．96°B．98°C．102°D．100°二、填空题13．如图，在扇形AOB中，OA＝4，⊙AOB＝90°，点P是弧AB上的动点，连接OP，点C是线段OP的中点，连接BC并延长交OA于点D，则图中阴影部分面积最小值为.14．如图，在边长为√2的正方形ABCD中，分别以四个顶点为圆心，以边长为半径画弧，分别与正方形的边和对角线相交，则图中阴影部分的面积为（结果保留π）.15．如图，⊙ABC的顶点A，B，C均在⊙O上，若⊙ABC+⊙AOC=90°，则⊙AOC的大小是．16．如图：⊙O为⊙ABC的内切圆，⊙C＝90°，AO的延长线交BC于点D，AC＝4，CD＝1，则⊙O的半径为.17．如图，在正八边形ABCDEFGH中，AC、GC是两条对角线，则tan⊙ACG=．18．如图，菱形ABCD中，已知AB=2，∠DAB=60°将它绕着点A逆时针旋转得到菱形ADEF，使AB与AD重合，则点C运动的路线CE⌢的长为．三、综合题19．如图，AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C，点D为AP的中点，连结AC．求证：（1）⊙P=⊙BAC（2）直线CD是⊙O的切线．20．如图，以△ABC的边AB为直径的⊙O交AC于点F，点E是BF⌢的中点，连接BE并延长交AC于点D，若∠CBD=12∠CAB．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为2，cos∠BAC=25，求CD的长．21．如图，⊙O是⊙ABC的外接圆，AC是O的直径，BD＝BA＝12，BC＝5，BE⊙DC，交D的延长线于点E，BD交直径AC于点F．（1）求证：⊙BCA＝⊙BAD．（2）求证：BE是⊙O的切线．（3）若BD平分⊙ABC，交⊙O于点D，求AD的长．22．如图，⊙OAB中，OA=OB=10cm，⊙AOB=80°，以点O为圆心，半径为6cm的优弧弧MN分别交OA，OB于点M，N．（1）点P在右半弧上（⊙BOP是锐角），将OP绕点O逆时针旋转80°得OP′．求证：AP=BP′；（2）点T在左半弧上，若AT与弧相切，求A T的长．23．如图，有一直径是√2米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC，则：（1）AB的长为米；（2）用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为米.⌢的中点，CE⊥AB于点E，BD交CE于点F．24．如图，AB是⊙O的直径，C是BD（1）求证：CF=BF；（2）若CD﹦5，AC﹦12，求⊙O的半径和CE的长．参考答案1．【答案】D2．【答案】D3．【答案】B4．【答案】C5．【答案】A6．【答案】D7．【答案】B8．【答案】C9．【答案】C10．【答案】D11．【答案】A12．【答案】D13．【答案】4π−8√3314．【答案】4-π15．【答案】60°16．【答案】0.817．【答案】118．【答案】2√33π19．【答案】（1）解：证明：∵AB是⊙O的直径∴⊙ACB=90°∴⊙ACP=90°∴⊙P+⊙CAP=90°∵AP⊙O是切线∴⊙BAP=90°即⊙CAP+⊙BAC=90°∴⊙P=⊙BAC；（2）解：∵CD是Rt⊙PAC斜边PA的中线∴CD=AD∴⊙DCA=⊙DAC连接OC∵OC=OA∴⊙OCA=⊙OAC∴⊙DCO=⊙DAO=90°∴CD是⊙O的切线．20．【答案】（1）证明：连接AE，如图所示：∵AB是⊙O的直径∴∠AEB=90°∴∠BAE+∠ABE=90°．∵点E为弧BF的中点∴EF⌢=EB⌢∴∠BAE=∠DAE=12∠CAB．又∵∠CBD=12∠CAB∴∠BAE=∠CBD∴∠CBD+∠ABE=90°∴AB⊥CB∴BC是⊙O的切线．（2）解：∵∠BAE=∠DAE，∠AED=∠AEB=90°∴∠ADE=∠ABE∴AD=AB=2×2=4．∵cos∠BAC=2 5∴在Rt△ABC中即4AC=25，得AC=10∴CD=AC−AD=10−4=6．21．【答案】（1）证明：∵BD=BA ∴∠BDA=∠BAD．∵∠BCA=∠BDA∴∠BCA=∠BAD．（2）证明：连结OB，如图∵∠BCA=∠BAD又∵∠BCE=∠BAD∴∠BCA=∠BCE∵OB=OC∴∠BCO=∠CBO∴∠BCE=∠CBO∴OB//ED．∵BE⊥ED∴EB⊥BO．∴BE是⊙O的切线．（3）解：∵AC是⊙O的直径∴∠ABC=90°∴AC=√AB2+BC2=√122+52=13．∵∠BDE=∠CAB∴△BED∽△CBA∴BDAC=DEAB，即1213=DE12∴DE=14413∴BE=√BD2−DE2=6013∴CE=√BC2−BE2=2513∴CD=DE−CE=119 13∵BD平分⊙ABC ∴∠CBD=∠ABD∴AD=CD=119 13．22．【答案】（1）证明：∵⊙AOB=⊙POP′=80°∴⊙AOB+⊙BOP=⊙POP′+⊙BOP即⊙AOP=⊙BOP′在⊙AOP 与⊙BOP′中 OA=OB ⊙AOP=⊙BOP OP=OP′∴⊙AOP⊙⊙BOP′ ∴AP=BP′（2）解：∵A T 与弧相切，连结OT ．∴OT⊙A T在Rt⊙AOT 中，根据勾股定理得，A T= √OA 2−OT 2 ∵OA=10，OT=6 ∴AT=823．【答案】（1）1 （2）1424．【答案】（1）证明：∵AB 是 ⊙O 的直径∴∠ACB =90° ∴∠A +∠ABC =90° 又∵CE ⊥AB ∴∠CEB =90° ∴∠BCE +∠ABC =90° ∴∠BCE =∠A∵C 是 BD ⌢ 的中点 ∴CD⌢=CB ⌢ ∴∠DBC =∠A ∴∠DBC =∠BCE ∴CF =BF（2）解：∵CD⌢=CB ⌢，CD =5 ∴∠DBC =∠BDC∴BC=CD=5∵∠ACB=90°∴AB=√AC2+BC2=√122+52=13∴AO=6.5∵∠BCE=∠A，∠ACB=∠CEB=90°∴△CEB⊙ △ACB∴CE=AC⋅BCAB=12×513=6013故⊙O的半径为6.5，CE的长是6013.第11页共11。

一、圆的综合 真题与模拟题分类汇编（难题易错题）1．如图1，已知扇形MON 的半径为2，∠MON=90°，点B 在弧MN 上移动，联结BM ，作OD ⊥BM ，垂足为点D ，C 为线段OD 上一点，且OC=BM ，联结BC 并延长交半径OM 于点A ，设OA=x ，∠COM 的正切值为y.（1）如图2，当AB ⊥OM 时，求证：AM=AC ；（2）求y 关于x 的函数关系式，并写出定义域；（3）当△OAC 为等腰三角形时，求x 的值.【答案】 (1)证明见解析;(2) 2=+y x 02<≤x 1422=x . 【解析】 分析：（1）先判断出∠ABM =∠DOM ，进而判断出△OAC ≌△BAM ，即可得出结论； （2）先判断出BD =DM ，进而得出DM ME BD AE =，进而得出AE =122x （），再判断出2OA OC DM OE OD OD==，即可得出结论； （3）分三种情况利用勾股定理或判断出不存在，即可得出结论．详解：（1）∵OD ⊥BM ，AB ⊥OM ，∴∠ODM =∠BAM =90°．∵∠ABM +∠M =∠DOM +∠M ，∴∠ABM =∠DOM ．∵∠OAC =∠BAM ，OC =BM ，∴△OAC ≌△BAM ，∴AC =AM ．（2）如图2，过点D 作DE ∥AB ，交OM 于点E ．∵OB =OM ，OD ⊥BM ，∴BD =DM ．∵DE ∥AB ，∴DM ME BD AE =，∴AE =EM ．∵OM 2，∴AE =122x （）． ∵DE ∥AB ，∴2OA OC DM OE OD OD==， ∴22DM OA y OD OE x =∴=+，02x ≤＜（3）（i）当OA=OC时．∵111222DM BM OC x===．在Rt△ODM中，222124OD OM DM x=-=-．∵2121224xDMyOD xx=∴=+-，．解得1422x-=，或1422x--=（舍）．（ii）当AO=AC时，则∠AOC=∠ACO．∵∠ACO＞∠COB，∠COB=∠AOC，∴∠ACO＞∠AOC，∴此种情况不存在．（ⅲ）当CO=CA时，则∠COA=∠CAO=α．∵∠CAO＞∠M，∠M=90°﹣α，∴α＞90°﹣α，∴α＞45°，∴∠BOA=2α＞90°．∵∠BOA≤90°，∴此种情况不存在．即：当△OAC为等腰三角形时，x的值为1422-．点睛：本题是圆的综合题，主要考查了相似三角形的判定和性质，圆的有关性质，勾股定理，等腰三角形的性质，建立y关于x的函数关系式是解答本题的关键．2．四边形ABCD 的对角线交于点E，且AE＝EC，BE＝ED，以AD 为直径的半圆过点E，圆心为O．（1）如图①，求证：四边形ABCD 为菱形；（2）如图②，若BC 的延长线与半圆相切于点F，且直径AD＝6，求弧AE 的长．【答案】（1）见解析；（2）π2【解析】试题分析：（1）先判断出四边形ABCD是平行四边形，再判断出AC⊥BD即可得出结论；（2）先判断出AD=DC且DE⊥AC，∠ADE=∠CDE，进而得出∠CDA=30°，最后用弧长公式即可得出结论．试题解析：证明：（1）∵四边形ABCD的对角线交于点E，且AE=EC，BE=ED，∴四边形ABCD 是平行四边形．∵以AD 为直径的半圆过点E ，∴∠AED =90°，即有AC ⊥BD ，∴四边形ABCD 是菱形；（2）由（1）知，四边形ABCD 是菱形，∴△ADC 为等腰三角形，∴AD =DC 且DE ⊥AC ，∠ADE =∠CDE ．如图2，过点C 作CG ⊥AD ，垂足为G ，连接FO ．∵BF 切圆O 于点F ，∴OF ⊥AD ，且132OF AD ==，易知，四边形CGOF 为矩形，∴CG =OF =3． 在Rt △CDG 中，CD =AD =6，sin ∠ADC =CG CD =12，∴∠CDA =30°，∴∠ADE =15°． 连接OE ，则∠AOE =2×∠ADE =30°，∴3031802AE ππ⋅⨯==．点睛：本题主要考查菱形的判定即矩形的判定与性质、切线的性质，熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键．3．等腰Rt △ABC 和⊙O 如图放置，已知AB=BC=1，∠ABC=90°，⊙O 的半径为1，圆心O 与直线AB 的距离为5．（1）若△ABC 以每秒2个单位的速度向右移动，⊙O 不动，则经过多少时间△ABC 的边与圆第一次相切？（2）若两个图形同时向右移动，△ABC 的速度为每秒2个单位，⊙O 的速度为每秒1个单位，则经过多少时间△ABC 的边与圆第一次相切？（3）若两个图形同时向右移动，△ABC 的速度为每秒2个单位，⊙O 的速度为每秒1个单位，同时△ABC 的边长AB 、BC 都以每秒0.5个单位沿BA 、BC 方向增大．△ABC 的边与圆第一次相切时，点B 运动了多少距离？【答案】（152-；（2） 52；（32042- 【解析】 分析：（1）分析易得，第一次相切时，与斜边相切，假设此时，△ABC 移至△A′B′C′处，A′C′与⊙O 切于点E ，连OE 并延长，交B′C′于F ．由切线长定理易得CC′的长，进而由三角形运动的速度可得答案；（2）设运动的时间为t 秒，根据题意得：CC′=2t ，DD′=t ，则C′D′=CD+DD′-CC′=4+t -2t=4-t ，由第（1）的结论列式得出结果；（3）求出相切的时间，进而得出B 点移动的距离．详解：（1）假设第一次相切时，△ABC 移至△A′B′C′处，如图1，A′C′与⊙O 切于点E ，连接OE 并延长，交B′C′于F ，设⊙O 与直线l 切于点D ，连接OD ，则OE ⊥A′C′，OD ⊥直线l ，由切线长定理可知C′E=C′D ，设C′D=x ，则C′E=x ，∵△ABC 是等腰直角三角形，∴∠A=∠ACB=45°，∴∠A′C′B′=∠ACB=45°，∴△EFC′是等腰直角三角形，∴C′F=2x ，∠OFD=45°， ∴△OFD 也是等腰直角三角形，∴OD=DF ，∴2x+x=1，则x=2-1，∴CC′=BD -BC-C′D=5-1-（2-1）=5-2，∴点C 运动的时间为522-； 则经过52-秒，△ABC 的边与圆第一次相切； （2）如图2，设经过t 秒△ABC 的边与圆第一次相切，△ABC 移至△A′B′C′处，⊙O 与BC 所在直线的切点D 移至D′处，A′C′与⊙O 切于点E ，连OE 并延长，交B′C′于F ，∵CC′=2t ，DD′=t ，∴C′D′=CD+DD′-CC′=4+t -2t=4-t ，由切线长定理得C′E=C′D′=4-t ，由（1）得：4-t=2-1， 解得：t=5-2，答：经过5-2秒△ABC 的边与圆第一次相切；（3）由（2）得CC′=（2+0.5）t=2.5t ，DD′=t ，则C′D′=CD+DD′-CC′=4+t -2.5t=4-1.5t ，由切线长定理得C′E=C′D′=4-1.5t ，由（1）得：4-1.5t=2-1，解得：t=10223-， ∴点B 运动的距离为2×10223-=20423-．点睛：本题要求学生熟练掌握圆与直线的位置关系，并结合动点问题进行综合分析，比较复杂，难度较大，考查了学生数形结合的分析能力．4．如图，AB 是⊙O 的直径，弦BC ＝OB ，点D 是AC 上一动点，点E 是CD 中点，连接BD 分别交OC ，OE 于点F ，G ．（1）求∠DGE 的度数；（2）若CF OF ＝12，求BF GF的值； （3）记△CFB ，△DGO 的面积分别为S 1，S 2，若CF OF＝k ，求12S S 的值．（用含k 的式子表示）【答案】(1)∠DGE ＝60°；(2)72；(3)12S S =211k k k +++.【解析】【分析】（1）根据等边三角形的性质，同弧所对的圆心角和圆周角的关系，可以求得∠DGE 的度数；（2）过点F 作FH ⊥AB 于点H 设CF ＝1，则OF ＝2，OC ＝OB ＝3,根据勾股定理求出BF 的长度，再证得△FGO ∽△FCB ，进而求得BF GF的值； （3）根据题意，作出合适的辅助线，然后根据三角形相似、勾股定理可以用含k 的式子表示出12S S 的值． 【详解】解：(1)∵BC ＝OB ＝OC ，∴∠COB ＝60°，∴∠CDB ＝12∠COB ＝30°， ∵OC ＝OD ，点E 为CD 中点，∴OE ⊥CD ，∴∠GED ＝90°，∴∠DGE ＝60°；(2)过点F 作FH ⊥AB 于点H设CF ＝1，则OF ＝2，OC ＝OB ＝3∵∠COB ＝60°∴OH ＝12OF ＝1， ∴HFHB ＝OB ﹣OH ＝2，在Rt △BHF 中，BF ==由OC ＝OB ，∠COB ＝60°得：∠OCB ＝60°，又∵∠OGB ＝∠DGE ＝60°，∴∠OGB ＝∠OCB ，∵∠OFG ＝∠CFB ，∴△FGO ∽△FCB ， ∴OF GF BF CF=， ∴， ∴BF GF =72. (3)过点F 作FH ⊥AB 于点H ，设OF ＝1，则CF ＝k ，OB ＝OC ＝k+1，∵∠COB ＝60°，∴OH ＝12OF=12， ∴HF＝330H =，HB ＝OB ﹣OH ＝k+12， 在Rt △BHF 中， BF ＝222HB HF k k 1+=++， 由(2)得：△FGO ∽△FCB ，∴GO OF CB BF=，即211GO k k k =+++， ∴GO 21k k =++，过点C 作CP ⊥BD 于点P∵∠CDB ＝30°∴PC ＝12CD ， ∵点E 是CD 中点，∴DE ＝12CD ， ∴PC ＝DE ，∵DE ⊥OE ， ∴12S S =BF GO =22111k k k k k +++++=211k k k +++【点睛】圆的综合题，解答本题的关键是明确题意，找出所求问题需要的条件，利用三角形相似和勾股定理、数形结合的思想解答．5．已知P 是O 的直径BA 延长线上的一个动点，∠P 的另一边交O 于点C 、D ，两点位于AB 的上方，AB ＝6，OP=m ，1sin 3P ＝，如图所示．另一个半径为6的1O 经过点C 、D ，圆心距1OO n ＝．（1）当m=6时，求线段CD 的长；（2）设圆心O 1在直线AB 上方，试用n 的代数式表示m ； （3）△POO 1在点P 的运动过程中，是否能成为以OO 1为腰的等腰三角形，如果能，试求出此时n 的值；如果不能，请说明理由．【答案】(1)CD=25;(2)m=23812n n- ;(3) n 的值为955或9155 【解析】分析：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．解Rt △POH ，得到OH 的长．由勾股定理得CH 的长，再由垂径定理即可得到结论；（2）解Rt △POH ，得到Rt 3m OH OCH ＝．在和Rt △1O CH 中，由勾股定理即可得到结论；（3）△1POO 成为等腰三角形可分以下几种情况讨论：① 当圆心1O 、O 在弦CD 异侧时，分1OP OO ＝和11O P OO ＝．②当圆心1O 、O 在弦CD 同侧时，同理可得结论． 详解：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．在Rt △1sin 63POH P PO =中，＝，，∴2OH =．∵AB ＝6，∴3OC ＝．由勾股定理得： 5CH =∵OH ⊥DC ，∴225CD CH ==．（2）在Rt △1sin 3POH P PO m 中，＝，＝，∴3m OH ＝．在Rt △OCH 中，2293m CH ⎛⎫- ⎪⎝⎭＝． 在Rt △1O CH 中，22363m CH n ⎛⎫-- ⎪⎝⎭＝． 可得： 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭＝，解得23812n m n -：＝． （3）△1POO 成为等腰三角形可分以下几种情况：① 当圆心1O 、O 在弦CD 异侧时i ）1OP OO ＝，即m n ＝，由23812n n n -＝，解得9n ：＝． 即圆心距等于O 、1O 的半径的和，就有O 、1O 外切不合题意舍去．ii ）11O P OO ＝ n ＝，解得：23m n ＝，即23n 23812n n-＝，解得n ： ②当圆心1O 、O 在弦CD 同侧时，同理可得： 28132n m n-＝．∵1POO ∠是钝角，∴只能是m n =，即28132n n n-＝，解得n ：综上所述：n 点睛：本题是圆的综合题．考查了圆的有关性质和两圆的位置关系以及解直径三角形．解答（3）的关键是要分类讨论．6．如图1，是用量角器一个角的操作示意图，量角器的读数从M 点开始（即M 点的读数为0），如图2，把这个量角器与一块30°（∠CAB ＝30°）角的三角板拼在一起，三角板的斜边AB 与量角器所在圆的直径MN 重合，现有射线C 绕点C 从CA 开始沿顺时针方向以每秒2°的速度旋转到与CB ，在旋转过程中，射线CP 与量角器的半圆弧交于E ．连接BE ． （1）当射线CP 经过AB 的中点时，点E 处的读数是 ，此时△BCE 的形状是 ； （2）设旋转x 秒后，点E 处的读数为y ，求y 与x 的函数关系式；（3）当CP 旋转多少秒时，△BCE 是等腰三角形？【答案】（1）60°，直角三角形；（2）y＝4x（0≤x≤45）；（3）7.5秒或30秒【解析】【分析】（1）根据圆周角定理即可解决问题；（2）如图2﹣2中，由题意∠ACE＝2x，∠AOE＝y，根据圆周角定理可知∠AOE＝2∠ACE，可得y＝2x（0≤x≤45）；（3）分两种情形分别讨论求解即可；【详解】解：（1）如图2﹣1中，∵∠ACB＝90°，OA＝OB，∴OA＝OB＝OC，∴∠OCA＝∠OAC＝30°，∴∠AOE＝60°，∴点E处的读数是60°，∵∠E＝∠BAC＝30°，OE＝OB，∴∠OBE＝∠E＝30°，∴∠EBC＝∠OBE+∠ABC＝90°，∴△EBC是直角三角形；故答案为60°，直角三角形；（2）如图2﹣2中，∵∠ACE＝2x，∠AOE＝y，∵∠AOE＝2∠ACE，∴y＝4x（0≤x≤45）．（3）①如图2﹣3中，当EB＝EC时，EO垂直平分线段BC，∵AC⊥BC，∵EO∥AC，∴∠AOE＝∠BAC＝30°，∠AOE＝15°，∴∠ECA＝12∴x＝7.5．②若2﹣4中，当BE＝BC时，易知∠BEC＝∠BAC＝∠BCE＝30°，∴∠OBE＝∠OBC＝60°，∵OE＝OB，∴△OBE是等边三角形，∴∠BOE＝60°，∴∠AOB＝120°，∴∠ACE＝12∠ACB＝60°，∴x＝30，综上所述，当CP旋转7.5秒或30秒时，△BCE是等腰三角形；【点睛】本题考查几何变换综合题、创新题目、圆周角定理、等腰三角形的判定和性质等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考压轴题．7．如图，线段BC所在的直线是以AB为直径的圆的切线，点D为圆上一点，满足BD＝BC，且点C、D位于直径AB的两侧，连接CD交圆于点E. 点F是BD上一点，连接EF，分别交AB、BD于点G、H，且EF＝BD.(1)求证：EF∥BC；(2)若EH＝4，HF＝2，求BE的长.【答案】(1)见解析；(2) 233【解析】【分析】（1）根据EF＝BD可得EF＝BD，进而得到BE DF，根据“在同圆或等圆中，同弧或等弧所对的圆周角相等”即可得出角相等进而可证.（2）连接DF，根据切线的性质及垂径定理求出GF、GE的长，根据“在同圆或等圆中，同弧或等弧所对的圆周角相等”及平行线求出相等的角，利用锐角三角函数求出∠BHG，进而求出∠BDE的度数，确定BE所对的圆心角的度数，根据∠DFH＝90°确定DE为直径，代入弧长公式即可求解.【详解】(1)∵EF＝BD，∴EF＝BD∴BE DF∴∠D＝∠DEF又BD＝BC，∴∠D＝∠C，∴∠DEF=∠CEF∥BC(2)∵AB是直径，BC为切线，∴AB⊥BC又EF∥BC，∴AB⊥EF，弧BF=弧BE,GF＝GE＝12(HF+EH)=3，HG=1DB平分∠EDF，又BF∥CD，∴∠FBD＝∠FDB＝∠BDE＝∠BFH ∴HB＝HF＝2∴cos∠BHG＝HGHB ＝12，∠BHG＝60°.∴∠FDB＝∠BDE＝30°∴∠DFH＝90°，DE为直径，DE＝3BE所对圆心角＝60°.∴弧BE＝163π＝233π【点睛】本题是圆的综合题，主要考查圆周角、切线、垂径定理、弧长公式等相关知识，掌握圆周角的有关定理，切线的性质，垂径定理及弧长公式是解题关键.8．如图，已知△ABC，23BC=，∠B=45°，点D在边BC上，联结AD，以点A 为圆心，AD为半径画圆，与边AC交于点E，点F在圆A上，且AF⊥AD．（1）设BD为x，点D、F之间的距离为y，求y关于x的函数解析式，并写出定义域；（2）如果E是DF的中点，求:BD CD的值；（3）联结CF，如果四边形ADCF是梯形，求BD的长．【答案】(1) 2442y x x (0≤x≤3); (2) 45; (3) BD 的长是1或1+5. 【解析】【分析】 （1）过点A 作AH ⊥BC ，垂足为点H ．构造直角三角形，利用解直角三角形和勾股定理求得AD 的长度．联结DF ，点D 、F 之间的距离y 即为DF 的长度，在Rt △ADF 中，利用锐角三角形函数的定义求得DF 的长度，易得函数关系式．（2）由勾股定理求得：AC=22AH DH +．设DF 与AE 相交于点Q ，通过解Rt △DCQ 和Rt △AHC 推知12DQ CQ =．故设DQ=k ，CQ=2k ，AQ=DQ=k ，所以再次利用勾股定理推知DC 的长度，结合图形求得线段BD 的长度，易得答案．（3）如果四边形ADCF 是梯形，则需要分类讨论：①当AF ∥DC 、②当AD ∥FC ．根据相似三角形的判定与性质，结合图形解答．【详解】（1）过点A 作AH ⊥BC ，垂足为点H ．∵∠B =45°，AB 2∴·cos 1BH AH AB B ===．∵BD 为x ，∴1DH x =-．在Rt △ADH 中，90AHD ∠=︒，∴22222AD AH DH x x =+=-+． 联结DF ，点D 、F 之间的距离y 即为DF 的长度．∵点F 在圆A 上，且AF ⊥AD ，∴AD AF =，45ADF ∠=︒．在Rt △ADF 中，90DAF ∠=︒，∴2442cos AD DF x x ADF==-+∠ ∴2442y x x =-+．()03x ≤≤ ;（2）∵E 是DF 的中点，∴AE DF ⊥，AE 平分DF ．∵BC=3，∴312HC =-=．∴225AC AH HC =+=． 设DF 与AE 相交于点Q ，在Rt △DCQ 中，90DQC ∠=︒，tan DQ DCQ CQ ∠=． 在Rt △AHC 中，90AHC ∠=︒，1tan 2AH ACH HC ∠==． ∵DCQ ACH ∠=∠，∴12DQ CQ =． 设,2DQ k CQ k ==，AQ DQ k ==，∵35k =，5k =，∴2253DC DQ CQ =+=． ∵43BD BC DC =-=，∴4:5BD CD =． （3）如果四边形ADCF 是梯形 则①当AF ∥DC 时，45AFD FDC ∠=∠=︒．∵45ADF ∠=︒，∴AD BC ⊥，即点D 与点H 重合． ∴1BD =．②当AD ∥FC 时，45ADF CFD ∠=∠=︒．∵45B ∠=︒，∴B CFD ∠=∠．∵B BAD ADF FDC ∠+∠=∠+∠，∴BAD FDC ∠=∠．∴ABD ∆∽DFC ∆．∴AB AD DF DC =． ∵2DF AD =，DC BC BD =-． ∴2AD BC BD =-．即()222-23x x x +=-,整理得 210x x --=，解得 15x ±=（负数舍去）． 综上所述，如果四边形ADCF 是梯形，BD 的长是1或1+52． 【点睛】此题属于圆的综合题，涉及了平行四边形的性质、相似三角形的判定与性质、三角函数值以及勾股定理等知识，综合性较强，解答本题需要我们熟练各部分的内容，对学生的综合能力要求较高，一定要注意将所学知识贯穿起来．9．如图，是大半圆的直径，是小半圆的直径，点是大半圆上一点，与小半圆交于点，过点作于点. （1）求证：是小半圆的切线； （2）若，点在上运动（点不与两点重合），设，. ①求与之间的函数关系式，并写出自变量的取值范围； ②当时，求两点之间的距离.【答案】（1）见解析；（2）①，，②两点之间的距离为或.【解析】【分析】（1）连接CO、CM，只需证到CD⊥CM．由于CD⊥OP，只需证到CM∥OP，只需证到CM 是△AOP的中位线即可．（2）①易证△ODC∽△CDP，从而得到CD2=DP•OD，进而得到y与x之间的函数关系式．由于当点P与点A重合时x=0，当点P与点B重合时x=4，点P在大半圆O上运动（点P不与A，B两点重合），因此自变量x的取值范围为0＜x＜4．②当y=3时，得到-x2+4x=3，求出x．根据x的值可求出CD、PD的值，从而求出∠CPD，运用勾股定理等知识就可求出P，M两点之间的距离．【详解】（1）连接，如图1所示∵是小半圆的直径，∴即∵∴∵∴∴，∵∴，∴∴.，即∵经过半径的外端，且∴直线是小半圆的切线.（2）①∵，，∴∴∴∽∴∴∵,,，∴当点与点重合时，；当点与点重合时，∵点在大半圆上运动（点不与两点重合），∴∴与之间的函数关系式为，自变量的取值范围是.②当时，解得,Ⅰ当时，如图2所示在中，∵，∴，∴∵，∴是等边三角形∵∴∴.Ⅱ当时，如图3所示，同理可得∵∴∴过点作，垂足为，连接，如图3所示∵，∴同理在中，∵，∴综上所述，当时，两点之间的距离为或.【点睛】考查了切线的判定、平行线的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质、特殊角的三角函数值、勾股定理等知识，综合性比较强．10．如图，AN是⊙M的直径，NB∥x轴，AB交⊙M于点C．（1）若点A（0，6），N（0，2），∠ABN=30°，求点B的坐标；（2）若D为线段NB的中点，求证：直线CD是⊙M的切线．【答案】(1) B（，2）．(2)证明见解析.【解析】试题分析：（1）在Rt△ABN中，求出AN、AB即可解决问题；（2）连接MC，NC．只要证明∠MCD=90°即可试题解析：（1）∵A的坐标为（0，6），N（0，2），∴AN=4，∵∠ABN=30°，∠ANB=90°，∴AB=2AN=8，∴由勾股定理可知：NB=，∴B（，2）．（2）连接MC，NC∵AN是⊙M的直径，∴∠ACN=90°，∴∠NCB=90°，在Rt△NCB中，D为NB的中点，∴CD=NB=ND，∴∠CND=∠NCD，∵MC=MN，∴∠MCN=∠MNC，∵∠MNC+∠CND=90°，∴∠MCN+∠NCD=90°，即MC⊥CD．∴直线CD是⊙M的切线．考点：切线的判定；坐标与图形性质．。

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，在△ABC中，AB＝AC，以AB为直径作⊙O，⊙O交BC于点D，交CA的延长线于点E．过点D作DF⊥AC，垂足为F．（1）求证：DF为⊙O的切线；（2）若AB＝4，∠C＝30°，求劣弧BE的长．【答案】（1）证明见解析（2）4 3【解析】分析：（1）连接AD、OD，根据直径所对的圆周角为直角，可得∠ADB=90°，然后根据等腰三角形的性质求出BD=CD，再根据中位线的性质求出OD⊥DF，进而根据切线的判定证明即可；（2）连接OE，根据三角形的外角求出∠BAE的度数，然后根据圆周角定理求出∠BOE的度数，根据弧长公式求解即可.详解：（1）连接AD、OD．∵AB是直径，∴∠ADB＝90°．∵AB＝AC，∴BD＝CD，又∵OA＝OB，∴OD是△ABC的中位线，∴OD∥AC，∵DF⊥AC，∴OD⊥DF即∠ODF＝90°．∴DF为⊙O的切线；（2）连接OE．∵AB＝AC，∴∠B＝∠C＝30°，∴∠BAE＝60°，∵∠BOE＝2∠BAE，∴∠BOE＝120°，∴＝·4π＝π．点睛：本题是圆的综合题，考查了等腰三角形的性质和判定、切线的性质和判定、三角形的中位线、圆周角定理，灵活添加辅助线是解题关键．2．如图,四边形ABCD是⊙O的内接四边形,AB=CD．(1)如图(1),求证:AD∥BC；(2)如图(2),点F是AC的中点,弦DG∥AB,交BC于点E,交AC于点M,求证:AE=2DF；(3)在(2)的条件下,若DG平分∠ADC,GE=53,tan∠ADF=43,求⊙O的半径。

【答案】(1)证明见解析；（2）证明见解析；（3）129【解析】试题分析：(1)连接AC．由弦相等得到弧相等，进一步得到圆周角相等，即可得出结论．（2）延长AD到N，使DN=AD，连接NC．得到四边形ABED是平行四边形，从而有AD=BE，DN=BE．由圆内接四边形的性质得到∠NDC=∠B．即可证明ΔABE≌ΔCND，得到AE=CN，再由三角形中位线的性质即可得出结论．（3）连接BG，过点A作AH⊥BC，由（2）知∠AEB=∠ANC，四边形ABED是平行四边形，得到AB=DE．再证明ΔCDE是等边三角形，ΔBGE是等边三角形，通过解三角形ABE，得到AB，HB，AH，HE的长，由EC=DE=AB，得到HC的长．在Rt△AHC中，由勾股定理求出AC的长．作直径AP，连接CP，通过解△APC即可得出结论．试题解析：解：(1)连接AC．∵AB=CD，∴弧AB=弧CD，∴∠DAC=∠ACB，∴AD∥BC．（2）延长AD到N，使DN=AD，连接NC．∵AD∥BC，DG∥AB，∴四边形ABED是平行四边形，∴AD=BE，∴DN=BE．∵ABCD是圆内接四边形，∴∠NDC=∠B．∵AB=CD，∴ΔABE≌ΔCND，∴AE=CN．∵DN=AD，AF=FC，∴DF=1CN，∴AE=2DF．2（3）连接BG，过点A作AH⊥BC，由（2）知∠AEB=∠ANC，四边形ABED是平行四边形，∴AB=DE．∵DF∥CN，∴∠ADF=∠ANC，∴∠AEB=∠ADF，∴tan∠AEB= tan∠ADF=43，DG平分∠ADC，∴∠ADG=∠CDG．∵AD∥BC，∴∠ADG=∠CED，∠NDC=∠DCE．∵∠ABC=∠NDC，∴∠ABC=∠DCE．∵AB∥DG，∴∠ABC=∠DEC，∴∠DEC=∠ECD=∠EDC，∴ΔCDE是等边三角形，∴AB=DE=CE．∵∠GBC=∠GDC=60°，∠G=∠DCB=60°，∴ΔBGE是等边三角形，BE= GE=53．∵tan∠AEB= tan∠ADF=43，设HE=x，则AH=43x．∵∠ABE=∠DEC=60°，∴∠BAH=30°，∴BH=4x，AB=8x，∴4x+x=53，解得：x=3，∴AB=83，HB=43，AH=12，EC=DE=AB=83，∴HC=HE+EC=383+=93．在Rt△AHC中，AC=222212(93)AH HC+=+=343．作直径AP，连接CP，∴∠ACP=90°，∠P=∠ABC=60°，∴sin∠P=AC AP，∴3432129sin6032ACAP===︒，∴⊙O的半径是129．3．某居民小区的一处圆柱形的输水管道破裂，维修人员为更换管道，需要确定管道圆形截面的半径．如图，若这个输水管道有水部分的水面宽AB=16cm，水最深的地方的高度为4cm，求这个圆形截面的半径．【答案】10cm【解析】分析：先过圆心O作半径CO⊥AB，交AB于点D设半径为r，得出AD、OD的长，在Rt△AOD中，根据勾股定理求出这个圆形截面的半径．详解：解：过点O作OC⊥AB于D，交⊙O于C，连接OB，∵OC⊥AB∴BD=12AB=12×16=8cm由题意可知，CD=4cm∴设半径为xcm，则OD=（x﹣4）cm在Rt△BOD中，由勾股定理得：OD2+BD2=OB2（x﹣4）2+82=x2解得：x=10．答：这个圆形截面的半径为10cm．点睛：此题考查了垂经定理和勾股定理，关键是根据题意画出图形，再根据勾股定理进行求解．4．如图，AB是圆O的直径，射线AM⊥AB，点D在AM上，连接OD交圆O于点E，过点D作DC=DA交圆O于点C（A、C不重合），连接O C、BC、CE．（1）求证：CD是⊙O的切线；（2）若圆O的直径等于2，填空：①当AD=时，四边形OADC是正方形；②当AD=时，四边形OECB是菱形．【答案】(1)见解析；（2）①1；②3．【解析】试题分析：（1）依据SSS证明△OAD≌△OCD，从而得到∠OCD=∠OAD=90°；（2）①依据正方形的四条边都相等可知AD=OA；②依据菱形的性质得到OE=CE，则△EOC为等边三角形，则∠CEO=60°，依据平行线的性质可知∠DOA=60°，利用特殊锐角三角函数可求得AD的长．试题解析：解：∵AM⊥AB，∴∠OAD=90°．∵OA=OC，OD=OD，AD=DC，∴△OAD≌△OCD，∴∠OCD=∠OAD=90°．∴OC⊥CD，∴CD是⊙O的切线．（2）①∵当四边形OADC是正方形，∴AO=AD=1．故答案为：1．②∵四边形OECB是菱形，∴OE=CE．又∵OC=OE，∴OC=OE=CE．∴∠CEO=60°．∵CE∥AB，∴∠AOD=60°．在Rt△OAD中，∠AOD=60°，AO=1，∴AD=．故答案为：．点睛：本题主要考查的是切线的性质和判定、全等三角形的性质和判定、菱形的性质、等边三角形的性质和判定，特殊锐角三角函数值的应用，熟练掌握相关知识是解题的关键．5．如图，AD是△ABC的角平分线，以AD为弦的⊙O交AB、AC于E、F，已知EF∥BC．（1）求证：BC是⊙O的切线；（2）若已知AE=9，CF=4，求DE长；（3）在（2）的条件下，若∠BAC=60°，求tan∠AFE的值及GD长．【答案】（1）证明见解析（2）DE=6（318367【解析】试题分析：（1）连接OD ，由角平分线的定义得到∠1=∠2，得到DE DF =，根据垂径定理得到OD ⊥EF ，根据平行线的性质得到OD ⊥BC ，于是得到结论；（2）连接DE ，由DE DF =，得到DE=DF ，根据平行线的性质得到∠3=∠4，等量代换得到∠1=∠4，根据相似三角形的性质即可得到结论；（3）过F 作FH ⊥BC 于H ，由已知条件得到∠1=∠2=∠3=∠4=30°，解直角三角形得到FH=12DF=12×6=3，=，根据三角函数的定义得到tan ∠AFE=tan ∠C=HF CH =；根据相似三角形到现在即可得到结论． 试题解析：（1）连接OD ，∵AD 是△ABC 的角平分线，∴∠1=∠2，∴DE DF =，∴OD ⊥EF ，∵EF ∥BC ，∴OD ⊥BC ，∴BC 是⊙O 的切线；（2）连接DE ，∵DE DF =，∴DE=DF ，∵EF ∥BC ，∴∠3=∠4，∵∠1=∠3，∴∠1=∠4，∵∠DFC=∠AED ，∴△AED ∽△DFC ， ∴AE DE DF CF =，即94DE DE =， ∴DE 2=36，∴DE=6；（3）过F 作FH ⊥BC 于H ，∵∠BAC=60°，∴∠1=∠2=∠3=∠4=30°， ∴FH=12DF=162⨯=3，∴=，∵EF ∥BC ，∴∠C=∠AFE ，∴tan ∠AFE=tan ∠C=377HF CH =； ∵∠4=∠2．∠C=∠C ，∴△ADC ∽△DFC ，∴AD CD DF CF=， ∵∠5=∠5，∠3=∠2，∴△ADF ∽△FDG ，∴AD DF DF DG =， ∴CD DF CF DG =，即33764DG+=， ∴DG=183675-．点睛：本题考查了切线的判定、圆周角定理、相似三角形的判定与性质、解直角三角形、平行线的性质，正确作出辅助线是解题的关键.6．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点G ，点F 是CD 上一点，且满足若13CF DF =,连接AF 并延长交⊙O 于点E ，连接AD 、DE ，若CF=2，AF=3.（1）求证：△ADF ∽△AED ；（2）求FG 的长；（3）求tan ∠E 的值．【答案】(1)证明见解析5【解析】分析：（1）由AB是 O的直径，弦CD⊥AB，根据垂径定理可得：弧AD=弧AC，DG=CG，继而证得△ADF∽△AED；（2）由13CFFD= ,CF=2，可求得DF的长，继而求得CG=DG=4，则可求得FG=2；（3）由勾股定理可求得AG的长，即可求得tan∠ADF的值，继而求得tan∠E=5 4.本题解析：①∵AB是⊙O的直径，弦CD⊥AB，∴DG=CG，∴AD AC=，∠ADF=∠AED，∵∠FAD=∠DAE（公共角），∴△ADF∽△AED；②∵13CFFD=，CF=2，∴FD=6，∴CD=DF+CF=8，∴CG=DG=4，∴FG=CG-CF=2；③∵AF=3，FG=2，∴AG=225AF FG-=，点睛：本题考查了相似三角形的判定与性质、圆周角定理、垂径定理、勾股定理以及三角函数等知识点，考查内容较多，综合性较强，难度适中，注意掌握数形结合的思想.7．如图，已知：AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D，E 是AB延长线上一点，CE交⊙O于点F，连接OC、AC．（1）求证：AC平分∠DAO．（2）若∠DAO=105°，∠E=30°①求∠OCE的度数；②若⊙O的半径为22，求线段EF的长．【答案】（1）证明见解析；（2）①∠OCE=45°；②EF =23【解析】【试题分析】（1）根据直线与⊙O相切的性质，得OC⊥CD.又因为AD⊥CD，根据同一平面内，垂直于同一条直线的两条直线也平行，得：AD//OC. ∠DAC=∠OCA.又因为OC=OA，根据等边对等角，得∠OAC=∠OCA.等量代换得：∠DAC=∠OAC.根据角平分线的定义得：AC平分∠DAO.（2）①因为 AD//OC，∠DAO=105°，根据两直线平行，同位角相等得，∠EOC=∠DAO=105°，在OCE∆中，∠E=30°，利用内角和定理，得：∠OCE=45°.②作OG⊥CE于点G，根据垂径定理可得FG=CG，因为OC=22，∠OCE=45°.等腰直角三角形的斜边是腰长的2倍，得CG=OG=2. FG=2.在Rt△OGE中，∠E=30°，得GE=23，则EF=GE-FG=23-2.【试题解析】（1）∵直线与⊙O相切，∴OC⊥CD.又∵AD⊥CD，∴AD//OC.∴∠DAC=∠OCA.又∵OC=OA，∴∠OAC=∠OCA.∴∠DAC=∠OAC.∴AC平分∠DAO.（2）解：①∵AD//OC，∠DAO=105°，∴∠EOC=∠DAO=105°∵∠E=30°，∴∠OCE=45°.②作OG⊥CE于点G，可得FG=CG∵OC=22，∠OCE=45°.∴CG=OG=2.∴FG=2.∵在Rt△OGE中，∠E=30°，∴GE=23.∴EF=GE-FG=23-2.【方法点睛】本题目是一道圆的综合题目，涉及到圆的切线的性质，平行线的性质及判定，三角形内角和，垂径定理，难度为中等.8．如图，AB为⊙O的直径，且AB＝m（m为常数），点C为AB的中点，点D为圆上一动点，过A点作⊙O的切线交BD的延长线于点P，弦CD交AB于点E．（1）当DC⊥AB时，则DA DBDC+＝；（2）①当点D在AB上移动时，试探究线段DA，DB，DC之间的数量关系；并说明理由；②设CD长为t，求△ADB的面积S与t的函数关系式；（3）当9220PDAC=时，求DEOA的值．【答案】（12；（2）①DA+DB 2DC ，②S ＝12t 2﹣14m 2 ；（3）242DE OA =. 【解析】【分析】 （1）首先证明当DC ⊥AB 时，DC 也为圆的直径，且△ADB 为等腰直角三角形，即可求出结果；（2）①分别过点A ，B 作CD 的垂线，连接AC ，BC ，分别构造△ADM 和△BDN 两个等腰直角三形及△NBC 和△MCA 两个全等的三角形，容易证出线段DA ，DB ，DC 之间的数量关系；②通过完全平方公式（DA+DB ）2＝DA 2+DB 2+2DA•DB 的变形及将已知条件AB ＝m 代入即可求出结果；（3）通过设特殊值法，设出PD 的长度，再通过相似及面积法求出相关线段的长度，即可求出结果．【详解】解：（1）如图1，∵AB 为⊙O 的直径，∴∠ADB ＝90°，∵C 为AB 的中点，∴AC BC =，∴∠ADC ＝∠BDC ＝45°，∵DC ⊥AB ，∴∠DEA ＝∠DEB ＝90°，∴∠DAE ＝∠DBE ＝45°，∴AE ＝BE ，∴点E 与点O 重合，∴DC 为⊙O 的直径，∴DC ＝AB ，在等腰直角三角形DAB 中，DA ＝DB 2AB ， ∴DA+DB 2AB 2CD ， ∴DA DB DC +2；（2）①如图2，过点A 作AM ⊥DC 于M ，过点B 作BN ⊥CD 于N ，连接AC ，BC ， 由（1）知AC BC =，∴AC ＝BC ，∵AB 为⊙O 的直径，∴∠ACB ＝∠BNC ＝∠CMA ＝90°，∴∠NBC+∠BCN ＝90°，∠BCN+∠MCA ＝90°，∴∠NBC ＝∠MCA ，在△NBC 和△MCA 中，BNC CMA NBC MCA BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△NBC ≌△MCA （AAS ），∴CN ＝AM ，由（1）知∠DAE ＝∠DBE ＝45°，AM ＝22DA ，DN＝22DB ， ∴DC ＝DN+NC ＝2DB+2DA ＝2（DB+DA ）， 即DA+DB ＝2DC ；②在Rt △DAB 中，DA 2+DB 2＝AB 2＝m 2，∵（DA+DB ）2＝DA 2+DB 2+2DA•DB ，且由①知DA+DB 2DC 2t ，∴2t ）2＝m 2+2DA•DB ，∴DA•DB ＝t 2﹣12m 2，∴S △ADB ＝12DA•DB ＝12t 2﹣14m 2， ∴△ADB 的面积S 与t 的函数关系式S ＝12t 2﹣14m 2； （3）如图3，过点E 作EH ⊥AD 于H ，EG ⊥DB 于G ，则NE ＝ME ，四边形DHEG 为正方形， 由（1）知AC BC =，∴AC ＝BC ，∴△ACB 为等腰直角三角形，∴ABAC ，∵20PD AC =，设PD ＝，则AC ＝20，AB ＝，∵∠DBA ＝∠DBA ，∠PAB ＝∠ADB ，∴△ABD ∽△PBA ， ∴AB BD AD PB AB PA ==，∴=， ∴DB ＝， ∴AD＝， 设NE ＝ME ＝x ，∵S △ABD ＝12AD•BD ＝12AD•NE+12BD•ME ， ∴12＝12•x+12•x ，∴x ＝7， ∴DEHE x ＝967，又∵AO ＝12AB ＝，∴96735DE OA ==．【点睛】本题考查了圆的相关性质，等腰直三角形的性质，相似的性质等，还考查了面积法及特殊值法的运用，解题的关键是认清图形，抽象出各几何图形的特殊位置关系．9．在平面直角坐标系xOy中，对于点P和图形W，如果以P为端点的任意一条射线与图形W最多只有一个公共点，那么称点P独立于图形W．（1）如图1，已知点A（-2，0），以原点O为圆心，OA长为半径画弧交x轴正半轴于点 B．在P1（0，4），P2（0，1），P3（0，-3），P4（4，0）这四个点中，独立于AB的点是；（2）如图2，已知点C（-3，0），D（0，3），E（3，0），点P是直线l：y=2x+8上的一个动点．若点P独立于折线CD-DE，求点P的横坐标x p的取值范围；（3）如图3，⊙H是以点H（0，4）为圆心，半径为1的圆．点T（0，t）在y轴上且t＞-3，以点T为中心的正方形KLMN的顶点K的坐标为（0，t+3），将正方形KLMN在x轴及x轴上方的部分记为图形W．若⊙H上的所有点都独立于图形W，直接写出t的取值范围．【答案】（1）P2，P3；（2）x P＜-5或x P＞-53．（3）-3＜t＜2或2＜t＜2【解析】【分析】（1）根据点P独立于图形W的定义即可判断；（2）求出直线DE，直线CD与直线y=2x+8的交点坐标即可判断；（3）求出三种特殊位置时t的值，结合图象即可解决问题.【详解】（1）由题意可知：在P1（0，4），P2（0，1），P3（0，-3），P4（4，0）这四个点中，独立于AB的点是P2，P3．（2）∵C（-3，0），D（0，3），E（3，0），∴直线CD的解析式为y=x+3，直线DE的解析式为y=-x+3，由283y xy x+⎧⎨+⎩＝＝，解得52xy-⎧⎨-⎩＝＝，可得直线l与直线CD的交点的横坐标为-5，由283y xy x+⎧⎨-+⎩＝＝，解得53143xy⎧-⎪⎪⎨⎪⎪⎩＝＝，可得直线l与直线DE的交点的横坐标为-53，∴满足条件的点P的横坐标x p的取值范围为：x P＜-5或x P＞-53．（3）如图3-1中，当直线KN与⊙H相切于点E时，连接EH，则EH=EK=1，HK=2，∴22-1，∴T（0，22∴当-3＜t＜2时，⊙H上的所有点都独立于图形W．如图3-2中，当线段KN与⊙H相切于点E时，连接EH．OT=OH+KH-KT=4+2-3=1+2，∴T（0，1+2），此时t=1+2，如图3-3中，当线段MN与⊙H相切于点E时，连接EH．22∴T（0，22∴当2＜t＜2时，⊙H上的所有点都独立于图形W．综上所述，满足条件的t的值为-3＜t＜2或2＜t＜2【点睛】本题属于圆综合题，考查了切线的性质，一次函数的应用，点P独立于图形W的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题，学会利用特殊位置解决实际问题.10．如图，已知等边△ABC，AB=16，以AB为直径的半圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连结GD．（1）求证：DF是⊙O的切线；（2）求FG的长；（3）求tan∠FGD的值．【答案】(1)证明见解析；（2）6；（3）．【解析】试题分析：(1)连接OD，根据等边三角形得出∠A=∠B=∠C=60°，根据OD=OB得到∠ODB=60°，得到OD∥AC，根据垂直得出切线；(2)根据中位线得出BD=CD=6，根据Rt△CDF的三角函数得出CF的长度，从而得到AF的长度，最后根据Rt△AFG的三角函数求出FG的长度；(3)过点D作DH⊥AB，根据垂直得出FG∥DH，根据Rt△BDH求出BH、DH的长度，然后得出∠GDH的正切值，从而得到∠FGD的正切值.试题解析：(1)如图①，连结OD，∵△ABC为等边三角形，∴∠C＝∠A＝∠B＝60°，而OD＝OB，∴△ODB是等边三角形，∠ODB＝60°，∴∠ODB＝∠C，∴OD∥AC，∵DF⊥AC，∴OD⊥DF，∴DF是⊙O的切线(2)∵OD∥AC，点O为AB的中点，∴OD为△ABC的中位线，∴BD＝CD＝6.在Rt△CDF中，∠C＝60°，∴∠CDF＝30°，∴CF＝CD＝3，∴AF＝AC－CF＝12－3＝9 在Rt△AFG中，∵∠A＝60°，∴FG＝AF·sinA＝9×＝(3)如图②，过D作DH⊥AB于H.∵FG⊥AB，DH⊥AB，∴FG∥DH，∴∠FGD＝∠GDH.在Rt△BDH中，∠B＝60°，∴∠BDH＝30°，∴BH＝BD＝3，DH＝BH＝3.∴tan∠GDH＝＝＝，∴tan∠FGD＝tan∠GDH＝考点：(1)圆的基本性质；(2)三角函数.。