MATLAB分支定界法求解例题

完整word版,分支定界法的Matlab实现

一个调用例子：ifint=[0 1];f=[10 9];a=[1 0;0 1;-5 -3];b=[8 10 -45];[x,fval,exitflag] = linprogdis(ifint,f,a,b,[],[],[],[],[],[])function r=checkint(x)%算法：如果x(i)是整数，则返回r(i)=1；否则返回r(i)=0function r=ifrowinmat(arow,amat)%输入参数：% arow 向量，% amat 矩阵%%设计：如果 arow与矩阵amat中的某一行相等，则返回1，如果找不到现等的一行，则返回0可以使用ismember(arrow,amat,’rows’)替换ifrowinmat的调用，2005-10-28标注使用时，将下面的代码存入文件：linprogdis.mfunction [x,fval,exitflag,output,lambda]=... linprogdis(ifint,f,A,b,Aeq,beq,lb,ub,x0,options)%Title:% 分支定届法求解混合整数线性规划模型%%初步完成：2002年12月%最新修订: 2004-03-06%最新注释：2004-11-20%数据处理[t1,t2] = size(b);if t2~=1,b=b';%将b转置为列向量end%调用线性规划求解[x,fval,exitflag,output,lambda] =linprog(f,A,b,Aeq,beq,lb,ub,x0,options);if exitflag<=0,%如果线性规划失败，则本求解也失败returnend%得到有整数约束的决策变量的序号v1=find(ifint==1);%整数变量的indextmp=x(v1);%【整数约束之决策变量】的当前值if isempty(tmp),%无整数约束，则是一般的线性规划，直接返回即可returnendv2=find(checkint(tmp)==0);%寻找不是整数的index if isempty(v2),%如果整数约束决策变量确实均为整数，则调用结束returnend%第k个决策变量还不是整数解%注意先处理第1个不满足整数约束的决策变量k=v1(v2(1));%分支1：左分支tmp1=zeros(1,length(f));%线性约束之系数向量tmp1(k)=1;low=floor(x(k));%thisA 分支后实际调用线性规划的不等式约束的系数矩阵A%thisb 分支后实际调用线性规划的不等式约束向量b if ifrowinmat([tmp1,low],[A,b])==1%如果分支的约束已经存在旧的A，b中，则不改变约束thisA= A;thisb= b;elsethisA=[A;tmp1];thisb=b;thisb(end+1)=low;end%disp('fenzhi1'),thisA,thisb%递归调用[x1,fval1,exitflag1,output1,lambda1]= ...linprogdis(ifint,f,thisA,thisb,Aeq,beq,lb,ub,x0,o ptions);%分支2：右分支tmp2=zeros(1,length(f));%tmp1;tmp2(k)=-1;high= - ceil(x(k));if ifrowinmat([tmp2,high],[A,b])==1thisA= A;thisb= b;elsethisA=[A;tmp2];thisb=b;thisb(end+1)=high;end%disp('fenzhi2'),thisA,thisb[x2,fval2,exitflag2,output2,lambda2]= ...linprogdis(ifint,f,thisA,thisb,Aeq,beq,lb,ub,x0,o ptions);if isempty(v2) & ((exitflag1>0 & exitflag2<=0 & fval<=fval1 ) ...| (exitflag2>0 & exitflag1<=0 &fval<=fval2 )...| (exitflag1>0 & exitflag2>0 &fval<=fval1 & fval<=fval2 )),disp('error call')return %isempty(v2) 表示都是整数 2002-12-7非常重要end%下面分别根据返回标志exitflag确定最终的最优解%case 1if exitflag1>0 & exitflag2<=0 %【左分支有】最优解，右分支无最优解x = x1;fval = fval1;exitflag = exitflag1;output = output1;lambda = lambda1;%case 2elseif exitflag2>0 & exitflag1<=0 %【右分支有】最优解，左分支无最优解x = x2;fval = fval2;exitflag = exitflag2;output = output2;lambda = lambda2;%case 3elseif exitflag1>0 & exitflag2>0 %【左、右分支均有】最优解，则比较选优if fval1<fval2,%【左】分支最优（min）x = x1;fval = fval1;exitflag = exitflag1;output = output1;lambda = lambda1;else x = x2;,%【右】分支最优（min）fval = fval2;exitflag = exitflag2;output = output2;lambda = lambda2;end%fval1<fval2endfunction r=checkint(x)%算法：如果x(i)是整数，则返回r(i)=1；否则返回r(i)=0%输入参数：x 向量%输出参数：r 向量for i=1:length(x),ifmin(abs(x(i)-floor(x(i))),abs(x(i)-ceil(x(i))))<1 e-03%这里用于判定是否为0的参数可以调整，如改为1e-6r(i)=1;elser(i)=0;endendfunction r=ifrowinmat(arow,amat)%输入参数：% arow 向量，% amat 矩阵%%设计：如果 arow与矩阵amat中的某一行相等，则返回1，如果找不到现等的一行，则返回0r = 0;rows = size(amat,1);for i=1:rows,temp = (amat(i,:)==arow);%利用 Matlab的==操作，如果相等，则为1向量；if length(find(temp==0))==0,%没有为0的，即temp元素全部是1r=1;return end%end %for。

python分支定界算法解决问题范例

Python分支定界算法解决问题范例一、概述分支定界算法是一种用于解决组合优化问题的算法。

它通过不断地分解问题和减少搜索空间来找到最优解。

Python是一种广泛应用的编程语言，其简洁、灵活的特性使其成为实现分支定界算法的理想工具。

本文将以一个例子来展示如何使用Python实现分支定界算法解决问题，以帮助读者更好地理解和运用这一算法。

二、问题描述假设有一个物品清单，每个物品有其对应的价值和重量。

同时有一个背包，其最大承重为W。

现需要将物品放入背包，使得背包中的物品总价值最大，但总重量不能超过背包的承重。

如何选择物品并放置到背包中才能使得总价值最大化呢？三、分支定界算法解决方案1. 定义问题我们需要明确问题的定义和目标。

通过对问题进行数学建模，可以将其表示为一个0-1背包问题。

具体而言，我们可以定义以下几个参数：- n：物品的数量- weight[i]：第i个物品的重量- value[i]：第i个物品的价值- W：背包的最大承重通过以上定义，我们可以将问题表述为，在给定n个物品、其对应的重量和价值以及背包的最大承重情况下，如何选择物品并放置到背包中，使得背包中的物品总价值最大，但总重量不能超过背包的承重。

2. 分支定界算法实现接下来，我们将使用Python实现分支定界算法来解决上述问题。

具体步骤如下：我们定义一个Node类来表示搜索树的节点，其中包括以下几个属性：level、value、weight、bound和include。

- level表示当前节点所处的层级；- value表示当前节点已获得的总价值；- weight表示当前节点已获得的总重量；- bound表示当前节点的价值上界；- include表示一个列表，记录了每个物品是否被选择放入背包中。

```pythonclass Node:def __init__(self, level, value, weight, bound, include):self.level = levelself.value = valueself.weight = weightself.bound = boundself.include = include```我们定义一个bound函数来计算当前节点的价值上界。

分支定界法的Matlab实现

一个调用例子：ifint=[0 1];f=[10 9];a=[1 0;0 1;-5 -3];b=[8 10 -45];[x,fval,exitflag] = linprogdis(ifint,f,a,b,[],[],[],[],[],[])function r=checkint(x)%算法：如果x(i)是整数，则返回r(i)=1；否则返回r(i)=0function r=ifrowinmat(arow,amat)%输入参数：% arow 向量，% amat 矩阵%%设计：如果 arow与矩阵amat中的某一行相等，则返回1，如果找不到现等的一行，则返回0可以使用ismember(arrow,amat,’rows’)替换ifrowinmat的调用，2005-10-28标注使用时，将下面的代码存入文件：linprogdis.mfunction [x,fval,exitflag,output,lambda]=... linprogdis(ifint,f,A,b,Aeq,beq,lb,ub,x0,options)%Title:% 分支定届法求解混合整数线性规划模型%%初步完成：2002年12月%最新修订: 2004-03-06%最新注释：2004-11-20%数据处理[t1,t2] = size(b);if t2~=1,b=b';%将b转置为列向量end%调用线性规划求解[x,fval,exitflag,output,lambda] =linprog(f,A,b,Aeq,beq,lb,ub,x0,options);if exitflag<=0,%如果线性规划失败，则本求解也失败returnend%得到有整数约束的决策变量的序号v1=find(ifint==1);%整数变量的indextmp=x(v1);%【整数约束之决策变量】的当前值if isempty(tmp),%无整数约束，则是一般的线性规划，直接返回即可returnendv2=find(checkint(tmp)==0);%寻找不是整数的index if isempty(v2),%如果整数约束决策变量确实均为整数，则调用结束returnend%第k个决策变量还不是整数解%注意先处理第1个不满足整数约束的决策变量k=v1(v2(1));%分支1：左分支tmp1=zeros(1,length(f));%线性约束之系数向量tmp1(k)=1;low=floor(x(k));%thisA 分支后实际调用线性规划的不等式约束的系数矩阵A%thisb 分支后实际调用线性规划的不等式约束向量b if ifrowinmat([tmp1,low],[A,b])==1%如果分支的约束已经存在旧的A，b中，则不改变约束thisA= A;thisb= b;elsethisA=[A;tmp1];thisb=b;thisb(end+1)=low;end%disp('fenzhi1'),thisA,thisb%递归调用[x1,fval1,exitflag1,output1,lambda1]= ...linprogdis(ifint,f,thisA,thisb,Aeq,beq,lb,ub,x0,o ptions);%分支2：右分支tmp2=zeros(1,length(f));%tmp1;tmp2(k)=-1;high= - ceil(x(k));if ifrowinmat([tmp2,high],[A,b])==1thisA= A;thisb= b;elsethisA=[A;tmp2];thisb=b;thisb(end+1)=high;end%disp('fenzhi2'),thisA,thisb[x2,fval2,exitflag2,output2,lambda2]= ...linprogdis(ifint,f,thisA,thisb,Aeq,beq,lb,ub,x0,o ptions);if isempty(v2) & ((exitflag1>0 & exitflag2<=0 & fval<=fval1 ) ...| (exitflag2>0 & exitflag1<=0 &fval<=fval2 )...| (exitflag1>0 & exitflag2>0 &fval<=fval1 & fval<=fval2 )),disp('error call')return %isempty(v2) 表示都是整数 2002-12-7非常重要end%下面分别根据返回标志exitflag确定最终的最优解%case 1if exitflag1>0 & exitflag2<=0 %【左分支有】最优解，右分支无最优解x = x1;fval = fval1;exitflag = exitflag1;output = output1;lambda = lambda1;%case 2elseif exitflag2>0 & exitflag1<=0 %【右分支有】最优解，左分支无最优解x = x2;fval = fval2;exitflag = exitflag2;output = output2;lambda = lambda2;%case 3elseif exitflag1>0 & exitflag2>0 %【左、右分支均有】最优解，则比较选优if fval1<fval2,%【左】分支最优（min）x = x1;fval = fval1;exitflag = exitflag1;output = output1;lambda = lambda1;else x = x2;,%【右】分支最优（min）fval = fval2;exitflag = exitflag2;output = output2;lambda = lambda2;end%fval1<fval2endfunction r=checkint(x)%算法：如果x(i)是整数，则返回r(i)=1；否则返回r(i)=0%输入参数：x 向量%输出参数：r 向量for i=1:length(x),ifmin(abs(x(i)-floor(x(i))),abs(x(i)-ceil(x(i))))<1 e-03%这里用于判定是否为0的参数可以调整，如改为1e-6r(i)=1;elser(i)=0;endendfunction r=ifrowinmat(arow,amat)%输入参数：% arow 向量，% amat 矩阵%%设计：如果 arow与矩阵amat中的某一行相等，则返回1，如果找不到现等的一行，则返回0r = 0;rows = size(amat,1);for i=1:rows,temp = (amat(i,:)==arow);%利用 Matlab的==操作，如果相等，则为1向量；if length(find(temp==0))==0,%没有为0的，即temp元素全部是1r=1;return end%end %for。

Matlab中的最优化问题求解方法

Matlab中的最优化问题求解方法近年来，最优化问题在各个领域中都扮演着重要的角色。

无论是在工程、经济学还是科学研究中，我们都需要找到最优解来满足特定的需求。

而Matlab作为一种强大的数值计算软件，在解决最优化问题方面有着广泛的应用。

本文将介绍一些Matlab中常用的最优化问题求解方法，并探讨其优缺点以及适用范围。

一. 无约束问题求解方法1. 最速下降法最速下降法是最简单且直观的无约束问题求解方法之一。

其基本思想是沿着梯度的反方向迭代求解，直到达到所需的精度要求。

然而，最速下降法的收敛速度通常很慢，特别是在局部极小值点附近。

2. 共轭梯度法共轭梯度法是一种改进的最速下降法。

它利用了无约束问题的二次函数特性，通过选择一组相互共轭的搜索方向来提高收敛速度。

相比于最速下降法，共轭梯度法的收敛速度更快，尤其适用于大规模优化问题。

3. 牛顿法牛顿法是一种基于二阶导数信息的优化方法。

它通过构建并求解特定的二次逼近模型来求解无约束问题。

然而，牛顿法在高维问题中的计算复杂度较高，并且需要矩阵求逆运算，可能导致数值不稳定。

二. 线性规划问题求解方法1. 单纯形法单纯形法是一种经典的线性规划问题求解方法。

它通过在可行域内进行边界移动来寻找最优解。

然而，当问题规模较大时，单纯形法的计算复杂度会大幅增加，导致求解效率低下。

2. 内点法内点法是一种改进的线性规划问题求解方法。

与单纯形法不同，内点法通过将问题转化为一系列等价的非线性问题来求解。

内点法的优势在于其计算复杂度相对较低，尤其适用于大规模线性规划问题。

三. 非线性规划问题求解方法1. 信赖域算法信赖域算法是一种常用的非线性规划问题求解方法。

它通过构建局部模型，并通过逐步调整信赖域半径来寻找最优解。

信赖域算法既考虑了收敛速度，又保持了数值稳定性。

2. 遗传算法遗传算法是一种基于自然进化过程的优化算法。

它模拟遗传操作，并通过选择、交叉和变异等操作来搜索最优解。

遗传算法的优势在于其适用于复杂的非线性规划问题，但可能需要较长的计算时间。

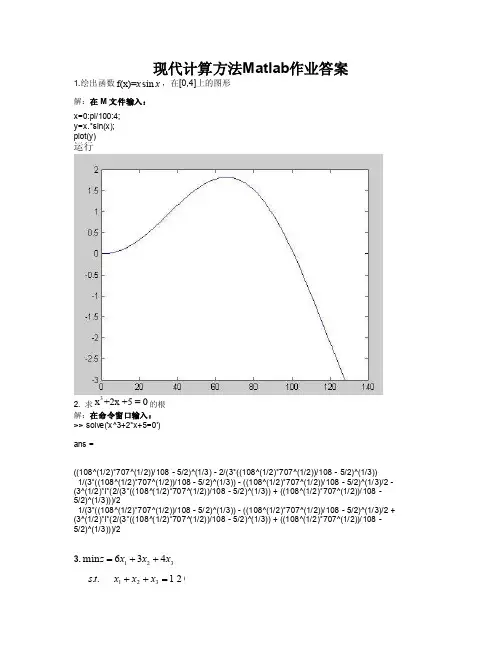
Matlab习题及答案

现代计算方法Matlab 作业答案1.绘出函数f(x)=sin x x ，在[0,4]上的图形解：在M 文件输入：x=0:pi/100:4;y=x.*sin(x);plot(y)运行2. 求3x +2x +5 = 0的根解：在命令窗口输入：>> solve('x^3+2*x+5=0')ans =((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3) - 2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3))1/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 -(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/21/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 +(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/23.321436min x x x z ++=120..321=++x x x t s301≥x5002≤≤x203≥x解：运用单纯形法计算此题，首先把约束条件化成标准形式：,,,,,205030120654321635241321≥=-=+=-=++x x x x x x x x x x x x x x x（1）在M 文件输入SimpleMthd 函数：function [x,minf] = SimpleMthd(A,c,b,baseVector)sz = size(A);nVia = sz(2);n = sz(1);xx = 1:nVia;nobase = zeros(1,1);m = 1;for i=1:nViaif (isempty(find(baseVector == xx(i),1)))nobase(m) = i;m = m + 1;else;endendbCon = 1;M = 0;while bConnB = A(:,nobase);ncb = c(nobase);B = A(:,baseVector);cb = c(baseVector);xb = inv(B)*b;f = cb*xb;w = cb*inv(B);for i=1:length(nobase)sigma(i) = w*nB(:,i)-ncb(i);end[maxs,ind] = max(sigma);if maxs <= 0minf = cb*xb;vr = find(c~=0 ,1,'last');for l=1:vrele = find(baseVector == l,1);if (isempty(ele))x(l) = 0;elsex(l)=xb(ele);endendbCon = 0;elsey = inv(B)*A(:,nobase(ind));if y <= 0disp('不存在最优解!');x = NaN;minf = NaN;return;elseminb = inf;chagB = 0;for j=1:length(y)if y(j)>0bz = xb(j)/y(j);if bz<minbminb = bz;chagB = j;endendendtmp = baseVector(chagB);baseVector(chagB) = nobase(ind);nobase(ind) = tmp;endendM = M + 1;if (M == 1000000)disp('找不到最优解!');x = NaN;minf = NaN;return;endend（2）在命令窗口输入：clear allA=[1 1 1 0 0 0;1 0 0 -1 0 0;0 1 0 0 1 0;0 0 1 0 0 -1];c=[6 3 4 0 0 0];b=[120;30;50;20];[xm,mf]=SimpleMthd(A,c,b,[3 4 5 6])xm =0 50 70mf =4304.计算下面函数在区间(0，1)内的最小值。

Matlab求解边值问题方法+例题

y1 y , y2 y1
原方程组等价于以下标准形式的方程组：
y y 1 2 y2 (1 x 2 ) y1 1
边界条件为：
y1 (0) 1 0 y1 (1) 3 0
边值问题的求解
求解：
c=1; solinit=bvpinit(linspace(0,4,10),[1 1]); sol=bvp4c(@ODEfun,@BCfun,solinit,[],c); x=[0:0.1:4]; y=deval(sol,x); plot(x,y(1,:),'b-',sol.x,sol.y(1,:),'ro') legend('解曲线','初始网格点解') % 定义ODEfun函数 function dydx=ODEfun(x,y,c) dydx=[y(2);-c*abs(y(1))]; % 定义BCfun函数 function bc=BCfun(ya,yb,c) bc=[ya(1);yb(1)+2];
z(0) 1, z (0) 0, z ( ) 0
本例中，微分方程与参数λ的数值有关。一般而言，对于任意的λ值，该问题无解，但对于特殊的λ值（特征值），它存在一个解，这也称为微分方程的特征值问题。对于此问题，可在bvpinit中提供参数的猜测值，然后重复求解BVP得到所需的参数，返回参数为sol.parameters
边值问题的求解
如果取1，计算结果如何?
infinity=6; solinit=bvpinit(linspace(0,infinity,5),[0 0 1]); options=bvpset('stats','on'); sol=bvp4c(@ODEfun,@BCfun,solinit,options); eta=sol.x; f=sol.y; fprintf('\n'); 2 求解： f ff (1 ( f ) ) 0 fprintf('Cebeci & Keller report f''''(0)=0.92768.\n') fprintf('Value computed here is f''''(0)=%7.5f.\n',f(3,1)) 0.5 clf reset plot(eta,f(2,:)); axis([0 infinity 0 1.4]); title... f (0) 0, f (0) 0, ('Falkner-Skan equation, positive wall shear,\beta=0.5.') 边界条件： f ( ) 1, xlabel('\eta'),ylabel('df/d\eta'),shg % 定义ODEfun函数 function dfdeta=ODEfun(eta,f) beta=0.5; dfdeta=[f(2);f(3);-f(1)*f(3)-beta*(1-f(2)^2)]; % 定义BCfun函数 function res=BCfun(f0,finf) res=[f0(1);f0(2);finf(2)-1];

分支定界算法优化一维下料问题

211 算法的基本思想
1 一维优化下料问题的具体模型分析
原材料长度为 L , 数量充足。需要切割成
n ( n ≥0 )种不同规格的零件 , 根据既省材料又容易
操作的原则 ,人们已经设计好了 n 种不同的下料方式。设第 j种下料方式中可下得第 i种零件 aij 个 , 又已知第 i种零件得需要量为 bi 个 , xj 表示第 B j 种下料方式所消耗得零件数目 , cj 表示第 B j 种下料方
x = 20 51 0 9 0 24 0 1。
3 实例
设某车间有一批长度为 180 cm 的钢管 ,为制造零件的需要将其裁成 3 种不同长度的零件 , 分别为
70, 52, 35 cm。这三种零件的需要量分别为 100, 150, 100 根。问如何下料才使得原材料的消耗
m in f =
n
∑c x
j j =1
j
if nargin < 10, op tions = op tim set( { } ) ; op tions . D isp lay = ’ off’ ; op tions . LargeScale = ’ off’ ; end
∑a
j =1
ij
xj = bi
最少 ? 分析 :对于一维下料问题都可以用组合最优化的方法给出合理的下料方式。设 x1 , x2 , x3 分别表示在已知钢管上下 3 种不同长度的零件数 ,则 70 x1 +
52 x2 + 35 x3 ≤ 180 ( xi ∈ Z , i = 1, 2, 3 ) 。其中 x1 ≤ 2 ,表 1给出下料方案。
xj > 0 xj < xj ∈ Z

MATLAB习题及参考答案经典.doc

习题：1，计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。

2，对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。

3，已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。

4，角度[]604530=x ，求x 的正弦、余弦、正切和余切。

(应用sin,cos,tan.cot)5，将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵：（1）组合成一个4⨯3的矩阵，第一列为按列顺序排列的a 矩阵元素，第二列为按列顺序排列的b 矩阵元素，第三列为按列顺序排列的c 矩阵元素，即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574（2）按照a 、b 、c 的列顺序组合成一个行矢量，即 []2965318772546，将(x -6)(x -3)(x -8)展开为系数多项式的形式。

(应用poly,polyvalm)7，求解多项式x 3-7x 2+2x +40的根。

(应用roots)8，求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。

(应用poly,polyvalm)9，计算多项式9514124234++--x x x x 的微分和积分。

(应用polyder,polyint ，poly2sym)10，解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。

(应用x=a\b)11，求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。

(应用pinv) 12，矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ，计算a 的行列式和逆矩阵。

(应用det,inv)13， y =sin(x )，x 从0到2π，∆x =0.02π，求y 的最大值、最小值、均值和标准差。

关于MATLAB整数规划分支定界法

关于MATLAB整数规划分支定界法一、编程利用Matlab的线性规划指令:[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub)编写计算整数规划函数，输入与输出与上述指令相同分枝定界法(递归实现)function [x,fval,status] = intprog(f,A,B,I,Aeq,Beq,lb,ub,e)%整数规划求解函数 intprog()% 其中 f为目标函数向量% A和B为不等式约束 Aeq与Beq为等式约束 % I为整数约束% lb与ub分别为变量下界与上界% x为最优解，fval为最优值%例子:% maximize 20 x1 + 10 x2 % S.T.% 5 x1 + 4 x2 <=24 % 2 x1 + 5 x2 <=13 % x1, x2 >=0 % x1, x2是整数 % f=[-20, -10];% A=[ 5 4; 2 5];% B=[24; 13];% lb=[0 0];% ub=[inf inf];% I=[1,2];% e=0.000001;% [x v s]= IP(f,A,B,I,[],[],lb,ub,,e) % x = 4 1 v = -90.0000 s = 1% 控制输入参数if nargin < 9, e = 0.00001;if nargin < 8, ub = [];if nargin < 7, lb = [];if nargin < 6, Beq = [];if nargin < 5, Aeq = [];if nargin < 4, I = [1:length(f)];end, end, end, end, end, end%求解整数规划对应的线性规划,判断是否有解 options = optimset('display','off'); [x0,fval0,exitflag] = linprog(f,A,B,Aeq,Beq,lb,ub,[],options);if exitflag < 0disp('没有合适整数解');x = x0;fval = fval0;status = exitflag;return;else%采用分支定界法求解bound = inf;[x,fval,status] =branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);end子函数function [newx,newfval,status,newbound] =branchbound(f,A,B,I,x,fval,bound,Aeq,Beq,lb,ub,e)% 分支定界法求解整数规划% f,A,B,Aeq,Beq,lb,ub与线性规划相同 % I为整数限制变量的向量% x为初始解，fval为初始值options = optimset('display','off');[x0,fval0,status0]=linprog(f,A,B,Aeq,Beq,lb,ub,[],options);%递归中的最终退出条件%无解或者解比现有上界大则返回原解 if status0 <= 0 || fval0 >= bound newx = x;newfval = fval;newbound = bound;status = status0;return;end%是否为整数解,如果是整数解则返回 intindex = find(abs(x0(I) -round(x0(I))) > e);if isempty(intindex)newx(I) = round(x0(I));newfval = fval0;newbound = fval0;status = 1;return;end%当有非整可行解时，则进行分支求解 %此时必定会有整数解或空解%找到第一个不满足整数要求的变量n = I(intindex(1));addA = zeros(1,length(f));addA(n) = 1;%构造第一个分支 x<=floor(x(n))A = [A;addA];B = [B,floor(x(n))];[x1,fval1,status1,bound1] =branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);A(end,:) = [];B(:,end) = [];%解得第一个分支，若为更优解则替换，若不是则保持原状status = status1;if status1 > 0 && bound1 < boundnewx = x1;newfval = fval1;bound = fval1;newbound = bound1;elsenewx = x0;newfval = fval0;newbound = bound;end%构造第二分支A = [A;-addA];B = [B,-ceil(x(n))];[x2,fval2,status2,bound2] =branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);A(end,:) = [];B(:,end) = [];%解得第二分支，并与第一分支做比较，如果更优则替换 if status2 > 0 && bound2 < boundstatus = status2;newx = x2;newfval = fval2;newbound = bound2;end二、求解利用上述指令求解下列问题:汽车厂生产三种类型的汽车，已知各类型每辆车对钢材、劳动时间的需求，利润及工厂每月的现有量小型中型大型现有量钢材(吨) 1 2 5 1000劳动时间(小时) 250 125 150 120000利润(万元) 3 5 121、若每月生产的汽车必须为整车，试制订月生产计划，使工厂的利润最大2、如果生产某一类型汽车，则至少要生产50辆，那么最优的生产计划应作何改变, 解:1f = [-3 -5 -12];A = [1 2 5;250 125 150];B = [1000 120000];I = [1:length(f)];lb = [0 0 0];[x,fval,status] = intprog(f,A,B,I,[],[],lb)答案为 x =307 344 1 fval = -2653 status =12lb = [50 50 50]答案为 x =350 200 50 fval =-2.6500e+003 status =1用分枝定界法求解整数线性规划问题%%问题的标准形式:%% min c'*x%% s.t. A*x<=b%% Aeq*x=beq%% 要求是整数%%function [y,fval]=BranchBound(c,A,b,Aeq,beq)%NL=length(c);UB=inf;LB=-inf;FN=[0];AA(1)={A};BB(1)={b};k=0;flag=0;while flag==0;[x,fval,exitFlag]=linprog(c,A,b,Aeq,beq); if (exitFlag == -2) | (fval >= UB)FN(1)=[];if isempty(FN)==1flag=1;elsek=FN(1);A=AA{k};b=BB{k};endelsefor i=1:NLif abs(x(i)-round(x(i)))>1e-7kk=FN(end);FN=[FN,kk+1,kk+2];temp_A=zeros(1,NL);temp_A(i)=1;temp_A1=[A;temp_A];AA(kk+1)={temp_A1};b1=[b;fix(x(i))];BB(kk+1)={b1};temp_A2=[A;-temp_A];AA(kk+2)={temp_A2};b2=[b;-(fix(x(i))+1)];BB(kk+2)={b2};FN(1)=[];k=FN(1);A=AA{k};b=BB{k};break;endendif (i==NL) & (abs(x(i)-round(x(i)))<=1e-7) UB=fval;y=x;FN(1)=[];if isempty(FN)==1flag=1;elsek=FN(1);A=AA{k};b=BB{k};endendendendy=round(y);fval=c*y;。

matlab求边值问题例题

matlab求边值问题例题
【最新版】
目录
1.MATLAB 求边值问题的基本概念
2.边值问题的例题解析
3.MATLAB 求解边值问题的步骤
4.总结
正文
一、MATLAB 求边值问题的基本概念
边值问题是数学物理中常见的一种问题，它是指在给定的边界条件下，求解偏微分方程的数值解。

在 MATLAB 中，我们可以通过边界元方法或者有限元方法来求解这类问题。

二、边值问题的例题解析
假设我们有一个二维的 Laplace 方程，给定边界条件为：x=0 时，y"=0；x=1 时，y"=0；y=0 时，x"=0；y=1 时，x"=0。

我们可以通过以下步骤在 MATLAB 中求解该问题。

1.定义边界和区域：在 MATLAB 中，我们首先需要定义问题的边界和区域。

我们可以使用边界元方法，将边界和区域定义为一个二维矩阵。

2.定义方程：然后，我们需要定义 Laplace 方程。

在 MATLAB 中，我们可以使用 PDE 工具箱中的函数来定义方程。

3.定义边界条件：接下来，我们需要定义边界条件。

在 MATLAB 中，我们可以使用边界元方法中的函数来定义边界条件。

4.求解：最后，我们可以使用 MATLAB 中的函数来求解该问题。

我们可以使用 PDE 工具箱中的函数，或者使用我们自己编写的函数来求解。

三、MATLAB 求解边值问题的步骤
1.定义边界和区域
2.定义方程
3.定义边界条件
4.求解
四、总结
MATLAB 是一个强大的数学软件，它可以帮助我们求解各种各样的数学问题，包括边值问题。

分支定界解析

MATLAB 解整数规划问题——分支定界法柯伟敏 G012012348一、问题分析在线性规划问题中，有些最优解可能是分数或小数，事实上，线性规划是连续变量的线性优化问题。

但在实际问题中，常有要求解答必须是整数的情形。

例如，所求解是机器人的台数，完成工作的人数或者装货的车数等，分数或者小数的解答就不符合要求。

为了满足整数解的要求，初看起来，似乎只要把已得到的带有分数的或小数的解经过‘舍入化整’就可以了。

但这常常是不行的，因为化整之后不见得就是可行解，或虽是可行解，但不一定是最优解。

因此，对求最优整数解问题，有必要另行研究。

我们称这样的问题为整数规划问题。

学习运筹学过后，我们学习了笔算这类问题，但是当对于一个问题的约束条件有很多个时，手算必然耗费很大个工作量。

但是用 MATLAB 解题却可以达到事半功倍的效果，省去了很多繁琐的运算过程。

二、数学原理下面我主要介绍分支定界解法。

分支定界法的基本思想是不断将可行域分割成小的集合，然后再小的集合上找整数最优解，在分割可行域时，整数解并不会丢失。

其算法过程如下： 1、置矩阵NF_lb 为原整数的的lb ，NF_ ub 为原整数规划的ub ，置最优解=*x ∅，目标函数的最优上界F=+∞。

2、设NF_lb 的第一列为l 0b ，NF_ub 第一列为u 0b ，求解线性规划min f （x ）=cx ， b Ax ≤s.t. 00ub x lb ≤≤ ，设最优解为-x ，最优值为_f ，如果不存在最优解，则设_f =+∞；0≥x3、若_f =+∞，则将NF_lb 的第一列和NF_ub 的第一列去掉，转7，否则，转44、若_f ≥F ，则将NF_lb 的第一列去掉，和NF_ub 的第一列去掉，转7，否则，转5.5、若_f <F ，且-x 的各分量都为整数，则置F=_f ,=*x -x ，将NF_lb 的第一列和NF_ub 的第一列去掉，转7，否则转6。

6、若_f <F ，但-x 的有些分量不是整数，任选择-x 中一个不是整数的分量_k x ，将此问题分解为两个问题Q1Q2；第一个问题的ub 等于u 0b ，而lb 是将NF_lb 中的第一列分量_k x 对应的下界改为[_k x ]+1;第二个问题的lb 等于l 0b ，而ub 是将NF_ub 中的第一列_k x ，对应的上界改为[_k x ]，再将NF_lb 的第一列和NF_ub 的第一列去掉，把Q1，Q2对应的lb ，ub 作为新列分别添加到NF_lb 和NF_ub 的后面，转27、若NF_lb不为空，则转2，若为空，且*x不为空，则*x为原整数规划的最优解，F=最优值，如果*x为空，则原整数规划不存在最优解。

分支定界法----整数规划matlab

分支定界法的思想是：首先确定目标值的上下界发布人：chengxu0921 发布时间：2008-7-21 18:16:27 新闻类别：分支-界限法例1：设有A,B,C,D,E 5人从事j1,j2,j3,j4,j5 5项工作每人只能从事一项,它们的效益表如下:求最佳安排,使效益最高？原文代码重写如下，希望增加点可读性。

program PlanJob;const MAX_SIZE = 20;typeTIntArray = array[1..MAX_SIZE] of Integer;PNode = ^Node;Node = recordJob2Man: TIntArray; // Job2Man[n] = m, job-n assign to person-m Man2Job: TIntArray; // Man2Job[n] = m, person-n assign to job-m UpperVal: Integer; // upper valueJobsDep: Integer; // jobs decided, as search depthNext: PNode;end;varCurNode: PNode; // Current nodeNewNode: PNode; // New branch nodeDelNode: PNode; // for deleteGoalNode: PNode; // the goalGoalMaxVal: Integer; // goal max valueCurMan, CurJob: Integer; // Current Man and Job of current NodeSize: Integer; // Person number, also task numberValues: array[1..MAX_SIZE, 1..MAX_SIZE] of Integer;function CalUpperValue(ANode: PNode): Integer;varRes: Integer;Man, Job: Integer;JobMaxVal: Integer;beginRes := 0;with ANode^ dobeginfor Job := 1 to Size dobeginif Job <= JobsDep thenbeginMan := Job2Man[Job];Res := Res + Values[Man, Job];Continue;end;// else find the max value for JobJobMaxVal := 0;for Man := 1 to Size dobeginif (JobMaxVal < Values[Man,Job]) and (Man2Job[Man] = 0) then JobMaxVal := Values[Man,Job];end;Res := Res + JobMaxVal;end; // for Jobend; // with ANode^CalUpperValue := Res;end;function InitNode(): PNode;varMan, Job: Integer;FInput: Text;Res: PNode;beginAssign(FInput, 'input.txt');Reset(FInput);Read(FInput, Size);Readln(FInput);for Man := 1 to Size dobeginfor Job := 1 to Size doRead(FInput, Values[Man,Job]);Readln(FInput);New(Res);with Res^ dobeginfor Man := 1 to Size dobeginMan2Job[Man] := 0;Job2Man[Man] := 0;end;JobsDep := 0;UpperVal := CalUpperValue(Res);Next := nil;end;InitNode := Res;end;procedure Insert(ANode: PNode; From: PNode);varPrevNode, NextNode: PNode;beginNextNode := From;repeatPrevNode := NextNode;NextNode := PrevNode^.Next;until (NextNode = nil) or (ANode^.UpperVal >= NextNode^.UpperVal); PrevNode^.Next := ANode;ANode^.Next := NextNode;end;procedure PrintNode(ANode: PNode);varMan, Job: Integer;AllJobAssigned: Boolean;beginAllJobAssigned := true;for Job := 1 to Size dobeginMan := ANode^.Job2Man[Job];if 0 <> Man thenWriteln('Job ', Job, ' assign to man ',Man, ', value ', Values[Man, Job])elseAllJobAssigned := false;Writeln;if AllJobAssigned thenWriteln('Value = ', ANode^.UpperVal)elseWriteln('UpperVal = ', ANode^.UpperVal);end;beginCurNode := InitNode();GoalMaxVal := 0;repeatCurJob := CurNode^.JobsDep + 1;for CurMan := 1 to Size dobeginif CurNode^.Man2Job[CurMan] <> 0 thenContinue;// New search branchNew(NewNode);NewNode^ := CurNode^;NewNode^.JobsDep := CurJob;NewNode^.Man2Job[CurMan] := CurJob;NewNode^.Job2Man[CurJob] := CurMan;NewNode^.UpperVal := CalUpperValue(NewNode);if NewNode^.UpperVal < GoalMaxVal thenDispose(NewNode) // discard this branch if smaller than limit elseInsert(NewNode, CurNode);if CurJob < Size then Continue; // for CurMan// all job assigned, update goalif NewNode^.UpperVal > GoalMaxVal thenbeginGoalNode := NewNode;GoalMaxVal := GoalNode^.UpperValend; // ifend; // for CurManDelNode := CurNode;CurNode := CurNode^.Next;Dispose(DelNode);until (CurNode^.UpperVal <= GoalMaxVal)or (CurNode = nil); // end of repeatPrintNode(GoalNode);Readln;end.input.txt:513 11 10 4 713 10 10 8 55 9 7 7 415 12 10 11 510 11 8 8 4output:Job 1 assign to man 4, value 15Job 2 assign to man 5, value 11Job 3 assign to man 2, value 10Job 4 assign to man 3, value 7Job 5 assign to man 1, value 7Value = 50如果扩展为10*10,input.txt:1013 11 10 4 7 13 11 10 4 713 10 10 8 5 13 10 10 8 55 9 7 7 4 5 9 7 7 415 12 10 11 5 15 12 10 11 5 10 11 8 8 4 10 11 8 8 413 11 10 4 7 13 11 10 4 713 10 10 8 5 13 10 10 8 55 9 7 7 4 5 9 7 7 415 12 10 11 5 15 12 10 11 5 10 11 8 8 4 10 11 8 8 4运行约两分钟。

matlab解决整数规划问题（蒙特卡洛法）

matlab解决整数规划问题（蒙特卡洛法）整数规划：clc,clear;c = [-40;-90];A = [9 7;7 20];b = [56;70];lb = zeros(2,1);[x,fval]= intlinprog(c,1:2,A,b,[],[],lb);fval = -fvalx分⽀定界法或者割平⾯法求解纯或者混合整数线性规划问题；输出：当条件A,B之间不是且关系⽽是或的时候：固定成本问题（最优化函数中含有与xi⽆关的常量，相当于固定成本，优化函数可以写成总固定成本加上总可变成本之和）：0-1整数规划问题（过滤隐枚举法，分枝隐枚举法）指派问题（0-1规划特殊情形：匈⽛利法）蒙特卡洛法（求解各种类型规划）下⾯主要介绍蒙特卡洛法（随机取样法）：例题：如果⽤显枚举法试探，需要计算1010个点，计算量巨⼤。

但是⽤蒙特卡洛去计算106个点便可以找到满意解。

前提：整数规划的最优点不是孤⽴的奇点；⽽采集106个点后，我们有很⼤把握最优值点在106个点之中；function [f,g] = mengte(x);f = x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)-8*x(1)-2*x(2)-3*x(3)-...x(4)-2*x(5);g = [sum(x)-400x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-8002*x(1)+x(2)+6*x(3)-200x(3)+x(4)+5*x(5)-200];rand('state',sum(clock));p0 = 0;ticfor i = 1:10^6x = 99*rand(5,1);x1 = floor(x);x2 = ceil(x);[f,g] = mengte(x1);if sum(g<=0)==4if p0<=fx0 = x1;p0=f;endend[f,g] = mengte(x2);if sum(g<=0)==4if p0 <= fx0 = x2;p0 = f;endendendx0,p0toc输出：蒙特卡洛法得到的解为最优解的近似解，10^6个数据已经⽤了将近7s的时间，所以如果增加⼗倍，可能得70s时间才能得到结果。

研究生数学建模E题

货运车物流运输计划问题在整数线性规划的基础上建立适当的模型、再运用分支定界法找到满足约束条件的较优变量，同时比较两种算法的迭代次数和运行时间，为进一步提高算法的利用率提供了依据。

最后通过MATLABGUI做成软件模拟在不同配置下相对应的分配方案，在总费用最小的前提下，程序运行时间短、效率高、能够较精确快速的找到合适的解决方案。

通过分析相应的整数线性规划建立相关的数学模型最后通过软件计算得到理想的效果，但是考虑到装箱调度决策过程中有多种可能，保证所有运输任务完成的情况下分配尽可能少的车辆来运输，因此，我们选择在货运车尽可能满载的情况下的分配方案。

这样可以减程序中少大量的矩阵运算和程序运行时间以及变量的迭代次数。

随着变量个数的增多，约束条件下不能得到较优的目标值，因此我们采用分支定界法先定出可选择的分配方案，再在优化的分配方案中找出相对较优的分配方案，例如运用整数线性规划得到不同车配置方案，运用分支定界法改变约束条件得到结果，在有路径的约束条件下我们运用两阶段法考虑整个分配方案。

先考虑第一阶段数量上的优化再考虑第二阶段路径上的优化。

运用逐步调优的策略在相同路程下就不优先考虑路径的优化，进一步调整配置方案。

在给定装配任务和分配任务的同时我们运用关联分类器先按题目要求将两张表建立关联，通过所给轿用车型的长、宽、高建立一个分类器。

按照表二中长、宽、高的不同分类分为12类，根据调度经验改用启发式算法将分类数降低至10类。

在满足题目要求的前提下我们采用货运车车型混装的形式，在一定程度上减少货运车的使用数量。

从而达到最充分的发挥资源的效能去获取最佳的经济效益。

对整车装箱调度问题进行研究从而降低运输成本具有一定的意义。

1、问题重述智能装载的问题描述：在一个配送中心，有N件货物需要分别配送至目的地A，B，C……，可以使用M辆车。

问如何规划车辆的配送路线，以及如何合理分配车辆的货物装载情况，提高车辆的实载率，减少车辆的数量。

利用Matlab解决数学问题

利用Matlab 解决数学问题一、线性规划求解线性规划的Matlab 解法单纯形法是求解线性规划问题的最常用、最有效的算法之一。

单纯形法是首先由George Dantzig 于1947年提出的，近60年来，虽有许多变形体已被开发，但却保持着同样的基本观念。

由于有如下结论：若线性规划问题有有限最优解，则一定有某个最优解是可行区域的一个极点。

基于此，单纯形法的基本思路是：先找出可行域的一个极点，据一定规则判断其是否最优；若否，则转换到与之相邻的另一极点，并使目标函数值更优；如此下去，直到找到某一最优解为止。

这里我们不再详细介绍单纯形法，有兴趣的读者可以参看其它线性规划书籍。

下面我们介绍线性规划的Matlab 解法。

Matlab5.3中线性规划的标准型为bAx x c T x ≤ such that min 基本函数形式为linprog(c,A,b)，它的返回值是向量x 的值。

还有其它的一些函数调用形式（在 Matlab 指令窗运行 help linprog 可以看到所有的函数调用形式），如： [x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X 0,OPTIONS)这里fval 返回目标函数的值，Aeq 和beq 对应等式约束beq x Aeq =*，LB 和UB 分别是变量x 的下界和上界，x 是x 的初始值，OPTIONS 是控制参数。

例2 求解下列线性规划问题321532m ax x x x z -+=⎪⎩⎪⎨⎧≥≥+-=++0,,10527321321321x x x x x x x x x解（i ）编写M 文件 c=[2;3;-5];a=[-2,5,-1]; b=-10; aeq=[1,1,1]; beq=7;x=linprog(-c,a,b,aeq,beq,zeros(3,1)) value=c'*x（ii ）将M 文件存盘，并命名为example1.m 。

matlab分支定界法

题目:min (4*x1+4*x2); 约束条件:2*x1+5*x2<=15,2*x1-2*x2<=5,x1,x2>=0,且都为整数把以下程序存为ILP.m，%============================function [x,y]=ILp(f,G,h,Geq,heq,lb,ub,x,id,options)%整数线性规划分支定界法，可求解纯整数规划和混合整数规划。

%y=minf’*x s.t. G*x<=h Geq*x=heq x为全整数或混合整数列向量%用法%[x,y]=ILp(f,G,h,Geq,heq,lb,ub,x,id,options)%参数说明%lb:解的下界列向量（Default:-int）%ub:解的上界列向量（Default:int）%x:迭代初值列向量%id：整数变量指标列向量，1-整数，0-实数（Default:1）global upper opt c x0 A b Aeq beq ID options;if nargin<10,options=optimset({});options.Display='off';rgeScale='off';endif nargin<9,id=ones(size(f));endif nargin<8,x=[];endif nargin<7 |isempty(ub),ub=inf*ones(size(f));endif nargin<6 |isempty(lb),lb=zeros(size(f));endif nargin<5,heq=[];endif nargin<4,Geq=[];endupper=inf;c=f;x0=x;A=G;b=h;Aeq=Geq;beq=heq;ID=id;ftemp=ILP(lb(:),ub(:));x=opt;y=upper;%下面是子函数function ftemp=ILP(vlb,vub)global upper opt c x0 A b Aeq beq ID options;[x,ftemp,how]=linprog(c,A,b,Aeq,beq,vlb,vub,x0,options);if how <=0return;end;if ftemp-upper>0.00005 %in order to avoid errorreturn;end;if max(abs(x.*ID-round(x.*ID)))<0.00005if upper-ftemp>0.00005 %in order to avoid erroropt=x';upper=ftemp;return;elseopt=[opt;x'];return;end;end;notintx=find(abs(x-round(x))>=0.00005); %in order to avoid errorintx=fix(x);tempvlb=vlb;tempvub=vub;if vub(notintx(1,1),1)>=intx(notintx(1,1),1)+1;tempvlb(notintx(1,1),1)=intx(notintx(1,1),1)+1;ftemp=IntLP(tempvlb,vub);end;if vlb(notintx(1,1),1)<=intx(notintx(1,1),1)tempvub(notintx(1,1),1)=intx(notintx(1,1),1);ftemp=IntLP(vlb,tempvub);end;%====================================然后：clc;clearf=[4 4]A=[2 5;2 -2]b=[15;5]Aeq=[];beq=[];LB=[0 0];UB=[];[xn,yn]=ILp(f,A,b,Aeq,beq,LB,UB,[1 1],1,[])[x,fval,exitflag]=linprog(f,A,b,Aeq,beq,LB,UB)结果：xn =0 0yn =Optimization terminated.x =1.0e-013 *0.2990040786747590.503948216933779fval =3.211809182434153e-013 exitflag =1。

（完整版）matlab经典习题及解答

（完整版）matlab经典习题及解答第1章 MATLAB 概论1.1 与其他计算机语⾔相⽐较，MATLAB 语⾔突出的特点是什么？MATLAB 具有功能强⼤、使⽤⽅便、输⼊简捷、库函数丰富、开放性强等特点。

1.2 MATLAB 系统由那些部分组成？MATLAB 系统主要由开发环境、MATLAB 数学函数库、MATLAB 语⾔、图形功能和应⽤程序接⼝五个部分组成。

1.4 MATLAB 操作桌⾯有⼏个窗⼝？如何使某个窗⼝脱离桌⾯成为独⽴窗⼝？⼜如何将脱离出去的窗⼝重新放置到桌⾯上？在MATLAB 操作桌⾯上有五个窗⼝，在每个窗⼝的右上⾓有两个⼩按钮，⼀个是关闭窗⼝的Close 按钮，⼀个是可以使窗⼝成为独⽴窗⼝的Undock 按钮，点击Undock 按钮就可以使该窗⼝脱离桌⾯成为独⽴窗⼝，在独⽴窗⼝的view 菜单中选择Dock ……菜单项就可以将独⽴的窗⼝重新防⽌的桌⾯上。

1.5 如何启动M ⽂件编辑/调试器？在操作桌⾯上选择“建⽴新⽂件”或“打开⽂件”操作时，M ⽂件编辑/调试器将被启动。

在命令窗⼝中键⼊edit 命令时也可以启动M ⽂件编辑/调试器。

1.6 存储在⼯作空间中的数组能编辑吗？如何操作？存储在⼯作空间的数组可以通过数组编辑器进⾏编辑：在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器，再选中要修改的数据单元，输⼊修改内容即可。

1.7 命令历史窗⼝除了可以观察前⾯键⼊的命令外，还有什么⽤途？命令历史窗⼝除了⽤于查询以前键⼊的命令外，还可以直接执⾏命令历史窗⼝中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M ⽂件中。

1.8 如何设置当前⽬录和搜索路径，在当前⽬录上的⽂件和在搜索路径上的⽂件有什么区别？当前⽬录可以在当前⽬录浏览器窗⼝左上⽅的输⼊栏中设置，搜索路径可以通过选择操作桌⾯的file 菜单中的Set Path 菜单项来完成。

在没有特别说明的情况下，只有当前⽬录和搜索路径上的函数和⽂件能够被MATLAB 运⾏和调⽤，如果在当前⽬录上有与搜索路径上相同⽂件名的⽂件时则优先执⾏当前⽬录上的⽂件，如果没有特别说明，数据⽂件将存储在当前⽬录上。