【2014丰台一模】北京市丰台区2014届高三下学期期中练习 理综 Word版含答案

丰台区2014英2014.31．答题前，考生务必先将答题卡上的学校、班级、姓名、准考证号用黑色字迹签字笔填写清楚，并认真核对条形码上的准考证号、姓名，在答题卡的“条形码2．本次考试所有答题均在答题卡上完成。

选择题必须使用2B铅笔以正确填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦除干净后再选涂其它选项。

非3．请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，4第一部分：听力理解（共三节，30第一节（共5小题；每小题1.5分，共7.5听下面5段对话。

每段对话后有一道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你将有10秒钟的时间来回答有关小题和阅读下一1. What will the man do tonight?A. Go to a movie.B. Read books.C. Watch TV.2. Where will the bookshelf probably be put?A. Near the window.B. In the bedroom.C. Beside the fireplace.3. What does the man want to be?A. A dancer.B. A singer.C. A waiter.4. Who is the man?A. A taxi driver.B. A policeman.C. A front desk clerk.5. Where are the two speakers?A. In a hospital.B. In a supermarket.C. In a post office.第二节（共10小题；每小题1.5分，共15听下面4段对话或独白。

每段对话或独白后有几道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听每段对话或独白前，你将有5秒钟的时间阅读每小题。

听完后，每小题将给出5秒钟的作答时间。

q :函数g(x)在区间(a,b)内有最值.则命题 p 是命题q 成立的丰台区2012年高三年级第二学期统一练习(一)2012.3数学(理科)第一部分(选择题共40 分)一、选择题共8小题，每小题5分，共40分•在每小题列出的四个选项中，选出符合题目要求的一项.21.已知集合 A={x I x <1}, B={a}，若A n B=._ ,则a 的取值范围是(A) ( -：：， (C) (-1,1)(D) [-1,1]2.若变量x ,卄 八0,卄y 满足约束条件{x-2yX1,则z=3x+5y 的取值范围是X —4層 3,(B) [-8,3](D) [-8,9]的二项展开式中，常数项是(C) 201I4.已知向量 a = (sin ,cosR , b = (3,4)，若 a _ b ，则 tan2二等于(A) 10(B) 15(D) 3024 6 24 (A)(B)(C)77255•若正四棱锥的正视图和俯视图如右图所示，则该几何体的表面积是24(D)(A) 4 (B) 4 4,10 (C) 8(D) 4 4116.学校组织高一年级 4个班外出春游，每个班从指定的甲、乙、丙、丁 四个景区中任选一个游览，则恰有两个班选择了甲景区的选法共有 (A) (B) A A 2 种(C)2 2(D) C 4 A 3 种7.已知 a :: b ，函数 f(x)二sin X ， g(x)=cos X .命题 p ： f (a) f(b) ：： 0，命题(A)充分不必要条件(C)充要条件(B)必要不充分条件(D)既不充分也不必要条件8.已知定义在R 上的函数y=f(x)满足 f(x+2)= f(x),当-1<x < 1 时,f(x)=x 3.若函数 g(x) = f (x) _ log a x 恰有6个零点，贝U a114.定义在区间［a,b ］上的连续函数y 二f(x)，如果 ［a,b ］，使得f (b) - f (a)二f'( J(b - a)，则称 为区间［a,b ］上的"中值点”.下列函数：① f (x) =3x 2 :②f (x) = x 2 -x • 1 :③f (x)二ln(x 1):④f (x) ^(x-1)3中，在区间［0,1］上“中值点”多于一个的函数序号为2(A) a= 5 或 a=—(B) a (0,：)U ［5,：：)5 1 1(D) a 匕,匚山［5,7)7 5二、填空题共6小题，每小题 第二部分(非选择题共110分)5分，共30分.9.已知双曲线的中心在原点,3焦点在x 轴上，一条渐近线方程为 y x , 4则该双曲线的离心率是10.已知等比数列{a n }的首项为1，若4a i , 2a 2,觅成等差数列，则数列 {-} 的前5项和为 a n11.在直角坐标系xOy 中，直线I 的参数方程是y 占 x=1 旦，2 (t 为参数)1. -2，.以O 为极点，x 轴正方向极轴的极坐标系中，圆 C 的极坐标方程是 p -4 pcos 肝3=0 .则圆心到直线的距离是12.如图所示，Rt △ ABC 内接于圆，• ABC =60；, PA 是圆的切线，A 为切点，PB 交AC 于E ,交圆于 D .若 FA=AE , PD=、3 , BD=3.3 , 贝UAF= ____13.执行如下图所示的程序框图，则输出的 i 值为.(写出所有.满足条件的函数2 的菱形，侧面 FAD 丄底面 ABCD ，/ BCD=60o, FA=PD=、2 ,E 是BC 中点，点Q 在侧棱FC 上.（I ）求证：AD 丄FB ;（n ）若Q 是FC 中点，求二面角 E-DQ-C 的余弦值；FQ（川）若，当FA //平面DEQ 时，求入的值.FC17.（本小题共13分）某班共有学生40人，将一次数学考试成绩（单位：分）绘制成频率分布直方图，如图所示. （I ）请根据图中所给数据，求出a 的值；（n ）从成绩在［50,70）内的学生中随机选 3名学生，求这3名学生的成绩都在［60,70）内的概率；的序号）三、解答题共6小题，共80分•解答应写出文字说明，演算步骤或证明过程. 15.（本小题共13分）在厶ABC 中，角A , B, C 所对的边分别为 （I ）判断△ ABC 的形状； 12 1f （x ） cos2x cosx ,2 32(n)若16.（本小题共14分）a ,b ,c ,且 a sin B _bcosC =ccosB . 求f （A ）的取值范围.四棱锥P —ABCD 中,底面ABCD 是边长为AB（川）为了了解学生本次考试的失分情况，从成绩在［50,70）内的学生中随机选取3人的成绩进行分析，用X表示所选学生成绩在［60,70）内的人数，求X的分布列和数学期望.即 sin As in B = si n C cos B cosCs in B ,......................... 2分 所以 sin(C B) = sin Asin B .................... 4分因为在△ ABC 中，A • B • C 二二， 所以 sin A =sinAsinB 又sinA = 0,................... 5分JI所以 sin B = 1 , B =— 2所以△ ABC 为B的直角三角形.2................... 6分(法 2)因为 asin B —bcosC =ccosB ,2.2 2 2 a ____ —j- rq a由余弦疋理可得 asin B = bc2abc 2- b 22ac '................... 4分即 a sin B = a . 因为a = 0,所以sin B =1 ................... 5分所以在△ ABC 中，B =~ .2所以△ ABC 为B的直角三角形.2................... 6分1 2 1 2 2n)因为 f (x) cos2x cosxcos xcosx......2 3 23................... 8分 = (cosx _丄)2.3 9................ 10分所以 0 :： A ，且 0 :：: cos A ：1 ,........................ 11 分211所以 当cos A 时，f(A)有最小值是.............. 12分391 1所以f (A)的取值范围是［-1,1) ......................... 13分9 316.证明：(I)取AD 中点O ,连结OP , OB , BD .因为PA=PD , 所以PO 丄AD . ........................... 1分因为菱形 ABCD 中，/ BCD=60o,所以AB=BD , 所以BO 丄AD . ........................... 2分 因为 BO n PO=O ,........................... 3 分 所以AD 丄平面POB. ................................. 4分 A所以AD 丄PB. ........................... 5分(H)由(I)知 B0 丄 AD , PO 丄 AD . 因为 侧面PAD 丄底面ABCD ,且平面 PAD n 底面 ABCD=AD , 所以PO 丄底面ABCD ............................以O 为坐标原点，如图建立空间直角坐标系 O.......................... 7分则 D(-1,0,0) , E(-1,、3,0)，P(0,0,1),C （-2八 3,0）,因为Q 为PC 中点，所以Q (_1，乜，丄).2 2所以"DE =（0^3,0）, DQ =（0,^」）,2 2所以平面DEQ 的法向量为m = (1,0,0).因为 DC=（-1八 3,0） , DQ^。

北京市丰台区2014届高三第二学期统一练习（一）英语试卷 2014.3第一部分：听力理解（共三节，30分）第一节（共5小题；每小题l.5分，共7.5分)听下面5段对话。

每段对话后有一道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你将有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话你将听一遍。

1. What will the man do tonight?A. Go to a movie.B. Read books.C. Watch TV.2. Where will the bookshelf probably be put?A. Near the window.B. In the bedroom.C. Beside the fireplace.3. What does the man want to be?A. A dancer.B. A singer.C. A waiter.4. Who is the man?A. A taxi driver.B. A policeman.C. A front desk clerk.5. Where are the two speakers?A. In a hospital.B. In a supermarket.C. In a post office.第二节（共10小题；每小题1.5分，共15分）听下面4段对话或独白。

每段对话或独白后有几道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听每段对话或独白前，你将有5秒钟的时间阅读每小题。

听完后，每小题将给出5秒钟的作答时间。

每段对话或独白你将听两遍。

听下面一段对话，回答第6至7两道小题。

6. What is the woman doing?A. Seeing a doctor.B. Doing a survey.C. Making an appointment.7. How does the man keep fit?A. By eating a healthy diet.B. By taking enough sleep.C. By riding the bike to work.听下面一段独白，回答第8至9两道小题。

北京市丰台区2014届高三第二学期统一练习（一）英语试卷2014.3第一部分：听力理解（共三节，30分）第一节（共5小题；每小题l.5分，共7.5分)听下面5段对话。

每段对话后有一道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你将有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话你将听一遍。

1. What will the man do tonight?A. Go to a movie.B. Read books.C. Watch TV.2. Where will the bookshelf probably be put?A. Near the window.B. In the bedroom.C. Beside the fireplace.3. What does the man want to be?A. A dancer.B. A singer.C. A waiter.4. Who is the man?A. A taxi driver.B. A policeman.C. A front desk clerk.5. Where are the two speakers?A. In a hospital.B. In a supermarket.C. In a post office.第二节（共10小题；每小题1.5分，共15分）听下面4段对话或独白。

每段对话或独白后有几道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听每段对话或独白前，你将有5秒钟的时间阅读每小题。

听完后，每小题将给出5秒钟的作答时间。

每段对话或独白你将听两遍。

听下面一段对话，回答第6至7两道小题。

6. What is the woman doing?A. Seeing a doctor.B. Doing a survey.C. Making an appointment.7. How does the man keep fit?A. By eating a healthy diet.B. By taking enough sleep.C. By riding the bike to work.听下面一段独白，回答第8至9两道小题。

13
2
14、
干涉图样与衍射图样的根本区别在于：干涉是由两列波通过双峰形成的，
波的波长越长条纹的宽度就越大，衍射图样中中间的条纹以及两边的条文相应的随之增宽；
16、
2
3
4
17
有匀强磁场，一带负电的粒子（不计重力）以速度水平匀速穿过两极板。

下列说法正确的是：（Array 2、
3
4
5
6
8
若将
18、
7、求解质量与密度的规律，往往是求解“中心球”的质量和密度的，需要已知几个物理量
20
所示是实验中打出的一条纸带的一部分，从比较清晰的点
，相邻的两个计数点之间都有4个点迹没有标出，测出各计数点之间的距离。

已知打点计时器接在频率为50的交流电源两端，则此次实
2
两导轨间接有阻值为的电阻。

一质量为的均匀金属棒放在两导轨上并与两导轨垂直。

整①
23（
（1）
（2
（3
（1）液体从出水口出来后做平抛运动，
（2
（3
24(20分)如图所示，直角坐标系位于竖直平面内，轴正向竖直向上，轴正向水平向右。

空间存
（2
（3
（1
（2
（3）
〖。

丰台区2013—2014学年度第二学期期中练习高 三 数 学（理科） 2014．3第一部分 （选择题 共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的4个选项中，选出符合题目要求的一项． （1）设集合{|11}A x x =∈-≤≤R ，{|(3)0}B x x x =∈-≤R ，则A B I 等于（ ）． A ． {|13}x x ∈-≤≤R B ． {|03}x x ∈≤≤R C ． {|10}x x ∈-≤≤R D ． {|01}x x ∈≤≤R（2）在极坐标系中，点(1,π)A 到直线cos 2ρθ=的距离是（ ）． A ．1 B ．2 C ．3 D ．4（3）执行如图所示的程序框图，输出的x 值为（ ）．A ．85B ．2912C ．53D ．138（4）已知函数()f x 是定义在[6,6]-上的偶函数，且(3)(1)f f >，则下列各式中一定成立的是（ ）．A ．(0)(6)f f <B ．(-3)(-2)f f >C ．(1)(3)f f -<D ．(-2)(1)f f >（5）“1m n >>”是 “log 2log 2m n <”的（ ）．A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件（6）某企业开展职工技能比赛，并从参赛职工中选1人参加该行业全国技能大赛．经过6轮选拔，甲、乙两人成绩突出，得分情况如茎叶图所示．若甲乙两人的平均成绩分别是x 甲，x 乙，则下列说法正确的是（ ）．A ．x x >甲乙，乙比甲成绩稳定，应该选乙参加比赛B ．x x >甲乙，甲比乙成绩稳定，应该选甲参加比赛C ．x x <甲乙，甲比乙成绩稳定，应该选甲参加比赛D ．x x <甲乙，乙比甲成绩稳定，应该选乙参加比赛（7）棱长为2 的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是（ ）．A ．143 B ．4C ．103D ．3（8）如果某年年份的各位数字之和为7，我们称该年为“七巧年”．例如，今年年份2014的各位数字之和为7，所以今年恰为“七巧年”．那么从2000年到2999年中“七巧年”共有（ ）．A ．24个B ．21 个C ．19 个D ．18个侧视图俯视图主视图221111第二部分 （非选择题 共110分）二、填空题共6小题，每小题5分，共30分．（9）已知tan 2α=，则sin cos sin cos αααα-+的值为_______________．（10）已知等比数列{}n a 中， 358a a +=，154a a =，则139a a = ．（11）如图，已知圆的两条弦AB 与CD 相交于点F ，E 是AB 延长线上一点，且2DF CF ==，::4:2:1AF FB BE =．若CE 与圆相切，则线段CE 的长为 ．（12）已知点F ，B 分别为双曲线2222:1(0,0)x y C a b a b -=>>的焦点和虚轴端点，若线段FB 的中点在双曲线C 上，则双曲线C 的离心率是_______．（13）已知平行四边形ABCD 中，点E 为CD 的中点，AM mAB =uuu r uu u r ，AN nAD =uuu r uuu r （0m n ⋅≠），若//MN BE uuu r uu u r，则nm=______________．（14）设不等式组22100x y y ⎧+-≤⎨≥⎩，表示的平面区域为M ，不等式组201t x t y t -≤≤⎧⎪⎨≤≤-⎪⎩，表示的平面区域为N ．在M 内随机取一个点，这个点在N 内的概率的最大值是_________．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． （15）（本小题共13分）已知函数2π()cos(2)2sin 13f x x x =--+．（Ⅰ）求函数()f x 的最小正周期；（Ⅱ）求函数()f x 在区间π[0,]2上的最大值和最小值．FE DCB A（16）（本小题共13分）年龄在60岁（含60岁）以上的人称为老龄人，某地区老龄人共有35万，随机调查了该地区700名老龄人的健康状况，结果如下表：健康指数2101-60岁至79岁的人数250260652580岁及以上的人数20452015其中健康指数的含义是：2表示“健康”，1表示“基本健康”，0表示“不健康，但生活能够自理”，1-表示“生活不能自理”．（Ⅰ）估计该地区80岁以下老龄人生活能够自理的概率．（Ⅱ）若一个地区老龄人健康指数的平均值不小于1.2，则该地区可被评为“老龄健康地区”．请写出该地区老龄人健康指数X分布列，并判断该地区能否被评为“老龄健康地区”．（17）（本小题共14分）如图，在棱长为1的正方体1111ABCD A B C D -中，点E 是棱AB 上的动点． （Ⅰ）求证：11DA ED ⊥；（Ⅱ）若直线1DA 与平面1CED 成角为45︒，求AEAB的值；（Ⅲ）写出点E 到直线1D C 距离的最大值及此时点E 的位置（结论不要求证明）．（18）（本小题共13分）已知曲线()e x f x ax =-(0)a ≠．（Ⅰ）求曲线在点（0,(0)f ）处的切线方程； （Ⅱ）若存在0x 使得0()0f x ≥，求a 的取值范围．（19）（本小题共14分）如图，已知椭圆:E 22221(0)x y a b a b+=>>的离心率为32，过左焦点(3,0)F -且斜率为k 的直线交椭圆E 于A ，B 两点，线段AB 的中点为M ，直线l ：40x ky +=交椭圆E 于C ，D 两点． （Ⅰ）求椭圆E 的方程；（Ⅱ）求证：点M 在直线l 上；（Ⅲ）是否存在实数k ，使得三角形BDM 的面积是三角形ACM 的3倍？若存在，求出k 的值；若不存在，说明理由．（20）（本小题共13分）从数列{}n a 中抽出一些项，依原来的顺序组成的新数列叫数列{}n a 的一个子列． （Ⅰ）写出数列{31}n -的一个是等比数列的子列；（Ⅱ）若{}n a 是无穷等比数列，首项11a =，公比0q >且1q ≠，则数列{}n a 是否存在一个子列为无穷等差数列？若存在，写出该子列的通项公式；若不存在，证明你的结论．丰台区2014年高三年级第二学期统一考试（一）数学（理科）答案 2014．3一、选择题题号1 2 3 4 5 6 7 8 答案D C A C A D B B二、填空题9． 13 10． 9 11． 72 12． 5 13． 2 14．2π三、解答题 15．解：（Ⅰ）()cos2cos sin 2sincos233f x x x x ππ=++13cos 2sin 2cos 222x x x =++ 33sin 2cos 222x x =+ 133(sin 2cos 2)22x x =+3(sin 2coscos2sin )33x x ππ=+3sin(2)3x π=+——————————————————————————————————5分 所以()f x 的最小正周期为π．————————————————————————————7分（Ⅱ）由（Ⅰ）知()3sin(2)3f x x π=+因为[0,]2x π∈，所以ππ4π2[,]333x +∈，当ππ232x +=，即π12x =时，函数()f x 取最大值3，当π4π233x +=，即π2x =时，函数()f x 取最小值32-．所以，函数()f x 在区间[0,]2π上的最大值为3，最小值为32-．——————————————13分16．解：（Ⅰ）该地区80岁以下老龄人生活能够自理的频率为2502606523250260652524++=+++，所以该地区80岁以下老龄人生活能够自理的概率约为2324．——————————————5分（Ⅱ）该地区老龄人健康指数X 的可能取值为2，1，0，1-，其分布列为（用频率估计概率）：X 2 1 0 1-P270700 305700 85700 40700EX =2703058540210(1)700700700700⨯+⨯+⨯+-⨯ 1.15= 因为 1.2EX <，所以该地区不能被评为“老龄健康地区”．———————————————13分17． 解：以D 为坐标原点，建立如图所示的坐标系，则D (0,0,0)，(1,0,0)A ，(1,1,0)B ，(0,1,0)C ，1(0,1,2)D ，1(1,0,1)A ，设(1,,0)E m (01)m ≤≤（Ⅰ）证明：1(1,0,1)DA =u u u r，1(1,,1)ED m =--u u u r111(1)0()110DA ED m ⋅=⨯-+⨯-+⨯=u u u r u u u r所以11DA ED ⊥————————————————————4分（Ⅱ）设平面1CED 的一个法向量为(,,)v x y z =r，则100v C D v C E ⎧⋅=⎪⎨⋅=⎪⎩r uuu r r uu u r ，而1(0,1,1)CD =-u u u r ，(1,1,0)CE m =-u u u r所以0,(1)0,y z x m y -+=⎧⎨+-=⎩取1z =，得1y =，1x m =-，得(1,1,1)v m =-r ． 因为直线1DA 与平面1CED 成角为45︒，所以1sin 45|cos ,|DA v ︒=<>u u u r r所以11||22||||DA v DA v ⋅=⋅uuu r r uuu r r ，所以2|2|22223m m m -=-+，解得12m = ．—————11分 （Ⅲ）点E 到直线1D C 距离的最大值为62，此时点E 在A 点处．——————14分 18．解：（Ⅰ）因为(0)1f =-，所以切点为(0,1)-．()x f x a e '=-，(0)1f a '=-，所以曲线在点(0,(0))f 处的切线方程为：(1)1y a x =--．———————————————4分 （Ⅱ）（1）当0a >时，令()0f x '=，则ln x a =．因为()x f x a e '=-在(,)-∞+∞上为减函数，所以在(,ln )a -∞内()0f x '>，在(ln ,)a +∞内()0f x '<，所以在(,ln )a -∞内()f x 是增函数，在(ln ,)a +∞内()f x 是减函数， 所以()f x 的最大值为(ln )ln f a a a a =-因为存在0x 使得0()0f x ≥，所以ln 0a a a -≥，所以a e ≥．（2）当0a <时，()0x f x a e '=-<恒成立，函数()f x 在R 上单调递减，而11()10a f e a=->，即存在0x 使得0()0f x ≥，所以0a <．综上所述，a 的取值范围是(,0)[e,)-∞+∞U ————————————————————13分19． 解：（Ⅰ）由题意可知32c e a ==，3c =，于是2,1a b ==． 所以，椭圆的标准方程为2214x y +=．——————————————————————3分（Ⅱ）设11(,)A x y ，22(,)B x y ，00(,)M x y ，22(3)14y k x x y ⎧=+⎪⎨+=⎪⎩即2222(41)831240k x k x k +++-=． 所以，21228341k x x k -+=+，2120243241x x k x k +-==+，0023(3)41ky k x k =+=+， 于是222433(,)4141k kM k k -++．因为222433404141k kk k k -+⋅=++，所以M 在直线l 上． —————————————————8分（Ⅲ）由（Ⅱ）知点A 到直线CD 的距离与点B 到直线CD 的距离相等，若BDM △的面积是ACM △面积的3倍，则3DM CM =，因为OD OC =，于是M 为OC 中点，；设点C 的坐标为33(,)x y ，则302y y =．因为22414x kyx y =-⎧⎪⎨+=⎪⎩，解得32141y k =±+． 于是2213||41241k k k =++，解得218k =，所以24k =±．————————————————14分 20． 解：（Ⅰ）212n n a -=（若只写出2，8，32三项也给满分）．————————————4分（Ⅱ）证明：假设能抽出一个子列为无穷等差数列，设为{}n b ，通项公式为1(1)n b b n d =+-．因为11a =，所以1n n a q -=．（1）当01q <<时，1n n a q -=∈（0，1]，且数列{}n a 是递减数列， 所以{}n b 也为递减数列且n b ∈（0，1]，0d <，令1(1)0b n d +-<，得111bn d>->，即存在*(1)n N n ∈>使得0n b <，这与n b ∈（0，1]矛盾． （2）当1q >时，1n n a q -=≥1，数列{}n a 是递增数数列，所以{}n b 也为递增数列且n b ≥1，0d >． 因为d 为正的常数，且1q >，所以存在正整数m 使得11(1)m m m a a q q d -+-=->． 令()k p b a p m =>，则11k p b a ++≥，因为111(1)(1)p m p p a a q q q q d --+-=->->=1k k b b +-，所以1p p a a +->1k k b b +-，即11p k a b ++>，但这与11k p b a ++≥矛盾，说明假设不成立．综上，所以数列{}n a 不存在是无穷等差数列的子列．—————————————————13分丰台区2014年高三年级第二学期统一考试（一）数学（理科）选填解析 2014．3一、 选择题 1． 【答案】D【解析】解：{|(3)0}{|03}B x x x x x =∈-≤=≤≤R 又{|11}A x x =∈-≤≤R 所以{|01}A B x x =≤≤I 故答案选D ．2． 【答案】C【解析】解：因为(1,π)A ，所以1cos π1x =⨯=-，1sin π0y =⨯=，所以A 对应的直角坐标为(1,0)-； 由cos 2ρθ=，得2x =，所以A 到直线的距离为3． 故选C ．3． 【答案】A【解析】解：列表法：i 0 1 2 3 4循环结束 x 1 232 53 85故选A4． 【答案】C【解析】因为()f x 是偶函数，所以(1)(1)f f -=， 又(3)(1)f f >，则(3)(1)f f >-，即(1)(3)f f -< ． 故选C5． 【答案】A【解析】解：因为1m n >> ，则22log log 0m n >>，所以2211log log m n<，即log 2log 2m n <． 即“1m n >>”⇒“log 2log 2m n <”另一方面，若log 2log 20m n<<，即22110log log m n<<，所以22log log 0n m <<，则1n m << 即“log 2log 2m n <”推不出“1m n >>”．所以“1m n >>”是 “log 2log 2m n <”充分不必要条件． 故答案选A ．6． 【答案】D【解析】解：由茎叶图，知703802901289562826x ⨯+⨯+⨯++++++==甲，70180390286881326263x ⨯+⨯+⨯++++++==乙所以x x <甲乙，由图知，乙的数据更集中，所以乙的成绩稳定； 故选D7． 【答案】B【解析】由三视图知，几何体如图所示，其体积为正方体体积的一半，即122242⨯⨯⨯=．故选B ．8． 【答案】B【解析】解：依题意，只需个位、十位，百位数字之和为5即可． 又5500410320311221=++=++=++=++=++当后三位数字为5、0、0或3、1、1或2、2、1时，各有133A =个； 当后三位数字为4、1、0或3、2、0时，各有336A =个； 所以共有336221⨯+⨯=个． 故选B ．二、 解答题9． 【答案】13【解析】解：sin cos tan 11sin cos tan 13αααααα--==++． 故答案为13．10．【答案】9【解析】解：因为{}n a 为等比数列，所以21534a a a ==，又358a a += 所以3526a a =⎧⎨=⎩或35210a a =-⎧⎨=⎩（舍），所以2533a q a == ，所以41399a q a ==． 故答案为9．11．【答案】72【解析】解：因为::4:2:1AF FB BE =，可设BE k =，2FB k =，4AF k =；由相交弦定理，得DF CF AF BF ⋅=⋅，所以282k =，所以12k =，由切割线定理，得227774EC EB EA k k k =⋅=⋅==．所以72EC =．故答案为7212．【答案】5【解析】解：不妨设(,0)F c ，(0,)B b ，则FB 的中点为(,)22c b，又因为线段FB 的中点在双曲线C 上，则2222144c b a b-=，解得5c a =故答案为5．13．【答案】2【解析】解：如图，显然当M 为AB 中点，N 与D 重合时，//MN BE uuu r uu u r．此时11,2n m ==．所以2nm=．故答案为2．14．【答案】2π【解析】画出不等式组22100x y y ⎧+-≤⎨≥⎩表示的平面区域，如图所示，不等式组201t x t y t -≤≤⎧⎪⎨≤≤-⎪⎩，表示的区域为阴影部分， 由几何概型的知识，在M 内随机取一个点，这个点在N 内的概率为22222141412πππ2π2t t t t t t --+-=≤⨯=，当且仅当22t =时取等号． 故答案为2π．。

北京市丰台区2014届高三英语下学期期中练习（丰台一模）新人教版第一部分：听力理解（共三节，30分）第一节（共5小题；每小题l.5分，共7.5分)听下面5段对话。

每段对话后有一道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你将有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话你将听一遍。

1. What will the man do tonight?A. Go to a movie.B. Read books.C. Watch TV.2. Where will the bookshelf probably be put?A. Near the window.B. In the bedroom.C. Beside the fireplace.3. What does the man want to be?A. A dancer.B. A singer.C. A waiter.4. Who is the man?A. A taxi driver.B. A policeman.C. A front desk clerk.5. Where are the two speakers?A. In a hospital.B. In a supermarket.C. In a post office.第二节（共10小题；每小题1.5分，共15分）听下面4段对话或独白。

每段对话或独白后有几道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听每段对话或独白前，你将有5秒钟的时间阅读每小题。

听完后，每小题将给出5秒钟的作答时间。

每段对话或独白你将听两遍。

听下面一段对话，回答第6至7两道小题。

6. What is the woman doing?A. Seeing a doctor.B. Doing a survey.C. Making an appointment.7. How does the man keep fit?A. By eating a healthy diet.B. By taking enough sleep.C. By riding the bike to work.听下面一段独白，回答第8至9两道小题。

北京市丰台区2014届高三二模物理13. 一个氢原子从基态跃迁到n=2的激发态．该氢原子A ．放出光子，能量增加B ．放出光子，能量减少C ．吸收光子，能量增加D ．吸收光子，能量减少14. 下列说法中正确的是A ．温度升高时，每个分子的动能都增大B ．在两分子间距离增大的过程中，分子间引力增大，斥力减小C ．在两分子间距离增大的过程中，分子势能一定增大D ．用N 表示阿伏伽德罗常数，M 表示铜的摩尔质量，ρ表示铜的密度，那么一个铜原子所占的体积可表示为MρN15. 物理学是一门以实验为基础的科学，任何理论和学说的建立都离不开实验。

下面有关物理实验与物理理论或学说关系的说法中正确的是A ．双缝干涉现象的发现表明光是电磁波B ．光电效应实验证实了光是横波C ．α 粒子散射实验表明了原子具有核式结构D ．天然放射现象的发现证实了玻尔原子理论16．在如图甲所示电路的MN 间加如图乙所示正弦交流电，负载电阻为200Ω，若不考虑电表内阻对电路的影响，则交流电压表和交流电流表的读数分别为 A ．311V ，1.10 A B ．220 V ，1.10 A C ．220V ，3.11A17．“嫦娥三号”探测器已成功在月球表面预选着陆区实现软着陆，“嫦娥三号”着陆前在月球表面附近绕月球做匀速圆周运动，经测量得其周期为T 。

已知引力常量为G ，根据这些数据可以估算出A ．月球的质量B ．月球的半径C ．月球的平均密度D ．月球表面的重力加速度18．如图甲所示，闭合电路由电阻R 和阻值为r 环形导体构成，其余电阻不计。

环形导体所围的面积为S 。

环形导体位于一垂直纸面向里的匀强磁场中，磁感应强度的大小随时间变化的规律如图乙所示。

在0-t 0时间内，下列说法正确的是0 B B ×10-2s 甲 乙A ．通过R 的电流方向由B 指向A ，电流大小为10B SR r t （+）B ．通过R 的电流方向由A 指向B ，电流大小为20B SR r t （+）C ．通过R 的电流方向由B 指向A ，电流大小为210()B B SR r t +2（+）D ．通过R 的电流方向由A 指向B ，电流大小为210()B B SR r t －（+）19．如图甲所示是用沙摆演示振动图像的实验装置，此装置可视为摆长为L 的单摆，沙摆的运动可看作简谐运动，实验时在木板上留下图甲所示的结果。

中国威望高考信息资源门户北京市丰台区 2014 年高三一模物理参照答案一、选择题：1314151617181920B A B DC CD D21.（ 18 分）（ 1） 5.44cm 5.694~5.698mm（2）① 长木板②均衡摩擦力③0.1s0.46m/s2④砂和砂桶质量较大，没知足砂和砂桶质量远小于小车质量的条件。

⑤F M m g m 1 MM m922.（ 16 分）解：（ 1）在Δt时间内， ab 棒向右挪动的距离为，vΔt这个过程中线框的面积变化量是S=Lv t(2 分)穿过闭合回路的磁通量的变化量是=B S=B LvΔt(2 分)依据法拉第电磁感觉定律 E n BLv(2 分)t（2）①当导体棒的速度为v 时，产生的感觉电动势为E=BLv回路中的电流大小为BLv(2 分) IR由右手定章可知电流方向为从N 到 M(2 分)②导体棒在磁场中运动时，所受安培力大小为F BIL B 2 L2 v（2分）R由左手定章可知，安培力方向沿斜面向上当导体棒的加快度为零时，速度最大即：B 2 L2 v m（2 分）mg sin R可解得最大速度为 v m mgR sin（2 分）B 2L223.（ 18 分）解：（ 1）液体喷出后做平抛运动h 1 g2t（1 分）2x vt（1 分）解得： x v 2h（2 分）g（ 2）设活塞运动速度v0由2v S（2 分）v0 L得 v0S2 v（1 分）L设在时间 t 内有质量为△m 的液体从喷口射出m vtS（2 分）时间 t 内装置对△m 做功Pt1mv21mv02（2 分）22P 13L4－ S2（2 分）2v s (L4)（ 3）金属棒在磁场中受力F＝ BIL（1 分）13S (1S2（2分）2v4 )＝ BILv 0L得 Bv2 ( L4S2 )（2 分）2IL 324.（ 20 分）解：（ 1）由题意知小球做匀速直线运动f (2 分)受力剖析如图f qvB2mgqE (2 分)匀速直线运动速度大小v 2mg(1 分)v qB mg方向如图，斜向下与x 轴方向夹角 45°(1 分)（2）小球做直线运动的条件为：洛仑兹力与电场力和重力的协力为一对均衡力。

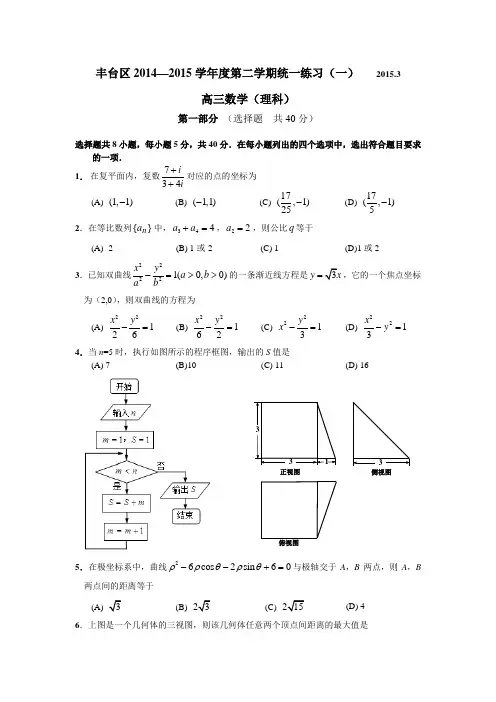
丰台区2014—2015学年度第二学期统一练习（一） 2015.3高三数学（理科）第一部分 （选择题 共40分）选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1． 在复平面内，复数734ii++对应的点的坐标为 (A) (1,1)-(B) (1,1)-(C) 17(,1)25- (D) 17(,1)5- 2．在等比数列}{n a 中，344a a +=，22a =，则公比q 等于(A) -2(B) 1或-2(C) 1(D)1或23．已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程是y =，它的一个焦点坐标为（2,0），则双曲线的方程为(A)22126x y -= (B)22162x y -= (C)2213y x -= (D) 2213x y -= 4．当n =5时，执行如图所示的程序框图，输出的S 值是(A) 7 (B)10 (C) 11(D) 16俯视图侧视图正视图5．在极坐标系中，曲线26cos 2sin 60ρρθρθ--+=与极轴交于A ，B 两点，则A ，B 两点间的距离等于(A)(B)(C) (D) 46．上图是一个几何体的三视图，则该几何体任意两个顶点间距离的最大值是(A) 4 (B) 5(C)(D)7．将函数1cos()26y x π=-图象向左平移3π个长度单位，再把所得图象上各点的横坐标缩短到原来的一半（纵坐标不变），所得图象的函数解析式是 (A) cos(+)6y x π=(B) 1cos4y x = (C) cos y x =(D) 1cos()43y x π=-8．如图所示，在平面直角坐标系xOy 中，点B ，C 分别在x 轴和y 轴非负半轴上，点A 在第一象限，且90BAC ︒∠=，4AB AC ==，那么O ，A 两点间距离的(A) 最大值是，最小值是4 (B) 最大值是8，最小值是4(C) 最大值是，最小值是2 (D) 最大值是8，最小值是2第二部分 （非选择题 共110分）一、填空题共6小题，每小题5分，共30分． 9．定积分(cos )x x dx π+=⎰____．10．已知二项式2()nx x+的展开式中各项二项式系数和是16，则n =____，展开式中的常数项是____．11．若变量x ，y 满足约束条件40,40,0,y x y x y -≤⎧⎪+-≤⎨⎪-≤⎩则2z x y =+的最大值是____．12．已知函数()f x 是定义在R 上的偶函数，当x ≥0时， 2()2f x x x =-， 如果函数()()g x f x m =- ( m ∈R ) 恰有4个零点，则m 的取值范围 是____．13．如图，AB 是圆O 的直径，CD 与圆O 相切于点D ，AB =8，BC =1，则 CD=____；AD=____．14．已知平面上的点集A 及点P ，在集合A 内任取一点Q ，线段PQ 长度的最小值称为点P 到集合A 的距离，记作(,)d P A ．如果集合={(,)|1(01)}A x y x y x +=≤≤，点P 的坐标为(2,0)，那么(,)d P A =____；如果点集A 所表示的图形是边长为2的正三角形及其内部，那么点集{|0(,)1}D P d P A =<≤所表示的图形的面积为____．二、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知函数21()coscos2222xxx f x ωωω=-(0)ω>的最小正周期为π．（Ⅰ）求ω的值及函数()f x 的最大值和最小值； （Ⅱ）求函数()f x 的单调递增区间．16. （本小题共13分）甲、乙两人为了响应政府“节能减排”的号召，决定各购置一辆纯电动汽车．经了解目前市场上销售的主流纯电动汽车，按续驶里程数R （单位：公里）可分为三类车型，A ：80≤R ＜150，B ：150≤R ＜250， C ：R ≥250．甲从A ，B ，C 三类车型中挑选，乙从B ，C 两类车型中挑选，甲、乙二人选择各类车型的概率如下表：若甲、乙都选C 类车型的概率为310. （Ⅰ）求p ，q 的值；（Ⅱ）求甲、乙选择不同车型的概率；记甲、乙两人购车所获得的财政补贴和．为X ，求X 的分布列．17. （本小题共14分）在如图所示的几何体中，四边形ABCD 为正方形，PA ⊥平面ABCD ，PA //BE ，AB =P A =4，BE =2．（Ⅰ）求证：CE //平面PAD ；（Ⅱ）求PD 与平面PCE 所成角的正弦值； （Ⅲ）在棱AB 上是否存在一点F ，使得平面DEF ⊥平面PCE ？如果存在，求AFAB的值； 如果不存在，说明理由．PEDCBA18.（本小题共13分）设函数()x f x e ax =-，x R ∈．（Ⅰ）当2a =时，求曲线()f x 在点(0,(0))f 处的切线方程； （Ⅱ）在（Ⅰ）的条件下，求证： ()0f x >； （Ⅲ）当1a >时，求函数()f x 在[0,]a 上的最大值．19.（本小题共14分）已知椭圆C ：22221(0)x y a b a b+=>>的离心率为，右顶点A 是抛物线28y x =的焦点．直线l ：(1)y k x =-与椭圆C 相交于P ，Q 两点．（Ⅰ）求椭圆C 的方程；（Ⅱ）如果AM AP AQ =+，点M 关于直线l 的对称点N 在y 轴上，求k 的值．20.（本小题共13分）如果数列A ：1a ，2a ，…，m a (Z m ∈，且3)m ≥，满足：①Z i a ∈，22i m ma -≤≤(1,2,,)i m =； ②121m a a a +++=，那么称数列A 为“Ω”数列．（Ⅰ）已知数列M ：-2，1，3，-1；数列N ：0，1，0，-1，1．试判断数列M ，N 是否为“Ω”数列；（Ⅱ）是否存在一个等差数列是“Ω”数列？请证明你的结论；（Ⅲ）如果数列A 是“Ω”数列，求证：数列A 中必定存在若干项之和为0．（考生务必将答案答在答题卡上，在试卷上作答无效）丰台区2015年高三年级第二学期数学统一练习（一）数 学（理科）参考答案一、填空题：本大题共6小题，每小题5分，共30分．9．22π 10．4，24 11．612．(1,0)- 13．3 14．1，6π+ 注：第10，13，14题第一个空填对得3分，第二个空填对得2分．二、解答题：15.（本小题共13分）解：（Ⅰ）21()coscos2222xxx f x ωωω=+-21sin 232cos 1-++=x x ωω x x ωωc o s 21s i n 23+=)6s i n (πω+=x ． 因为πωπ==2T ，0>ω，所以2=ω．因为)62sin()(π+=x x f ，R x ∈，所以1)62sin(1≤+≤-πx ．所以函数()f x 的最大值为1，最小值为-1． ……………………8分（Ⅱ）令226222πππππ+≤+≤-k x k )(Z k ∈， 得322322ππππ+≤≤-k x k )(Z k ∈， 所以63ππππ+≤≤-k x k )(Z k ∈．所以函数()f x 的单调递增区间为3[ππ-k ，]6ππ+k )(Z k ∈．……………………13分16.（本小题共13分）解：（Ⅰ）因为33410115q p q =⎧⎪+=⎨+⎪⎪⎪⎩所以25p =，25q =． ……………………4分 （Ⅱ）设“甲、乙选择不同车型”为事件A ，则121233()554545P A ⨯+⨯=+=．答：所以甲、乙选择不同车型的概率是35． ……………………7分 （Ⅲ）X 可能取值为7，8，9，10．111(7)5420P X ==⨯=， 13211(8)54544P X ==⨯+⨯=， 21232(9)54545P X ==⨯+⨯=； 233(10)5410P X ==⨯=．……………………13分17.（本小题共14分） 解：（Ⅰ）设PA 中点为G ，连结EG ，DG ．因为PA //BE ，且4PA =，2BE =， 所以BE //AG 且BE AG =，所以四边形BEGA 为平行四边形． 所以EG //AB ，且EG AB =．因为正方形ABCD ，所以CD //AB ，CD AB =所以EG //CD ，且EG CD =． 所以四边形CDGE 为平行四边形． 所以CE //DG ．因为DG ⊂平面PAD ，CE ⊄平面PAD ，所以CE //平面PAD ． ……………………4分（Ⅱ）如图建立空间坐标系，则(4,0,0)B ，(4,4,0)C ，(4,0,2)E ，(0,0,4)P ，(0,4,0)D ，所以(4,4,4)PC =-，(4,0,2)PE =-，(0,4,4)PD =-．设平面PCE 的一个法向量为(,,)m x y z =，所以00200m PC x y z x z m PE ⎧⋅=+-=⎧⎪⇒⎨⎨-=⋅=⎩⎪⎩．令1x =，则112x y z =⎧⎪=⎨⎪=⎩，所以(1,1,2)m =．设PD 与平面PCE 所成角为α，则sin cos ,6m PD m PD PD mα⋅=<>===． 所以PD与平面P C 所成角的正弦值是． ……………………9分 （Ⅲ）依题意，可设(,0,0)F a ，则(4,0,2)FE a =-，(4,4,2)DE =-．设平面DEF 的一个法向量为(,,)n x y z =，则0220(4)200n DE x y z a x z n FE ⎧⋅=-+=⎧⎪⇒⎨⎨-+=⋅=⎩⎪⎩．令2x =，则224x a y z a =⎧⎪⎪=⎨⎪=-⎪⎩，所以)4,2,2(-=a a n ．因为平面DEF ⊥平面PCE ，所以0m n ⋅=，即08222=-++a a，所以4512<=a ， 点12(,0,0)5F ． 所以35AF AB =． ……………………14分18.（本小题共13分）解：（Ⅰ）当2a =时，()2x f x e x =-，(0)1f =，所以()2x f x e '=-．因为0(0)21f e '=-=-，即切线的斜率为1-， 所以切线方程为1(0)y x -=--，即10x y +-=． ……………………4分（Ⅱ）证明：由（Ⅰ）知()2x f x e '=-．令()0f x '=，则0ln 2x =．当(,ln 2)x ∈-∞时，0)('<x f ，()f x 在(,ln 2)-∞上单调递减， 当(ln 2,)x ∈+∞时，0)('>x f ，()f x 在(ln 2,)+∞上单调递增， 所以当ln 2x =时，函数最小值是ln 2(ln 2)2ln 222ln 20f e =-=->．命题得证． ……………………8分（Ⅲ）因为()x f x e ax =-，所以()x f x e a '=-．令()0f x '=，则ln 0x a =>．当1a >时，设()ln M a a a =-，因为11()10a M a a a-'=-=>， 所以()ln M a a a =-在(1,)+∞上单调递增，且(1)1ln11M =-=，所以()ln 0M a a a =->在(1,)+∞恒成立，即ln a a >． 所以当(0,ln )x a ∈，()0f x '<，()f x 在(0,ln )a 上单调递减；当(ln ,)x a a ∈，()0f x '>，()f x 在(ln ,)a a 上单调递增． 所以()f x 在[0,]a 上的最大值等于{(0),()}max f f a ， 因为0(0)01f e a =-⋅=，2()a f a e a =-，不妨设2()()(0)1a h a f a f e a =-=--(1a >)， 所以()2a h a e a '=-．由（Ⅱ）知()20a h a e a '=->在(1,)+∞恒成立，所以2()()(0)1a h a f a f e a =-=--在(1,)+∞上单调递增． 又因为12(1)1120h e e =--=->，所以2()()(0)10a h a f a f e a =-=-->在(1,)+∞恒成立，即()(0)f a f >． 所以当1a >时，()f x 在[0,]a 上的最大值为2()a f a e a =-． ……………………13分19.（本小题共14分）解：（Ⅰ）抛物线28y x =，所以焦点坐标为(2,0)，即(2,0)A ， 所以2a =．又因为c e a ==，所以c = 所以2221b a c =-=， 所以椭圆C的方程为2214x y +=． ……………………4分 （Ⅱ）设11(,)P x y ，22(,)Q x y ，因为AM AP AQ =+，(2,0)A ，所以11(2,)AP x y =-，22(2,)AQ x y =-，所以1212(4,+)AM AP AQ x x y y =+=+-， 所以()12122,M x x y y +-+．由2214(1)x y y k x ⎧+=⎪⎨⎪=-⎩，得2222(41)8440k x k x k +-+-=（判别式0∆>），得2122282224141k x x k k -+-=-=++，121222(2)4+1ky y k x x k -+=+-=， 即2222(,)4141k M k k --++． 设3(0,)N y ， 则MN 中点坐标为3221(,)41412y kk k --+++，因为M ，N 关于直线l 对称，所以MN 的中点在直线l 上，所以3221(1)41241k y k k k --+=-++，解得32y k =-，即(0,2)N k -． 由于M ，N 关于直线l 对称，所以M ，N 所在直线与直线l 垂直，所以 222(2)4112041kk k k k ---+⋅=---+，解得2k =±． ……………………14分20.（本小题共13分）解：（Ⅰ）数列M 不是“Ω”数列；数列N 是“Ω”数列． ……………………2分（Ⅱ）不存在一个等差数列是“Ω”数列． 证明：假设存在等差数列是“Ω”数列，则由121m a a a +++= 得12m a a Z m+=∉，与i a Z ∈矛盾， 所以假设不成立，即不存在等差数列为“Ω”数列． ……………………7分 （Ⅲ）将数列A 按以下方法重新排列：设n S 为重新排列后所得数列的前n 项和（n Z ∈且1n m ≤≤），任取大于0的一项作为第一项，则满足1122m mS -+≤≤， 假设当2,n m n N ≤≤∈时，1122n m mS --+≤≤若10n S -=，则任取大于0的一项作为第n 项，可以保证122n m mS -+≤≤，若10n S -≠，则剩下的项必有0或与1n S -异号的一项，否则总和不是1， 所以取0或与1n S -异号的一项作为第n 项，可以保证122n m m S -+≤≤． 如果按上述排列后存在0n S =成立，那么命题得证；否则1S ，2S ，…，m S 这m 个整数只能取值区间[1,]22m m -+内的非0整数， 因为区间[1,]22m m -+内的非0整数至多m -1个，所以必存在i j S S =(1)i j m ≤<≤，那么从第1i +项到第j 项之和为0i j S S -=，命题得证．综上所述，数列A 中必存在若干项之和为0． ……………………13分（若用其他方法解题，请酌情给分）。