
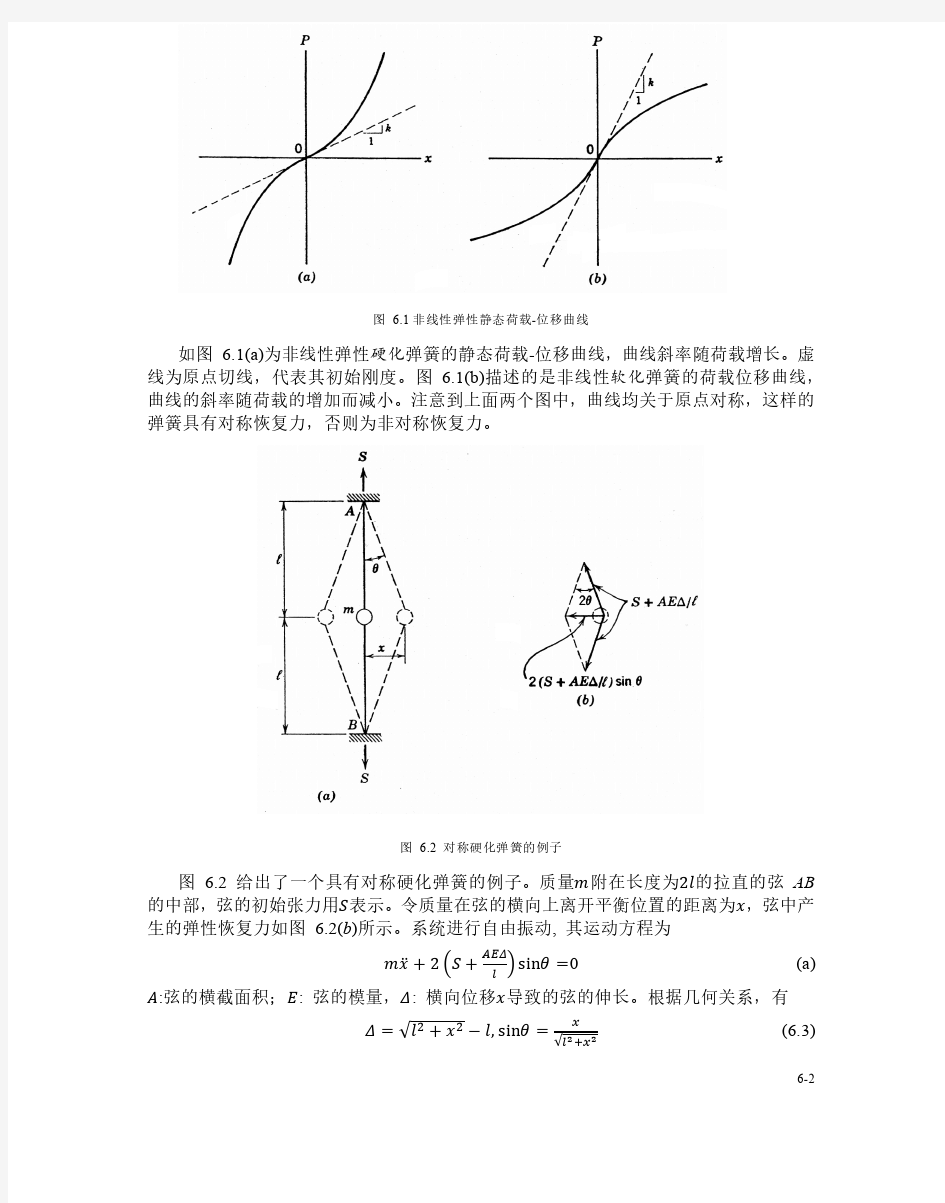
目录 1.两端铰支偏置转子的瞬态涡动分析 (1) 1.1转子动力学模型三维立体示意图:(UG) (3) 1.2转子动力学模型二维平面示意图:(CAD) (4) 1.3导出两端弹性支承刚性薄单盘偏置转子的瞬态涡动微分方程: (5) 1.3.1偏置转子在平动坐标系中的动量矩 (5) 1.3.2在平动坐标系中外力矩的表达 (7) 1.3.3在平动坐标系中定点转动微分方程 (7) 1.4形心稳态自由涡动时的频率方程,画出涡动角速度与自转角速度的关系曲线图: . 8 1.4.1同步涡动的临界转速: (9) 1.4.2稳态自由涡动角速度与自转角速度的关系: (9) 1.4.3涡动角速度与自转角速度的关系曲线如下: (10) 1.5mathematic源代码 (11) 2. 威尔逊-- 法求解等加速时的瞬态涡动幅频特性 (12) 2.1 分析 (12) 2.2 MATLAB编程求解 (16)
两端铰支偏置转子的瞬态涡动分析 已知:设有两端铰支偏置单盘转子,两端的滚动轴承简化为铰支座,弹性轴跨长57,l cm =直径 1.5,d cm =弹性模量62622.110/20.5810/E Kg cm N cm =?=?,材料密度337.810/Kg cm ρ-=?。固定在离支承1/4处的圆盘厚2cm =,直径16D cm =,若不计重力影响与系统阻尼,圆盘的转动惯量近似按薄圆盘计算。?为自转角位移,取222 5.7/35.814/rad s rad s ?π=?=。假设无质量偏心,不计重力影响,外力矩的作用是保证转子作等加速转动。 求: ①画出转子动力学模型三维立体示意图,导出两端铰支承刚性薄单盘偏置转子的瞬态涡动微分方程; ②应用Mathematic 软件求解该转子形心稳态自由涡动时的频率方程,画出涡动角速度与自转角速度的关系曲线图; ③应用Wilson θ-数值方法求解等加速度时的瞬态涡动的幅频特性,并画出涡动振幅与自转角速度的幅频关系曲线图和瞬态涡动响应时间历程曲线。
非线性振动的研究包括理论分析方法和数值分析方法。其中理论分析方法有是沿着两个方向发展,第一是定性方法,第二是定量方法,也称为解析法。 定性方法是对方程解的存在性、唯一性、周期性和稳定性等的研究;定量方法是对方程解的具体表达形式、数量大小和解的数目等的研究。数值方法目前已广泛用于计算非线性振动系统,是一种求解非线性方程的有效方法。 本文在查询相关文献的基础上,对非线性振动理论的分析方法最新研究成果做简要概括和分析比较。 1、平均法 平均法是求解非线性振动最常见和最实用的近似方法之一。其基本思想是设待解微分方程与派生方程具有相同形式的解,只是振幅和相位随时间缓慢变化。将振幅和相位的导数用一个周期的平均值替代,得到平均化方程,求解平均化方程,得到振幅和相位的表达式,从而求解出原方程的近似解析解。 1.1利用平均法分析多自由度非线性振动 平均法主要是用在单自由度非线性振动的分析中,是一种求近似解的方法,虽然精度较低,但可避免繁琐的中间运算,具有便于应用的突出优点。将其推广的到多自由度系统,导出了平均化方程,由此能够得到多自由度非线性振动的幅频特性。 1.2用改进平均法求解自由衰减振动 用平均法求解自由衰减振动方程时,无论是线性阻尼还是平方阻尼,
在阻尼常量很小的情况下,平均法解均有较高的精度。但随阻尼常量的增加,阻尼对振动周期的影响已不能忽略,此时平均法解的结果与实际振动情况有了明显的偏离,需要改进。改进平均法是将待解微分方程的圆频率与派生方程圆频率的差异函数表示为阻尼系数的多项式。 2、FFT多谐波平衡法分析非线性系统 非线性动力系统的响应可能含有几个主导频率,且有可能与激振频率不成倍数关系。现有的单一谐波法和多谐波法仅限于系统响应主导频率为激振频率的非线性系统,因此在某些情况下使用单一谐波法或多谐波法研究非线性系统动力学特性是不可靠的,而基于快速傅立叶变换(FFT)和主导频率的 FFT 多谐波平衡法能够依据所有的主导频率构筑多谐波平衡方程,因此其解析解精确度高,并能广泛适用于单倍周期、多倍周期、与初始条件有关的多解性及拟周期响应等典型的非线性特征响应。 3、等效小参数法求解强非线性系统 等效小参量法是将谐波平衡法和扰动法相结合用于求高阶非线性系 统近似解的一种比较有效的方法,这种方法不仅适用于弱非线性系统,而且适用于强非线性系统,其近似解能较好地反映系统特性。在求解弱非线性系统时,扰动法和等效小参量法均具有较高的精确度,但对于强非线性系统,等效小参量法表现出较明显的优势。 参考文献: 【1】王海期.非线性振动.高等教育出版社.1992
%% Let N=10 clear N=10; %this control the plane size %generate the alpha-beta plane; [a b]=meshgrid(-0.5:1/N:0.5,0.5:-1/N:-0.5); x=-0.5:0.01:0.5; y=zeros(1,length(x)); x_old=-0.6; counter=1; w=1/(N*(N-1))/2; %x increases for i=1:1:length(x) for j=1:N-1 for k=1:N-j if x(i)>=b(j,k) temp=1; elseif x(i)<=a(j,k) temp=0; else if x_old<=a(j,k) temp=0; elseif x_old>=b(j,k) temp=1; end end y(counter)=y(counter)+temp*w; end end counter=counter+1; end % figure % % plot(x,y,'r') x1=x; y1=y; %x decreases x=0.5:-0.01:-0.5; y=zeros(1,length(x));
x_old=0.6; counter=1; for i=1:1:length(x) for j=1:N-1 for k=1:N-j if x(i)>=b(j,k) temp=1; elseif x(i)<=a(j,k) temp=0; else if x_old<=a(j,k) temp=0; elseif x_old>=b(j,k) temp=1; end end y(counter)=y(counter)+temp*w; end end counter=counter+1; end figure plot([x1 x],[y1 y],'r'); %% Let N=100 N=100; %this control the plane size [a b]=meshgrid(-0.5:1/N:0.5,0.5:-1/N:-0.5);%generate the alpha-beta plane; x=-0.5:0.01:0.5; y=zeros(1,length(x)); x_old=-0.6; counter=1; w=1/(N*(N-1))/2; %x increases for i=1:1:length(x) for j=1:N-1 for k=1:N-j if x(i)>=b(j,k)
考虑由非线性弹簧和线性阻尼组成的质量-弹簧系统在简谐激振力作用下的受迫振动,动力学方程为: 30mx cx kx F cos t ++=ω 30mx cx kx F cos t '''++=ω 取参数值:m=1.0,c=0.05,k=1.0,F 0=7.5,ω=1.0,以及初始条件:()()11x 0 3.0,x 0 4.0== 求解:令()()()()12 u t x t u t x t =??'=?,则原方程变换为: ()()()()()()()()()121123022121212u t u t f t,u ,u F c k u t cos t-u t u t f t,u ,u m m m u 0 3.0u 0 4.0 '==???'=ω-=???=?=?? 根据Runge-Kutta 方法构造如下数值迭代计算公式: [][]1,i 11,i 111213142,i 12,i 21222324h u u k 2k 2k k 6h u u k 2k 2k k 6++?=++++????=++++?? 其中 ()() 111i 1,i 2,i 121i 1,i 112,i 21131i 1,i 122,i 22141i 1,i 132,i 23k f x ,u ,u h h h k f x ,u k ,u k 222h h h k f x ,u k ,u k 222k f x h,u hk ,u hk ?=????=+++ ???????? ?=+++ ?????=+++??
() () 212i 1,i 2,i 222i 1,i 112,i 21232i 1,i 122,i 22242i 1,i 132,i 23k f x ,u ,u h h h k f x ,u k ,u k 222h h h k f x ,u k ,u k 222k f x h,u hk ,u hk ?=?? ? ?=+++ ??????? ? ?=+++ ???? ?=+++?? 020406080100120140160 1 2 3 4 -4-3 -2 -1 1 2 3 4
振动与冲击 第!"卷第#期$%&’()*%+,-.’)/-%()(012%34,567!"(57#!88 ! !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! #非对称转子9轴承9基础系统的非线性振动" 沈松:郑兆昌!应怀樵" (:7北京大学力学与工程科学系,北京:88;<:;!7清华大学工程力学系,北京:888;#; "7东方振动和噪声技术研究所,北京:888;=) 摘要对柔性轴两端支承在滑动轴承上的转子,考虑非对称圆盘的陀螺力矩和弹性基础的振动,使用圆短轴承的非稳态非线性油膜力模型,建立了:8自由度的转子9轴承9基础系统运动方程,并通过数值方法计算系统稳态响应,分析了系统的非线性振动形式以及弹性基础的振幅调制对转子振动的影响。 关键词:转子系统,非线性振动,分叉,基础 中图分类号:/2:""7",%"!!文献标识码:) 8引言 在工程旋转机械中,研究转子系统稳定性的一个重要方面就是由滑动轴承非线性油膜力的作用而产生的各种非线性振动,目前已有大量文献对此进行了多方面的研究,文[:]研究了柔性轴支承的对称转子非线性特性,文[!]使用了非稳态油膜模型描述滑动轴承的非线性油膜力,文["]研究了非稳态油膜力下柔性轴支承的非对称陀螺转子模型,文[#]则建立了包括基础的简化的"自由度转子系统。 虽然转子系统的非线性振动常常由于滑动轴承的油膜力引起,但近年来许多理论和试验表明[=],为更好地反映转子系统动力特性,应当考虑基础的影响。基础部分的振动将与转子9轴承部分的振动相互影响,根据文["]的结果,转子9轴承部分的振动除旋转频率成分外,当出现油膜涡动时还会有半频或大约半频的成分,该半频可能同基础的固有频率比较接近,因此转子9轴承9基础系统中除旋转频率和半频外,不仅可能出现一阶临界转速频率,还可能出现基础的固有频率,这两种由于共振出现的频率都会对系统的稳定性造成不良影响。 为此本文在柔性轴非对称转子系统的基础上,又考虑弹性基础在垂直方向上的振动对整个转子系统的作用,使用文[!]的非稳态油膜力模型,建立了:8个自由度的非对称转子9非稳态油膜轴承9基础系统运动方程,并通过(>?@ABC9!积分和(>?D5E9’AFGH I5E法相结合的数值方法,计算转子在不同转速参数的瞬态响应,反映了弹性基础的共振形式。 :转子9轴承9基础系统模型 通常建立的转子轴承系统,两端的轴承座是不运动的。现在假设轴承座是固定在一个大质量的刚体基础上,基础与地面为弹性连接,个有一定的位移和转动,形成一个转子9轴承9基础系统。由于工程实际中基础位移在水平方向远小于垂直方向,因此本文仅考虑基础垂直方向的振动。 图:表示的是转子9轴承9基础系统在%JK(垂直面)和%LK(水平面)平面上的投影,).为柔性轴, 图:转子9轴承9基础系统力学模型示意 圆盘位于轴的%点,由于%点不处于).的中点,而具有陀螺力矩作用。30为基础,轴与基础通过在)、.两点的滑动轴承油膜力相互作用,基础在垂直方向J 上考虑位移和转动,将其视作平面内的刚体运动,假设具有位移和转角,在水平方向L上的位移和转动一般较J方向小得多而忽略。这样的转子9轴承9基础系统就成为一个:8自由度系统。 "国家重点基础研究项目((57M:NN;8!8":O)和国家自然科学基金项目((57:NN
非线性振动 期 末 作 业 任课老师: 姓名: 学号: 专业: 课程:非线性振动
非线性振动的理论研究方法 非线性振动是指恢复力与位移不成正比或阻尼力不与速度一次方成正比的系统的振动。尽管线性振动理论早已相当完善,在工程上也已取得广泛和卓有成效的应用,但在实际问题中,总有一些用线性理论无法解释的现象。一般说,线性模型只适用于小运动范围,超出这一范围,按线性问题处理就不仅在量上会引起较大误差,而且有时还会出现质上的差异,这就促使人们研究非线性振动。 通过理论分析对非线性振动进行研究是目前最有效最基本最直接的方式。理论研究分析最主要的任务是通过理论的研究分析来揭示各类非线性系统振动的基本理论和主要特点。非线性振动理论研究分析的最重要的数学工具就是微分方程。学者们在微分方程发展过程中发现用初等函数表达方程解的可能性极为有限之后,出现了三个比较重要的方向。其一是引入新的函数作为解的表达,并研究这些函数的性质和数值解。非线性振动中有个别的问题就可以用这种方法来求解方程,例如摆的大幅振动解用椭圆函数表达。然而这方面的例子是极为有限的。这就说明只有极少数非线性微分方程能够求出方程的解,所以通常必须用近似的求解方法求出非线性微分方程的近似解,这就需要用到求解非线性微分方程的两个最基本的方法,这就是定性方法和定量方法。定性理论不通过解的表达式来研究分析解的性质,比如利用几何法作出微分方程所定义的积分曲线,运用稳定性理论引入另外的函数中,通过它们去研究解的性质。把常微分方程定性理论与非线性振动联系起来主要应归功于前苏联的Andronov等建立起来的学派。这些学者们把定性理论用来解决电学和力学中出现的大量非线性振动问题。定性理论在发展的过程中,一方面在理论上形成了许多讨论奇点、周期解、极限环的定理、判据等,一方面形成了一些实用的作图方法,例如等倾线法、Lienard法、点映射等。 求解非线性微分方程近似解的方法中定量分析的方法包括数值解法以及解析法。定量分析方法中的解析法是最基本的分析研究方法,使用解析法来进行研究分析最主要的任务是通过理论的研究分析来揭示各类非线性系统振动的基本理论和主要特点。使用解析方法法求解非线性微分方程近似解的方法有:频闪法、平均法、小参数法、多尺度法、渐近法、谐波平衡法等研究分析方法。下面简单叙述一下几种分析非线性振动的方法:
第31卷第2期 Vol.31 No.2 工 程 力 学 2014年 2 月 Feb. 2014 ENGINEERING MECHANICS 190 ——————————————— 收稿日期:2012-08-24;修改日期:2013-01-29 通讯作者:曹 晖(1969―),男,四川内江市人,教授,博士,博导,从事结构抗震及结构健康监测研究(E-mail: caohui@https://www.doczj.com/doc/211526451.html,). 作者简介:郑 星(1986―),男,湖北荆州市人,硕士生,从事结构健康监测研究(E-mail: zhengx_cqu@https://www.doczj.com/doc/211526451.html,); 华建民(1974―),男,河南商丘市人,副教授,博士,从事结构工程及施工技术研究(E-mail: hjm191@https://www.doczj.com/doc/211526451.html,); 文章编号:1000-4750(2014)02-0190-05 基于非线性振动特性的预应力混凝土梁损伤识别 曹 晖1,2,郑 星1,华建民1,2,胡芝茂1 (1. 重庆大学土木工程学院,重庆 400045;2. 山地城镇建设与新技术教育部重点实验室(重庆大学),重庆 400045) 摘 要:对2根后张有粘结预应力混凝土简支梁分别进行单调加载和二级等幅值疲劳加载试验,在各级加载后对试验梁进行动测得到自由振动加速度信号,对加速度信号进行盲源分离并进行Hilbert 变换,得到各损伤状态下梁的频率-振幅曲线簇,分析其非线性振动特性随损伤状态的变化规律。结合裂缝开展情况和钢绞线的应力变化,探讨梁的非线性振动特性的变化与其损伤之间的关系。结果表明非线性振动特性适合于预应力混凝土梁的损伤 检测。 关键词:预应力混凝土梁;损伤检测;非线性动力特性;盲源分离;Hilbert 变换 中图分类号:TU311 文献标志码:A doi: 10.6052/j.issn.1000-4750.2012.08.0611 DAMAGE DETECTION OF PRESTRESSED CONCRETE BEAMS BASED ON NONLINEAR DYNAMIC CHARACTERISTICS CAO Hui 1,2 , ZHENG Xing 1 , HUA Jian-min 1,2 , HU Zhi-mao 1 (1. College of Civil Engineering, Chongqing University, Chongqing 400045, China; 2. Key Laboratory of New Technology for Construction of Cities in Mountain Area (Chongqing University), Ministry of Education, Chongqing 400045, China) Abstract: Two post-tensioning tests for bond prestressed concrete beams were used to carry out a static test and a two-stage fatigue test respectively. Under each damage level, the beams were excited by a hammer and their acceleration signals of free vibration were recorded. Then the signals were processed by the blind source separation algorithm and Hilbert transform to obtain frequency-amplitude curves, from which the change of nonlinear dynamic characteristics of the beams with the damage level was analyzed. The strain of the prestressing strand and cracking of the beams under each damage level were utilized to investigate the relation between the change of the nonlinear dynamic characteristics and the damage of the beams. The results prove that the nonlinear dynamic characteristics can be used to detect the damage of prestressed concrete beams. Key words: prestressed concrete beam; damage detection; nonlinear dynamic characteristics; blind source separation; Hilbert transform 预应力混凝土结构在使用期间,由于荷载、疲劳、腐蚀、老化及其它环境条件等众多不利因素的影响,将不可避免地产生损伤积累,导致混凝土开裂、预应力损失,甚至破坏等事故。因此,在役预应力混凝土构件的工作性能评价,是当前结构健康 监测的一个重要方面。 当混凝土构件出现裂缝后,会产生呼吸裂缝效应[1]。所谓呼吸裂缝,即裂缝在振动中时张时合。振幅小的时候,裂缝闭合,此时结构刚度较大;振幅大的时候,裂缝张开,此时结构刚度变小。随着
收稿日期:20030710 基金项目:航空科学基金项目(02C53019)资助 作者简介:刘晓宁(1976-),男(汉),山东, 博士研究生 刘晓宁 文章编号:100328728(2004)1021191203 三自由度齿轮传动系统的非线性振动分析 刘晓宁,王三民,沈允文 (西北工业大学,西安 710072) 摘 要:在建立三自由度齿轮间隙非线性动力学模型的基础上,利用增量谐波平衡法获得了受到参数激励和外部谐波激励的三自由度齿轮传动系统模型的周期响应,包括稳定和不稳定的周期轨道,并利用Floquet 理论研究其稳定性、分岔类型,对系统的参数变化进行分析,研究了系统通向混沌的倍周期分岔道路和拟周期分岔道路,绘制了系统周期解分岔图。关 键 词:齿轮转子轴承传动系统;增量谐波平衡法;Floquet 理论中图分类号:TH13 文献标识码:A N onlinear Vibrations of 32DOF G eared R otor 2B earing System LI U X iao 2ning ,W ANG San 2min ,SHE N Y un 2wen (N orthwestern P olytechnical University ,X i ′an 710072) Abstract :The incremental harm onic balance (IH B )method is used to obtain periodic m otions of a 32DOF non 2linear m odel of a geared rotor system subjected to parametric and external harm onic excitations.The stability of the periodic m otions is investigated by the Floquet theory ,the bifurcation behavior is traced.Parametric studies are performed to understand the effect of system parameters such as excitation frequency on the nonlinear dy 2namic behaviors. K ey w ords :G eared rotor bearing system ;Incremental harm onic balance (IH B )method ;Floquet theory 齿轮传动是应用最为广泛的一种机械传动形式。在齿轮传动系统中,由于齿侧间隙、支承间隙、时变刚度等因素的存在,导致系统产生强非线性振动,这种振动往往表现为系统的分叉、混沌振动现象,会对机械传动系统的工作性能和可靠性产生很大影响。因此,齿轮传动非线性系统的非线性振动研究引起了广泛的关注[2~5]。 从齿轮传动系统间隙非线性动力学研究来说,大部分的研究都是借助数值方法探讨系统分叉、混沌等现象的存在。增量谐波平衡法(IH B )作为求解非线性微分方程周期解的解析方法,具有精度高,适用于求解周期激励问题的特点,尤为重要的是能够求解出混沌吸引子内部的不稳定周期轨道,这也恰恰是实现混沌控制的目标稳定轨道。 本文综合利用增量谐波平衡法和数值方法研究三自由度齿轮传动系统的动态特性,考察系统参数对动态性能的影响,并结合应用Floquet 理论探讨了通向混沌的倍周期和拟周期分叉道路。 1 三自由度齿轮转子轴承系统的间隙非线性模型及方程 图1 三自由度非线性齿轮传动系统模型 如图1所示的三自由度非线性齿轮传动系统模型,齿轮部分包括齿轮惯量I g 1和I g 2,齿轮质量m g 1和m g 2,基圆直径d g 1和d g 2。齿轮啮合由非线性位移函数f h 和时变刚度 k h (t - ),线性粘性阻尼c h 描述。轴承和支撑轴的模型则由 等效的阻尼元件和非线性刚度元件表述。阻尼元件具有线 第23卷 第10期 机械科学与技术 V ol.23 N o.10 2004年 10月 MECH ANIC A L SCIE NCE AND TECH NO LOGY October 2004
一维非线性振动的数值求解 高雁军1吴少平2 (1.湖北民族学院物理系,恩施,445000;2.华中师范大学物理系,武汉,430079) 摘要利用四阶龙格-库塔方法数值求解了一维阻尼振动方程,所得到的结果与用解析方法得到的结果完全一致,验证了四阶龙格-库塔方法的可靠性和精度。在此基础上,数值求解了在物理中有广泛应用的几个非线性方程,说明了非线性效应对于振动的影响。 关键词振动;非线性;龙格-库塔方法 振动是一种很常见的物理现象。在线性振动理论中,研究的是系统在平衡位置附近的微小振动,它的特点之一是描述物质运动状态的物理量在某一数值附近作周期性的变化。振动的例子有很多,比如,钟摆的摆动,活塞的往复运动,固体中原子的振动,交流电路中的电流在某一电流值附近作周期性的变化等,所以振动问题具有很重要、很广泛的应用。在普通物理中讲的振动都是线性的,对于这种振动,从物理上说,非线性效应还不明显,从数学上说,振动方程中
的非线性项被忽略掉了,因而振动方程求解起来也比较容易。但严格地说,物质世界没有真正的线性振动,它只是非线性振动的近似。如果某一物理量对平衡位置有较大偏离,在处理这类振动问题时,就必须考虑非线性项的作用,从而会产生新的物理现象,因此非线性振动有重要的理论和实际意义。不过,除了少数可以精确求解的非线性方程外,对于非线性问题,在数学上要得到解析解,也只能采取一些近似的、特别的方法(如摄动法、平均法、多尺度法、KMB法等),还缺乏一种普遍的、行之有效的解析方法。随着计算机技术的飞速发展和人们对数值计算方法的深入研究,数值方法作为一种重要的手段日益受到人们的重视,数值计算也被应用到非线性振动的研究中来。 对于常微分方程的初值问题,数值方法的基本思想就是离散化,即将求解区域分成各离散点,然后直接求出各离散点上的、满足精度要求的未知函数的近似值。求解常微分方程的初值问题的数值方法有:欧拉方法、龙格-库塔法、阿达姆斯法等,其中四阶龙格-库塔法具有计算稳定、精度高的特点。本文中,采用四阶龙格-库塔方法求解了一维阻尼振动方程和在物理中有广泛应用的几个非线性方程,说明了非线性效应对于振动的影响。 1.四阶龙格-库塔公式
A.1 传递距阵法分析程序 %main_critical.m %该程序使用Riccati传递距阵法计算转子系统的临界转速及振型 %本函数中均采用国际单位制 % 第一步:设置初始条件(调用函数shaft_parameters) %初始值设置包括:轴段数N,搜索次数M %输入轴段参数:内径d,外径D,轴段长度l,支撑刚度K,单元质量mm,极转动惯量Jpp[N,M,d,D,l,K,mm,Jpp]=shaft_parameters; % 第二步:计算单元的5个特征值(调用函数shaft_pra_cal) %单元的5个特征值: %m_k::质量 %Jp_k:极转动惯量 %Jd_k:直径转动惯量 %EI:弹性模量与截面对中性轴的惯性矩的乘积 %rr:剪切影响系数 [m_k,Jp_k,EI,rr]=shaft_pra_cal(N,D,d,l,Jpp,mm); % 第三步:计算剩余量(调用函数surplus_calculate),并绘制剩余量图 %剩余量:D1 for i=1:1:M ptx(i)=0; pty(i)=0; end for ii=1:1:M wi=ii/1*2+50; [D1,SS,Sn]=surplus_calculate(N,wi,K,m_k,Jp_k,JD_k,l,EI,rr); D1; pty(ii)=D1; ptx(ii)=w1 end ylabel(‘剩余量’); plot(ptx,pty) xlabel(‘角速度red/s’); grid on % 第四步:用二分法求固有频率及振型图 %固有频率:Critical_speed wi=50; for i=1:1:4 order=i [D1,SS,Sn]=surplus_calculate(N,wi,k,m_k,Jp_k,Jd_k,l,EI,rr); Step=1; D2=D1; kkk=1; while kkk<5000
目录 一选择题部分 (2) 第一、二章非线性系统理论基础、相平面分析法 (2) 第三章Lyapunov理论基础 (4) 第四章近似线性化与精确线性化 (6) 第五章滑膜变结构部分 (7) 二判断题部分 (10) 第一、二章非线性系统理论基础、相平面分析法 (10) 第三章Lyapunov理论基础 (11) 第四章近似线性化与精确线性化 (12) 第五章滑膜变结构部分 (13)
一 选择题部分 第一、二章 非线性系统理论基础、相平面分析法 1. 在非线性系统中,系统在平衡状态下的稳定性与下列哪些因素有关:(ABC) A 结构 B 参数 C 初始条件 D 约束条件 2. 如果二阶自治系统的一条轨线驻留在一个有限域内,则下面哪些情况成立:(ABC ) A 轨线趋于一个平衡点。 B 轨线趋于一个渐进稳定极限环。 C 轨线本身就是一个极限环。 D 轨线趋于多个平衡点。 3. 下列属于非线性的现象有:(B ) A 暂态响应由系统的自然模态组成,能够得到一般解的表达式。 B 多个平衡点或多个操作点 C 存在外部输入时,系统的响应满足叠加性。 D 存在外部输入时,系统的响应满足正弦输入产生同频率正弦输出。 4. 下面哪些是常见的非线性系统性态:(ABCD ) A 多平衡点 B 极限环 C 分岔 D 混沌 5. 下列属于静态分岔的是:(D ) A 霍普夫分岔 B 庞卡莱分岔 C 闭轨分岔 D 鞍结分岔 6. 下列属于动态分岔的是:(C ) A 鞍结分岔 B 跨临界分岔 C 同宿异宿分岔 D 叉型分岔 7. 下面哪些系统是非线性的?(BC ) A. 0x x += B. 2x x x =- C.2 2(1)0mx c x x kx +-+= D. 0x ax bx ++= 8. 下面哪些说法是正确的(A ) A 自激振荡的幅值与初值无关,而线性震荡依赖于初值。 B 自激振荡的幅值与初值无关,线性震荡同样不依赖于初值。 C 自激振荡的幅值与初值相关,而线性震荡依赖于初值。
1-3单自由度系统的非线性振动 主要问题 1-3-1非线性问题的力学描述1-3-2相轨迹与奇点 1-3-3静态分叉 1-3-5 非线性系统的受迫振动1-3-4 有阻尼系统的自由振动
1-3-1 非线性问题的力学描述 力学模型 ? 非小变形 ? 非粘滞阻尼 对于振动系统的基本元素 弹簧 质量体 保守系统 阻尼 非保守系统 非线性振动问题
数学模型 0),(=+x x f x 单自由度系统动力学方程的一般形式 1-3-2 相轨迹与奇点 相平面内的相轨迹 单自由度系统振动问题 运动微分方程——解析法 相平面法——几何法 定量分析 定性分析 ),(x x f -——单位质量物体上作用的恢复力和阻尼力的合力 方程不显含时间变量,则系统称为自治系统
状态变量 令 x y =?? ?-==),(x x f y y x 则 初始条件为 0)0(,)0(: 0y y x x t ===y x (位置) (速度) 系统的运动状态 相平面 相点 相轨迹 相轨迹族方程 y x x f dx dy ),( -=!相轨迹与x 轴正交 ∞→=0 y dx dy (不同初始条件)
设(x s ,y s ) ? 由柯西微分方程解的存在唯一性定理,除奇点外,相平面上 的任何点只能通过一条积分曲线 相平面的奇点 ),(,0==s s s y x f y 相轨迹的奇点 ? 奇点处无积分曲线通过,或无数条积分曲线通过 ? 奇点处相点的移动速度为零,即相点沿通往奇点的相轨迹 运动须经过无限长时间才能到达奇点 ? 奇点的物理意义即系统的平衡状态。奇点亦称其为相平面的 平衡点 )(0==x y )0==x y (相平面内使相轨迹族的一阶微分方程的分子与分母同时为零的点
利用状态空间法对一类非线性振动系统的 数值方法研究 王建平1,2 刘宏昭2 原大宁2 苏志霄3 (1同济大学机械学院 上海,200092)(2西安理工大学机仪学院 西安,710048) (3国电电力建设研究所 北京,100055) 摘 要 提出了一类非线性振动系统的隐式解,导出了相应的数值计算方法,并对该数值方法的收敛性、误差和稳定性进行了研究。与传统的非线性振动系统的数值求解方法如:Ho ubo lt法、Wilson-θ法、New mar k-β法以及考虑高阶余项的连续线性化模型及其T ay lo r变换法相比,该方法具有更高的求解精度和效率。将该数值方法应用到结晶器四偏心式振动机构这样复杂的弹性机构非线性振动系统的研究中,取得了良好的效果,说明该方法具有一定的工程实用价值。 关键词:非线性振动;数值方法;隐式解;状态空间法 中图分类号:T H113.5;O322 目前,对于线性振动系统的理论研究已经发展得相当完善,但是对于非线性振动系统,特别是强非线性系统和非线性高阶系统,解的形式究竟有几种,至今还没有完全搞清楚[1]。然而对于部分弱非线性振动系统,目前已经发展了多种有效的近似解法,如Lindstedt-Poincaré(L-P)法、平均法、多尺度法、KBM法(三级数法)、谐波平衡法等[2]。对于一般的强非线性系统,近年来国内外学者在这一方面也开展了一系列理论研究工作,取得了不少成果。如S E Jones用参数变换法研究了大参数Duffing方程的自由振动问题[3];T D Burto n等提出了一种改进的多尺度法,分析了大参数强非线性系统的自由振动和强迫振动[4];S Brav o Yuste提出一种带有Jaco bi 椭圆函数的谐波平衡法[5]。但是无论是弱非线性问题,还是强非线性问题,所有的近似解法都有各自的特点,都是针对某一类特定的振动问题提出的近似解法。由于求解非线性方程本身的复杂性,目前还没有一种适应各种不同类型方程的通用解析法,仅有极少数非线性振动方程可以求得其精确解[1]。 因此,对于非线性系统的研究通常是首先利用数值计算方法得到系统的数值解,再采用点映射、胞映射等方法进行全局分析[6]。目前常用的数值方法有Houbo lt法、Wilso n-θ法和New mark-β法等,这些方法首先是将非线性微分方程化为对每一时间步长Δt内的线性方程(或称为线性化方程),然后按中心差分法等递推算法及各种修正形式计算非线性方程的数值解[2]。由于基于系统线性化的各种算法本身存在着一定的模型误差,即忽略线性化后高阶余项带来的误差,而中心差分法等各种算法及其修正形式只能提高线性化方程的计算精度,不能从根本上改进或修正这类模型误差[6]。另外,针对局部非线性动力系统的分块Ho ubolt法、分块Wilso n-θ和分块New mark-U法及其周期解方法也存在着同样的问题[8,9]。本文从非线性振动系统的物理空间出发,导出了一类非线性振动系统改进的状态空间模型,基于此模型提出了该类非线性振动系统的隐式解析解,给出了相应的数值计算格式,并对数值计算方法的收敛性、误差和稳定性进行了分析。与现有的非线性振动系统数值计算方法如:Houbo lt法、Wilson-θ法和New mark-U法相比,本文提出的数值计算方法具有更高的计算精度和效率。 1 非线性振动方程状态空间模型 对于自然界广泛存在的非线性振动问题,可以用下面的二阶非线性方程进行描述 第17卷第2期2004年6月 振 动 工 程 学 报 Jo urnal o f Vibra tion Engineering V ol.17No.2 Jun.2004 国家自然科学基金资助项目(编号:50075068)、陕西省教育厅科研基金资助项目(编号:O O JK181)、中国博士后基金资助项目(编号:200303321) 收稿日期:2002-06-24;修改稿收到日期:2003-11-27 DOI:10.16385/https://www.doczj.com/doc/211526451.html, k i.i ssn.1004-4523.2004.02.023
东北大学《非线性振动》学习总结 第一章非线性振动的定性分析方法 1.1 稳定性理论的基本概念 特定的运动成为系统的未受干扰的运动,简称为稳态运动,而受扰运动则是偏离稳态运动的系统的运动。李雅普诺夫关于稳定性的定义有:稳定的、渐进稳定、不稳定 李雅普诺夫直接方法的理论基础由三个定理组成:(1)若能够早可谓征订函数V(x),使得沿扰动方程解曲线计算的全导数V为半负定或等于零,则系统的未扰运动稳定。(2)若能构造可微正定函数V(x),使得沿扰动方程解曲线计算的全导数V为负定,则系统的未扰运动渐进稳定。(3)若能构造可微正定、半正定函数V(x),使得沿扰动方程解曲线计算的全导数V为正定,则系统的未扰运动不稳定。 定理:若保守系统的势能在平衡状态处有孤立极小值,则平衡状态稳定。 对于复杂的非线性系统,可以以近似的线性系统代替 可以根据一次近似方程的稳定性,判断原方程的稳定性:(1)若一次方程的所有本征实部均为负,则原方程的零解渐进稳定(2)若一次近似方程至少有一本征实部为正,则原方程的零解不稳定(3)若一次近似方程存在零实部的本征值,其余根的实部为负,则不能判断原方程的零解的稳定性 1.2相平面、相轨迹和奇点 与系统的运动状态一一对应的像平面上的点称为系统的相点,相点的移动轨迹称为相轨迹。像 平面内能使方程右边分子分母同时为零的特殊点称为相轨迹的奇点。 保守系统的相轨迹有以下特点: (1)相轨迹曲线相对横坐标对称;(2)势能曲线z=V(x)与横坐标轴的平行线z=E交点的横坐标C1,C2,C3,处,相轨迹与横坐标轴相交;(3)横坐标轴上与势能曲线的驻点相对应的点S1,
S2,S3,为奇点,因为他们满足几点的定义;(4)在势能取极小值处,设E>V(S1),则在x= S1的某个小领域内都有E大于等于V(x)。这种类型的奇点是稳定的,称为中心。(5)在势能取极大值的点x= S2处,设E小于V(S2)则在区间(C1,C2),内没有对应的相轨迹,这种类型的奇点是不稳定的,称为鞍点。通过鞍点的相轨迹称为分割线。在势能曲线的拐点x= S3,奇点为退化的鞍点,对应于不稳定的平衡态 保守系统的势能在平衡状态处有非孤立极小值,则平衡状态不稳定。 线性系统存在等时性。 分段线性系统是一类特殊的非线性振动系统,其恢复力f(x)为x的分段线性函数。 f(x)=Fsgn x 这类最简单的分段线性恢复力常见于自动控制系统,称为邦邦控制。 具有线性恢复力的保守系统的相轨迹为椭圆族。对于更复杂的分段线性系统,其相轨迹可由直线、抛物线和椭圆线拼接形成。 定理:如果区域f(x s,μ)>0位于曲线f(x s,μ)=0的上方,则平衡位置稳定,奇点为中心。如果f(x s,μ)=0的下方,则平衡位置不稳定,起点为鞍点。 曲线是那个dμ/d x s为零或取不定值所对应的点μ=μ1,μ2,μ3,都具有临界性质,因为当μ经过这些点时,奇点的个数和类型都发生突变,因此μ1,μ2,μ3,就是相轨迹的分叉点。若f(x,μ)为线性函数,则不存在分叉点,所以分叉现象只发生于非线性系统。 1.2.5相轨迹的作图法 等倾线法:另方程右边等于常数C,得到(x,y)两平面内以C为参数的曲线族,称为相轨迹的等倾线族。 列纳法:只用于线性恢复力的特殊情形 1.2.6耗散系统的自由振动 1、粘性阻尼 运动过程伴随能量耗散的机械系统称为耗散系统,如带有粘性阻尼活干摩擦的系统。 图a相轨迹是朝原点趋紧的螺线,它围绕奇点(远点)转动却始终达不到奇点的位置,这类奇点称为稳定焦点。系统的运动为衰减振动。 图b相轨迹尚未完成绕奇点转动一周既接近奇点,这类奇点称为稳定节点,系统的运动为衰减的非往复运动。
doi :10.3969/j.issn.1673-3142.2010.01.001 悬架非线性振动研究综述 周继磊,任传波 (山东理工大学交通与车辆工程学院,山东淄博255049) 摘要:现代的悬架系统的非线性是无处不在的,悬架减振器、弹簧、轮胎等都存在着明显的非线性特点,因此使用精确的非线性模型进行理论方面的研究变得很有意义,对此许多学者对非线性悬架进行了大量的理论和实验研究。本文主要阐述了当前国内外悬架非线性振动的理论研究概况和实验成果,提出了研究中所存在的一些问题和今后的发展方向,对悬架非线性振动研究具有重要意义。关键词:非线性振动;悬架系统;非线性模型;研究进展中图分类号:U463.33 文献标识码:A 文章编号:1673-3142(2010)01-0003-04 Summary of Nonlinear Dynamics Systems of Vehicle Suspension ZHOU Ji-lei ,REN C huan-bo (School of Traffic and Vehicle Engineering ,Shandong University of Technology ,Zibo 255049,China ) Abstrac t :The nonlinearity of modern suspension system is widespread.There is a clear non-linear characteristics in suspension shock absorber ,springs ,tires and so on.So it becomes very significant to use more precise theoretical nonlinear model for designing a reasonable control strategy.Many scholars have carried out a large number of theoretical and experimental research for non-linear suspension.The current theoretical and experimental research of non-linear suspension vibration at home and abroad are mainly described ,and some problems as well as the future direction of development which are to be of great significance for the Study on Nonlinear Vibration of the suspension are put forward. Keywords :non-linear dynamics ;suspension systems ;non-linear models ;summarizations 收稿日期:2009-09-08 作者简介:周继磊,男(1982-),研究生,专业:工程力学,研究方向:车辆动力学。 农业装备与车辆工程 AGRICULTURAL EQUIPMENT &VEHICLE ENGINEERING 2010年第1期(总第222期) No.12010(Totally 222) 1引言 当前汽车工业对悬架系统的机理研究在线性 分析方面已十分成熟,其结构得到不断改进,性能及控制技术也得到了提高,但在非线性研究方面还很贫乏[1] 。实际上悬架具有很强的非线性特性,如压缩阻尼小于伸张阻尼的减振器、具有干摩擦效应的变刚度钢板弹簧悬架等,这些部件的非线性特性恰恰改善了汽车的振动特性,对悬架系统的线性分析已不能精确反映实际工作情况。另外,随着悬架控制技术的发展,高性能的控制器设计是建立在对悬架系统精确的振动分析基础上的。所以,针对悬架系统,研究更符合实际的非线性模型,并分析其非线性特性对平顺性、安全性和操作舒适性的影响,不仅对悬架动力学理论发展具有重要作用,而且对悬架系统的设计与控制规划等 都具有使用价值。 2汽车悬架的力学模型 在研究汽车悬架非线性振动特性时,根据研 究情况需建立汽车悬架的力学模型。常用的汽车悬架模型有三种,即1/4车悬架模型、1/2车悬架模型和整车悬架模型。 【设计与研究】