2012年桂林市、防城港市高三第一次调研考试数学(文)试题

广西桂林市、崇左市、防城港市2013届高考第一次联合模拟考试数学试卷（文科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷注意事项：第Ⅰ卷共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

参考公式：如果事件A 、B 互斥，那么 P （A+B ）=P （A ）+P （B ） 如果事件A 、B 相互独立，那么P （A·B）＝P （A ）·P（B ）如果事件A 在一次试验中发生的概率是p ，那么n 次独立重复试验中事件A 恰好发生k次的概率k n kk n n p p C k P --=)1()(（k=0，1，2…，n ）球的表面积公式S ＝4πR 2其中R 表示球的半径 球的体积公式V ＝334R π其中R 表示球的半径一、选择题1. 已知集合A ＝{x ｜|x|≤2，x∈R}，B ＝{x ｜x ≤2，x∈Z}，则A∩B＝ A. （0，2）B. [0，2]C. {0，2}D. {0，1，2}2. 如果函数f （x ）=sin ⎪⎭⎫⎝⎛+6πωx （ω>0）的最小正周期为2π，则ω的值为A. 8B. 4C. 2D. 13. 函数y=1+2x-的反函数为y=g （x ），则g （5）=A. 2B. －2C. －4D. 44. 设S n 是等差数列{a n }的前n 项和，S 5=3（a 2+a 8），则35a a 的值为 A.61 B.31C.53 D.65 5. 在正三棱柱ABC －A 1B 1C 1中，已知AB=2，AA 1=3，则BB 1与平面AB 1C 1所成的角为A.6π B.4π C.3π D.2π 6. 下列4个数中，最大的是A. lg （lg2）B. （lg2）2C. lg 2D. lg27. 已知双曲线x 2－m 2y 2=m 2（m>0）的一条渐近线与直线2x －y+3=0垂直，则该双曲线的准线方程为A. x=±334B. x=±554C. x=±23 D. x=±25 8. 设（x －b ）8=b 0+b 1x+b 2x 2+…+b 8x 8，如果b 5+b 8=－6，则实数b 的值为A.21 B. －21 C.2 D. －29. 在△ABC 中，D 为BC 边上的点，=λ+μ，则λμ的最大值为A. 1B.21 C.31D.41 10. 已知抛物线y 2=4px （p>0）与双曲线22a x －22by =1（a>0，b>0）有相同的焦点F ，点A是两曲线的交点，且AF⊥x 轴，则双曲线的离心率为A.215+ B.2122+ C. 12+ D. 13+11. 已知三棱锥S －ABC 的所有顶点都在球O 的球面上，SA⊥平面ABC ，SA=23，AB=1，AC=2，∠BAC=60°，则球O 的表面积为A. 4πB. 12πC. 16πD. 64π12. 在8×8棋盘的64个方格中，共有由整数个小方格组成的大小或位置不同的正方形的个数为A. 64B. 128C. 204D. 408第Ⅱ卷注意事项：第Ⅱ卷共10小题，共90分。

2012 年高考文科数学真题及答案全国卷1注息事项 :1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷 (非选择题 )两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.问答第Ⅰ卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动 .用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效.3.回答第Ⅱ卷时。

将答案写在答题卡上.写在本试卷上无效·4.考试结束后 .将本试卷和答且卡一并交回。

第1 卷一、选择题：本大题共 12 小题，每小题 5 分，在每小题给同的四个选项中，只有一项是符合题目要求的。

（1）已知集合 A={ x|x2－ x－ 2<0} ， B={ x|－ 1<x<1} ，则（A）A B（B）BA（C）A=B（D）A∩B=【命题意图】本题主要考查一元二次不等式解法与集合间关系，是简单题.【解析】 A= （－ 1,2），故 B A ，故选 B.（ 2）复数 z＝3i的共轭复数是2 i（ A ）2 i（ B ）2 i（C）1 i（ D）1 i【命题意图】本题主要考查复数的除法运算与共轭复数的概念，是简单题.【解析】∵ z =3 ii ，∴ z 的共轭复数为 1 i ，故选D.= 12i（3）在一组样本数据（ x1， y1），（ x2， y2），⋯，（ x n， y n）（n≥ 2， x1,x2, ⋯ ,x n不全相等）的散点图中，若所有样本点（x i，y i）(i=1,2, ⋯, n) 都在直线y 1x 1 y=1x+1上，则这组样本22数据的样本相关系数为（A）－ 1（B）0（C）1（D）1 2【命题意图】本题主要考查样本的相关系数，是简单题.【解析】有题设知，这组样本数据完全正相关，故其相关系数为1，故选 D.12x2y2=1（a＞ b ＞0）的左、右焦点，P 为直线 x3a（4）设F,F是椭圆E：a2b2上一2点，△ F2PF1是底角为300的等腰三角形，则 E 的离心率为A .1B .2C .3D .4 2345【命题意图】本题主要考查椭圆的性质及数形结合思想，是简单题.【解析】∵△F2 PF1是底角为300的等腰三角形，∴ PF 2A600， | PF 2 | | F 1F 2 | 2c ，∴ | AF 2 | = c ，∴2c3a ，∴e =3，故选 C.24（ 5）已知正三角形 ABC 的顶点 A(1,1) ，B(1,3) ，顶点 C 在第一象限，若点（x ，y ）在△ ABC内部，则 zxy 的取值范围是（A ）(1－ 3，2)（ B ） (0， 2)（ C ）( 3－ 1，2)（ D ） (0， 1+ 3)【命题意图】本题主要考查简单线性规划解法，是简单题.【解析】有题设知C(1+ 3 ,2)，作出直线l 0：xy 0 ，平移直线l 0，有图像知，直线 l : zx y 过B点时， z max=2，过 C 时，z min =1 3 ，∴ z x y 取值范围为(1－3，2)，故选 A.（ 6）如果执行右边的程序框图，输入正整数N ( N ≥2)和实数a 1，a 2，⋯，a N ，输出A ，B ，则A . A + B 为a 1，a 2，⋯，a N 的和ABB .为a 1，a 2，⋯，a N 的算术平均数C .A 和B 分别为a 1，a 2，⋯，a N 中的最大数和最小数D . A 和 B 分别为a 1，a 2，⋯，a N 中的最小数和最大数【命题意图】本题主要考查框图表示算法的意义，是 简单题 .【解析】由框图知其表示的算法是找大值和最小值，A 和B分别为 a 1， a 2，⋯， a N 中 的最大数和最小数，故选C.（7）如图，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则几何体的体积为A .6B .9C .12D .18【命题意图】本题主要考查简单几何体的三视图及体积计算，是简单题 .【解析】由三视图知，其对应几何体为三棱锥，其底面为一边长为 6，这边上高为 3，棱锥的高为 3，故其体积为116 33 =9，32故选 B.(8) 平面α截球 O 的球面所得圆的半径为1，球心 O 到平面α的距离为 2，则此球的体积为（ A ） 6π（ B ） 4 3π（C ） 4 6π（ D ） 6 3π【命题意图】【解析】N 个数中的最（ 9）已知>0，0，直线x =和x =5是函数f ( x) sin( x ) 图像的两条44相邻的对称轴，则=（ A ）ππ π 3π4（B ）3 （C ）2 （D ）4【命题意图】本题主要考查三角函数的图像与性质，是中档题.【解析】由题设知，5，∴ =1，∴= k（ k Z ），=4442∴= k （ kZ ），∵0，∴ =，故选 A.44（ 10）等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 216x 的准线交于 A 、B 两点，| AB |=4 3，则C 的实轴长为A .2B .2 2C .4D .8.【命题意图】本题主要考查抛物线的准线、直线与双曲线的位置关系，是简单题【解析】由题设知抛物线的准线为： x 4 ，设等轴双曲线方程为：x 2 y 2 a 2，将x 4代入等轴双曲线方程解得y =16 a 2 ，∵| AB|=43，∴2 16a 2 = 4 3 ，解得 a =2，∴ C 的实轴长为4，故选 C.(11)当 0< x ≤1时，4xlog a x ，则a 的取值范围是222（A ）(0，2 ) （B ）( 2 ， 1) （C ） (1， 2) （D ） ( 2，2)【命题意图】本题主要考查指数函数与对数函数的图像与性质及数形结合思想， 是中档题 .0 a12 【解析】由指数函数与对数函数的图像知11，解得a2 ，故选 A.loga242（ 12）数列 { a n } 满足a n 1( 1)n a n2n 1 ，则{ a n }的前60项和为（ A ）3690 （B ） 3660（ C ） 1845 （ D ） 1830 【命题意图】本题主要考查灵活运用数列知识求数列问题能力，是难题 . 【解析】【法 1】有题设知a 2 a 1=1，① a 3a 2=3②a 4 a 3=5③a 5 a 4=7， a 6 a 5=9， a 7 a 6=11， a 8a 7=13， a 9 a 8=15， a 10 a 9=17， a 11a 10=19， a 12a1121 ，⋯⋯∴②－①得 a 1a 3=2，③+②得 a 4 a 2=8，同理可得 a 5 a 7=2， a 6 a 8=24， a 9a 11=2，a10a 12=40，⋯，∴ a 1 a 3，a 5 a 7，a 9 a 11，⋯，是各项均为 2 的常数列，a 2a 4，a 6a 8，a 10a 12，⋯是首项为8，公差为 16 的等差数列，∴ { a n } 的前 60 项和为 15 215 8116 15 14 =1830.2【法 2】可证明：bn 1a4 n 1a4n 2a4 n 3a4 n 4a4 n 3a4n 2a4 n 2a 4n 16b n16b 1a 1a 2 a 3 a 4 1 01 5 1 4 S 1510 1516 18302第Ⅱ卷二．填空题：本大题共 4 小题，每小题 5 分。

绝密*启用前2012年普通高等学校招生全国统一考试（新课标卷）文科数学注息事项:1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.问答第Ⅰ卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动.用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效.3.回答第Ⅱ卷时。

将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

1、已知集合A={x |x 2－x －2<0}，B={x |－1<x <1}，则（A ）A ⊂≠B （B ）B ⊂≠A （C ）A=B （D ）A ∩B=∅ （2）复数z ＝－3+i2+i 的共轭复数是（A ）2+i （B ）2－i （C ）－1+i （D ）－1－i 3、在一组样本数据（x 1，y 1），（x 2，y 2），…，（x n ，y n ）（n ≥2，x 1,x 2,…,x n 不全相等）的散点图中，若所有样本点（x i ，y i ）(i =1,2,…,n )都在直线y =12x +1上，则这组样本数据的样本相关系数为（A ）－1 （B ）0 （C ）12 （D ）1（4）设F 1、F 2是椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，P 为直线x =3a2上一点，△F 1PF 2是底角为30°的等腰三角形，则E 的离心率为（ ） （A ）12 （B ）23 （C ）34 （D ）455、已知正三角形ABC 的顶点A(1,1)，B(1,3)，顶点C 在第一象限，若点（x ，y ）在△ABC 内部，则z =－x+y 的取值范围是（A ）(1－3，2) （B ）(0，2) （C ）(3－1，2) （D ）(0，1+3)（6）如果执行右边的程序框图，输入正整数N(N ≥2)和实数a 1,a 2,…,a N ，输出A,B ，则 （A ）A+B 为a 1,a 2,…,a N 的和（B ）A ＋B2为a 1,a 2,…,a N 的算术平均数（C ）A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数 （D ）A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数（7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（A）6（B）9（C）12（D）18(8)平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π（9）已知ω>0，0<φ<π，直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴，则φ= （A ）π4 （B ）π3 （C ）π2 （D ）3π4（10）等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 2=16x 的准线交于A ，B 两点，|AB|=43，则C 的实轴长为（A ） 2 （B ）2 2 （C ）4 （D ）8(11)当0<x ≤12时，4x <log a x ，则a 的取值范围是（A ）(0，22) （B ）(22，1) （C ）(1，2) （D ）(2，2) （12）数列{a n }满足a n +1＋(－1)n a n ＝2n －1，则{a n }的前60项和为（A ）3690 （B ）3660 （C ）1845 （D ）1830第Ⅱ卷本卷包括必考题和选考题两部分。

广西老牌高中2012届高三第一次调研联考卷（语文）1下列词语中加点的字，读音全都正确的一项是（）A．渐染（jiān）绮丽（qǐ）前倨后恭（jù）矫揉造作（jiā）B．发酵（iào）档案（dàng）杀一儆百（jǐng）解甲归田（jiě）C．瞻仰（zhān）术讷（nè）瑕瑜互见（jiàn）剑拔弩张（nù）D．削价（xuē）内讧（hòng）厚古薄今（bó）不容置喙（huì）【答案解析】D2下列各句中，加点的成语使用恰当的一项是（）A．蒂姆·库克长勒以来其实已在掌管苹果公司，乔布斯两次病休期间，实干家库克都临危授命负责苹果的日常运营工作。

B．近年来，高考、英语四六级考试、各种资格证考试的作弊现象蔚然成风，国家对此应加大执法力度，以保障考试的严肃性和公信力。

C．袁隆平培育出杂交水稻亩产9266公斤，再创新纪录，用“大师”一词已不足以形容其贡献，称他为“活着的国宝”才是实至名归。

D．购物能给女人带来幸福感，特别是面对打折等促销活动，那种以便宜的价格买到自己心仪的物品的快乐，更是男人所不可理喻的。

【答案解析】C3下列各句中，没有语病的一句是（）A．以文化产业的升级推动城市软实力的提升，最根本的就是耍抓住文化产业的本质属性，在经营性和公益性上做好文章。

B．只有新闻工作者走出高楼大院，跳出文山会梅，走进基层的广阔天地，才能挖掘到取之不尽的鲜活素材，采写出打动人心的精品报道。

C．中国经济能否顺利渡过危机，不仅取决于宏观经济政策调整是否及时得当，而且取决于整个社会的和谐稳定．这也考验著各级政府的执政能力。

D．据中央电视台报道，中国第一艘航母此次试航为厂方测试，具体测试包括引擎、电子系统、导航设备、大力控制等内容组成。

【答案解析】A4依次填入下面一段文字横线处的语句，衔接最恰当的一组是（）我国已进入老龄化社会，65岁及以上的老年人已达1.5亿。

广西防城港市数学高三文数第一次高考模拟统一考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）已知集合，则（）A . {x｜0＜x＜}B . {x｜＜x＜1}C . {x｜0＜x＜1}D . {x｜1＜x＜2}2. （2分） (2019高二下·宁夏月考) 计算的结果是（）A .B .C .D .3. （2分） (2018高二上·马山期中) 等比数列中，，，则与的等比中项是A .B . 4C .D .4. （2分）从5双不同的手套中任取4只，恰有两只是同一双的概率为（）A .B .C .D .5. （2分） (2015高三上·滨州期末) 如图，是一个程序框图，运行这个程序，则输出的结果为（）A .B .C .D .6. （2分） (2019高一上·蚌埠月考) 函数，，则函数的最大值与最小值之差为（）A .B .C .D .7. （2分）已知，若向区域上随机投一点P，则点P落入区域A的概率为（）A .B .C .D .8. （2分）(2019·定远模拟) 定义：如果函数的导函数为，在区间上存在，使得，，则称为区间上的“双中值函数“ 已知函数是上的“双中值函数“，则实数m的取值范围是A .B .C .D .9. （2分） (2017高二上·大庆期末) 将8个半径为1实心铁球溶化成一个大球，则这个大球的半径是（）A . 8B . 2C . 2D .10. （2分）设分别为双曲线的左，右顶点，若双曲线上存在点使得两直线斜率，则双曲线的离心率的取值范围为（）A .B .C .D .11. （2分）(2017·菏泽模拟) 一个几何体的三视图如图所示，则该几何体的体积为（）A . 3B . 4C . 5D . 612. （2分）(2018·河北模拟) 若函数图像上存在两个点，关于原点对称，则对称点为函数的“孪生点对”，且点对与可看作同一个“孪生点对”.若函数恰好有两个“孪生点对”，则实数的值为（）A . 0B . 2C . 4D . 6二、填空题 (共4题；共4分)13. （1分） (2016高一下·枣阳期中) 已知向量与的夹角是，且| |=1，| |=4，若（3+λ ）⊥ ，则实数λ=________．14. （1分） (2019高一上·浙江期中) 已知函数是奇函数，则实数m的值是________；若函数f（x）在区间[-1，a-2]上满足对任意x1≠x2 ，都有成立，则实数a的取值范围是________．15. （1分）(2017·鄂尔多斯模拟) 过抛物线C：y2=8x的焦点F作直线与C交于A、B两点，线段AB的垂直平分线交x轴于点P，则| |=________．16. （1分）定义：F（x，y）=yx（x＞0，y＞0），设数列{an}满足an= ，设Sn为数列{ }的前n项和，则Sn________1（填“＞”、“=”、“＜”）．三、解答题 (共7题；共40分)17. （5分）(2020·湖南模拟) 在中，分别为内角的对边，且.（1）求角的大小；（2）若，为的内心，求的最大值.18. （5分）如图，AB是半圆O的直径，C是半圆O上除A、B外的一个动点，DC垂直于半圆O所在的平面，DC∥EB，DC=EB=1，AB=4．（Ⅰ）证明：平面ADE⊥平面ACD；（Ⅱ）若AC=BC，求二面角D﹣AE﹣B的余弦值．19. （5分） (2017高一下·池州期末) 为了了解初三女生身高情况，某中学对初三女生身高情况进行了一次测量，所得数据整理后列出了频率分布表如下：组别频数频率145.5～149.510.02149.5～153.540.08153.5～157.5200.40157.5～161.5150.30161.5～165.580.16165.5～169.5m n合计M N（1）求出表中m，n，M，N所表示的数分别是多少？（2）画出频率分布直方图；（3）全体女生中身高在哪组范围内的人数最多？20. （5分） (2017高二上·靖江期中) 在平面直角坐标系xOy中，如图，已知椭圆C： +y2=1的上、下顶点分别为A、B，点P在椭圆C上且异于点A、B，直线AP、PB与直线l：y=﹣3分别交于点M、N．（1）设直线AP、PB的斜率分别为k1，k2，求证：k1•k2为定值；（2）求线段MN长的最小值；（3）当点P运动时，以MN为直径的圆是否经过某定点？请证明你的结论．21. （5分） (2018高二下·张家口期末) 已知，函数（是自然对数的底数）.（1）若有最小值，求的取值范围，并求出的最小值；（2）若对任意实数，不等式恒成立，求实数的取值范围.22. （10分） (2017高三上·荆州期末) 在直角坐标系xOy中，圆C的参数方程（φ为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．（1）求圆C的极坐标方程；（2）直线l的极坐标方程是2ρsin（θ+ ）=3 ，射线OM：θ= 与圆C的交点为O、P，与直线l 的交点为Q，求线段PQ的长．23. （5分）已知函数f（x）=2|x﹣2|+3|x+3|．（1）解不等式：f（x）＞15；（2）若函数f（x）的最小值为m，正实数a，b满足4a+25b=m，证明： + ≥ ．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题；共40分) 17-1、17-2、18-1、19-1、19-2、19-3、20-1、20-2、20-3、21-1、21-2、22-1、22-2、23-1、23-2、。

广西桂林市、防城港市2012届高三第一次调研联合考试语文第I卷（选择题，共30分）一、选择题（12分，每小题3分）1．下列词语中加点的字，读音完全相同的一项是（）A．绯．闻斐．然缠绵悱．恻蜚．短流长B．腈．纶粳．米数茎．华发泾．渭分明C．掮．客歼．灭熏陶渐．染三缄．其口D．韧．性烹饪．色厉内荏．万仞．高山2．下列词语中，没有错别字的一项是（）A．肇事擀面杖旁证博引迅雷不及掩耳B．诡秘吊书袋开源截流吃一堑，长一智C．玷污杀风景并行不悖口惠而实不至D．辐射忘年交作壁上观毕其功于一役3．下列各句中，加点的成语使用恰当的一项是（）A．我们来到了实习工厂，厂领导和工人们对我们的工作和生活早已做了周密的安排，他们对我们的关心真是无所不至。

B．近年很多名牌大学毕业生，除了书本知识外便身无长物，被认为缺乏一技之长而在现代职场中难以立足。

C．受“限购”政策影响，不少地产商开始对艺术品收藏蠢蠢欲动，有人预测，今后几年艺术品的拍卖价格将会持续走高。

D．近来，台湾当局领导人数典忘祖，制造麻烦，转移视线，妄图隔断中华民族的血脉，切断两岸同胞的骨肉联系。

4．下列各句中，没有语病的一句是（）A．国家财政对教育的投入必须加大，否则，投入不加大，教育产业化就一定会“泛滥成灾”。

B．那天欧盟的大使跟龙永图谈话以后，他一夜没睡着；第二天到经贸大学去作报告，血压也因此升得很高。

C．随着信息技术的日益普及，电脑成为人们学习和工作不可或缺的工具已经是不争的事实。

D．中央电视台“今日说法”栏目将推出七期特别节目，目的就是要加强未成年人的安全教育，提高他们自护自救的法律意识和能力。

二、（9分，每小题3分）阅读下面的文字，完成5～7题。

网络电影互联网已经把触角伸向了传统的娱乐方式——人们只需用鼠标点击几下，有如电影宽银幕般效果的网络电影就会扑面而来。

越来越多背负工作重压的上班族开始把每天上网看电影作为日常生活习惯，因为能在院线放映的电影毕竟有限。

2012年普通高等学校招生全国统一考试（新课标全国卷）文科数学试题一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x |x 2−x −2<0}，B={x |−1<x <1}，则（A ）A ⊂≠B （B ）B ⊂≠A （C ）A=B （D ）A ∩B=∅ （2）复数z ＝32ii-++的共轭复数是 （A ）2i + （B ）2i - （C ）1i -+ （D ）1i --（3）在一组样本数据（x 1，y 1），（x 2，y 2），…，（x n ，y n ）（n ≥2，x 1,x 2,…,x n 不全相等）的散点图中，若所有样本点（x i ，y i ）(i =1,2,…,n )都在直线112y x =+上，则这组样本数据的样本相关系数为（A ）−1 （B ）0 （C ）12（D ）1（4）设1F ,2F 是椭圆E ：2222x y a b+=1（a ＞b ＞0）的左、 右焦点，P 为直线32ax =上一点，△21F PF 是底角为030的等腰三角形，则E 的离心率为 （A ）12 （B ）23 （C ）34 D .45（5）已知正三角形ABC 的顶点A (1,1)，B (1,3)，顶点C 在第一象限，若点（x ，y ）在△ABC内部，则z x y =-+的取值范围是（A ）(1－3，2) （B ）(0，2) （C ）(3－1，2) （D ）(0，1+3) （6）如果执行右边的程序框图，输入正整数N (N ≥2)和实数1a ，2a ，…，N a ，输出A ，B ，则 （A ）A +B 为1a ，2a ，…，N a 的和 （B ）2A B+为1a ，2a ，…，N a 的算术平均数 （C ）A 和B 分别为1a ，2a ，…，N a 中的最大数和最小数（D ）A 和B 分别为1a ，2a ，…，N a 中的最小数和最大数 （7）如图，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为 （A ）6 （B ）9 （C ）12 （D ）18(8)平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π （9）已知ω>0，0ϕπ<<，直线x =4π和x =54π是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴，则ϕ=（A ）π4 （B ）π3 （C ）π2 （D ）3π4（10）等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线216y x =的准线交于A 、B 两点，||AB =43，则C 的实轴长为（A ）2 （B ）22 （C ）4 （D ）8 (11)当0<x ≤12时，4log xa x <，则a 的取值范围是（A ）(0，22) （B ）(22，1) （C ）(1，2) （D ）(2，2) （12）数列{n a }满足1(1)21nn n a a n ++-=-，则{n a }的前60项和为（A ）3690 （B ）3660 （C ）1845 （D ）1830二．填空题：本大题共4小题，每小题5分。

桂林市、防城港市2012年高三第一次调研理科综合能力测试本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题)两部分。

考试结束后，将本试题卷和答题卡一并交回。

第Ⅰ卷注意事项：1．答题前，考生在答题卡上务必用直径0．5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。

请认真核准条形码的准考证号、姓名和科目。

2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动，用橡皮擦干净后,再选涂其他答案标号，在试题卷上作答无效。

3．第Ⅰ卷共21小题,每小题6分，共126分。

可能用到的相对原子质量：H一1 C一12 N-14 O-16 Al一27 S一32 K一39 Cr 一52 I一127 Ba-137一、选择题（本题包括13小题一每小题给出的四个选项中，只有一项是符合题目要求的)1．胸腺嘧啶脱氧核苷(简称胸苷）在细胞内可以转化为胸腺嘧啶脱氧核糖核苷酸，后者足合成DNA的原料。

用含有3H-胸苷的营养液，处理活的菜豆的幼根处，一定时间后洗去游离的3H-胸苷。

连续48小时检测F图a和b部位（a是分生区)，则随生长进程，a和b部位的放射性含量变化情况为( ）2．下列有关植物生长素的说法，正确的是( ）A．能合成生长素的细胞一定能进行光合作用B．生长素的化学本质是吲哚乙酸，该化合物含有矿质元素C、H、O、NC．适宜茎生长的一定浓度的生长素也一定促进根的生长D．植物的向光性现象不能体现生长素作用的两重性3．下列关于人类疾病的叙述,正确的是A．糖尿病患者血糖浓度过高，组织细胞供糖过剩，出现糖尿B．肝脏分泌胆汁不足是患脂肪肝的原因C．用DNA探针检测镰刀型细胞贫血症，利用了DNA分子杂交的原理D．艾滋病是遗传病，因HIV使效应B细胞大量死亡，导致患者免疫能力低下4．对基因型为Aa的二倍体生物相关图的叙述中,正确的是( ）A．甲图细胞含有1个染色体组，其子细胞为次级精母细胞B．甲图有可能含有等位基冈（不考虑变异）C．乙图b过程，一个细胞可能出现两条X染色体D．乙图d过程，染色体复制导致染色体数量加倍5．北极比目鱼中有抗冻基因,其编码的抗冻蛋白具有11个氨基酸的重复序列，科研人员利用比目鱼抗冻基因成功获得转基因抗冻番茄植株,有关叙述正确的是( )A．每个插入的抗冻基因至少表达一个抗冻蛋白分子B．每个限制性内切酶识别位点至少插入一个抗冻基因C．不考虑变异，抗冻番茄成熟植株所有细胞中表达基因无差异D．通过反转录获取的目的基因,一定可用于基因工程和比目鱼基因组测序6．日本核泄漏事故发生后,核电站附近检测到放射性原子131I。

（11）已知 ， ， ，则（ ）.
【考点】对数函数
【难度】中等
【点评】本题考查对数函数的相关性质。在高一数学强化提高班上学期课程讲座2，第四章《初等函数》有详细讲解，在高考精品班数学（文）强化提高班中有对指数函数、对数函数相关知识的总结讲解。
（12）正方形 的边长为1，点 在边AB上，点 在边 上， ，动点 从 出发沿直线向 运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角，当点p第一次碰到E时，p与正方形的边碰撞的次数为（ ）.
面授课程
·1对1个性化辅导
·小升初：中小学教育网学习中心
2012年普通高等学校招生全国统一考试
文科数学（必修+选修Ⅰ）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页，第Ⅱ卷3至4页。考试结束后，将本卷和答题卡一并交回。
第Ⅰ卷
注意事项：
1、答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。请认真核准条形码上的准考证号、姓名和科目。
（7）6位选手依次演讲，其中选手甲不在第一个也不在最后一个演讲，则不同的演讲次序共有（ ）.
(A)240种(B)360种(C)480种(D)720种
【考点】排列
【难度】中等
【点评】本题考查排列的定义及计算方法。在高二数学（文）强化提高班，第三章《概率》有详细讲解，在高考精品班数学（文）强化提高班中对概率、排列、组合相关知识的总结讲解。
【考点】三角函数与偶函数的结合
【难度】中等
【点评】本题考查三角函数变换，及偶函数的性质。在高一数学强化提高班上学期课程讲座1，第五章《三角函数》中有详细讲解，在高考精品班数学（文）强化提高班、百日冲刺班中均有对三角函数及向量相关知识的总结讲解。

2012年全国统一高考数学试卷（文科）（新课标）一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A={x|x2﹣x﹣2＜0}，B={x|﹣1＜x＜1}，则（）A．A⊊B B．B⊊A C．A=B D．A∩B=∅2．（5分）复数z=的共轭复数是（）A．2+i B．2﹣i C．﹣1+i D．﹣1﹣i3．（5分）在一组样本数据（x1，y1），（x2，y2），…，（x n，y n）（n≥2，x1，x2，…，x n不全相等）的散点图中，若所有样本点（x i，y i）（i=1，2，…，n）都在直线y=x+1上，则这组样本数据的样本相关系数为（）A．﹣1B．0C．D．14．（5分）设F1、F2是椭圆E：+=1（a＞b＞0）的左、右焦点，P为直线x=上一点，△F2PF1是底角为30°的等腰三角形，则E的离心率为（）A．B．C．D．5．（5分）已知正三角形ABC的顶点A（1，1），B（1，3），顶点C在第一象限，若点（x，y）在△ABC内部，则z=﹣x+y的取值范围是（）A．（1﹣，2）B．（0，2）C．（﹣1，2）D．（0，1+）6．（5分）如果执行下边的程序框图，输入正整数N（N≥2）和实数a1，a2，…，a n，输出A，B，则（）A．A+B为a1，a2，…，a n的和B．为a1，a2，…，a n的算术平均数C．A和B分别是a1，a2，…，a n中最大的数和最小的数D．A和B分别是a1，a2，…，a n中最小的数和最大的数7．（5分）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（）A．6B．9C．12D．188．（5分）平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为（）A．πB．4πC．4πD．6π9．（5分）已知ω＞0，0＜φ＜π，直线x=和x=是函数f（x）=sin（ωx+φ）图象的两条相邻的对称轴，则φ=（）A．B．C．D．10．（5分）等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于点A和点B，|AB|=4，则C的实轴长为（）A．B．C．4D．811．（5分）当0＜x≤时，4x＜log a x，则a的取值范围是（）A．（0，）B．（，1）C．（1，）D．（，2）12．（5分）数列{a n}满足a n+1+（﹣1）n a n=2n﹣1，则{a n}的前60项和为（）A．3690B．3660C．1845D．1830二．填空题：本大题共4小题，每小题5分．13．（5分）曲线y=x（3lnx+1）在点（1，1）处的切线方程为．14．（5分）等比数列{a n}的前n项和为S n，若S3+3S2=0，则公比q=．15．（5分）已知向量夹角为45°，且，则=．16．（5分）设函数f（x）=的最大值为M，最小值为m，则M+m=．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（12分）已知a，b，c分别为△ABC三个内角A，B，C的对边，c=asinC ﹣ccosA．（1）求A；（2）若a=2，△ABC的面积为，求b，c．18．（12分）某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售．如果当天卖不完，剩下的玫瑰花做垃圾处理．（Ⅰ）若花店一天购进17枝玫瑰花，求当天的利润y（单位：元）关于当天需求量n（单位：枝，n∈N）的函数解析式．（Ⅱ）花店记录了100天玫瑰花的日需求量（单位：枝），整理得如表：日需求量n14151617181920频数10201616151310（i）假设花店在这100天内每天购进17枝玫瑰花，求这100天的日利润（单位：元）的平均数；（ii）若花店一天购进17枝玫瑰花，以100天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于75元的概率．19．（12分）如图，三棱柱ABC﹣A1B1C1中，侧棱垂直底面，∠ACB=90°，AC=BC=AA1，D是棱AA1的中点．（Ⅰ）证明：平面BDC1⊥平面BDC（Ⅱ）平面BDC1分此棱柱为两部分，求这两部分体积的比．20．（12分）设抛物线C：x2=2py（p＞0）的焦点为F，准线为l，A∈C，已知以F为圆心，FA为半径的圆F交l于B，D两点；（1）若∠BFD=90°，△ABD的面积为，求p的值及圆F的方程；（2）若A，B，F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m，n距离的比值．21．（12分）设函数f（x）=e x﹣ax﹣2．（Ⅰ）求f（x）的单调区间；（Ⅱ）若a=1，k为整数，且当x＞0时，（x﹣k）f′（x）+x+1＞0，求k的最大值．22．（10分）如图，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点，若CF∥AB，证明：（1）CD=BC；（2）△BCD∽△GBD．23．选修4﹣4；坐标系与参数方程已知曲线C1的参数方程是（φ为参数），以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C2的坐标系方程是ρ=2，正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为（2，）．（1）求点A，B，C，D的直角坐标；（2）设P为C1上任意一点，求|PA|2+|PB|2+|PC|2+|PD|2的取值范围．24．已知函数f（x）=|x+a|+|x﹣2|①当a=﹣3时，求不等式f（x）≥3的解集；②f（x）≤|x﹣4|若的解集包含[1，2]，求a的取值范围．。

2012年高考桂林市、崇左市、贺州市、防城港市联合调研考试文科综合能力测试本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至6页。

第Ⅱ卷第6至8页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项：1.答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。

请认真核准条形码上的准考证号、姓名和科目.2.每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效.3.第I卷共35小题，每小题4分，共140分。

在每题给出的四个选项中，只有一项是符合题目要求。

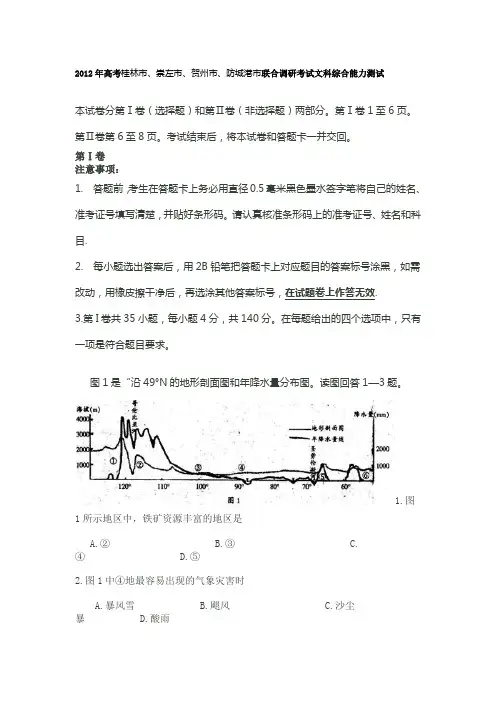
图1是“沿49°N的地形剖面图和年降水量分布图。

读图回答1—3题。

1.图1所示地区中，铁矿资源丰富的地区是A.②B.③C.④D.⑤2.图1中④地最容易出现的气象灾害时A.暴风雪B.飓风C.沙尘暴D.酸雨3.下列有关图示地区说法不正确的是A.①地比⑥地多地震，且①地比⑥地大陆架狭窄B.②地因西风溯河而上受山地抬升，降水量较大C.③地以大牧场放牧业为主，⑥地渔业资源丰富D.④地和⑤地均是以乳畜业为主的农业地域类型读图2“内蒙古山路煤炭集团光伏发电产业链模式图”，回答4～6题。

4．产业链模式图中的①②分别为A．粉煤灰、新型建筑材料厂B．供气、液化气站，C．供水、农田灌溉D．钢材、轧钢厂5．关于此发展模式的叙述，不正确的是A．立足于煤炭资源的深加工B．实现了光伏发电循环发展C．最终产出绿色环保电能D．达到了废弃物的零排放6．关于此产业链各环节的叙述，不正确的是A．煤矸石和秸秆等废弃物用于热电厂锅炉燃烧B．热电厂的蒸汽都用于多晶硅生产C．污水处理厂再生水用作热电厂冷却水源D．热电厂发电作为多晶硅生产的动力读图3“我国某地多年月平均降水量、蒸发量与各作物生育期内平均需水量关系图”，回答7~9题。

图37．该地的耕作制度为A．一年一熟B．两年三熟或一年两熟C．一年三熟D．一年两熟或一年三熟8．有关该地水资源最缺乏月份的叙述，正确的是A．降水少，只有80毫米左右B．气温回升快，大风天气多C．一年中光照最强的时候，蒸发旺盛D．正值夏玉米生长后期，需水量大9．有关该地农业可持续发展的叙述，正确的是①为缓解水资源短缺状况，扩大夏玉米的比重，降低冬小麦的比重②建设良好的水利基础设施③大规模扩大水田面积，增产粮食④推广海水淡化技术，增加水资源供给A．①② B．②③ C．①③ D．②④图4表示某地某日树影变化，F1表示当地日出时的树影，F2表示当地17时的树影，F2与F1等长，读图回答10、11题。

广西防城港市高三数学第一次模拟（期末)试卷姓名:________ 班级:________ 成绩:________一、单选题 (共4题；共8分)1. （2分）如果那么 xy>0 是 |x+y|=|x|+|y| 成立的（）A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件2. （2分） (2016高一下·汕头期末) 要得到y=sin（﹣2x+ ）的图象，只需将y=sin（﹣2x）的图象（）A . 向左平移个单位B . 向右平移个单位C . 向左平移个单位D . 向右平移个单位3. （2分）若，其中，是虚数单位，则（）A . 1B . 2C .D . 54. （2分） (2019高三上·朝阳月考) 在平面直角坐标系中，设为边长为1的正方形内部及其边界的点构成的集合．从中的任意点P作x轴、y轴的垂线，垂足分别为，．所有点构成的集合为M，M中所有点的横坐标的最大值与最小值之差记为；所有点构成的集合为N，N中所有点的纵坐标的最大值与最小值之差记为．给出以下命题：① 的最大值为：② 的取值范围是；③ 恒等于0．其中所有正确结论的序号是（）A . ①②B . ②③C . ①③D . ①②③二、填空题 (共12题；共12分)5. （1分） (2016高一上·南京期中) 函数f（x）= 的定义域为________．6. （1分）(2017·上海模拟) 若关于x，y，z的三元一次方程组有唯一解，则θ的取值的集合是________．7. （1分） (2019高一下·安徽月考) 已知函数为幂函数，则 ________．8. （1分） (2018高二下·巨鹿期末) 若复数 ,其中是虚数单位,则 ________.9. （1分）(2020·西安模拟) 若圆锥的底面半径为1，体积为，则圆锥的母线与底面所成的角等于________.10. （1分）(2017·榆林模拟) 二项式（﹣）n的展开式中所有项的二项式系数之和是64，则展开式中的常数项为________．11. （1分）(2019高一下·佛山月考) 内角的对边分别为，若，则的面积 ________．12. （1分）(2017·松江模拟) 已知数列{an}满足a1=1，a2=3，若|an+1﹣an|=2n（n∈N*），且{a2n﹣1}是递增数列、{a2n}是递减数列，则 =________．13. （1分） (2019高二下·上海月考) 已知向量，，若，且，，则 ________.14. （1分）(2020·杨浦期末) 己知六个函数:① ;② ;③ ;④ ;⑤;⑥ ,从中任选三个函数,则其中既有奇函数又有偶函数的选法共有________种.15. （1分）(2017高二下·沈阳期末) 已知为定义在上的偶函数，当时，有，且当时，，给出下列命题：① 的值为；②函数在定义域上为周期是2的周期函数；③直线与函数的图像有1个交点；④函数的值域为 .其中正确的命题序号有________ .16. （1分）(2020·海安模拟) 在平面直角坐标系中，点集A＝{（x，y）|x2+y2≤1}，B＝{（x，y）|x≤4，y≥0，3x﹣4y≥0}，则点集Q＝{（x，y）|x＝x1+x2 ， y＝y1+y2 ，（x1 ， y1）∈A，（x2 ， y2）∈B}所表示的区域的面积为________．三、解答题 (共5题；共60分)17. （10分）已知函数f（x）=2sinxsin（x+）．（1）求函数f（x）的最小正周期和单调递增区间；（2）当x∈[0，]时，求f（x）的值域．18. （10分） (2016高一上·西湖期中) 函数f（x）=loga（3﹣ax）（a＞0，a≠1）（1）当a=3时，求函数f（x）的定义域；（2）若g（x）=f（x）﹣loga（3+ax），请判定g（x）的奇偶性；（3）是否存在实数a，使函数f（x）在[2，3]递增，并且最大值为1，若存在，求出a的值；若不存在，请说明理由．19. （10分）在中，角，，所对的边分别为，，，且．（1）求角；（2）若，求及的面积．20. （15分） (2019高二上·四川期中) 已知圆C的圆心在轴的正半轴上，且轴和直线均与圆C相切．（1）求圆C的标准方程；（2）设点，若直线与圆C相交于M，N两点，且为锐角，求实数m的取值范围．21. （15分） (2019高一下·上海月考) 是定义在上且满足如下条件的函数组成的集合：①对任意的，都有②存在常数使得对任意的，都有 .（1）设问是否属于？说明理由;（2）若如果存在使得证明：这样的是唯一的；（3）设且试求的取值范围.参考答案一、单选题 (共4题；共8分)1-1、2-1、3-1、4-1、二、填空题 (共12题；共12分)5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共5题；共60分)17-1、18-1、18-2、18-3、19-1、19-2、20-1、20-2、21-1、21-2、21-3、。

2012年高考桂林市毕业班第一次模拟考试理科数学（必修+选修Ⅱ)第I 卷注意事项:1．答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。

请认真核准条形码上的准考证号、姓名和科目。

2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后，再选涂其他答案标号,在试题卷．．．．上作答无效．．．．．. 3．第I 卷共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

参考公式：如果事件A 、B 互斥,那么 球的表面积公式()()()P A B P A P B +=+ 24S R π=如果事件A 、B 相互独立，那么 其中R 表示球的半径()()()P A B P A P B = 球的体积公式如果事件A 在一次试验中发生的概率是p ，那么 343V R π=n 次独立重复试验中事件A 恰好发生k 次的概率 其中R 表示球的半径()(1)(0,1,2,)k k n kn nP k C p p k n -=-=…一．选择题(1) 点P （o300cos ，o300sin ）在直角坐标平面上位于(A)第一象限 （B ）第二象限 （C)第三象限 （D)第四象限(2） 投掷两颗骰子,得到其向上的点数分别为m 和n ，则复数2()m ni +为纯虚数的概率为（A ）13 (B)14 (C ）16 （D)112(3) 等差数列}{na 的公差为2,若a 1,a 3,a 4成等比数列，则a 2=（A ）－6 (B ）－8 （C ）8 (D ）6（4） 对于定义在R 上的奇函数)(x f ，满足)3(+x f =)(x f ,若)1(-f =1，则(1)(2)f f ++(10)f +=(A ）0 （B ）1- （C)1 (D ）10（5） 如果随机变量ξ～N (μ,σ2），且Eξ=3，Dξ=1，则P （－1＜ξ≤1）=(A ）2Φ（1）－1 (B)Φ（4）－Φ（2） （C ）Φ（2）－Φ（4) (D)Φ（－4）－Φ(－2) （6） 设函数2()()f x g x x =+,曲线()y g x =在点(1,(1))g 处的切线方程为21y x =+，则曲线()y f x =在点(1,(1))f 处切线的斜率为（A ）3 （B ）5 （C ）2 （D ）4(7) 用0，1，2，3，4这五个数字组成无重复数字的五位数,其中恰有1个偶数夹在两个奇数之间的五位数有(A ）12个 （B ）28个 （C ）36个 (D ）48个（8） 已知直线422=+=+y xa y x 与圆交于A 、B 两点，O 是坐标原点，向量OA 、OB 满足OA OB OA OB +=-，则实数a 的值是（A ）2 （B ）－2 （C ）6或－6 (D ）2或－2（9） 将函数x x f 2sin )(=的图象按向量(,0)4π=n 平移得到)(x g 的图象，则函数)(x f 与)(x g 的图象（A)关于直线83π=x 对称 (B)关于直线43π=x 对称（C)关于直线4π=x 对称 （D ）关于y 轴对称 （10） 在矩形ABCD 中，1,DC AD ==在DC 上截取1DE =，沿AE 将AED ∆翻折得到1AED ∆，使点1D 在平面ABC 上的射影落在AC 上，则二面角1D AE B --的平面角的余弦值为（A)（B)（C ）2(D)2 （11) 已知)(x f y =是其定义域上的单调递增函数,它的反函数是1()y f x -=，且(1)y f x =+ 的图象过()4,0A -、()2,3B 两点，若3|)1(|1≤+-x f ，则x 的取值范围是（A ）[0,3] （B)［－4，2] （C ）[1，3] （D ）[－1，2］ (12 ) 已知直线l 交椭圆224580xy +=于M 、N 两点，椭圆与y 轴的正半轴交于B 点，若△BMN 的重心恰好落在椭圆的右焦点上，则直线l 的方程是（A ）65280x y --= （B ）65280x y +-= （C ）56280x y +-= （D ）56280x y --=绝密★启用2012年高考桂林市第一次模拟考试理科数学(必修+选修Ⅱ）第Ⅱ卷注意事项：1．答题前，考生先在答题卡上用直径0。

广西老牌高中2012届高三第一次调研联考卷数 学 试 题（文）考生注意：1．本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，满分150分。

考试时间120分钟。

2．考生作答时，请将答案答在答题卡上，第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；第II 卷请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效。

3．本试卷主要命题范围，以集合与常用逻辑用语、函数与导数、三角函数、解三角形、平面向量、数列、不等式为主。

第I 卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．不等式1x x ≥的解集是（ ）A ．(,1)(0,1)-∞-B ．(](,1)0,1-∞-C ．(,1)[0,1]-∞-D ．(](],10,1-∞- 2．已知集合2{,},{1}M m n N ==，若M N φ≠，则M N =（ ）A ．{-1}B ．1C ．{-1，1}D ．{1，0}3．一支田径队有男运动员44人，女运动员33人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为14的样本，则抽取女运动员的人数为（ ）A ．6B ．8C ．10D ．124．若a ，b 均为正实数，则“1b a<”是“01ab <<”的 （ ） A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 5．已知等差数列{}n a 的前n 项和n S ，且*22232848,n n S S a a n N --++=∈且1n >，则1n a +等于（ ） A ．212 B ．424C ．848D ．1016 6．已知角α的终边上有一点21(,)(0)4P t t t +>，则tan α的最小值为（ ）A ．12B ．1CD ．27．在ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，且,(0)a b λ==>，45A =︒，则满足条件的三角形个数是（ ）A ．0B ．1C ．2D ．无数个 8．已知cos sin 1x x +=，则cos2x 等于（ ）A ．0B ．1C ．-1D ．1± 9．若10()x a +展开式中8x 的系数为90，则负数a 的值等于（ ）A ．B ．C ．-1D ．12- 10．在正四面体ABCD 中，点Q 在线段AD 上运动，当QB QC ⋅取得最小值时，点Q 的位置位于（ ）A ．点A 处B ．点D 处C ．靠近D 点的三等分点处 D ．线段AD 中点处11．定义在R 上的奇函数()f x 满足对任意的x 都有(1)(4)f x f x -=-且3(),(0,)2f x x x =∈，则(2012)(2010)f f -等于 （ ） A ．-1 B ．0 C ．1 D ．212．已知实数,s t 满足不等式()(2)0.s t s t -+-≥若14s ≤≤，则t s 的取值范围是（ ）A ．1[,1]4-B ．1,14⎛⎤- ⎥⎝⎦C ．1[,1]2-D ．1,12⎛⎤-⎥⎝⎦ 第II 卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分。