递延年金终值与现值的计算(有图解)

现值系数有2种：
b.复利现值系数：n
)
/
=)
(.
1(
F
P-
+
i
终值系数也有2种：
b.复利终值系数：n i
(+
/
=.
P
)
F)
1(
其中i表示利率
一般题目中现值、终值系数都会给出,但表示的方式为(P/A,i,n ),(F/A,i,n ),所以你只需记住这些公式符号代表的含义.
A是年金P是现值F是终值P/A是已知年金求现值P/F是已知终值求现值
P/A指的是年金现值，如果现金流量有多期，且每期的现金流量相同，此时计算现值时就应该使用年金现值。

P/F指的是复利现值，如果现金流量只有一期，对其进行折现时应该使用复利现值系数。

两者区分的关键是看现金流量是一期还是多期，如果是一期，就用复利现值P/F；
如果是多期，且每期的数值相等，则使用年金现值，即P/A。

其中：P=本金；i=利率；n=持有期限
THANKS !!!
致力为企业和个人提供合同协议，策划案计划书，学习课件等等
打造全网一站式需求
欢迎您的下载，资料仅供参考。

一、年金终值：年金终值是指在一段时间内，定期支付一定金额的现金流，经过一定的利率增长后所积累的总金额。

年金终值计算的目的是评估未来一段时间内现金流的价值。

年金终值的计算可以通过如下的公式进行：FV=P*((1+r)^n-1)/r其中，FV表示年金终值，P表示每期支付的金额，r表示每期支付的利率，n表示支付的期数。

例如，每年支付1000元，利率为5%，持续支付10年，则年金终值的计算为：年金终值的计算方法可以应用于各种不同的现金流情况，如每月、每季度、每半年等的现金支付。

二、年金现值：年金现值是指将未来一段时间内的现金流按照一定的利率折算到现在的价值，将未来的现金流所得到的总金额。

年金现值的计算的目的是评估未来现金流的现值，以便做出更加准确的投资决策。

年金现值的计算可以通过如下的公式进行：PV=P*(1-(1+r)^(-n))/r其中，PV表示年金现值，P表示每期支付的金额，r表示每期支付的利率，n表示支付的期数。

例如，每年支付1000元，利率为5%，持续支付10年，则年金现值的计算为：所以，每年支付1000元，利率为5%，持续支付10年，年金现值为7721.73元。

年金现值的计算方法也可以适用于各种不同的现金流情况。

三、年金终值和年金现值的应用：在投资决策中，投资者可以利用年金终值和年金现值来比较不同投资方案的收益。

通过计算不同方案的年金终值和年金现值，可以判断哪种投资方案更加有利可图，从而做出更加明智的决策。

在退休规划中，个人可以利用年金终值和年金现值来评估自己的退休金需求和储蓄目标。

通过计算所需的年金终值和现值，可以规划合理的退休储蓄计划，确保在退休时有足够的资金支持。

总之，年金终值和年金现值是评估一定时间内或一系列现金流价值的重要工具。

通过运用年金终值和年金现值的计算方法，可以帮助人们做出更加准确的投资决策和退休规划。

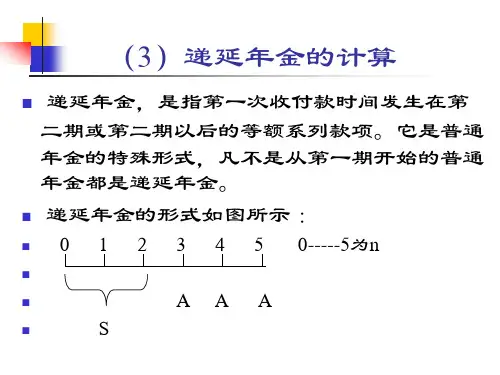
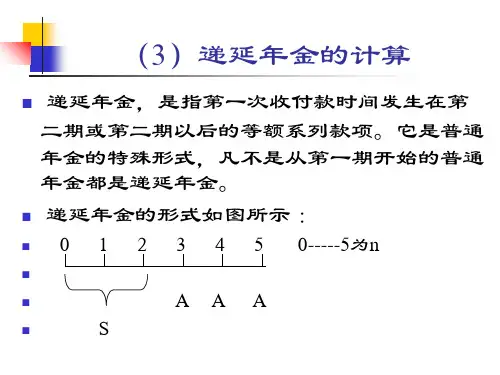
财务管理》第二章重难点讲解及例题：递延年金终值和现值递延年金终值和现值（1）递延年金终值（已知从第二期或第二期以后等额收付的普通年金A，求FA）递延年金是指第－次等额收付发生在第二期或第二期以后的普通年金。

图示如下：求递延年金的终值与求普通年金的终值没有差别（要注意期数），递延年金终值与递延期无关。

如上图中，递延年金的终值为：FA＝AX（F／A，i，n），其中，“n，，表示的是A的个数，与递延期无关。

（2）递延年金现值（已知从第二期或第二期以后等额收付的普通年金A，求PA）方法－：把递延期以后的年金套用普通年金公式求现值，这时求出的现值是第－次等额收付前－期的数值，再往前推递延期期数就得出递延年金的现值。

图示如下：PA＝AX（P／A，i，n）×（P／F，i，m）方法二：把递延期每期期末都当作有等额的收付，把递延期和以后各期看成是－个普通年金，计算这个普通年金的现值，再把递延期多算的年金现值减去即可。

图示如下：PA＝AX（P／A，i，m＋n）－A×（P／A，i，m）【提示】方法－、方法二求递延年金现值的思路是把递延年金的现值问题转换为普通年金的现值问题，再求递延年金现值。

方法三：先求递延年金的终值，再将终值换算成现值，图示如下：PA＝A×（F／A，i，n）×（P／F，i，m＋n）【提示】递延年金现值计算公式中的“n”指的是等额收付的次数，即A的个数；递延期“m”的含义是，把普通年金（第－次等额收付发生在第1期期末）递延m期之后，就变成了递延年金（第－次等额收付发生在第W期期末，W>1）。

因此，可以按照下面的简便方法确定递延期m的数值：（1）确定该递延年金的第－次收付发生在第几期末（假设为第W期末）（此时应该注意“下－期的期初相当于上－期的期末”）；（2）根据（W－1）的数值确定递延期m的数值。

【例题7.单选题】下列关于递延年金的说法中，错误的是（）。

A.递延年金是指隔若干期以后才开始发生的系列等额收付款项B.递延年金没有终值C.递延年金现值的大小与递延期有关，递延期越长，现值越小D.递延年金终值与递延期无关【答案】B【解析】递延年金是指隔若干期以后才开始发生的系列等额收付款项；递延年金存在终值，其终值的计算与普通年金是相同的；终值的大小与递延期无关；但是递延年金的现值与递延期是有关的，递延期越长，递延年金的现值越小，所以选项B的说法是错误的。

年金是指一定时期内定期支付的固定金额的现金流，可以分为年金的终值和现值两种计算方式。

一、年金的终值计算年金的终值是指在一定时期内，以固定利率计算，连续不断地进行定期支付的现金流的总金额。

假设有一个年金，每年支付2000元，年利率为5%，计算5年后的年金终值需要使用以下公式：FV=PMT×[(1+r)^n-1]/r其中FV表示年金的终值；PMT表示每年支付的金额；r表示年利率；n表示年数。

将数据代入计算公式，得到年金的终值：FV=2000×[(1+0.05)^5-1]/0.05=2000×[1.276-1]/0.05=2000×0.276/0.05二、年金的现值计算年金的现值是指在一定时期内，以固定利率计算，连续不断地定期支付的现金流的当前金额。

假设有一个年金，每年支付2000元，年利率为5%，计算当前的年金现值需要使用以下公式：PV=PMT×[1-(1+r)^-n]/r其中PV表示年金的现值；PMT表示每年支付的金额；r表示年利率；n表示年数。

将数据代入计算公式，得到年金的现值：PV=2000×[1-(1+0.05)^-5]/0.05=2000×[1-0.7835]/0.05=2000×0.2165/0.05=8659所以，当前该年金的现值为8659元。

年金的终值和现值的计算是财务管理中常用的计算方法，可以帮助人们进行投资决策和规划个人财务。

通过计算年金的终值，可以了解到未来收益的总金额，帮助人们判断投资的价值和收益能力；而通过计算年金的现值，可以了解到当前年金的价值，帮助人们做出合理的投资决策。

在实际应用中，可以使用电子表格软件（如Excel）中的相应函数或者金融计算器来进行年金的终值和现值的计算，这样更加简便和快捷。

不过，理解计算公式的推导过程对于掌握计算方法和理解计算结果的正确性是很重要的。

年金是指在一定期限内定期支付的一系列等额现金流。

年金可以分为两类：年金终值和年金现值。

年金终值是指在未来一些特定时间点的一系列等额现金流的总和。

计算年金终值的公式如下：FV=PMT*[(1+r)^n-1]/r其中FV是年金终值PMT是每期支付的金额r是每期的利率n是支付期数。

我们可以通过以下例子来说明如何计算年金终值：假设你决定每个月从现在开始存入500元，存款期限是10年，年利率是5%。

现在我们来计算这个年金的终值。

PMT=500,r=0.05/12,n=10*12=120。

带入公式计算得到：FV=500*[(1+0.05/12)^120-1]/(0.05/12)年金现值是指将未来的一系列等额现金流折算到现在的总金额。

计算年金现值的公式如下：PV=PMT*[1-(1+r)^(-n)]/r其中PV是年金现值PMT是每期支付的金额r是每期的利率n是支付期数。

以下是一个年金现值的实例：假设你决定每个月从现在开始存入500元，存款期限是10年，年利率是5%。

现在我们来计算这个年金的现值。

PMT=500,r=0.05/12,n=10*12=120。

带入公式计算得到：PV=500*[1-(1+0.05/12)^(-120)]/(0.05/12)在计算年金终值和现值时，需要注意以下几个要点：1.利率的表示方式：通常利率是年利率，需要根据支付频率进行调整。

例如，如果利率是年利率，而支付频率是每个月，则利率需要除以122.支付期数的计算：支付期数等于存款期限乘以支付频率。

例如，如果存款期限是10年，支付频率是每个月，则支付期数为10乘以12，即120期。

3.利率和支付期数的单位要一致：利率和支付期数的单位要保持一致，比如，如果利率是年利率，支付期数应该是年份；如果利率是月利率，支付期数应该是月份。

4.汇率调整：如果计算的是国际性的年金，涉及到不同货币的转换，需要根据汇率进行调整。

综上所述，年金终值和现值的计算可以通过相应的公式进行完成。

递延年金求现值方法递延年金求现值方法是在计算基于递延年金的金融产品价格时经常使用的一种数学方法。

递延年金指的是从某一未来时间点开始支付的一系列固定金额的付款。

这篇文章将介绍递延年金的定义，递延年金的现值计算方法，以及实际应用中的一些问题。

一、递延年金的定义递延年金指的是从某一未来时间点开始支付的一系列固定金额的付款。

递延年金可以用于金融产品的定价和计算，如养老金、保险等。

递延年金的关键是确定未来支付的金额和支付的时间，这两个变量通常是固定的。

二、递延年金的现值计算方法计算递延年金的现值需要考虑时间价值和递延效应。

递延效应指的是递延期间未支付的付款会产生利息，而这些利息会在付款开始后的一段时间内计算出现值，因此必须从递延年金中扣除。

递延年金的现值的计算公式如下：现值= ∑(每期支付的金额 / (1 + r) ^ n)其中，r 是折现率，n 是离现在的年数。

现值表示递延年金在当前时间点的价值。

通过计算递延年金的现值，我们可以知道，从现在开始，如果我们投资相同数量的资金，我们可以获得多少收益。

三、实际应用中的一些问题在实际应用中计算递延年金的现值时，有几个问题需要注意：1. 支付期间需要一致。

递延年金的支出必须在一定的间隔时间内一致地支付，否则现值的计算会受到影响。

2. 递延期间需要一致。

递延期间必须是固定的，否则现值的计算也会受到影响。

3. 折现率的选择对现值的计算有很大的影响。

折现率是投资者希望获得收益的利率，但通常选择的利率因人而异。

总之，递延年金是一种用于计算基于递延年金的金融产品价格的数学方法。

现值计算方法需要考虑递延效应和时间价值，而实际应用中需要注意支付期间和递延期间的一致性，并选择合适的折现率以获得正确的现值计算结果。

2015年全国会计专业技术中级资格考试内部资料财务管理第二章 财务管理基础知识点：货币时间价值的计算——递延年金终值和现值● 详细描述：（1）递延年金终值【结论】递延年金终值只与A的个数（n）有关，与递延期（m）无关。

F递=A（F/A,i,n）（2）递延年金现值方法1：两次折现。

递延年金现值P= A×（P/A, i, n）×（P/F, i, m）递延期m（第一次有收支的前一期），连续收支期n方法2：先加上后减去。

递延年金现值P=A×（P/A，i，m + n）-A×（P/A，i，m）例题：1.有一项年金，前3年无流入，后5年每年年初流入500万元，假设年利率为10%，其现值为（）万元。

A.1994.59B.1566.36C.1813.48D.1423.21正确答案：B解析：现值＝500×（P/A，10%，5）×（P/F，10%，2）＝1566.36（万元）2.某递延年金，前3年没有现金流入，后5年每年年初有等额的现金流入100万元，折现×率为10%，下列关于该递延年金现值的表达式中，不正确的是（） 。

A.100×(P/A,10%,5)×(P/F,10%,2)B.100×(P/A,10%,5)×(P/F,10%,3)C.100×[(P/A,10%,4)+1]×(P/F,10%,3)D.100×(F/A,10%,5)×(P/F,10%,7)正确答案：B解析：本题中，第一次现金流入发生在第4年初，相当于第3年末。

100×(P/A,10%,5)表示的是第3年初的现值，进一步折现到第1年初，还需要折现2期，因此，选项A的表达式正确，选项B的表达式不正确；100×[(P/A,10%,4)+1]表示的是第4年初的现值，进一步折现到第1年初，还需要折现3期，因此，选项C的表达式正确；100×(F/A，10%,5)表示的是第7年末的终值，进一步折现到第1年初，需要折现7期，因此，选项D的表达式正确。

答：
1.定义递延年金：递延年金是指以未来的货币价值来确定的一种金融产品，即受益人的金融权利在未来一些特定的时点上才发放的金融付款。

2.递延年金现值的计算方法：递延年金现值是指投资者在当前时点上将未来收取的延迟支付的金融付款转换为现在价值的过程，可以用贴现现值公式来表示：
V=P/(1+i)^n
其中：
V表示现值；
P表示未来可能收取的金融付款金额；
i表示贴现率；
n表示未来支付延期的时间。

3.根据贴现原理，同样本金及利息水平的情况下，贴现现值越高，说明未来支付的延迟时间越长，同时也是投资者收益越低。

因此，投资者在计算递延年金现值时，应根据投资的期望收益率合理设定贴现率，以确定贴现现值大小。

4.投资者不仅应根据未来可能收取的金融付款金额、未来延期支付的时间和贴现率来计算递延年金现值，而且还应根据自身的投资能力和投资目标，计算出最佳的递延年金现值，以实现投资的最佳收益。

第四节递延年金终值与现值的计算第四节递延年金终值与现值的计算钭志斌丽水职业技术学院一、递延年金递延年金（Deferred Annuity）是指第一次年金收付形式发生在第二期或第二期以后的年金。

递延年金的支付形式如图2-8所示。

12 …mm+1m+2 …m+n递延期递延年金发生的期数二、递延年金终值计算由于递延期m与终值无关只需考虑递延年金发生的期数n。

计算公式如下：12 …mm+1m+2 …m+n递延期递延年金发生的期数【例2-11】农庄的累计净收益为多少？假设江南公司拟一次性投资开发某农庄，预计该农庄能存续15年，但是前5年不会产生净收益，从第6年开始，每年的年末产生净收益5万元。

在考虑资金时间价值的因素下，若农庄的投资报酬率为10%，该农庄给企业带来累计收益为多少？12 …55+15+2 …5+10递延期5递延年金发生的期数10求该农庄给企业带来的累计收益，实际上就是求递延年金终值。

根据＝50000×（F/A，10%，10）＝50000×153>.937＝796850（元）12 …55+15+2 …5+10递延期5递延年金发生的期数10三、递延年金现值的计算递延年金的现值与递延期数相关，递延的期数越长，其现值越低。

递延年金的现值计算有三种方法：方法1：把递延期以后的年金套用普通年金公式求现值，然后再向前折现。

即：12 …mm+1m+2 …m+n递延期递延年金发生的期数方法2：把递延期每期期末都当作有等额的年金收付A，把递延期和以后各期看成是一个普通年金，计算出这个普通年金的现值再把递延期虚增的年金现值减掉即可。

即：12 …mm+1m+2 …m+n假设递延期内每期都有A收付方法3：先求递延年金终值，再折现为现值即12 …mm+1m+2 …m+n【例2-12】农庄的累计投资限额为多少？接例2-11，假设江南公司决定投资开发该农庄，根据其收益情况，该农庄的累计投资限额为多少？实质上，求现值12 …55+15+2 …5+10递延期5递延年金发生的期数10按第一种方法计算：P＝50000×（P/A，10%，10）×（P/F，10%，5）＝50000×6.1446×0.6209＝190759.11（元）按第二种方法计算：P＝50000×（P/A，10%，15）－50000×（P/A，10%，5）＝50000×7.6061－50000×3.7908＝190765.00（元）按第三种方法计算：P＝50000×（F/A，10%，10）×（P/F，10%，15）＝50000×15.9370×0.2394＝190765.89（元）计算结果表明，该农庄的累计投资限额为190759.11元。

（5）递延年金终值和现值的计算递延年金由普通年金递延形成，递延的期数称为递延期，用m表示（m为大于0的整数）。

递延年金的第一次收付发生在第（m+1）期期末。

递延年金的形式如下图：递延年金终值递延年金的终值=A×（F/A，i，n），只与年金期有关，与递延期无关。

递延年金的现值递延年金的现值，与递延期有关。

递延年金的现值计算方法【应用举例】【例题】某递延年金为从第4期开始，每期期末支付10万元，共计支付6次，假设利率为4%，相当于现在一次性支付的金额是多少？（P/A，4%，6）=5.2421，（P/F，4%，3）=0.8890，（P/A，4%，9）=7.4353，（P/A，4%，3）=2.7751。

【分析】从图上可看出，递延期m=3，年金A=10万元，n=6。

第一种方法分段折现：将6个10万元按普通年金求现值的方法折算到第3期期末，再将6年期的普通年金现值由按复利现值的方法折算到第0年。

递延年金现值P=10×（P/A，4%，6）×（P/F，4%，3）=10×5.2421×0.8890=46.60（万元）第二种方法用减法：假设递延期每期期末也都有年金10万元，这样在0时点看就构成了普通年金的形式，一共有9个10万元，可将这9个10万元求普通年金的现值，然后再减去递延期3个10万元的普通年金现值，就可求出本题递延年金的现值。

即：递延年金现值P=10×（P/A，4%，9）-10×（P/A，4%，3）=10×7.4353-10×2.7751=46.602（万元）【例题】某递延年金为从第4期开始，每期期初支付10万元，共计支付6次，假设利率为4%，相当于现在一次性支付的金额是多少？（P/F，4%，2）=0.9246，（P/A，4%，6）=5.2421。

【分析】从图上可看出，递延期m=3，年金A=10万元，n=6。

递延年金现值P=10×（P/A，4%，6）×（P/F，4%，2）=10×5.2421×0.9246=48.47（万元）递延年金现值P=10×（P/A，4%，8）-10×（P/A，4%，2）=48.47（万元）递延年金的现值计算方法【应用举例】【例题】DL公司2019年12月10日欲购置一批电脑，销售方提出三种付款方案，具体如下：方案1：2019年12月10日付款10万元，从2021年开始，每年12月10日付款28万元，连续支付5次。

终值现值系数公式终值和现值系数公式，这俩家伙在财务和金融领域那可是相当重要！咱先来说说啥是终值。

简单来讲，终值就是一笔钱在未来某个时间点的价值。

比如说，你现在有 1000 块钱，存到银行里年利率是 5%，存 3 年，那 3 年后这笔钱会变成多少呢？这就得用到终值系数公式来算一算啦。

终值系数公式是：F = P × (1 + i)^n 。

这里的 F 就是终值，P 是现值，也就是你最初的那笔钱，i 是利率，n 是期数。

举个例子哈，我有个朋友小李，他特别想攒钱买一辆心仪已久的摩托车，价格大概是 2 万块。

他现在手里有 1 万块，他想着把这 1 万块存到银行里，银行年利率是 4%。

那他得存几年才能攒够买摩托车的钱呢？咱们用终值系数公式来算算。

P = 10000，i = 4% = 0.04，F = 20000，代入公式就是 20000 = 10000 × (1 + 0.04)^n 。

先化简一下，2 = (1.04)^n 。

这时候就得用到对数来求解啦，n = log₁.₀₄ 2 。

算出来 n 大概是17.67 年。

哎呀，小李一看，这可不行，得想办法多赚点钱或者找个更高利率的存钱方式。

再来说说现值。

现值呢，就是未来的一笔钱在现在的价值。

比如说，你知道 3 年后能收到 5000 块钱，年利率还是 5%，那这 5000 块钱在现在值多少钱呢？这就用到现值系数公式：P = F / (1 + i)^n 。

还是我那朋友小李，他听说有个投资项目，3 年后能给他带来15000 块的收益，但是需要他现在投入 12000 块。

他就犯愁了，不知道这投资划不划算。

咱们用现值系数公式来帮他算算。

F = 15000，i = 5%，n = 3，P = 15000 / (1 + 0.05)^3 ，算出来 P 大概是 12957.58 块。

这说明，如果按照 5%的利率来算，3 年后的 15000 块钱在现在只值 12957.58 块，而他现在要投入 12000 块，看起来还是有点小赚的。