
例1 证明下面诸命题推得的结论是有效的: 如果今天是星期三, 那么我有一次离散数学或数字逻辑测验; 如果离散数学课老师有事, 那么没有离散数学测验; 今天是星期三且离散数学老师有事, 所以, 我有一次数字逻辑测验。
证明先将各命题形式化。
设A: 今天是星期三。B: 我有一次离散数学测验。
C: 我有一次数字逻辑测验。D: 离散数学课老师有事。
则本题要求证: A→B∨C , D→┐B , A∧D C。
(1) A∧D(前提)
(2) A ((1),I1)
(3) A→B∨C(前提)
(4) B∨C ((2), (3), I11)
(5) D ((1), I2)
(6) D→┐B(前提)
(7) ┐B((5), (6), I11)
(8) C((4), (7),I10)
例2 证明三段论方法的正确性:
凡人要死。
苏格拉底是人。
苏格拉底要死。
令H(x): x是人。
M(x): x要死。
a: 苏格拉底。
则本题要证明:x(H (x)→M (x )) , H (a ) M (a )
证明
(1) H (a ) (前提)
(2) x (H (x )→M (x ))(前提)
(3) H (a )→M (a ) ((2),US)
(4) M ( a ) ((1), (3), I11
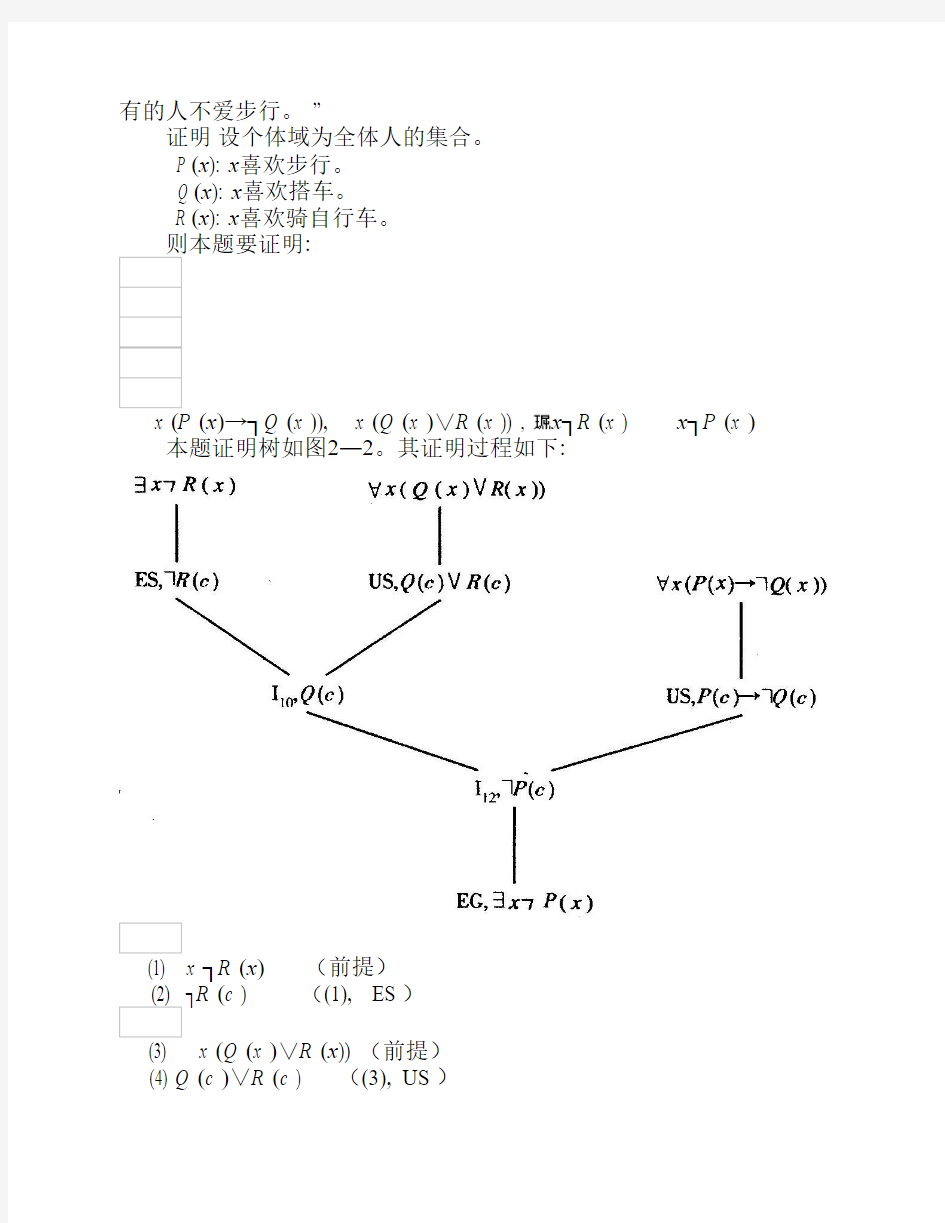
例3 用形式证明的方法证明“任何人如果他喜欢步行, 他就不喜欢乘汽车,每个人或者喜欢乘汽车或者喜欢骑自行车。有的人不爱跨自行车, 所以
有的人不爱步行。 ”
证明设个体域为全体人的集合。
P (x): x喜欢步行。
Q (x): x喜欢搭车。
R (x): x喜欢骑自行车。
则本题要证明:
x (P (x)→┐Q (x )), x (Q (x )∨R (x )) , x┐R (x ) x┐P (x )本题证明树如图2―2。其证明过程如下:
(1) x ┐R (x)(前提)
(2) ┐R (c ) ((1), ES)
(3) x (Q (x )∨R (x)) (前提)
(4) Q (c )∨R (c ) ((3), US)
(5) Q (c)((2), (4),I10)
(6) x (P (x )→┐Q (x )) (前提)
(7) P (c )→┐Q (c)((6), US)
(8) ┐P (c ) ((5), (7), I12)
(9)x┐P (x) ((8), EG)
例4 将下列推理符号化, 并推证其结论:
所有有理数是实数, 某些有理数是整数, 因此某些实数是整数。
解:设
R(x):x是实数。
Q(x):x是有理数。
I(x):x是整数。
则上述推理可符号化为:x(Q(x)→R(x)),x(Q(x)∧I(x)) x(R(x)∧I(x))。
结论推证如下:
① x(Q(x)∧I(x)) (前提)
②Q(a)∧I(a) (①,ES)
③Q(a) (②,I1)
④I(a) (②,I2)
⑤x(Q(x)→R(x)) (前提)
⑥Q(a)→R(a) (⑤,US)
⑦R(a) (③,⑥,I11)
⑧R(a)∧I(a) (④,⑦,I9)
⑨ x(R(x)∧I(x)) (⑧,EG)
∴x(Q(x)→R(x)), x(Q(x)∧I(x)) x(R(x)∧I(x))。
谓词逻辑习题 1. 将下列命题用谓词符号化。 (1)小王学过英语和法语。 (2)2大于3仅当2大于4。 (3)3不是偶数。 (4)2或3是质数。 (5)除非李键是东北人,否则他一定怕冷。 解: (1) 令)(x P :x 学过英语,Q(x):x 学过法语,c :小王,命题符号化为)()(c Q c P ∧ (2) 令),(y x P :x 大于y, 命题符号化为)3,2()4,2(P P → (3) 令)(x P :x 是偶数,命题符号化为)3(P ? (4) 令)(x P :x 是质数,命题符号化为)3()2(P P ∨ (5) 令)(x P :x 是北方人;)(x Q :x 怕冷;c :李键;命题符号化为)()(x P c Q ?→ 2. 设个体域}{c b a D ,, =,消去下列各式的量词。 (1)))()((y Q x P y x ∧?? (2)))()((y Q x P y x ∨?? (3))()(y yQ x xP ?→? (4)))()((y yQ y x P x ?→?, 解: (1) 中))()(()(y Q x P y x A ∧?=,显然)(x A 对y 是自由的,故可使用UE 规则,得到 ))()(()(y Q y P y y A ∧?=,因此))()(())()((y Q y P y y Q x P y x ∧?∧?? ,再用ES 规则, )()())()((z Q z P y Q y P y ∧∧? ,D z ∈,所以)()())()((z Q z P y Q x P y x ∧∧?? (2)中))()(()(y Q x P y x A ∨?=,它对y 不是自由的,故不能用UI 规则,然而,对 )(x A 中约束变元y 改名z ,得到))()((z Q x P z ∨?,这时用UI 规则,可得: ))()((y Q x P y x ∨?? ))()((z Q x P z x ∨??? ))()((z Q x P z ∨? (3)略 (4)略 3. 设谓词)(y x P ,表示“x 等于y ”,个体变元x 和y 的个体域都是}321 {,,=D 。求下列各式的真值。 (1))3(,x xP ? (2))1(y yP ,? (3))(y x yP x ,?? (4))(y x yP x ,?? (5))(y x yP x , ?? (6))(y x xP y , ?? 解:
§2.2 谓词公式及其解释 习题2.2 1. 指出下列谓词公式的指导变元、量词辖域、约束变元和自由变元。 (1)))()((y x Q x P x ,→? (2))()(y x yQ y x xP ,,?→? (3))())()((z y x xR z y Q y x P y x ,,,,?∨∧?? 解 (1)x ?中的x 是指导变元;量词x ?的辖域是),()(y x Q x P →;x 是约束变元,y 是自由变元。 (2)x ?中的x ,y ?中的y 都是指导变元;x ?的辖域是)(y x P ,,y ?的辖域是)(y x Q ,;)(y x P ,中的x 是x ?的约束变元,y 是自由变元; )(y x Q ,中的x 是自由变元,y 是y ?的约束变元。 (3)x ?中的x ,y ?中的y 以及x ?中的x 都是指导变元;x ?的辖域是))()((z y Q y x P y ,,∧?,y ?的辖域是)()(z y Q y x P ,,∧,x ?的辖域是)(z y x R ,,;)(y x P ,中的x ,y 都是约束变元;)(z y Q ,中的y 是约束变元;z 是自由变元, )(z y x R ,,中的x 为约束变元,y ,z 是自由变元。 2. 设个体域}21 {,=D ,请给出两种不同的解释1I 和2I ,使得下面谓词公式在1I 下都是真命题,而在2I 下都是假命题。 (1)))()((x Q x P x →? (2)))()((x Q x P x ∧? 解(1)解释1I :个体域}21 {,=D ,0:)(,0:)(>>x x Q x x P 。 (2)解释2I :个体域}21 {,=D ,2:)(,0:)(>>x x Q x x P 。 3. 对下面的谓词公式,分别给出一个使其为真和为假的解释。 (1))))()(()((y x R y Q y x P x ,∧?→? (2))),()()((y x R y Q x P y x →∧?? 解 (1)成真解释:个体域D ={1,2,3},0:)(
第五章谓词逻辑 习题5.1 1. a)每个自然数都有唯一的后继; 解:“每个”是全称的概念;“自然数”需引进一个特性谓词;“有”表示存在;“唯一”表示所有具有该性质的元素均相等(即若x具有该性质,y也具有该性质,则x等于y);“后继”用谓词表示。于是,可令: N(x):x是自然数; Q(x, y):y是x的后继; E(x, y):x等于y; 则上述命题可以符号化为: (? x) ( N ( x ) → (? y) (Q ( x, y ) ∧ (? z) (Q ( x, z ) → E ( y, z ) ) b) 没有以0为后继的自然数; 解:“没有”表示不存在;“自然数”用特性谓词表示;“后继”用谓词表示。于是,可令:N(x):x是自然数; Q(x, y):y是x的后继; 则上述命题可以符号化为: ? (? x)( N ( x ) ∧ Q ( x, 0 ) ) 注意:①对于引进的特性谓词,在全称量词约束下要用逻辑联结词“→”,在存在量词约束下要用逻辑联结词“∧”。 ②“唯一”概念的符号化。 2. a)存在唯一的偶素数; 解:“存在”是存在量词的概念;“唯一”可参照上题;“偶数”、“素数”用谓词表示。于是,可令: E(x):x是偶数; S(x):x是素数; R(x, y):x等于y; 则上述命题可以符号化为: (? x) ( E ( x ) ∧ S ( x ) ∧ (? y) ( E ( y ) ∧ S ( y ) → R ( x, y ) ) b)没有既是奇数又是偶数的数; 解:“没有”表示不存在;“奇数”、“偶数”、“数”用谓词表示。于是,可令: O(x):x是奇数; E(x):x是偶数; Q(x):x是数;
谓词逻辑表示法是把一些知识表示为经典逻辑中的谓词表示式。它只能表示出精确的知识,而对不确定的知识无法有效表示,同时这种表示方式也不能很好地体现知识的内在联系。在进行教学时,首先需要通过实例让学生了解什么是命题和命题公式,什么是谓词和谓词公式,然后用实例来分析讲解将知识表示为谓词公式的过程: 1)定义谓词和个体 例:王先生是李文的老师。首先定义谓词:TEACHER(X,Y):X 是Y 的老师,而后定义个体:王先生(Wang),李文(LiWen ); 2)为每个谓词中的变元赋以特定的值:TEACHER(Wang,LiWen); 3)根据所要表达的知识语义,以适当的连接词和量词符号将各个谓词连接起来,得到知识的谓词公式:TEACHER(Wang,LiWen)。 在理解连接词∧(逻辑与)、∨(逻辑或)、┐(逻辑非)时可以参考我们平时的语言 中的“并且”、“或者”、“不”,对P →Q 的理解可以参考┐P ∨Q 。在此节只要求学生对谓词表示法有了解,命题的证明等内容不做要求,可以将相关内容放在辅助教学网站的拓展篇,以满足不同学生的需求。 在教学中除了书本中介绍的例子之外,还可以使用以下例子。 例1:用谓词逻辑和公式表达意境。 分析如下命题和谓词逻辑,并尽可能正确表达它的含义: (1) 蓝的(天)∧飘(白云)∧奔跑(马儿)∧飞翔歌唱(鸟儿); 答:这是一个由“与”关系连接起来的谓词逻辑公式,它表达了一种大自然的景观:蓝色的天上白云飘飘,马儿在奔跑,鸟儿在飞翔歌唱。 (2) )(x {好姑娘(x )∧居住的地方(z,x) ∧遥远的(z) ∧(y)[人(y) ∧行走 经过(y,z) →回头留恋地张望(y)]} 答:这是一个既有谓词表示,又有命题逻辑表达,既有连接词,又有全称量词和存在量词的较复杂的谓词公式,它表达的意思是:在那遥远的地方,有位好姑娘,人们经过她的身旁,都要回头留恋地张望。这就是青海民歌《在那遥远的地方》(王洛宾词曲)中的意境。 例2:用谓词逻辑表示知识单元。 设有下述记录:①小李给小王送礼物;②小李是工程师;③小王是程序员;④小李的地址是南京路115号;⑤小王的地址是黄山路458号。 请用谓词逻辑(中或英文)表示上述记录,并分成必要的知识单元。 答:1)定义谓词,GIVE(x,y,p),x 给Y 送礼物p ; OCCUPATION(x,y),X 是Y 职业; ADDRESS (x,y ),x 的地址是Y ; 2)定义个体 小李(xiaoli),小王(xiaowang),工程师(engineer ),程序员(programmer)、 南京路115号(115-nianjing-road ),黄山路458号(458-huangshan-road)。 3)知识谓词公式: ① GIVE(xiaoli,xiaowang,presents); ② OCCUPATION(xiaoli,engineer); ③ OCCUPATION (xiaowang,programmer ); ④ ADDRESS (xiaoli,115-nianjing-road ); ⑤ ADDRESS(xiaowang,458-huangshan-road);
? 离散数学基础 2017-11-19 ?定义:个体和谓词 ?在原子命题中,描述的对象称为个体,用于描述个体的性质或个体之间的关系部分称为谓词。 ?例:张三是个大学生。 ?个体:张三;谓词:是个大学生 ?例:张三和李四是表兄弟。 ?个体:张三、李四;谓词:是表兄弟(关系) ?习惯上,用小写字母 a, b, c, … 表示个体,大写字母 P, Q, R, … 表示谓词。 ?例:a:张三;b:李四; P(x):x 是个大学生;Q(x, y):x 和 y 是表兄弟。 则:P(a):张三是个大学生; P(b):李四是个大学生; Q(a, b):张三和李四是表兄弟。 ?定义:原子命题的谓词形式 ?一个原子命题用一个谓词常项(如 P)和 n 个有次序的个体常量(如 a1, a2, …, a n)表示成 P(a1, a2, …, a n),称为该原子命题的谓词形式。 ?例:Q(a, b):张三和李四是表兄弟。 ?当讨论的个体处于一个论述范围时,个体常量被个体变量取代。如 Q(x, y)。?定义:n 元原子谓词 ?由一个谓词(如 P)和 n 个个体变量(如 x1, x2, …, x n)组成的 P(x1, x2, …, x n),称为 n 元原子谓词,或简称 n 元谓词,或 n 元命题函数。 ?一个 n 元谓词 P(x1, …, x n) 只有 P 取谓词常项,且其中所有个体变量均取得个体常项时,该谓词才成为命题。 ?特别地将命题看成是0元谓词。 ?定义:个体论域 ?个体变量 x i 的论述范围(取值范围)称为 x i 的论域或变程。 ?全总论域:将一个 n 元谓词的各个个体论域综合在一起,称为该谓词的全总
一. 利用代换实例判断下列公式的类型 (1) (?xA(x)→?xA(x))→(??yB(y)∨?yB(y)) (2) ?(?xF(x)→?xB(x))∧?xB(x) 二. 利用等值演算, 求证?x?y(P(x)→Q(y))??xP(x)→?yQ(y) 三. 利用等值演算, 求证??x?y(F(x) ∧(G(y) →H(x,y))) ??x?y((F(x) →G(y))∧( F(x) →? H(x,y))) 一. 利用代换实例判断下列公式的类型 (1) (?xA(x)→?xA(x))→(??yB(y)∨?yB(y)) (2) ?(?xF(x)→?xB(x))∧?xB(x) 二. 利用等值演算, 求证?x?y(P(x)→Q(y))??xP(x)→?yQ(y) 三. 利用等值演算, 求证??x?y(F(x) ∧(G(y) →H(x,y))) ??x?y((F(x) →G(y))∧( F(x) →? H(x,y))) 一. 利用代换实例判断下列公式的类型 (1) (?xA(x)→?xA(x))→(??yB(y)∨?yB(y)) (2) ?(?xF(x)→?xB(x))∧?xB(x) 二. 利用等值演算, 求证?x?y(P(x)→Q(y))??xP(x)→?yQ(y) 三. 利用等值演算, 求证??x?y(F(x) ∧(G(y) →H(x,y))) ??x?y((F(x) →G(y))∧( F(x) →? H(x,y))) 一. 利用代换实例判断下列公式的类型 (1) (?xA(x)→?xA(x))→(??yB(y)∨?yB(y)) (2) ?(?xF(x)→?xB(x))∧?xB(x) 二. 利用等值演算, 求证?x?y(P(x)→Q(y))??xP(x)→?yQ(y) 三. 利用等值演算, 求证??x?y(F(x) ∧(G(y) →H(x,y))) ??x?y((F(x) →G(y))∧( F(x) →? H(x,y))) 一. 利用代换实例判断下列公式的类型 (1) (?xA(x)→?xA(x))→(??yB(y)∨?yB(y)) (2) ?(?xF(x)→?xB(x))∧?xB(x) 二. 利用等值演算, 求证?x?y(P(x)→Q(y))??xP(x)→?yQ(y) 三. 利用等值演算, 求证??x?y(F(x) ∧(G(y) →H(x,y))) ??x?y((F(x) →G(y))∧( F(x) →? H(x,y))) 一. 利用代换实例判断下列公式的类型 (1) (?xA(x)→?xA(x))→(??yB(y)∨?yB(y)) (2) ?(?xF(x)→?xB(x))∧?xB(x) 二. 利用等值演算, 求证?x?y(P(x)→Q(y))??xP(x)→?yQ(y) 三. 利用等值演算, 求证??x?y(F(x) ∧(G(y) →H(x,y))) ??x?y((F(x) →G(y))∧( F(x) →? H(x,y))) 一. 利用代换实例判断下列公式的类型 (1) (?xA(x)→?xA(x))→(??yB(y)∨?yB(y)) (2) ?(?xF(x)→?xB(x))∧?xB(x) 二. 利用等值演算, 求证?x?y(P(x)→Q(y))??xP(x)→?yQ(y) 三. 利用等值演算, 求证??x?y(F(x) ∧(G(y) →H(x,y))) ??x?y((F(x) →G(y))∧( F(x) →? H(x,y))) 一. 利用代换实例判断下列公式的类型 (1) (?xA(x)→?xA(x))→(??yB(y)∨?yB(y)) (2) ?(?xF(x)→?xB(x))∧?xB(x) 二. 利用等值演算, 求证?x?y(P(x)→Q(y))??xP(x)→?yQ(y) 三. 利用等值演算, 求证??x?y(F(x) ∧(G(y) →H(x,y))) ??x?y((F(x) →G(y))∧( F(x) →? H(x,y)))
第二节 谓词公式的分类与解释 为了给出谓词公式的定义,先给出项和原子公式的定义。 定义2.1 项: (1) 个体常项和个体变项是项; (2) 设),...,,(21n x x x ?是任意的n 元函数,n t t t ,...,,21是项,则),...,,(21n t t t ?是项; (3) 有限地使用(1),(2)形成的符号串是项。 定义2.2 设),...,,(21n x x x R 是任意的n 元谓词,n t t t ,...,,21是项,则称),...,,(21n t t t R 是原子公式。 定义2.3合式公式: (1) 原子公式是合式公式; (2) 若A 是合式公式,则)(A ?也是合式公式; (3) 若B A ,是合式公式,则)(),(),(),(B A B A B A B A ?→∨∧也是合式公式; (4) 若A 是合式公式,则(),()xA xA ??也是合式公式。其中x 为任意的个体变项; (5) 有限次地应用(1)~(4)形成的字符串是合式公式。 这样定义的合式公式又称作谓词公式,简称公式。合式公式的最外层括号可以省去。 定义2.4 (1) 在公式xA ?和xA ?中,A 是相应量词的辖域,x 称为指导变量。 (2) 在公式xA ?和xA ?中,x 的所有出现都是约束出现的,不是约束出现的变项称 为自由出现的。 例如:在公式))),,()((),((z y x L y G y y x F x ∧?→?中,?的辖域为 ))),,()((),((z y x L y G y y x F ∧?→ ?的辖域为 )),,()((z y x L y G ∧ x ?中的x 和y ?中的y 都是指导变量。x 的出现都是约束的,),(y x F 中的y 是自由出现的,)(y G 与),,(z y x L 中的y 是约束出现的,z 的出现是自由的。 一般情况下,在一个谓词公式A 中,除了可能含若干个个体常项,函数常项,谓词常 项外,还可能含个体变项,函数变项,谓词变项等。用下面定义对公式进行解释。 定义2.5 一个解释I 由下面4个部分构成: (1) 非空的个体域D ; (2) D 上一部分特定的元素; (3) D 上一些特定的函数;
第二章谓词逻辑 练习一 1、指出下列谓词公式中的量词及其辖域,指出各自由变元和约束变元,并回答它们是否是命题: (1)?x(P(x)∨Q(x))∧R (R为命题常元) (2)?x(P(x)∧Q(x))∧?xS(x)→T(x) (3)?x(P(x)→?y(B(x,y)∧Q(y))∨T(y)) (4)P(x)→(?y?x(P(x)∧B(x,y))→P(x)) 解(1)全称量词?,辖域P(x)∨Q(x),其中x为约束变元,?x(P(x)∨Q(x))∧R是命题。 (2)全称量词?,辖域P(x)∨Q(x),其中x为约束变元。 存在量词?,辖域S(x) ,其中x为约束变元。 T(x)中x为自由变元。?x(P(x)∧Q(x))∧?xS(x)→T(x)不是命题。 (3)全称量词?,辖域P(x)→?y(B(x,y)∧Q(y))∨T(y),其中x为约束变元,T(y)中y为自由变元。存在量词?,辖域B(x,y)∧Q(y),其中y为约束变元。?x(P(x)→?y(B(x,y)∧Q(y))∨T(y))是命题。 (4)全称量词?,辖域?x(P(x)∧B(x,y)),其中y为约束变元。 存在量词?,辖域P(x)∧B(x,y),其中x为约束变元。 不在量词辖域中的P(x)中的x为自由变元。P(x)→(?y?x(P(x)∧B(x,y))→P(x)) 不是命题。 2、对个体域{0,1}判定下列公式的真值, E(x)表示“x是偶数”: (1)?x(E(x)→┐x=1) (2)?x(E(x)∧┐x=1) (3)?x(E(x)∧x=1) (4)?x(E(x)→x=1) 再将它们的量词消去,表示成合取或析取命题公式,鉴别你所确定的真值是否正确。
排列组合公式/排列组合计算公式 2008-07-08 13:30 公式P是指排列,从N个元素取R个进行排列。 公式C是指组合,从N个元素取R个,不进行排列。 N-元素的总个数 R参与选择的元素个数 !-阶乘,如9!=9*8*7*6*5*4*3*2*1 从N倒数r个,表达式应该为n*(n-1)*(n-2)..(n-r+1); 因为从n到(n-r+1)个数为n-(n-r+1)=r 举例: Q1:有从1到9共计9个号码球,请问,可以组成多少个三位数? A1: 123和213是两个不同的排列数。即对排列顺序有要求的,既属于“排列P”计算范畴。 上问题中,任何一个号码只能用一次,显然不会出现988,997之类的组合,我们可以这么看,百位数有9种可能,十位数则应该有9-1种可能,个位数则应该只有9-1-1种可能,最终共有9*8*7个三位数。计算公式=P(3,9)=9*8*7,(从9倒数3个的乘积) Q2: 有从1到9共计9个号码球,请问,如果三个一组,代表“三国联盟”,可以组合成多少个“三国联盟”? A2: 213组合和312组合,代表同一个组合,只要有三个号码球在一起即可。即不要求顺序的,属于“组合C”计算范畴。 上问题中,将所有的包括排列数的个数去除掉属于重复的个数即为最终组合数C(3,9)=9*8*7/3*2*1 排列、组合的概念和公式典型例题分析 例1设有3名学生和4个课外小组.(1)每名学生都只参加一个课外小组;(2)每
名学生都只参加一个课外小组,而且每个小组至多有一名学生参加.各有多少种不同方法? 解(1)由于每名学生都可以参加4个课外小组中的任何一个,而不限制每个课外小组的人数,因此共有种不同方法. (2)由于每名学生都只参加一个课外小组,而且每个小组至多有一名学生参加,因此共有种不同方法. 点评由于要让3名学生逐个选择课外小组,故两问都用乘法原理进行计算. 例2 排成一行,其中不排第一,不排第二,不排第三,不排第四的不同排法共有多少种? 解依题意,符合要求的排法可分为第一个排、、中的某一个,共3类,每一类中不同排法可采用画“树图”的方式逐一排出: ∴ 符合题意的不同排法共有9种. 点评按照分“类”的思路,本题应用了加法原理.为把握不同排法的规律,“树图”是一种具有直观形象的有效做法,也是解决计数问题的一种数学模型. 例3判断下列问题是排列问题还是组合问题?并计算出结果. (1)高三年级学生会有11人:①每两人互通一封信,共通了多少封信?②每两人互握了一次手,共握了多少次手? (2)高二年级数学课外小组共10人:①从中选一名正组长和一名副组长,共有多少种不同的选法?②从中选2名参加省数学竞赛,有多少种不同的选法? (3)有2,3,5,7,11,13,17,19八个质数:①从中任取两个数求它们的商可以有多少种不同的商?②从中任取两个求它的积,可以得到多少个不同的积? (4)有8盆花:①从中选出2盆分别给甲乙两人每人一盆,有多少种不同的选法?②从中选出2盆放在教室有多少种不同的选法? 分析(1)①由于每人互通一封信,甲给乙的信与乙给甲的信是不同的两封信,所以与顺序有关是排列;②由于每两人互握一次手,甲与乙握手,乙与甲握手是同一次握手,与顺序无关,所以是组合问题.其他类似分析. (1)①是排列问题,共用了封信;②是组合问题,共需握手(次). (2)①是排列问题,共有(种)不同的选法;②是组合问题,共有种不同的选法. (3)①是排列问题,共有种不同的商;②是组合问题,共有种不同的积. (4)①是排列问题,共有种不同的选法;②是组合问题,共有种不同的选法. 例4证明. 证明左式
谓词公式的解释
2.2.3 谓词公式的解释 定义2.12 谓词逻辑中公式A的每一个解释(赋值)I由以下几部分构成: 1)非空个体域D; 2)D中的某些特定元素; 3)D中的某些特定的函数; 4)D中某些特定的谓词。 用一个解释I解释一个谓词公式A包括:将I的个体域D作为A的个体域,A中的个体常元用I中的特定元素代替,A中的函数用I中的特定函数代替,谓词用I上的特定谓词代替。把这样得到的公式记作A*。称A*为A在I下的解释,或A在I下被解释成A*。
给定解释I如下: 1)个体域为实数集合R; 2)R中的特定元素a=0; 3)R上的特定函数f(x, y) =x+y, g(x, y)=xy; 4)R上的特定谓词F(x, y):x=y。 在解释I下,求下列各式的真值: 1)?xF(f(x, a), g(x, a)) 2)?x?y(F(f(x, y), g(x, y))→F(x, y)) 3)?xF(g(x, y), a)
给定解释I如下: 1)个体域为实数集合R; 2)R中的特定元素a=0; 3)R上的特定函数f(x, y) =x+y, g(x, y)=xy; 4)R上的特定谓词F(x, y):x=y。在解释I下,公式分别解释为: 1)?xF(f(x, a), g(x, a)) 解释为: 2)?x?y(F(f(x, y), g(x, y))→F(x, y)) )) 解释为: 3)?xF(g(x, y), a) 解释为: 封闭的公式在任何解释下都成为命题。 定理2.1 在实数集合R中,?x(x+0=x?0) 真值为1; 在实数集合R中,?x?y(x+y=x?y→x=y) 真值为0; 在实数集合R中,?x(x?y=0) 真值不确定。
第2章谓词逻辑 一、教学要求 1. 理解谓词、量词、个体词、个体域、原子公式、谓词公式和变元等概念。会将不太复杂的命题符号化。 2. 掌握在有限个体域下求公式的真值和某些公式在给定解释下真值的方法,判别公式类型(永真式、永假式和可满足式)的方法。 3. 掌握谓词演算的等值式和重言蕴含式(六种情况:(1)命题公式的推广;(2)量词否定式的等值式;(3)量词辖域扩张和收缩的等值式;(4)量词与联结词∨,∧,→的等值式;(5)量词与联结词的重言蕴含式;(6)两个量词公式间的等值式与重言蕴含式)。会进行谓词公式的等值演算。 4. 了解前束范式的概念,会求公式的前束范式。 5. 了解谓词逻辑推理的规则:全量词消去规则(US规则);全量词附加规则(UG规则);存在量词消去规则(ES规则);存在量词附加规则(EG规则) 本章重点:谓词与量词,公式与解释,前束范式,谓词逻辑推理证明。 二、学习辅导 在命题逻辑中,我们把原子命题作为基本研究单位,对原子命题不再进行分解,只有复合命题才可以分解,揭示了一些有效的推理过程. 但是进一步研究发现,仅有命题逻辑是无法把一些常见的推理形式包括进去. 例如 “凡人要死,张三是人,张三要死” 显然是正确推理. 用命题逻辑解释三段式. 设 P:人要死;Q张三是人;R:张三要死。 表示成复合命题有 P∧Q→R 这不是重言式,即R不是前提P,Q的有效结论. 这反映了命题逻辑的局限性,其原因是把本来有内在联系的命题P,Q,R,视为独立的命题。要反映这种内在联系,就要对命题逻辑进行分析,分析出其中的个体词、谓词和量词,再研究它们之间的逻辑关系,总结出正确的推理形式和规则,这就是谓词逻辑的研究内容。 1. 谓词与量词 学习这一部分要反复理解谓词和量词引入的意义,概念的含义。 在谓词逻辑中,原子命题分解成个体词和谓词。个体词是可以独立存在的客体,它可以是具体事物或抽象的概念,如小张,房子,南京,大米,思想,实数2等等。谓词是用来刻划个体词的性质或事物之间的关系的词。例如 (1)(1)ln5是无理数; (2)(2)高可比李木相高4cm; (3) 郑州位于北京和广州之间。 这时三个简单命题,其中ln5,高可,李木相,郑州,北京,广州等都是个体词,而“是无理数”,“……比……高4cm”,“……位于……和……之间”等都是谓词。 个体词分个体常项(用a,b,c,d,…表示)和个体变项(用x,y,z,…表示);谓词分谓词常项(表
1、指出下列公式?x?y(F(x,y)∧G(y,z)) ∨?xH(x,y,z)中的指导变元,量词的辖域,约束变元是哪些, 自由变元是哪些, 各个体变项的自由出现和约束出现的次数。 2. 在谓词逻辑中将下列命题符号化: (1)火车都比轮船快. (2)有的火车比汽车快. (3)不存在比所有火车都快的汽车. (4)说凡是汽车比火车慢是不对的.(明天下午放学我交给助教) 1指出下列公式?x?y(F(x,y)∧G(y,z)) ∨?xH(x,y,z)中的指导变元,量词的辖域,约束变元是哪些, 自由变元是哪些, 各个体变项的自由出现和约束出现的次数。 2.在谓词逻辑中将下列命题符号化: (1)火车都比轮船快. (2)有的火车比汽车快. (3)不存在比所有火车都快的汽车. (4)说凡是汽车比火车慢是不对的.(明天下午放学我交给助教) 1指出下列公式?x?y(F(x,y)∧G(y,z)) ∨?xH(x,y,z)中的指导变元,量词的辖域,约束变元是哪些, 自由变元是哪些, 各个体变项的自由出现和约束出现的次数。 2. 在谓词逻辑中将下列命题符号化: (1)火车都比轮船快. (2)有的火车比汽车快. (3)不存在比所有火车都快的汽车. (4)说凡是汽车比火车慢是不对的.(明天下午放学我交给助教) 1指出下列公式?x?y(F(x,y)∧G(y,z)) ∨?xH(x,y,z)中的指导变元,量词的辖域,约束变元是哪些, 自由变元是哪些, 各个体变项的自由出现和约束出现的次数。 2. 在谓词逻辑中将下列命题符号化: (1)火车都比轮船快. (2)有的火车比汽车快. (3)不存在比所有火车都快的汽车. (4)说凡是汽车比火车慢是不对的.(明天下午放学我交给助教) 1指出下列公式?x?y(F(x,y)∧G(y,z)) ∨?xH(x,y,z)中的指导变元,量词的辖域,约束变元是哪些, 自由变元是哪些, 各个体变项的自由出现和约束出现的次数。 2. 在谓词逻辑中将下列命题符号化: (1)火车都比轮船快. (2)有的火车比汽车快. (3)不存在比所有火车都快的汽车. (4)说凡是汽车比火车慢是不对的.(明天下午放学我交给助教) 1指出下列公式?x?y(F(x,y)∧G(y,z)) ∨?xH(x,y,z)中的指导变元,量词的辖域,约束变元是哪些, 自由变元是哪些, 各个体变项的自由出现和约束出现的次数。 2. 在谓词逻辑中将下列命题符号化: (1)火车都比轮船快. (2)有的火车比汽车快.
实验三化为子句集的九步法实验 一、实验目的 理解和掌握消解原理,熟悉谓词公式化为子句集的九个步骤,理解消解推理规则,能把任意谓词公式转换成子句集。 二、实验原理 消解是可用于一定的子句公式的重要推理规则,任一谓词演算公式可以化成一个子句集。通过九步法消解可以从这两个父辈子句推导出一个新子句。 九步法消解包括消去蕴涵符号、减否定符辖域、对变量标准化、消去存在量词、化为前束型、化为合取范式、消去全程量词、消去合取符、更换变量名,依次变换即可得到子句集。具体为: (1)消去连接词“→”和“?” P→Q?﹁P∨QP?Q?(P∧Q)∨(﹁P∧﹁Q) (2)将否定符号“﹁”移到仅靠谓词的位置 ﹁(﹁P)?P ﹁(P∧Q)?﹁P∨﹁Q ﹁(P∨Q)?﹁P∧﹁Q ﹁(?x)P(x)?(?x)﹁P(x) ﹁(?x)P(x)?(?x)﹁P(x) (?x)(﹁(?y)P(x,y)∨﹁(?y)(﹁Q(x,y)∨R(x,y)))?(?x)((?y)﹁P(x,y)∨(?y)(Q(x,y)∧﹁R(x,y))) (3)对变元标准化 (?x)((?y)﹁P(x,y)∨(?z)(Q(x,z)∧﹁R(x,z))) (4)化为前束范式 (?x)(?y)(?z)(﹁P(x,y)∨(Q(x,z)∧﹁R(x,z))) (5)消去存在量词 (?x)(﹁P(x,f(x))∨(Q(x,g(x))∧﹁R(x,g(x)))) (6)化为Skolem标准形P∨(Q∧R)?(P∨Q)∧(P∨R) (?x)((﹁P(x,f(x))∨Q(x,g(x))∧(﹁P(x,f(x))∨﹁R(x,g(x)))) (7)消去全称量词 (?x)((﹁P(x,f(x))∨Q(x,g(x))∧(﹁P(x,f(x))∨﹁R(x,g(x)))) (8)消去合取词 ﹁P(x,f(x))∨Q(x,g(x)) ﹁P(x,f(x))∨﹁R(x,g(x)) (9)更换变量名称 ﹁P(x,f(x))∨Q(x,g(x)) ﹁P(y,f(y))∨﹁R(y,g(y)) 三、实验内容 (1)可以采用自己熟悉的C#、C++、JAVA等任一种语言编写出Windows应用程序,演示子句消解推理演示程序。 (2)界面中可以通过实例按钮,由程序指定具体的实例,给出原始谓词公式; (3)设计九个步骤的按钮,每按一步按钮,给出这一步消解的结果; (4)该程序主要帮助初学者学习、掌握九步法谓词公式化为子句集的过程。 四、实验要求 (1)提交实验报告,以word文档形式“学号+姓名”命名; (2)报告中要有程序源代码; (3)有程序运行结果截图; (4)报告提交到:ftp://192.168.129.253/xstjzy/任建平/人工智能