线性代数应用实例
- 格式:doc
- 大小:234.50 KB
- 文档页数:9

线性代数在数学建模中的应用举例1 基因间“距离”的表示在ABO 血型的人们中,对各种群体的基因的频率进行了研究。
如果我们把四种等位基因A 1,A 2,B ,O 区别开,有人报道了如下的相对频率,见表1.1。
表1.1基因的相对频率问题 一个群体与另一群体的接近程度如何?换句话说,就是要一个表示基因的“距离”的合宜的量度。
解 有人提出一种利用向量代数的方法。
首先,我们用单位向量来表示每一个群体。
为此目的,我们取每一种频率的平方根,记ki ki f x =.由于对这四种群体的每一种有141=∑=i ki f ,所以我们得到∑==4121i kix .这意味着下列四个向量的每个都是单位向量.记.44434241,34333231,24232221,141312114321⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=x x x x a x x x x a x x x x a x x x x a在四维空间中,这些向量的顶端都位于一个半径为1的球面上. 现在用两个向量间的夹角来表示两个对应的群体间的“距离”似乎是合理的.如果我们把a 1和a 2之间的夹角记为θ,则由于| a 1|=| a 2|=1,再由内只公式,得21cos a a ⋅=θ而.8307.03464.02943.03216.0,8228.01778.00000.05398.021⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=a a 故 9187.0cos 21=⋅=a a θ 得 2.23=θ°. 按同样的方式,我们可以得到表1.2.表1.2基因间的“距离”爱斯基摩人班图人 英国人 朝鲜人 爱斯基摩人 0° 23.2° 16.4° 16.8° 班图人 23.2° 0° 9.8° 20.4° 英国人 16.4° 9.8° 0° 19.6° 朝鲜人16.8°20.4°19.6°0°由表1.2可见,最小的基因“距离”是班图人和英国人之间的“距离”,而爱斯基摩人和班图人之间的基因“距离”最大.2 Euler 的四面体问题问题 如何用四面体的六条棱长去表示它的体积?这个问题是由Euler (欧拉)提出的.解 建立如图2.1所示坐标系,设A ,B ,C 三点的坐标分别为(a 1,b 1,c 1),( a 2,b 2,c 2)和(a 3,b 3,c 3),并设四面体O-ABC 的六条棱长分别为.,,,,,r q p n m l 由立体几何知道,该四面体的体积V 等于以向量→→→OC OB OA ,,组成右手系时,以它们为棱的平行六面体的体积V 6的16.而)(.3332221116c b a c b a c b a OC OB OA V =⋅⨯= 于是得 .6333222111c b a c b a c b a V = 将上式平方,得.362323233232323231313232322222221212131313121212121212133322211133322211122c b a c c b b a a c c b b a a c c b b a a c b a c c b b a a c c b b a a c c b b a a cb ac b a c b a c b a c b a c b a c b a V ++++++++++++++++++=⋅=根据向量的数量积的坐标表示,有.,,,,232323323232222222313131212121212121c b a OC OC c c b b a a OC OB c b a OB OB c c b b a a OC OA c c b b a a OB OA c b a OA OA ++=⋅++=⋅++=⋅++=⋅++=⋅++=⋅ 于是362OC OC OB OC OB OBOB OBOA OB OA OAV ⋅⋅⋅= (2.1)由余弦定理,可行.2cos 222n q p q p OB OA -+=⋅⋅=⋅θ同理.2,2222222l r q OC OB m r p OC OA -+=⋅-+=⋅将以上各式代入(2.1)式,得.222222362222222222222222222222r l r p m r p l r p p n q p m r p n q p pV -+-+-+-+-+-+=(2.2)这就是Euler 的四面体体积公式.例 一块形状为四面体的花岗岩巨石,量得六条棱长分别为l =10m, m =15m, n =12m, p =14m, q =13m, r =11m.则.952222,462222,5.1102222=-+=-+=-+l r p m r p n q p代入(2.1)式,得.75.13698291219546951695.110465.110196236==V 于是.)195(82639.38050223m V ≈≈即花岗岩巨石的体积约为195m 3.古埃及的金字塔形状为四面体,因而可通过测量其六条棱长去计算金字塔的体积.3 动物数量的按年龄段预测问题问题 某农场饲养的某种动物所能达到的最大年龄为15岁,将其分成三个年龄组:第一组,0~5岁;第二组,6~10岁;第三组,11~15岁.动物从第二年龄组起开始繁殖后代,经过长期统计,第二组和第三组的繁殖率分别为4和3.第一年龄和第二年龄组的动物能顺利进入下一个年龄组的存活率分别为12 和14 .假设农场现有三个年龄段的动物各100头,问15年后农场三个年龄段的动物各有多少头?问题分析与建模 因年龄分组为5岁一段,故将时间周期也取为5年.15年后就经过了3个时间周期.设)(k i x 表示第k 个时间周期的第i 组年龄阶段动物的数量(k =1,2,3;i =1,2,3).因为某一时间周期第二年龄组和第三年龄组动物的数量是由上一时间周期上一年龄组存活下来动物的数量,所以有).3,2,1(41,21)1(2)(3)1(1)(2===--k x x x x k k k k又因为某一时间周期,第一年龄组动物的数量是由于一时间周期各年龄组出生的动物的数量,所以有).3,2,1(34)1(3)1(2)(1=+=--k x x x k k k于是我们得到递推关系式:⎪⎪⎪⎩⎪⎪⎪⎨⎧==+=----.41,21,34)1(2)(3)1(1213)1(2)(1k k k k k k k x x x x x x x 用矩阵表示).3,2,1(0410021340)1(3)1(2)1(1)(3)(2)(1=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---k x x x x x x k k k k k k则).3,2,1()1()(==-k Lx x k k其中.100010001000,04100021340)0(⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=x L 则有),3,2,1()(3)(2)(1)(=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=k x x x x k k k k,250500700010001000100004100021340)0()1(⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡==Lx x,12535002750250500700004100021340)1()2(⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡==Lx x .8751375143751253500275004100021340)2()3(⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡==Lx x 结果分析 15年后,农场饲养的动物总数将达到16625头,其中0~5岁的有14375头,占86.47%,6~10岁的有1375头,占8.27%,11~15岁的有875头,占 5.226%.15年间,动物总增长16625-3000=13625头,总增长率为13625/3000=454.16%.注 要知道很多年以后的情况,可通过研究式)0()1()(x L Lx x k k k ==-中当趋于无穷大时的极限状况得到.关于年龄分布的人口预测模型 我们将人口按相同的年限(比如5年)分成若干年龄组,同时假设各年龄段的田、女人口分布相同,这样就可以通过只考虑女性人口来简化模型.人口发展随时间变化,一个时间周期的幅度使之对应于基本年龄组间距(如先例的5年),令)(k i x 是在时间周期k 时第i 个年龄组的(女性)人口,i =1,2,…,n .用1表示最低年龄组,用n 表示最高年龄组,这意味着不考虑更大年龄组人口的变化.假如排除死亡的情形,则在一个周期内第i 个年龄组的成员将全部转移到i +1个年龄组.但是,实际上必须考虑到死亡率,因此这一转移过程可由一存活系数所衰减. 于是,这一转移过程可由下述议程简单地描述:),1,,2,1()1()(1-==-+n i x b x k ii k i其中i b 是在第i 个年龄组在一个周期的存活率,因子i b 可由统计资料确定.惟一不能由上述议程确定的年龄组是,)(1k x 其中的成员是在后面的周期内出生的,他们是后面的周期内成员的后代,因此这个年龄组的成员取决于后面的周期内各组的出生率及其人数.于是有方程,)1(122)1(11)(1---+++=k n n k k k x a x a x a x (3.1)这里),,2,1(n i a i =是第i 个年龄组的出生率,它是由每时间周期内,第i 个年龄组的每一个成员的女性后代的人数来表示的,通常可由统计资料来确定.于是我们得到了单性别分组的人口模型,用矩阵表示便是,00000000000)1()1(3)1(2)1(11211321)()(3)(2)(1⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------k n k k k n n n k n k k k x x x x b b b a a a a a x x x x 或者简写成.)1()(-=k k Lx x (3.2)矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--000000000001211321n n n b b b a a a a a L称为Leslie 矩阵.由(3.2)式递推可得)0()1()(x L Lx x k k k ==-这就是Leslie 模型.4 企业投入产生分析模型问题 某地区有三个重要产业,一个煤矿、一个发电厂和一条地方铁路.开采一元钱的煤,煤矿要支付0.25元的电费及0.25元的运输费.生产一元钱的电力,发电厂要支付0.65元的煤费,0.05元的电费及0.05元的运输费.创收一元钱的运输费,铁路要支付0.55元的煤费及0.10元的电费.在某一周内,煤矿接到外地金额为50000元的定货,发电厂接到外地金额为25000元的定货,外界对地方铁路没有需求.问三个企业在这一周内总产值多少才能满足自身及外界的需求?数学模型 设x 1为煤矿本周内的总产值,x 2为电厂本周的总产值,x 3为铁路本周内的总产值,则⎪⎩⎪⎨⎧=⨯++-=++-=++⨯-,0)005.025.0(,25000)10.005.025.0(,50000)55.065.00(321332123211x x x x x x x x x x x x (4.1) 即.02500050000005.025.010.005.025.055.065.00321321⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡x x x x x x 即.025********,005.025.010.005.025.055.065.00,321⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Y A x x x X 矩阵A 称为直接消耗矩阵,X 称为产出向量,Y 称为需求向量,则方程组(4.1)为,Y AX X =-即Y X A E =-)(, (4.2)其中矩阵E 为单位矩阵,(E-A )称为列昂杰夫矩阵,列昂杰夫矩阵为非奇异矩阵.投入产出分析表 设,00000,)(3211⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=--=-x x x A C E A E B D=(1,1,1)C.矩阵B 称为完全消耗矩阵,它与矩阵A 一起在各个部门之间的投入产生中起平衡作用.矩阵C 可以称为投入产出矩阵,它的元素表示煤矿、电厂、铁路之间的投入产出关系.向量D 称为总投入向量,它的元素是矩阵C 的对应列元素之和,分别表示煤矿、电厂、铁路得到的总投入.由矩阵C ,向量Y ,X 和D ,可得投入产出分析表4.1.表4.1 投入产出分析表 单位:元 煤矿电厂铁路外界需求总产出煤矿 11c 12c 13c 1y 1x电厂 21c 22c 23c 2y 2x 铁路 31c32c33c 3y3x总投入1d 2d 3d计算求解 按(4.2)式解方程组可得产出向量X ,于是可计算矩阵C 和向量D ,计算结果如表4.2.表4.2 投入产出计算结果 单位:元 煤矿 电厂 铁路 外界需求 总产出 煤矿 0 36505.96 15581.51 50000 102087.48 电厂 25521.87 2808.15 2833.00 25000 56163.02 铁路 25521.87 2808.15 0 0 28330.02总投入51043.7442122.2718414.525 交通流量的计算模型问题 图5.1给出了某城市部分单行街道的交通流量(每小时过车数).假设:(1)全部流入网络的流量等于全部流出网络的流量;(2)全部流入一个节点的流量等于全部流出此节点的流量.试建立数学模型确定该交通网络未知部分的具体流量.建模与计算 由网络流量假设,所给问题满足如下线方程组:234457612157891091083630050020080080010004002006001000x x x x x x x x x x x x x x x x x x x x -+=⎧⎪+=⎪⎪-=⎪+=⎪⎪+=⎪⎨+=⎪⎪=⎪-=⎪⎪=⎪++=⎪⎩ 系数矩阵为11100000000011000000000011000110000000010001000000000001100000000001000000000110000000001010010100A -⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ 增广矩阵阶梯形最简形式为1000100000800010010000000010000000200000110000050000000101008000000001100100000000000104000000000001600000000000000000000000B ⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦其对应的齐次方程组为1525345687891000000000x x x x x x x x x x x x x +=⎧⎪-=⎪⎪=⎪+=⎪⎨+=⎪⎪+=⎪=⎪⎪=⎩取(x 5,x 8)为自由取值未知量,分别赋两组值为(1,0),(0,1),得齐次方程组基础解系中两个解向量()11,1,0,1,1,0,0,0,0,0,'η=--()20,0,0,0,0,1,1,1,0,0'η=--其对应的非齐次方程组为1525345687891080002005008001000400600x x x x x x x x x x x x x +=⎧⎪-=⎪⎪=⎪+=⎪⎨+=⎪⎪+=⎪=⎪⎪=⎩赋值给自由未知量(x 5,x 8)为(0,0)得非齐次方程组的特解()800,0,200,500,0,800,1000,0,400,600'x *=于是方程组的通解,*2211x k k x ++=ηη其中k 1,k 2为任意常数,x 的每一个分量即为交通网络未知部分的具体流量,它有无穷多解.6 小行星的轨道模型问题 一天文学家要确定一颗小行星绕太阳运行的轨道,他在轨道平面内建立以太阳为原点的直角坐标系,在两坐标轴上取天文测量单位(一天文单位为地球到太阳的平均距离:1.4959787×1011m ).在5个不同的时间对小行星作了5次观察,测得轨道上5个点的坐标数据如表6.1.表6.1 坐标数据由Kepler (开普勒)第一定律知,小行星轨道为一椭圆.现需要建立椭圆的方程以供研究(注:椭圆的一般方程可表示为012225423221=+++++y a x a y a xy a x a .问题分析与建立模型 天文学家确定小行星运动的轨道时,他的依据是轨道上五个点的坐标数据:(x 1, y 1), (x 2, y 2), (x 3, y 3), (x 4, y 4), (x 5, y 5).由Kepler 第一定律知,小行星轨道为一椭圆.而椭圆属于二次曲线,二次曲线的一般方程为012225423221=+++++y a x a y a xy a x a .为了确定方程中的五个待定系数,将五个点的坐标分别代入上面的方程,得2211211314151221222232425222132333343532214244344454221525535455522212221222122212221a x a x y a y a x a y a x a x y a y a x a y a x a x y a y a x a y a x a x y a y a x a y a x a x y a y a x a y ⎧++++=-⎪++++=-⎪⎪++++=-⎨⎪++++=-⎪⎪++++=-⎩这是一个包含五个未知数的线性方程组,写成矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡11111222222222222222543215525552544244424332333232222222211211121a a a a a y x y y x x y x y y x x y x y y x x y x y y x x y x y y x x 求解这一线性方程组,所得的是一个二次曲线方程.为了知道小行星轨道的一些参数,还必须将二次曲线方程化为椭圆的标准方程形式:12222=+bY a X 由于太阳的位置是小行星轨道的一个焦点,这时可以根据椭圆的长半轴a 和短半轴b 计算出小行星的近日点和远日点距离,以及椭圆周长L .根据二次曲线理论,可得椭圆经过旋转和平移两种变换后的方程如下:[]22120D X Y C λλ++=所以,椭圆长半轴:C D a 1λ=;椭圆短半轴: CDb 2λ=;椭圆半焦矩:22b ac -=.计算求解 首先由五个点的坐标数据形成线性方程组的系数矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=7200.69600.142896.112656.509504.550520.53360.143807.62127.363802.516460.35180.133233.36433.246841.454040.25720.124448.11115.155138.39292.1528.114199.04701.72237.33A使用计算机可求得12345(,,,,)(0.6143,0.3440,0.6942, 1.6351,0.2165)a a a a a =---从而⎪⎪⎭⎫⎝⎛--=⎥⎦⎤⎢⎣⎡=6942.03440.03440.06143.03221a a a a C C C ,3081.0=的特征值120.3080, 1.0005λλ==123235450.61430.3440 1.63510.34400.69420.21651 1.63510.21651a a a D a a a a a ---⎡⎤⎡⎤⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦.8203.1-=D于是,椭圆长半轴a=19.1834,短半轴b=5.9045,半焦距c=18.2521.小行星近日点距和远日点距为039313,37.4355h a c H a c =-==+=最后,椭圆的周长的准确计算要用到椭圆积分,可以考虑用数值积分解决问题,其近似值为84.7887.7 人口迁移的动态分析问题 对城乡人口流动作年度调查,发现有一个稳定的朝向城镇流动的趋势:每年农村居民的2.5%移居城镇,而城镇居民的1%迁出.现在总人口的60%位于城镇.假如城乡总人口保持不变,并且人口流动的这种趋势继续下去,则一年以后住在城镇人口所占比例是多少两年以后呢十年以后呢最终呢解 设开始时,令乡村人口为,0y 城镇人口为,0z 一年以后有乡村人口,10011000975100y z y =+ 城镇人口 ,10099100025100z z y =+或写成矩阵形式⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡00111009910002510011000975z y z y . 两年以后,有.100991000251001100097510099100025100110009750021122⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡z y z y z y . 十年以后,有.100991000251001100097500101010⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡z y z y 事实上,它给出了一个差分方程:k k Au u =+1.我们现在来解这个差分方程.首先,1009910002510011000975⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Ak 年之后的分布(将A 对角化):.75757275100200193115210000⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡z y z y A z y k k k k 这就是我们所要的解,而且容易看出经过很长一个时期以后这个解会达到一个极限状态.7572)(00⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=⎥⎦⎤⎢⎣⎡∞∞z y z y 总人口仍是00z y +,与开始时一样,但在此极限中人口的75在城镇,而72在乡村.无论初始分布是什么样,这总是成立的.值得注意这个稳定状态正是A 的属于特征值1的特征向量.上述例子有一些很好的性质:人口总数保持不变,而且乡村和城镇的人口数决不能为负.前一性质反映在下面事实中:矩阵每一列加起来为1;每个人都被计算在内,而没有人被重复或丢失.后一性质则反映在下面事实中:矩阵没有负元素;同样地0y 和0z 也是非负的,从而1y 和21,y z 和2z 等等也是这样.8 常染色体遗传模型为了揭示生命的奥秘,遗传学的研究已引起了人们的广泛兴趣.动植物在产生下一代的过程中,总是将自己的特征遗传给下一代,从而完成一种“生命的延续”.在常染色体遗传中,后代从每个亲体的基因对中各继承一个基因,形成自己的基因对.人类眼睛颜色即是通过常染色体控制的,其特征遗传由两个基因A 和a 控制.基因对是AA 和Aa 的人,眼睛是棕色,基因对是aa 的人,眼睛为蓝色.由于AA 和Aa 都表示了同一外部特征,或认为基因A 支配a ,也可认为基因a 对于基因A 来说是隐性的(或称A 为显性基因,a 为隐性基因).下面我们选取一个常染色体遗传——植物后代问题进行讨论.某植物园中植物的基因型为AA ,Aa ,aa .人们计划用AA 型植物与每种基因型植物相结合的方案培育植物后代.经过若干年后,这种植物后代的三种基因型分布将出现什么情形我们假设),2,2,0(,, =n c b a n n n 分别代表第n 代植物中,基因型为AA ,Aa 和aa 的植物占植物总数的百分率,令),,()('=n n n n c b a x为第n 代植物的基因分布, ),,(000)0('=c b a x 表示植物基因型的初始分布,显然,我们有.1000=++c b a (8.1)先考虑第n 代中的AA 型,第1-n 代AA 型与AA 型相结合,后代全部是AA 型;第1-n 代的Aa 型与和与AA 相结合,后代是AA 型的可能性为21;1-n 代的aa 型与AA 型相结合,后代不可能是AA 型。


浅谈线性代数的一些应用实例一、关于矩阵运算的应用1.数学期望值准则。
把各种行动方案看成不同的随机变量,每个方案对应若干种状态,假设它们的概率是已知的,每个方案在各种状态下的效益看成随机变量的取值。
数学期望准则就是将每个行动方案的数学期望计算出来,视其决策目标的情况选择最优行动方案。
如果决策目标是利润、效益等最大,则采用期望值最大的行动方案;如果决策目标是成本、损失等最小,则采用期望值最小的行动方案。
用X表示各行动方案的集合,N表示各具体行动方案所处各种状态的集合,它们的概率写成向量P,效益值写成矩阵A(其中,列向量代表不同的随机变量在各种状态的取值):N=(N1,・・・,Nn),P=(P1(N1),・・・,Pn(Nn)),X=(X1,・・・,Xm),A=(aij)m×n。
则数学期望E(X)=(E(X1),・・・,E(Xn))=PA,决策就是确定向量E(X)的最大分量或最小分量所对应的行动方案。
例某投资者要在两种产品间作投资选择:生产领带或旅游鞋。
生产领带需投资800万元,生产旅游鞋需投资1000万元。
两者的生产年限都是8年,估计在此期间两个方案的产品销售状况出现好、中、差的概率都是0.5、0.3、0.2。
生产领带在好、中、差的状况下的年纯利润分别为400万元、300万元、50万元;生产旅游鞋在好、中、差的状况下的年纯利润分别为500万元、400万元、120万元。
试按数学期望值准则对这两种方案进行决策。
解:P=(0.5,0.3,0.2),A=■T,X1=产领带,X2=产旅游鞋。
令Y=8X-Y0,这里Y0=(800,1000),则EY=8(EX)-Y0=8PA-Y0=(1600,2152),因此应采取生产旅游鞋方案。
2.矩阵乘幂的应用。
例某高校所在地本地学生度周末有回家和在校两种选择。
统计数据显示,本周末回家的学生,下周末回家的几率为2/5,本周末在校的学生下周末在校的几率是1/5。
已知第一周末有30%本地学生回家。


应用线性代数解决实际问题线性代数作为数学的一个重要分支,广泛应用于各个领域,包括计算机科学、物理学、经济学等。
它不仅是数学家们研究的重要工具,更是解决实际问题的有效途径。
本文将通过具体案例,介绍线性代数在实际问题中的应用,从而展示其强大的解决能力。
案例一:网络流量优化现代社会离不开互联网,而网络流量的优化是提高互联网服务质量的重要问题之一。
假设我们有一组服务器,每个服务器的带宽和消耗成本有所不同,现在需要将用户的请求合理地分配到这些服务器上,以最大化带宽利用率并最小化消耗成本。
这就可以转化为一个线性代数中的线性规划问题。
首先,我们可以用一个向量表示服务器的带宽,用另一个向量表示服务器的消耗成本。
设请求到达的向量为x,那么我们的目标就是最大化带宽利用率和最小化消耗成本,可以构建如下优化模型:maximize cᵀx subject to Ax ≤ b其中,c是服务器的消耗成本向量,x是请求到达的向量,A是服务器带宽的矩阵,b是服务器的带宽上限。
通过求解这个线性规划问题,我们可以得到最佳的请求分配方案,从而实现网络流量的优化。
案例二:图像处理线性代数在图像处理中有着广泛的应用。
以黑白图片为例,可以将其表示为一个矩阵,其中的元素代表每个像素点的灰度值。
通过矩阵的加减、乘除运算,以及线性变换等操作,可以实现图像的平移、旋转、缩放等处理效果。
举个例子,假设我们想要将一张黑白图片的亮度增加一倍。
我们可以将这张图片表示为一个矩阵A,然后构造一个倍增矩阵B,即每个元素都是2。
通过这两个矩阵的乘法运算,即可实现亮度的增加。
这个过程可以用下面的表达式表示:A' = BA其中,A'表示亮度增加后的图像矩阵。
通过线性代数的运算,我们可以方便地实现图像处理中的各种效果。
总结线性代数作为数学的重要分支,具有广泛的应用领域。
本文通过网络流量优化和图像处理两个具体案例,展示了线性代数在实际问题中的应用。
线性代数的强大解决能力不仅能帮助我们解决现实生活中的问题,同时也为我们提供了一种思维方式和方法论。
论线性代数的应用实例线性代数(Linear Algebra)是数学的一个分支,它的研究对象是向量,向量空间(或称线性空间),线性变换和有限维的线性方程组。
向量空间是现代数学的一个重要课题;因而,线性代数被广泛地应用于抽象代数和泛函分析中;通过解析几何,线性代数得以被具体表示。
线性代数的理论已被泛化为算子理论。
由于科学研究中的非线性模型通常可以被近似为线性模型,使得线性代数被广泛地应用于自然科学和社会科学中。
线性代数是理工类、经管类数学课程的重要内容。
在日常学习、工作和生活中,有很多问题,运用线性代数的方法就可以使问题简化,以下举一些线性代数的应用实例。
一、药方配制问题问题:某中药厂用9种中草药(A-I),根据不同的比例配制成了7种特效药,各用量成分见表1(单位:克)已经卖完,请问能否用其他特效药配制出这两种脱销的药品。
(2)现在该医院想用这7种草药配制三种新的特效药,表2给出了三种新的特效药的成分,请问能否配制?如何配制?解:(1)把每一种特效药看成一个九维列向量,分析7个列向量构成向量组的线性相关性。
若向量组线性无关,则无法配制脱销的特效药;若向量组线性相关,并且能找到不含3u,6u的一个最大线性无关组,则可以配制3号和6号药品。
可使用matlab软件进行运算:在Matlab窗口输入1 2 3 4 5 6 7[10;12;5;7;0;25;9;6;8];[2;0;3;9;1;5;4;5;2];[14;12;11;25;2;35;17;16;12]; [12;25;0;5;25;5;25;10;0]; [20;35;5;15;5;35;2;10;0]; [38;60;14;47;33;55;39;35;6]; [100;55;0;35;6;50;25;10;20];u u u u u u u =======1234567 [,,,,,,]u u u u u u u u =[0u ,r]=rref(u )计算结果为0u =10100000120030000101000001100000001⎛⎫⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭从矩阵中可以看出,有四个零行,r=1、2、4、5、7从最简行阶梯型0u 中可以看 出,R (u )=5,向量组线性 相关,一个最大无关组为: 1u 2u 4u 5u 7u3u = 1u +22u 6u =32u +4u +5u故可以配制新药。
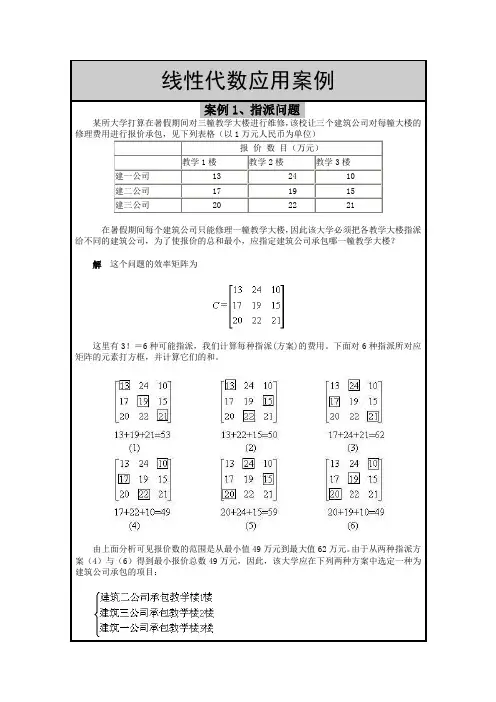
线性代数应用案例案例1、指派问题某所大学打算在暑假期间对三幢教学大楼进行维修,该校让三个建筑公司对每幢大楼的修理费用进行报价承包,见下列表格(以1万元人民币为单位)报价数目(万元)教学1楼教学2楼教学3楼建一公司 13 24 10建二公司 17 19 15建三公司 20 22 21在暑假期间每个建筑公司只能修理一幢教学大楼,因此该大学必须把各教学大楼指派给不同的建筑公司,为了使报价的总和最小,应指定建筑公司承包哪一幢教学大楼?解这个问题的效率矩阵为这里有3!=6种可能指派,我们计算每种指派(方案)的费用。
下面对6种指派所对应矩阵的元素打方框,并计算它们的和。
由上面分析可见报价数的范围是从最小值49万元到最大值62万元。
由于从两种指派方案(4)与(6)得到最小报价总数49万元,因此,该大学应在下列两种方案中选定一种为建筑公司承包的项目:或案例2、交通问题设有A,B,C三国,它们的城市,之间的交通联接情况(不考虑国内交通)如图:根据上图,A国和B国城市之间交通联接情况可用矩阵表示,其中同样,B国和C国城市之间的交通情况可用矩阵用P来表示矩阵M与N的乘积,那么可算出案例3、圆锥曲线方程平面上圆锥曲线(椭圆、双曲线、抛物线)的一般方程为这方程含有六个待定系数,用它们之中不为零的任意一个系数去除其它系数,实际上此方程只有五个独立的待定系数。
用与上面类似的方法,通过五个不同点:的一般圆锥曲线方程为:(9)例一天文学家要确定一颗小行星绕太阳运行的轨道,他在轨道平面内建立一个以太阳为原点的直角坐标系,在两坐标轴上取天文测量单位(1天文单位为地球到太阳的平均距离:9300万里)。
他五个不同时间对小行星作五次观测,得到轨道上五个点的坐标分别为(5.764,0.648)(6.286,1.202)(6.759,1.823)(7.168,2.562)与(7.408,3.360)。
由开普勒第一定律知小行星轨道为一椭圆,试建立它的方程。

线性代数建模案例汇编目录案例一. 交通网络流量分析问题1案例二. 配方问题4案例三. 投入产出问题6案例四. 平板的稳态温度分布问题7案例五. CT图像的代数重建问题11案例六. 平衡结构的梁受力计算13案例七. 化学方程式配平问题16案例八. 互付工资问题17案例九. 平衡价格问题19案例十. 电路设计问题20案例十一. 平面图形的几何变换22案例十二. 太空探测器轨道数据问题24案例十三. 应用矩阵编制Hill密码25案例十四. 显示器色彩制式转换问题27案例十五. 人员流动问题29案例十六. 金融公司支付基金的流动31案例十七. 选举问题33案例十八. 简单的种群增长问题34案例十九. 一阶常系数线性齐次微分方程组的求解36 案例二十. 最值问题38附录数学实验报告模板错误!未定义书签。
案例一. 交通网络流量分析问题城市道路网中每条道路、每个交叉路口的车流量调查,是分析、评价及改善城市交通状况的基础。
根据实际车流量信息可以设计流量控制方案,必要时设置单行线,以免大量车辆长时间拥堵。
【模型准备】 某城市单行线如下图所示, 其中的数字表示该路段每小时按箭头方向行驶的车流量(单位: 辆).图3 某城市单行线车流量(1) 建立确定每条道路流量的线性方程组.(2) 为了唯一确定未知流量, 还需要增添哪几条道路的流量统计? (3) 当x 4 = 350时, 确定x 1, x 2, x 3的值.(4) 若x 4 = 200, 则单行线应该如何改动才合理?【模型假设】 (1) 每条道路都是单行线. (2) 每个交叉路口进入和离开的车辆数目相等.【模型建立】 根据图3和上述假设, 在①, ②, ③, ④四个路口进出车辆数目分别满足500 = x 1 + x 2① 400 + x 1 = x 4 + 300 ② x 2 + x 3 = 100 + 200 ③ x 4 = x 3 + 300 ④ 【模型求解】根据上述等式可得如下线性方程组12142334500100300300x x x x x x x x +=⎧⎪-=-⎪⎨+=⎪⎪-+=⎩其增广矩阵(A , b ) =1100500100110001103000011300⎛⎫ ⎪--⎪ ⎪ ⎪-⎝⎭−−−−→初等行变换10011000101600001130000000--⎛⎫ ⎪⎪-- ⎪⎪⎝⎭由此可得142434100600300x x x x x x -=-⎧⎪+=⎨⎪-=-⎩ 即142434100600300x x x x x x =-⎧⎪=-+⎨⎪=-⎩. 为了唯一确定未知流量, 只要增添x 4统计的值即可. 当x 4 = 350时, 确定x 1 = 250, x 2 = 250, x 3 = 50.若x 4 = 200, 则x 1 = 100, x 2 = 400, x 3 = -100 < 0. 这表明单行线“③←④”应该改为“③→④”才合理.【模型分析】(1) 由(A , b )的行最简形可见, 上述方程组中的最后一个方程是多余的. 这意味着最后一个方程中的数据“300”可以不用统计.(2) 由142434100600300x x x x x x =-⎧⎪=-+⎨⎪=-⎩可得213141500200100x x x x x x =-+⎧⎪=-⎨⎪=+⎩, 123242500300600x x x x x x =-+⎧⎪=-+⎨⎪=-+⎩, 132343200300300x x x x x x =+⎧⎪=-+⎨⎪=+⎩, 这就是说x 1, x 2, x 3, x 4这四个未知量中, 任意一个未知量的值统计出来之后都可以确定出其他三个未知量的值.Matlab 实验题某城市有下图所示的交通图, 每条道路都是单行线, 需要调查每条道路每小时的车流量. 图中的数字表示该条路段的车流数. 如果每个交叉路口进入和离开的车数相等, 整个图中进入和离开的车数相等.图4 某城市单行线车流量(1)建立确定每条道路流量的线性方程组.(2)分析哪些流量数据是多余的.(3)为了唯一确定未知流量, 需要增添哪几条道路的流量统计.案例二. 配方问题在化工、医药、日常膳食等方面都经常涉及到配方问题. 在不考虑各种成分之间可能发生某些化学反应时, 配方问题可以用向量和线性方程组来建模. 【模型准备】一种佐料由四种原料A 、B 、C 、D 混合而成. 这种佐料现有两种规格, 这两种规格的佐料中, 四种原料的比例分别为2:3:1:1和1:2:1:2. 现在需要四种原料的比例为4:7:3:5的第三种规格的佐料. 问: 第三种规格的佐料能否由前两种规格的佐料按一定比例配制而成?【模型假设】 (1) 假设四种原料混合在一起时不发生化学变化. (2) 假设四种原料的比例是按重量计算的. (3) 假设前两种规格的佐料分装成袋, 比如说第一种规格的佐料每袋净重7克(其中A 、B 、C 、D 四种原料分别为2克, 3克, 1克, 1克), 第二种规格的佐料每袋净重6克(其中A 、B 、C 、D 四种原料分别为1克, 2克, 1克, 2克). 【模型建立】 根据已知数据和上述假设, 可以进一步假设将x 袋第一种规格的佐料与y 袋第二种规格的佐料混合在一起, 得到的混合物中A 、B 、C 、D 四种原料分别为4克, 7克, 3克, 5克, 则有以下线性方程组24,327,3,2 5.x y x y x y x y +=⎧⎪+=⎨+=⎪+=⎩ 【模型求解】上述线性方程组的增广矩阵(A , b ) =214327113125⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭−−−−→初等行变换101012000000⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭,可见{1,2.x y == 又因为第一种规格的佐料每袋净重7克, 第二种规格的佐料每袋净重6克, 所以第三种规格的佐料能由前两种规格的佐料按7:12的比例配制而成. 【模型分析】(1) 若令α1 = (2, 3, 1, 1)T , α2 = (1, 2, 1, 1)T , β = (4, 7, 5, 3)T , 则原问题等价于“线性方程组Ax = b 是否有解”, 也等价于“β能否由α1, α2线性表示”.(2) 若四种原料的比例是按体积计算的, 则还要考虑混合前后体积的关系(未必是简单的叠加), 因而最好还是先根据具体情况将体积比转换为重量比, 然后再按上述方法处理.(3) 上面的模型假设中的第三个假设只是起到简化运算的作用. 如果直接设x 克第一种规格的佐料与y 克第二种规格的佐料混合得第三种规格的佐料, 则有下表因而有如下线性方程组214(),7619327(),7619113(),7619125().7619x y x y x y x y x y x y x y x y ⎧+=+⎪⎪⎪+=+⎪⎨⎪+=+⎪⎪⎪+=+⎪⎩(*) 【模型检验】把x = 7, y = 12代入上述方程组(*), 则各等式都成立. 可见模型假设中的第三个假设不影响解的正确性.Matlab 实验题蛋白质、碳水化合物和脂肪是人体每日必须的三种营养, 但过量的脂肪摄入不利于健康.人们可以通过适量的运动来消耗多余的脂肪. 设三种食物(脱脂牛奶、大豆面粉、乳清)每100克中蛋白质、碳水化合物和脂肪的含量以及慢跑5分钟消耗蛋白质、碳水化合物和脂肪的量如下表.问怎样安排饮食和运动才能实现每日的营养需求?案例三. 投入产出问题在研究多个经济部门之间的投入产出关系时, W. Leontief 提出了投入产出模型. 这为经济学研究提供了强有力的手段. W. Leontief 因此获得了1973年的Nobel 经济学奖.【模型准备】某地有一座煤矿, 一个发电厂和一条铁路. 经成本核算, 每生产价值1元钱的煤需消耗0.3元的电; 为了把这1元钱的煤运出去需花费0.2元的运费; 每生产1元的电需0.6元的煤作燃料; 为了运行电厂的辅助设备需消耗本身0.1元的电, 还需要花费0.1元的运费; 作为铁路局, 每提供1元运费的运输需消耗0.5元的煤, 辅助设备要消耗0.1元的电. 现煤矿接到外地6万元煤的订货, 电厂有10万元电的外地需求, 问: 煤矿和电厂各生产多少才能满足需求? 【模型假设】假设不考虑价格变动等其他因素.【模型建立】设煤矿, 电厂, 铁路分别产出x 元, y 元, z 元刚好满足需求. 则有下表根据需求, 应该有(0.60.5)60000(0.30.10.1)100000(0.20.1)0x y z y x y z z x y -+=⎧⎪-++=⎨⎪-+=⎩, 即0.60.5600000.30.90.11000000.20.10x y z x y z x y z --=⎧⎪-+-=⎨⎪--+=⎩ 【模型求解】在Matlab 命令窗口输入以下命令>> A = [1,-0.6,-0.5;-0.3,0.9,-0.1;-0.2,-0.1,1]; b = [60000;100000;0]; >> x = A\bMatlab 执行后得 x =1.0e+005 *1.99661.84150.5835可见煤矿要生产1.9966⨯105元的煤, 电厂要生产1.8415⨯105元的电恰好满足需求.【模型分析】令x =xyz⎛⎫⎪⎪⎝⎭, A =00.60.50.30.10.10.20.10⎛⎫⎪⎪⎝⎭, b =60000100000⎛⎫⎪⎪⎝⎭, 其中x称为总产值列向量,A称为消耗系数矩阵, b称为最终产品向量, 则Ax =00.60.50.30.10.10.20.10⎛⎫⎪⎪⎝⎭xyz⎛⎫⎪⎪⎝⎭=0.60.50.30.10.10.20.1y zx y zx y+⎛⎫⎪++⎪+⎝⎭根据需求, 应该有x-Ax = b, 即(E-A)x = b. 故x = (E-A)-1b.Matlab实验题某乡镇有甲、乙、丙三个企业. 甲企业每生产1元的产品要消耗0.25元乙企业的产品和0.25元丙企业的产品. 乙企业每生产1元的产品要消耗0.65元甲企业的产品, 0.05元自产的产品和0.05元丙企业的产品. 丙企业每生产1元的产品要消耗0.5元甲企业的产品和0.1元乙企业的产品. 在一个生产周期内, 甲、乙、丙三个企业生产的产品价值分别为100万元, 120万元, 60万元, 同时各自的固定资产折旧分别为20万元, 5万元和5万元.(1) 求一个生产周期内这三个企业扣除消耗和折旧后的新创价值.(2) 如果这三个企业接到外来订单分别为50万元, 60万元, 40万元, 那么他们各生产多少才能满足需求?案例四. 平板的稳态温度分布问题在热传导的研究中, 一个重要的问题是确定一块平板的稳态温度分布. 根据…定律, 只要测定一块矩形平板四周的温度就可以确定平板上各点的温度.图8 一块平板的温度分布图【模型准备】如图9所示的平板代表一条金属梁的截面. 已知四周8个节点处的温度(单位°C), 求中间4个点处的温度T 1, T 2, T 3, T 4.图9 一块平板的温度分布图【模型假设】假设忽略垂直于该截面方向上的热传导, 并且每个节点的温度等于与它相邻的四个节点温度的平均值.【模型建立】根据已知条件和上述假设, 有如下线性方程组1232143144231(90100)41(8060)41(8060)41(5050)4T T T T T T T T T T T T ⎧=+++⎪⎪⎪=+++⎪⎨⎪=+++⎪⎪=+++⎪⎩ 【模型求解】将上述线性方程组整理得1231241342344190414041404100T T T T T T T T T T T T --=⎧⎪-+-=⎪⎨-+-=⎪--+=⎪⎩. 在Matlab 命令窗口输入以下命令T 1T 2 T 3 T 4 10080908060506050>> A = [4,-1,-1,0;-1,4,0,-1;-1,0,4,-1;0,-1,-1,4]; b = [190;140;140;100];>> x = A\b; x’Matlab执行后得ans =82.9167 70.8333 70.8333 60.4167可见T1 = 82.9167, T2 = 70.8333, T3 = 70.8333, T4 = 60.4167.参考文献陈怀琛, 高淑萍, 杨威, 工程线性代数,: 电子工业, 2007. 页码: 15-16.Matlab实验题假定下图中的平板代表一条金属梁的截面, 并忽略垂直于该截面方向上的热传导. 已知平板内部有30个节点, 每个节点的温度近似等于与它相邻的四个节点温度的平均值. 设4条边界上的温度分别等于每位同学学号的后四位的5倍, 例如学号为16308209的同学计算本题时, 选择T l = 40, T u = 10, T r = 0, T d = 45.图10 一块平板的温度分布图(1) 建立可以确定平板内节点温度的线性方程组.(2) 用Matlab软件求解该线性方程组.(3) 用Matlab中的函数mesh绘制三维平板温度分布图.案例五. CT图像的代数重建问题X射线透视可以得到3维对象在2维平面上的投影, CT则通过不同角度的X射线得到3维对象的多个2维投影, 并以此重建对象内部的3维图像. 代数重建方法就是从这些2维投影出发, 通过求解超定线性方程组, 获得对象内部3维图像的方法.图11双层螺旋CT 图12 CT图像这里我们考虑一个更简单的模型, 从2维图像的1维投影重建原先的2维图像. 一个长方形图像可以用一个横竖均匀划分的离散网格来覆盖, 每个网格对应一个像素, 它是该网格上各点像素的均值. 这样一个图像就可以用一个矩阵表示,其元素就是图像在一点的灰度值(黑白图像). 下面我们以3⨯3图像为例来说明.3⨯3图像各点的灰度值水平方向上的叠加值x1 = 1 x2 = 0 x3 = 0 x1 + x2 + x3 = 1x4 = 0 x5 = 0.5 x6 = 0.5 x4 + x5 + x6 = 1x7 = 0.5 x8 = 0 x9 = 1 x7 + x8 + x9 = 1.5 竖直方向上的叠加值x1 + x4 + x7= 1.5x2 + x5 + x8= 0.5x3 + x6 + x9= 1.5i色. 如果我们不知道网格中的数值, 只知道沿竖直方向和水平方向的叠加值, 为了确定网格中的灰度值, 可以建立线性方程组(含有6个方程, 9个未知数)123456369111x x xx x xx x x++=⎧⎪++=⎪⎨⎪++=⎪⎩显然该方程组的解是不唯一的, 为了重建图像, 必须增加叠加值. 如我们增加从右上方到左下方的叠加值, 则方程组将增加5个方程x1 = 1,x2 + x4 = 0,x3 + x5 + x7 = 1,x 6 + x 8 = 0.5, x 9 = 1,和上面的6个方程放在一起构成一个含有11个方程, 9个未知数的线性方程组. 【模型准备】设3⨯3图像中第一行3个点的灰度值依次为x 1, x 2, x 3, 第二行3个点的灰度值依次为x 4, x 5,x 6, 第三行3个点的灰度值依次为x 7, x 8, x 9. 沿竖直方向的叠加值依次为1.5, 0.5, 1.5, 沿水平方向的叠加值依次为1, 1, 1.5, 沿右上方到左下方的叠加值依次为1, 0, 1, 0.5, 1. 确定x 1, x 2, …, x 9的值.【模型建立】由已知条件可得(含有11个方程, 9个未知数的)线性方程组1234569111x x x x x x x ++=⎧⎪++=⎪⎨⎪=⎪⎩ 【模型求解】在Matlab 命令窗口输入以下命令>> A = [1,1,1,0,0,0,0,0,0;0,0,0,1,1,1,0,0,0;0,0,0,0,0,0,1,1,1;1,0,0,1,0,0,1,0,0;0,1,0,0,1,0,0,1,0;0,0,1,0,0,1,0,0,1; 1,0,0,0,0,0,0,0,0;0,1,0,1,0,0,0,0,0;0,0,1,0,1,0,1,0,0; 0,0,0,0,0,1,0,1,0;0,0,0,0,0,0,0,0,1];>> b = [1;1;1.5;1.5;0.5;1.5;1;0;1;0.5;1]; >> x = A\b; x ’Matlab 执行后得Warning: Rank deficient, rank = 8 tol =4.2305e-015. ans =1.0000 0.0000 0 -0.0000 0.5000 0.5000 0.5000 -0.0000 1.0000 可见上述方程组的解不唯一. 其中的一个特解为x 1 = 1, x 2 = 0, x 3 = 0, x 4 = 0, x 5 = 0.5, x 6 = 0.5, x 7 = 0.5, x 8 = 0, x 9 = 1.【模型分析】上述结果表明, 仅有三个方向上的叠加值还不够.可以再增加从左上方到右下方的叠加值. 在实际情况下, 由于测量误差, 上述线性方程组可能是超定的. 这时可以将超定方程组的近似解作为重建的图像数据.Matlab 实验题给定一个3⨯3图像的2个方向上的灰度叠加值: 沿左上方到右下方的灰度叠加值依次为0.8, 1.2, 1.7, 0.2, 0.3; 沿右上方到左下方的灰度叠加值依次为0.6, 0.2, 1.6, 1.2, 0.6.(1) 建立可以确定网格数据的线性方程组, 并用Matlab 求解. (2) 将网格数据乘以256, 再取整, 用Matlab 绘制该灰度图像.案例六. 平衡结构的梁受力计算在桥梁、房顶、铁塔等建筑结构中, 涉及到各种各样的梁. 对这些梁进行受力分析是设计师、工程师经常做的事情.图14 埃菲尔铁塔局部下面以双杆系统的受力分析为例, 说明如何研究梁上各铰接点处的受力情况. 【模型准备】在图15所示的双杆系统中, 已知杆1重G1 = 200牛顿, 长L1 = 2米, 与水平方向的夹角为θ1 = π/6, 杆2重G2 = 100牛顿, 长L2 = 2米, 与水平方向的夹角为θ2 = π/4. 三个铰接点A, B, C所在平面垂直于水平面. 求杆1, 杆2在铰接点处所受到的力.图15双杆系统【模型假设】假设两杆都是均匀的. 在铰接点处的受力情况如图16所示.【模型建立】对于杆1:水平方向受到的合力为零, 故N1 = N3,竖直方向受到的合力为零, 故N2 + N4 = G1,以点A为支点的合力矩为零, 故(L1sinθ1)N3 + (L1cosθ1)N4 = (12L1cosθ1)G1.图16 两杆受力情况对于杆2类似地有AC杆1杆2CN1N2N3N5N6G1G2A B杆1杆2π/6π/4N 5 = N 7, N 6 = N 8 + G 2, (L 2sin θ2)N 7 = (L 2cos θ2)N 8 + (12L 2cos θ2)G 2.此外还有N 3 = N 7, N 4 = N 8. 于是将上述8个等式联立起来得到关于N 1, N 2, …, N 8的线性方程组:132414800N N N N G N N -=⎧⎪+=⎪⎨⎪⎪-=⎩ 【模型求解】在Matlab 命令窗口输入以下命令>> G1=200; L1=2; theta1=pi/6; G2=100; L2=sqrt(2); theta2=pi/4; >> A = [1,0,-1,0,0,0,0,0;0,1,0,1,0,0,0,0;0,0,L1*sin(theta1),L1*cos(theta1),0,0,0,0;0,0,0,0,1,0,-1,0; 0,0,0,0,0,1,0,-1;0,0,0,0,0,0,L2*sin(theta2),-L2*cos(theta2); 0,0,1,0,0,0,-1,0;0,0,0,1,0,0,0,-1];>> b = [0;G1;0.5*L1*cos(theta1)*G1;0;G2;0.5*L2*cos(theta2)*G2;0;0]; >> x = A\b; x ’ Matlab 执行后得 ans =95.0962 154.9038 95.0962 45.0962 95.0962 145.0962 95.0962 45.0962【模型分析】最后的结果没有出现负值, 说明图16中假设的各个力的方向与事实一致. 如果结果中出现负值, 则说明该力的方向与假设的方向相反. 参考文献陈怀琛, 高淑萍, 杨威, 工程线性代数,: 电子工业, 2007. 页码: 157- 158.Matlab 实验题有一个平面结构如下所示, 有13条梁(图中标号的线段)和8个铰接点(图中标号的圈)联结在一起. 其中1号铰接点完全固定, 8号铰接点竖直方向固定, 并在2号, 5号和6号铰接点上, 分别有图示的10吨, 15吨和20吨的负载. 在静平衡的条件下,任何一个铰接点上水平和竖直方向受力都是平衡的. 已知每条斜梁的角度都是45º.(1) 列出由各铰接点处受力平衡方程构成的线性方程组. (2) 用Matlab 软件求解该线性方程组, 确定每条梁受力情况.图17 一个平面结构的梁案例七. 化学方程式配平问题在用化学方法处理污水过程中, 有时会涉及到复杂的化学反应. 这些反应的化学方程式是分析计算和工艺设计的重要依据. 在定性地检测出反应物和生成物之后,可以通过求解线性方程组配平化学方程式.【模型准备】某厂废水中含K, 其浓度为650mg/L. 现用氯氧化法处理, 发生如下反应:K + 2KOH + Cl 2 = KO+ 2KCl + H 2O.投入过量液氯, 可将氰酸盐进一步氧化为氮气. 请配平下列化学方程式:KO +KOH +Cl 2 ===CO 2+N 2+KCl +H 2O.(注: 题目摘自XX 省XX 外国语学校2008-2009学年高三第三次月考化学试卷) 【模型建立】设x 1KO +x 2KOH +x 3Cl 2 === x 4CO 2 +x 5N 2 +x 6KCl +x 7H 2O,则1261247141527362222x x x x x x xx x x x x x x x +=⎧⎪+=+⎪⎪=⎪⎨=⎪⎪=⎪=⎪⎩, 即1261247141527360200202020x x x x x x x x x x x x x x x +-=⎧⎪+--=⎪⎪-=⎪⎨-=⎪⎪-=⎪-=⎪⎩ 【模型求解】在Matlab 命令窗口输入以下命令>> A = [1,1,0,0,0,-1,0;1,1,0,-2,0,0,-1;1,0,0,-1,0,0,0;1,0,0,0,-2,0,0;0,1,0,0,0,0,-2;0,0,2,0,0,-1,0];>> x = null(A,’r ’); format rat, x ’Matlab 执行后得 ans =1 2 3/2 1 1/2 3 1 可见上述齐次线性方程组的通解为x = k (1, 2, 3/2, 1, 1/2, 3, 1)T .取k = 2得x = (2, 4, 3, 2, 1, 6, 2)T . 可见配平后的化学方程式如下2KO + 4KOH + 3Cl 2 ===2CO 2+ N 2+ 6KCl + 2H 2O.【模型分析】利用线性方程组配平化学方程式是一种待定系数法. 关键是根据化学方程式两边所涉及到的各种元素的量相等的原则列出方程. 所得到的齐次线性方程组Ax = θ中所含方程的个数等于化学方程式中元素的种数s , 未知数的个数就是化学方程式中的项数n .当r(A ) = n -1时, Ax = θ的基础解系中含有1个(线性无关的)解向量. 这时在通解中取常数k 为各分量分母的最小公倍数即可. 例如本例中1, 2, 3/2, 1, 1/2, 3, 1分母的最小公倍数为2, 故取k = 2.当r(A ) ≤n -2时, Ax = θ的基础解系中含有2个以上的线性无关的解向量. 这时可以根据化学方程式中元素的化合价的上升与下降的情况, 在原线性方程组中添加新的方程. Matlab 实验题配平下列反应式(1) FeS + KMnO 4 + H 2SO 4—— K 2SO 4 + MnSO 4 + Fe 2(SO 4)3 + H 2O + S ↓ (2) Al 2(SO 4)3 + Na 2CO 3 + H 2O —— Al(OH)3↓+ CO 2↑+ Na 2SO 4案例八. 互付工资问题互付工资问题是多方合作相互提供劳动过程中产生的. 比如农忙季节, 多户农民组成互助组, 共同完成各户的耕、种、收等农活. 又如木工, 电工, 油漆工等组成互助组, 共同完成各家的装潢工作. 由于不同工种的劳动量有所不同, 为了均衡各方的利益, 就要计算互付工资的标准.【模型准备】现有一个木工, 电工, 油漆工. 相互装修他们的房子, 他们有如下协议:(1) 每人工作10天(包括在自己家的日子), (2) 每人的日工资一般的市价在60~80元之间, (3) 日工资数应使每人的总收入和总支出相等.求每人的日工资. 【模型假设】假设每人每天工作时间长度相同. 无论谁在谁家干活都按正常情况工作, 既不偷懒, 也不加班.【模型建立】设木工, 电工, 油漆工的日工资分别为x , y , z 元, 则由下表可得2610451044310x y z xx y z y x y z z++=⎧⎪++=⎨⎪++=⎩, 即8604504470x y z x y z x y z -++=⎧⎪-+=⎨⎪+-=⎩【模型求解】在Matlab 命令窗口输入以下命令>> A = [-8,1,6;4,-5,1;4,4,-7];>> x = null(A,’r ’); format rat, x ’ Matlab 执行后得ans =31/36 8/9 1可见上述齐次线性方程组的通解为x = k (31/36, 8/9, 1)T . 因而根据“每人的日工资一般的市价在60~80元之间”可知60 ≤3631k <98k < k ≤ 80, 即 312160≤k ≤ 80.也就是说, 木工, 电工, 油漆工的日工资分别为3631k 元, 98k 元, k 元, 其中312160≤k ≤ 80. 为了简便起见, 可取k = 72, 于是木工, 电工, 油漆工的日工资分别为62元, 64元, 72元.【模型分析】事实上各人都不必付自己工资, 这时各家应付工资和各人应得收入如下6845447y z x x z y x y z +=⎧⎪+=⎨⎪+=⎩, 即8604504470x y z x y z x y z -++=⎧⎪-+=⎨⎪+-=⎩ 可见这样得到的方程组与前面得到的方程组是一样的.Matlab 实验题甲, 乙, 丙三个农民组成互助组, 每人工作6天(包括为自己家干活的天数), 刚好完成他们三人家的农活, 其中甲在甲, 乙, 丙三家干活的天数依次为: 2, 2.5, 1.5; 乙在甲, 乙, 丙三家各干2天活, 丙在甲, 乙, 丙三家干活的天数依次为: 1.5, 2, 2.5. 根据三人干活的种类, 速度和时间, 他们确定三人不必相互支付工资刚好公平. 随后三人又合作到邻村帮忙干了2天(各人干活的种类和强度不变), 共获得工资500元.问他们应该怎样分配这500元工资才合理?案例九. 平衡价格问题为了协调多个相互依存的行业的平衡发展, 有关部门需要根据每个行业的产出在各个行业中的分配情况确定每个行业产品的指导价格, 使得每个行业的投入与产出都大致相等.【模型准备】假设一个经济系统由煤炭、电力、钢铁行业组成, 每个行业的产出在各个行业中的分配如下表所示:等的平衡价格.【模型假设】假设不考虑这个系统与外界的联系.【模型建立】把煤炭、电力、钢铁行业每年总产出的价格分别用x 1,x 2, x 3表示, 则123212331230.40.60.60.10.20.40.50.2x x x x x x x x x x x =+⎧⎪=++⎨⎪=++⎩, 即1231231230.40.600.60.90.200.40.50.80x x x x x x x x x --=⎧⎪-+-=⎨⎪--+=⎩. 【模型求解】在Matlab 命令窗口输入以下命令>> A = [1,-0.4,-0.6;-0.6,0.9,-0.2;-0.4,-0.5,0.8]; >> x = null(A,’r ’); format short, x ’ Matlab 执行后得ans =0.9394 0.8485 1.0000 可见上述齐次线性方程组的通解为x = k(0.9394, 0.8485, 1)T.这就是说, 如果煤炭、电力、钢铁行业每年总产出的价格分别0.9394亿元, 0.8485亿元, 1亿元, 那么每个行业的投入与产出都相等.【模型分析】实际上, 一个比较完整的经济系统不可能只涉及三个行业, 因此需要统计更多的行业间的分配数据.Matlab实验题假设一个经济系统由煤炭、石油、电力、钢铁、机械制造、运输行业组成, 每个行业的产出在各个行业中的分配如下表所示:产出分配购买者煤炭石油电力钢铁制造运输0 0 0.2 0.1 0.2 0.2 煤炭0 0 0.1 0.1 0.2 0.1 石油0.5 0.1 0.1 0.2 0.1 0.1 电力0.4 0.1 0.2 0 0.1 0.4 钢铁0 0.1 0.3 0.6 0 0.2 制造0.1 0.7 0.1 0 0.4 0 运输等的平衡价格.案例十. 电路设计问题电路是电子元件的神经系统. 参数的计算是电路设计的重要环节. 其依据来自两个方面: 一是客观需要, 二是物理学定律.图22 USB扩展板【模型准备】假设图23中的方框代表某类具有输入和输出终端的电路. 用11vi⎛⎫⎪⎝⎭记录输入电压和输入电流(电压v以伏特为单位, 电流i以安培为单位), 用22vi⎛⎫⎪⎝⎭记录输出电压和输入电流. 若22vi⎛⎫⎪⎝⎭= A11vi⎛⎫⎪⎝⎭,则称矩阵A为转移矩阵.图23 具有输入和输出终端的电子电路图图24给出了一个梯形网络, 左边的电路称为串联电路, 电阻为R 1(单位: 欧姆). 右边的电路是并联电路, 电路R 2. 利用欧姆定理和楚列斯基定律, 我们可以得到串联电路和并联电路的转移矩阵分别是1101R -⎛⎫ ⎪⎝⎭和2101/1R ⎛⎫ ⎪-⎝⎭串联电路 并联电路图24 梯形网络设计一个梯形网络, 其转移矩阵是180.55-⎛⎫⎪-⎝⎭. 【模型假设】假设导线的电阻为零.【模型建立】设A 1和A 2分别是串联电路和并联电路的转移矩阵, 则输入向量x 先变换成A 1x , 再变换到A 2(A 1x ). 其中A 2A 1 =2101/1R ⎛⎫ ⎪-⎝⎭1101R -⎛⎫ ⎪⎝⎭=121211/1/R R R R -⎛⎫ ⎪-+⎝⎭就是图22中梯形网络的转移矩阵.于是, 原问题转化为求R 1, R 2的值使得121211/1/R R R R -⎛⎫ ⎪-+⎝⎭=180.55-⎛⎫ ⎪-⎝⎭. 【模型求解】由121211/1/R R R R -⎛⎫ ⎪-+⎝⎭=180.55-⎛⎫ ⎪-⎝⎭可得121281/0.51/5R R R R -=-⎧⎪-=-⎨⎪+=⎩. 根据其中的前两个方程可得R 1 = 8, R 2 = 2. 把R 1 = 8, R 2 = 2代入上面的第三个方程确实能使等式成立. 这就是说在图22中梯形网络中取R 1 = 8, R 2 = 2即为所求.【模型分析】若要求的转移矩阵改为180.54-⎛⎫⎪-⎝⎭, 则上面的梯形网络无法实现. 因为v 2这时对应的方程组是121281/0.51/4R R R R -=-⎧⎪-=-⎨⎪+=⎩. 根据前两个方程依然得到R 1 = 8, R 2 = 2, 但把R 1= 8, R 2 = 2代入上第三个方程却不能使等式成立.练习题根据基尔霍夫回路电路定律(各节点处流入和流出的电流强度的代数和为零, 各回路中各支路的电压降之和为零), 列出下图所示电路中电流i 1, i 2, i 3所满足的线性方程组, 并用矩阵形式表示:图25简单的回路案例十一. 平面图形的几何变换随着计算机科学技术的发展, 计算机图形学的应用领域越来越广, 如仿真设计、效果图制作、动画片制作、电子游戏开发等.图形的几何变换, 包括图形的平移、旋转、放缩等, 是计算机图形学中经常遇到的问题. 这里暂时只讨论平面图形的几何变换.【模型准备】平面图形的旋转和放缩都很容易用矩阵乘法实现, 但是图形的平移并不是线性运算, 不能直接用矩阵乘法表示. 现在要求用一种方法使平移、旋转、放缩能统一用矩阵乘法来实现. 【模型假设】设平移变换为(x , y ) → (x +a , y +b )旋转变换(绕原点逆时针旋转θ角度)为(x , y ) → (x cos θ-y sin θ, x sin θ + y cos θ)放缩变换(沿x 轴方向放大s 倍, 沿y 轴方向放大t 倍)为(x , y ) → (sx , ty )【模型求解】R 2中的每个点(x , y )可以对应于R 3中的(x , y , 1). 它在xOy 平面上方1单E 12位的平面上. 我们称(x , y , 1)是(x , y )的齐次坐标. 在齐次坐标下, 平移变换(x , y ) → (x +a , y +b )可以用齐次坐标写成(x , y , 1) → (x +a , y +b , 1).于是可以用矩阵乘积1001001a b ⎛⎫ ⎪ ⎪⎝⎭1x y ⎛⎫ ⎪ ⎪⎝⎭=1x a y b +⎛⎫⎪+ ⎪⎝⎭实现.旋转变换(x , y ) → (x cos θ-y sin θ, x sin θ + y cos θ)可以用齐次坐标写成(x , y , 1) → (x cos θ-y sin θ, x sin θ + y cos θ, 1). 于是可以用矩阵乘积cos sin 0sin cos 0001θθθθ-⎛⎫ ⎪ ⎪⎝⎭1x y ⎛⎫ ⎪ ⎪⎝⎭=cos sin sin cos 1x y x y θθθθ-⎛⎫⎪+ ⎪⎝⎭实现.放缩变换(x , y ) → (sx , ty )可以用齐次坐标写成(x , y , 1) → (sx , ty , 1).于是可以用矩阵乘积0000001s t ⎛⎫ ⎪ ⎪⎝⎭1x y ⎛⎫ ⎪ ⎪⎝⎭=1sx ty ⎛⎫⎪ ⎪⎝⎭实现.【模型分析】由上述求解可以看出, R 2中的任何线性变换都可以用分块矩阵1⎛⎫⎪⎝⎭A O O 乘以齐次坐标实现, 其中A 是2阶方阵. 这样, 只要把平面图形上点的齐次坐标写成列向量, 平面图形的每一次几何变换, 都可通过左乘一个3阶变换矩阵来实现.参考文献David C. Lay, 线性代数及其应用, 沈复兴, 傅莺莺等译,: 人民邮电, 2009. 页码: 139-141.Matlab 实验题在Matlab 命令窗口输入以下命令 >>clear all , clc,>>t=[1,3,5,11,13,15]*pi/8; >>x=sin(t); y=cos(t); >>fill(x,y,'r'); >>grid on ;>>axis([-2.4, 2.4, -2, 2])运行后得图25.图26Matlab绘制的图形(1) 写出该图形每个顶点的齐次坐标;; 最后进行横(2) 编写Matlab程序, 先将上面图形放大0.9倍; 再逆时针旋转3坐标加0.8, 纵坐标减1的图形平移. 分别绘制上述变换后的图形.案例十二. 太空探测器轨道数据问题太空航天探测器发射以后, 可能需要调整以使探测器处在精确计算的轨道里. 雷达监测到一组列向量x1, …, x k,它们给出了不同时刻探测器的实际位置与预定轨道之间的偏差的信息.图28 火星探测器【模型准备】令X k = [x1, …, x k]. 在雷达进行数据分析时需要计算出矩阵G k = X k X k T. 一旦接收到数据向量x k+1,必须计算出新矩阵G k+1. 因为数据向量到达的速度非常快, 随着k的增加, 直接计算的负担会越来越重. 现需要给出一个算法, 使得计算G k的负担不会因为k的增加而加重.【模型求解】因为G k = X k X k T=[x 1, …, x k ]T 1T k⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦x x =T 1k i i i =∑x x ,G k +1 = X k +1T1k +X =[X k , x k +1]T T 1k k +⎡⎤⎢⎥⎣⎦X x = X k X k T +x k +1T 1k +x =G k +x k +1T 1k +x ,所以一旦接收到数据向量x k +1, 只要计算x k +1T1k +x , 然后把它与上一步计算得到的G k相加即可. 这样计算G k 的负担不会因为k 的增加而加重.【模型分析】计算机计算加法的时间与计算乘法的时间相比可以忽略不计. 因此在考虑计算矩阵乘积的负担时, 只要考察乘法的次数就可以了. 设x k 的维数是n , 则X k = [x 1, …, x k ]是n ⨯k 的矩阵, G k = X k X k T 是n ⨯n 的矩阵. 直接计算G k = X k X k T 需要做n 2k 次乘法. 因而计算的负担会随着k 的增加而增加. 但是对于每一个k , 计算x k Tk x 始终只要做n 2次乘法.Matlab 实验题用Matlab 编写一个程序用于处理这个问题.案例十三. 应用矩阵编制Hill 密码密码学在经济和军事方面起着极其重要的作用. 现代密码学涉及很多高深的数学知识. 这里无法展开介绍.图29 XX 通信的基本模型密码学中将信息代码称为密码, 尚未转换成密码的文字信息称为明文, 由密码表示的信息称为密文. 从明文到密文的过程称为加密, 反之为解密. 1929年, 希尔(Hill)通过线性变换对待传输信息进行加密处理, 提出了在密码史上有重要地位的希尔加密算法. 下面我们略去一些实际应用中的细节, 只介绍最基本的思想.【模型准备】若要发出信息action, 现需要利用矩阵乘法给出加密方法和加密后得到的密文, 并给出相应的解密方法.。



线性代数应用实例求插值多项式右表给出函数f(t)上4个点的值,试求三次插值多项式p(t) a 0 a-|t a 2t 2 a 3t 3 ,并求f (1.5)的近似值。
角军:令三次多项式函数 p(t) a 0 a 1t a 2t 2表中已知的4点,可以得到四元线性方程组:a 。
3 a o a 1 a 2 a 3 0 a o2a 1 4a 2 8a 3 1 a o3a 19a 227a 36对于四元方程组,笔算就很费事了。
应该用计算机求解了,键入:2 32,a 3 1,三次多项函数为 p(t) 3 2t2t t ,故f(1.5)近似等于 p(1.5) 3 2(1.5) 2(1.5)2 (1.5)31.125。
在一般情况下,当给出函数f(t)在n+1个点t i (i 1,2,卅,n 1)上的值f(tj 时,就可以用n 次多项式p(t) a 。
a 1t a ?t 2卅 a n t n对f (t)进行插值。
在数字信号处理中的应用——数字滤波器系统函数数字滤波器的网络结构图实际上也是一种信号流图。
它的特点在于所有的相加节点都 限定为双输入相加器;另外,数字滤波器器件有一个迟延一个节拍的运算,它也是一个线 性算子,它的标注符号为z 1o 根据这样的结 构图,也可以用类似于例 7.4的方法,求它的输入输出之间的传递函数,在数字信号处 理中称为系统函数。
图1表示了某个数字滤波器的结构图, 现在要求出它的系统函数,即输出 y 与输入 u 之比。
先在它的三个中间节点上标注信号 的名称x1,x2,x3,以便对每个节点列写方程。
t i0 1 2 3 f(t i )3-16得到x = 1 0 0 0 30 10 -20 0 1 0 -20 0 0 1 1 um ---2X 1y-i ---- 11 -- 1—z 1■ V1/4J 1 1/4■* x 2二―]X3z 1,.3/8图1某数字滤波器结构图>>A=[1,0,0,0;1,1,1,1;1,2,4,8;1,3,9,27], b=[3;0;-1;6], s=rref([A,b]) 得到 a 0 3,a 12, a 2描述n 阶线性时不变(LTI )连续系统的微分方程为d n yd n 1ydy」d mu」du 」an ,an 1 y b1 mbmbm 1u,a1 n a 2dt dtdt dt dty 及其各阶导数的初始值为 y (0),y ⑴(0),…,y (n -1)(0),求系统的零输入响应。
线性代数应用案例线性代数是数学中的一个重要分支,它在各个领域都有着重要的应用。
从最基础的向量运算到高级的矩阵理论,线性代数贯穿于整个数学体系,并且在物理、工程、计算机科学等领域中有着广泛的应用。
本文将通过几个实际案例,展示线性代数在不同领域的应用。
案例一,图像处理中的线性代数应用。
在图像处理领域,线性代数有着重要的应用。
例如,图像可以表示为一个矩阵,其中每个元素代表一个像素的数值。
通过对这个矩阵进行线性变换,可以实现图像的旋转、缩放、平移等操作。
此外,线性代数还可以用于图像的压缩和去噪,通过对图像矩阵进行特定的变换,可以实现对图像信息的提取和优化。
案例二,机器学习中的线性代数应用。
在机器学习领域,线性代数是必不可少的工具。
例如,在回归分析中,线性代数可以用来解决最小二乘法的问题,通过对数据矩阵进行变换,可以得到最优的回归系数。
此外,线性代数还可以用于主成分分析、奇异值分解等高级机器学习算法中,帮助我们理解和处理复杂的数据结构。
案例三,通信系统中的线性代数应用。
在通信系统中,线性代数也有着重要的应用。
例如,在信号处理中,线性代数可以用来描述信号的传输和变换过程,通过对信号矩阵进行运算,可以实现信号的编解码、调制解调等操作。
此外,线性代数还可以用于设计和分析通信系统中的滤波器、编码器等模块,帮助我们优化通信系统的性能。
通过上述案例的介绍,我们可以看到线性代数在不同领域都有着重要的应用。
它不仅可以帮助我们理解和解决实际问题,还可以为各种工程技术提供强大的数学工具支持。
因此,对线性代数的深入理解和应用将对我们的工作和研究产生重要的影响。
希望本文所介绍的案例能够帮助读者更好地理解线性代数的应用,并激发大家对这一领域的兴趣和研究。
行列式的应用案例1 大学生在饮食方面存在很多问题,多数大学生不重视吃早餐,日常饮食也没有规律,为了身体的健康就需要注意日常饮食中的营养。
大学生每天的配餐中需要摄入一定的蛋白质、脂肪和碳水化合物,下表给出了这三种食物提供的营养以及大学生的正常所需营养(它们的质量以适当的单位计量)。
试根据这个问题建立一个线性方程组,并通过求解方程组来确定每天需要摄入的上述三种食物的量。
解:设123,,x x x 分别为三种食物的摄入量,则由表中的数据可以列出下列方程组12323123365113337 1.1352347445x x x x x x x x ++=⎧⎪+=⎨⎪++=⎩ 利用matlab 可以求得 x =0.27722318361443 0.39192086163701 0.23323088049177案例2 一个土建师、一个电气师、一个机械师组成一个技术服务社。
假设在一段时间,每个人收入1元人民币需要支付给其他两人的服务费用以及每个人的实际收入如下表所示,问这段时间,每人的总收入是多少?(总收入=实际收入+支付服务费)解:设土建师、电气师、机械师的总收入分别是123,,x x x 元,根据题意,建立方程组1232133120.20.35000.10.47000.30.4600x x x x x x x x x --=⎧⎪--=⎨⎪--=⎩ 利用matlab 可以求得 x =1.0e+003 *1.25648414985591 1.44812680115274 1.55619596541787案例3医院营养师为病人配制的一份菜肴由蔬菜、鱼和肉松组成,这份菜肴需含1200cal 热量,30g 蛋白质和300mg 维生素c ,已知三种食物每100g 中的有关营养的含量如下表,试求所配菜肴中每种食物的数量。
解:设所配菜肴中蔬菜、鱼和肉松的数量分别为123,,x x x 百克,根据题意,建立方程组12312312360300600120039630906030300x x x x x x x x x ++=⎧⎪++=⎨⎪++=⎩利用matlab 可以求得 x =1.521739130434782.39130434782609 0.65217391304348矩阵的应用案例1 矩阵概念的引入 (1)线性方程组11112211211222221122n n n n n n nn n na x a x a xb a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩的系数(,1,2,,),(1,2,,)i j j a i j n b j n ==按原来的位置构成一数表11121121222212n n n n nnn a a a b aa ab a a a b ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦该数表决定着上述方程组是否有解,以及如果有解,解是什么等问题,因而研究这个数表就很重要。
线性代数应用实例 ● 求插值多项式右表给出函数()f t 上4个点的值,试求三次插值多项式230123()p t a a t a t a t =+++,并求(1.5)f 的近似值。
解:令三次多项式函数230123()p t a a t a t a t =+++过表中已知的4点,可以得到四元线性方程组:⎪⎪⎩⎪⎪⎨⎧=+++-=+++=+++=627931842033210321032100a a a a a a a a a a a a a 对于四元方程组,笔算就很费事了。
应该用计算机求解了,键入: >>A=[1,0,0,0;1,1,1,1;1,2,4,8;1,3,9,27], b=[3;0;-1;6], s=rref([A,b]) 得到x = 1 0 0 0 3 0 1 0 0 -2 0 0 1 0 -2 0 0 0 1 1得到01233,2,2,1a a a a ==-=-=,三次多项函数为23()322p t t t t =--+,故(1.5)f 近似等于23(1.5)32(1.5)2(1.5)(1.5) 1.125p =--+=-。
在一般情况下,当给出函数()f t 在n+1个点(1,2,,1)i t i n =+上的值()i f t 时,就可以用n 次多项式2012()n n p t a a t a t a t =++++对()f t 进行插值。
● 在数字信号处理中的应用----- 数字滤波器系统函数数字滤波器的网络结构图实际上也是一种信号流图。
它的特点在于所有的相加节点都限定为双输入相加器;另外,数字滤波器器件有一个迟延一个节拍的运算,它也是一个线性算子,它的标注符号为z -1。
根据这样的结构图,也可以用类似于例7.4的方法,求它的输入输出之间的传递函数,在数字信号处理中称为系统函数。
图1表示了某个数字滤波器的结构图,现在要求出它的系统函数,即输出y 与输入u 之比。
先在它的三个中间节点上标注信号的名称x1,x2,x3,以便对每个节点列写方程。
由于迟延算子z -1不是数,要用符号代替,所以取q = z -1,按照图示情况,可以写出:1223312311844x qx ux q x u x x =+⎛⎫=-+ ⎪⎝⎭=写成矩阵形式为11223300231100844010q x x x q x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎛⎫⎢⎥⎢⎥⎢⎥⎢⎥==-+⇒ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎝⎭⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦x u x =Qx -Pu经过移项后,系统函数W 可以写成:W =x/u =inv(I -Q)*P 现在可以列写计算系统函数的MATLAB 程序ea705,syms q% 规定符号变量Q(1,2)=q; Q(2,3)=3/8*q -1/4; Q(3,1)=1; % 给非零元素赋值 Q(3,3)=0; % 给右下角元素Q (3,3)赋值后,矩阵中未赋值元素都自动置零 P=[2;1/4;0]% 给P 赋值W=inv(eye(3)-Q)*P% 用信号流图求传递函数的公式程序运行的结果为W = [-16/(-8+3*q^2-2*q)-2*q/(-8+3*q^2-2*q) ][ -2*(3*q -2)/(-8+3*q^2-2*q)-2/(-8+3*q^2-2*q)] [-16/(-8+3*q^2-2*q)-2*q/(-8+3*q^2-2*q)]我们关心的是以y =x3作为输出的系统函数,故再键入 pretty(W(3)) 整理后得到 1222116288(3)832 1.54 1.54y q q z W u q q q q z z -----++====-+--++-++用线性代数方法的好处是适用于任何复杂系统,并能用计算机解决问题。
信号与系统课程中的应用-----线性时不变系统的零输入响应描述n 阶线性时不变(LTI )连续系统的微分方程为,d d d d d d d d d d 111121u b t u b tu b y a t y a t y a t y a m m m m n n n n n ++-+++=++++ n ≥m已知y 及其各阶导数的初始值为y (0),y (1)(0),…,y (n -1)(0),求系统的零输入响应。
解:当LTI 系统的输入为零时,其零输入响应为微分方程的齐次解(即令微分方程等号右端为0),其形式为(设特征根均为单根)t p n t p t p n C C C t y e e e )(2121+++=其中p 1,p 2,…,p n 是特征方程a 1λn +a 2λn -1+…+ a n λ+ a n +1 =0的根,它们可用roots(a)语句求得。
各系数C 1,…,C n 由y 及其各阶导数的初始值来确定。
对此有C 1+ C 2+…+C n = y 0 y 0 = y (0)p 1C 1+ p 2C 2+…+ p n C n =D y 0 (D y 0表示y 的导数的初始值y (1)(0)) …………………………………011212111D y C p C p C p n n n n n n ----=+++写成矩阵形式为 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----0100211121121D D 111y y y C C C p p p p p p n n n n n n n 即 V ·C = Y 0 , 其解为 C =V \ Y 0式中 112000[,,,];[,D ,,D ]n n C C C y y y -==T T 0C Y⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=---1121121111n n n n n p p p p p pV V 为范德蒙矩阵,在MATLAB 的特殊矩阵库中有vander 函数可直接生成。
MATLAB 程序ea703.ma=input('输入分母系数向量a=[a1,a2,...]= '); n=length(a)-1;Y0=input('输入初始条件向量 Y0=[y0,Dy0,D2y0,...]= '); p=roots(a);V=rot90(vander(p));c= V\Y0'; dt=input('dt='); tf=input('tf= ') t=0:dt:tf; y=zeros(1,length(t)); for k=1:n y= y+c(k)*exp(p(k)*t);end plot(t ,y),grid⏹ 程序运行结果用这个通用程序来解一个三阶系统,运行此程序并输入a=[3,5,7,1]; dt=0.2; tf=8;而Y0取[1,0,0];[0,1,0];[0,0,1]三种情况,用hold on 语句使三次运行生成的图形画在一幅图上,得到图2。
● 减肥配方的实现设三种食物每100克中蛋白质、碳水化合物和脂肪的含量如下表,表中还给出了80年代美国流行的剑桥大学医学院的简捷营养处方。
现在的问题是:如果用这三种食物作为每天的主要食物,那么它们的用量应各取多少?才能全面准确地实现这个营养要求。
营养 每100g 食物所含营养(g)减肥所要求的每日营养量脱脂牛奶 大豆面粉乳清 蛋白质 36 51 13 33 碳水化合物 52 34 74 45 脂肪71.13设脱脂牛奶的用量为x 1个单位(100g ),大豆面粉的用量为x 2个单位(100g ),乳清的用量为x 3个单位(100g ),表中的三个营养成分列向量为:图2 三阶系统的零输入响应12136511352,34,74,07 1.1a a a ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦则它们的组合所具有的营养为11223312336511352347407 1.1x a x a x a x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥++=++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦使这个合成的营养与剑桥配方的要求相等,就可以得到以下的矩阵方程:123365113335234744507 1.13x x Ax b x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⇒=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦用MATLAB 解这个问题非常方便,列出程序ag763如下:A=[36,51,13;52,34,74;0,7,1.1] b=[33;45;3] x=A\b程序执行的结果为:0.2772 0.3919 0.2332x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦即脱脂牛奶的用量为27.7g ,大豆面粉的用量为39.2g ,乳清的用量为23.3g ,就能保证所需的综合营养量。
人口迁徙模型设在一个大城市中的总人口是固定的。
人口的分布则因居民在市区和郊区之间迁徙而变化。
每年有6%的市区居民搬到郊区去住,而有2%的郊区居民搬到市区。
假如开始时有30%的居民住在市区,70%的居民住在郊区,问十年后市区和郊区的居民人口比例是多少?30年、50年后又如何?这个问题可以用矩阵乘法来描述。
把人口变量用市区和郊区两个分量表示,即,ck k sk x x x ⎡⎤=⎢⎥⎣⎦其中x c 为市区人口所占比例,x s 为郊区人口所占比例,k 表示年份的次序。
在k=0的初始状态:0000.30.7c s x x x ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦。
一年以后,市区人口为x c1= (1-0.02) x c0+0.06x s0,郊区人口x s1= 0.02x c0 + (1-0.06)x s0,用矩阵乘法来描述,可写成:11010.940.020.3 0.29600.060.980.7 0.7040c s x x Ax x ⎡⎤⎡⎤⎡⎤⎡⎤==⋅==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦此关系可以从初始时间到k 年,扩展为2120k k k k x Ax A x A x --====,用下列MATLAB 程序进行计算:A=[0.94,0.02;0.06,0.98] x0=[0.3;0.7] x1=A*x0, x10=A^10*x0 x30=A^30*x0 x50=A^50*x0程序运行的结果为:1103050 0.2960 0.2717 0.2541 0.2508,,,, 0.7040 0.7283 0.7459 0.7492x x x x ⎡⎤⎡⎤⎡⎤⎡⎤====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦无限增加时间k ,市区和郊区人口之比将趋向一组常数 0.25/0.75。
为了弄清为什么这个过程趋向于一个稳态值,我们改变一下坐标系统。
在这个坐标系统中可以更清楚地看到乘以矩阵A 的效果。
选u 1为稳态向量[0.25,0.75]T 的任意一个倍数,令u 1=[1,3]T 和u 2=[-1,1]T 。