当前位置：文档之家› 应用回归分析课后答案

应用回归分析课后答案

第二章一元线性回归

解答：EXCEL结果:

SUMMARY OUTPUT

回归统计

Multiple R

R Square

Adjusted R Square

标准误差

观测值5

方差分析

df SS MS F Significance F

回归分析125

残差3

总计410

Coefficients标准误差t Stat P-value Lower 95%Upper 95%下限%上限% Intercept

X Variable 15

RESIDUAL OUTPUT

观测值预测Y残差

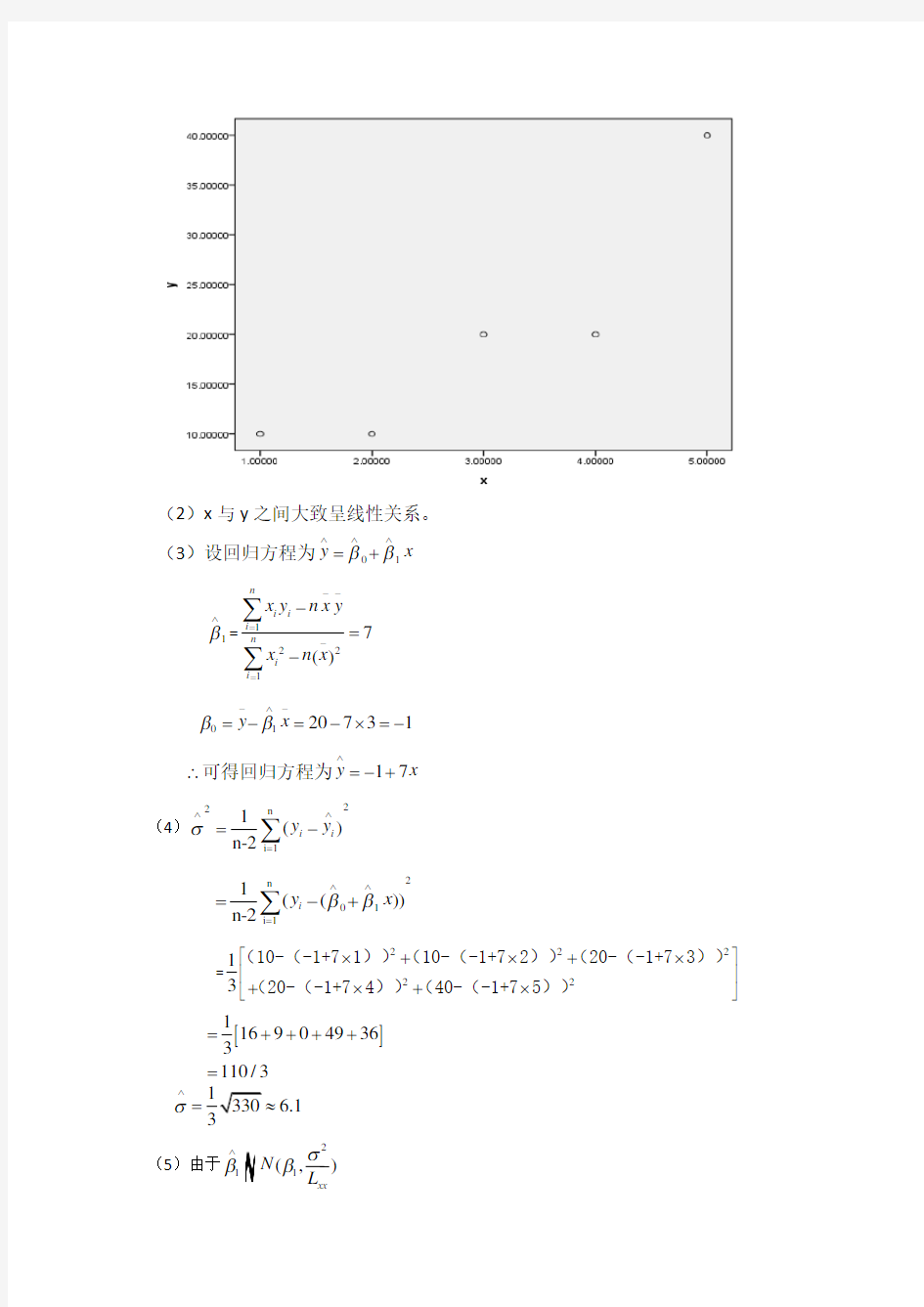
SPSS结果：（1）散点图为：

（2）x 与y 之间大致呈线性关系。（3）设回归方程为01y x ββ∧

∧

1β∧

7()n

i i

i n

i x y n x y

n x --

=-=-∑∑

0120731y x ββ-∧-

=-=-?=-

17y x ∧

∴=-+可得回归方程为

（4）22

i=1

1()n-2i i y y σ∧∧=-∑

01i=1

1(())n-2i y x ββ∧∧=-+∑ =222

13???+?+???+?+???

（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1

169049363

110/3=

++++=

330 6.13

σ∧=≈ （5）由于2

11(,

)xx

N L σββ∧

∧

服从自由度为n-2的t分布。因而

|(2)1

P t n

<-=-

也即：

1/211/2

(p t t

αα

βββ

∧∧

-<<+=1α

可得

95%

β∧的置信度为的置信区间为（7-2.3537+2.353即为：（，）

1()

(,())

n L

ββσ

∧

∧∧

服从自由度为n-2的t分布。因而

(2)1

P t n

∧

<-=-

即

0/200/2

()1

pβσββσα

∧∧∧∧

-<<+=-

可得

95%7.77,5.77

β∧-

的置信度为的置信区间为（）

（6）x与y的决定系数

()

490/6000.817

()

y y

∧-

==≈

∑

（7）

线性项加权的1.056

偏差.8331.833.326

组内2.500

总数4

由于(1,3)

F F

>,拒绝

H,说明回归方程显着，x与y有显着的线性关系。

（8

）t

∧

==其中

()

n n

i i i

i i

e y y

n n

σ∧∧

==-

∑∑

3.66

==≈

2.353

3.66

t t

∴接受原假设

:0,

Hβ=认为

β显着不为0，因变量y对自变量x的一元线性回归成立。（9）相关系数

()()

i i

xx yy

x x y y

L L

∑

0.904

=≈

r小于表中1%

α=的相应值同时大于表中5%

α=的相应值，∴x与y有显着的线性关系.

残差图为：

从图上看，残差是围绕e=0随机波动，从而模型的基本假定是满足的。

（11）当广告费0x =万元时，销售收入028.4y =万元，

95%置信度为的置信区间 y 2σ∧

∧

±近似为，即（，）解答：

（1）散点图为：

（2）x 与y 之间大致呈线性关系。（3）设回归方程为01y x ββ∧

∧

1β∧

(2637021717)

0.0036(71043005806440)

()n

i i

i n

i x y n x y

n x --

=--=

=--∑∑

01 2.850.00367620.1068y x ββ-∧-

=-=-?=

0.10680.0036y x ∧

∴=+可得回归方程为

(4) 22

i=1

1()n-2i i y y σ∧∧=-∑

01i=1

1(())n-2i y x ββ∧∧=-+∑ =

σ∧

(5) 由于2

11(,

)xx

N L σββ∧

t σ

∧

服从自由度为n-2的t 分布。因而

/2|(2)1P t n αασ????<-=-??

也即：1/2

11/2

(p t t ααβββ∧

∧

-<<+=1α-

可得195%β∧

的置信度为的置信区间为

0.4801/0.4801/??（0.0036-1.8600.0036+1.860

即为：（，）

001()(,())xx

x N n L ββσ-

∧

t ∧

∧

服从自由度为n-2的t 分布。因而

/2(2)1P t n αα∧??????<-=-??????????

即0/200/2()1p βσ

ββσα∧∧

∧

-<<+=- 可得195%0.3567,0.5703β∧

-的置信度为的置信区间为（）

(6)x 与y 的决定系数 2

()

i n

i y y r y y ∧-

=-=-=

-∑∑16.82027

18.525

(7)

ANOVA x

平方和df

均方F

显着性组间（组合）7.168

线性项加权的1.027

偏差6.315.885组内2

总数9

由于(1,9)

F F

>,拒绝

H,说明回归方程显着，x与y有显着的线性关系。

(8) t

∧

==其中

()

n n

i i i

i i

e y y

n n

σ∧∧

==-

∑∑

8.542

1.895

8.542

t t

∴接受原假设

:0,

Hβ=认为

β显着不为0，因变量y对自变量x的一元线性回归成立。

(9) 相关系数

()()

i i

x x y y

∑

0.9489

r小于表中1%

α=的相应值同时大于表中5%

α=的相应值，∴x与y有显着的线性关系.

8 325 9 670 3 10

1215

从图上看，残差是围绕e=0随机波动，从而模型的基本假定是满足的。

(11)001000 3.7x ∧

==新保单时，需要加班的时间为y 小时。

（12）00/200y (2)1y t n h αα∧

∧

±-+的置信概率为1-的置信区间精确为, 即为（，）

近似置信区间为：02y σ∧∧

±，即（，）

（13）可得置信水平为α1-的置信区间为0/200(2)y t n h α∧

∧

±-，即为（，）.

可以用直线回归描述y 与x 之间的关系. (2)回归方程为:12112.629 3.314y x ∧

(3)

从图上可看出，检验误差项服从正态分布。

第三章多元线性回归

初始数据：

编号y x1x2x3

116070351

22607540

321065402

426574423

52407238

62206845

727578424

816066362

92757044

1025065423

解：（1）用SPSS算出y，x1，x2,x3相关系数矩阵：

数值分析课后答案

1、解：将)(x V n 按最后一行展开，即知)(x V n 是n 次多项式。由于 n i i i n n n n n i n x x x x x x x x x x V ...1...1... ......... ...... 1 )(21110 20 0---= ，.1,...,1,0-=n i 故知0)(=i n x V ，即110,...,,-n x x x 是)(x V n 的根。又)(x V n 的最高次幂 n x 的系数为 )(...1...1... ...... .........1),...,,(101 1 21 11 2 2221 02001101j n i j i n n n n n n n n n n n x x x x x x x x x x x x x x V -== ∏-≤<≤-----------。故知).)...()()(,...,,()(1101101------=n n n n x x x x x x x x x V x V 6、解：（1）设 .)(k x x f =当n k ,...,1,0=时，有.0)()1(=+x f n 对 )(x f 构造Lagrange 插值多项式， ),()(0 x l x x L j n j k j n ∑== 其 0)()! 1() ()()()(1)1(=+=-=++x w n f x L x F x R n n n n ξ， ξ介于j x 之间，.,...,1,0n j = 故 ),()(x L x f n =即 .,...,1,0,)(0 n k x x l x k j n j k j ==∑= 特别地，当0=k 时， 10) (=∑=n j x j l 。（2） 0)()1(1) ()1()()(0000=-=??? ? ??-??? ? ??-=--=-===∑∑∑∑k j j i j i k j k i i j i i k j n j k i i j k n j j x x x x i k x l x x i k x l x x ）利用（。 7、证明：以b a ,为节点进行线性插值，得 )()()(1 b f a b a x a f b a b x x P --+--= 因 0)()(==b f a f ，故0)(1=x P 。而 ))()(("2 1 )()(1b x a x f x P x f --= -ξ，b a <<ξ。故)("max )(8 122)("max )(max 2 2 x f a b a b x f x f b x a b x a b x a ≤≤≤≤≤≤-=??? ??-≤。 14、解：设 ))...()(()(21n n x x x x x x a x f ---=， k x x g =)(，记)() (1 ∏=-=n j j n x x x w ，则 ),()(x w a x f n n =).()(' j n n j x w a x f = 由差商的性质知 [])! 1()(1,..,,1) (' 1 )(')('1 211 11 -== ==-===∑∑∑ n g a x x x g a x w x a x w a x x f x n n n n n j j n k j n n j j n n k j n j j k j ξ， ξ介于n x x ,...,1之间。当20-≤≤ n k 时，0)()1(=-ξn g ，当 1-=n k 时，)!1()(1-=-n g n ξ，故 ???-=-≤≤=-= --=∑1,,20,0)!1()(1) ('1 11 n k a n k n g a x f x n n n n j j k j ξ 16、解：根据差商与微商的关系，有 [] 1! 7! 7!7)(2,...,2,2)7(7 10===ξf f ， [ ] 0! 80 !8)(2,...,2,2)8(8 1 ===ξf f 。（ 13)(47+++=x x x x f 是7次多项式，故 ,!7)()7(=x f 0)()8(=x f ）。 25、解：（1）右边= [][]dx x S x f x S dx x S x f b a b a ??-+-)(")(")("2)(")("2 = [] d x x S x f x S x S x S x f x f b a ?-++-)("2)(")("2)(")(")("2)(" 222 = [] d x x S x f b a ?-)(")(" 22 = [][]dx x S dx x f b a b a 2 2 )(")("??- =左边。（2）左边= ? -b a dx x S x f x S ))(")(")(("

数值分析课后题答案

数值分析第二章 2．当1,1,2x =-时，()0,3,4f x =-,求()f x 的二次插值多项式。解： 0120121200102021101201220211,1,2, ()0,()3,()4;()()1 ()(1)(2)()()2()()1 ()(1)(2) ()()6 ()()1 ()(1)(1) ()()3 x x x f x f x f x x x x x l x x x x x x x x x x x l x x x x x x x x x x x l x x x x x x x ==-===-=--==-+-----==------= =-+-- 则二次拉格朗日插值多项式为 2 20 ()()k k k L x y l x ==∑ 0223()4() 14 (1)(2)(1)(1)23 537623 l x l x x x x x x x =-+=---+ -+= +- 6．设,0,1,,j x j n =L 为互异节点，求证：（1） 0()n k k j j j x l x x =≡∑ (0,1,,);k n =L （2）0 ()()0n k j j j x x l x =-≡∑ (0,1,,);k n =L 证明（1）令()k f x x = 若插值节点为,0,1,,j x j n =L ，则函数()f x 的n 次插值多项式为0 ()()n k n j j j L x x l x == ∑。插值余项为(1)1() ()()()()(1)! n n n n f R x f x L x x n ξω++=-= + 又,k n ≤Q

(1)()0 ()0 n n f R x ξ+∴=∴= 0()n k k j j j x l x x =∴=∑ (0,1,,);k n =L 0 000 (2)()() (())()()(()) n k j j j n n j i k i k j j j i n n i k i i k j j i j x x l x C x x l x C x x l x =-==-==-=-=-∑∑∑∑∑ 0i n ≤≤Q 又由上题结论可知 ()n k i j j j x l x x ==∑ ()()0 n i k i i k i k C x x x x -=∴=-=-=∑原式 ∴得证。 7设[]2 (),f x C a b ∈且()()0,f a f b ==求证： 21 max ()()max ().8 a x b a x b f x b a f x ≤≤≤≤''≤- 解：令01,x a x b ==，以此为插值节点，则线性插值多项式为 10 101010 ()() ()x x x x L x f x f x x x x x --=+-- =() () x b x a f a f b a b x a --=+-- 1()()0()0 f a f b L x ==∴=Q 又插值余项为1011 ()()()()()()2 R x f x L x f x x x x x ''=-= -- 011 ()()()()2 f x f x x x x x ''∴= --

数值分析习题集及答案[1].(优选)

数值分析习题集（适合课程《数值方法A 》和《数值方法B 》）长沙理工大学第一章绪论 1. 设x >0,x 的相对误差为δ,求ln x 的误差. 2. 设x 的相对误差为2％,求n x 的相对误差. 3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字: *****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====? 4. 利用公式(3.3)求下列各近似值的误差限: ********12412324(),(),()/,i x x x ii x x x iii x x ++其中**** 1234 ,,,x x x x 均为第3题所给的数. 5. 计算球体积要使相对误差限为1％,问度量半径R 时允许的相对误差限是多少? 6. 设028,Y =按递推公式 1n n Y Y -=( n=1,2,…) 计算到100Y .27.982(五位有效数字),试问计算100Y 将有多大误差? 7. 求方程2 5610x x -+=的两个根,使它至少具有四位有效数字27.982). 8. 当N 充分大时,怎样求2 1 1N dx x +∞+?? 9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2 ? 10. 设 212S gt = 假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对误差增加,而相对误差却减小. 11. 序列 {}n y 满足递推关系1101n n y y -=-(n=1,2,…),若0 1.41y =≈(三位有效数字), 计算到 10y 时误差有多大?这个计算过程稳定吗? 12. 计算6 1)f =, 1.4≈,利用下列等式计算,哪一个得到的结果最好? 3 -- 13. ()ln(f x x =,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若

26、回归分析测试题及答案

中级经济师基础知识第 1题：单选题(本题1分) 某公司产品当产量为1000单位时，其总成本为4000元；当产量为2000单位时，其总成本为5000，则设产量为x，总成本为y，正确的一元回归方程表达式应该是（）。 A、y = 3000 + x B、y = 4000 + 4x C、y = 4000 + x D、y = 3000 + 4x 【正确答案】：A 【答案解析】：本题可列方程组：设该方程为y = a + bx，则由题意可得：4000 = a + 1000b5000 = a + 2000b 解该方程，得b=1，a=3000，所以方程为y = 3000 + x 第 2题：单选题(本题1分) 在回归分析中，估计回归系数的最小二乘法的原理是（）。 A、使得因变量观测值与均值之间的离差平方和最小 B、使得因变量估计值与均值之间的离差平方和最小 C、使得观测值与估计值之间的乘积和最小 D、使得因变量观测值与估计值之间的离差平方和最小【正确答案】：D 【答案解析】：较偏较难的一道题目。最小二乘法就是使得因变量的观测值与估计值之间的离差平方和最小来估计参数的一种方法第 3题：多选题(本题2分) 关于相关分析和回归分析的说法，正确的的有（） A、相关分析可以从一个变量的变化来推测另一个变量的变化 B、相关分析研究变量间相关的方向和相关的程度 C、相关分析中需要明确自变量和因变量 D、回归分析研究变量间相互关系的具体形式 E、相关分析和回归分析在研究方法和研究目的有明显区别【正确答案】：BDE 【答案解析】：相关分析与回归分析在研究目的和方法上具有明显的区别。（1）、相关分析研究变量之间相关的方向和相关的程度，无法从一个变量的变化来推测另一变量的变化情况。（2）、回归分析是研究变量之间相关关系的具体形式

数值分析课后题答案

数值分析 2?当x=1,—1,2时，f(x)=O, 一3,4,求f(x)的二次插值多项式。解： X 0 =1,x j = — 1,x 2 = 2, f(X。)= 0, f (xj = -3, f (x2)= 4; l o(x)=(x-xi^~x2\=-1(x 1)(x-2) (x o -X/X o _x2) 2 (x -x0)(x -x2) 1 l i(x) 0 2(x-1)(x-2) (x i ~x0)(x i ~x2) 6 (x—x0)(x—x,) 1 l2(x) 0 1(x-1)(x 1) (X2 -X°)(X2 - X i) 3 则二次拉格朗日插值多项式为 2 L 2(X)= ' y k 1 k ( x) kz0 = -3l°(x) 4l2(x) 1 4 =(x_1)(x—2) 4 (x-1)(x 1) 2 3 5 2 3 7 x x - 6 2 3 6?设Xj, j =0,1,||(,n 为互异节点，求证： n (1 )7 x：l j(x) =x k(k =0,1川,n); j=0 n (2 )7 (X j -x)k l j(x)三0 (k =0,1川,n); j ￡证明 (1)令f(x)=x k

n 若插值节点为X j, j =0,1,|l(, n，则函数f (x)的n次插值多项式为L n(x)八x k l j(x)。 j=0 f (n 十)(?) 插值余项为R n(X)二f(X)-L n(X) n1(X) (n +1)!

.f(n1)( ^0 R n(X)=O n 二瓦x k l j(x) =x k(k =0,1川,n); j ：o n ⑵、(X j -x)k l j(x) j卫 n n =為(' C?x j(—x)k_L)l j(x) j =0 i =0 n n i k i i =為C k( -x) (、X j l j(x)) i =0 j=0 又70 _i _n 由上题结论可知 n .原式二''C k(-x)k_L x' i=0 =(X -X)k =0 -得证。 7设f (x) c2 la,b 1且f (a) =f (b)二0,求证: max f(x)兰一(b-a) max a $至小一*丘f (x). 解：令x^a,x^b，以此为插值节点，则线性插值多项式为 L i(x^ f(x o) x x f (xj X o —人x -X o X —X o x-b x-a ==f(a) f(b)- a - b x -a 又T f (a) = f (b)二0 L i(x) = 0 1 插值余项为R(x)二f (x) - L,(x) f (x)(x - X Q)(X - xj 1 f(x) = 2 f (x)(x -X g)(X -xj

数值分析习题集及答案

（适合课程《数值方法A 》和《数值方法B 》）第一章绪论 1. 设x >0,x 的相对误差为δ,求ln x 的误差. 2. 设x 的相对误差为2％,求n x 的相对误差. 3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字: ***** 123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====? 4. 利用公式(3.3)求下列各近似值的误差限: * * * * * * * * 12412324(),(),()/,i x x x ii x x x iii x x ++其中* * * * 1234,,,x x x x 均为第3题所给的数. 5. 计算球体积要使相对误差限为1％,问度量半径R 时允许的相对误差限是多少? 6. 设028,Y =按递推公式 11783 100 n n Y Y -=- ( n=1,2,…) 计算到100Y .若取783≈27.982(五位有效数字),试问计算100Y 将有多大误差? 7. 求方程2 5610x x -+=的两个根,使它至少具有四位有效数字(783≈27.982). 8. 当N 充分大时,怎样求 2 11N dx x +∞+?? 9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2 ? 10. 设2 12S gt = 假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对误差增加, 而相对误差却减小. 11. 序列{}n y 满足递推关系1101 n n y y -=-(n=1,2,…),若02 1.41y =≈(三位有效数字),计算到10 y 时误差有多大?这个计算过程稳定吗? 12. 计算6 (21)f =-,取 2 1.4≈,利用下列等式计算,哪一个得到的结果最好? 3 6 3 11,(322), ,9970 2. (21) (322) --++ 13. 2 ()ln(1)f x x x =- -,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若改用另一等价公式 2 2 ln(1)ln(1)x x x x - -=-+ + 计算,求对数时误差有多大? 14. 试用消元法解方程组{ 10 10 12121010; 2. x x x x +=+=假定只用三位数计算,问结果是否可靠? 15. 已知三角形面积 1sin , 2 s ab c = 其中c 为弧度, 02c π << ,且测量a ,b ,c 的误差分别为,,.a b c ???证明面积的误差s ?满足 . s a b c s a b c ????≤ ++ 第二章插值法 1. 根据( 2.2)定义的范德蒙行列式,令

应用回归分析,第8章课后习题参考答案

第8章非线性回归思考与练习参考答案 8.1 在非线性回归线性化时，对因变量作变换应注意什么问题？答：在对非线性回归模型线性化时，对因变量作变换时不仅要注意回归函数的形式，还要注意误差项的形式。如： (1) 乘性误差项，模型形式为 e y AK L αβε =， (2) 加性误差项，模型形式为y AK L αβ ε = + 对乘法误差项模型（1）可通过两边取对数转化成线性模型，（2）不能线性化。一般总是假定非线性模型误差项的形式就是能够使回归模型线性化的形式，为了方便通常省去误差项，仅考虑回归函数的形式。 8.2为了研究生产率与废料率之间的关系，记录了如表8.15所示的数据，请画出散点图，根据散点图的趋势拟合适当的回归模型。表8.15 生产率x （单位/周） 1000 2000 3000 3500 4000 4500 5000 废品率y （%） 5.2 6.5 6.8 8.1 10.2 10.3 13.0 解：先画出散点图如下图： 5000.00 4000.003000.002000.001000.00x 12.00 10.00 8.006.00 y

从散点图大致可以判断出x 和y 之间呈抛物线或指数曲线，由此采用二次方程式和指数函数进行曲线回归。（1）二次曲线 SPSS 输出结果如下： Model Summ ary .981 .962 .942 .651 R R Square Adjusted R Square Std. E rror of the Estimate The independent variable is x. ANOVA 42.571221.28650.160.001 1.6974.424 44.269 6 Regression Residual Total Sum of Squares df Mean Square F Sig.The independent variable is x. Coe fficients -.001.001-.449-.891.4234.47E -007.000 1.417 2.812.0485.843 1.324 4.414.012 x x ** 2 (Constant) B Std. E rror Unstandardized Coefficients Beta Standardized Coefficients t Sig. 从上表可以得到回归方程为：72? 5.8430.087 4.4710y x x -=-+? 由x 的系数检验P 值大于0.05，得到x 的系数未通过显著性检验。由x 2的系数检验P 值小于0.05，得到x 2的系数通过了显著性检验。（2）指数曲线 Model Summ ary .970 .941 .929 .085 R R Square Adjusted R Square Std. E rror of the Estimate The independent variable is x.

数值分析课后习题答案

习题一解答 1．取3.14，3.15， 227，355113 作为π的近似值，求各自的绝对误差，相对误差和有效数字的位数。分析：求绝对误差的方法是按定义直接计算。求相对误差的一般方法是先求出绝对误差再按定义式计算。注意，不应先求相对误差再求绝对误差。有效数字位数可以根据定义来求，即先由绝对误差确定近似数的绝对误差不超过那一位的半个单位，再确定有效数的末位是哪一位，进一步确定有效数字和有效数位。有了定理2后，可以根据定理2更规范地解答。根据定理2，首先要将数值转化为科学记数形式，然后解答。解：（1）绝对误差: e(x)=π－3.14＝3.14159265…－3.14＝0.00159…≈0.0016。相对误差： 3()0.0016 ()0.51103.14r e x e x x -==≈? 有效数字：因为π＝3.14159265…=0.314159265…×10，3.14＝0.314×10，m=1。而π－3.14＝3.14159265…－3.14＝0.00159… 所以│π－3.14│＝0.00159…≤0.005=0.5×10－2＝21311 101022 --?=? 所以，3.14作为π的近似值有3个有效数字。（2）绝对误差: e(x)=π－3.15＝3.14159265…－3.14＝－0.008407…≈－0.0085。相对误差： 2()0.0085 ()0.27103.15r e x e x x --==≈-? 有效数字：因为π＝3.14159265…=0.314159265…×10，3.15＝0.315×10，m=1。而π－3.15＝3.14159265…－3.15＝－0.008407… 所以│π－3.15│＝0.008407……≤0.05=0.5×10－1 ＝11211101022 --?=? 所以，3.15作为π的近似值有2个有效数字。（3）绝对误差: 22 () 3.14159265 3.1428571430.0012644930.00137e x π=-=-=-≈- 相对误差：

回归分析练习试题和参考答案解析

1 下面是7个地区2000年的人均国内生产总值（GDP）和人均消费水平的统计数据：求：(1)人均GDP作自变量，人均消费水平作因变量，绘制散点图，并说明二者之间的关系形态。 (2)计算两个变量之间的线性相关系数，说明两个变量之间的关系强度。 (3)求出估计的回归方程，并解释回归系数的实际意义。 (4)计算判定系数，并解释其意义。 α=)。 (5)检验回归方程线性关系的显著性(0.05 (6)如果某地区的人均GDP为5000元，预测其人均消费水平。 (7)求人均GDP为5000元时，人均消费水平95％的置信区间和预测区间。解：（1）

可能存在线性关系。（2）相关系数：系数a 模型非标准化系数标准系数 t Sig. 相关性 B标准误差试用版零阶偏部分 1(常量).003 人均GDP.309.008.998.000.998.998.998 a. 因变量: 人均消费水平有很强的线性关系。（3）回归方程：734.6930.309 y x =+ 系数a 模型非标准化系数标准系数t Sig.相关性

回归系数的含义：人均GDP没增加1元，人均消费增加元。%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。系数(a) 模型非标准化系数标准化系数 t显著性B标准误Beta 1（常量）人均GDP（元） %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%（4）模型汇总模型R R 方调整 R 方标准估计的误差 1.998a.996.996 a. 预测变量: (常量), 人均GDP。人均GDP对人均消费的影响达到%。%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。模型摘要模型R R 方调整的 R 方估计的标准差

数值分析第四版习题及答案

第四版数值分析习题第一章绪论 1. 设x >0,x 的相对误差为δ,求ln x 的误差. 2. 设x 的相对误差为2％,求n x 的相对误差. 3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字: *****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====? 4. 利用公式求下列各近似值的误差限: ********12412324(),(),()/,i x x x ii x x x iii x x ++其中**** 1234 ,,,x x x x 均为第3题所给的数. 5. 计算球体积要使相对误差限为1％,问度量半径R 时允许的相对误差限是多少? 6. 设028,Y =按递推公式 1n n Y Y -=…) 计算到100Y .(五位有效数字),试问计算100Y 将有多大误差? 7. 求方程2 5610x x -+=的两个根,使它至少具有四位有效数字. 8. 当N 充分大时,怎样求 2 11N dx x +∞ +? ? 9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2 ? 10. 设 212S gt = 假定g 是准确的,而对t 的测量有±秒的误差,证明当t 增加时S 的绝对误差增加,而相对误差却减小. 11. 序列 {}n y 满足递推关系1101n n y y -=-(n=1,2,…),若0 1.41y =≈(三位有效数字), 计算到 10y 时误差有多大?这个计算过程稳定吗? 12. 计算61)f =, 1.4≈,利用下列等式计算,哪一个得到的结果最好? 3 -- 13. ()ln(f x x =,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若改用另一等价公式 ln(ln(x x =- 计算,求对数时误差有多大?

多元线性回归模型习题及答案

多元线性回归模型一、单项选择题 1.在由30n =的一组样本估计的、包含3个解释变量的线性回归模型中，计算得多重决定系数为，则调整后的多重决定系数为（ D ） A. B. C. 下列样本模型中，哪一个模型通常是无效的（B ） A. i C （消费）=500+i I （收入） B. d i Q （商品需求）=10+i I （收入）+i P （价格） C. s i Q （商品供给）=20+i P （价格） D. i Y （产出量）=0.6i L （劳动）0.4i K （资本） 3.用一组有30个观测值的样本估计模型01122t t t t y b b x b x u =+++后，在的显著性水平上对 1b 的显著性作t 检验，则1b 显著地不等于零的条件是其统计量t 大于等于（ C ） A. )30(05.0t B. )28(025.0t C. )27(025.0t D. )28,1(025.0F 4.模型 t t t u x b b y ++=ln ln ln 10中，1b 的实际含义是（ B ） A.x 关于y 的弹性 B. y 关于x 的弹性 C. x 关于y 的边际倾向 D. y 关于x 的边际倾向 5、在多元线性回归模型中，若某个解释变量对其余解释变量的判定系数接近于１，则表明模型中存在（ C ） A.异方差性 B.序列相关 C.多重共线性 D.高拟合优度 6.线性回归模型01122......t t t k kt t y b b x b x b x u =+++++ 中，检验0:0(0,1,2,...) t H b i k ==时，所用的统计量服从( C ) (n-k+1) (n-k-2) (n-k-1) (n-k+2) 7. 调整的判定系数与多重判定系数之间有如下关系( D ) A.2 211n R R n k -=-- B. 22111 n R R n k -=--- C. 2211(1)1n R R n k -=-+-- D. 2211(1)1n R R n k -=---- 8．关于经济计量模型进行预测出现误差的原因，正确的说法是（ C ）。 A.只有随机因素 B.只有系统因素 C.既有随机因素，又有系统因素、B 、C 都不对 9．在多元线性回归模型中对样本容量的基本要求是(k 为解释变量个数)：（ C ） A n ≥k+1 B n

数值分析第四版习题及答案

第四版数值分析习题第一章绪论 1.设x>0,x得相对误差为δ,求得误差、 2.设x得相对误差为2％,求得相对误差、 3.下列各数都就是经过四舍五入得到得近似数,即误差限不超过最后一位得半个单位,试指出它们就是几位有效数字: 4.利用公式(3、3)求下列各近似值得误差限: 其中均为第3题所给得数、 5.计算球体积要使相对误差限为1％,问度量半径R时允许得相对误差限就是多少? 6.设按递推公式 ( n=1,2,…) 计算到、若取≈27、982(五位有效数字),试问计算将有多大误差? 7.求方程得两个根,使它至少具有四位有效数字(≈27、982)、 8.当N充分大时,怎样求? 9.正方形得边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝? 10.设假定g就是准确得,而对t得测量有±0、1秒得误差,证明当t增加时S得绝对误差增加,而相对误差却减小、 11.序列满足递推关系(n=1,2,…),若(三位有效数字),计算到时误差有多大?这个计算过程稳定吗? 12.计算,取,利用下列等式计算,哪一个得到得结果最好? 13.,求f(30)得值、若开平方用六位函数表,问求对数时误差有多大?若改用另一等价公式计算,求对数时误差有多大? 14.试用消元法解方程组假定只用三位数计算,问结果就是否可靠? 15.已知三角形面积其中c为弧度,,且测量a ,b ,c得误差分别为证明面积得误差满足第二章插值法 1.根据(2、2)定义得范德蒙行列式,令证明就是n次多项式,它得根就是,且、 2.当x= 1 , -1 , 2 时, f(x)= 0 , -3 , 4 ,求f(x)得二次插值多项式、 3. 4., 研究用线性插值求cos x 近似值时得总误差界、

回归分析练习题(有答案)

1.1回归分析的基本思想及其初步应用一、选择题 1. 某同学由x 与y 之间的一组数据求得两个变量间的线性回归方程为y bx a =+，已知：数据x 的平均值为2，数据 y 的平均值为3，则 ( ) A ．回归直线必过点（2，3） B ．回归直线一定不过点（2，3） C ．点（2，3）在回归直线上方 D ．点（2，3）在回归直线下方 2. 在一次试验中，测得(x,y)的四组值分别是A(1,2),B(2,3),C(3,4),D(4,5)，则Y 与X 之间的回归直线方程为（）A ． y x 1=+ B ． y x 2=+ C ． y 2x 1=+ Ｄ． y x 1=-3. 在对两个变量x ，y 进行线性回归分析时，有下列步骤： ①对所求出的回归直线方程作出解释； ②收集数据(i x 、i y ），1,2i =，…，n ； ③求线性回归方程； ④求未知参数； ⑤根据所搜集的数据绘制散点图如果根据可行性要求能够作出变量,x y 具有线性相关结论，则在下列操作中正确的是（） A ．①②⑤③④ B ．③②④⑤① C ．②④③①⑤ D ．②⑤④③① 4. 下列说法中正确的是（） A ．任何两个变量都具有相关关系 B ．人的知识与其年龄具有相关关系 C ．散点图中的各点是分散的没有规律 D ．根据散点图求得的回归直线方程都是有意义的 5. 给出下列结论：（1）在回归分析中，可用指数系数2 R 的值判断模型的拟合效果，2 R 越大，模型的拟合效果越好；（2）在回归分析中，可用残差平方和判断模型的拟合效果，残差平方和越大，模型的拟合效果越好；（3）在回归分析中，可用相关系数r 的值判断模型的拟合效果，r 越小，模型的拟合效果越好；（4）在回归分析中，可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适．带状区域的宽度越窄，说明模型的拟合精度越高．以上结论中，正确的有（）个． A ．1 B ．2 C ．3 D ．4 6. 已知直线回归方程为2 1.5y x =-，则变量x 增加一个单位时（） A.y 平均增加1.5个单位 B.y 平均增加2个单位 C.y 平均减少1.5个单位 D. y 平均减少2个单位 7. 下面的各图中，散点图与相关系数r 不符合的是（）

数值分析课后习题答案

第一章题12 给定节点01x =-，11x =，23x =，34x =，试分别对下列函数导出拉格朗日插值余项：（1）（1） 3 ()432f x x x =-+ （2）（2） 4 3 ()2f x x x =- 解（1）(4) ()0f x =，由拉格朗日插值余项得(4)0123() ()()()()()()0 4!f f x p x x x x x x x x x ξ-=----=；（2）(4) ()4!f x = 由拉格朗日插值余项得 01234! ()()()()()() 4! f x p x x x x x x x x x -= ----(1)(1)(3)(4)x x x x =+---. 题15 证明：对于()f x 以0x ，1x 为节点的一次插值多项式()p x ，插值误差 012 10()()()max () 8x x x x x f x p x f x ≤≤-''-≤. 证由拉格朗日插值余项得 01() ()()()()2!f f x p x x x x x ξ''-= --，其中01x x ξ≤≤， 01 0101max ()()()()()()()() 2!2!x x x f x f f x p x x x x x x x x x ξ≤≤''''-=--≤-- 01210()max () 8x x x x x f x ≤≤-''≤. 题22 采用下列方法构造满足条件(0)(0)0p p '==，(1)(1)1p p '==的插值多项式 ()p x ：（1）（1）用待定系数法；（2）（2）利用承袭性，先考察插值条件(0)(0)0p p '==，(1)1p =的插值多项式 ()p x . 解（1）有四个插值条件，故设230123()p x a a x a x a x =+++，2 123()23p x a a x a x '=++，代入得方程组001231123010231 a a a a a a a a a =? ?+++=?? =? ?++=? 解之，得01230 021 a a a a =??=?? =??=-?

(参考资料)数值分析课后答案1

1第一章习题解答 1 设x >0，x 的相对误差限为δ，求 ln x 的误差。解：设 x 的准确值为x *，则有 ( | x – x * | /|x *| ) ≤ δ 所以 e (ln x )=| ln x – ln x * | =| x – x * | ×| (ln x )’|x=ξ·≈ ( | x – x * | / | x *| ) ≤ δ 另解： e (ln x )=| ln x – ln x * | =| ln (x / x *) | = | ln (( x – x * + x *)/ x *) | = | ln (( x – x * )/ x * + 1) |≤( | x – x * | /|x *| ) ≤ δ 2 设 x = – 2.18 和 y = 2.1200 都是由准确值经四舍五入而得到的近似值。求绝对误差限ε( x ) 和 ε( y ) 。解：| e (x ) | = |e (– 2.18)|≤ 0.005，| e (y ) | = |e ( 2.1200)|≤ 0.00005，所以 ε( x )=0.005， ε( y ) = 0.00005。 3 下近似值的绝对误差限都是 0.005，问各近似值有几位有效数字 x 1=1.38，x 2= –0.0312，x 3= 0.00086 解：根据有效数字定义，绝对误差限不超过末位数半个单位。由题设知，x 1，x 2， x 3有效数末位数均为小数点后第二位。故x 1具有三位有效数字，x 2具有一位有效数字，x 3具有零位有效数字。 4 已知近似数x 有两位有效数字，试求其相对误差限。解：| e r (x ) | ≤ 5 × 10– 2 。 5 设 y 0 = 28，按递推公式 y n = y n-1 – 783/ 100 ( n = 1，2，…) 计算到y 100。若取≈78327.982 （五位有效数字），试问，计算 y 100 将有多大的误差？解：由于初值 y 0 = 28 没有误差，误差是由≈78327.982所引起。记 x = 27.982，783?=x δ。则利用理论准确成立的递推式 y n = y n-1 – 783/ 100 和实际计算中递推式 Y n = Y n-1 – x / 100 (Y 0 = y 0) 两式相减，得 e ( Y n ) = Y n – y n = Y n-1 – y n-1 – ( x – 783)/ 100 所以，有 e ( Y n ) = e ( Y n-1) – δ / 100 利用上式求和 δ?=∑∑=?=100111001)()(n n n n Y e Y e 化简，得 e ( Y 100) = e ( Y 0) – δ = δ 所以，计算y 100 的误差界为 4100105001.05.0)(?×=×=≤δεY 6 求方程 x 2 – 56x + 1 = 0的两个根，问要使它们具有四位有效数字，D=ac b 42 ?至少要取几位有效数字？如果利用韦达定理，D 又应该取几位有效数字？解：在方程中，a = 1，b = – 56，c = 1，故D=4562?≈55.96427，取七位有效数字。

回归分析练习题及参考答案

1 下面是7个地区2000年的人均国生产总值（GDP）和人均消费水平的统计数据：地区人均GDP/元人均消费水平/元北京上海 22460 11226 34547 4851 5444 2662 4549 7326 4490 11546 2396 2208 1608 2035 求：(1)人均GDP作自变量，人均消费水平作因变量，绘制散点图，并说明二者之间的关系形态。 (2)计算两个变量之间的线性相关系数，说明两个变量之间的关系强度。 (3)求出估计的回归方程，并解释回归系数的实际意义。 (4)计算判定系数，并解释其意义。 (5)检验回归方程线性关系的显著性(0.05 α=)。 (6)如果某地区的人均GDP为5000元，预测其人均消费水平。 (7)求人均GDP为5000元时，人均消费水平95％的置信区间和预测区间。解：（1）可能存在线性关系。（2）相关系数：

（3）回归方程：734.6930.309 y x =+ 回归系数的含义：人均GDP没增加1元，人均消费增加0.309元。%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意：图标不要原封不动的完全复制软件中的图标，要按规排版。系数(a) 模型非标准化系数标准化系数 t 显著性B 标准误Beta 1 （常量）734.693 .540 5.265 0.003 人均GDP（元）0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平（元）%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% （4）模型汇总模型R R 方调整 R 方标准估计的误差 1 .998a.996 .996 247.303 a. 预测变量: (常量), 人均GDP。人均GDP对人均消费的影响达到99.6%。%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意：图标不要原封不动的完全复制软件中的图标，要按规排版。模型摘要模型R R 方调整的 R 方估计的标准差 1 .998(a) 0.996 0.996 247.303 a. 预测变量:(常量), 人均GDP（元）。%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

文档之家

应用回归分析课后答案

数值分析课后答案

数值分析课后题答案

数值分析习题集及答案[1].(优选)

26、回归分析测试题及答案

数值分析课后题答案

数值分析习题集及答案

应用回归分析,第8章课后习题参考答案

数值分析课后习题答案

回归分析练习试题和参考答案解析

数值分析第四版习题及答案

多元线性回归模型习题及答案

数值分析第四版习题及答案

回归分析练习题(有答案)

数值分析课后习题答案

最新数值分析课程第五版课后习题答案(李庆扬等)1

(参考资料)数值分析课后答案1

回归分析练习题及参考答案