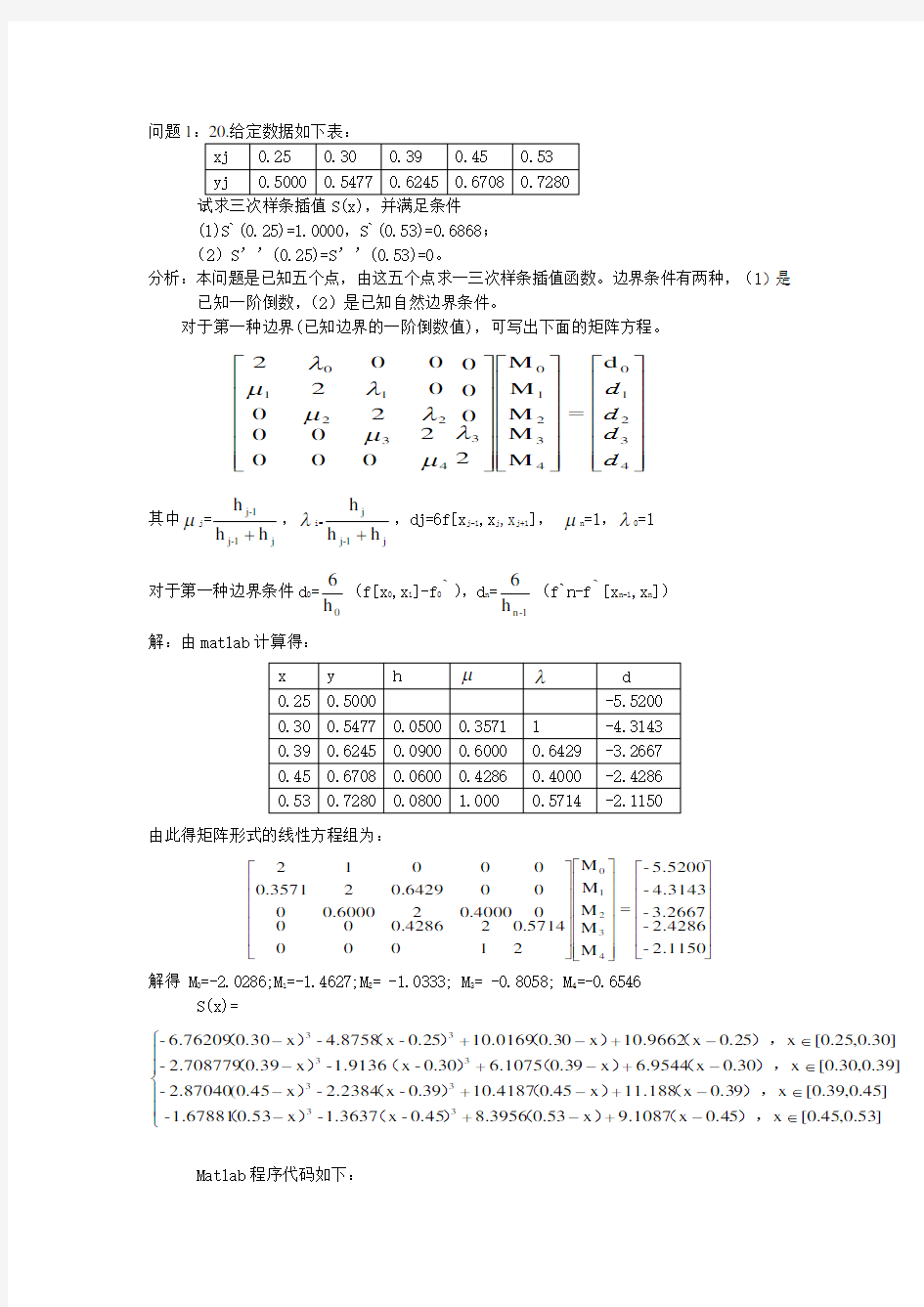

问题1:20.给定数据如下表:
试求三次样条插值S(x),并满足条件
(1)S`(0.25)=1.0000,S`(0.53)=0.6868; (2)S ’’(0.25)=S ’’(0.53)=0。
分析:本问题是已知五个点,由这五个点求一三次样条插值函数。边界条件有两种,(1)是
已知一阶倒数,(2)是已知自然边界条件。
对于第一种边界(已知边界的一阶倒数值),可写出下面的矩阵方程。
????????????????=????????
??
???
???????????????????4321043210343
22
110d M M M M M 2000200
00
02
002
2d d d d λμμλμλμλ
其中μj =
j
1-j 1-j h h h +,λi=
j
1-j j h h h +,dj=6f[x j-1,x j ,x j+1], μn =1,λ0=1
对于第一种边界条件d 0=
0h 6(f[x 0,x 1]-f 0`),d n =1
-n h 6
(f`n-f `[x n-1,x n ]) 解:由matlab 计算得:
由此得矩阵形式的线性方程组为:
?
?????????????=????????????????????????
?????? 2.1150-2.4286-3.2667-4.3143-5.5200-M M M M M 25714.0000
120
4286.0000
04000.02
6000.0006429.023571.00
012
432
10
解得 M 0=-2.0286;M 1=-1.4627;M 2= -1.0333; M 3= -0.8058; M 4=-0.6546
S(x)=
???
????∈-+-+-∈-+-+-∈-+-+-∈-+-+-]53.0,45.0[x 5.40x 9.1087x 35.03956.8.450-x 1.3637-x .5301.67881- ]45.0,39.0[x 9.30x 11.188x 54.010.418793.0-x 2.2384
-x .450(2.87040-]39.0,30.0[x 03.0x 6.9544x 9.30 6.107503.0-x 1.9136-x .3902.708779
-]30.0,25.0[x 5.20x 10.9662x 0.3010.01695.20-x 4.8758-x .3006.76209-333
33
33
3),()()()(),()()()),()()()(),()()()(
Matlab 程序代码如下:
function tgsanci(n,s,t) %n代表元素数,s,t代表端点的一阶导。x=[0.25 0.30 0.39 0.45 0.53];
y=[0.5 0.5477 0.6245 0.6708 0.7280];
n=5,s=1.0,t=0.6868
for j=1:1:n-1
h(j)=x(j+1)-x(j);
end
for j=2:1:n-1
r(j)=h(j)/(h(j)+h(j-1));
end
for j=1:1:n-1
u(j)=1-r(j);
end
for j=1:1:n-1
f(j)=(y(j+1)-y(j))/h(j);
end
for j=2:1:n-1
d(j)=6*(f(j)-f(j-1))/(h(j-1)+h(j));
end
d(1)=6*(f(1)-s)/h(1)
d(n)=6*(t-f(n-1))/h(n-1)
a=zeros(n,n);
for j=1:1:n
a(j,j)=2;
end
r(1)=1;
u(n)=1;
for j=1:1:n-1
a(j+1,j)=u(j+1);
a(j,j+1)=r(j);
end
b=inv(a)
m=b*d'
p=zeros(n-1,4); %p矩阵为S(x)函数的系数矩阵
for j=1:1:n-1
p(j,1)=m(j)/(6*h(j));
p(j,2)=m(j+1)/(6*h(j));
p(j,3)=(y(j)-m(j)*(h(j)^2/6))/h(j);
p(j,4)=(y(j+1)-m(j+1)*(h(j)^2/6))/h(j);
end
对于第二中边界,已知边界二阶倒数,可写出下面的矩阵:
???
????
?
????????=??????????
??????????????????????4321043210343
22
1
10d M M M M M 200020
00
02
002
00
2d d d d λμμλμλμλ 其中μj =
j
1-j 1-j h h h +,λi=
j
1-j j h h h +,dj=6f[x j-1,x j ,x j+1],μn =λ0=0 d 0=d n =0
解:由matlab 计算得:
由此得矩阵形式的线性方程组为:
?
??????
???????=????????????????????????
??????0 2.4286-3.2667-4.3143-0M M M M M 25714.0000
020
4286.0000
04000.02
6000.0006429.023571.00
02
43
2
10
解得M 0=0 ;M 1= -1.8795;M 2= -0.8636; M 3= -1.0292; M 4=0
S(x)=
???
????∈-+-+--∈-+-+---∈-+-+---∈-+-+--]53.0,45.0[x )45.0(1000.953.03987.845.00-x .5302.1442-]45.0,39.0[x 9.30x 1903.11x 54.0417.1093.0-x 8590.2x .4503990
.2]39.0,30.0[x 03.0x 9518.6x 9.301137.603.0-x 5993.1x .3904806
.3]30.0,25.0[x )25.0(9697.1030.0 010.25-x 2652.6x 0.30 0333
33
33
3,)()()(),()()()(),()()()(,)()()(x x x x x matlab 程序代码如下:
function tgsanci(n,s,t) %n 代表元素数, x=[0.25 0.30 0.39 0.45 0.53];
y=[0.5 0.5477 0.6245 0.6708 0.7280];
n=5
for j=1:1:n-1
h(j)=x(j+1)-x(j);
end
for j=2:1:n-1
r(j)=h(j)/(h(j)+h(j-1));
end
for j=1:1:n-1
u(j)=1-r(j);
end
for j=1:1:n-1
f(j)=(y(j+1)-y(j))/h(j);
end
for j=2:1:n-1
d(j)=6*(f(j)-f(j-1))/(h(j-1)+h(j));
end
d(1)=0
d(n)=0
a=zeros(n,n);
for j=1:1:n
a(j,j)=2;
end
r(1)=0;
u(n)=0;
for j=1:1:n-1
a(j+1,j)=u(j+1);
a(j,j+1)=r(j);
end
b=inv(a)
k=a
m=b*d'
p=zeros(n-1,4); %p矩阵为S(x)函数的系数矩阵
for j=1:1:n-1
p(j,1)=m(j)/(6*h(j));
p(j,2)=m(j+1)/(6*h(j));
p(j,3)=(y(j)-m(j)*(h(j)^2/6))/h(j);
p(j,4)=(y(j+1)-m(j+1)*(h(j)^2/6))/h(j);
end
p
由下面的一段程序,画出自然边界与第一边界的图形:
程序代码如下:
x=[0.25 0.30 0.39 0.45 0.53];
y=[0.5 0.5477 0.6245 0.6708 0.7280];
s=csape(x,y,'variational')
fnplt(s,'r')
hold on
xlabel('x')
ylabel('y')
gtext('三次样条自然边界')
plot(x,y,'o',x,y,':g')
hold on
s.coefs
r=csape(x,y,'complete',[1.0 0.6868])
fnplt(r,'b')
gtext('三次样条第一边界')
hold on r.coefs
图中的三条线几乎重合。
x
y
图20-1 在一小段区间内的图形
x
y
图20-2 在整个给出的区间的图形
问题2:1已知函数在下列各点的值为
试用4次牛顿插值多项式P 4(x )及三次样条函数S (x )(自然边界条件)对数据进行
插值。用图给出{(x i ,y i ),x i =0.2+0.08i ,i=0,1, 11, 10},P 4(x )及S (x )。 分析:(1)要用4次牛顿插值多项式处理数据,
P n =f(x 0)+f[x 0,x 1](x-x 0)+ f[x 0,x 1,x 2](x-x 0) (x-x 1)+···+
f[x 0,x 1,···x n ](x-x 0) ···(x-x n-1)
首先我们要知道牛顿插值多项式的系数,即均差表中得部分均差。 解:由matlab 计算得:
P 4(x )=0.98-0.3(x-0.2)-0.62500 (x-0.2)(x-0.4) -0.20833
(x-0.2)(x-0.4)(x-0.6)-0.52083 (x-0.2)(x-0.4)(x-0.6)(x-0.8)
计算牛顿插值中多项式系数的程序如下: function varargout=newtonliu(varargin) clear,clc
x=[0.2 0.4 0.6 0.8 1.0];
fx=[0.98 0.92 0.81 0.64 0.38]; newtonchzh(x,fx);
function newtonchzh(x,fx) %由此函数可得差分表 n=length(x);
fprintf('*****************差分表*****************************\n'); FF=ones(n,n); FF(:,1)=fx'; for i=2:n
for j=i:n
FF(j,i)=(FF(j,i-1)-FF(j-1,i-1))/(x(j)-x(j-i+1)); end end
for i=1:n
fprintf('%4.2f',x(i)); for j=1:i
fprintf('%10.5f',FF(i,j)); end
fprintf('\n'); end
(2)用三次样条插值函数由上题分析知,要求各点的M 值: 有matlab 编程计算求出个三次样条函数:
????
?????????
?=??????????????????????????????06.7500-4.5000-3.7500-0M M M M M 2.5000000020.50000000.50002.500000.50002.5000000 2
432
10 解得:M 0=0 ;M 1= -1.6071;M 2= -1.0714; M 3= -3.1071; M 4=0
???
????∈-+-+--∈-+-+-∈-+-+--∈-+-+---]0.1,8.0[x )8.0(9.10.1 3036.38.00-x 0.12.5893-]8.0,6.0[x 6.0x 3036.3x 8.00857.4.60-x 5893.2-x .800.8929
-]6.0,4.0[x 4.0x 7508.4x 6.04.6536 .40-x 8929.0x .601.3393
- ]4.0,2.0[x )2.0(6536.44.0900.42.0 1.33934.00 333
33
33
,)()()(),()()()(),()()()(,)()()(x x x x x x x 三次样条插值函数计算的程序如下:
function tgsanci(n,s,t) %n 代表元素数,s,t 代表端点的一阶导。
x=[0.2 0.4 0.6 0.8 1.0];
y=[0.98 0.92 0.81 0.64 0.38];
n=5
for j=1:1:n-1
h(j)=x(j+1)-x(j);
end
for j=2:1:n-1
r(j)=h(j)/(h(j)+h(j-1));
end
for j=1:1:n-1
u(j)=1-r(j);
end
for j=1:1:n-1
f(j)=(y(j+1)-y(j))/h(j);
end
for j=2:1:n-1
d(j)=6*(f(j)-f(j-1))/(h(j-1)+h(j));
end
d(1)=0 d(n)=0 a=zeros(n,n);
for j=1:1:n
a(j,j)=2;
end
r(1)=0; u(n)=0;
for j=1:1:n-1
a(j+1,j)=u(j+1); a(j,j+1)=r(j);
end b=inv(a) m=b*d'
p=zeros(n-1,4); %p 矩阵为S(x)函数的系数矩阵 for j=1:1:n-1
p(j,1)=m(j)/(6*h(j));
p(j,2)=m(j+1)/(6*h(j));
p(j,3)=(y(j)-m(j)*(h(j)^2/6))/h(j);
p(j,4)=(y(j+1)-m(j+1)*(h(j)^2/6))/h(j);
end
p
下面是画牛顿插值以及三次样条插值图形的程序:
x=[0.2 0.4 0.6 0.8 1.0];
y=[0.98 0.92 0.81 0.64 0.38];
plot(x,y)
hold on
for i=1:1:5
y(i)=0.98-0.3*(x(i)-0.2)-0.62500*(x(i)-0.2)*(x(i)-0.4)
-0.20833*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)-0.52083*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0 .6)*(x(i)-0.8)
end
k=[0 1 10 11]
x0=0.2+0.08*k
for i=1:1:4
y0(i)=0.98-0.3*(x(i)-0.2)-0.62500*(x(i)-0.2)*(x(i)-0.4)
-0.20833*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)-0.52083*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0 .6)*(x(i)-0.8)
end
plot( x0,y0,'o',x0,y0 )
hold on
y1=spline(x,y,x0)
plot(x0,y1,'o')
hold on
s=csape(x,y,'variational')
fnplt(s,'r')
hold on
gtext('三次样条自然边界')
gtext('原图像')
gtext('4次牛顿插值')
运行上述程序可知:给出的{(x i,y i),x i=0.2+0.08i,i=0,1, 11, 10}点,S(x)及P4(x)图形如下所示:
问题3 :3
(1)用这9各点作8次多项式插值L 8(x).
(2)用三次样条(自然边界条件)程序求S (x )。从结果看在[0,64]上,那个插值更
精确;在区间[0,1]上,两种哪个更精确? 分析:L 8(x)可由公式L n (x)=
∑=n
k k
k )(l y
j x 得出。
三次样条可以利用自然边界条件。写成矩阵:
???
????
?
????????=????????????????????????????????4321043210343
22
1
10d M M M M M 200020
00
02
002
00
2d d d d λμμλμλμλ 其中μj =
j
1-j 1-j h h h +,λi=
j
1-j j h h h +,dj=6f[x j-1,x j ,x j+1],μn =λ0=0 d 0=d n =0
解:l 0(x)=)
640)(490)(360)(250)(160)(90)(40)(10()64)(49)(36)(25)(16)(9)(4)(1-(x ---------------x x x x x x x
l 1(x)=
)641)(491)(361)(251)(161)(91)(41)(01()
64)(49)(36)(25)(16)(9)(4)(0-(x ---------------x x x x x x x
l 2(x)= )644)(494)(364)(254)(164)(94)(14)(04()
64)(49)(36)(25)(16)(9)(1)(0-(x ---------------x x x x x x x
l 3(x)=
)
649)(499)(369)(259)(169)(49)(19)(09()
64)(49)(36)(25)(16)(4)(1)(0-(x ---------------x x x x x x x
l 4(x)=
)
6416)(4916)(3616)(2516)(916)(416)(116)(016()
64)(49)(36)(25)(9)(4)(1)(0-(x ---------------x x x x x x x
l 5(x)= )
6425)(4925)(3625)(1625)(925)(425)(125)(025()
64)(49)(36)(16)(9)(4)(1-(x )0-x (--------------x x x x x x
l 6(x)= )
6436)(4936)(2536)(1636)(936)(436)(136)(036()
64)(49)(25)(16)(9)(4)(1)(0-(x ---------------x x x x x x x
l 7(x)= )
6449)(3649)2549)(1649)(949)(449)(149(049)
64)(36)(25)(16)(9)(4)(1-(x 0-x --------------()()(x x x x x x
l 8(x)= )
4964)(3664)(2564)(1664)(964)(464)(164)(064()49)(36)(25)(16)(9)(4)(1-0)(x -x (--------------x x x x x x L 8(x)= l 1(x)+2 l 2(x)+3 l 3(x)+4 l 4(x)+5 l 5(x)+6 l 6(x)+7 l 7(x)+8 l 8(x) 求三次样条插值函数由matlab 计算: 可得矩阵形式的线性方程组为:
?????????
????
?
???
???
??
??????-------=????????????????????????????????????????????????????????00022.00035.00061.0191.000286.01.00.10M M M M M M M M M 000.0200000000573.50000.02634.40000000
0417.50000.02583.400000000500.50000.02500.400000
005625.0000.02375.400000000833.500000.2167.400000000250.60000.02750.300000000500.70000.02500.2000000000000.028********解得:
M 0=0;M 1=-0.5209;M 2=0.0558;M 3=-0.0261;M 4=0.0006;M 5=-0.0029;M 6=-0.0008;M 7=--0.0009; M 8=0
S(x)= ????
??????
?????∈+-+-+-∈+-+--∈+-+--∈+---∈-+-+-∈-+-+--∈-+-+-∈+-+--+-]64,48[x 48)-0.5333(x 640.4689)48(0640]48,36[x 36)-0.5404(x 480.4633360-480]
36,25[x 25)-0.5470(x 364599.0250-360]25,16[x 16)-0.5600(x 250.4436-160.0001-250]16,9[x 9)-0.5708(x -164590.090160.0006-]
9,4[x 4x 0.6271x 90.35354-x 0009.0x 90019.0]4,1[x 1x 0.6388x 40.59381-x 0.0031-x 40.0289
-]1,0[x 0)-1.0868(x 100)(0868.0100333
3333
33
3333
333
,)()(
,)()()(,)()()(,)()()(
,)()()(),()()()(),()()()(,)()(x x x x x x x x x x x x x x x x x x
拉格朗日插值函数与三次样条插值函数如图中所示,绿色实线条为三次样条插值曲线,
蓝色虚线条为x=y 2
的曲线,另外一条红色线条为拉格朗日插值曲线。图3-1为[0 1]的曲线,图3-2为[0 64]区间上的曲线。由图3-1可以看出,红色的线条与蓝色虚线条几乎重合,所以可知拉格朗日插值函数的曲线更接近开平方根的函数曲线,在[0 1]朗格朗日插值更精确。而在区间[0 64]上从图3-2中可以看出蓝色虚线条和绿色线条是几乎重合的,而红色线条在[30 70]之间有很大的振荡,所在在区间[0 64]三次样条插值更精确写。
图3-1
图3-2
Matlab程序代码如下:
求三次样条插值函数的程序:
function tgsanci(n,s,t) %n代表元素数,s,t代表端点的一阶导。
y=[0 1 2 3 4 5 6 7 8];
x=[0 1 4 9 16 25 36 49 64];
n=9
for j=1:1:n-1
h(j)=x(j+1)-x(j);
end
for j=2:1:n-1
r(j)=h(j)/(h(j)+h(j-1));
end
for j=1:1:n-1
u(j)=1-r(j);
end
for j=1:1:n-1
f(j)=(y(j+1)-y(j))/h(j);
end
for j=2:1:n-1
d(j)=6*(f(j)-f(j-1))/(h(j-1)+h(j));
end
d(1)=0
d(n)=0
a=zeros(n,n);
for j=1:1:n
a(j,j)=2;
end
r(1)=0;
u(n)=0;
for j=1:1:n-1
a(j+1,j)=u(j+1);
a(j,j+1)=r(j);
end
b=inv(a)
m=b*d'
t=a
p=zeros(n-1,4); %p矩阵为S(x)函数的系数矩阵
for j=1:1:n-1
p(j,1)=m(j)/(6*h(j));
p(j,2)=m(j+1)/(6*h(j));
p(j,3)=(y(j)-m(j)*(h(j)^2/6))/h(j);
p(j,4)=(y(j+1)-m(j+1)*(h(j)^2/6))/h(j);
end
p
%画图形比较那个插值更精确的函数:
x0=[0 1 4 9 16 25 36 49 64];
y0=[0 1 2 3 4 5 6 7 8];
x=0:64;y=lagr1(x0,y0,x);
plot(x0,y0,'o')
hold on
plot(x,y,'r');
hold on;
pp=csape(x0,y0,'variational')
fnplt(pp,'g');
hold on;
plot(x0,y0,':b');hold on
%axis([0 2 0 1]); %看[0 1]区间的图形时加上这条指令gtext('三次样条插值')
gtext('原图像')
gtext('拉格朗日插值')
%下面是求拉格朗日插值的函数
function y=lagr1(x0,y0,x)
n=length(x0); m=length(x); for i=1:m z=x(i); s=0.0; for k=1:n p=1.0; for j=1:n if j~=k
p=p*(z-x0(j))/(x0(k)-x0(j)); end end
s=p*y0(k)+s; end y(i)=s; end
分析:由所给的数据在坐标纸上描出如图16-1所示。 从图中可以看到各点在一条直线的附近,故可以选择线性函数作拟合曲线,即令s(t)=a+bt ,这里m=5,n=1。法方程矩阵为下面的形式:
n ??? ,,10的线性无关性,知道该方程存在唯一解
b Ax =
解:由上面的分析以及通过matlab 计算得: 法方程矩阵如下:
??
????=????????????107828063.537.147.146
b a 解之得:a=-7.8550 ,b=22.2538 。
由此可得运动方程为:S(t)=22.2538t-7.8550 . 在matlab 中拟合的曲线如图16-2所示:
()()()()()
()
???
?
? ??=????? ??????? ??D n D n D n n D n D n D f f a a ??????????,,,,,,000000 11
(,),(,)m
m
j k ji ki j ji i
i i f y ??????====∑∑
t
s (x )
源数据点
t
s (x )
最小二乘拟合曲线
图16-1 图16-2 Matlab 源程序代码: 计算部分的程序代码:
x=[0 0.9 1.9 3.0 3.9 5.0]; y=[0 10 30 50 80 110]; r=zeros(2,2); for i=1:1:6;
r(1,1)=r(1,1)+1; end
for i=1:1:6
r(1,2)=r(1,2)+x(i); end
for i=1:1:6
r(2,1)=r(2,1)+x(i); end
for i=1:1:6
r(2,2)=r(2,2)+x(i)^2; end
a=zeros(2,1); for i=1:1:6
a(1,1)=a(1,1)+y(i);
a(2,1)=a(2,1)+y(i)*x(i) end k=r t=a
d=inv(r);a=d*a 画图的程序代码:
x=[0 0.9 1.9 3.0 3.9 5.0]; y=[0 10 30 50 80 110]; xx=0:0.02:5.0; pp=polyfit(x,y,1);
yy=polyval(pp,xx); plot(x,y,'o',xx,yy)
问题:18在某化学反应中,由试验得分解物浓度与时间的关系如下: 时间(t/s) 0 5
10
15
20
25
30
35
40
45
50
55
浓度
y/(10-4
)
1.27
2.16 2.86
3.44 3.87
4.15 4.37 4.51 4.58 4.62 4.64
用最小二乘法求y=f(t)。
分析:首先要选择拟合曲线,作出给定数据的散点图如下:
10
20
3040
50
60
00.5
11.5
22.5
3
3.5
44.5
5t
y (t )
图18-1 给定数据的散点图
通过对散点图的分析可以看出,数据点的分布为一条单调上升的曲线。具有这种特性的曲线很多,我们选取如下三种函数来拟合:
① 多项式 (x ) = a 0 a 1x … a m x m
,m 为适当选取的正整数; ② b
ax x
x +=
)(?; ③ x
b ae x =)(?(a >0, b <0)。
在matlab 中分别用上述拟合函数拟合曲线,本题应采用倒指数拟合,即y(t)=a*exp(bt -1
)拟合曲线。
对y(t)=a*exp(bt -1
)两边取对数有 ㏑y=㏑a+b/t ; 如令Y=㏑y ,A=㏑a ,则得Y=A+b/t;为确定A ,b,先将(t i ,y i )转化为(t i ,Y i ). 根据最小二乘法,取1)(0=t ?,t t /1)(1=?。
用lsqcurvefit 函数拟合曲线,程序代码如下:
创建M 文件:
function F=mf(a,t)
F=a(1)*exp(a(2).*t.^(-1)); 在命令窗口中敲入如下代码: t=[5:5:55]
y=[ 1.27 2.16 2.86 3.44 3.87 4.15 4.37 4.51 4.58 4.62 4.64]; a0=[0.5,0.5];
a=lsqcurvefit('pf',a0,t,y)
回车后可得:
a(1)= 5.5031 ,a(2)= -8.7872
下面的计算问题用matlab编程实现:
x=[5 10 15 20 25 30 35 40 45 50 55 ];
y0=[1.27 2.16 2.86 3.44 3.87 4.15 4.37 4.51 4.58 4.62 4.64];
y=log(y0)
y(1)=0
r=zeros(2,2);
for i=1:1:12;
r(1,1)=r(1,1)+1;
end
for i=2:1:12
r(1,2)=r(1,2)+1/x(i);
end
for i=2:1:12
r(2,1)=r(2,1)+1/x(i);
end
for i=2:1:12
r(2,2)=r(2,2)+1/x(i)^2;
end
a=zeros(2,1);
for i=2:1:12
a(1,1)=a(1,1)+y(i);
a(2,1)=a(2,1)+y(i)*(1/x(i)) ;
end
k=r
t=a
d=inv(r);m=d*a
由matlab软件计算得:a= 3.9864,b= -4.8922。所以y(t)= 3.9864e-4.8922/t。有下面的语句给出拟合后的图形:
x=[0 5 10 15 20 25 30 35 40 45 50 55 ];
y0=[0 1.27 2.16 2.86 3.44 3.87 4.15 4.37 4.51 4.58 4.62 4.64];
fplot('5.5031*exp((-8.7872)*(x).^(-1))',[0,55]);
hold on
plot(x,y0,'o',x,y0,'r')
hold on
gtext('倒指数拟合曲线')
gtext('原图像')
图18-2
(注:素材和资料部分来自网络,供参考。请预览后才下载,期待你的好评与关注!)
大作业 三 1. 给定初值 0x 及容许误差 ,编制牛顿法解方程f (x )=0的通用 程序. 解:Matlab 程序如下: 函数m 文件:fu.m function Fu=fu(x) Fu=x^3/3-x; end 函数m 文件:dfu.m function Fu=dfu(x) Fu=x^2-1; end 用Newton 法求根的通用程序Newton.m clear; x0=input('请输入初值x0:'); ep=input('请输入容许误差:'); flag=1; while flag==1 x1=x0-fu(x0)/dfu(x0); if abs(x1-x0) while flag1==1 && m<=10^3 x1=x0-fu(x0)/dfu(x0); if abs(x1-x0) 数值分析习题集 (适合课程《数值方法A 》和《数值方法B 》) 长沙理工大学 第一章 绪 论 1. 设x >0,x 的相对误差为δ,求ln x 的误差. 2. 设x 的相对误差为2%,求n x 的相对误差. 3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出 它们是几位有效数字: *****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====? 4. 利用公式(3.3)求下列各近似值的误差限: ********12412324(),(),()/,i x x x ii x x x iii x x ++其中**** 1234 ,,,x x x x 均为第3题所给的数. 5. 计算球体积要使相对误差限为1%,问度量半径R 时允许的相对误差限是多少? 6. 设028,Y =按递推公式 1n n Y Y -=( n=1,2,…) 计算到100Y .27.982(五位有效数字),试问计算100Y 将有多大误差? 7. 求方程2 5610x x -+=的两个根,使它至少具有四位有效数字27.982). 8. 当N 充分大时,怎样求2 1 1N dx x +∞+?? 9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2 ? 10. 设 212S gt = 假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对 误差增加,而相对误差却减小. 11. 序列 {}n y 满足递推关系1101n n y y -=-(n=1,2,…),若0 1.41y =≈(三位有效数字), 计算到 10y 时误差有多大?这个计算过程稳定吗? 12. 计算6 1)f =, 1.4≈,利用下列等式计算,哪一个得到的结果最好? 3 -- 13. ()ln(f x x =,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若 大作业 三 1. 给定初值 0x 及容许误差 ,编制牛顿法解方程f (x )=0的通用程序. 解:Matlab 程序如下: 函数m 文件:fu.m function Fu=fu(x) Fu=x^3/3-x; end 函数m 文件:dfu.m function Fu=dfu(x) Fu=x^2-1; end 用Newton 法求根的通用程序Newton.m clear; x0=input('请输入初值x0:'); ep=input('请输入容许误差:'); flag=1; while flag==1 x1=x0-fu(x0)/dfu(x0); if abs(x1-x0) while flag==1 sigma=k*eps; x0=sigma; k=k+1; m=0; flag1=1; while flag1==1 && m<=10^3 x1=x0-fu(x0)/dfu(x0); if abs(x1-x0) end end fprintf('最大的sigma 值为:%f\n',sigma); 2.求下列方程的非零根 5130.6651()ln 05130.665114000.0918 x x f x x +?? =-= ?-???解: Matlab 程序为: (1)主程序 clear clc format long x0=765; N=100; errorlim=10^(-5); x=x0-f(x0)/subs(df(),x0); n=1; 数值分析作业答案 插值法 1、当x=1,-1,2时,f(x)=0,-3,4,求f(x)的二次插值多项式。 (1)用单项式基底。 (2)用Lagrange插值基底。 (3)用Newton基底。 证明三种方法得到的多项式是相同的。 解:(1)用单项式基底 设多项式为: , 所以: 所以f(x)的二次插值多项式为: (2)用Lagrange插值基底 Lagrange插值多项式为: 所以f(x)的二次插值多项式为: (3) 用Newton基底: 均差表如下: xk f(xk) 一阶均差二阶均差 1 0 -1 -3 3/2 2 4 7/ 3 5/6 Newton插值多项式为: 所以f(x)的二次插值多项式为: 由以上计算可知,三种方法得到的多项式是相同的。 6、在上给出的等距节点函数表,若用二次插值求ex的近似值,要使截断误差不超过10-6,问使用函数表的步长h应取多少? 解:以xi-1,xi,xi+1为插值节点多项式的截断误差,则有 式中 令得 插值点个数 是奇数,故实际可采用的函数值表步长 8、,求及。 解:由均差的性质可知,均差与导数有如下关系: 所以有: 15、证明两点三次Hermite插值余项是 并由此求出分段三次Hermite插值的误差限。 证明:利用[xk,xk+1]上两点三次Hermite插值条件 知有二重零点xk和k+1。设 确定函数k(x): 当或xk+1时k(x)取任何有限值均可; 当时,,构造关于变量t的函数 显然有 在[xk,x][x,xk+1]上对g(x)使用Rolle定理,存在及使得 在,,上对使用Rolle定理,存在,和使得 再依次对和使用Rolle定理,知至少存在使得 而,将代入,得到 推导过程表明依赖于及x 综合以上过程有: 确定误差限: 记为f(x)在[a,b]上基于等距节点的分段三次Hermite插值函数。在区间[xk,xk+1]上有 而最值 进而得误差估计: 16、求一个次数不高于4次的多项式,使它满足,,。 ¥ 数值分析思考题1 1、讨论绝对误差(限)、相对误差(限)与有效数字之间的关系。 2、相对误差在什么情况下可以用下式代替 3、查阅何谓问题的“病态性”,并区分与“数值稳定性”的不同点。 4、取 ,计算 ,下列方法中哪种最好为什么(1)(3 3-,(2)(2 7-,(3) ()3 1 3+ ,(4) ()6 1 1 ,(5)99- , 数值实验 数值实验综述:线性代数方程组的解法是一切科学计算的基础与核心问题。求解方法大致可分为直接法和迭代法两大类。直接法——指在没有舍入误差的情况下经过有限次运算可求得方程组的精确解的方法,因此也称为精确法。当系数矩阵是方的、稠密的、无任何特殊结构的中小规模线性方程组时,Gauss消去法是目前最基本和常用的方法。如若系数矩阵具有某种特殊形式,则为了尽可能地减少计算量与存储量,需采用其他专门的方法来求解。 Gauss消去等同于矩阵的三角分解,但它存在潜在的不稳定性,故需要选主元素。对正定对称矩阵,采用平方根方法无需选主元。方程组的性态与方程组的条件数有关,对于病态的方程组必须采用特殊的方法进行求解。 数值计算方法上机题目1 1、实验1. 病态问题 实验目的: 算法有“优”与“劣”之分,问题也有“好”和“坏”之别。所谓坏问题就是问题本身的解对数据变化的比较敏感,反之属于好问题。希望读者通过本实验对此有一个初步的体会。 数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。 $ r e x x e x x ** * ** - == 141 . ≈)61 目录 第一章非线性方程求根 (3) 1.1迭代法 (3) 1.2牛顿法 (4) 1.3弦截法 (5) 1.4二分法 (6) 第二章插值 (7) 2.1线性插值 (7) 2.2二次插值 (8) 2.3拉格朗日插值 (9) 2.4分段线性插值 (10) 2.5分段二次插值 (11) 第三章数值积分 (13) 3.1复化矩形积分法 (13) 3.2复化梯形积分法 (14) 3.3辛普森积分法 (15) 3.4变步长梯形积分法 (16) 第四章线性方程组数值法 (17) 4.1约当消去法 (17) 4.2高斯消去法 (18) 4.3三角分解法 (20) 4.4雅可比迭代法 (21) 4.5高斯—赛德尔迭代法 (23) 第五章常积分方程数值法 (25) 5.1显示欧拉公式法 (25) 5.2欧拉公式预测校正法 (26) 5.3改进欧拉公式法 (27) 5.4四阶龙格—库塔法 (28) 数值计算方法 第一章非线性方程求根 1.1迭代法 程序代码: Private Sub Command1_Click() x0 = Val(InputBox("请输入初始值x0")) ep = Val(InputBox(请输入误差限ep)) f = 0 While f = 0 X1 = (Exp(2 * x0) - x0) / 5 If Abs(X1 - x0) < ep Then Print X1 f = 1 Else x0 = X1 End If Wend End Sub 例:求f(x)=e2x-6x=0在x=0.5附近的根(ep=10-10) 1.2牛顿法 程序代码: Private Sub Command1_Click() b = Val(InputBox("请输入被开方数x0")) ep = Val(InputBox(请输入误差限ep)) f = 0 While f = 0 X1 = x0 - (x0 ^ 2 - b) / (2 * b) If Abs(X1 - x0) < ep Then Print X1 f = 1 Else x0 = X1 End If Wend End Sub 例:求56的值。(ep=10-10) 《数值分析B》大作业一 SY1103120 朱舜杰 一.算法设计方案: 1.矩阵A的存储与检索 将带状线性矩阵A[501][501]转存为一个矩阵MatrixC[5][501] . 由于C语言中数组角标都是从0开始的,所以在数组MatrixC[5][501]中检索A的带内元素a ij的方法是: A的带内元素a ij=C中的元素c i-j+2,j 2.求解λ1,λ501,λs ①首先分别使用幂法和反幂法迭代求出矩阵按摸最大和最小的特征值λmax和λmin。λmin即为λs; 如果λmax>0,则λ501=λmax;如果λmax<0,则λ1=λmax。 ②使用带原点平移的幂法(mifa()函数),令平移量p=λmax,求 出对应的按摸最大的特征值λ,max, 如果λmax>0,则λ1=λ,max+p;如果λmax<0,则λ501=λ,max+p。 3.求解A的与数μk=λ1+k(λ501-λ1)/40的最接近的特征值λik (k=1,2,…,39)。 使用带原点平移的反幂法,令平移量p=μk,即可求出与μk最接近的特征值λik。 4.求解A的(谱范数)条件数cond(A)2和行列式d etA。 ①cond(A)2=|λ1/λn|,其中λ1和λn分别是矩阵A的模最大和 最小特征值。 ②矩阵A的行列式可先对矩阵A进行LU分解后,detA等于U所有对角线上元素的乘积。 二.源程序 #include 数值计算方法第一次作业及参考答案 1. 已测得函数()y f x =的三对数据:(0,1),(-1,5),(2,-1), (1)用Lagrange 插值求二次插值多项式。(2)构造差商表。(3)用Newton 插值求二次插值多项式。 解:(1)Lagrange 插值基函数为 0(1)(2)1 ()(1)(2)(01)(02)2 x x l x x x +-= =-+-+- 同理 1211 ()(2),()(1)36 l x x x l x x x = -=+ 故 2 20 2151 ()()(1)(2)(2)(1) 23631 i i i p x y l x x x x x x x x x =-==-+-+-++=-+∑ (2)令0120,1,2x x x ==-=,则一阶差商、二阶差商为 011215 5(1) [,]4, [,]20(1) 12 f x x f x x ---= =-= =----- 0124(2) [,,]102 f x x x ---= =- 实际演算中可列一张差商表: (3)用对角线上的数据写出插值多项式 2 2()1(4)(0)1*(0)(1)31P x x x x x x =+--+-+=-+ 2. 在44x -≤≤上给出()x f x e =的等距节点函数表,若用二次插值求x e 的近似值,要使 截断误差不超过6 10-,问使用函数表的步长h 应取多少 解: ()40000(), (),[4,4],,,, 1.x k x f x e f x e e x x h x x h x x th t ==≤∈--+=+≤考察点及 (3) 2000 4 43 4 3 () ()[(()]()[()] 3! (1)(1) (1)(1) 3!3! .(4,4). 6 f R x x x h x x x x h t t t e t h th t h e h e ξ ξ =----+ -+ ≤+??-= ≤∈- 则 4 36 ((1)(1) 100.006. t t t h - -+± << Q在点 得 3.求2 () f x x =在[a,b]上的分段线性插值函数() h I x,并估计误差。 解: 22 22 11 1 111 22 11 11 1 () () k k k k h k k k k k k k k k k k k k k k k k k x x x x x x I x x x x x x x x x x x x x x x x x x x x x ++ + +++ ++ ++ + --- =+= --- ?-? -=+- - [] 2 11 22 11 ()()()[()] 11 ()() 44 h h k k k k k k k k R x f x I x x x x x x x x x x x x x h ++ ++ =-=-+- =--≤-= 4.已知单调连续函数() y f x =的如下数据 用插值法计算x约为多少时() 1. f x=(小数点后至少保留4位) 解:作辅助函数()()1, g x f x =-则问题转化为x为多少时,()0. g x=此时可作新 的关于() i g x的函数表。由() f x单调连续知() g x也单调连续,因此可对() g x的数值进行反插。的牛顿型插值多项式为 1()0.110.097345( 2.23)0.451565( 2.23)( 1.10) 0.255894( 2.23)( 1.10)(0.17) x g y y y y y y y - ==-+++++ -++- 数值分析报大作业 班级:铁道2班 专业:道路与铁道工程 姓名:蔡敦锦 学号:13011260 一、序言 该数值分析大作业是通过C语言程序编程在Microsoft Visual C++ 6.0编程软件上运行实现的。本来是打算用Matlab软间来计算非线性方程的根的。学习Matlab也差不多有一个多月了,感觉自己编程做题应该没什么问题了;但是当自己真心的去编程、运行时才发现有很多错误,花了一天时间修改、调试程序都没能得到自己满意的结果。所以,我选择了自己比较熟悉的C程序语言来编程解决非线性的求值问题,由于本作业是为了比较几种方法求值问题的收敛速度和精度的差异,选择了一个相对常见的非线性函数来反映其差异,程序运行所得结果我个人比较满意。编写C语言,感觉比较上手,程序出现问题也能比较熟练的解决。最终就决定上交一份C程序语言编程的求值程序了! 二、选题 本作业的目的是为了加深对非线性方程求根方法的二分法、简单迭代法、、牛顿迭代法弦截法等的构造过程的理解;能将各种方法的算法描述正确并且能够改编为程序并在计算机上实现程序的正确合理的运行,能得到自己满意的结果,并且能调试修改程序中可能出现的问题和程序功能的增减修改。本次程序是为了比较各种方法在求解同一非线性方程根时,在收敛情况上的差异。 为了达到上面的条件我选择自己比较熟悉的语言—C语言来编程,所选题目为计算方程f(x)=x3-2x-5=0在区间[2,3]内其最后两近似值的差的绝对值小于等于5 ?的根的几种方法的比较。 110- 本文将二分法、牛顿法、简单迭代法、弦截法及加速收敛法这五种方法在同一个程序中以函数调用的方式来实现,比较简洁明了,所得结果能很好的比较,便于分析;发现问题和得出结论。 6.4.设??? ? ? ??=5010010a b b a A ,0det ≠A ,用a ,b 表示解线性方程组f Ax =的雅可比迭代与 高斯—塞德尔迭代收敛的充分必要条件。 解 雅可比迭代法的迭代矩阵 ? ??? ??? ? ??----=???? ? ??----????? ??=-050100100100000001010101 a b b a a b b a B J , ?? ? ?? -=-1003||2ab B I J λλλ,10||3)(ab B J = ρ。 雅可比迭代法收敛的充分必要条件是3 100 || 数值分析习题集 (适合课程《数值方法A 》和《数值方法B 》) 长沙理工大学 第一章 绪 论 1. 设x >0,x 的相对误差为δ,求ln x 的误差. 2. 设x 的相对误差为2%,求n x 的相对误差. 3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指 出它们是几位有效数字: *****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====? 4. 利用公式(3.3)求下列各近似值的误差限: ********12412324(),(),()/,i x x x ii x x x iii x x ++其中**** 1234 ,,,x x x x 均为第3题所给的数. 5. 计算球体积要使相对误差限为1%,问度量半径R 时允许的相对误差限是多少? 6. 设028,Y =按递推公式 1n n Y Y -=…) 计算到100Y .27.982(五位有效数字),试问计算100Y 将有多大误差? 7. 求方程2 5610x x -+=的两个根,使它至少具有四位有效数字27.982). 8. 当N 充分大时,怎样求2 1 1N dx x +∞+?? 9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2 ? 10. 设 212S gt = 假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对 误差增加,而相对误差却减小. 11. 序列 {}n y 满足递推关系1101n n y y -=-(n=1,2,…),若0 1.41y =≈(三位有效数字), 计算到 10y 时误差有多大?这个计算过程稳定吗? 12. 计算6 1)f =, 1.4≈,利用下列等式计算,哪一个得到的结果最好? 3 -- 13. ()ln(f x x =,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大? 1、 方程组中,,则求解方程组的Jacobi 迭代与Gauss-Seidel 迭代均收敛的a 的范围是___________。 2、,则A 的LDL T 分解中,。 3、,则__________,_______________. 4、已 知,则用复合梯形公式计算求 得,用三点式求得____________. 5、,则_________ ,三点高斯求积公式______________. 6设* 2.40315x =是真值 2.40194x =的近似值,则* x 有________位有效数字。 7 3()1,[0,1,2,3]f x x x f =+-=设 则差商(均差)_____________,[0,1,2,3,4]f =________________。 8 求方程()x f x =根的牛顿迭代格式是__________________。 9.梯形求积公式和复化梯形公式都是插值型求积公式_____(对或错)。 10.牛顿—柯特斯求积公式的系数和()0n n k k C ==∑__________________。 11.用二次拉格朗日插值多项式2()sin0.34L x 计算的值。插值节点和相应的函数值是(0,0),(0.30,0.2955),(0.40,0.3894)。 12.用二分法求方程3()10[1.0,1.5]f x x x =--=在 区间内的一个根,误差限 210ε-=。 13.用列主元消去法解线性方程组 1231231 232346,3525,433032.x x x x x x x x x ++=??++=??++=? 14. 确定求积公式 012()()(0)()h h f x dx A f h A f A f h -≈-++? 。 中待定参数i A 的值(0,1,2)i =,使求积公式的代数精度尽量高;并指出此时求积公式的代数精度。 15、 试求使求积公式的代数精度 尽量高,并求其代数精度。 16.证明区间[a,b]上带权()x ρ的正交多项式(),1,2,n P x n = 的n 个根都是单根,且位于区间(a,b)内。 17.设()()[,],max ()n n a x b f x C a b M f x ≤≤∈=,若取 21cos ,1,2,,222k a b a b k x k n n +--=+= 作节点,证明Lagrange 插值余项有估计式21()max ()!2n n n a x b M b a R x n -≤≤-≤ 18用n=10的复化梯形公式计算时, (1)试用余项估计其误差 (2)用n=10的复化梯形公式计算出该积分的近似值。 19已知方程组AX =f,其中 (1)列出Jacobi 迭代法和Gauss-Seidel 迭代法的分量形式。 (2)求出Jacobi 迭代矩阵的谱半径,SOR 迭代法的最佳松弛参数 和SOR 法 的谱半径(可直接用现有结论) 20试确定常数A ,B ,C 和,使得数值积分公式 有尽可能高的代数精度。试问所得的数值积分公式代数精度是多少? 21证明方程=)(x f x 2-x -3=0在区间(2,3)内有且仅有一个根,并用迭代法求方程在区间(2,3)内的根,精确到小数点后4位。 22设f (1)=2,f (3)=4,f (4)=6,用拉格朗日插值法求f (x )的二次插值多项式P 2(x ),并求f (2)的近似值。 数值分析第三次大作业 一、算法的设计方案: (一)、总体方案设计: x y当作已知量代入题目给定的非线性方程组,求(1)解非线性方程组。将给定的(,) i i 得与(,)i i x y 相对应的数组t[i][j],u[i][j]。 (2)分片二次代数插值。通过分片二次代数插值运算,得到与数组t[11][21],u[11][21]]对应的数组z[11][21],得到二元函数z=(,)i i f x y 。 (3)曲面拟合。利用x[i],y[j],z[11][21]建立二维函数表,再根据精度的要求选择适当k 值,并得到曲面拟合的系数矩阵C[r][s]。 (4)观察和(,)i i p x y 的逼近效果。观察逼近效果只需要重复上面(1)和(2)的过程,得到与新的插值节点(,)i i x y 对应的(,)i i f x y ,再与对应的(,)i i p x y 比较即可,这里求解 (,)i i p x y 可以直接使用(3)中的C[r][s]和k 。 (二)具体算法设计: (1)解非线性方程组 牛顿法解方程组()0F x =的解* x ,可采用如下算法: 1)在* x 附近选取(0) x D ∈,给定精度水平0ε>和最大迭代次数M 。 2)对于0,1, k M =执行 ① 计算() ()k F x 和()()k F x '。 ② 求解关于() k x ?的线性方程组 () ()()()()k k k F x x F x '?=- ③ 若() () k k x x ε∞∞ ?≤,则取*()k x x ≈,并停止计算;否则转④。 ④ 计算(1) ()()k k k x x x +=+?。 ⑤ 若k M <,则继续,否则,输出M 次迭代不成功的信息,并停止计算。 (2)分片双二次插值 给定已知数表以及需要插值的节点,进行分片二次插值的算法: 设已知数表中的点为: 00(0,1,,) (0,1,,)i j x x ih i n y y j j m τ=+=???=+=?? ,需要插值的节点为(,)x y 。 1) 根据(,)x y 选择插值节点(,)i j x y : 若12h x x ≤+ 或12 n h x x ->-,插值节点对应取1i =或1i n =-, 第二章 1. 题目:运用MATLAB编程实现牛顿迭代 2. 实验操作 1、打开MATLAB程序软件。 2、在MATLAB中编辑如下的M程序。 function [p1,err,k,y]=newton(f,df,p0,delta,max) %f 是要求根的方程(f(x)=0); %df 是f(x)的导数; %p0是所给初值,位于x*附近; %delta是给定允许误差; %max是迭代的最大次数; %p1是newton法求得的方程的近似解; %err是p0的误差估计; %k是迭代次数; p0 for k=1:max p1=p0-feval('f',p0)/feval('df',p0); err=abs(p1-p0); p0=p1; k p1 err y=feval('f',p1) if (err p0 = 1.2000 k =1 p1=1.1030 err=0.0970 y=0.0329 k= 2 p1=1.0524 err=0.0507 y=0.0084 k =3 p1=1.0264 err=0.0260 y=0.0021 k =4 p1=1.0133 err=0.0131 y=5.2963e-004 k =5 p1=1.0066 err=0.0066 y=1.3270e-004 k =6 p1=1.0033 err=0.0033 y=3.3211e-005 k =7 p1=1.0017 err=0.0017 y=8.3074e-006 k =8 p1=1.0008 err=8.3157e-004 y = 2.0774e-006 k =9 p1=1.0004 err=4.1596e-004 y =5.1943e-007 k=10 p1=1.0002 err=2.0802e-004 y= 1.2987e-007 k=11 p1=1.0001 err=1.0402e-004 y =3.2468e-008 k=12 p1=1.0001 err=5.2014e-005 y=8.1170e-009 k=13 p1=1.0000 err=2.6008e-005 y= 2.0293e-009 k=14 p1=1.0000 err=1.3004e-005 y=5.0732e-010 k=15 p1 =1.0000 err=6.5020e-006 y=1.2683e-010 k=16 p1 =1.0000 err=3.2510e-006 y=3.1708e-011 k=17 p1 =1.0000 err=1.6255e-006 y =7.9272e-012 k=18 p1 =1.0000 err =8.1279e-007 y= 1.9820e-012 ans = 1.0000 结果说明:经过18次迭代得到精确解为1,误差为8.1279e-007。 目标:使用带双步位移的QR 分解法求矩阵10*10[]ij A a =的全部特征值,并对其中的每一个实特征值求相应的特征向量。已知:sin(0.50.2)() 1.5cos( 1.2)(){i j i j ij i j i j a +≠+== (i,j=1,2, (10) 算法: 以上是程序运作的逻辑,其中具体的函数的算法,大部分都是数值分析课本上的逻辑,在这里特别写出矩阵A 的实特征值对应的一个特征向量的求法: ()[]()() []()[]()111111I 00000 i n n n B A I gause i n Q A I u Bu u λλ-?-?-=-?-?? ?-=????→=??????→= ?? ? 选主元的消元 检查知无重特征值 由于=0i A I λ- ,因此在经过选主元的高斯消元以后,i A I λ- 即B 的最后一行必然为零,左上方变 为n-1阶单位矩阵[]()()11I n n -?-,右上方变为n-1阶向量[]()11n Q ?-,然后令n u 1=-,则 ()1,2,,1j j u Q j n ==???-。 这样即求出所有A所有实特征值对应的一个特征向量。 #include 《数值分析》计算实习题目 第一题: 1. 算法设计方案 (1)1λ,501λ和s λ的值。 1)首先通过幂法求出按模最大的特征值λt1,然后根据λt1进行原点平移求出另一特征值λt2,比较两值大小,数值小的为所求最小特征值λ1,数值大的为是所求最大特征值λ501。 2)使用反幂法求λs ,其中需要解线性方程组。因为A 为带状线性方程组,此处采用LU 分解法解带状方程组。 (2)与140k λλμλ-5011=+k 最接近的特征值λik 。 通过带有原点平移的反幂法求出与数k μ最接近的特征值 λik 。 (3)2cond(A)和det A 。 1)1=n λλ2cond(A),其中1λ和n λ分别是按模最大和最小特征值。 2)利用步骤(1)中分解矩阵A 得出的LU 矩阵,L 为单位下三角阵,U 为上三角阵,其中U 矩阵的主对角线元素之积即为det A 。 由于A 的元素零元素较多,为节省储存量,将A 的元素存为6×501的数组中,程序中采用get_an_element()函数来从小数组中取出A 中的元素。 2.全部源程序 #include 数值分析大作业(2013年5月) 金洋洋(12721512),机自系 1.下列各数都是经过四舍五入得到的近似值,试分别指出它 们的绝对误差限, 相对误差限和有效数字的位数。 X1 =5.420, x 2 =0.5420, x 3=0.00542, x 4 =6000, x 5=50.610? 解:根据定义:如果*x 的绝对误差限 不超过x 的某个数位的半个单位,则从*x 的首位非零数字到该位都是有效数字。 显然根据四舍五入原则得到的近视值,全部都是有效数字。 因而在这里有:n1=4, n2=4, n3=3, n4=4, n5=1 (n 表示x 有效数字的位数) 对x1:有a1=5, m1=1 (其中a1表示x 的首位非零数字,m1表示x1的整数位数) 所以有绝对误差限 143 11 (1)101022 x ε--≤ ?=? 相对误差限 31() 0.510(1)0.00923%5.4201 r x x x εε-?= == 对x2:有a2=5, m2=0 所以有绝对误差限 044 11 (2)101022 x ε--≤ ?=? 相对误差限 42() 0.510(2)0.00923%0.54202 r x x x εε-?= == 对x3:有a3=5, m3=-2 所以有绝对误差限 235 11 (3)101022 x ε---≤ ?=? 相对误差限 53() 0.510(3)0.0923%0.005423 r x x x εε-?= == 对x4:有a4=0, m4=4 所以有绝对误差限 4411(4)1022 x ε-≤?= 相对误差限 4() 0.5 (4)0.0083%6000 4 r x x x εε= = = 对x5:有a5=6, m5=5 所以有绝对误差限 514 11(5)101022 x ε-≤ ?=? 相对误差限 45() 0.510(5)8.3%600005 r x x x εε?= == 5.1.设A 是对称矩阵且011≠a ,经过一步高斯消去法后,A 约化为 ?? ????21 110 A a a T 证明2A 是对称矩阵。 证明 由消元公式及A 的对称性,有 ,,,3,2,,)2(111 11111 )2(n j i a a a a a a a a a a ji i j ji j i ij ij ==-=- = 故2A 对称。 5.2.设n ij a A )(=是对称正定矩阵,经过高斯消去法一步后,A 约化为 ?? ????21 110 A a a T 其中1)2(2)(-=n ij a A 。证明: (1).A 的对角元素;,,2,1,0n i a ii => (2).2A 是对称正定矩阵。 证明 (1).因为A 对称正定,所以 n i e Ae a i i ii ,,2,1,0),( =>=, 其中T i e )0,,0,1,0,,0( =为第i 个单位向量。 (2).由A 的对称性及消元公式,有 ,,,3,2,,)2(111 11111 )2(n j i a a a a a a a a a a ji i j ji j i ij ij ==-=- = 故2A 也对称。 又由A L A a a T 121110=????? ?,其中 ??? ?????- =? ????? ? ?????????--=-111 1 11111 21101 1011n n I a a a a a a L , 可见1L 非奇异,因而对任意0≠x ,由A 的正定性,有 ,0),(),(,011111>=≠x AL x L x AL L x x L T T T T 故T AL L 11正定。 由,000110211 111121111 1?? ? ?? ?=????????-??????=-A a I a a A a a AL L n T T T 而011>a ,故知2A 正定 北京航空航天大学 数值分析大作业八 学院名称自动化 专业方向控制工程 学号 学生姓名许阳 教师孙玉泉 日期2014 年11月26 日 一.题目 关于x , y , t , u , v , w 的方程组(A.3) ???? ?? ?=-+++=-+++=-+++=-+++79 .0sin 5.074.3cos 5.007.1cos sin 5.067.2cos 5.0y w v u t x w v u t y w v u t x w v u t (A.3) 以及关于z , t , u 的二维数表(见表A-1)确定了一个二元函数z =f (x , y )。 表A-1 二维数表 t z u 0 0.4 0.8 1.2 1.6 2 0 -0.5 -0.34 0.14 0.94 2.06 3.5 0.2 -0.42 -0.5 -0.26 0.3 1.18 2.38 0.4 -0.18 -0.5 -0.5 -0.18 0.46 1.42 0.6 0.22 -0.34 -0.58 -0.5 -0.1 0.62 0.8 0.78 -0.02 -0.5 -0.66 -0.5 -0.02 1.0 1.5 0.46 -0.26 -0.66 -0.74 -0.5 1. 试用数值方法求出f (x , y ) 在区域}5.15.0,8.00|), {≤≤≤≤=y x y x D (上的近似表达式 ∑∑===k i k j s r rs y x c y x p 00 ),( 要求p (x , y )以最小的k 值达到以下的精度 ∑∑==-≤-=10020 7210)],(),([i j i i i i y x p y x f σ 其中j y i x i i 05.05.0,08.0+==。 2. 计算),(),,(* ***j i j i y x p y x f (i =1,2,…,8 ; j =1,2,…,5) 的值,以观察p (x , y ) 逼 近f (x , y )的效果,其中j y i x j i 2.05.0,1.0**+==。数值分析习题集及答案[1].(优选)
数值分析大作业三 四 五 六 七
数值分析作业答案
数值分析作业思考题汇总
数值计算方法大作业
北航数值分析大作业一
数值分析第一次作业及参考答案
数值分析大作业
数值分析作业答案part
数值分析习题集及答案Word版
数值分析模拟试题
北航数值分析报告第三次大作业
数值分析作业
北航数值分析大作业第二题精解
北航数值分析大作业第一题幂法与反幂法
上海大学_王培康_数值分析大作业
数值分析作业答案(第5章)
北航数值分析报告大作业第八题