
第七章 格与布尔代数
1. 说明什么叫格?
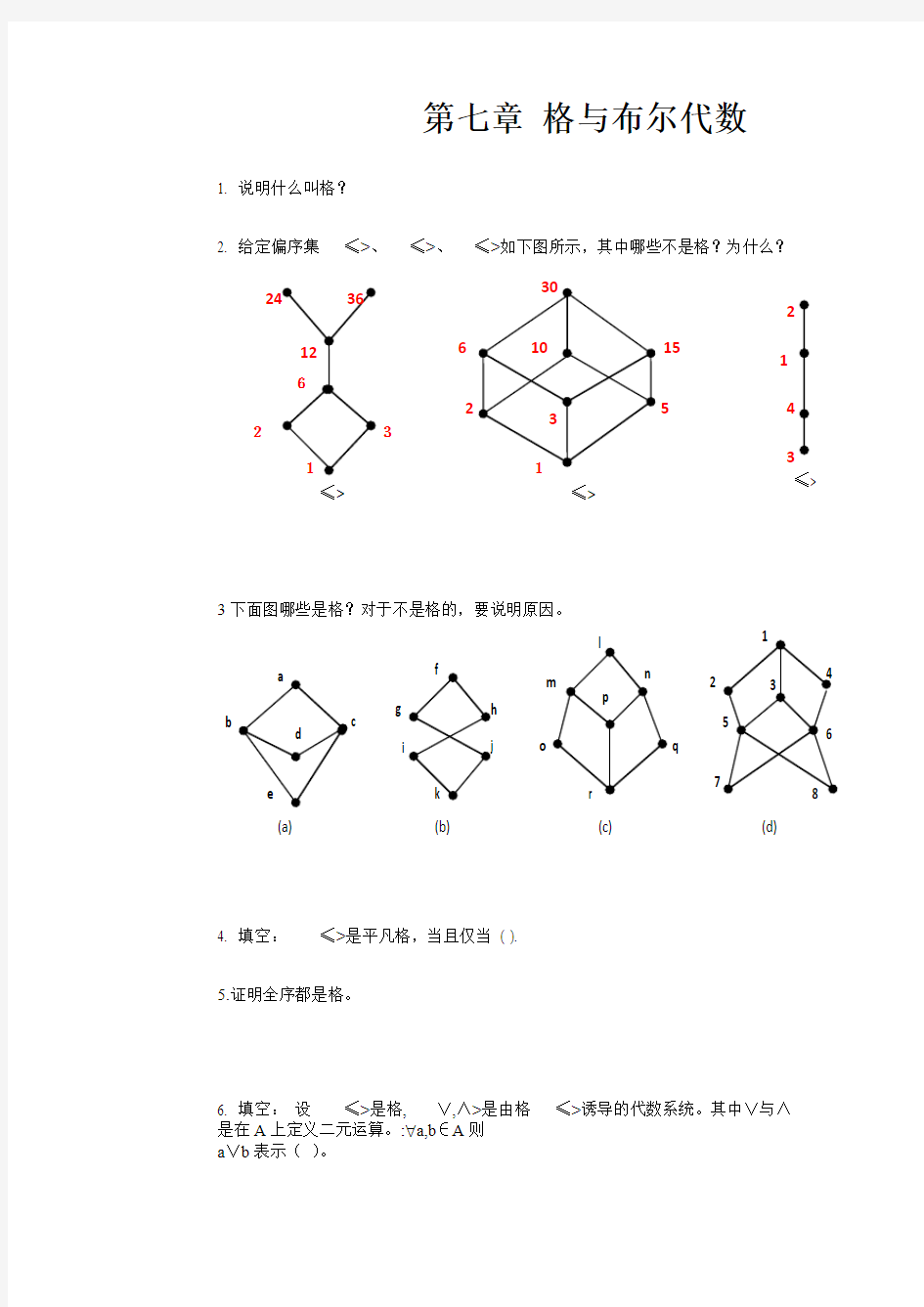
2. 给定偏序集
3下面图哪些是格?对于不是格的,要说明原因。
4. 填空:
5.证明全序都是格。
6. 填空: 设
q
(a)
(b)
(c)
(d)
3
2
5
15
6
4
1 2
3
a ∧
b 表示( )。
7. 说明什么叫子格?
8. 给定偏序集
9.设
10.具有一、二、三个元素的格各有几种不同构形式?请分别请画出它们的哈斯图。
11.具有四个元素的格有几种不同构形式?请分别请画出它们的哈斯图。
12具有五个元素的格有几种不同构形式?请分别请画出它们的哈斯图。
13. 证明格中下面式子成立: (a ∧b)∨(c ∧d)≤(a ∨c)∧(b ∨d)
a
a
c
a
14. 请说出什么叫分配格?
15. 指出判定一个格是分配格的充分且必要条件是在该格中没有任何子格与两个五元素非分配格之一同构。请画出这两个五元素非分配格。
16. 下面具有五个元素的格中,哪些是分配格?
17.具有五个元素的格中,有几个不是分配格?请画出这些非分配格的图。
18. 验证下面格不是分配格。
19. 验证下面格不是分配格。
a b c d
e
20.下面图中哪个是分配格?对不是分配格的,说明原因。
21. 给定集合如下:
A 1={1,2,4,8,16} A 2={1,2,3,5,6,10,15,30}
A 3={1,2,3,5,30} A 4={1,2,3,5,10,15,30} A 5={1,2,3,4,9,36}
令≤是上述集合上的整除关系。
1. 请分别画出各个偏序集的哈斯图(i=1,2,3,4,5)
22. 设 (a) 3 4 (b) b (c) d a c 23 给出有界格如图(1)所示。问 a) 哪些元素有补元? b) 该格是分配格吗? c) 该格是有补格吗? 24. 证明具有两个或更多个元素的格中 不存在以自身为补元的元素。 25. 在有界分配格中,证明具有补元的那些元素组成一个子格。 26. 设 27. 填空 1. 28. 下面(a),(b),(c)三个格是布尔格吗?如果是,请指出各个格的原子。 c b d g e d a f (1) (2) 29.下面的说法是否正确?为什么? 1.不是所有格都是有界格。 2.少于五个元素的格,都是分配格。 30. 设 31. 设 32. 判断下面命题的真值,并说明原因。 所有链都不是有补格。 33.判断下面命题的真值,并说明原因。 34.判断下面命题的真值,并说明原因。 d f c 1 b (a) (b) 35.设 1.化简表达式 a b a a b a *****)(())(( 2. 36. 设 x ≤y 当且仅当 x y ≤ 37. 举例说明并非有补格都是分配格。并非分配格都是有补格。(画出图说明即可) 38. 给定布尔代数<{0,1},∨,∧,―>中的布尔表达式E(x,y,z)如下,请用最简单的方法对它化简。(提示:考虑析取范式与合取范式的关系) )()()()()()(),,(z y x z y x z y x z y x z y x z y x z y x E ∧∧∨∧∧∨∧∧∨∧∧∨∧∧∨∧∧= 39.给定布尔代数<{0,1},∨,∧,―>中的布尔表达式E(x,y,z)如下,请用最简单的方法对它化简。(提示:考虑析取范式与合取范式的关系) )()()()()()(),,(z y x z y x z y x z y x z y x z y x z y x E ∧∧∨∧∧∨∧∧∨∧∧∨∧∧∨∧∧= 40.给定布尔代数<{0,1},∨,∧, ˉ >上的一个布尔表达式如下: ) ()()(),,(323221321x x x x x x x x x E ∧∨∧∨∧= 分别写出它的析取范式与合取范式。 1.答案: 2.答案: 3.(a) 不是格,因为d 和e 没有下确界,也没有上确界. (d) 不是格,因为5和6没有下确界,7和8既没下确界,也没上确界. 4.答案:( 即{x,y}的最大下界为较小元素,最小上界为较大元素。所以全序都是格。 6.答案:a ∨b 表示(LUB {a,b}, 或者{a,b}的最小上界) a ∧ b 表示(GLB {a,b}, 或者{a,b}的最大下界) 7.答案:设 因为在 任取x,y ∈B, 由B 的构成得a ≤x ≤b,a ≤y ≤b, 于是由格的性质得,a ≤x ∨y ≤b , a ≤x ∧y ≤b, 于是有 x ∨y ∈B ,x ∧y ∈B , 说明∨和∧在B 上封闭 。 所以 10.答案:含有一、二、三个元素的格都是链。都各有一种不同构形式。 它们的哈斯图如下: 11.答案:具有四个元素的格不同构形式有2钟。 任何一个具有四个元素的格必同构于下面两种格形式之一: 它们的哈斯图如下: ? a a b a b c 12.答案:具有五个元素的格有五种不同构的形式,其图形如下: 设a,b 是格 b). a ∧b :a) 充分性:已知a ∨b=a ,b=b ∧(b ∨a)= b ∧(a ∨b) =b ∧a=a ∧b 必要性:已知a ∧b=b , a=a ∨(a ∧b)=a ∨b b) 充分性:已知a 与b 是不可比较的. 因a ∧b ≤b, a ∧b ≤a, 如果a ∧b=b, 则有b ≤a, 如果a ∧b=a, 则有a ≤b,都与a 与b 是不可比较的矛盾. 所以有: a ∧ b ≤b ∧ a ∧b ≠b,于是有 a ∧b 必要性:已知a ∧b ∵ (a ∧b)≤a ≤(a ∨c) ∴ (a ∧b)≤(a ∨c) ∵ (c ∧d)≤c ≤(a ∨c) ∴ (c ∧d)≤(a ∨c) ∴ (a ∧b)∨(c ∧d)≤(a ∨c) 同理 (a ∧b)≤(b ∨d) (c ∧d)≤(b ∨d) ∴ (a ∧b)∨(c ∧d)≤(b ∨d) ∴(a ∧b)∨(c ∧d)≤(a ∨c)∧(b ∨d) 14.答案: 则称 16.答案:a,d,e 是分配格。 17.答案:有两个。图形如下: d a c d a b 18.答案:2∧(3∨5)=2∧30=2 (2∧3)∨(2∧5)=1∨1=1 2∧(3∨5)≠ (2∧3)∨(2∧5) 19.答案:c ∧(b ∨d)=c ∧a=c (c ∧b)∨(c ∧d)=e ∨d=d c ∧(b ∨d) ≠(c ∧b)∨(c ∧d) 20.答案:(a)和(b)是分配格。 (c)不是分配格。 因为(c)图等价于下面图(d),而其中结点bfged 构成的子格就是与五元素非分配格(e)同构的子格。所以它不是分配格。 21.答案: 1.各个偏序集的哈斯图如下:(i=1,2,3,4,5) 先证 f 是从A 到B 的映射:任取x ∈A, 由f 的定义得f(x)=(x ∨a)∧b) 显然 (x ∨a)∧b ≤b ,而 (x ∨a)∧b=(x ∧b)∨(a ∧b)=(x ∧b)∨a ( 因a a ≤(x ∨a)∧ b ≤b 即a ≤f(x)≤b ∴f(x)∈B ,∴ dom f=A. 又由于∨和∧的定义知(x ∧b)∨a 是唯一的。 即f(x)是唯一的 . 所以f 是从A 到B 的映射。 1 4 2 8 16 5 10 9 f a (d) 2 1 3 (e) d a c 再证f 满足同态等式:任取x 1,x2∈A, f(x 1∧x 2)=((x 1∧x 2)∨a)∧b=((x 1∨a)∧(x 2∨a))∧b =((x 1∨a)∧b)∧((x 2∨a)∧b) =f(x 1)∧f(x 2) f(x 1∨x 2)=((x 1∨x 2)∨a)∧b=((x 1∨a)∨(x 2∨a))∧b =((x 1∨a)∧b)∨((x 2∨a)∧b) =f(x 1)∨f(x 2) ∴f 是同态映射。 23.答案:解 :a) a 、c 、d 、f 、g 无补元 ; b 和e 互为补元; 0和1互为补元。 b) 不是分配格, 因为它含有如图(2)所示的子格。 c) 它不是有补格,因为很多元素无补元。 24.答案:证明:设 1=a ∨a =a ∨a=a 0=a ∧a =a ∧a=a 产生矛盾. 所以不存在以自身为补元的元素. 25.证明: 设 任取a,b ∈B, ,,,,A b a A b a B b a ∈∨∈∧∈ 下面证明∨和∧在B 上封闭,即a ∨b 和a ∧b 都有补元: 所以 a) x=x ∧(x ∨y)=x ∧0=0 y=y ∧(y ∨x)=y ∧0=0 b) x=x ∨(x ∧y)=x ∨1=1 y=y ∨(y ∧x)=y ∨1=1 27.答案: 1.(有补分配)。 2.(x ∧a=a )(x ∧a=0)。 28.答案:都是是布尔格。 (a):1是原子。(b):a,b 是原子。(c):d,e,f 是原子。 29.答案: 1.是正确的。 因为有的格就不是有界格。例如 因为少于五个元素的格,它们不可能与五元素的非分配格同构。所以都是分配格。 30.答案:证明:设 而 (a ∨b)∧(a ∨c) = ((a ∨b)∧a)∨((a ∨b)∧c) (分配) =a ∨((a ∨b)∧c)=a ∨((a ∧c)∨(b ∧c)) (吸收、分配) = (a ∨(a ∧c))∨(b ∧c) (结合) = a ∨(b ∧c) (吸收) 所以∨对∧也可分配。 31.答案:证明:任取a,b,c ∈A, 设有 a ∧b=a ∧c 及 a ∨b=a ∨c B b a b a b a ∈∧∨∧所以有补元所以000)()()( )(=∨=∧∧∨∧∧=∨∧∧b b a a b a b a b a 111)()()()(=∧=∨∨∧∨∨=∨∨∧b a b b a a b a b a B b a b a b a ∈∨∧∨ 所以有补元所以000)()()()(=∨=∧∧∨∧∧=∧∧∨b a b b a a b a b a 1 11)()()()(=∧=∨∨∧∨∨=∧∨∨b b a a b a b a b a b=b ∨(a ∧b) (吸收律) =b ∨(a ∧c) (代换) =(b ∨a)∧(b ∨c) (分配) =(a ∨b)∧(b ∨c) (交换) =(a ∨c)∧(b ∨c) (代换) = (a ∧b)∨c (分配) = (a ∧c)∨c (代换) =c (吸收律) 32.答案:真值为真。 因为任何链都不会含有与五元素非分配格之一同构的子格,所以链必是分配格。 33.答案:真值为真。因为 如果|A|=3,则它的哈斯图是链。中间元素没有补员。所以它不是有补格; 如果|A|<5,则它都不会含有与五元素非分配格之一同构的子格,所以它们必是分配格。 34.答案:真值为真。因为 根据stone(钻石)定理的推论1可得:有限布尔格,它的元素个数为2n 。(n 是正整数) 35.答案 1.化简表达式: . a a a a a a b a a b a a b a a b a a b a a b a =∨=*=∨∧*∨∧=∨∨*∨∨=*****))(())(())(())(()(())(( 2. a) 证明 * 满足封闭性:这显然成立。因为 任何a,b ∈A ,在布尔代数中并和补运算封闭,所以a *b=a ∨b ∈A ,a *b ∈A 。 b) 证明 * 满足结合性: 任取a,b,c ∈A , ) ()()()())(()()(c b a c b a c b c a c b a c b a c b a ∨∨=**∨∧∨=∨∧=∨∨=** (a *b )*c ≠ a *(b *c ), 可见*不满足可结合性。 所以 充分性:已知x y ≤。 必要性:已知x ≤y 37.答案: x y x y x x y x x y x ≤=∨=∧∴=∧∴所以即y x y x y y y x y y x y ≤=∨==∧=∧∴所以即 38.答案: )()()()()()(),,(z y x z y x z y x z y x z y x z y x z y x E ∧∧∨∧∧∨∧∧∨∧∧∨∧∧∨∧∧= =m 7∨m 3∨ m 5∨ m 2∨ m 4∨ m 0 = M 1∧M 6 = )()(z y x z y x ∨∨∧∨∨ 39.答案: )()()()()()(),,(z y x z y x z y x z y x z y x z y x z y x E ∧∧∨∧∧∨∧∧∨∧∧∨∧∧∨∧∧= =m 7∨m 3∨ m 6∨ m 5∨ m 4∨ m 2 = M 0∧M 1 = )()(z y x z y x ∨∨∧∨∨ =)(z z y x ∧∨∨ =x ∨y 40.答案:先列出真值表如下: 1 4 2 8 16 5 E(x 1,x 2,x 3)= )()()(321321321x x x x x x x x x ∨∨∧∨∨∧∨∨ )()()()()(),,(321321321321321321x x x x x x x x x x x x x x x x x x E ∧∧∨∧∧∨∧∧∨ ∧∧∨∧∧= 离散数学习题解答 习题五(第五章 格与布尔代数) 1.设〈L ,?〉是半序集,?是L 上的整除关系。问当L 取下列集合时,〈L ,?〉是否是格。 a) L={1,2,3,4,6,12} b) L={1,2,3,4,6,8,12} c) L={1,2,3,4,5,6,8,9,10} [解] a) 〈L ,?〉是格,因为L 中任两个元素都有上、下确界。 b) 〈L ,?〉不是格。因为L 中存在着两个元素没有上确界。 例如:8 12=LUB{8,12}不存在。 c) 〈L ,?〉不是格。因为L 中存在着两个元素没有上确界。 1 6 3 1 2 4 8 63 1 2 4 1 1 倒例如:46=LUB{4,6}不存在。 2.设A ,B 是两个集合,f 是从A 到B 的映射。证明:〈S ,?〉是〈2B ,?〉的子格。其中 S={y|y=f (x),x ∈2A } [证] 对于任何B 1∈S ,存在着A 1∈2A ,使B 1=f (A 1),由于f(A 1)={y|y ∈B ∧(x)(x ∈A 1∧f (x)=y)}?B 所以B 1∈2B ,故此S ?2B ;又B 0=f (A)∈S (因为A ∈2A ),所以S 非空; 对于任何B 1,B 2∈S ,存在着A 1,A 2∈2A ,使得B 1=f (A 1),B 2=f (A 2),从而 L ∪B{B 1,B 2}=B 1∪B 2=f (A 1)f (A 2) =f (A 1∪A 2) (习题三的8的1)) 由于A 1∪A 2?A ,即A 1∪A 2∈2A ,因此f (A 1∪A 2)∈S ,即上确界L ∪B{B 1,B 2}存在。 对于任何B 1,B 2∈S ,定义A 1=f –1 (B 1)={x|x ∈A ∧f (x)∈B 1},A 2=f -1 (B 2)={x|x ∈A ∧f (x)∈B 2},则A 1,A 2∈2A ,且显然B 1=f (A 1),B 2=f (A 2),于是 GLB{B 1,B 2}=B 1∩B 2=f (A 1)∩f (A 2) ?f (A 1∩A 2) (习题三的8的2)) 又若y ∈B 1∩B 2,则y ∈B ,且y ∈B 2。由于y ∈B 1=f (A 1)={y|y ∈B ∧(x)(x ∈A 1∧f (x)=y)},于是存在着x ∈A 1,使f (x)=y ,但是f (x)=y ∈B 2。故此x ∈A 2=f -1 (B 2)={x|x ∈A ∧f(x)∈B 2},因此x ∈A 1∩A 2,从而y=f (x)∈f (A 1∩A 2),所以 GLB{B 1,B 2}=B 1∩B 2=f (A 1)∩f (A 2) ?f (A 1∩A 2) 9 7 31 第七章 格与布尔代数 1. 说明什么叫格? 2. 给定偏序集 a ∧ b 表示( )。 7. 说明什么叫子格? 8. 给定偏序集 14. 请说出什么叫分配格? 15. 指出判定一个格是分配格的充分且必要条件是在该格中没有任何子格与两个五元素非分配格之一同构。请画出这两个五元素非分配格。 16. 下面具有五个元素的格中,哪些是分配格? 17.具有五个元素的格中,有几个不是分配格?请画出这些非分配格的图。 18. 验证下面格不是分配格。 19. 验证下面格不是分配格。 a b c d e 、选择题(每小题2分,共30分) 1、N 是自然数集, 是小于等于关系, 则 N, 是(C )。 (A)有界格 (B) 有补格 (C)分配格 (D) 2、在有界格中,若只有一个元素有补元, 有补分配格 则补元( C ) (A)必唯 (B) 不唯 (C)不一定唯 (D) 可能唯 3、 F 面是一些偏序集的哈斯图,判断哪一个为格( C ) d c e e e c D A C B D ) (A)分配格 (B)有补格 (C)布尔格 (D) 有界格 6设L,是一条链,其中L -3,贝U L, ( C ) (A)不是格 (B) 是有补格 5、只含有有限个元素的格称为有限格, 有限格必是( (C)是分配格 (D) 是布尔格 7、 设A 为一个集合, P(A), 为有补格,P(A)中每个元素的补元(A ) (A) 存在且唯一 (B) 不存在 (C)存在但不唯一 (D)可能存在 8、 设 代 是一个有界格,若它也是有补格,只要满足( B ) (A)每个元素都有一个补元 (B)每个元素都至少有一个补元 9、如下哈斯图(C )表示的关系构成有补格。 (C)每个元素都无补元 (D)每个元素都有多个补元 10、如图给出的哈斯图表示的格中( (A)a (C)e (D) f 11、设格 B, 2如图所示,它们的运算分别为 和,。令 f(a) X !, f(b) X 2, f (c) X 4, f (d) X 8,则 f ( B ) B )元素无补元。 d g c (A)是格同态映射 (B)不是格同态映射 系。贝U 30的补元为 (B) 30 (D) 70 f (a) 2 f(b)是格同构的( (B)充分条件 ,其中定义为:对于n 1 , n 2 L, n 1 n 2 当且仅当n 1是n 2的因子。问其中哪几个偏序集是格(说明理由)。(共6 分) a)、L {1,2,3,4,6,12} b)、L {1,2,3,4,6,8,12,14} C)、L {1,2,3,4,5,6,7,8,9,10,11,12} 、图中为格L 所对应的哈斯图。(共10分) (C) 是格同构映射 (D) 是自同态映射 (A) 2n (B) (C) 2n (D) 4n 13、在布尔格 A, 中有3个原子a 1,a 2,a 3则6 ( B ) (A) a 2 a 3 (B) a 2 a 3 (C) a 2 a 3 (D) a 2 a 3 14、在布尔格 代 中, A {X | X 是5的整数倍且是210的正因子} , |为整除关 (A)15 (C)35 15、设A, 1和 B, 2 是两个格, f 是A 到B 的双射,则对任意的a,b A ,有 (A)必要条件 (C)充要条件 (D)既不充分也不必要 、由下列集合L 构成的偏序集 L, 格与布尔代数试题1 一、选择题(每小题2分,共30分) 1、N 是自然数集,≤是小于等于关系,则≤><,N 是(C )。 )(A 有界格 )(B 有补格 )(C 分配格 )(D 有补分配格 2、在有界格中,若只有一个元素有补元,则补元(C )。 )(A 必唯一 )(B 不唯一 )(C 不一定唯一 )(D 可能唯一 3、下面是一些偏序集的哈斯图,判断哪一个为格(C ) f g c e a e c d f d e b c a e b A B C D 4、以下为4个格对应的哈斯图,( D )是分配格。 A B C D 5、只含有有限个元素的格称为有限格,有限格必是( D ) )(A 分配格 )(B 有补格 )(C 布尔格 )(D 有界格 6、设≤><,L 是一条链,其中3≥L ,则≤><,L ( C ) )(A 不是格 )(B 是有补格 )(C 是分配格 )(D 是布尔格 7、设A 为一个集合,?><),(A P 为有补格,)(A P 中每个元素的补元( A ) )(A 存在且唯一 )(B 不存在 )(C 存在但不唯一 )(D 可能存在 8、设≤><,A 是一个有界格,若它也是有补格,只要满足( B ) )(A 每个元素都有一个补元 )(B 每个元素都至少有一个补元 )(C 每个元素都无补元 )(D 每个元素都有多个补元 9、如下哈斯图( C )表示的关系构成有补格。 A B C D 10、如图给出的哈斯图表示的格中( B )元素无补元。 a b d f g )(A a )(B c )(C e )(D f 11、设格>≤<>≤<21,,B A 和如图所示,它们的运算分别为?⊕∧∨,和,。令8421)(,)(,)(,)(x d f x c f x b f x a f ====,则f ( B ) )(A 是格同态映射 )(B 不是格同态映射 )(C 是格同构映射 )(D 是自同态映射 12、有限布尔代数的元素的个数必定等于( C ) )(A n 2 )(B 2n )(C n 2 )(D n 4 13、在布尔格≤><,A 中有3个原子321,,a a a 则=1a ( B ) )(A 32a a ∧ )(B 32a a ∨ )(C 32a a ∧ )(D 32a a ∨ 14、在布尔格≤><,A 中,}2105|{的正因子的整数倍且是是X X A =,|为整除关系。则30的补元为( C ) )(A 15 )(B 30 )(C 35 )(D 70 15、设>≤<>≤<21,,B A 和是两个格,的双射到是B A f ,则对任意的A b a ∈,,有)()(21b f a f b a ≤?≤是格同构的( C ) )(A 必要条件 )(B 充分条件 )(C 充要条件 )(D 既不充分也不必要 二、由下列集合L 构成的偏序集≤><,L ,其中≤定义为:对于1n , 2n ,L ∈1n ≤2n 当且仅当1n 是2n 的因子。问其中哪几个偏序集是格(说明理 由)。(共6分) 第十章 格和布尔代数 习题10.1 1.解 ⑴不是,因为L 中的元素对{2,3}没有最小上界; ⑵是,因为L={1,2,3,4,6,9,12,18,36}任何一对元素a ,b ,都有最小上界和最大下界; ⑶是,与⑵同理; ⑷不是,因为L 中的元素对{6,7}没有最小上界不存在最小上界。 2.证明 ⑴因为,a ≤b,所以,a ∨b=b ;又因为,b ≤c,所以,b ∧c=b 。故a ∨b=b ∧c ; ⑵因为,a ≤b ≤c,所以,a ∧b=a,b ∧c=b,而a ∨b=b ,因此,(a ∧b )∨(b ∧c )=b ; 又a ∨b=b,b ∨c=c,而b ∧c=b, 因此,(a ∨b )∧(b ∨c )=b 。即 (a ∧b)∨(b ∧c)=(a ∨b)∧(b ∨c)。 习题10.2 1.解 由图1知:<S 1,≤>不是<L,≤>的子格,这是因为,e ∨f=g ?S 1; <S 2,≤>不是<L,≤>的子格, ∵e ∧f=c ?S 2; <S 3,≤>是<L,≤>的子格. 2.解 S 24的包含5个元素的子格有如下的8个: S 1={1,3,6,12,24}, S 2={1,2,6,12,24}, S 3={1,2,4,12,24}, S 4={1,2,4,8,24}, S 5={1,2,3,6,12}, S 6={1,2,4,6,12}, S 7={2,4,6,12,24}, S 7={2,4,8,12,24}. 3.证明 因为,一条线上的任何两个元素都有(偏序)关系,所以,都有最大下界和最小上界,故它是格,又因为它是 第七章 格与布尔代数 1. 说明什么叫格? 2. 给定偏序集 a ∧ b 表示( )。 7. 说明什么叫子格? 8. 给定偏序集 14. 请说出什么叫分配格? 15. 指出判定一个格是分配格的充分且必要条件是在该格中没有任何子格与两个五元素非分配格之一同构。请画出这两个五元素非分配格。 16. 下面具有五个元素的格中,哪些是分配格? 17.具有五个元素的格中,有几个不是分配格?请画出这些非分配格的图。 18. 验证下面格不是分配格。 19. 验证下面格不是分配格。 a b c d e 一、选择题(每小题2分,共30分) 1、N 是自然数集,≤是小于等于关系,则≤><,N 是(C )。 )(A 有界格 )(B 有补格 )(C 分配格 )(D 有补分配格 2、在有界格中,若只有一个元素有补元,则补元(C )。 )(A 必唯一 )(B 不唯一 )(C 不一定唯一 )(D 可能唯一 3、下面是一些偏序集的哈斯图,判断哪一个为格(C ) f g c e a e c d f d e b c a e b A B C D 4、以下为4个格对应的哈斯图,( D )是分配格。 A B C D 5、只含有有限个元素的格称为有限格,有限格必是( D ) )(A 分配格 )(B 有补格 )(C 布尔格 )(D 有界格 6、设≤><,L 是一条链,其中3≥L ,则≤><,L ( C ) )(A 不是格 )(B 是有补格 )(C 是分配格 )(D 是布尔格 7、设A 为一个集合,?><),(A P 为有补格,)(A P 中每个元素的补元( A ) )(A 存在且唯一 )(B 不存在 )(C 存在但不唯一 )(D 可能存在 8、设≤><,A 是一个有界格,若它也是有补格,只要满足( B ) )(A 每个元素都有一个补元 )(B 每个元素都至少有一个补元 )(C 每个元素都无补元 )(D 每个元素都有多个补元 9、如下哈斯图( C )表示的关系构成有补格。 A B C D 10、如图给出的哈斯图表示的格中( B )元素无补元。 a b d f g )(A a )(B c )(C e )(D f 11、设格>≤<>≤<21,,B A 和如图所示,它们的运算分别为?⊕∧∨, 和,。令8421)(,)(,)(,)(x d f x c f x b f x a f ====,则f ( B ) 第九章 格与布尔代数 习题提示 9.1 下面整数集合对于整除关系都构成偏序集,判断哪些偏序集是格。 (1)L={1,2,3,4,5} (2)L={1,2,3,6,12} (3)L={1,2,3,4,6,9,12,18,38} (4)L={} 2 3 1,2,2,2,,2n 解:(1)不是格。(2)是格。(3)不是格。(4)是格。 9.2.试问下面哈斯图所示的偏序集是否是格? 图9.2 解:(1)是格。(2)不是格。(3)不是格。(4)是格。(5)是格。(6)是格。 9.4 设G 是群,L (G )表示G 的所有子群组成的集合,L (G)的偏序关系定义为:对于任意 ,G 当且仅当,证明12,()G G L G ∈12G ≤21G G ?((),)L G ≤是格。 提示:直接验证。 9.5 设S 是非空集合,T S 是S 的非空子集,证明?()(),P T ?是()() ,P S ?的子格。 提示:关键要证格()() ,P T ?中运算与()() ,P S ?子格()P T 的运算也一致。 9.7 在格(,)+ ?Z 中(其中是正整数集合,偏序“+ Z ?”定义为:a b a b ??) ,下面的集合是否是它的子格。 (1)S={1,2,3,9,12,72} (2)S={1,2,3,12,18} (3)S={} 2 3 1,2,2,2,,2n 解:(1)和(2)都不是子格。(3)是子格。 9.10 证明如果L 是有界格,并且2L ≥,则0I ≠。 证明:如果0I =, 因为对任意L 中元x ,0x I ??,所以x I ?,I x ?。从而I x =。于2L ≥矛盾。 9.12 判断下面图所示的格是否是分配格,是否是补格。 图 9.4 解:(1)不是分配格,也不是补格。 (2)不是分配格,也不是补格。 (3)不是分配格,是补格。 9.16 在同构的意义下确定所有4个元素的格,并证明它们都是分配格。 解:(1), 其中不可比较。(2){0,,,}S b c =I I ,b c {0,,,}S b c =, 其中b c ?。 9.17 找出所有不同构的5元格。 解:不同构的5元格共有五个,它们的哈斯图如下:离散数学习题解答(第五章)格与布尔代数
第七章格与布尔代数
格与布尔代数试题
格与布尔代数试题1电子版本
离散数学答案 第十章 格和布尔代数
第七章 格与布尔代数
格与布尔代数试题
第九章格与布尔代数