2009年第七届小学希望杯全国数学邀请赛五年级第1试试题及详细解答

2009年第7届希望杯5年级二试试题1.(2009年第7届希望杯5年级2试第1题，5分)四个数2008200720092008,,,2007200820082009其中最大的数是，最小的数是．2.(2009年第7届希望杯5年级2试第2题，5分)若0.24 2.814A=+，则循环小数A的每个循环节有___位数字，循环节的首位数字和末位数字分别是___和___．3.(2009年第7届希望杯5年级2试第3题，5分)100以内的自然数中．所有是3的倍数的数的平均数是．4.(2009年第7届希望杯5年级2试第4题，5分)一个十位数字是0的三位数，等于它的各位数字之和的67倍，交换这个三位数的个位数字和百位数字，得到的新三位数是它的各位数字之和的倍．5.(2009年第7届希望杯5年级2试第5题，5分)如图1，圆圈内分别填有1，2，……，7这7个数．如果6个三角形的顶点处圆圈内的数字的和是64，那么，中间圆圈内填入的数是．6.(2009年第7届希望杯5年级2试第6题，5分)如图2所示，4盏霓虹灯安装在大正方形的4个小正方形框里，3秒后，上下的灯互换图案，又过了3秒，左右的等互换图案，……，重复这样的变化规律．请画出经过1分钟霓虹灯的排列图案．7.(2009年第7届希望杯5年级2试第7题，5分)五（1）班共有学生40人，其中，既会轮滑又会游泳的学生有8人，这两项运动都不会的学生有12人，只会轮滑与只会游泳的人数之比是3：2．那么，五（1）班会轮滑的而又人，会游泳的有人．8.(2009年第7届希望杯5年级2试第8题，5分)两个篮子中分别装有很多同样的牵牛花和月季花，从中选出6朵串成花环（图3是其中的一种情况），可以得到不同的花环种．（通过旋转和翻转能重合的算同一种花环）．9.(2009年第7届希望杯5年级2试第9题，5分)如图4，李明和王亮从同一跑道的起点同时同向出发，结果李明比王亮晚到终点0.5秒．则跑道长米．10.(2009年第7届希望杯5年级2试第10题，5分)用若干个棱长为1的小正方体铁框架焊接成的几何体，从正面、侧面、上面看到的视图均如图5所示．那么这个几何体至少是个小正方体铁框架焊接而成．11.(2009年第7届希望杯5年级2试第11题，5分)用{x}表示数x的小数部分，[x]表示x的整数部分．如{2.3}=0.3，[2.3]=2．若a+[b]=15.3，{a}+b=7.8，则a= ，b= ．12.(2009年第7届希望杯5年级2试第12题，5分)通常，汽车经销商对所销售汽车的报价中已经计入了增值税，即报价等于纯车价与增值税之和．消费者在购买汽车后还需要缴纳购置税．增值税和购置税都是按照纯车价来计算的．根据以上信息完成下表．13.(2009年第7届希望杯5年级2试第13题，15分)图6，在一张方格纸上画若干个1×2的阴影方块，可留下一定数量的1×1的空方块□．要求：1×2的阴影方块的阴影部分不重叠，1×1的空方块不相连．请根据图（a）、图（b）的示例，在图（c）、图（d）、图（e）的方格纸上画一个或更多个1×2的阴影方块，使各图留下的1×1的空方块的数量最多．14.(2009年第7届希望杯5年级2试第14题，15分)甲、乙两车间生产同一种零件，若按4：1向甲乙车间分配生产任务，这两个车间能同时完成任务．实际生产时，乙车间每天生产15个零件，由于甲车间抽调一部分工人去完成另外的任务，实际每天生产50个零件．若干天后，乙车间完成了任务，甲车间还剩一部分未完成，这时，甲乙两车间合作，2天后全部完成．问：这批零件有多少个？15.(2009年第7届希望杯5年级2试第15题，15分)如图7，梯形ABCD与正方形DEFC拼在一起，AF与DE交于点G．已知BC=CD=4，三角形AGD的面积是三角形DGF面积的2倍．（1）求梯形ABCD的面积；（2）比较三角形GEF和三角形AGD的面积大小．16.(2009年第7届希望杯5年级2试第16题，15分)如图8，甲、乙两艘快船不断往返于A、B两港之间．若甲、乙同时从A港出发，它们能否同时到达下列地点？若能，请推出它们何时到达该地点；若不能，请说明理由：（1）A港口；（2）B港口；（3）在两港口之间且距离B港30千米的大桥．试题答案1. 【分析】20082007；200720082. 【分析】6；0；93. 【分析】100以内的自然数中是3的倍数的数有0，3,6,9,99 共33个，他们的和是()09934179916832+⨯=⨯=，则他们的平均数为1683÷34=49.5． 4. 【分析】令这个三位数为0a b ，则由题意可知，10067()a b a b +=+，可得2a b =，而调换个位和百位之后变为：0100102b a b a b =+=，而3a b b +=，则得到的新三位数是它的各位数字之和的102334b b ÷=倍．5. 【分析】26. 【分析】7. 【分析】20；168. 【分析】考虑月季花的数量有0、1、2、3、4、5、6共类情况，分类讨论：（１） 有0朵月季花，则有1种；（２） 有1朵月季花，则有1种；（３） 有2朵月季花，2朵月季花中间可包夹有0、1、2朵月季花，共有3种情况．（包夹3、4朵分与包夹1、0朵相同）；（４） 有3朵月季花，3多月季花中间可包含有0、1、2朵月季花，共有3种情况．（包含 （５） 3朵月季花与包含0朵相同）；（６） 有4朵月季花，同（3），有3种情况；（７） 有5朵月季花，有1种；（８） 有6朵月季花，有1种；所以共有1+1+3+3+3+1+1=13（种）9. 【分析】20810. 【分析】注意，此题是焊接而成，而不是堆砌，则中间可以空，所以用9个小正方体铁框架即可焊接而成．11. 【分析】8.3；7.512. 【分析】84000；420013. 【分析】图（c ）、图（d ）、图（e ）分别最多留下0个、2个、6个11⨯的空房快，如下图所示．（画法不唯一，每个图6分．）14. 【分析】如果甲车间不抽调一部分工人去完成另外的任务，每天能生产零件 151460÷⨯=（个） （5分） 原计划完成任务所用的时间是()()50152605013+⨯÷-=（天） （10分） 这批零件有 ()60153975+⨯1=（个）．（15分） 15. 【分析】（1）因为三角形AGD 的面积是三角形DGF 的面积的2倍，两个三角形有相同的底边DG ，所以三角形AGD 的高是三角形DGF 的高的2倍，则()42112AB =⨯+=．梯形ABCD 的面积是()4124232+⨯÷=．（2）正方形DEFC 的面积是4416⨯=，三角形AFB 的面积是()4412248+⨯÷=．又因为ABCD 的面积是32，而三角形DCF 的面积为8，所以三角形ADF 的面积为8，又三角形DEF 的面积为8，所以三角形GEF 的面积与三角形ADG 的面积相等．16. 【分析】（1）甲往返一次的时间是()18018013.5h 3010300+=+-1， 乙往返一次的时间是()180180.5h 5010500+=7+-1， 13.5和7.5的最小公倍数是67.5，所以，在甲、乙出发后的()67.51,2,a a = 小时，它们又同时回到A 港． （5分） （2）设甲、乙能同时到达B 港，此时，甲、乙各完成了,m n 次往返（,m n 是自然数），则有 18018013.57.530105010m n +=+++ 即 915m n +=．当m 的个位数是6或1时，有满足上式的自然数n ．，最小的=1,最少需要4.5+13.5=18小时．则在甲、乙出发后18+67.5小时，它们同时到达港口．（10分） （3）设甲、乙能同时到达大桥，且分别完成了,m n 次往返（,m n 是自然数）． ①若此时甲、乙向下游行驶，则15015013.57.530105010m n +=+++， 即 13512.575m n +=，没有满足上式的自然数,m n ．②若此时甲、乙向上游行驶，则180301803013.57.53010301050105010m n ++=+++-+-， 即 13522.575m n +=，没有满足上式的自然数,m n ．③若此时甲向上游行驶，乙向下游行驶，则1803015013.57.5301030105010m n ++=++-+ 即 27715m n +=没有满足上式的自然数,m n ．④若此时甲向下游行驶，乙向上游行驶，则1501803013.57.5301050105010m n +=++++- 即 95m n =当m 的个位数是0或5时，有满足上式的自然数n ，所以在甲、乙出发后的 ()15013.55 3.7567.50,1,2,3010c c c +⨯=+=+ 小时，它们同时到达大桥．。

五年级数学希望杯试题第五届“希望杯”全国数学邀请赛（五年级第1试）1．2007÷＝______。

2．对不为零的⾃然数a，b，c ，规定新运算“☆”：☆（a，b ，c）= ，则☆（1，2，3）＝______。

3．判断：“⼩明同学把⼀张电影票夹在数学书的51页⾄52页之间”这句话是______的。

(填“正确”或“错误”)4．已知a，b，c是三个连续⾃然数，其中a是偶数。

则a+1，b+2，c+3的积是奇数还是偶数5．某个⾃然数除以2余1，除以3余2，除以4余1，除以5也余1，则这个数最⼩是______。

6．当p和p3＋5都是质数时，＋5＝______.7．下列四个图形是由四个简单图形A、B、C、D（线段和正⽅形）组合（记为*）⽽成。

则图中①～④中表⽰A*D的是______。

（填序号）8．下⾯四幅图形中不是轴对称图形的是______。

（填序号）9．⼩华⽤相同的若⼲个⼩正⽅形摆成⼀个⽴体（如图）。

从上⾯看这个⽴体，看到的图形是图①～③中的______。

（填序号）10．图中内部有阴影的正⽅形共有______个。

11．下图中的阴影部分BCGF是正⽅形，线段FH长18厘⽶，线段AC长24厘⽶，则长⽅形ADHE的周长是______厘⽶。

12．图中的熊猫图案的阴影部分的⾯积是______平⽅厘⽶。

(注：阴影部分均由半圆和正⽅形组成，图中⼀个⼩正⽅形的⾯积是1平⽅厘⽶，π取3.14) 13．⼩红看⼀本故事书，第⼀天看了这本书的⼀半⼜10页，第⼆天看了余下的⼀半⼜10页，第三天看了10页正好看完。

这本故事书共有______页。

14．有⼀副扑克牌中（去掉⼤、⼩王），最少取______张牌就可以保证其中3张牌的点数相同。

15．如图，摩托车⾥程表显⽰的数字表⽰摩托车已经⾏驶了24944千⽶，经过两⼩时后，⾥程表上显⽰的数字从左到右与从右到左的读数相同，若摩托车的时速不超过90千⽶，则摩托车在这两⼩时内的平均速度是______千⽶/时。

历届五年级希望杯答案及解析2010年第八届2011年第九届1、解：原式=1.25 ×31.3 ×3 ×8 = 100 ×93.9 = 9392、解：将循环节多写一次即可逐位比较3、解：十位数之前应该有1 + 2 + 3 +……+9 = 45位。

1位数有9位，10—19有20位，20—27有16位，所以十位数的开头应为28，为28293031324、解：从A到B一定会经过三步，第一步要从A走到中间，最后一步应该是从中间走到B，而第二步为从中间走到中间只能有一种走法。

从A到中间一条线上共有5种走法，从B到中间一条线上也有5种走法。

所以共有5 ×1 ×5 = 25种走法。

5、解：在3 ×4的长方形中有20个横平竖直的正方形。

斜着的有1 ×1正方形17个，2 ×2的正方形8个，还有1个3 ×3的大正方形。

共46个。

6、解：47 ÷b = c ……c ，即b ×c + c = 47，即c ×( b + 1 ) = 47，所以c一定是47的约数，c为47肯定不符合条件，所以c = 1，即除数是46，余数是1.7、解：能被90整除说明即能被9整除也能被10整除，被10整除说明最后一位是0，被9整除说明数字和应为9的倍数，即2 + 0 + 1 + 1 + a +0 是9的倍数，所以a = 5，即后两位是50.8、解：约数个数为奇数说明这个自然数为完全平方数，1000以内最大的完全平方数是31²= 9619、解：首先最下面的一个角肯定没有，最上面的中部也会少一部分，所以是丁。

10、解：一圈共400米，甲是乙速度的1.5倍，所以甲共走了240米，乙走了160米。

DE为60米，CE为40米。

SADE = 3000平方米，SBCE = 2000平方米，差为1000平方米。

11、解：弟弟如果不多跑半小时应比哥哥少跑80 ×30 — 900 = 1500米，所以哥哥共跑了1500 ÷（110—80）= 50分钟，共跑了50 ×110 = 5500米。

第七届小学“希望杯”全国数学邀请赛六年级 第1试1.计算：2.009×13＋20.09×2.9＋200.9×0.28＝ 。

2.规定：如果A 大于B ，则|A-B|＝ A-B ；如果A 等于B ，则|A-B|＝0；如果A 小于B ，则|A-B|＝B-A 。

根据上述规律计算：|4.2-1.3|+|2.3-5.6|+|3.2-3.2|＝ 。

3.图1中的扇形图分别表示小羽在寒假的前两周阅读《漫话数学》一书的页数占全书总页数的比例。

由图1可知，这本书共有 页。

4.根据图2的信息回答，剩下的糖果是原来糖果重量的 。

图25．本届“希望杯”全国数学邀请赛第1试于3月15日举行。

观察下面一列数：112123123412345121321432154321，，，，，，，，，，，，，，，…… 根据发现的规律，从左往右数，315是第 个分数。

6.将小数0.987654321改为循环小数。

如果小数点后的第20位上的数字是5，那么表示循环节的两个点应分别加在数字 和 的上面。

7.如果现在时刻是8点55分，那么，第一次到10点整时，秒针旋转了 周。

8.将一个分数的分子减少10%，分母增加50%，变化后，得到的新分数比原分数减少 %。

9.春天幼儿园中班小朋友的平均身高是115厘米，其中男孩比女孩多15，女孩的平均身高比男孩高10%，这个班男孩的平均身高是 厘米。

10.甲乙两校参加数学竞赛的人数之比是7：8，获奖人数之比是2：3，两校各有320人未获奖，那么两校参赛的学生共有 人。

11.某项目的成本包括：人力成本、差旅费、活动费、会议费、办公费、招待费以及其他营运费用，它们所占比例如图4所示，其中的活动费是10320元，则该项目的成本是元。

12.联欢会上有一则数字谜语，谜底是一个八位数。

现已猜出：□54□7□39，主持人提示：“这个无重复数字的八位数中，最小的数是2。

”要猜出这个谜语，最多还要猜次。

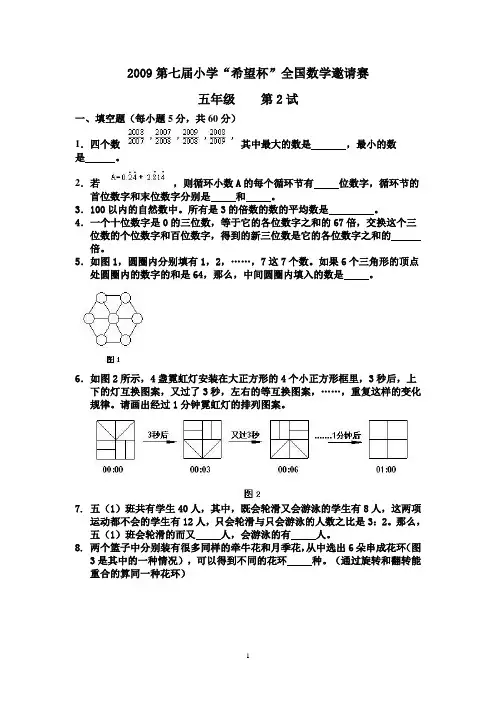
2009第七届小学“希望杯”全国数学邀请赛五年级第2试一、填空题（每小题5分，共60分）1．四个数其中最大的数是，最小的数是。

2．若，则循环小数A的每个循环节有位数字，循环节的首位数字和末位数字分别是和。

3．100以内的自然数中。

所有是3的倍数的数的平均数是。

4．一个十位数字是0的三位数，等于它的各位数字之和的67倍，交换这个三位数的个位数字和百位数字，得到的新三位数是它的各位数字之和的倍。

5．如图1，圆圈内分别填有1，2，……，7这7个数。

如果6个三角形的顶点处圆圈内的数字的和是64，那么，中间圆圈内填入的数是。

6．如图2所示，4盏霓虹灯安装在大正方形的4个小正方形框里，3秒后，上下的灯互换图案，又过了3秒，左右的等互换图案，……，重复这样的变化规律。

请画出经过1分钟霓虹灯的排列图案。

7. 五（1）班共有学生40人，其中，既会轮滑又会游泳的学生有8人，这两项运动都不会的学生有12人，只会轮滑与只会游泳的人数之比是3：2。

那么，五（1）班会轮滑的而又人，会游泳的有人。

8. 两个篮子中分别装有很多同样的牵牛花和月季花，从中选出6朵串成花环（图3是其中的一种情况），可以得到不同的花环种。

（通过旋转和翻转能重合的算同一种花环）9. 如图4，李明和王亮从同一跑道的起点同时同向出发，结果李明比王亮晚到终点0.5秒。

则跑道长米。

10.用若干个棱长为1的小正方体铁框架焊接成的几何体，从正面、侧面、上面看到的视图均如图5所示。

那么这个几何体至少是个小正方体铁框架焊接而成。

11.用{x}表示数x的小数部分，[x]表示x的整数部分。

如{2.3}=0.3，[2.3]=2。

若a+[b]=15.3，{a}+b=7.8，则a=，b=。

12.通常，汽车经销商对所销售汽车的报价中已经计入了增值税，即报价等于纯车价与增值税之和。

消费者在购买汽车后还需要缴纳购置税。

增值税和购置税都是按照纯车价来计算的。

根据以上信息完成下表。

二、解答题（每小题15分，共60分）每题都要写出推算过程。

第七届小学“希望杯”全国数学邀请赛五年级 第1试以下每题6分，共120分。

1、计算：...0.30.030.003--＝ 。

(结果写成分数形式) 2、计算：100÷1.2×3÷541615⨯＝ 。

3、如右图，从起点走到终点，要求取走每个站点上的棋子，并且每个站点只允许通过一次，有_________种不同的走法。

4、三个数：23，51，72，各除以大于1的同一个自然数，得到同一个余数。

则这个除数是___________。

5、有2克、5克、20克的砝码各1个，只用砝码和一架已经调节平衡了的天平能称出___________种不同的质量。

6××商品销售计划进价(元／件)销售方式 售价(元／件)利润率(％)利润(元／件)原价 1800 20 九折7、中心对称图形是:绕某一点旋转180°后能和原来的图形重合的图形。

轴对称图形是:沿着一条直线对折后两部分完全重合的图形。

图2的4个图形中,既是中心对称图形又是轴对称图形的有__________个。

图28、如图3,小明做减法时看错了减数.这个减数应当是___________。

图3 9、已知A ＝1+11111112345678++++++,则A 的整数部分是___________。

10、小羽和小曼分别住在一座山两侧的山脚下。

一天，小羽在上午9：00从家里出发到小曼家做客。

小羽在小曼家玩了2个半小时后回家，到家时是下午14：00。

若小羽山每小时走2里地，下山每小时走3里地，则小羽家和小曼家之间的山路长__________里。

11、今年，小军和小勇的年龄的比是3：5，两年后，两人的年龄的比是2：3。

那么，小军今年________岁，小勇________岁。

12、一只蚂蚁“侦察兵”在洞外发现了食物，他立刻回到洞穴通知同伴。

假设一只蚂蚁在1分钟内可以把消息传达给4个同伴，那么，不超过_______分钟，蚁穴里的全部2000只蚂蚁都知道了这个消息。

2011年第九届初赛1.计算：1.25×31.3×24=。

2.把0.123,0.2,0.1,0.12按照从小到大的顺序排列：<<<3.先将从1开场的自然数排成一列：1415......然后按一定的规律分组：1,23,456,7891,01112,131415，......在分组后的数中，有一个十位数,这个十位数是。

4.如图1,从A到B,有条不同的路线。

〔不能重复经过同一个点〕5.数数，图2中有个正方形。

6.—个除法算式中.被除数、除数、商与余数都是自然数，并且商与余数相等假设被除数是47.则除数是,余数是。

7.如果六位数2011□□能被90整除.则它的最后两位数是。

8.如果一个自然数的约数的个数是奇数，我们称这个自然数为“希望数〞。

则，1000以最大的“希望数〞是。

9.将等边三角形纸片按图3所示步骤折叠3次〔图3中的虚线是三边的中点的连线然后沿过两边的中点的直线减去一角〔如图4〕将剩下的纸片展开，平铺.得到的图形是。

10.如图5,甲、乙两人按箭头方向从A点问时出发，沿着正方形ABCD的边行走，正方形ABCD 的边长是100米，甲的速度是乙的速度的1.5倍，两人在E点第一次相遇，则三角形ADE 的面积比EBC三角形的面积大平方米。

11.星期天早晨，哥哥和弟弟去练习跑步。

哥哥每分钟跑110米，弟弟每分钟跑80米。

弟弟比哥哥多跑了半小时,结果比哥哥多跑了900米。

则，哥哥跑了米。

12.小明带了30元钱去买文具，买了3个笔记本和5支笔,剩余的钱，如果再买2支笔还差0.4元，如果再买2个笔记本则还差2元。

则，笔记本每个元，笔每支元。

13.数学家维纳是控制论的创始人。

在他获得哈佛大学博士学位的授予仪式上，有人看他一脸稚气的样子，好奇地询问他的年龄。

维纳的问答很有趣，他说：“我的年龄的立方是一个四位数，年龄的四次方是一个六位数，这两个数刚好把0〜9这10个数字全都用上了，不重也不漏。

小学“希望杯” 全国数学邀请赛五年级一试 试卷解析1、计算：2015201.520.152.015--＝2、9个13相乘，积的个位数字是 。

3、如果自然数a 、b 、c 除以14都余5，则a ＋b ＋c 除以14，得到的余数是 。

4、将1到25这25个数随意排成一行，然后将它们依次和1，2，3，…，25相减，并且都是大数减小数，则在这25个差中，偶数最多有 个。

5、如图l ，有3个长方形，长方形①的长为16厘米，宽为8厘米；长方形②的长、宽分别是长方形①长、宽的一半；长方形③的长、宽分别是长方形②长、宽的一半，则这个图形的周长是 厘米。

6．字母a ，b ，c ，d ，e ，f ，g 分别代表1至7中的一个数字，若a ＋b ＋c ＝c ＋d ＋e ＝e ＋f ＋g ，则c 可取的值有 个。

7、用64个体积为l 立方米的小正方体拼成一个大正方体，如果将大正方体8个顶点处的小正方体都去掉，则此时的几何体的表面积是____平方米。

8、有一个三位数，百位数字是最小的质数，十位数字是算式（0.3＋π×13）的结果中的小数点后第1位数字，个位数字是三位数中能被17整除的最小数的个位数字，则这个三位数是 。

（π取3.14）9、循环小数0.0142857 的小数部分的前2015位数字之和是10、如图2，用若干个相同的小正方体摆成一个几何体，从上面、前面、左面看分别是图形①、②、③，则至少需要 个小正方体。

11、已知a 和b 的最大公约数是4，a 与c 及b 与c 的最小公倍数都是100，而且a 小于等于b，则满足条件的有序自然数对（a，b，c）共有组。

12、从写有1、2、3、4、5的五张卡片中，任取3张组成一个三位数，其中不能被3整除的有个。

因此，不能被3整除的共有：6×6＝36（个）。

13、两位数ab和ba都是质数，则ab有个。

14、ab和cde分别表示两位数和三位数，如果ab＋cde＝1079，则a＋b＋c＋d＋e＝。

1.计算：2.009×13＋20.09×2.9＋200.9×0.28＝ 。

2.规定：如果A 大于B ，则|A-B|＝ A-B ；如果A 等于B ，则|A-B|＝0；如果A 小于B ，则|A-B|＝B-A 。

根据上述规律计算：|4.2-1.3|+|2.3-5.6|+|3.2-3.2|＝ 。

3.图1中的扇形图分别表示小羽在寒假的前两周阅读《漫话数学》一书的页数占全书总页数的比例。

由图1可知，这本书共有 页。

4.根据图2的信息回答，剩下的糖果是原来糖果重量的 。

图25．本届“希望杯”全国数学邀请赛第1试于3月15日举行。

观察下面一列数：112123123412345121321432154321，，，，，，，，，，，，，，，…… 根据发现的规律，从左往右数，315是第 个分数。

6.将小数0.987654321改为循环小数。

如果小数点后的第20位上的数字是5，那么表示循环节的两个点应分别加在数字 和 的上面。

7.如果现在时刻是8点55分，那么，第一次到10点整时，秒针旋转了 周。

8.将一个分数的分子减少10%，分母增加50%，变化后，得到的新分数比原分数减少( )%。

9.春天幼儿园中班小朋友的平均身高是115厘米，其中男孩比女孩多15，女孩的平均身高比男孩高10%，这个班男孩的平均身高是厘米。

10.甲乙两校参加数学竞赛的人数之比是7：8，获奖人数之比是2：3，两校各有320人未获奖，那么两校参赛的学生共有人。

11.某项目的成本包括：人力成本、差旅费、活动费、会议费、办公费、招待费以及其他营运费用，它们所占比例如图4所示，其中的活动费是10320元，则该项目的成本是元。

12.联欢会上有一则数字谜语，谜底是一个八位数。

现已猜出：□54□7□39，主持人提示：“这个无重复数字的八位数中，最小的数是2。

”要猜出这个谜语，最多还要猜次。

13.如图5，正方形ABCD的边长是5厘米，点E、F分别是AB和BC的中点，EC与DF交于点G，则四边形BEGF的面积等于平方厘米。

2009年第七届六年级“希望杯”培训试题1、211⨯+321⨯+431⨯+…+200720061⨯＝ 20062007 。

2、（1＋20021＋20041＋20061）×（20021＋20041＋20061＋20081）－（1＋20021＋20041＋20061＋20081）×（20021＋20041＋20061）= 12008 。

3、（220071×3.6＋353×720072006）÷43÷53= 80 。

4、从21＋41＋61＋81＋101＋121 中去掉 81 和 101 ，余下的分数之和为1.5、99…9×55…5乘积的各位数字之和是 18063 。

6、20031200412005120061 200711±±±±的整数部分是 400 。

（分母中只有加号）7、已知除法算式：÷，它的计算结果的小数点后的前三位分别是 3、9、5 。

8、一个整数与它的倒数和等于20.05，这个数是 20 ，它的倒数是 0.05 。

9、在如图1的加法算式中，每个汉字分别代表1至9中的一个数字，且相同的汉字代表相同的数字，不同的汉字代表不同的数字，那么这个加法算式的和是 。

我 爱 希 望 杯 数 学 竞 赛 ＋ 8 6 4 1 9 7 5 3 2 赛 竞 学 数 杯 望 希 爱 我 10、有一个分数，它的分子加2,可以约简为74；它的分母减2,可以约简为2514。

这个分数是 4277 。

11、四个非零自然数的和为38,这四个自然数的乘积的最小值是 35 ，最大值是 8100 。

12、已知a 是质数，b 是偶数，且a 2+b=2008,则a+b+1= 2007 。

13、当a ＝2007时，a-1,a,a+1,a+2中的合数有 4 个。

14、从1到30这30个自然数连乘各的末尾共 7 个连续的数码0.2007个9 2007个515、一个质数p ，使得p+2,p+4同时都是质数，则p1＋21±p ＋41±p = 71105 .16、三个质数的倒数之和是20061155，则这三个质数中最大的是 5917、彼此不等且大于0的偶数a,b,c,d 满足a+b+c+d=20，样的偶数组（a,b,c,d ）共有 24 组。