Toward a Method of Selecting Among Computational Models of Cognition
- 格式:pdf
- 大小:231.10 KB
- 文档页数:20

心理学专业英语复习资料I. Translate the Following English Phrases into Chinese1. Research Methods 研究方法2. Psychophysics 心理物理学3. Theories of Learning 学习理论4. Social Cognition 社会认知5.Personality Test 人格测试6. Extraneous Variable 无关变量7. Longitudinal Study 纵向研究8. Crystallized Intelligence 晶体智力9. Motor control 运动控制10. Corpus Callosum 胼胝体11. Group Thinking 群体思维12. Social Loafing 社会懈怠13. Social Exchange 社会交换14. Social Approval 社会赞许15. Diffusion of Responsibility 责任分散16. Recency Effec 近因效应17.Trace Decay 痕迹消退18. Retrograde Amnesia 倒摄遗忘19. Social Support 社会支持20. Self-efficacy 自我效能21. Case Study 个案研究II. Translate the Following Chinese Word Groups into English1. 机能主义functionalism2. 自我实现self—actualization3.一般规律研究法nomothetic method4. 分层抽样stratified sampling5. 外在信度external reliability6. 选择性注意selective attention7. 知觉恒常性perceptual constancy8. 自我概念self concept9. 液体智力fluid intelligence10. 安全型依恋secure attachment11. 性别图示gender schema12. 亲社会行为pro social behavior13. 从众实验conformity experiment14. 头脑风暴brain storming15. 社会助长social facilitation16. 旁观者效应bystander effect17. 标准差standard deviation18. 柱状图bar chart19. 正态分布normal distribution20. 临界值critical value21. 知觉适应perceptual adaptationIII. Multiple Choices1. Like Carl Rogers, I believe people choose to live more creative and meaningful lives. My name isa. Wertheimer.b. Washburn.c. Skinner.d. Maslow.2. The goals of psychology are toa. develop effective methods of psychotherapy.b. describe, predict, understand, and control behavior.c. explain the functioning of the human mind.d. compare, analyze, and control human behavior.3. The "father" of psychology and founder of the first psychological laboratory wasa. Wilhelm Wundt.b. Sigmund Freud.c. John B. Watson.d. B. F. Skinner.4. You see a psychologist and tell her that you are feeling depressed. She talks to you about the goals you have for yourself, about your image of yourself, and about the choices that you make in your life and that you could make in your life. This psychologist would probably belong to the __________ school of psychology.a. humanisticb. psychodynamicc. behavioristicd. Gestalt5. Biopsychologistsa. limit the scope of their study to animals.b. are concerned with self-actualization and free will.c. stress the unconscious aspect of behavior.d. attempt to explain behavior in terms of biological or physical mechanisms.6. In a study of effects of alcohol on driving ability, the control group should be givena. a high dosage of alcohol.b. one-half the dosage given the experimental group.c. a driving test before and after drinking alcohol.d. no alcohol at all.7.The phrase "a theory must also be falsifiable" meansa. researchers misrepresent their data.b. a theory must be defined so it can be disconfirmed.c. theories are a rich array of observations regarding behavior but with few facts to support them.d. nothing.8. A common method for selecting representative samples is to select thema. randomly from the larger population.b. strictly from volunteers.c. by threatening or coercing institutionalized populations.d. from confidential lists of mail order firms.9. The chief function of the control group in an experiment is that ita. allows mathematical relationships to be established.b. provides a point of reference against which the behavior of the experimental group can be compared.c. balances the experiment to eliminate all extraneous variables.d. is not really necessary.10. Which of the following best describes a double-blind experimental procedure?a. All subjects get the experimental procedure.b. Half the subjects get the experimental procedure, half the placebo; which they receive is known only to the experimenter.c. Half the subjects get the experimental procedure, half the placebo; which they receive is not known to subjects or experimenters.d. All subjects get the control procedure.11. A simple experiment has two groups of subjects calleda. the dependent group and the independent group.b. the extraneous group and the independent group.c. the before group and the after group.d. the control group and the experimental group.12. One of the limitations of the survey method isa. observer bias.b. that it sets up an artificial situation.c. that replies may not be accurate.d. the self-fulfilling prophecy.13. To replicate an experiment means toa. use control groups and experimental groups.b. use statistics to determine the effect of chance.c. control for the effects of extraneous variables.d. repeat the experiment using either identical or improved research methods.14. Information picked up by the body's receptor cells is termeda. cognitionb. perception.c. adaptation.d. sensation.15. The incoming flow of information from our sensory systems is referred to asa. sensation.b. perception.c. adaptation.d. cognition.16. A researcher presents two lights of varying brightness to a subject who is asked to respond "same" or "different" by comparing their intensities. The researcher is seeking thea. just noticeable difference.b. absolute threshold.c. subliminal threshold.d. minimal threshold.17. Film is to camera as __________ is to eye.a. retinab. irisc. lensd. pupil18. Black and white vision with greatest sensitivity under low levels of illumination describes the function ofa. the cones.b. the visual pigments.c. the rods.d. the phosphenes.19. Unpleasant stimuli may raise the threshold for recognition. This phenomenon is calleda. aversive stimulation.b. absolute threshold.c. perceptual defense.d. unconscious guard.20. When infants are placed in the middle of a visual cliff, they usuallya. remain still.b. move to the shallow side of the apparatus.c. move to the deep side of the apparatus.d. approach their mothers when called, whether that requires moving to the shallow or deep side.21.The fact that objects that are near each other tend to be grouped together is known asa. closure.b. continuation.c. similarity.d. nearness.22. An ability to "read" another person's mind is termeda. clairvoyance.b. telepathy.c. precognition.d. psychokinesis.23. The fact that infants will often crawl off tables or beds shows thata. depth perception is completely learned.b. human depth perception emerges at about 4 months of age.c. integration of depth perception with motor skills has not yet been accomplished.d. depth perception is completely innate.24. Sensations are organized into meaningful perceptions bya. perceptual constancies.b. localization of meaning.c. perceptual grouping (Gestalt) principles.d. sensory adaptation.25. The analysis of information starting with features and building into a complete perception is known asa. perceptual expectancy.b. top-down processing.c. bottom-up processing.d. Gregory's phenomenon.26.One recommended way for parents to handle problems of occasional bed wetting in children is toa. limit the amount of water they drink in the evening.b. punish them for "wet" nights.c. wake them up during the night to use the toilet.d. consider medication or psychotherapy.27. Teachers, peers, and adults outside the home become important in shaping attitudes toward oneself in Erikson's stage ofa. trust versus mistrust.b. initiative versus guilt.c. industry versus inferiority.d. integrity versus despair.28. With aging there is a decline of __________ intelligence, but not of __________ intelligence.a. fluid; fixedb. fixed; fluidc. fluid; crystallizedd. crystallized; fluid29. The single most important thing you might do for a dying person is toa. avoid disturbing that person by not mentioning death.b. allow that person to talk about death with you.c. tell that person about the stages of dying.d. keep your visits short and infrequent in order to avoid tiring that person.30. The five-factor model of personality includesa. social interactionism.b. neuroticism.c. agreeableness.d. sense of humor.31. An adjective checklist would most likely be used by aa. psychodynamic therapist.b. behaviorist.c. humanistic therapist.d. trait theorist.32. Jung believed that there are basic universal concepts in all people regardless of culture calleda. persona.b. collective consciousness.c. archetypes.d. mandalas.33. Behaviorists are to the external environment as humanists are toa. stress.b. personal growth.c. humankind.d. internal conflicts.34. Self-actualization refers toa. a tendency that causes human personality problems.b. what it is that makes certain men and women famous.c. anyone who is making full use of his or her potentials.d. the requirements necessary for becoming famous, academically distinguished, or rich.35. If you were asked to describe the personality of your best friend, and you said she was optimistic, reserved, and friendly, you would be using the __________ approach.a. psychodynamicb. analyticalc. humanisticd. trait36. The halo effect refers toa. the technique in which the frequency of various behaviors is recorded.b. the use of ambiguous or unstructured stimuli.c. the process of admitting experience into consciousness.d. the tendency to generalize a favorable or unfavorable first impression to unrelated details of personality.37.A truck gets stuck under a bridge. Several tow-trucks are unable to pull it out. At last a little boy walks up and asks the red-faced adults trying to free the truck why they haven't let the air out of the truck's tires. Their oversight was due toa. divergent thinking.b. cognitive style.c. synesthesia.d. fixation.38. __________ thinking goes from specific facts to general principles.a. Deductiveb. Inductivec. Divergentd. Convergent39. In most anxiety disorders, the person's distress isa. focused on a specific situation.b. related to ordinary life stresses.c. greatly out of proportion to the situation.d. based on a physical cause.40. The antisocial personalitya. avoids other people as much as possible.b. is relatively easy to treat effectively by psychotherapy.c. tends to be selfish and lacking remorse.d. usually gives a bad first impression.41. One who is quite concerned with orderliness, perfectionism, and a rigid routine might be classified as a(n) __________ personality.a. histrionicb. obsessive-compulsivec. schizoidd. avoidant42.In psychoanalysis, patients avoid talking about certain subjects. This is calleda. avoidance.b. transference.c. analysis.d. resistance.43. In psychoanalysis, an emotional attachment to the therapist that symbolically represents other important relationships is calleda. resistance.b. transference.c. identification.d. empathy.44. In aversion therapy a person __________ to associate a strong aversion with an undesirable habit.a. knowsb. learnsc. wantsd. hopes45. Behavior modification involvesa. applying non-directive techniques such as unconditional positive regard to clients.b. psychoanalytic approaches to specific behavior disturbances.c. the use of learning principles to change behavior.d. the use of insight therapy to change upsetting thoughts and beliefs.46. A cognitive therapist is concerned primarily with helping clients change theira. thinking patterns.b. behaviors.c. life-styles.d. habits.47.__________ is best known for his research on conformity.a. Aschb. Rubinc. Schachterd. Zimbardo48. Solomon Asch's classic experiment (in which subjects judged a standard line and comparison lines) was arranged to test the limits ofa. social perception.b. indoctrination.c. coercive power.d. conformity.49. Aggression is best defined asa. hostility.b. anger.c. any action carried out with the intent of harming another person.d. none of these50. Which of the following is the longest stage of grieving for most people?a. shockb. angerc. depressiond. agitation51. Which of the following is NOT part of the definition of psychology?A) scienceB) therapyC) behaviorD) mental process52.The term psychopathology refers toA) the study of psychology.B) study of psychological disorders.C) the distinction between psychologists and psychiatrists.D) the focus of counseling psychology.53. In which area of psychology would a researcher interested in how individuals persist to attain a difficult goal (like graduating from college) most likely specialize?A) motivation and emotionB) physiological psychologyC) social psychologyD) community psychology54. A psychologist who focused on the ways in which people's family background related to their current functioning would be associated with which psychological approach?A) the behavioral approachB) the psychodynamic approachC) the humanistic approachD) the cognitive approach55. The researcher most associated with functionalism isA) William James.B) Wilhelm Wundt.C) Charles Darwin.D) E. B. Titchener.56. A psychologist is attempting to understand why certain physical characteristics are rated as attractive. The psychologist explains that certain characteristics have been historically adaptive, and thus are considered attractive. This explanation is consistent with which of the following approaches?A) the sociocultural approachB) the humanistic approachC) the cognitive approachD) the evolutionary approach57. Which approach would explain depression in terms of disordered thinking?A) the humanistic approachB) the evolutionary approachC) the cognitive approachD) the sociocultural approach58. Which of the following would a sociocultural psychologist be likely to study?A) the impact of media messages on women's body imageB) the way in which neurotransmitters are implicated in the development of eating disordersC) the impact of thinking patterns on weight managementD) the benefits of exercise in preventing obesity59. Why is psychology considered a science?A) It focuses on internal mental processes.B) It classifies mental disorders.C) It focuses on observation, drawing conclusions, and prediction.D) It focuses on behavior.60. Why is it important to study positive psychology?A) Psychologists are only interested in the experiences of healthy persons.B) We get a fuller understanding of human experience by focusing on both positive and negativeaspects of life.C) Negative experiences in people's lives tell us little about people's mental processes.D) Psychology has been too focused on the negativeIV. Blank filling1.The perspective that focuses on how perception is organized is called psychology.2.A(n) is a broad explanation and prediction concerning a phenomenon of interest.3.The variable is expected to change as a result of the experimenter's manipulation.4.Bill refuses to leave his house because he knows spiders live outside. Bill is most clearlysuffering from a .5.Learned _______ may develop when a person is repeatedly exposed to negative events overwhich he/she has no control.6.Troublesome thoughts that cause a person to engage in ritualistic behaviors are called________.7.Psychologists consider deviant, maladaptive, and personally distressful behaviors to be______.8.Ken is impulsive, reckless, and shows no remorse when he hurts other people. He is often introuble with the law. Kevin is most likely to be diagnosed with _______ personality disorder.9.The researcher known as the "father of modern psychology" was Wilhelm _______.10.Asking someone to think about their conscious experience while listening to poetry wouldbe an example of _______.11.The field of psychology that is interested in workplace behavior is called Industrial and___________ psychology.12.________ is a statistic that measures the strength of the relationship between two variables.13.In a set of data, the number that occurs most often is called the ______.14.In a set of data, the average score is called the _______.15.A study that collects data from participants over a period of time is known as a(n) ______.16.The variable that a researcher manipulates is called the _______ variable.17._______statistics are used to test a hypothesis.18.A mental framework for how a person will think about something is called a ______.19.Rapid skeletal and sexual development that begins to occur around ages nine to eleven iscalled _______.20.A generalization about a group that does not take into account differences among membersof that group is called a(n) ________.21.Feeling the same way as another, or putting yourself in someone else's shoes, is called______.22.Feelings or opinions about people, objects, and ideas are called _______.23.When you saw a movie in a crowded theater you found yourself laughing out loud witheveryone else. When you saw it at home, though, you still found it funny but didn't laugh as much. This is an example of ________ contagion.24.When Carlos first sat next to Brenda in class he didn't think much of her. After sitting nextto her every day for a month he really likes her. This is best explained by the ________ effect.V.True or false (10 points, 1 point each)1 Positive psychology is not interested in the negative things that happen in people's lives.A) True2 The behavioral approach is interested in the ways that individuals from different cultures behave.A) TrueB) False3. Developmental psychologists focus solely on the development of children.A) TrueB) False4. Psychologists study behavior and mental processes.A) TrueB) False5. Meta-analysis examines many studies to draw a conclusion about an effect.A) TrueB) False6. The 50th percentile is the same as the median.A) TrueB) False7. The standard deviation is a measure of central tendency.A) TrueB) False8. Variables can only have one operational definition.A) TrueB) False9. The scores for 5 participants are 3, 2, 6, 3, and 7. The range is 4.A) TrueB) False10. In correlational research, variables are not manipulated by the researcher.A) TrueB) False11. The placebo effect refers to experimenter bias influencing the behavior of participants.A) TrueB) FalseCarol and Armando work together, go to school together, and socialize together. Carol notices that Armando is always on time to work and class and is never late when they make plans. One day, Armando is late to class. It is likely that Carol would make an external attribution about Armando's lateness.A) TrueB) False12. Violence in movies and television has no effect on people's levels of aggression.A) TrueB) False13. Rioting behavior is usually understood to occur because of groupthink.A) TrueB) False14. Small groups are more prone to social loafing than larger groups.A) TrueB) False15. Piaget believed that children were active participants in their cognitive development.A) True16 A strong ethnic identity helps to buffer the effects of discrimination on well-being.A) TrueB) False17. Older adults experience more positive emotions than younger adults.A) TrueB) False18. Harlow's research showed that infant monkeys preferred to spend time with the "mother" (wireor cloth) on which they were nursed.A) TrueB) False19. To help adolescents research their full potential, parents should be effective managers of theirchildren.A) TrueB) False20. Emerging adulthood is the period between 18 and 30 years of age.A) TrueB) False21. Health psychologists work only in mental health domains.A) TrueB) FalseVI. Essays questions (20 points, 10 points each)1. What is qualitative research interview?2. What is bystander effect? When is it most likely to occur? How can its effects be minimized?3. How important is fathering to children?。
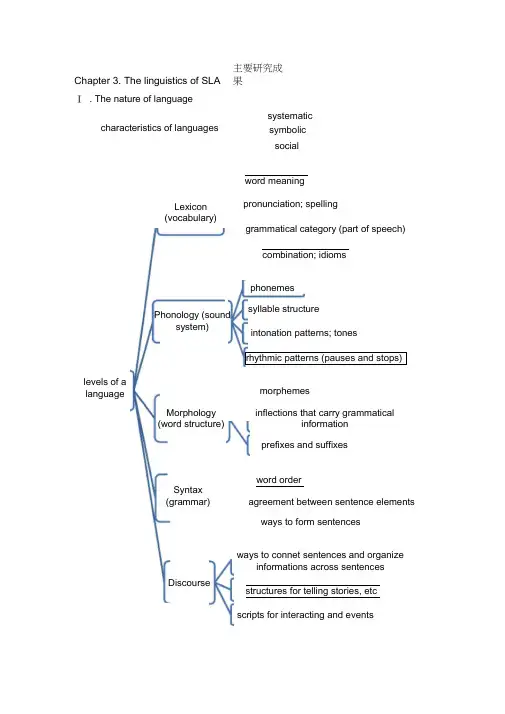
Chapter 3. The linguistics of SLA Ⅰ . The nature of languagecharacteristics of languages主要研究成果 systematic socialword meaningpronunciation; spellingMorphology (word structure)Lexicon(vocabulary)Phonology (soundsystem)levels of a languageSyntax (grammar)grammatical category (part of speech)combination; idioms phonemesintonation patterns; tonessyllable structurerhythmic patterns (pauses and stops)morphemesprefixes and suffixesinflections that carry grammaticalinformation word orderagreement between sentence elements ways to form sentencesDiscourseways to connet sentences and organizeinformations across sentencesstructures for telling stories, etc scripts for interacting and eventssymbolicⅡ . Early approaches to SLA1. Contrastive Analysis (CA)1) . as a beginning of the survey:aspects of its procedures are still incorporated in more recent approaches. It introduced the influence of L1 on L2 (Chomsky)2) . CA: an approach to the study of SLA which involves predicting andexplaining learner problems based on a comparison of L1 and L2 to determine similarities and differences.(Based on idealized linguistic structures attributed to native speakers of L1 and L2)3) . influenced by Structuralism and Behaviorism.4) . Goal of CA was primarily pedagogical in nature: to increase efficiency in L2teaching and testing.structuralist linguisticsthe surface forms of L1 and L2 systems phonology → morphology → syntax → lexion → bottom- updiscourseCAassumptionsbehaviorist psychologyLA essentially invoves habit formationstimulus- response- reinofrcement Llinguistic inputrespond habituate... transfer(S-R-R)practice makesperfect5). Process:Describing L1 and L2 at different levelAnalyzing comparable segment of the language for elements that may cause6). Assessment:Cannot explain the logical problem of language learning (how learners know more than they ' ve heard and been taught) Not always validated byevidence from actual learner errors.Stimulated the preparation of comparative grammarIts analytic procedures have been usefully applied to descriptive studies and to translation2. Error analysis (EA)1) . EA: the first approach to the study of SLA which includes aninternal focus on learner 's creative ability to construct language. (based on the description and analysis of actual learner errors inL2)2) . CA → EAPredictions by CA not always correct; many real learner errors are nottransferred from L1Focus on surface-level forms and patterns → underlying rulesBehaviorism →mentalism (emphasis on the innate capacity) Teachingconcerns as motivation ↓3) . Procedures for analyzing learner errors:Collection of a sample of learner languageIdentification of errorsDescription of errorsExplanation of errorsEvaluation of errors4) . ShortcomingsAmbiguity in classificationLack of positive dataPotential for avoidance3. Interlanguage (IL)1) . IL refers to the intermediate states (interim grammars) of a learner ' slanguage as it moves toward the target L2.2) . Characteristics:SystematicDynamicVariableReduced system, both in form and function3) . Differences between SLA and L1 acquisition by childrenLanguage transfer from L1 to L2Transfer of training, or how the L2 is taughtStrategies of 2 nd language learningOvergeneralization of the target language linguistic materials4) . L1 as fossilization for L2 learners:Fossilization: the probability that they 'll cease their IL development in somerespects before they reach target language norms, in spite of continuing L2input and passage time.Relates to: the age of learning; social identity; communicative need.4. Morpheme order studies1) . Refers to :an important Q in the study of SLA, whether there is a naturalorder (or universal sequence) in the grammatical development of L2 learners.2) . Inflection: it adds one or more units of meaning to the base form of a word, togive it a more specific meaning. (plural nouns, past tense etc.)3) . The order of morpheme acquisition reported was similar in L1 and L2It supports an Identity Hypothesis (L1=L2): that processes involved in L1 and L2 acquisition are the same.4) . The concept of natural order remains very important for understanding SLA.(both from linguistic and cognitive approaches)5. Monitor model1) . One of the last of the early approaches which has an internal focus in theMonitor Model.(Stephen Krashen)2) . It explicitly and essentially adopts the notion of a language acquisition device(LAD) (Chomsky used for children 's innate knowledge of language)3) . Krashen 's approach: 5 hypotheses6. Consensus:1) . What is being acquired in SLA is a“rule0governed ” languagesystems2) . How SLA take place involves creative mental processes.3) . Why some learners are more (less) successful in SLA than others relatesprimarily to the age of the learner.Ⅲ . Universal Grammar (UG)1. UG (Chomsky): what all languages have in common.1) . Two important concepts linguistic competence (speaker-hearers 'underlying knowledge of language) needs to be accounted for LA such knowledge of language > what could be learned from the input. (the logic problem of language learning/ the poverty-of-the stimulus argument)2) . The nature of speaker-hearers ' competence in native language can be explained only by innate knowledge that human genetically endowed with. 3) . The innate knowledge is in the language facultyLanguage faculty: a component of the human mind, physically represented in the brain and part of the biological endowment of the species.2. Principles and Parameters1) . With Chomsky ' s reconceptualization of UG in the Principles andParameters framework [often called the Government and Binding (GB)subconsciousinnate language acquisition deviceconsciousexemplified by theL2 learningwhat is "learned" is availableonly as a monitor acquire the rules of languagein a predictable order inputcomprehensiviblehypothesisinputenough understandableinput may not be processed if theaffective filter is "up"natral order hypothesisaffective filter hypothesismonitor hypothesis 5hypothesisacquisitionacquisition-learning hypothesislearningmodel] and the subsequent introduction of the Minimalist program, there came a new idea about the acquisition process.2) . UG has been conceptualized as a set of principles which are properties of all languages in the world.Some of these principles contain parameters3) . What is acquired in L1 acquisition (not UG itself):LA includes a process of selecting among the limited parametric options in UG that match the settings which are encountered in linguistic input. 4) . How acquisition occurs for children: natural; instinctive; internal to the cognitive system5) . Why some learners are more successful:Irrelevant with L1 acquisition, for all native speakers attain essentially the same final state. (For SLA, attitudes; motivation and social context matters)Ⅳ . Functional approaches1. Functional approach1) . Based on: the framework of Functionalism2) . Characteristics of functional approaches to SLAstructural such as which element is the object or subject functionsuch as convey information or express emotioFocus on the use of language in real situations (performance) and underlying knowledge (competence)Assumption: purpose of language is communication; LA and SLA requirecommunicative useConcern about the sentence, discourse structure, how language is used ininteraction; include aspects of communication beyond language2. Systemic linguistics (M.A.K.Halliday)1) . Systemic linguistics is a model for analyzing language in terms of theinterrelated systems of choices that are available forexpressing meaning.“ language acquisition needs to be seen as the mastery of linguisticfunctions ”2) . What language learners acquire: meaning potential3) . Process of acquisition:mastering certain basic functions of language developing a meaning potential for each4) . pragmatic functions development in L1 acquisition: instrumental →regulatory → interactional → personal → heuristic → imagination →representational5) . linguistic structures: directly reflections of the functions that language serves;related to the social and personal needs3. Functional Typology1) . Based on: the comparative study of a wide range of the world 's language2) . Goal: to describe patterns of similarities and differences among languages;to determine which types and patterns occur more/less frequently or areuniversal in distribution.3) . Application: why some L2 constructions are more/less difficult than others forL2 learners to acquire; for the selectivety of crosslinguistic influence or transfer4) . important concept: markedness (deals with whether any specific feature oflanguage is marked or unmarked)5) . Markedness differential prediction for SLAIn SLA, unmarked elements are easier to master than marked ones.6) . Compared with CA:Functional typology goes beyond the surface-level structural (CA)to more abstract patterns, principles and constraints; the Markedness Differential Hypothesis 7) . implications:some aspects of some languages are more difficultwhy some types and patterns of features are more/less frequent in native and 2 nd language (factors: perceptual salience, ease of cognitive processing, physical constraints, communicative needs)4. Function-to-form mapping1) . Basic concept: L1 and L2 acquisition involves a process of grammaticalization. 2) . Grammaticalization: a grammatical function is first conveyed byshared extralinguistic knowledge and inferencing based on the context of discourse, then by a lexical word, and only later by a grammatical marker. Driven by: communicative need and use.Related to : the development of more efficient cognitive process3) . Pragmatic mode: a style of expressing meaning which relies more on context.Syntactic mode: a style which relies more on formal grammatical elementtopic- comment → subject -predict structure loose conjunction → tight subordinationslow rate of delivery → fast rate of delivery word order governed by pragmatic principle of old information then new information → word order used to signal semantic case functionsroughly one-to-one ratio of verbs → nouns in discourse toa larger ratio of nouns over verbs4) . According to function-to-mapping approach, LAimportantly involves developing linguistic forms to fulfill semantic or pragmatic functions.5. Information organization1). Focus on: utterance structure (the way learners put their words together.)2). Includes:describing the structures of interlanguage (learner varieties)discovering what organizational principles guide learners ' production atIn all languages: to express functions (such as time)reliance on grammatical forms ↑ liance on context and lexical words ↓no use of grammatical morphology↓elavorate useofgrammatical morphologyvarious stages of developmentanalyzing how these principles interact with one another.3) . European Science Foundation (ESF) projectdevelopmental levels: in this study, no matter what their L1 andL2, the learners go through a remarkably similar sequence of development in their interlanguage.organizing principles:* there is a limited set of principles (phrasal constraints; semanticconstraints; pragmatic constraints) which learners make use of fororganizing information.* Individual variation: how the principles apply in their L1 and influence the interlanguage use.。

Transportation Systems交通运输系统Transportation system in a developed nation consists of a network of modes that have evolved over many years. The system consists of vehicles,guideways,terminal facilities, and control systems; these operate according to established procedures and schedules in the air, on land and on water. The system also requires interaction with the user, the operator,and the environment. The system that are in place reflect the multitude of decisions made by shippers,earners, government, individual travelers, and affected nonusers concerning the investment in or the use of transportation. The transportation system that has evolved has produced a variety of modes that complement each other.在发达国家,经过多年发展交通运输系统已经形成了一个网络模式。
这一体系由车辆、导轨、码头设施和控制系统构成并根据已建立的程序和时间表在水陆空进行运作。
该系统还需要用户、操作员和环境的之间的相互作用。

U1 AToward a brighter future for all奔向更加光明的未来Good afternoon! As president of the university, I am proud to welcome you to this university. Your achievement is the triumph of years of hard work, both of your own and of your parents and teachers. Here at the university, we pledge to make your educational experience as rewarding as possible.下午好!作为校长,我非常自豪地欢迎你们来到这所大学。
你们所取得的成就是你们自己多年努力的结果,也是你们的父母和老师们多年努力的结果。
在这所大学里,我们承诺将使你们学有所成。
In welcoming you to the university, I am reminded of my own high school graduation and the photograph my mom took of my dad and me. "Pose naturally." Mom instructed us. "Wait!" said Dad, "Let's take a picture of me handing him an alarm clock." The clock woke me up every morning in college. It is still on my office desk.在欢迎你们到来的这一刻,我想起自己高中毕业时的情景,还有妈妈为我和爸爸拍的合影。

Unit 1 Section Ⅰ一、语言基础训练Ⅰ.单句语法填空1.(2020·新高考全国Ⅰ卷)And in Karakalpakstan, he is saddened by the dust storms, diseases and fishing boats __stuck__(stick) miles from the sea.2.Some people have drawn the __conclusion__ (conclude) from Bowlby’s work that children should not be sent to day care before the age of three.3.(2018·全国Ⅰ卷)The living-room television is replaced and gets __planted__ (plant) in the kids’ room.4.__Apparently__ (apparent), he was not satisfied with the result.5.He refused to acknowledge __being defeated__ (defeat) in the match, but in vain.6.__It__ is acknowledged that the shortest distance between persons is a sincere smile.7.The results of the survey fell into __distinct__ groups. The old were scholars of great __distinction__ while the young were the opposite. (distinct) 8.That is why it is vital that we __(should) observe__ (observe) the traffic lights.9.It is said that the building program __has been evaluated__ (evaluate) for its usefulness and effect it would have.10.(2021·1月浙江卷)In 1985, urban men and women in more than three quarters of the countries __studied__(study) had higher BMIs than men and women in rural areas.Ⅱ.完成句子1.__The expert insisted that he (should) analyse the extract in public__.那位专家坚持要当众分析那些提取物。

U1 AToward a brighter future for all奔向更加光明的未来Good afternoon! As president of the university, I am proud to welcome you to this university. Your achievement is the triumph of years of hard work, both of your own and of your parents and teachers. Here at the university, we pledge to make your educational experience as rewarding as possible.下午好!作为校长,我非常自豪地欢迎你们来到这所大学。
你们所取得的成就是你们自己多年努力的结果,也是你们的父母和老师们多年努力的结果。
在这所大学里,我们承诺将使你们学有所成。
In welcoming you to the university, I am reminded of my own high school graduation and the photograph my mom took of my dad and me. "Pose naturally." Mom instructed us. "Wait!" said Dad, "Let's take a picture of me handing him an alarm clock." The clock woke me up every morning in college. It is still on my office desk.在欢迎你们到来的这一刻,我想起自己高中毕业时的情景,还有妈妈为我和爸爸拍的合影。

Marketing StrategyMarket Segmentation and Target StrategyA market consists of people or organizations with wants,money to spend,and the willingness to spend it.However,within most markets the buyer’ needs are not identical。
Therefore,a single marketing program starts with identifying the differences that exist within a market,a process called market segmentation, and deciding which segments will be pursued ads target markets.Marketing segmentation enables a company to make more efficient use of its marketing resources.Also,it allows a small company to compete effectively by concentrating on one or two segments.The apparent drawback of market segmentation is that it will result in higher production and marketing costs than a one-product,mass—market strategy。
However, if the market is correctly segmented,the better fit with customers' needs will actually result in greater efficiency。

教育硕士开题报告英文IntroductionEducation plays a crucial role in shaping the future of individuals, societies, and nations. As a result, the pursuit of advanced degrees in education, such as a Master's in Education, has become increasingly popular. This report aims to provide a comprehensive overview of the proposed research study for the Education Master's thesis.BackgroundTraditional teaching methods often fail to capture the attention and engage students effectively in the learning process. With the advancement of technology, schools have seen a shift towards integrating digital tools and resources into the classroom environment. This digital transformation has brought forth several benefits, including improved student engagement and enhanced learning outcomes. However, it is essential to evaluate the impact and effectiveness of these digital tools on education comprehensively.Research ProblemThe primary focus of this study is to investigate the impact of integrating digital tools, specifically interactive multimedia, in primary classrooms. The goal is to assess the effectiveness of these tools in enhancing student engagement, developing critical thinking skills, and improving academic performance. It is essential to understand the challenges and opportunities associatedwith implementing these digital tools to inform pedagogical practices and ensure successful integration into the classroom. Research Questions1. What is the impact of interactive multimedia tools on student engagement in primary classrooms?2. How do interactive multimedia tools contribute to the development of critical thinking skills in primary students?3. Do interactive multimedia tools improve academic performance in primary students?4. What challenges and opportunities arise from the implementation of interactive multimedia tools in primary classrooms?Research Objectives1. To evaluate the impact of interactive multimedia tools on student engagement in primary classrooms.2. To assess the contribution of interactive multimedia tools to the development of critical thinking skills.3. To examine the correlation between the use of interactive multimedia tools and academic performance in primary students.4. To identify the challenges and opportunities associated with implementing interactive multimedia tools in primary classrooms. Research MethodologyTo accomplish the research objectives, a mixed-methods approach will be employed. The study will involve both quantitative andqualitative data collection and analysis. Questionnaires will be administered to primary school teachers and students to measure student engagement, critical thinking skills, and academic performance. Additionally, interviews and focus groups will be conducted to gather qualitative data on the challenges and opportunities regarding the implementation of interactive multimedia tools in classrooms.Expected OutcomesBased on the analysis of the collected data, this study aims to provide insights into the effectiveness of integrating interactive multimedia tools in primary classrooms. It is anticipated that the research will demonstrate a positive impact on student engagement, critical thinking skills, and academic performance. Additionally, the study will identify potential challenges and opportunities to aid educators in effectively implementing these tools in their teaching practices.ConclusionWith the increasing prevalence of technology in education, it is crucial to evaluate the impact of digital tools, such as interactive multimedia, on primary students' educational experiences. Through this research, we hope to contribute to the knowledge base surrounding the integration of digital tools in classrooms and inform educators about the potential benefits and challenges associated with their implementation.。

对外经济贸易大学《跨文化交际(英)》期末考试I. True-False: Decide whether each of the following statements is true orfalse. Write T for “true” and F for “false”. (每题 1 分,共 20 分)1. The term “intercultural communication” was first used by Geert Hofstede in1959.2. Hall defines culture as the "software of the mind" that guides us in ourdaily interactions.3. In most of Africa, Argentina and Peru, putting one’s index finger to his templemeans ‘You are crazy.’4. Stereotyping is a complex form of categorization that mentally organizesyour experiences and guides your behavior toward a particular group of people.5. Values are social principles, goals, or standards accepted by persons in a culture.They are the innermost “skin of the onion.”6. People from some cultures may lower their gaze to convey respect, whereasthis may be understood as evading or even insulting in other cultures.7. Unbuttoning one’s coat is a sign of openness, friendliness or willingness to reachan agreement.8. In order for intercultural negotiation to be successful, the parties must providefor a win-lose situation.9. Edward Hall’s theory states that the four levels embody the total conceptof culture like an onion – symbols, heroes, rituals, and values.10. Successful intercultural business communication involves knowing theethnocentrisms of persons in other cultures. Understanding the mindsets of both oneself and the person of another culture will result in more efficient communication.11. Ethnocentrism is the belief that somebody else’s cultural background, includingways of analyzing problems, values, beliefs, language, and verbal and nonverbalcommunication, is better than our own.12. People in the United States place a greater emphasis on history and do notlike change as compared with people of Asian and Latin cultures.13. When dealing with German business people, you should avoid jokes andother forms of humor during the actual business sessions.14. In the business circle, American business people use first names immediately.15. Companies should avoid sending female employees to the Middle East, as inArab countries men may refuse to work with women.16. In Southeast Asia, you should avoid presenting your business card with your righthand.17. When accepting a business card, German business people carefully look at thecard, observe the title and organization, acknowledge with a nod that theyhave digested the information, and perhaps make a relevant comment or aska polite question.18. The OK sign may be interpreted as asking for money by Japanese businesspeople.19. Nonverbal communication is important to the study of interculturalcommunication because a great deal of nonverbal behavior speaks auniversal language.20. In short, intercultural communication competence requires sufficientawareness knowledge, motivations, and skills. Each of these components alone is sufficient to achieve intercultural communication competence.II. Translation: Translate the following Chinese terms into English and English terms into Chinese.(每题 1 分,共 20 分)1. stereotypes2. paralanguage3. ethnocentrism4. masculinity5. high-context culture6. monochronic time7. speech act 8. conversation taboos9. vocal qualifiers 10. power distance11. 译码12.偏见13. 文化震惊14.不确定性回避15. 概念意义16.语用错误17. 礼貌原则18.归纳法19. 空间语言20.礼仪与礼节III. Multiple Choice: Choose the ONE appropriate answer. (每题 1 分,共20 分)1. Understanding another culture .a. enables businesspeople to know why foreign associates believe andact as they dob. is best achieved through “do’s and don’ts” listsc. is important for businesspeople because they can appear to bebetter informedd. isn’t necessary for businesspeople2. Non-linear languages .a. are object orientedb. see time as a continuum of present, past andfuture c. are circular, tradition oriented andsubjectived. lead to short-range planning in business practices3. Which statement about values is incorrecta. Values are social principles, goals, or standards accepted by persons ina culture.b. Values are learned by contacts with family members, teachers,and religious leaders.c. Values will be influenced by what is seen on television or read innewspapers.d. People in various cultures have basically similar values.4. People from cultures that follow the monochronic time system tendto a. do one thing at a time.b. be committed to people.c. borrow and lend things often.d. build lifetime relationships.5. Which statement regarding haptics is incorrecta. In Thailand, it is offensive to touch the head.b. Japan is considered a "don't touch" culture.c. Greece is considered a "touch" culture.d. In Latin American countries, touching between men is unacceptable.6. The opinion that everyone has a position and clearly defined privileges is .a. a view of hierarchical structure of social relationshipb. a view of group orientation structure of social relationshipc. a view of individual orientation structure of social relationshipd. none of the above7. General guidelines to follow when conversing with someone fromanother culture include all of the following except:a. politics is a safe topic in most cultures.b. avoid telling jokes.c. avoid personal questions.d. keep the conversation positive.8. Which statement best describes an incorrect handshakea. In the ., a handshake should be firm.b.An Asian handshake is usually gentle.c. Germans repeat a brusque handshake upon arrival anddeparture. d. A British handshake is firm and repeated frequently.9. Which statement referring to thought patterns is incorrecta. Asians typically use the inductive method of reasoning.b. Thought patterns impact oral communication.c. When using the deductive method of reasoning, one starts with thefacts and goes to generalizations.d. Recognizing different thought patterns is important in negotiation withdifferent cultures.10. Which statement is incorrecta. Costly business blunders are often the result of a lack of knowledgeof another culture's nonverbal communication patterns.b. Processes of reasoning and problem solving are the same in all cultures.c. Attitudes toward time and use of space convey nonverbal messagesin intercultural encounters.d. When in another culture, an appropriate caution would be to watchthe behavior of the persons you are talking with and match their style.11. Language is important because ita. helps us shape concepts, controls how we think, and controls howwe perceive others.b. allows us to be understood by foreigners.c. is determined by colonialism.d. is stable, easily understood, and free of diversity.12. Which of the following countries uses high-context languagea. Canadab. Germanyc. Japand. United States13. Slang is generallya. understood by everyone.b. spoken by the masses.c. easily translated.d. used by subgroups.14. Nonverbal communication does not includea. chromatics.b. chronemics.c. haptics.d. semantics.15. Dominance, harmony, and subjugation are all value orientations that correspond to which of the following cultural problemsa. What is the nature of human beingsb. What is the relationship of humans to naturec. What is the orientation of humans to timed. What is the human orientation to activity16. Proverbs are significant to the study of intercultural communicationbecause .a. they provide a compact description of a culture’s valuesb. they tell a great deal about what a culture praises and what itrejects c. they unite a people with the wisdom of their ancestorsd. all of the above17. Which statement highlights weak uncertainty avoidancea. One group's truth should not be imposed onothers. b. Scientific opponents cannot be personalfriends.c. Citizen protest should be repressed.d. Negative attitudes are expressed toward young people.18. The main idea of the Sapir-Whorf Hypothesis is thata. language is just a device for reporting a person's experience.b. two languages can represent the same social reality.c. the social reality can be conveyed to a person who does not speakthe language.d. language functions as a way of shaping a person's experience.19. Many multinational firms find that cultural shock can be alleviated bya. sending only top executives abroad.b. sending only young, single associates on overseas assignments.c. testing associates to see who is most qualified.d. selecting employees for overseas assignments who possesscertain personal and professional qualifications.20. Which of the following statement is incorrecta. Knowing cultural variations in the use of silence is helpful whenconversing with persons in another culture.b. We need to keep things in perspective and not get offended each timewe deal with someone who has a different attitude toward touchingc. Good advice when communicating with persons in other cultures isto keep gestures to a minimumd. Although oral communication varies from culture to culture, non-verbal communication is almost always interpreted the same in eachculture.IV. Answer the following essay question. (共 20 分)Compare and contrast the following proverbs from two different cultures: “It is the duck that squawks that gets shot” and “The squeaky wheel gets the grease.”How do people from these cultures perceive silence and talk In light of their different perceptions, how might they view each other What problems might arise in their interactionsV. Case Analysis: Analyze the following conversation from an intercultural perspective. (共 20 分)The following conversation took place between two Chinese friends.A: We’re going to New Orleans this weekend.B: What fun! I wish we were going with you. How long are you going to be thereA: Three days.B: Do you need a ride to the airport I’ll take you.A: Are you sure it’s not too much troubleB: No, no. It’s no trouble at all.Case Analysis: Analyze the following conversation f rom an intercultural perspective.参考答案及评分标准A 卷VI. True-False: Decide whether each of the following statements is true or false. Write T for “true” a nd F for “false”. (每题 1 分,共 20 分)1. F2. F3. F4. T5. T6. T7. T8. F9. F 10. T11. F 12. F 13. T 15. T 16. F 17. F 18. T 19. T 20. FVII.Translation: Translate the following Chinese terms into English and English terms into Chinese.(每题 1 分,共20 分)1. stereotypes 定势/刻板印象2. paralanguage 辅助语言/副语言3. ethnocentrism 民族中心主义4. masculinity 男性特征5. high-context culture 高语境文化6. m onochronic t ime 单一时间观念7. speech act 言语行为8. conversation taboos 对话禁忌9. vocal qualifiers 声音修饰10. power distance 权力距离11. 译码 decoding 12. 偏见prejudice13. 文化震惊 cultural shock 14. 不确定性回避uncertaintyavoidance15. 概念意义 denotational meaning 16. 语用错误 pragmatic f ailure17. 礼貌原则 the Politeness Principle 18. 归纳法inductivepattern19. 空间语言 spatial language/proximics 20. 礼仪与礼节etiquette andprotocolVIII. Multiple Choice: Choose the ONE appropriate answer. (每题 1 分,共 20 分)1. a2. a3. d4. a5. d6. a7. a8. d9. c 10. b11. a 12. c 13. d 14. d 15. b 16. d 17. a 18. d 19. d 20. d IX. Answer the following essay question. (共 20 分)测试重点: Compare and contrast the proverbs “It is the duck that squawks that gets shot”and “The squeaky wheel gets the grease.”The former is an English proverbwhile the latter is a Chinese proverb. In light of their different perceptions, the two cultures might differ in terms of silence and talk etc. and problems might arise in their interactions.评分标准:从以上角度进行分析,其他根据具体答题情况酌情。

Unit 1, Book OneSection A: Toward a brighter future for all1. Teaching Objectives:To know the meaning and usage of some important words, phrases and patternsTo study Passage A and understand the main idea of the textTo understand the structure of the text and the devices for developing itTo talk about college education2.Time Allotment:Section A (3 periods):1st---2nd period: Pre-reading activities ( theme-related questions for warming up;)While-reading activities (cultural notes; useful words and expressions;difficult sentences)3rd period: While-reading activities (text structure; main ideas)Post-reading activities (comprehension questions; exercises)Section B(1period):4th periods: Practice of the reading skill (reading for the key idea in a sentence);T checks on Ss’ home reading by asking questions based on the passage.T explains some difficult sentences3.Teaching Procedures:Pre-reading ActivitiesStep 1. GreetingsGreet the whole class warmly.Step 2. Lead-in and preparation for readingLet them talk to each other about the following questions:1. What is the ideal university like in your eyes?2. What are your expectations of your college life?3. What advice did your parents give you before you left for college?Step 3. Fast readingAsk the Students to read the passage as quickly as they can and then answer the questions on the screen. Let them get the main idea of each paragraph and make clear about the text structure.Text structure: ( structured writing ) The passage can be divided into 3 parts.Part1 (para.1-3) Opening part of the welcome speechPart 2 (para.4-7) Making the best of what you have.Challenging yourself.Facing new experiences.Opportunities and responsibilities.Part 3 (Para.8) Concluding remarks of the welcome speech.Purpose: Improve the students’ reading and writing ability and understand the general idea of each paragraph.Method:Read the text individually and talk in groups; Use task-based language teaching method, reading approach, communicative approach and total physical response method.Step 4. Preparation for details of the text on the screenStudents are required to look at the Words and Phrases on the screen and give a brief presentation in class.Words and Phrases:Purpose: Train the Students’ ability of understandi ng and using foreign language.Method:Talk in groups, Use task-based language teaching method, communicative approach and total physical response method.1. (Para.1)pledge to do sth. 作保证,承诺China and the United states pledge to boost cooperation and exchange to ensure a better future for China-US ties.中美政府承诺将加强合作与交流以确保两国关系的未来更加美好。
Unit4TextA|工作、劳动和嬉戏Work,Labor,andPlay威斯坦·H·奥登PrefaceWegotoworkeverydayandwethinkweareworkers.However,afterreadingAuden'sdiscussionabout work,labor,andplay,themajorityofusmayfindthatwearenolonger"workers".Whatarewethen?就我所知,汉娜·阿伦特小姐是界定工作和劳动之间实质区其余第一人。
一个人要想快乐,第一要有自由感,第二要确信自己有价值。
假如社会迫使一个人去做他自己不喜爱的事,或许说,他所喜爱做的事被社会忽略,看作没有价值或不重要,那他就不会真实快乐。
在一个严格意义上已取销奴隶制的社会里,一个人做的事情能否拥有社会价值取决于他能否为达成此项工作获取了酬劳。
但是,今日的劳动者能够被称为货真价实的薪资奴隶。
假如社会给一个人供给一份他自己不感兴趣的工作,他出于养家生活的需要不得已才从事这项工作,那这个人就是一个劳动者。
SofarasIknow,MissHannahArendtwasthefirstpersontodefinetheessentialdifferencebetweenworkand labor.Tobehappy,amanmustfeel,firstly,freeand,secondly,important.Hecannotbereallyhappyifhei scompelledbysocietytodowhathedoesnotenjoydoing,orifwhatheenjoysdoingisignoredbysocietyasof novalueorimportance.Inasocietywhereslaveryinthestrictsensehasbeenabolished,whetherwhataman doeshassocialvaluedependsonwhetherheispaidmoneytodoit,butalaborertodaycanrightlybecalledaw ageslave.Amanisalaborerifthejobsocietyoffershimisofnointeresttohimselfbutheiscompelledtota keitbythenecessityofearningalivingandsupportinghisfamily.与劳动相对的是嬉戏。
Guest Editors’Introduction:Special Section on Learning Deep ArchitecturesSamy Bengio,Li Deng,Hugo Larochelle,Honglak Lee,and Ruslan SalakhutdinovÇT HE past seven years have seen a resurgence of research in the design of deep architecture models and learning algorithms,i.e.,methods that rely on the extraction of a multilayer representation of the data.Often referred to as deep learning,this topic of research has been building on and contributing to many different research topics,such as neural networks,graphical models,feature learning,un-supervised learning,optimization,pattern recognition,and signal processing.Deep learning is also motivated and inspired by neuroscience and has had a tremendous impact on various applications such as computer vision,speech recognition,and natural language processing.The clearly multidisciplinary nature of deep learning led to a call for papers for a special issue dedicated to learning deep architectures,which would provide a forum for the latest advances on the subject.Associate Editor in Chief(AEIC) Max Welling took the initiative for the special issue in an earlier attempt to collaborate with Editor In Chief of the IEEE Signal Processing Magazine(Li Deng)for a joint special issue.We were five guest editors to oversee the task of selecting among the submissions the eight papers that were included in this special section.We were assisted by a great team of dedicated reviewers.Former Editor in Chief (EIC)Ramin Zabih and current EIC David Forsyth have greatly assisted in the process of realizing this special section.We all thank them for their crucial role in making this special section a success.The guest editors were not allowed to submit their own papers to this special section.However,it was decided that our paper submissions on deep learning would be handled by AEIC Max Welling(who was not a guest editor)and go through the regular TPAMI review process.The last two papers in the list below resulted from this special arrangement.The first three papers in this special section present insightful overviews of general topics related to deep learning:representation learning,transformation learning, and the primate visual cortex.The first paper in our special section,“Representation Learning:A Review and New Perspectives,”written by Yoshua Bengio,Aaron Courville,and Pascal Vincent, reviews the recent work in deep learning,framing it in terms of representation learning.The paper argues that shallow representations can often entangle and hide the different underlying factors of variability behind the observed surface data,and deep learning has the capacity to disentangle such factors using powerful distributed representations,which are combinatorial in nature.The paper also provides interesting connections among deep learning,manifold learning,and learning based on density estimation.A short overview of recent work on learning to relate(a pair of)images is also presented in“Learning to Relate Images”by Roland Memisevic.The focus of the work is to learn local relational latent features via multiplicative interactions(using three factors that correspond to latent features and a pair of images).Specifically,the paper proposes a gated3-way sparse coding model to learn a dictionary of transformations between two or more image patches,and it provides insightful connections to other related methods,such as mapping units,motion energy models,and squared pooling.This work further provides an interesting geometric interpretation of learned transfor-mation dictionary,which represents a set of2D subspace rotations in eigenspace.The paper demonstrates that interesting filters(related to transformations such as translation and rotation)can be learned from pairs of transformed images.We look forward to exciting real-world applications of relational feature learning in the near future.The primate visual cortex,which has always been part of the inspiration behind deep learning research,is the subject of the next paper in this special section.The paper“Deep Hierarchies in the Primate Visual Cortex:What Can We Learn For Computer Vision?”by Norbert Kruger,Peter Janssen,Sinan Kalkan,Markus Lappe,Ales Leonardis, Justus Piater,Antonio J.Rodriguez-Sanchez,and Laurenz Wiskott is a great overview of known facts from the primate visual cortex that could help researchers in computer vision interested in deep learning approaches to their field.It shows how the primate visual system is organized in a deep hierarchy,in contrast to the flatter classical computer vision approach,with the hope that more interaction between biological and computer vision researchers may lead to better designs of actual computer vision systems..S.Bengio is with Google Research,1600Amphitheatre Parkway,MountainView,CA94043.E-mail:bengio@..L.Deng is with Microsoft Research,One Microsoft Way,Redmond,WA98052.E-mail:deng@.rochelle is with the De´partement d’Informatique,Universite´deSherbrooke,2500boul.de l’Universite´,Sherbrooke,QC,J1K2R1,Canada.E-mail:rochelle@usherbrooke.ca..H.Lee is with the Department of Electrical Engineering and ComputerScience,University of Michigan,2260Hayward St.,Ann Arbor,MI48109.E-mail:honglak@..R.Salakhutdinov is wth the Departments of Computer Science andStatistics,University of Toronto,6King’s College Rd.,Toronto,ON,M5S3G4,Canada.E-mail:rsalakhu@.For information on obtaining reprints of this article,please send e-mail to:tpami@.0162-8828/13/$31.00ß2013IEEE Published by the IEEE Computer SocietyThe next three papers in this section then move on to presenting novel deep architectures,designed in the context of image classification and object recognition.The paper“Invariant Scattering Convolution Networks”by Joan Bruna and Ste´phane Mallat describes a new deep convolutional architecture,which can extract a representa-tion that is shown to be locally invariant to translations and stable to deformations.It can also preserve high-frequency information within the input image,which is important in a classification setting.Unlike for deep convolutional models, however,the filters or convolutional kernel are not learned. This paper is a really interesting demonstration of how signal processing ideas can help in designing and theore-tically understanding deep architectures.One of the fundamental challenges of deep learning research is how to learn the structure of the underlying model,including the number of layers and number of hidden variables per layer.The paper“Deep Learning with Hierarchical Convolutional Factor Analysis”by Bo Chen, Gungor Polatkan,Guillermo Sapiro,David Blei,David Dunson,and Lawrence Carin takes a first step toward achieving this goal.It introduces a hierarchical convolu-tional factor-analysis model,where the factor scores from layer l serve as the inputs to layer l+1with a max-pooling operation.In particular,a key characteristic of the proposed model is that the number of hidden variables,or dictionary elements,at each layer is inferred from the data using a beta-Bernoulli implementation of the Indian buffet process. The authors further present an empirical evaluation on several image-processing applications.Next,the paper“Scaling Up Spike-and-Slab Models for Unsupervised Feature Learning,”written by Ian Good-fellow,Aaron Courville,and Yoshua Bengio,describes an interesting new deep architecture for object recognition.The (shallow)spike-and-slab sparse coding architecture devel-oped by the authors in previous work has been extended to its deep variant,called the partially directed deep Boltz-mann machine.Appropriate learning and inference proce-dures are described,and a demonstration is given of the ability of the architecture to scale up to very large problem sizes,even when the number of labeled examples is low.While image classification and object recognition is frequently the focus of deep learning research,this special issue also received papers that present deep architecture systems going beyond the typical object recognition setup.The paper“Learning Hierarchical Features for Scene Labeling”by Camille Couprie,Clement Farabet,Laurent Najman,and Yann Lecun describes a novel application of convolutional neural networks for scene labeling that jointly segments images and categorizes image regions.The proposed method first introduces a multiscale convolu-tional neural network(CNN)to automatically learn a feature hierarchy from raw images for pixel-wise label prediction.It then introduces a hierarchical tree-based segmentation algorithm(”optimal label purity cover”)to integrate the pixel-level outputs of a CNN from multiple scales.The proposed approach is very fast and achieves state-of-the-art results on several publicly available scene labeling datasets with varying complexity.Overall,this paper shows a compelling demonstration that a deep architecture is potentially capable of solving a very hard computer vision problem that traditionally has been handled only by more hand-engineered methods.A new application for deep learning to the medical imaging domain is also presented in“Stacked Autoenco-ders for Unsupervised Feature Learning and Multiple Organ Detection in a Pilot Study Using4D Patient Data”by Hoo-Chang Shin,Matthew R.Orton,David J.Collins, Simon J.Doran,and Martin O.Leach.They developed an approach to detect organs from magnetic resonance medical images.Medical imaging is a little-explored domain application for deep architecture models.It poses specific challenges,such as the presence of multiple modalities,the lack of labeled data,and the modeling of a variety of abnormalities in imaged tissues.The authors present a thorough empirical analysis of the success of their ap-proach,based on unsupervised learning of sparse,stacked autoencoders.Finally,we mention two other papers that were sub-mitted by guest editors but were handled through the regular TPAMI review process.The paper“Tensor Deep Stacking Networks”by Brian Hutchinson,Li Deng,and Dong Yu reports in detail the development and evaluation of a new type of deep architecture(T-DSN)and the related learning algorithm. The T-DSN makes effective use of its weight tensors to efficiently represent higher-order statistics in the hidden features,and it shifts the major computation in learning the network weights into a convex optimization problem amenable to a straightforward parallel implementation. An experimental evaluation on three tasks(image classifi-cation,phone classification,and phone recognition)demon-strates the importance of sufficient depth in the T-DSN and the symmetry in the two hidden layers’structure within each block of the T-DSN for achieving low error rates in all three tasks.The paper“Learning with Hierarchical-Deep Models”by Ruslan Salakhutdinov,Joshua Tenenbaum,and Antonio Torralba introduces an interesting compositional learning architecture that integrates deep learning models with structured hierarchical Bayesian models.Their model is capable of learning novel concepts from a few training examples by learning low-level generic features,high-level part-like features that capture correlations among low-level features,and a hierarchy of super-classes for sharing priors over the high-level features that are typical of different kinds of concepts.The authors further evaluate their model on three different perceptual domains,including CIFAR-100object recognition,handwritten character recognition, and human motion capture datasets.The papers in this section illustrate well the variety of topics and methods behind deep learning research.We hope that by gathering a variety of both insightful review and novel research papers,this special section will help in consolidating this multidisciplinarity and further stimulate innovative research in the field.Samy BengioLi DengHugo LarochelleHonglak LeeRuslan SalakhutdinovGuest EditorsSamy Bengio received the PhD degree in computer science from the University of Mon-treal in 1993.He has been a research scientist at Google since 2007.Before that,he was a senior researcher in statistical machine learning at the IDIAP Research Institute since 1999.His most recent research interests are in machine learning,in particular large scale online learning,learning to rank,image ranking and annotation,music information retrieval,and deep learning.He is action editor of the Journal of Machine Learning Research and on the editorial board of the Machine Learning Journal .He was an associate editor of the Journal of Computational Statistics ,general chair of the Workshops on Machine Learning for Multimodal Interactions (MLMI ’04,’05,and ’06),program chair of the IEEE Workshop on Neural Networks for Signal Processing (NNSP ’02),and on the program committee of several international conferences such as NIPS,ICML,and ECML.More information can be found on his website:.Li Deng received the PhD degree in electrical and computer engineering from the University of Wisconsin–Madison.He joined the Department of Electrical and Computer Engineering,Uni-versity of Waterloo,Ontario,Canada,in 1989as an assistant professor and became a full professor with tenure there in 1996.In 1999,he joined Microsoft Research (MSR),Redmond,Washington,as a Senior Researcher,where he is currently a Principal Researcher.Since 2000,he has also been an affiliate full professor and graduate committee member in the Department of Electrical Engineering at the University of Washington,Seattle.Prior to MSR,he also worked or taught at the Massachusetts Institute of Technology,ATR Interpreting Telecommu-nications Research Laboratory (Kyoto,Japan),and HKUST.His current research activities include deep learning and machine intelligence,automatic speech and speaker recognition,spoken language under-standing,speech-to-speech translation,machine translation,information retrieval,statistical signal processing,and human speech production and perception,and noise robust speech processing.He has been granted more than 60patents in acoustics/audio,speech/language technology,and machine learning.He is a fellow of the Acoustical Society of America,a fellow of the IEEE,and a fellow of ISCA.He served on the Board of Governors of the IEEE Signal Processing Society (2008-2010).More recently,he served as Editor in Chief for the IEEE Signal Processing Magazine (2009-2011),which ranked first in 2010and 2011among all IEEE publications in terms of its impact factor and for which he received the 2011IEEE SPS Meritorious Service Award.He currently serves as editor-in-chief for the IEEE Transactions on Audio,Speech,and Language Processing .Hugo Larochelle received the PhD degree in computer science from the University of Mon-treal in 2009.He is now an assistant professor at the University of Sherbrooke,Canada.He specializes in the development of deep and probabilistic neural networks for high-dimen-sional and structured data,with a focus on AI-related problems such as natural language processing and computer vision.He is currently an associate editor for the IEEE Pattern Analysisand Machine Intelligence (TPAMI )and a member of the program committee for the NIPS 2013conference.He also served on the senior program committee of UAI 2011.He received a Notable Paper Award at the AISTATS 2011conference and a Google Faculty Research Award.Honglak Lee received the PhD degree from the Computer Science Department at Stanford University in 2010,advised by Andrew Ng.He is now an assistant professor of computer science and engineering at the University of Michigan,Ann Arbor.His primary research interests lie in machine learning,which spans deep learning,unsupervised and semi-super-vised learning,transfer learning,graphical mod-els,and optimization.He also works onapplication problems in computer vision,audio recognition,and other perception problems.He has coorganized workshops and tutorials related to deep learning at NIPS,ICML,CVPR,and AAAI,and he has served as an area chair for ICML 2013.His work received best paper awards at ICML and CEAS.He received a Google Faculty Research Award and was selected by IEEE Intelligent Systems as one of the AI’s Top 10to Watch.Ruslan Salakhutdinov received the PhD de-gree in computer science from the University of Toronto in 2009.After spending two postdoctoral years at the Massachusetts Institute of Technol-ogy Artificial Intelligence Lab,he joined the University of Toronto as an assistant professor in the Departments of Statistics and Computer Science.His primary interests lie in artificial intelligence,machine learning,deep learning,and large-scale optimization.He is an actioneditor of the Journal of Machine Learning Research and served on the program committees for several learning conferences,including NIPS,UAI,and ICML.He is an Alfred P.Sloan Research Fellow and Microsoft Research New Faculty Fellow,a recipient of the Early Researcher Award,Connaught New Researcher Award,and is a Scholar of the Canadian Institute for Advanced Research.BENGIOET AL.:GUESTEDITORS’INTRODUCTION:SPECIAL SECTION ON LEARNING DEEP ARCHITECTURES 3。
英语专业八级考试TEM-8阅读理解练习册(1)(英语专业2012级)UNIT 1Text AEvery minute of every day, what ecologist生态学家James Carlton calls a global ―conveyor belt‖, redistributes ocean organisms生物.It’s planetwide biological disruption生物的破坏that scientists have barely begun to understand.Dr. Carlton —an oceanographer at Williams College in Williamstown,Mass.—explains that, at any given moment, ―There are several thousand marine species traveling… in the ballast water of ships.‖ These creatures move from coastal waters where they fit into the local web of life to places where some of them could tear that web apart. This is the larger dimension of the infamous无耻的,邪恶的invasion of fish-destroying, pipe-clogging zebra mussels有斑马纹的贻贝.Such voracious贪婪的invaders at least make their presence known. What concerns Carlton and his fellow marine ecologists is the lack of knowledge about the hundreds of alien invaders that quietly enter coastal waters around the world every day. Many of them probably just die out. Some benignly亲切地,仁慈地—or even beneficially — join the local scene. But some will make trouble.In one sense, this is an old story. Organisms have ridden ships for centuries. They have clung to hulls and come along with cargo. What’s new is the scale and speed of the migrations made possible by the massive volume of ship-ballast water压载水— taken in to provide ship stability—continuously moving around the world…Ships load up with ballast water and its inhabitants in coastal waters of one port and dump the ballast in another port that may be thousands of kilometers away. A single load can run to hundreds of gallons. Some larger ships take on as much as 40 million gallons. The creatures that come along tend to be in their larva free-floating stage. When discharged排出in alien waters they can mature into crabs, jellyfish水母, slugs鼻涕虫,蛞蝓, and many other forms.Since the problem involves coastal species, simply banning ballast dumps in coastal waters would, in theory, solve it. Coastal organisms in ballast water that is flushed into midocean would not survive. Such a ban has worked for North American Inland Waterway. But it would be hard to enforce it worldwide. Heating ballast water or straining it should also halt the species spread. But before any such worldwide regulations were imposed, scientists would need a clearer view of what is going on.The continuous shuffling洗牌of marine organisms has changed the biology of the sea on a global scale. It can have devastating effects as in the case of the American comb jellyfish that recently invaded the Black Sea. It has destroyed that sea’s anchovy鳀鱼fishery by eating anchovy eggs. It may soon spread to western and northern European waters.The maritime nations that created the biological ―conveyor belt‖ should support a coordinated international effort to find out what is going on and what should be done about it. (456 words)1.According to Dr. Carlton, ocean organism‟s are_______.A.being moved to new environmentsB.destroying the planetC.succumbing to the zebra musselD.developing alien characteristics2.Oceanographers海洋学家are concerned because_________.A.their knowledge of this phenomenon is limitedB.they believe the oceans are dyingC.they fear an invasion from outer-spaceD.they have identified thousands of alien webs3.According to marine ecologists, transplanted marinespecies____________.A.may upset the ecosystems of coastal watersB.are all compatible with one anotherC.can only survive in their home watersD.sometimes disrupt shipping lanes4.The identified cause of the problem is_______.A.the rapidity with which larvae matureB. a common practice of the shipping industryC. a centuries old speciesD.the world wide movement of ocean currents5.The article suggests that a solution to the problem__________.A.is unlikely to be identifiedB.must precede further researchC.is hypothetically假设地,假想地easyD.will limit global shippingText BNew …Endangered‟ List Targets Many US RiversIt is hard to think of a major natural resource or pollution issue in North America today that does not affect rivers.Farm chemical runoff残渣, industrial waste, urban storm sewers, sewage treatment, mining, logging, grazing放牧,military bases, residential and business development, hydropower水力发电,loss of wetlands. The list goes on.Legislation like the Clean Water Act and Wild and Scenic Rivers Act have provided some protection, but threats continue.The Environmental Protection Agency (EPA) reported yesterday that an assessment of 642,000 miles of rivers and streams showed 34 percent in less than good condition. In a major study of the Clean Water Act, the Natural Resources Defense Council last fall reported that poison runoff impairs损害more than 125,000 miles of rivers.More recently, the NRDC and Izaak Walton League warned that pollution and loss of wetlands—made worse by last year’s flooding—is degrading恶化the Mississippi River ecosystem.On Tuesday, the conservation group保护组织American Rivers issued its annual list of 10 ―endangered‖ and 20 ―threatened‖ rivers in 32 states, the District of Colombia, and Canada.At the top of the list is the Clarks Fork of the Yellowstone River, whereCanadian mining firms plan to build a 74-acre英亩reservoir水库,蓄水池as part of a gold mine less than three miles from Yellowstone National Park. The reservoir would hold the runoff from the sulfuric acid 硫酸used to extract gold from crushed rock.―In the event this tailings pond failed, the impact to th e greater Yellowstone ecosystem would be cataclysmic大变动的,灾难性的and the damage irreversible不可逆转的.‖ Sen. Max Baucus of Montana, chairman of the Environment and Public Works Committee, wrote to Noranda Minerals Inc., an owner of the ― New World Mine‖.Last fall, an EPA official expressed concern about the mine and its potential impact, especially the plastic-lined storage reservoir. ― I am unaware of any studies evaluating how a tailings pond尾矿池,残渣池could be maintained to ensure its structural integrity forev er,‖ said Stephen Hoffman, chief of the EPA’s Mining Waste Section. ―It is my opinion that underwater disposal of tailings at New World may present a potentially significant threat to human health and the environment.‖The results of an environmental-impact statement, now being drafted by the Forest Service and Montana Department of State Lands, could determine the mine’s future…In its recent proposal to reauthorize the Clean Water Act, the Clinton administration noted ―dramatically improved water quality since 1972,‖ when the act was passed. But it also reported that 30 percent of riverscontinue to be degraded, mainly by silt泥沙and nutrients from farm and urban runoff, combined sewer overflows, and municipal sewage城市污水. Bottom sediments沉积物are contaminated污染in more than 1,000 waterways, the administration reported in releasing its proposal in January. Between 60 and 80 percent of riparian corridors (riverbank lands) have been degraded.As with endangered species and their habitats in forests and deserts, the complexity of ecosystems is seen in rivers and the effects of development----beyond the obvious threats of industrial pollution, municipal waste, and in-stream diversions改道to slake消除the thirst of new communities in dry regions like the Southwes t…While there are many political hurdles障碍ahead, reauthorization of the Clean Water Act this year holds promise for US rivers. Rep. Norm Mineta of California, who chairs the House Committee overseeing the bill, calls it ―probably the most important env ironmental legislation this Congress will enact.‖ (553 words)6.According to the passage, the Clean Water Act______.A.has been ineffectiveB.will definitely be renewedC.has never been evaluatedD.was enacted some 30 years ago7.“Endangered” rivers are _________.A.catalogued annuallyB.less polluted than ―threatened rivers‖C.caused by floodingD.adjacent to large cities8.The “cataclysmic” event referred to in paragraph eight would be__________.A. fortuitous偶然的,意外的B. adventitious外加的,偶然的C. catastrophicD. precarious不稳定的,危险的9. The owners of the New World Mine appear to be______.A. ecologically aware of the impact of miningB. determined to construct a safe tailings pondC. indifferent to the concerns voiced by the EPAD. willing to relocate operations10. The passage conveys the impression that_______.A. Canadians are disinterested in natural resourcesB. private and public environmental groups aboundC. river banks are erodingD. the majority of US rivers are in poor conditionText CA classic series of experiments to determine the effects ofoverpopulation on communities of rats was reported in February of 1962 in an article in Scientific American. The experiments were conducted by a psychologist, John B. Calhoun and his associates. In each of these experiments, an equal number of male and female adult rats were placed in an enclosure and given an adequate supply of food, water, and other necessities. The rat populations were allowed to increase. Calhoun knew from experience approximately how many rats could live in the enclosures without experiencing stress due to overcrowding. He allowed the population to increase to approximately twice this number. Then he stabilized the population by removing offspring that were not dependent on their mothers. He and his associates then carefully observed and recorded behavior in these overpopulated communities. At the end of their experiments, Calhoun and his associates were able to conclude that overcrowding causes a breakdown in the normal social relationships among rats, a kind of social disease. The rats in the experiments did not follow the same patterns of behavior as rats would in a community without overcrowding.The females in the rat population were the most seriously affected by the high population density: They showed deviant异常的maternal behavior; they did not behave as mother rats normally do. In fact, many of the pups幼兽,幼崽, as rat babies are called, died as a result of poor maternal care. For example, mothers sometimes abandoned their pups,and, without their mothers' care, the pups died. Under normal conditions, a mother rat would not leave her pups alone to die. However, the experiments verified that in overpopulated communities, mother rats do not behave normally. Their behavior may be considered pathologically 病理上,病理学地diseased.The dominant males in the rat population were the least affected by overpopulation. Each of these strong males claimed an area of the enclosure as his own. Therefore, these individuals did not experience the overcrowding in the same way as the other rats did. The fact that the dominant males had adequate space in which to live may explain why they were not as seriously affected by overpopulation as the other rats. However, dominant males did behave pathologically at times. Their antisocial behavior consisted of attacks on weaker male,female, and immature rats. This deviant behavior showed that even though the dominant males had enough living space, they too were affected by the general overcrowding in the enclosure.Non-dominant males in the experimental rat communities also exhibited deviant social behavior. Some withdrew completely; they moved very little and ate and drank at times when the other rats were sleeping in order to avoid contact with them. Other non-dominant males were hyperactive; they were much more active than is normal, chasing other rats and fighting each other. This segment of the rat population, likeall the other parts, was affected by the overpopulation.The behavior of the non-dominant males and of the other components of the rat population has parallels in human behavior. People in densely populated areas exhibit deviant behavior similar to that of the rats in Calhoun's experiments. In large urban areas such as New York City, London, Mexican City, and Cairo, there are abandoned children. There are cruel, powerful individuals, both men and women. There are also people who withdraw and people who become hyperactive. The quantity of other forms of social pathology such as murder, rape, and robbery also frequently occur in densely populated human communities. Is the principal cause of these disorders overpopulation? Calhoun’s experiments suggest that it might be. In any case, social scientists and city planners have been influenced by the results of this series of experiments.11. Paragraph l is organized according to__________.A. reasonsB. descriptionC. examplesD. definition12.Calhoun stabilized the rat population_________.A. when it was double the number that could live in the enclosure without stressB. by removing young ratsC. at a constant number of adult rats in the enclosureD. all of the above are correct13.W hich of the following inferences CANNOT be made from theinformation inPara. 1?A. Calhoun's experiment is still considered important today.B. Overpopulation causes pathological behavior in rat populations.C. Stress does not occur in rat communities unless there is overcrowding.D. Calhoun had experimented with rats before.14. Which of the following behavior didn‟t happen in this experiment?A. All the male rats exhibited pathological behavior.B. Mother rats abandoned their pups.C. Female rats showed deviant maternal behavior.D. Mother rats left their rat babies alone.15. The main idea of the paragraph three is that __________.A. dominant males had adequate living spaceB. dominant males were not as seriously affected by overcrowding as the otherratsC. dominant males attacked weaker ratsD. the strongest males are always able to adapt to bad conditionsText DThe first mention of slavery in the statutes法令,法规of the English colonies of North America does not occur until after 1660—some forty years after the importation of the first Black people. Lest we think that existed in fact before it did in law, Oscar and Mary Handlin assure us, that the status of B lack people down to the 1660’s was that of servants. A critique批判of the Handlins’ interpretation of why legal slavery did not appear until the 1660’s suggests that assumptions about the relation between slavery and racial prejudice should be reexamined, and that explanation for the different treatment of Black slaves in North and South America should be expanded.The Handlins explain the appearance of legal slavery by arguing that, during the 1660’s, the position of white servants was improving relative to that of black servants. Thus, the Handlins contend, Black and White servants, heretofore treated alike, each attained a different status. There are, however, important objections to this argument. First, the Handlins cannot adequately demonstrate that t he White servant’s position was improving, during and after the 1660’s; several acts of the Maryland and Virginia legislatures indicate otherwise. Another flaw in the Handlins’ interpretation is their assumption that prior to the establishment of legal slavery there was no discrimination against Black people. It is true that before the 1660’s Black people were rarely called slaves. But this shouldnot overshadow evidence from the 1630’s on that points to racial discrimination without using the term slavery. Such discrimination sometimes stopped short of lifetime servitude or inherited status—the two attributes of true slavery—yet in other cases it included both. The Handlins’ argument excludes the real possibility that Black people in the English colonies were never treated as the equals of White people.The possibility has important ramifications后果,影响.If from the outset Black people were discriminated against, then legal slavery should be viewed as a reflection and an extension of racial prejudice rather than, as many historians including the Handlins have argued, the cause of prejudice. In addition, the existence of discrimination before the advent of legal slavery offers a further explanation for the harsher treatment of Black slaves in North than in South America. Freyre and Tannenbaum have rightly argued that the lack of certain traditions in North America—such as a Roman conception of slavery and a Roman Catholic emphasis on equality— explains why the treatment of Black slaves was more severe there than in the Spanish and Portuguese colonies of South America. But this cannot be the whole explanation since it is merely negative, based only on a lack of something. A more compelling令人信服的explanation is that the early and sometimes extreme racial discrimination in the English colonies helped determine the particular nature of the slavery that followed. (462 words)16. Which of the following is the most logical inference to be drawn from the passage about the effects of “several acts of the Maryland and Virginia legislatures” (Para.2) passed during and after the 1660‟s?A. The acts negatively affected the pre-1660’s position of Black as wellas of White servants.B. The acts had the effect of impairing rather than improving theposition of White servants relative to what it had been before the 1660’s.C. The acts had a different effect on the position of white servants thandid many of the acts passed during this time by the legislatures of other colonies.D. The acts, at the very least, caused the position of White servants toremain no better than it had been before the 1660’s.17. With which of the following statements regarding the status ofBlack people in the English colonies of North America before the 1660‟s would the author be LEAST likely to agree?A. Although black people were not legally considered to be slaves,they were often called slaves.B. Although subject to some discrimination, black people had a higherlegal status than they did after the 1660’s.C. Although sometimes subject to lifetime servitude, black peoplewere not legally considered to be slaves.D. Although often not treated the same as White people, black people,like many white people, possessed the legal status of servants.18. According to the passage, the Handlins have argued which of thefollowing about the relationship between racial prejudice and the institution of legal slavery in the English colonies of North America?A. Racial prejudice and the institution of slavery arose simultaneously.B. Racial prejudice most often the form of the imposition of inheritedstatus, one of the attributes of slavery.C. The source of racial prejudice was the institution of slavery.D. Because of the influence of the Roman Catholic Church, racialprejudice sometimes did not result in slavery.19. The passage suggests that the existence of a Roman conception ofslavery in Spanish and Portuguese colonies had the effect of _________.A. extending rather than causing racial prejudice in these coloniesB. hastening the legalization of slavery in these colonies.C. mitigating some of the conditions of slavery for black people in these coloniesD. delaying the introduction of slavery into the English colonies20. The author considers the explanation put forward by Freyre andTannenbaum for the treatment accorded B lack slaves in the English colonies of North America to be _____________.A. ambitious but misguidedB. valid有根据的but limitedC. popular but suspectD. anachronistic过时的,时代错误的and controversialUNIT 2Text AThe sea lay like an unbroken mirror all around the pine-girt, lonely shores of Orr’s Island. Tall, kingly spruce s wore their regal王室的crowns of cones high in air, sparkling with diamonds of clear exuded gum流出的树胶; vast old hemlocks铁杉of primeval原始的growth stood darkling in their forest shadows, their branches hung with long hoary moss久远的青苔;while feathery larches羽毛般的落叶松,turned to brilliant gold by autumn frosts, lighted up the darker shadows of the evergreens. It was one of those hazy朦胧的, calm, dissolving days of Indian summer, when everything is so quiet that the fainest kiss of the wave on the beach can be heard, and white clouds seem to faint into the blue of the sky, and soft swathing一长条bands of violet vapor make all earth look dreamy, and give to the sharp, clear-cut outlines of the northern landscape all those mysteries of light and shade which impart such tenderness to Italian scenery.The funeral was over,--- the tread鞋底的花纹/ 踏of many feet, bearing the heavy burden of two broken lives, had been to the lonely graveyard, and had come back again,--- each footstep lighter and more unconstrained不受拘束的as each one went his way from the great old tragedy of Death to the common cheerful of Life.The solemn black clock stood swaying with its eternal ―tick-tock, tick-tock,‖ in the kitchen of the brown house on Orr’s Island. There was there that sense of a stillness that can be felt,---such as settles down on a dwelling住处when any of its inmates have passed through its doors for the last time, to go whence they shall not return. The best room was shut up and darkened, with only so much light as could fall through a little heart-shaped hole in the window-shutter,---for except on solemn visits, or prayer-meetings or weddings, or funerals, that room formed no part of the daily family scenery.The kitchen was clean and ample, hearth灶台, and oven on one side, and rows of old-fashioned splint-bottomed chairs against the wall. A table scoured to snowy whiteness, and a little work-stand whereon lay the Bible, the Missionary Herald, and the Weekly Christian Mirror, before named, formed the principal furniture. One feature, however, must not be forgotten, ---a great sea-chest水手用的储物箱,which had been the companion of Zephaniah through all the countries of the earth. Old, and battered破旧的,磨损的, and unsightly难看的it looked, yet report said that there was good store within which men for the most part respect more than anything else; and, indeed it proved often when a deed of grace was to be done--- when a woman was suddenly made a widow in a coast gale大风,狂风, or a fishing-smack小渔船was run down in the fogs off the banks, leaving in some neighboring cottage a family of orphans,---in all such cases, the opening of this sea-chest was an event of good omen 预兆to the bereaved丧亲者;for Zephaniah had a large heart and a large hand, and was apt有…的倾向to take it out full of silver dollars when once it went in. So the ark of the covenant约柜could not have been looked on with more reverence崇敬than the neighbours usually showed to Captain Pennel’s sea-chest.1. The author describes Orr‟s Island in a(n)______way.A.emotionally appealing, imaginativeB.rational, logically preciseC.factually detailed, objectiveD.vague, uncertain2.According to the passage, the “best room”_____.A.has its many windows boarded upB.has had the furniture removedC.is used only on formal and ceremonious occasionsD.is the busiest room in the house3.From the description of the kitchen we can infer that thehouse belongs to people who_____.A.never have guestsB.like modern appliancesC.are probably religiousD.dislike housework4.The passage implies that_______.A.few people attended the funeralB.fishing is a secure vocationC.the island is densely populatedD.the house belonged to the deceased5.From the description of Zephaniah we can see thathe_________.A.was physically a very big manB.preferred the lonely life of a sailorC.always stayed at homeD.was frugal and saved a lotText BBasic to any understanding of Canada in the 20 years after the Second World War is the country' s impressive population growth. For every three Canadians in 1945, there were over five in 1966. In September 1966 Canada's population passed the 20 million mark. Most of this surging growth came from natural increase. The depression of the 1930s and the war had held back marriages, and the catching-up process began after 1945. The baby boom continued through the decade of the 1950s, producing a population increase of nearly fifteen percent in the five years from 1951 to 1956. This rate of increase had been exceeded only once before in Canada's history, in the decade before 1911 when the prairies were being settled. Undoubtedly, the good economic conditions of the 1950s supported a growth in the population, but the expansion also derived from a trend toward earlier marriages and an increase in the average size of families; In 1957 the Canadian birth rate stood at 28 per thousand, one of the highest in the world. After the peak year of 1957, thebirth rate in Canada began to decline. It continued falling until in 1966 it stood at the lowest level in 25 years. Partly this decline reflected the low level of births during the depression and the war, but it was also caused by changes in Canadian society. Young people were staying at school longer, more women were working; young married couples were buying automobiles or houses before starting families; rising living standards were cutting down the size of families. It appeared that Canada was once more falling in step with the trend toward smaller families that had occurred all through theWestern world since the time of the Industrial Revolution. Although the growth in Canada’s population had slowed down by 1966 (the cent), another increase in the first half of the 1960s was only nine percent), another large population wave was coming over the horizon. It would be composed of the children of the children who were born during the period of the high birth rate prior to 1957.6. What does the passage mainly discuss?A. Educational changes in Canadian society.B. Canada during the Second World War.C. Population trends in postwar Canada.D. Standards of living in Canada.7. According to the passage, when did Canada's baby boom begin?A. In the decade after 1911.B. After 1945.C. During the depression of the 1930s.D. In 1966.8. The author suggests that in Canada during the 1950s____________.A. the urban population decreased rapidlyB. fewer people marriedC. economic conditions were poorD. the birth rate was very high9. When was the birth rate in Canada at its lowest postwar level?A. 1966.B. 1957.C. 1956.D. 1951.10. The author mentions all of the following as causes of declines inpopulation growth after 1957 EXCEPT_________________.A. people being better educatedB. people getting married earlierC. better standards of livingD. couples buying houses11.I t can be inferred from the passage that before the IndustrialRevolution_______________.A. families were largerB. population statistics were unreliableC. the population grew steadilyD. economic conditions were badText CI was just a boy when my father brought me to Harlem for the first time, almost 50 years ago. We stayed at the hotel Theresa, a grand brick structure at 125th Street and Seventh avenue. Once, in the hotel restaurant, my father pointed out Joe Louis. He even got Mr. Brown, the hotel manager, to introduce me to him, a bit punchy强力的but still champ焦急as fast as I was concerned.Much has changed since then. Business and real estate are booming. Some say a new renaissance is under way. Others decry责难what they see as outside forces running roughshod肆意践踏over the old Harlem. New York meant Harlem to me, and as a young man I visited it whenever I could. But many of my old haunts are gone. The Theresa shut down in 1966. National chains that once ignored Harlem now anticipate yuppie money and want pieces of this prime Manhattan real estate. So here I am on a hot August afternoon, sitting in a Starbucks that two years ago opened a block away from the Theresa, snatching抓取,攫取at memories between sips of high-priced coffee. I am about to open up a piece of the old Harlem---the New York Amsterdam News---when a tourist。
Passage OneQuestions 51 to 55 are based on the following passage:Statuses are marvelous human inventions that enable us to get along with one another and to determine where we "fit" in society.As we go about our everyday lives,we mentally attempt to place people in terms of their statuses.For example,we must judge whether the person in the library is a reader or a librarian,whether the telephone caller is a friend or a salesman,whether the unfamiliar person on our property is a thief or a meter reader,and so on.身份是人类了不起的发明创造,它使得我们能够融洽相处,还能判断我们”适合“于社会的哪一部分。
在我们进行日常生活时,我们在心理上努力要把人们归入他们的身份。
比如说,我们必须判断在图书馆里的那个人是读者还是馆员,打电话来的人是朋友还是推销员,在我们财产边的陌生人是个贼还是测量员,等等。
我们假设的身份通常随我们所遇到的人而变化,而且它一生都在改变。
我们中大多数人可以很迅速地设想出不同情况下应有的身份。
许多社会上相互交流的情况就包括辨别合适的身份,并且加以选择,而且让其他人可以表现出与我们相处时相应的身份。
这就意味着我们根据他人的行为来调整自己的行为,而这是以思想中不断进行的估计与解释为基础的。
Toward a Method of Selecting Among Computational Models of CognitionMark A.Pitt,In Jae Myung,and Shaobo ZhangThe Ohio State UniversityThe question of how one should decide among competing explanations of data is at the heart of the scientific putational models of cognition are increasingly being advanced as explanations of behavior.The success of this line of inquiry depends on the development of robust methods to guide the evaluation and selection of these models.This article introduces a method of selecting among mathematical models of cognition known as minimum description length ,which provides an intuitive and theoretically well-grounded understanding of why one model should be chosen.A central but elusive concept in model selection,complexity,can also be derived with the method.The adequacy of the method is demonstrated in 3areas of cognitive modeling:psychophysics,information integration,and categorization.How should one choose among competing theoretical explana-tions of data?This question is at the heart of the scientific enter-prise,regardless of whether verbal models are being tested in an experimental setting or computational models are being evaluated in simulations.A number of criteria have been proposed to assist in this endeavor,summarized nicely by Jacobs and Grainger (1994).They include (a)plausibility (are the assumptions of the model biologically and psychologically plausible?);(b)explana-tory adequacy (is the theoretical explanation reasonable and con-sistent with what is known?);(c)interpretability (do the model and its parts—e.g.,parameters—make sense?are they understand-able?);(d)descriptive adequacy (does the model provide a good description of the observed data?);(e)generalizability (does the model predict well the characteristics of data that will be observed in the future?);and (f)complexity (does the model capture the phenomenon in the least complex—i.e.,simplest—possible manner?).The relative importance of these criteria may vary with the types of models being compared.For example,verbal models are likely to be scrutinized on the first three criteria just as much as the lastthree to thoroughly evaluate the soundness of the models and their putational models,on the other hand,may have already satisfied the first three criteria to a certain level of accept-ability earlier in their evolution,leaving the last three criteria to be the primary ones on which they are evaluated.This emphasis on the latter three can be seen in the development of quantitative methods designed to compare models on these criteria.These methods are the topic of this article.In the last two decades,interest in mathematical models of cognition and other psychological processes has increased tremen-dously.We view this as a positive sign for the discipline,for it suggests that this method of inquiry holds considerable promise.Among other things,a mathematical instantiation of a theory provides a test bed in which researchers can examine the detailed interactions of a model’s parts with a level of precision that is not possible with verbal models.Furthermore,through systematic evaluation of its behavior,an accurate assessment of a model’s viability can be obtained.The goal of modeling is to infer the structural and functional properties of a cognitive process from behavioral data that were thought to have been generated by that process.At its most basic level,then,a mathematical model is a set of assumptions about the structure and functioning of the process.The adequacy of a model is first assessed by measuring its ability to reproduce human data.If it does so reasonably well,then the next step is to compare its performance with competing models.It is imperative that the model selection method that is used to select among competing models accurately measures how well each model approximates the mental process.Above all else,the method must be valid.Otherwise,the purpose of modeling is undermined.One runs the risk of choosing a model that in actuality is a poor approximation of the underlying process of interest,leading researchers astray.The potential severity of this problem should make it clear that sound methodology is not only integral to but also necessary for theoretical advancement.In short,model selection methods must be as sophisticated and robust as the models themselves.In this article,we introduce a new quantitative method of model selection.It is theoretically well grounded and provides a clearMark A.Pitt,In Jae Myung,and Shaobo Zhang,Department of Psy-chology,The Ohio State University.Portions of this work were presented at the 40th annual meeting of the Psychonomic Society,Los Angeles,California,November 18–22,1999,and at the 31st and 32nd annual meetings of the Society for Mathematical Psychology,Nashville,Tennessee (August 6–9,1998)and Santa Cruz,California (July 29–August 1,1999),respectively.We thank D.Bamber,R.Golden,and Andrew Hanson for their valuable comments and attention to detail in reading earlier versions of this article.Mark A.Pitt and In Jae Myung contributed equally to the article,so order of authorship should be viewed as arbitrary.The section Three Application Examples is based on Shaobo Zhang’s doctoral dissertation submitted to the Department of Psychology at The Ohio State University.In Jae Myung and Mark A.Pitt were supported by National Institute of Mental Health Grant MH57472.Correspondence concerning this article should be addressed to Mark A.Pitt or In Jae Myung,Department of Psychology,The Ohio State Univer-sity,1885Neil Avenue Mall,Columbus,Ohio 43210-1222.E-mail:pitt.2@ or myung.1@Psychological ReviewCopyright 2002by the American Psychological Association,Inc.2002,Vol.109,No.3,472–4910033-295X/02/$5.00DOI:10.1037//0033-295X.109.3.472472understanding of why one model should be chosen over another. The purpose of the article is to provide a good conceptual under-standing of the problem of model selection and the solution being advocated.Consequently,only the most important(and new)tech-nical advances are discussed.A more thorough treatment of the mathematics can be found in other sources(Myung,Balasubrama-nian,&Pitt,2000;Myung,Kim,&Pitt,2000;Myung&Pitt, 1997,1998).After introducing the problem of model selection and identifying model complexity as a key property of a model that must be considered by any selection method,we introduce an intuitive statistical tool that assists in understanding and measuring complexity.Next,we develop a quantitative measure of complex-ity within the mathematics of differential geometry and show how it is incorporated into a powerful model selection method known as minimum description length(MDL).Finally,application exam-ples of MDL and the complexity measure are provided by com-paring models in three areas of cognitive psychology:psychophys-ics,information integration,and categorization.Generalizability Instead of Goodness of FitModel selection in psychology has largely been limited to a single criterion to measure the accuracy with which a set of models describes a mental process:goodness of fit(GOF).The model that fits a particular set of observed data the best(i.e.,accounts for the most variance)is considered superior because it is presumed to approximate most closely the mental process that generated the data.Typical measures of GOF include the root mean squared error(RMSE),which is the square root of the sum of squared deviations between observed and predicted data divided by the number of data points fitted,and the maximum likelihood,which is the probability of obtaining the observed data maximized with respect to the model’s parameter values.GOF as a selection criterion is attractive because it appears to measure exactly what one wants to know:How well does the model mimic human behavior?In addition,the GOF measure is easy to calculate. GOF is a necessary and important component of model selec-tion:Data are the only link to the underlying cognitive process,so a model’s ability to describe the output from this process must be considered in model selection.However,model selection based solely on GOF can lead to erroneous results and the choice of an inferior model.Just because a model fits data well does not necessarily imply that the regularity one seeks to capture in the data is well approximated by the model(Roberts&Pashler,2000). Properties of the model itself can enable it to provide a good fit to the data for reasons that have nothing to do with the model’s approximation to the cognitive process(Myung,2000).Two of these properties are the number of parameters in the model and its functional form(i.e.,the way in which the model’s parameters and data are combined in the model equation).Together they contrib-ute to a model’s complexity,which refers to the flexibility inherent in a model that enables it to fit diverse patterns of data.1The following simulation example demonstrates the independent con-tribution of these two properties to GOF.Three models were compared on their ability to fit data.Model M1(defined in Table1)generated the data to fit,and is thereforeconsidered the“true”model.Model M2differed from M1only inhaving one additional parameter,two instead of one;note that their functional forms are the same.Model M3had the same number ofparameters as M2,but a different functional form(a is an exponent of x rather than an additive component).Parameters were chosen for each of the three models to give the best fit to1,000randomlygenerated samples of data from the model M1.Each model’s mean fit to the samples is shown in the first row of Table1along with the percentage of time that particular model provided a better fitthan its two competitors.As can been seen,M2and M3,with onemore parameter than M1,always provided a better fit to the datathan M1.Because the data were generated by M1,M2and M3must have overfitted the data beyond what is necessary to capture theunderlying regularity.Otherwise,one would have expected M1tofit its own data best at least some of the time.After all,M1 generated the data!The improved fit of M2and M3occurred because the extra parameter,b,in these two models enabled them to absorb random error(i.e.,nonsystematic variation)in the data. Absorption of these random fluctuations is the only means bywhich M2and M3could have fitted the data better than the truemodel,M1.Note also that M3provided a better fit than M2.This improvement in fit must be due to functional form rather than the number of parameters,because these two models differ only in how the data(x)and the two parameters(a and b)are combined in the model equation.This example demonstrates clearly that GOF alone is inadequate as a model selection criterion.Because a model’s complexity is not evaluated by the method,the model capable of absorbing the most variation in the data,regardless of its source,will be chosen. Frequently this will be the most complex model.The simulation also highlights the point that model selection is particularly diffi-cult in psychology,and in other social sciences,precisely because random error is present in the data.Although this“noise”can be minimized(in the experimental design),it cannot be eliminated,so in any given data set,variation due to the cognitive process and variation due to random error are entangled,posing a significant obstacle to identifying the best model.To get around this problem,model selection must be based, instead,on a different criterion—that of generalizability.The goal1Cutting,Bruno,Brady,and Moore(1992)used the term scope,which is similar to our definition of complexity.They proposed to measure the scope by assessing a model’s ability“to account for all possible data functions,where those functions are generated by a reasonably large sample of random data sets”(p.364).Table1Goodness of Fit and Generalizability Measures of Three Models Differing in ComplexityModel M1(true model)M2M3 Goodness of fit 2.68(0%) 2.49(31%) 2.41(69%) Generalizability 2.99(52%) 3.08(28%) 3.14(20%) Note.Each cell contains the average root mean squared error of the fit of each model to the data and the percentage of samples(out of1,000)in which that particular model fitted the data best(in parentheses).The threemodels were as follows:M1:yϭln(xϩa)ϩerror;M2:yϭb*ln(xϩa)ϩerror;and M3:yϭbx aϩerror.The error was normally distributed,Mϭ0,SDϭ3.Samples were generated from model M1using aϭ1on the same 6points for x,which ranged from1to6in increments of1.473MODEL SELECTION AND COMPLEXITYof generalizability is to predict the statistics of new,as yet unseen,samples generated by the mental process being studied.The ratio-nale underlying the criterion is that the model should be chosen that fits all samples best,not the model that provides the best fit to one particular sample.Only when this condition is met can one be sure a model is accurately capturing the underlying process,not also the idiosyncracies (i.e.,random error)of a particular data sample.More formally,generalizability can be defined in terms of a discrepancy function that measures the expected error in predict-ing future data given the model of interest (Linhart &Zucchini,1986;also see their work for a discussion of the theoretical underpinnings of generalizability).The results of a second simulation illustrate the superiority of generalizability as a model selection criterion.After each of the data samples was fitted in the first simulation,the parameters of the three models were fixed,and generalizability was assessed by fitting the models to another 1,000samples of data generated from M 1.The average fits are shown in the second row of Table 1.As can be seen,poor generalizability is the cost of overfitting a specific sample of data.Not only are average fits now worse for M 2and M 3than for M 1,but these two models provided the best fit to the second sample much less often than M 1.Generalizability should be preferred over GOF because it does a better job of capturing the general trend in the data and ignoring random variation.This difference between these two selection criteria is shown in Figure 1.Dots in the panel represent observed data points.Lines are the functions generated by two models varying in complexity.The simpler model (thick line)captures the general trend in the data.If new data points (ϩ)are added to the sample,fit will remain similar.The more complex model (thin line)not only captures the general trend in the data,but also captures many of the idiosyn-cracies of each observation in the data set,which will cause fit to drop when additional observations are added to the sample.Gen-eralizability would favor the simple model,which fits with our intuitions.GOF,on the other hand,would favor the complex model.The goal of model selection,then,should be to maximize generalizability.This turns out to be quite difficult in practice,because the relationship between complexity and generalizability is not as straightforward as that between complexity and GOF.These differences are illustrated in Figure 2.Model complexity is represented along the horizontal axis and any fit index on the vertical axis,where larger values indicate a better fit (e.g.,percent variance accounted for),with the two functions representing the two selection criteria.As was demonstrated in the first simulation,as complexity increases,so does GOF.Generalizability will also increase positively with complexity,but only up to the point where the model is sufficiently complex to capture the regularities in the data caused by the cognitive process being modeled.Any addi-tional complexity will cause a drop in generalizability,because after that point the model will begin to capture random error,not just the underlying process.The difference between the GOF and generalizability curves represents the amount of overfitting that can occur.Only by taking complexity into account can a selection method accurately measure a model ’s generalizability.The task before the modeling community has been to develop an accurate and complete measure of model complexity,being sensitive not only to the number of parameters in the model but also to its functional form.Another way to interpret the preceding discussion is that the trademark of a good model is its ability to satisfy the two opposing selection pressures of GOF and complexity,with the end result being good generalizability.These two pressures can be thought of as the two edges of Occam ’s razor:A model must be complex enough to capture the underlying regularity yet simple enough to avoid overfitting the data sample and thus losing generalizability.In this regard,model selection methods should be evaluated on their success in implementing Occam ’s razor.The selection method that we introduce in this article,MDL,achieves this goal.Before we describe this method,we review prior approaches to model selection.Prior Approaches to Model SelectionWe begin this section with a formal definition of a model.From a statistical standpoint,data are a sample generated from a true but unknown probability distribution,which is the regularity underly-ing the data.A statistical model is defined as a collection of probability distributions defined on experimental data and indexed by the model ’s parameter vector,whose values range over the parameter space of the model.If the model contains as a special case the probability distribution that generated the data (i.e.,the “true ”model),then the model is said to be correctly specified;otherwise it is misspecified.Formally,define y ϭ(y 1,...,y N )as a vector of values of the dependent variable,ϭ(1,...,k )as the parameter vector of the model,f (y ͉)as the likelihood function as a function of the parameter .N is the number of observations and k is the number of parameters.Often it is possible to write y as a sum of a deterministic component plus random error:y ϭg ͑,x ͒ϩe .(1)In the equation,x ϭ(x 1,...,x N )is a vector of an independent variable x ,and e ϭ(e 1,...,e N )is the random error vector from a probability distribution with a mean of zero.Quite often themeanFigure 1.Illustration of the trade-off between goodness of fit and gen-eralizability.An observed data set (dots)was fitted to a simple model (thick line)and a complex model (thin line).New observations are shown by the plus symbol.474PITT,MYUNG,AND ZHANGfunction g (,x )itself is taken to define a mathematical model.However,the specification of the error distribution must be in-cluded in the definition of a model.Additional parameters may be introduced in the model to specify the shape of the error distribu-tion (e.g.,normal).Often its shape is determined by the experi-mental task or design.For example,consider a recognition mem-ory experiment in which the participant is required to respond “old ”or “new ”to a set of pictures presented across a series of n independent trials,with the number of correct responses recorded as the dependent variable.Suppose that a two-parameter model assumes that the probability of a correct response follows a logistic function of the time lag (x i ),for condition i (i ϭ1,...,N ),between initial exposure and recognition test,in the form of g (1,2,x i )ϭ[1ϩ1exp(Ϫ2⅐x i )]Ϫ1.In this case,the dependent variable y i will be binomially distributed with probability g (1,2,x i )and the number of binomial trials n ,so the shape of error function is completely specified by the experimental task.Six representative selection methods currently in use are shown in Table 2.They are the Akaike information criterion (AIC;Akaike,1973),the Bayesian information criterion (BIC;Schwarz,1978),the root mean squared deviation (RMSD),the information-theoretic measure of complexity (ICOMP;Bozdogan,1990),cross-validation (CV;Stone,1974),and Bayesian model selection (BMS;Kass &Raftery,1995;Myung &Pitt,1997).Each of these methods assesses a model ’s generalizability by combining a mea-sure of GOF with a measure of complexity.Each prescribes that the model that minimizes the given criterion be chosen.That is,the smaller the criterion value of a model,the better the model gen-eralizes.2A fuller discussion of these methods can be found in Myung,Forster,and Browne (2000;see also Linhart &Zucchini,1986).AIC and BIC are the two most commonly used selection meth-ods.The first term,Ϫ2ln(f (y ͉ˆ)),is a maximum likelihood mea-sure of GOF and the second term,involving k ,is a measure of complexity that is sensitive to the number of parameters in the model.As the number of parameters increases,so does the crite-rion.In BIC,the rate of increase is modified by the log of thesample size,n .3RMSD uses RMSE as the measure of GOF and also takes into account the number of parameters through k .4These three measures,AIC,BIC,and RMSD ,are all sensitive only to one aspect of complexity,number of parameters,but insensitive to functional form.This is clearly inadequate because,as demon-strated in Table 1,the functional form of a model influences generalizability.ICOMP is an improvement on this shortcoming.Its second and third terms together represent a complexity measure that takes into account the effects of parameter sensitivity through trace(⍀)and parameter interdependence through det(⍀),which,according to Li,Lewandowski,and DeBrunner (1996),are two principal components of the functional form that contribute to model complexity.However,ICOMP is also problematic because it is not invariant under reparameterization of the model,in par-ticular under nonlinear forms of reparameterization.52The model selection methods discussed in the present article do not require the assumption that the models being compared are correct or nested.(A model is said to be correct if there is a parameter value of the model that yields the probability distribution that has generated the ob-served data sample.A model is said to be nested within another model if the former can be reduced to a special case of the latter by setting one or more of its parameters to fixed values.)On the other hand,the generalized likelihood ratio test based on the G 2or chi-square statistics (e.g.,Bishop,Fienberg,&Holland,1975,pp.125–127),which are often used to compare two models,assumes that the models are nested and,further,that the reduced model is correct.When these assumptions are met,both types of selection methods should perform similarly.However,the methods should not be viewed as interchangeable because their goals differ.The selection methods presented in this article were designed to identify the model that generalizes best in some defined sense.The generalized likelihood ratio test,in contrast,is a null hypothesis significance test in which the hypoth-esis that the reduced model is correct is tested given a prescribed level of the Type 1error rate (i.e.,␣).Accordingly,the model chosen under this test may not necessarily be the one that generalizes best.3Sample size refers to the number of independent data samples (more accurately,errors,i.e.,e i s)drawn from the same probability distribution.Data size is the number of observed data points that are being fitted to evaluate a model and that may come from different probability distribu-tions,although from the same probability family.Often,the sample size is equal to the data size.A case in point is a linear regression model,y i ϭx i ϩe i (i ϭ1,...,N ),where e i ϳN (0,2).Note that errors,e i s,are independent and identically distributed according to the normal probability distribution with mean zero and variance 2.On the other hand,if it is assumed that each e i is normally distributed with zero mean but with a different value of the variance,that is,e i ϳN (0,i 2),(i ϭ1,...,N ),then the sample size,n ,will now be equal to 1whereas the data size,N ,remains unchanged.4The RMSD defined in Table 2differs from the RMSD that has often been used in the psychological literature (e.g.,Friedman,Massaro,Kitzis,&Cohen,1995)where it is defined as RMSD ϭ͌SSE/N ,in which (N Ϫk )is replaced by N ,and therefore does not take into account the number of parameters.This form of RMSD is nothing more than RMSE .As such,it is not appropriate to use as a method of model selection,especially when comparing models that differ in the number of parameters.5Reparameterization refers to transforming the parameters of a model so that it becomes another,behaviorally equivalent,model.For example,a one-parameter exponential model with normal error,y ϭe x ϩN (0,2)is a reparameterization of another model:y ϭ␣x ϩN (0,2).The latterisFigure 2.Illustration of the relationship between goodness of fit and generalizability as a function of model complexity (Myung &Pitt,2001).From Stevens’Handbook of Experimental Psychology (p.449,Figure 11.4),by J.Wixted (Editor),2001,New York:Wiley.Copyright 2001by Wiley.Adapted with permission.475MODEL SELECTION AND COMPLEXITYIn CV,the observed data are divided into two subsamples of equal sizes,calibration and validation.The former is used to estimate the best-fitting parameter values of a model.The param-eters are then fixed to these values and used by the model to fit the validation sample,yielding a model ’s CV index.CV is an easy-to-use,heuristic method of estimating a model ’s generalizability (for a brief tutorial,see Myung &Pitt,2001).The emphasis on generalizability makes it reasonable to suppose that CV somehow takes into account the effects of functional form.If,how,and how well it does this is not clear,however.BMS is a model selection method motivated from Bayesian inference.As such,the method chooses models based on the posterior probability of a model given the data.Calculation of the posterior probability requires the specification of the parameter prior density,(),creating the possibility that model selection will depend on the choice of the prior density.As with CV,complexity in BMS is elusive.The integral form of the measure indicates that BMS takes into account functional form and the number of parameters,but how this is achieved is not entirely clear.It can be shown that BIC performs equivalently to BMS as a large sample approximation.It is important to note that these selection criteria are themselves sample estimates of a true but unknown population parameter (i.e.,generalizability in the population),and thus their values can change from sample to sample.Under the model selection proce-dure described above,however,one is forced to choose one model no matter how small the difference is among models,even when the models are virtually equivalent in their approximation of the underlying regularity.One solution to this dilemma is to conduct a statistical test,before applying the model selection procedure,to decide if two given models provide equally good descriptions of the underlying process.Golden (2000)proposed such a method-ology,in which one can determine whether a subset of models areequally good approximations of the cognitive process.6If the number of comparisons is not small,however,it can be difficult to control experiment-wise error.The preceding selection methods represent important progress in tackling the model selection problem.All have shortcomings that limit their usefulness to various degrees.The complexity measure in AIC,BIC,and RMSD is incomplete,and the other three are either not invariant under reparameterization (ICOMP)or lack a clear complexity measure (CV,BMS).The remainder of this article is devoted to the development and testing of a model selection approach that overcomes these limitations.We begin by showing that differential geometry provides a theoretically well-justified and intuitive framework for understanding complexity and model selection in general.Model Complexity:A Distributional ApproachWe begin the discussion of complexity with a graphical defini-tion of the term,intended to clarify what it means for a model to be complex.Depicted in the top panel in Figure 3is the set of all data patterns that are possible given a particular experimental design.Every point in this multidimensional data space represents a particular data pattern in terms of a probability distribution,such as the shape of a frequency distribution of response times.All models occupy a section,or multiple sections,of data space,being able to fit a subset of the possible data patterns that could be observed.It is equally appropriate to think of data space as the universe of all models under consideration,because every model will occupy a region of this space,large or small.6This is a null hypothesis significance test,which,as an extension of the Wilke ’s generalized likelihood ratio test,tests the null hypothesis that all models under consideration fit the data equally well.This test,unlike the generalized likelihood ratio test,is applicable to comparing non-nested and misspecified models for a wide range of discrepancy functions,including the ones with penalty terms,such as AIC,BIC,and MDL.In the standard model selection procedure using these criteria,one is forced to decide between two models under comparison.This test allows for a third decision that both models are equally good or there is not enough evidence yet for choosing one model over the other.Table 2Six Prior Model Selection MethodsSelection methodCriterion equationAkaike information criterion (AIC)AIC ϭϪ2ln f (y ͉ˆ)ϩ2k Bayesian information criterion (BIC)BIC ϭϪ2ln f (y ͉ˆ)ϩk ln n Root mean square deviation (RMSD)RMSD ϭ͌SSE/(N Ϫk )Information-theoretic measure of complexity (ICOMP)ICOMP ϭϪln f (y ͉ˆ)ϩk 2ln ͩtrace [⍀(ˆ)]k ͪϪ12ln det(⍀(ˆ))Cross-validation (CV)CV ϭϪln f (y Val ͉ˆCal )Bayesian model selection (BMS)BMS ϭϪln ͐f (y ͉)()d Note.y ϭdata sample of size n ;ˆϭparameter value that maximizes the likelihood function f (y ͉);k ϭnumber of parameters;SSE ϭsum of the squared deviations between observed and predicted data;N ϭthe number of data points fitted;⍀ϭcovariance matrix of the parameter estimates;y Val ϭvalidation sample of observed data;ˆCal ϭmaximum likelihood parameter estimate for a calibration sample;ln ϭthe natural logarithm of base e ;()ϭthe prior probability density function of the parameter.obtained from the former by defining a new parameter,␣,as ␣ϭe .Whenever two models are related to each other through reparameterization,they become equivalent in the sense that both will fit any given data set identically,albeit with different parameter values.Statistically speaking,they are indistinguishable from one another.476PITT,MYUNG,AND ZHANG。