
人教版九年级数学下册相似三角形同步练习新人教版
专题一相似形中的开放题
1.如图,在正方形网
2.格中,点A﹨B﹨C﹨D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE= 时,以点A﹨D﹨E为顶点的三角形与△ABC相似.
1.已知:如图,△ABC中,点D﹨E分别在边AB﹨AC上.连接DE并延长交BC的延长线于点F,连接DC﹨BE,∠BDE+∠BCE=180°.
(1)写出图中三对相似三角形(注意:不得添加字母和线);
(2)请你在所找出的相似三角形中选取一对,说明它们相似
的理由.
专题二相似形中的实际应用题
3.如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求厚度x.
专题三相似形中的探究规律题
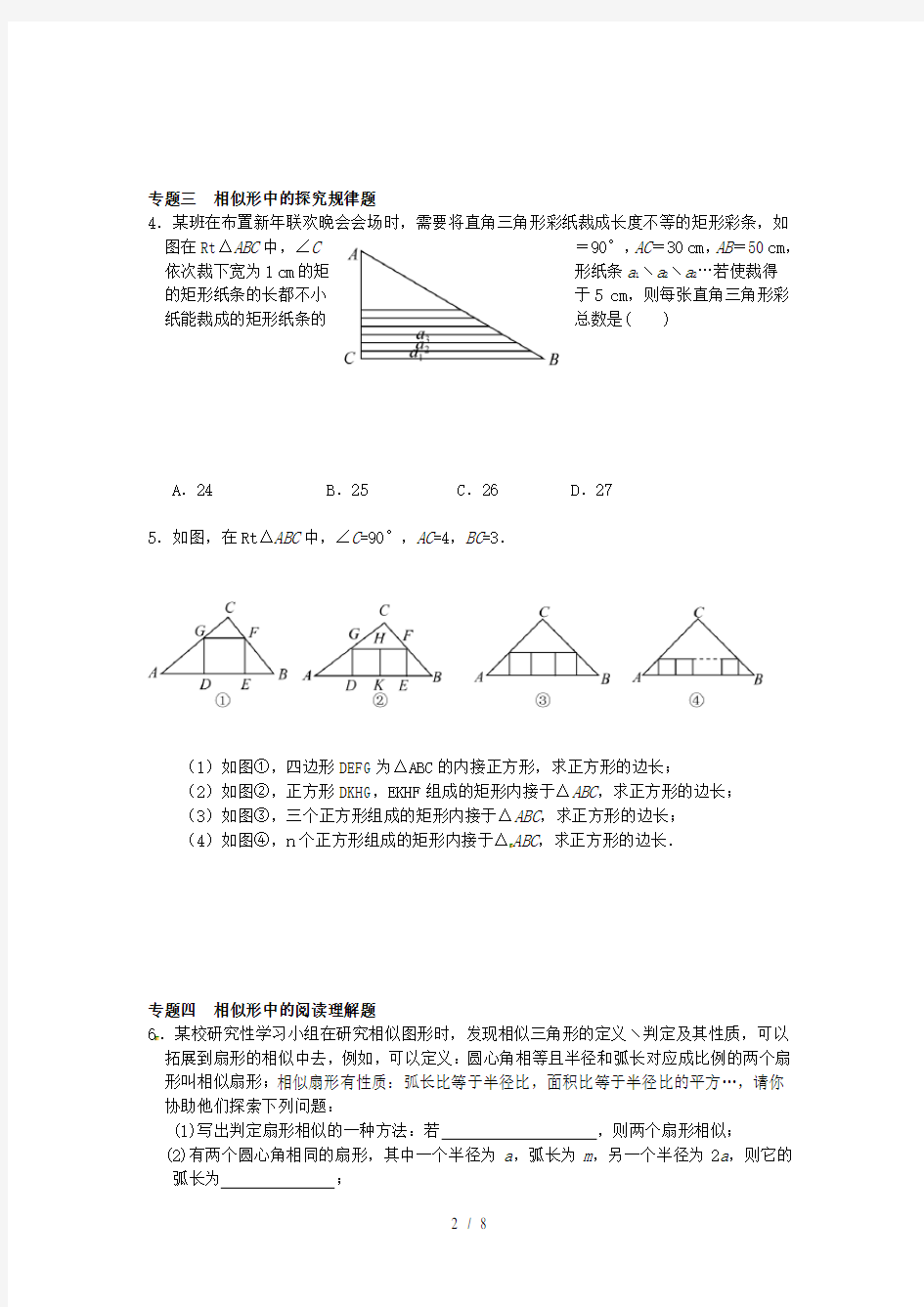
4.某班在布置新年联欢晚会会场时,需要将直角三角形彩纸裁成长度不等的矩形彩条,如图在Rt△ABC中,∠C=90°,AC=30 cm,AB=50 cm,依次裁下宽为1 cm的矩形纸条a1﹨a2﹨a2…若使裁得
的矩形纸条的长都不小于5 cm,则每张直角三角形彩纸能裁成的矩形纸条的总数是( )
A.24 B.25 C.26 D.27
5.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.
(1)如图①,四边形DEFG为△ABC的内接正方形,求正方形的边长;
(2)如图②,正方形DKHG,EKHF组成的矩形内接于△ABC,求正方形的边长;
(3)如图③,三个正方形组成的矩形内接于△ABC,求正方形的边长;
(4)如图④,n个正方形组成的矩形内接于△ABC,求正方形的边长.
专题四相似形中的阅读理解题
6.某校研究性学习小组在研究相似图形时,发现相似三角形的定义﹨判定及其性质,可以拓展到扇形的相似中去,例如,可以定义:圆心角相等且半径和弧长对应成比例的两个扇形叫相似扇形;相似扇形有性质:弧长比等于半径比,面积比等于半径比的平方…,请你协助他们探索下列问题:
(1)写出判定扇形相似的一种方法:若,则两个扇形相似;
(2)有两个圆心角相同的扇形,其中一个半径为a,弧长为m,另一个半径为2a,则它的
弧长为;
(3)如图1,是—完全打开的纸扇,外侧两竹条AB和AC的夹角为120°,AB为30cm,现要
做一个和它形状相同,面积是它的一半的纸扇(如图2),求新做纸扇(扇形)的圆心角和半径.
图1 图2
专题五相似形中的操作题
7.宽与长的比是
21
5
的矩形叫黄金矩形,心理测试表明:黄金矩形令人赏心悦目,它给我们以协调﹨匀称的美感.
现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以N为圆心,ND长为半径画弧,交BC的延长线于E;
第四步:过E作EF⊥AD,交AD的延长线于F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
8.如图①,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起.
(1)操作:如图②,将△ECF 的顶点F 固定在△ABD 的BD 边上的中点处,△ECF 绕点 F 在BD 边上方左右旋转,设旋转时FC 交BA 于点H (H 点不与B 点重合),FE 交DA 于点G
(G 点不与D 点重合).求证:BH?GD=BF 2;
(2)操作:如图③,△ECF 的顶点F 在△ABD 的BD 边上滑动(F 点不与B ﹨D 点重合), 且CF 始终经过点A ,过点A 作AG ∥CE ,交FE 于点G ,连接DG .
探究:FD +DG = DB ,请给予证明.
专题六 相似形中的综合题
9.正方形ABCD 的边长为4,M ﹨N 分别是BC ﹨CD 上的两个动点,且始终保持AM ⊥MN .当BM = 时,四边形ABCN 的面积最大.
10.如图,在锐角△ABC 中,AC 是最短边,以AC 的中点O 为圆心,
2
1AC 长为半径作⊙O ,交BC 于E ,过O 作OD ∥BC 交⊙O 于D ,连接AE ﹨AD ﹨DC .
(1)求证:D 是 ⌒AE 的中点;
(2)求证:∠DAO =∠B +∠BAD ;
(3)若21=??OCD CEF S S ,且AC =4,求CF 的长.
【知识要点】
1.平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例.
2.平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等.
3.平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
4.如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
5.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
6.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
7.相似三角形周长的比等于相似比.相似多边形周长的比等于相似比.
8.相似三角形对应高的比等于相似比.
9.相似三角形面积的比等于相似比的平方. 相似多边形面积的比等于相似比的平方.
【温馨提示】
1.平行线分线段成比例时,一定找准对应线段.
2.当已知两个三角形有一组对应角相等,利用夹这个角的两边对应成比例来判定它们相似时,比例式常有两种情况,考虑不全面是遗漏解的主要原因.
3.数学猜想需要严密的推理论证说明其正确性,规律的发现与提出需要从特殊到一般的数学归纳思想,平时要养成观察﹨分析问题的习惯.
【方法技巧】
1.相似三角形对应角平分线的比等于相似比;相似三角形对应中线的比等于相似比.
2.在平面几何中,求图形中等积式或等比式时,一般地首先通过观察找出图形中相似的三角形,再从理论上证明观察结论的正确性,最后运用相似形的性质来解决问题.
参考答案
1.22或4
2 【解析】根据题意得AD =1,AB=3,AC =2266+=26,
∵∠A=∠A ,∴若△ADE∽△ABC 时,AC AE AB AD =,即2631AE =,解得AE =22. 若△ADE∽△ACB 时,AB AE AC AD =,即1362AE =,解得AE=42. ∴当AE =22或42时,以点A ﹨D ﹨E 为顶点的三角形与△ABC 相似. 2.解:(1)△ADE∽△ACB ,△CEF∽△DBF ,△EFB∽△CFD (不唯一).
(2)由∠BDE+∠BCE =180°,可得∠ADE=∠BCE . ∵∠A=∠A,∴△ADE∽△ACB ; ∴AC AD =AB
AE .∵ ∠A=∠A , ∴△AEB∽△ADC ;∵∠BDE+∠BC E =180°,∠BCE+∠ECF =180°,
∴∠ECF=∠BDF ,
又∠F=∠F ,
∴△CEF∽△DBF ;∴BF EF =DF
CF ,而∠F=∠F ,∴△EFB∽△CFD . 3.解:∵ OA :OC =OB :OD =n 且∠AOB=∠COD,∴△AOB∽△COD .
∵ OA:OC =AB:CD =n ,
又∵CD =b,∴AB=CD ·n =nb ,∴x =a -AB 2 =a -nb 2
. 4.C 【解析】设裁成的矩形纸条的总数为n ,且每条纸条的长度都不小于5cm ,
2240(cm)BC AB AC =-=.设矩形纸条的长边分别与AC ﹨AB 交于点M ﹨N ,因为
△AMN ∽△ACB ,所以BC MN AC AM =.又因为AM=AC-1·n=30-n ,MN ≥5 cm ,所以4053030≥-n ,得n ≤26.25,所以n 最多取整数26.
5.解:(1)在题图①中过点C 作CN ⊥AB 于点N ,交GF 于点M .
因为∠C =90°,AC =4,BC =3,所以AB =5. 因为
21×5CN=21×3×4,所以CN=5
12. 因为GF∥AB ,所以∠CGF=∠A,∠CFG=∠B ,所以△CGF∽△CAB ,所以AB GF CN CM =. 设正方形的边长为x ,则1251255
x x -=,解得37
60=x .所以正方形的边长为3760. (2)同(1),有12251255
x x -=,解得49
60=x . (3)同(1),有12351255
x x -=,解得61
60=x .
(4)同(1),有1251255x nx -=,解得n x 122560+=. 6.解:(1)答案不唯一,如“圆心角相等” “半径和弧长对应成比例”
(2)由相似扇形的性质知半径和弧长对应成比例,设另一个扇形的弧长为x ,则a a 2=x m ,∴x =2m.
(3)∵两个扇形相似,∴新做扇形的圆心角与原来扇形的圆心角相等,等于120°.
设新做扇形的半径为γ,则2
30γ?? ???=21,γ=152,即新做扇形的半径为152㎝. 7.证明:在正方形ABCD 中,取AB=2a ,∵N 为BC 的中点,∴12
NC BC a =
=. 在Rt△DNC 中,2222(2)5.ND NC CD a a a =+=+=
∵NE=ND ,∴(51)CE NE CN a =-=-. ∴2
152)15(-=-=a a CD CE ,故矩形DCEF 为黄金矩形. 8.解:(1)证明:∵将菱形纸片AB (E )CD (F )沿对角线BD (EF )剪开,∴∠B =∠D . ∵将△ECF 的顶点F 固定在△ABD 的BD 边上的中点处,△ECF 绕点F 在BD 边上方
左右旋转,∴BF =DF .
∵∠HFG =∠B ,∴∠GFD =∠BHF ,∴△BFH∽△DGF ,∴
BF BH DG DF =, ∴BH?GD =BF 2.
(2)证明:∵AG∥CE ,∴∠FAG∥∠C .∵∠CFE=∠CEF ,∴∠AGF=∠CFE ,∴AF=AG . ∵∠BAD=∠C ,∴∠BAF=∠DAG ,△ABF≌△ADG ,∴FB=DG ,∴FD+DG=DB ,
9.2
10.解:(1)证明:∵AC 是⊙O 的直径,∴AE ⊥BC. ∵OD ∥BC ,∴AE ⊥OD ,∴D 是 ⌒AE 的中点.
(2)方法一:证明:如图,延长OD 交AB 于G ,则OG ∥BC .
∴∠AGD=∠B .
∵OA=OD ,∴∠DAO=∠ADO . ∵∠ADO=∠BAD+∠AGD ,∴∠DAO=∠B +∠BAD. 方法二:证明:如图,延长AD 交BC 于H ,则∠ADO=∠AHC .
∵∠AHC=∠B +∠BAD ,∴∠ADO =∠B +∠BAD . ∵OA=OD ,∴∠DAO=∠B +∠BAD .
(3) ∵AO=OC ,∴12
OCD ACD S S ??=.∵12CEF OCD S S ??=,∴14CEF ACD S S ??=. ∵∠ACD=∠FCE ,∠ADC=∠FEC =90°,∴△ACD∽△FCE .
∴
2
CEF
ACD
S CF
S AC
?
?
??
= ?
??
,即
2
1
44
CF
??
= ?
??
,∴CF=2.