
高中数学选修4-1切线长定理及弦切角练习题(一)填空
1.已知:如图7-143,直线BC切⊙O于B点,AB=AC,AD=BD,那么∠A=____.
2.已知:如图7-144,直线DC与⊙O相切于点C,AB为⊙O直径,AD⊥DC 于D,∠DAC=28°侧∠CAB=____ .
3.已知:直线AB与圆O切于B点,割线ACD与⊙O交于C和D
4.已知:如图7-145,PA切⊙O于点A,割线PBC交⊙O于B和C两点,∠P=15°,∠ABC=47°,则∠C= ____.
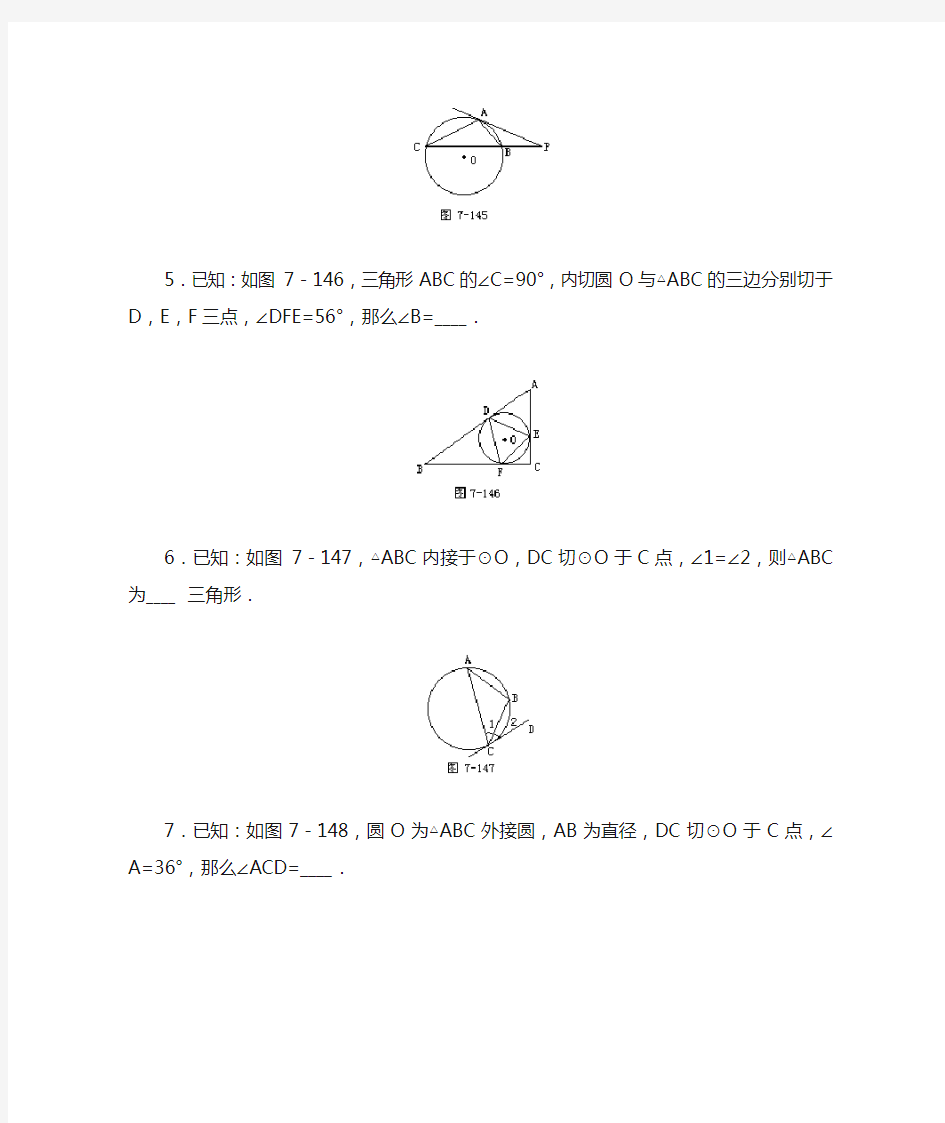
5.已知:如图7-146,三角形ABC的∠C=90°,内切圆O与△ABC的三边分别切于D,E,F三点,∠DFE=56°,那么∠B=____.
6.已知:如图 7-147,△ABC内接于⊙O,DC切⊙O于C点,∠1=∠2,则△ABC为____ 三角形.
7.已知:如图7-148,圆O为△ABC外接圆,AB为直径,DC切⊙O于C点,∠A=36°,那么∠ACD=____.
(二)选择
8.已知:△ABC内接于⊙O,∠ABC=25°,∠ACB= 75°,过A点作⊙O的切线交BC的延长线于P,则∠APB等于
[ ]
A.62.5°;B.55°;C.50°;D.40°.
9.已知:如图 7-149,PA,PB切⊙O于A,B两点,AC为直径,则图中与∠PAB相等的角的个数为
[ ]
A.1 个;B.2个;C.4个;D.5个.
10.已知如图7-150,四边形ABCD为圆内接四边形,AB是直径,MN切⊙O 于C点,∠BCM=38°,那么∠ABC的度数是
[ ]
A.38°;B.52°;C.68°;D.42°.
11.已知如图7-151,PA切⊙O于点A,PCB交⊙O于C,B两点,且 PCB 过点 O,AE⊥BP交⊙O于E,则图中与∠CAP相等的角的个数是
[ ]
A.1个;B.2个;C.3个;D.4个.
(三)计算
12.已知:如图7-152,PT与⊙O切于C,AB为直径,∠BAC=60°,AD为⊙O一弦.求∠ADC与∠PCA的度数.
13.已知:如图7-153,PA切⊙O于A,PO交⊙O于B,C,PD平分∠APC.求∠ADP的度数.
14.已知:如图7-154,⊙O的半径OA⊥OB,过A点的直线交OB于P,交⊙O于Q,过Q引⊙O的切线交OB延长线于C,且PQ=QC.求∠A的度数.
15.已知:如图7-155,⊙O内接四边形ABCD,MN切⊙O于C,∠BCM=38°,AB为⊙O直径.求∠ADC的度数.
16.已知:如图7-156,PA,PC切⊙O于A,C两点,B点
17.已知:如图 7-157,AC为⊙O的弦,PA切⊙O于点A,PC过O点与⊙O 交于B,∠C=33°.求∠P的度数.
18.已知:如图7-158,四边形ABCD内接于⊙O,EF切⊙O
19.已知 BA是⊙O的弦,TA切⊙O于点A,∠BAT= 100°,点M在圆周上但与A,B不重合,求∠AMB的度数.
20.已知:如图7-159,PA切圆于A,BC为圆直径,∠BAD=∠P,PA=15cm,PB=5cm.求 BD的长.
21.已知:如图7-160,AC是⊙O直径,PA⊥AC于A,PB切⊙O于B,BE ⊥AC于E.若AE=6cm,EC=2cm,求BD的长.
22.已知:如图7-161所示,P为⊙O外一点,PA切⊙O于A,从PA中点M 引⊙O割线MNB,∠PNA=138°.求∠PBA的度数.
23.已知:如图7-162,DC切⊙O于C,DA交⊙O于P和B两点,AC交⊙O 于Q,PQ为⊙O直径交BC于E,∠BAC=17°,∠D=45°.求∠PQC与∠PEC的度数.
24.已知:如图 7-163,QA切⊙O于点A,QB交⊙O于B
25.已知:如图7-164,QA切⊙O于A,QB交⊙O于B和C
26.已知:在图7-165中,PA切⊙O于A,AD平分∠BAC,PE平分∠APB,AD=4cm,PA=6cm.求EP的长.
27.已知;如图7-166,PA为△ABC外接圆的切线,A 为切点,DE∥AC,PE=PD.AB=7cm,AD=2cm.求DE的长.
28.已知:如图 7-167,BC是⊙O的直径,DA切⊙O于A,DA=DE.求∠BAE 的度数.
29.已知:如图 7-168,AB为⊙O直径,CD切⊙O于CAE∠CD于E,交BC 于F,AF=BF.求∠A的度数.
30.已知:如图7-169,PA,PB分别切⊙O于A,B,PCD为割线交⊙O于C,D.若 AC=3cm,AD=5cm,BC= 2cm,求DB的长.
ABCD的顶点A,D,C在圆O上,AB的延长线
31.已知:如图7-170,
与⊙O交于M,CB的延长线与⊙O交于点N,PD切⊙O于D,∠ADP=35°,∠ADC=108°.求∠M的度数.
32.已知:如图7-171,PQ为⊙O直径,DC切⊙O于C,DP交⊙O于B,交CQ延长线于A,∠D=45°,∠PEC=39°.求∠A的度数.
33.已知:如图 7-172,△ABC内接于⊙O,EA切⊙O于A,过B作BD∥AE 交AC延长线于D.若AC=4cm,CD= 3cm,求AB的长.
34.已知:如图7-173,△ABC内接于圆,FB切圆于B,CF⊥BF于F交圆于 E,∠1=∠2.求∠1的度数.
35.已知:如图7-174,PC为⊙O直径,MN切⊙O于A,PB⊥MN于B.若PC=5cm,PA=2cm.求PB的长.
36.已知:如图7-175,AD为⊙O直径,CBE,CD分别切⊙
37.已知:如图7-176,圆内接四边形ABCD的AB边经过圆心,AD,BC的延长线相交于E,过C点的切线CF⊥AE于F.求证:
(1)△ABE为等腰三角形;
(2)若 BC=1cm,AB=3cm,求EF的长.
38.已知:如图7-177,AB,AC切⊙O于B,C,OA交⊙O于F,E,交BC 于D.
(1)求证:E为△ABC内心;
(2)若∠BAC=60°,AB=a,求OB与OD的长.
(四)证明
39.已知:在△ABC中,∠C=90°,以C为圆心作圆切AB边于F点,AD,BC分别与⊙C切于D,E两点.求证:AD∥BE.
40.已知:PA,PB与⊙O分别切于A,B两点,延长OB到C,
41.已知:⊙O与∠A的两边分别相切于D,E.在线段AD,AE(或在它们的延长线)上各取一点B,C,使DB=EC.求证:OA⊥BC.
⊥EC于H,AO交BC于D.求证:
BC·AH=AD·CE.
*43.已知:如图7-178,MN切⊙O于A,弦BC交OA于E,过C点引BC的垂线交MN于D.求:AB∥DE.
44.已知:如图7-179,OA是⊙O半径,B是OA延长线上一点,BC切⊙O 于C,CD⊥OA于D.求证:CA平分∠BCD.
45.已知:如图7-180,BC是⊙O直径,EF切⊙O于A点,AD⊥BC于D.求证:AB平分∠DAE,AC平分∠DAF.
46.已知:如图7-181,在△ABC中,AB=AC,∠C= 2∠A,以 AB为弦的圆O与 BC切干点 B,与 AC交于 D点.求证:AD=DB=BC.
47.已知:如图7-182,过△ADG的顶点A作直线与DG的延长线相交于C,过G作△ADG的外接圆的切线二等分线段AC于E.求证:AG2=DG·CG.
48.已知:如图7-183,PA,PB分别切⊙O于A,B两点,PCD为割线.求证:AC·BD=BC·AD.
BC=BA,连结AC交圆于点E.求证:四边形ABDE是平行四边形.
50.已知:如图7-185,∠1=∠2,⊙O过A,D两点且交AB,AC于E,F,BC切⊙O于D.求证:EF∥BC.
51.已知:如图7-186,AB是半圆直径,EC切半圆于点C,BE⊥CE交AC 于F.求证:AB=BF.
52.已知:如图7-187,AB为半圆直径,PA⊥AB,PC切半圆于C点,CD⊥AB于D交PB于M.求证:CM=MD.
(五)作图
53.求作以已知线段AB为弦,所含圆周角为已知锐角∠α(见图7-188)的弧(不写作法,写出已知、求作,答出所求).
54.求作一个以α为一边,所对角为∠α,此边上高为h的三角形.
55.求作一个以a为一边,m为此边上中线,所对角为∠α的三角形(不写作法,答出所求).
切线长定理及弦切角练习题(答案)
(一)填空
1.36° 2.28° 3.50° 4.32°
5.22° 6.等腰 7.54°
(二)选择
8.C 9.D 10.B 11.C
(三)计算
12.30°,30°.
13.45°.提示:连接AB交PD于E.只需证明∠ADE=∠AED,证明时利用三角形外角定理及弦切角定理.
14.30°.提示:因为PQ=QC,所以∠QCP=∠QPC.连接OQ,则知∠POQ与∠QCP互余.又∠OAQ=∠OQA与∠QPC互余,所以∠POQ=∠OAQ=∠OQA.而它们的和为90°(因为∠AOC=90°).所以∠OAQ=30°
16.67.5°.提示:解法一连接AC,则∠PAC=∠PCA.又∠P=45°,所以∠PAC=∠PCA=67.5°.从而∠B=∠PAC=67.5°.
解法二连接OA,OC,则∠AOC=180°-∠P=135°,所以
17.24°.提示:连接OA,则∠POA=66°.
18.60°.提示:连接BD,则∠ADB=40°,∠DBC=20°.设∠ABD=∠BDC(因为AB//CD)=x°,则因∠B+∠D=180°,所以2x°+60°=180°,x°=60°,从而∠ADE=∠ABD=60°.
19.100°或80°.提示: M可在弦AB对的两弧的每一个上.
从而
22.42°.提示:∠ABM=∠NAM.于是显然△ABM∽△NAM,
NMP,所以△PMB∽△NMP,从而∠PBM=∠NPM.再由∠ABM=∠NAM,就有
∠PBA=∠PBM+∠NAM=∠NPM+∠NAM
=180°-∠PNA=42°.
23.28°,39°.提示:连接PC.
24.41°.提示:求出∠QAC和∠ACB的度数.
25.100°.
以DB=9.因为2DP2=2×9,由此得DP2=9.又DP>0,所以DP=3,从而,DE=2×3=6(cm).
28.45°.提示:连接AC.由于DA=DE,所以∠ABE+∠BAE=∠AED=∠EAD=∠CAD+∠CAE,但∠ABE=∠CAD,所以∠BAE=∠CAE.由于∠BAE+∠CAE=90°,所以∠BAE=45°.
29.60°.提示:解法一连接AC,则AC⊥BC.又AF⊥CE,所以∠ACE=∠F.又DC切⊙O于C,所以∠ACE=∠B.所以∠F=∠B.因为AF=BF,所以∠BAF=∠B=∠F.所以∠BAF=60°.
31.37°.提示:连接AC,则∠M=∠ACN=∠CAD.
32.17°.提示:连接PC,则∠QPC+∠PBC=90°.
45°=∠D=(∠BPQ+∠QPC)∠DCP
=(∠BPQ+∠QPC)-∠PBC
=[∠BPQ+(90°-∠PBC)]-∠PBC.
所以
2∠PBC-∠BPQ=45°.
(1)
又
∠PBC+∠BPQ=39°,
(2)
从而∠PBC=28°,∠BPQ=11°.于是∠A=∠PBC-∠BPQ=17°.
34.30°.提示:连接BE,由∠1=∠2,可推出∠EBF=∠ECB=∠EBC,而这三个角的和为90°,所以每个角为30°.
36.60°.提示:连接OB,则OB⊥CE,从而∠C=∠BOE= 60°.
37.(1)提示:连接OC,则∠E=∠OCB=∠OBC=∠CDE,所以△ABE为等腰三角形.
38.(1)提示:连接BE.只需证明∠ABE=∠DBE.
(四)证明
39.提示:AC,BC各平分∠A,∠B.设法证出∠A+∠B=180°.
40.提示:连接OP,设法证出∠BPC=∠BPO.
42.提示:在△BCE和△DAH中,∠BCE=∠DAH(它们都与∠DCH互补).又A,D,C,H共圆,所以∠CEB=∠ACB=∠AHD,从而△BCE∽△DAH.这就得所要证明的比例式.
43.提示:连接AC.先证明A,E,C,D四点共圆.由此得∠ADE=(∠ACE=)∠MAB,所以AB//DE.
44.提示:证法一延长AO交⊙O于点E,连接EC,则∠BCA=∠E,且∠ACD=∠E.所以∠BCA=∠ACD.
证法二连接OA,则∠BCA与∠OCA互余;又∠ACD与∠OAC互余,而∠OCA=∠OAC,所以∠BCA=∠ACD.
46.提示:由已知得∠A=36°,∠B=∠C=72°,∠DBC=∠A=36°,所以∠ABD=36°,从而AD=BD.又∠C=∠CDB=72°,所以BD=BC.
47.提示:过A作CD的平行线交BC于H,则AH=CG.然后证
AG2=DG·AH=DG·CG.
49.提示:因为BC=BA,所以∠A=(∠C=)∠D;又∠CED=∠DBF(BF是AB 的延长线),所以它们的补角∠DEA=∠ABD.从而四边形ABDE是平行四边形.
50.提示:连接DE,则∠BDE=∠1=∠2=∠FED.所以EF//BC.
51.提示:连接BC,则∠ACB=90°=∠FCB.因为CE⊥BE,所以∠F=∠ECB.因为EC切半圆于C,所以∠ECB=∠A,所以∠A=∠F,因此AB=BF.
52.提示:连接AC,BC并延长BC交AP延长线于点N.首先
所以CM=MD.
切线长定理典型练习题 一、填空题 1、如图AB 为⊙O 的直径,CA 切⊙O 于点A ,CD=1cm ,DB=3cm ,则AB=______cm 。 2、已知三角形的三边分别为 3、 4、5,则这个三角形的内切圆半径是 。 3、三角形的周长是12,面积是18,那么这个三角形的内切圆半径是 。 二、选择题 1、△ABC 内接于圆O ,AD ⊥BC 于D 交⊙O 于E ,若BD=8cm , CD=4cm ,DE=2cm ,则△ABC 的面积等于( ) A.248cm B.296cm C.2108cm D.232cm 2、正方形的外接圆与内切圆的周长比为( ) A. 1:2 B. 2:1 C. 4:1 D. 3:1 3、在三角形内,与三角形三条边距离相等的点,是这个三角形的 ( ) A.三条中线的交点, B.三条角平分线的交点, C.三条高的交点, D.三边的垂直平分线的交点。 4、△ABC 中,内切圆I 和边BC 、CA 、AB 分别相切于点D 、E 、F ,则∠FDE 与∠A 的关系 是 ( ) A. ∠FDE=21∠A B . ∠FDE+21∠A=180° C . ∠FDE+2 1∠A=90° D . 无法确定 三、解答题: 1、如图,AB 、CD 分别与半圆O 切于点A 、D ,BC 切⊙O 于点E ,若AB =4,CD =9,求⊙O 的半径。 2、等腰三角形的腰长为13cm ,底边长为10 cm ,求它的内切圆的半径。 3、如图,在△ABC 中,∠C=90°,以BC 上一点O 为圆心,以OB 为半径的圆交AB 于点M ,交BC 于点N 。 (1)求证:B A ·BM=BC ·BN ; (2)如果CM 是⊙O 的切线,N 为OC 的中点。当AC=3时,求AB 的值。
切线长定理弦切角定理切割线定理相交弦定理 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】
切线长定理、弦切角定理、切割线定理、相交弦定理 以及与圆有关的比例线段 [学习目标] 1.切线长概念 切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直 线,它不可以度量长度。 2.切线长定理 对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相 等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆 外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆 外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5) 圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。 3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。 直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢(四个) 4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。 5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。 6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定 理。 7.与圆有关的比例线段 定理图形已知结论证法 相交弦 定理 ⊙O中,AB、CD为 弦,交于P. PA·PB= PC·PD. 连结AC、BD,证: △APC∽△DPB.
相交弦定理的推论⊙O中,AB为直 径,CD⊥AB于P. PC2=PA·PB.用相交弦定理. 切割线定理⊙O中,PT切⊙O于 T,割线PB交⊙O于 A PT2=PA·PB连结TA、TB,证: △PTB∽△PAT 切割线定理推论PB、PD为⊙O的两 条割线,交⊙O于 A、C PA·PB= PC·PD 过P作PT切⊙O于 T,用两次切割线定 理 圆幂定理⊙O中,割线PB交 ⊙O于A,CD为弦 P'C·P'D=r2- OP'2 PA·PB=OP2- r2 r为⊙O的半径 延长P'O交⊙O于 M,延长OP'交⊙O 于N,用相交弦定理 证;过P作切线用 切割线定理勾股定 理证 8.圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数||(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。 【典型例题】 例1.如图1,正方形ABCD的边长为1,以BC为直径。在正方形内作半圆O,过A作半圆切线,切点为F,交CD于E,求DE:AE的值。 图1 解:由切线长定理知:AF=AB=1,EF=CE 设CE为x,在Rt△ADE中,由勾股定理
切线的判定与性质、切线长定理 1.如图,AB为⊙O的直径,CE切⊙O于点C,CD⊥AB,D为垂足,AB=12㎝,∠B =300,则∠ECB=,CD=。 2.如图,CA为⊙O的切线,切点为A。点B在⊙O上,如果∠CAB=550,那么∠AOB 等于。 3.如图,P是⊙O外一点,PA、PB分别和⊙O相切于点A、B,C是⌒ AB上任意一点,过C作⊙O的切线分别交PA、PB于点D、E,(1)若PA=12,则△PDE的周长为____; (2)若△PDE的周长为12,则PA长为;(3)若∠P=40°,则∠DOE=____度。 (1题图) (2题图) (3题图) 4.下列说法:①与圆有公共点的直线是圆的切线;②垂直与圆的半径的直线是切线;③与 圆心的距离等于半径的直线是切线;④过圆直径的端点,垂直于该直径的直线的是切线。 其中正确命题有() A.①②B.②③C.③④D.①④ 5.如图,AB、AC与⊙O相切与B、C,∠A=500,点P是圆上异于B、C的一动点,则 ∠BPC的度数是。 6.如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的 ( ) A.三条中线的交点B.三条高的交点 C.三条角平分线的交点D.三条边的垂直平分线的交点 7.如图,⊙O分别与△ABC的边BC、CA、AB相切于D、E、F,∠A=800,则∠EDF =。 (5题图)(6题图)(7题图) 8.点O是△ABC的内心,∠BAO=200,∠AOC=1300,则∠ACB=。 9.已知:Rt△ABC中,∠C=900,AC=4,BC=3,则△ABC内切圆的半径 为。
10.若直角三角形斜边长为10㎝,其内切圆半径为2㎝,则它的周长为。 11.如图,BA与⊙O相切于B,OA与⊙O 相交于E,若AB=5,EA=1,则⊙O的半 径为。 12.如图,在△ABC中,I是内心,∠BIC=1300,则∠A的度数是。 13.如图,△ABC的内切圆⊙O与各边相切于点D、E、F,若∠FOD=∠EOD=1350,则 △ABC是() A.等腰三角形; B.等边三角形; C.直角三角形; D. 等腰直角三角形; (11题图)(12题图)(13题图) 14.如果两圆的半径分别为6cm和4cm,圆心距为8cm,那么这两个圆的位置关系是() A. 外离 B. 外切 C. 相交 D. 内切 15.若已知Rt△ABC中,斜边为26cm,内切圆的半径为4cm,那么它的两条直角边的长分 别为()cm A、7、27 B、8、26 C、16、18 D、24、104 16.已知两圆的半径分别是方程0 2 3 2= + -x x的两根,圆心距为3,则两圆的位置关系是__________. 17.两圆半径分别为5cm和4cm,公共弦长为6cm,则两圆的圆心距等于()cm。 A. 7 4+ B. 7 4- C. 7 4+或7 4- D. 41 18.从圆外一点向半径为9的圆作切线,已知切线长为18,?从这点到圆的最短距离为 (). A.3 9B.()13 9-C.()1 5 9-D.9 19.如图,AB为⊙O的直径,BC是圆的切线,切点为 B,OC平行于弦AD,求证:DC 是⊙O的切线。
C B O A D C E O A B D 弦切角定理测试卷 姓名 _____ 1.已知一个圆的弦切角等于50°,那么这个弦切角所夹的弧所对的圆心角的度数为 _______ . 2.如图,AB 是直径,点D 在AB 的延长线上,BD=OB ,若CD 切⊙O 于C 点,则∠CAB 的度数为 ,∠DCB 的度数为 ,∠ECA 的度数为 ___ . 3.如图,AB , AC 是⊙O 的两条切线,切点分别为 B 、 C 、 D 是优弧BC 上的点,已知 ∠BAC=800,那么∠BDC =______. 4.如图,AB 是⊙ O 的弦, AD 是⊙ O 的切线,C 为弧AB 上任一点,∠ACB=1080,那么∠BAD =______. 5.如图,PA , PB 切⊙ O 于 A , B 两点, AC ⊥PB ,且与⊙ O 相交于 D ,若∠DBC=220,则∠APB==________. 2题图 3题图 4题图 5 题图 6、如图,CD 是⊙O 的直径,AE 切⊙O 于点B ,连接DB ,若20D ? ,则DBE D的大小为( ) A. 20° B. 40° C. 60° D. 70° 7、如图,AB 是半圆O 的直径,C 、D 是半圆上的两点,半圆O 的切线PC 交AB 的延长线于点P ,∠PCB =25°,则∠ADC 为( ) A.105° B.115° C.120° D.125° 8、如图,AB 是⊙O 的直径,EF 切⊙O 于C ,AD ⊥EF 于D ,AD=2,AB=6,则AC 的长为( ) A.2 B.3 C.23 D.4 9、如图,AB 是⊙ O 的直径, AC , BC 是⊙ O 的弦, PC 是⊙ O 的切线,切点为 C ,∠BAC=350 ,那么∠ACP 等于( )A. 350 B. 550 C. 650 D. 125 6题图 7题图 8题图 9题图 10、如图,在⊙ O 中, AB 是弦, AC 是⊙ O 的切线, A 是切点,过 B 作BD ⊥AC 于D ,BD 交⊙ O 于 E 点,若 AE 平分∠BAD ,则∠BAD=( ) A. 300 B. 450 C. 500 D. 600 11、如图,E 是⊙O 内接四边形 ABCD 两条对角线的交点,CD 延长线与过 A 点的⊙ O 的切线交于F 点,若 ∠ABD=440,∠AED=1000 ,弧AD=弧AB , 则∠AFC 的度数为( ) A.780 B.920 C.560 D. 1450 C B A D C B A D P O C B D E O A F B P C O A C B D A P O A E B C O D
弦切角定理及其推论 定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。 弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半. 证明:设圆心为O,连接OC,OB,。 ∵∠TCB=90°-∠OCB ∵∠BOC=180°-2∠OCB ∴∠BOC=2∠TCB (定理:弦切角的度数等于它所夹的弧所对的圆心角的度数的一半)∵∠BOC=2∠CAB(同一弧所对的圆心角等于圆周角的两倍) ∴∠TCB=∠CAB (定理:弦切角的度数等于它所夹的弧的圆周角) 弦切角定理推论:两弦切角所夹的弧相等,则这两个弦切角也相等。 应用举例:
第一个算出地球周长的人 ──埃拉托色尼 2000多年前,有人用简单的测量工具计算出地球的周长。这个人就是古希腊的埃拉托色尼。 埃拉托色尼博学多才,他不仅通晓天文,而且熟知地理;又是诗人、历史学家、语言学家、哲学家,曾担任过亚历山大博物馆的馆长。 细心的埃拉托色尼发现:离亚历山大城约800公里的塞恩城(今埃及阿斯旺附近),夏日正午的阳光可以一直照到井底,因而这时候所有地面上的直立物都应该没有影子。但是,亚历山大城地面上的直立物却有一段很短的影子。他认为:直立物的影子是由亚历山大城的阳光与直立物形成的夹角所造成。从地球是圆球和阳光直线传播这两个前提出发,从假想的地心向塞恩城和亚历山大城引两条直线,其中的夹角应等于亚历山大城的阳光与直立物形成的夹角。按照相似三角形的比例关系,已知两地之间的距离,便能测出地球的圆周长。埃拉托色尼测出夹角约为7度,是地球圆周角(360度)的五十分之一,由此推算地球的周长大约为4万公里,这与实际地球周长(40076公里)相差无几。他还算出太阳与地球间距离为1.47亿公里,和实际距离1.49亿公里也惊人地相近。这充分反映了埃拉托色尼的学说和智慧。 埃拉托色尼是首先使用“地理学”名称的人,从此代替传统的“地方志”,写成了三卷专著。书中描述了地球的形状、大小和海陆分布。埃拉托色尼还用经纬网绘制地图,最早把物理学的原理与数学方法相结合,创立了数理地理学。
切线长定理练习题 一、选择题 1.下列说法中,不正确的是( ) A.三角形的内心是三角形三条内角平分线的交点 B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部 C.垂直于半径的直线是圆的切线 D.三角形的内心到三角形的三边的距离相等 2.给出下列说法: ①任意一个三角形一定有一个外接圆,并且只有一个外接圆; ②任意一个圆一定有一个内接三角形,并且只有一个内接三角形; ③任意一个三角形一定有一个内切圆,并且只有一个内切圆; ④任意一个圆一定有一个外切三角形,并且只有一个外切三角形. 其中正确的有( ) A.1个B.2个C.3个D.4个 3.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( ) A.21 B.20 C.19 D.18 4. 如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP, 则与∠PAB相等的角(不包括∠PAB本身)有( ) A.1个B.2个C.3个D.4个 4题图5题图6题图 5.如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的( ) A.三条中线的交点B.三条高的交点 C.三条角平分线的交点D.三条边的垂直平分线的交点 6.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( ) A.21 B.20 C.19 D.18 二、填空题
6.如图,⊙I 是△ABC 的内切圆,切点分别为点D 、E 、F ,若∠DEF=52o , 则∠A 的度为________. 6题图 7题图 8题图 7.如图,一圆内切于四边形ABCD ,且AB=16,CD=10,则四边形ABCD 的周长为________. 8.如图,已知⊙O 是△ABC 的内切圆,∠BAC=50o ,则∠BOC 为____________度. 三、解答题 9. 如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,求△ABC 的周长. 10. 如图,PA 、PB 是⊙O 的两条切线,切点分别为点A 、B ,若直径AC= 12,∠P=60o ,求弦AB 的长. 11. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°. (1)求∠APB 的度数; (2)当OA =3时,求AP 的长. 12.已知:如图,⊙O 内切于△ABC ,∠BOC =105°,∠ACB =90°,AB =20cm .求BC 、 AC 的长.
弦切角 1、教材分析 (1)知识结构 (2)重点、难点分析 重点:弦切角定理是本节的重点也是本章的重点内容之一,它在证明角相等、线段相等、线段成比例等问题时,有重要的作用;它与圆心角和圆周角以及直线形角的性质构成了完美的角的体系,属于工具知识之一. 难点:弦切角定理的证明.因为在证明过程中包含了由“一般到特殊”的数学思想方法和完全归纳法的数学思想,虽然在圆周角定理的证明中应用过,但对学生来说是生疏的,因此它是教学中的难点. 2、教学建议 (1)教师在教学过程中,主要是设置学习情境,组织或引导学生发现问题、分析问题、研究问题和归纳结论,应用知识培养学生的数学能力;在学生主体参与的学习过程中,让学生学会学习,并获得新知识; (2)学习时应注意:(Ⅰ)弦切角的识别由三要素构成:①顶点为切点,②一边为切线,③一边为过切点的弦;(Ⅱ)在使用弦切角定理时,首先要根据图形准确找到弦切角和它们所夹弧上的圆周角;(Ⅲ)要注意弦切角定理的证明,体现了从特殊到一般的证明思路. 教学目标: 1、理解弦切角的概念; 2、掌握弦切角定理及推论,并会运用它们解决有关问题; 3、进一步理解化归和分类讨论的数学思想方法以及完全归纳的证明方法. 教学重点:弦切角定理及其应用是重点. 教学难点:弦切角定理的证明是难点. 教学活动设计: (一)创设情境,以旧探新
1、复习:什么样的角是圆周角? 2、弦切角的概念: 电脑显示:圆周角∠CAB,让射线AC绕点A旋转,产生无数个圆周角,当AC绕点A 旋转至与圆相切时,得∠BAE. 引导学生共同观察、分析∠BAE的特点: (1)顶点在圆周上;(2)一边与圆相交;(3)一边与圆相切. 弦切角的定义: 顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。 3、用反例图形剖析定义,揭示概念本质属性: 判断下列各图形中的角是不是弦切角,并说明理由: 以下各图中的角都不是弦切角. 图(1)中,缺少“顶点在圆上”的条件; 图(2)中,缺少“一边和圆相交”的条件; 图(3)中,缺少“一边和圆相切”的条件; 图(4)中,缺少“顶点在圆上”和“一边和圆相切”两个条件. 通过以上分析,使全体学生明确:弦切角定义中的三个条件缺一不可。 (二)观察、猜想
一、填空 1.已知:如图7-143,直线BC切⊙O于B点,AB=AC,AD=BD,那么∠A=____. 2.已知:如图7-144,直线DC与⊙O相切于点C,AB为直径,AD⊥DC于D,∠DAC=28°,则∠CAB=____ . 3.已知:如图7-145,PA切⊙O于点A,∠P=15°,∠ABC=47°,则∠C= ____. 4.已知:如图7-146,三角形ABC的∠C=90°,内切圆O与△ABC的三边分别切于D,E,F三点,∠DFE=56°,那么∠B=____. 二、选择 5.已知:△ABC内接于⊙O,∠ABC=25°,∠ACB= 75°,过A点作⊙O的切线交BC的延长线于P,则∠APB等于() A.62.5°B.55° C.50°D.40° 6.已知:如图 7-149,PA,PB切⊙O于A,B两点,AC为直径, 则图中与∠PAB相等的角的个数为() A.1 个B.2个C.4个D.5个 7.已知如图7-150,四边形ABCD为圆内接四边形,AB是直径, MN切⊙O于C点,∠BCM=38°,那么∠ABC的度数是 A.38°B.52°C.68°D.42° 三、解答 8.已知:如图7-152,PT与⊙O切于C,AB为直径,∠BAC=60°, AD为⊙O一弦.求∠ADC与∠PCA的度数. 9.已知:如图7-154,⊙O的半径OA⊥OB,过A点的直线交OB于 P,交⊙O于Q,过Q引⊙O的切线交OB延长线于C,且PQ=QC.求 ∠A的度数.
10.已知:如图7-160,AC是⊙O直径,PA⊥AC于A,PB切⊙O于B,BE⊥AC于E.若AE=6cm,EC=2cm,求BD的长. 2 11.已知:如图7-185,∠1=∠2,⊙O过A,D两点且交AB,AC于E,F,BC切⊙O于D.求证:EF∥BC. 12.已知:如图7-176,圆内接四边形ABCD的AB边经过圆心,AD,BC的延长线相交于E,过C点的切线CF⊥AE于F.求证: (1)△ABE为等腰三角形; (2)若 BC=1cm,AB=3cm,求EF的长.
2019年中考数学知识点过关培优训练:弦切角定理(圆) 一.选择题 1.如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是() A.50°B.55°C.60°D.65° 2.如图,BD为圆O的直径,直线ED为圆O的切线,A、C两点在圆上,AC平分∠BAD且交BD于F点.若∠ADE=19°,则∠AFB的度数为何?() A.97°B.104°C.116°D.142° 3.点P是⊙O外一点,PA、PB分别切⊙O于点A、B,∠P=70°,点C是⊙O上的点(不与点A、B重合),则∠ACB等于() A.70°B.55°C.70°或110°D.55°或125° 4.如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°, ∠B=60°,则的度数为何() A.50°B.60°C.100°D.120° 5.如图,AB是⊙O的直径,DE为⊙O的切线,切点为B,点C在⊙O上,若∠CBE=40°,则∠A的度数为() A.30°B.40°C.50°D.60° 6.如图,直线AD与△ABC的外接圆相切于点A,若∠B=60°,则∠CAD等于()
A.30°B.60°C.90°D.120° 7.如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于() A.40°B.50°C.60°D.70° 8.如图,四边形ABCD内接于⊙O,AB=BC.AT是⊙O的切线,∠BAT=55°,则∠D等于() A.110°B.115°C.120°D.125° 9.如图,AB为⊙O的直径,C、D为⊙O上的点,直线MN切⊙O于C点,图中与∠BCN互余的角有() A.1个B.2个C.3个D.4个 10.已知:如图,E是相交两圆⊙M和⊙N的一个交点,且ME⊥NE,AB为外公切线,切点分别为A,B 连接AE,BE,则∠AEB的度数为()
切线长定理、弦切角定理、切割线定理、相交弦定理 以及与圆有关的比例线段 [学习目标] 1.切线长概念 切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。(PA 长) 2.切线长定理 对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。 3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。 直线AB 切⊙O 于P ,PC 、PD 为弦,图中几个弦切角呢?(四个) 4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。 5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。 6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。 7.与圆有关的比例线段 定理 图形 已知 结论 证法 相交弦定理 ⊙O 中,AB 、CD 为弦,交于P. PA·PB=PC·PD . 连结AC 、BD ,证:△APC∽△DPB . 相交弦定理的推论 ⊙O 中,AB 为直径,CD⊥AB 于P. PC 2 =PA·PB . (特殊情况) 用相交弦定理.
切割线定理 ⊙O 中,PT 切⊙O 于T ,割线PB 交⊙O 于A PT 2 =PA·PB 连结TA 、TB ,证:△PTB∽△PAT 切割线定理推论 PB 、PD 为⊙O 的两条割线,交⊙O 于A 、C PA·PB=PC·PD 过P 作PT 切⊙O 于T ,用两次切割线定理 (记忆的方法方法) 圆幂定理 ⊙O 中,割线PB 交⊙O 于A ,CD 为弦 P'C·P'D =r 2 -OP'2 PA·PB=OP 2-r 2 r 为⊙O 的半径 延长P'O 交⊙O 于M ,延 长OP'交⊙O 于N ,用相交 弦定理证;过P 作切线用切割线定理勾股定理证 8.圆幂定理:过一定点P 向⊙O 作任一直线,交⊙O 于两点,则自定点P 到两交点的两条线段之积为常数||(R 为圆半径),因为叫做点对于⊙O 的幂,所以将上述定理统称为圆幂定理。 【典型例题】 例1.如图1,正方形ABCD 的边长为1,以BC 为直径。在正方形内作半圆O ,过A 作半圆切线,切点为F ,交CD 于E ,求DE :AE 的值。 图1 解:由切线长定理知:AF =AB =1,EF =CE 设CE 为x ,在Rt△ADE 中,由勾股定理 ∴, ,
切线长定理练习题 一、填空 1.已知:如图7-143,直线BC切⊙O于B点,AB=AC,AD=BD,那么∠A=____.2.已知:如图7-144,直线DC与⊙O相切于点C,AB为⊙O直径,AD⊥DC于D,∠DAC=28°侧∠CAB=____ . 3.已知:直线AB与圆O切于B点,割线ACD与⊙O交于C和 D 4.已知:如图7-145,PA切⊙O于点A,割线PBC交⊙O于B和C两点,∠P=15∠ABC=47°,则∠C= ____. 5.已知:如图7-146,三角形ABC的∠C=90°,内切圆O与△ABC的三边分别切于D,E,F三点,∠DFE=56°,那么∠B=____. 6.已知:如图7-147,△ABC内接于⊙O,DC切⊙O于C点,∠1=∠2,则△ABC为____ 三角形. 7.已知:如图7-148,圆O为△ABC外接圆,AB为直径,DC切⊙O于C点,∠A=36°,那么∠ACD=____. 8.一个边长为4cm的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC 相交于点E,则CE 的长为_________cm. 9.如图,⊙O 的半径为3,P是CB 延长线上一点,PO=5,PA 切⊙O于A点,则PA=_________.10.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是_________°. 11.如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD.若∠A=25°,则∠C=_________度. (9题)(10题)(11题) 12.如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是 _________.(结果保留π) 13. 如图,⊙I ABC △的内切圆,点D E ,分别为边AB AC ,上的点,且DE为⊙I的切线,若ABC △的周长为21,BC边的长为6,则ADE △的周长为 14 已知:PA、PB分别切⊙O于点A和B,C为弧AB上一点,过C与⊙O相切的直线分别交PA、PB于点D和E,若PA=2cm,∠APB=60° 则(1)△PDE的周长= (2)∠DOE= . 二、选择 1.下列说法正确的是() A.相切两圆的连心线经过切点B.长度相等的两条弧是等弧 C.平分弦的直径垂直于弦D.相等的圆心角所对的弦相等 2.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于() A.20°B.25°C.40°D.50°
初中数学:切线长定理练习题 一、选择题 1.如图K-27-1,PA,PB分别切⊙O于点A,B,PA=10,CD切⊙O于点E,与PA,PB 分别交于C,D两点,则△PCD的周长是( ) 图K-27-1 A.10 B.18 C.20 D.22 2.如图K-27-2,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O 与AB,BC,AC分别切于点D,E,F,则AF的长为() 图K-27-2 A.5 B.10 C.7.5 D.4 3.已知⊙O的半径是4,P是⊙O外一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB的长为() A.4 B.4 2 C.4 3 D.2 3 4.如图K-27-3,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中,错误的是( ) 图K-27-3 A.∠1=∠2 B.PA=PB C.AB⊥OP D.PA2=PC·PO 5.如图K-27-4,AB为半圆O的直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点
E,连接OD,OC.下列结论:①∠DOC=90°;②AD+BC=CD;③S ∶S△BOC=AD2∶AO2;④OD∶ △AOD OC=DE∶EC;⑤OD2=DE·CD.其中正确的有( ) 图K-27-4 A.2个 B.3个 C.4个 D.5个 二、填空题 6.如图K-27-5,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD 的周长为________. 图K-27-5 7.如图K-27-6所示,在Rt△ABC中,∠C=90°,AC长为8,BC长为15,则△ABC的内切圆⊙O的直径是________. 图K-27-6 8.如图K-27-7,P是⊙O的直径AB的延长线上的一点,PC,PD分别切⊙O于点C,D.若PA=6,⊙O的半径为2,则∠CPD=________°. 图K-27-7 9.如图K-27-8所示,已知PA,PB,EF分别切⊙O于点A,B,D,若PA=15 cm,则△PEF的周长是________ cm;若∠P=50°,则∠EOF=________°.
中考复习专题——切线长定理与弦切角定理 【知识要点】 切线长定理:过圆外一点P做该圆的两条切线,切点为A、B。AB交PO于点C,则有如下结论: PA=PB PO⊥AB,且PO平分AB APO BPO OAC OBC ∠=∠=∠=∠;AOP BOP CAP CBP ∠=∠=∠=∠ 弦切角定理:弦切角(切线与圆的夹角)等于它所夹的弧所对的圆周角 推论:若两弦切角所夹的弧相等,则这两个弦切角也相等 【典型例题】 【例1】如图1,AB,AC是⊙O的两条切线,切点分别为B、C、D是优弧BC上的点,已知∠BAC=800,那么∠BDC =______. 图1 图2 图3 举一反三: 1.如图2,AB是⊙ O的弦,AD是⊙ O的切线,C为AB上任一点,∠ACB=1080,那么∠BAD =______. 2.如图3,PA,PB切⊙ O于A,B两点,AC⊥PB,且与⊙ O相交于D,若∠DBC=220,则∠APB=________.【例2】如图,已知圆上的弧AC BD =,过C点的圆的切线与BA的延长线交于E点,证明: (1)∠ACE=∠BCD; (2)BC2=BE×CD. 举一反三: 1.如图,AB是圆O的直径,D为圆O上一点,过D作圆O的切线交 AB的延长线于点C,若DA=DC,求证:AB=2BC. C B O A D C B A D P O
P B A O 【例3】已知:如图 7-149,PA ,PB 切⊙O 于A ,B 两点,AC 为直径,则图中与∠PAB 相等的角的个数为 A . 1 个; B .2个; C .4个; D .5个. 【例4】如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,求△ABC 的周长. 举一反三: 1. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°. (1)求∠APB 的度数; (2)当OA =3时,求AP 的长. 2.已知:如图,⊙O 内切于△ABC ,∠BOC=105°,∠ACB=90°,AB=20cm .求BC 、AC 的长. 3.已知:如图,△ABC 三边BC=a ,CA=b ,AB=c ,它的内切圆O 的半径长为r .求△ABC 的面积S .
弦切角 .弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。 .弦切角定理:弦切角等于其所夹的弧所对的圆周角。 与圆有关的比例线段 圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数| |(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。 1.如图1,正方形ABCD的边长为1,以BC为直径。在正方形内作半圆O, 过A作半圆切线,切点为F,交CD于E,求DE:AE的值。 2.⊙O中的两条弦AB与CD相交于E,若AE=6cm, BE=2cm,CD=7cm,那么CE=_________cm。 3.已知PA是圆的切线,PCB是圆的割线, 则________。 4.如图3,P是⊙O外一点,PC切⊙O于点C,PAB是⊙O的割线,交⊙O 于A、B两点,如果PA:PB=1:4,PC=12cm,⊙O的半径为10cm,则 圆心O到AB的距离是___________cm。 5.如图4,AB为⊙O的直径,过B点作⊙O的切线BC,OC交⊙O于 点E,AE的延长线交BC于点D,(1)求证:; (2)若AB=BC=2厘米,求CE、CD的长。 6.如图5,AB为⊙O的直径,弦CD∥AB,AE切⊙O于A,交CD 的延长线于E。 求证: 7.如图6,PA、PC切⊙O于A、C,PDB为割线。求证:AD·BC=CD·AB 8.如图8,在正方形ABCD中,AB=1,是以点B为圆心,AB长为半径的圆的 一段弧。点E是边AD上的任意一点(点E与点A、D不重合),过E作所在 圆的切线,交边DC于点F,G为切点。 当∠DEF=45°时,求证点G为线段EF的中点; 9.如图2,△ABC中,AC=2cm,周长为8cm,F、K、N是△ABC与内切圆的 切点,DE切⊙O于点M,且DE∥AC,求DE的长。
第3课时切线长定理和三角形的切圆 知识点 1 切线长定理 1.如图24-2-34,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中,错误的是( ) 图24-2-34 A.∠1=∠2 B.PA=PB C.AB⊥OP D.∠PAB=2∠1 2.如图24-2-35所示,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( ) 图24-2-35 A.4 B.8 C.4 3 D.8 3 3.如图24-2-36,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为( ) 图24-2-36 A.50° B.65° C.100° D.130°
4.如图24-2-37,PA,PB是⊙O的两条切线,A,B是切点,若∠APB=60°,PO=2,则⊙O的半径等于________. 图24-2-37 知识点 2 三角形的切圆 5.2017·如图24-2-38,⊙O是△ABC的切圆,则点O是△ABC的( ) 图24-2-38 A.三条边的垂直平分线的交点 B.三条角平分线的交点 C.三条中线的交点 D.三条高的交点 6.如图24-2-39,点O是△ABC的切圆的圆心,若∠BAC=80°,则∠BOC的度数为( ) 图24-2-39 A.130° B.120° C.100° D.90° 7.如图24-2-40,△ABC的切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC=28 cm,CA=26 cm,求AF,BD,CE的长.
图24-2-40 8.如图24-2-41所示,O是△ABC的心,过点O作EF∥AB,与AC,BC分别交于点E,F,则( ) 图24-2-41 A.EF>AE+BF B.EF<AE+BF C.EF=AE+BF D.EF≤AE+BF 9.2016·《九章算术》是数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形切圆的直径是多少步.”该问题的答案是________步. 10.如图24-2-42,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为________.
圆周角定理及圆的内接四边形 副标题 一、选择题(本大题共5小题,共15.0分) 1.如图,A,B,C是上三个点,,则下列说 法中正确的是 A. B. 四边形OABC内接于 C. D. 【答案】D 【解析】解:过O作于D交于E, 则, ,, , , , , ,故C错误; , , , ,故A错误; 点A,B,C在上,而点O在圆心, 四边形OABC不内接于,故B错误; , , ,故D正确; 故选D. 过O作于D交于E,由垂径定理得到,于是得到,推出,根据三角形的三边关系得到,故C错误;根据三角形内 角和得到, ,推出,故A错误;由点A,B, C 在上,而点O在圆心,得到四边形OABC不内接于,故B错误;根据余角的性质得到,故D正确; 本题考查了圆心角,弧,弦的关系,垂径定理,三角形的三边关系,正确的作出辅助线
是解题的关键. 2.如图,四边形ABCD内接于,AC平分,则下列 结论正确的是 A. B. C. D. 【答案】B 【解析】解:A、与的大小关系不确定,与AD不一定相等,故本选项错误; B、平分,,,故本选项正确; C、与的大小关系不确定,与不一定相等,故本选项错误; D、与的大小关系不确定,故本选项错误. 故选:B. 根据圆心角、弧、弦的关系对各选项进行逐一判断即可. 本题考查的是圆心角、弧、弦的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等. 3.如图,四边形ABCD内接于,若四边形ABCO是平行四 边形,则的大小为 A. B. C. D. 【答案】C 【解析】解:设的度数,的度数; 四边形ABCO是平行四边形, ; ,;而, , 解得:,,, 故选:C. 设的度数,的度数,由题意可得,求出即可解决问 题. 该题主要考查了圆周角定理及其应用问题;应牢固掌握该定理并能灵活运用. 4.如图,已知AC是的直径,点B在圆周上不与A、 C重合,点D在AC的延长线上,连接BD交于 点E,若,则
、填空 1 已知:如图 7 — 143,直线BC 切O O 于B 点,AB=AC , AD=BD ,那么/ A= ___________ 2. 已知:如图7 — 144,直线DC 与O O 相切于点 C, AB 为直径,AD 丄DC 于D ,/ DAC=28 则/ CAB= _______ . 3. 已知:如图 7 — 145, PA 切O O 于点 A ,/ P=15°,/ ABC=47 °,则/ C= __________ . 4. 已知:如图 7 — 146,三角形 ABC 的/C=90 °,内切圆 0与厶ABC 的三边分别切于 D , E , F 三点,/ DFE=56 °,那么/ B= _______ . 延长线于P ,则/ APB 等于( ) A . 1个 B . 2个 C . 4个 D . 5个 7.已知如图7— 150,四边形ABCD 为圆内接四边形,AB 是直 径,MN 切O O 于C 点,/ BCM=38 °,那么/ ABC 的度数是 A . 38° B . 52° C . 68° D . 42° 三、解答 &已知:如图7 — 152 , PT 与O O 切于C, AB 为直径,/ BAC=60 AD 为O O 一弦.求/ ADC 与/ PCA 的度数. 9. 已知:如图7— 154,O O 的半径 OA 丄OB ,过A 点的直线交 OB 于P,交O O 于Q,过Q 引O O 的切线交OB 延长线于C,且PQ=QC .求 A . 62.5 B . 55° C . 50° 40° PB 切O O 于A , B 两点, 直径,则图中与/ PAB 相等的角的个数为( ) 6.已知: 如图 7 — 149, PA , 5. 已知:△ ABC 内接于O O ,Z ABC=25 ,/ ACB= 75。,过A 点作O O 的切线交 BC 的 團 7-150
切线长定理练习题 1. 如图,已知为的角平分线,=,,以为圆心,为半径的圆分别交 ,于点,,连接并延长交于点. (1)求证:是的切线;(2)求的值. (3)若的半径为,求的值. 2. 如图,直线、、分别与相切于、、,且,,.求: (1)的度数;(2)的长;(3)的半径. 3. 如图,的直径,和是它的两条切线,切于,交于,交于.设 ,.(1)求证:.(2)探究与的函数关系. 4. 如图,,是的切线,、为切点,是的直径,. (1)求的度数;(2)当时,求的长. 5. 已知,如图,、是得切线,、是切点,过上的任意一点作的切线与、 分别交于点、。(1)连接和,若,求的度数. (2)若,求的周长. 6. 如图,边长为的正方形的边是的直径,是的切线,为 切点,点在上,是的弦,求的面积. 7. 如图,是的直径,,连接,分别过、作圆的切线,两切线交于点,若 已知的半径为,求的周长. 8. 如图,是的直径,点在上,是的中点,交的切线于点. (1)判断直线和的位置关系,并证明你的结论; (2)若,的半径为,求线段的长.
参考答案与试题解析 2019年3月19日初中数学 一、解答题(本题共计 8 小题,每题 10 分,共计80分) 1. 【答案】 证明:作于. ∵平分,,, ∴=, ∴是的切线. ∵=, ∴可以假设=,=,则=, ∵=, ∴, ∴是的切线,∵是的切线, ∴==,=,设=, ∴=, 在中,=, ∴, ∴, 连接, ∵是直径, ∴=, ∴=,=, ∴=, ∵=, ∴==, ∴=, ∵=, ∴, ∴=, ∵=, ∴=, ∴=,=,=, ∴=,∴=, ∴==, ∴. 【解析】 (1)作于.只要证明=即可; (2)假设=,=,则=,因为是的切线,是的切线,推出==,=,设=,推出=,在中,=,求出与关系即可解决问题; (3)想办法求出、即可解决问题; 2. 【答案】 解:(1)连接;根据切线长定理得:,,,;∵, ∴, ∴, ∴; (2)由(1)知,. ∵,, ∴由勾股定理得到:, ∴. (3)∵, ∴. 【解析】 (1)根据切线的性质得到平分,平分,,再根据平行线的性质得 ,则有,即; (2)由勾股定理可求得的长,进而由切线长定理即可得到的长; (3)最后由三角形面积公式即可求得的长. 3. 【答案】 (1)证明:∵和是的两条切线, ∴, , ∴.
2019 中考数学专题练习-圆的 切线长定理(含解析) 、单选题 1.如图,△ ABC是一张周长为17cm 的三角形的纸片,BC=5cm ,△O是它的内切圆,小明准备用剪刀在△O的右侧沿着与△O相切的任意一条直线MN 剪下△ AMN,则剪下的三角形的 变化 2.下列说法正确的是() A.过任意一点总可以作圆的两条切线 C. 过圆外一点所画的圆的两条切线长相等大于圆的 半径 3.如图,PA,PB 切△O于A,B 两点, CD 切△O于点E,交PA,PB 于C,D.若△O 56 周长为( A. 12cm C. 6cm D. 随直线MN 的变化而 径为1,△ PCD的周长等于2 ,则线段AB 的长是() ABCD 的四条边都相切,且AB=16,CD=10, 则四边形ABCD 的周长为() B. 52 C. 54 D. B. 圆的切线长就是圆的切线的长度 D. 过圆外一点所画的圆的切线长一 的半
5.如图,PA,PB,CD 与△O相切于点为A,B,E,若PA=7,则△ PCD的周长为()
A.8 B. 18 C. 16 D. 14 7. 如图,四边形 ABCD 中,AD 平行 BC ,△ ABC=90°,AD=2 ,AB=6 ,以 AB 为直径的半 △O 切 CD 于点 E ,F 为弧 BE 上一动点, 过 F 点的直线 MN 为半 △O 的切线, MN 交 BC 于 M , 8. 圆外切等腰梯 形的一腰长是 8,则这个等腰梯形的上底与下底长的和为( ) A. 4 B. 8 C. 12 D. 16 9. 如图, △ ABC 是一张三角形的纸片, △O 是它的内切圆,点 D 是其中的一个切点,已知 AD=10cm , 小明准备用剪刀沿着与 △O 相切的任意一条直线 MN 剪下一块三角形 (△ AMN ),则剪下的 △AMN 的周长为( ) A. 7 D. 10 B. 14 C. 10.5 交 CD 于 N ,则 △ MCN 的周长为( A. 9 B. 10 C. 3 D. 2 6.如图, 的周长是