Shannon _Fano_ Elias编码的实现

云南大学数学与统计学院上机实践报告课程名称：信息论基础实验年级：2009级上机实践成绩：指导教师：xxx姓名：xxx上机实践名称：Shannon-Fano-Elias编码与Shannon编码学号：xxx上机实践日期：2012-5-15上机实践编号：No.2专业：xxxx上机实践时间：2学时一、实验目的1. 进一步熟悉Shannon-Fano-Elias编码算法2. 进一步熟悉Shannon编码算法3. 学习编码程序的调试二、实验内容1.编程实现Shannon-Fano-Elias编码算法2.编程实现Shannon编码算法三、实验环境Microsoft visual c++6.0和个人计算机四、实验结果1. Shannon-Fano-Elias编码算法的源代码：#include<stdio.h>#include<math.h>#define n 4void main(){int i,j,a,k,t,x[n],l[n],code[n][n]={0};float p[n],F[n],F1[n],F2[n],s,b,q;printf("输入一组数组符号：x[n]\n");for(i=0;i<n;i++)scanf("%d",&x[i]);printf("\n");printf("输入符号的相应概率：p[n]\n");for(i=0;i<n;i++)scanf("%f",&p[i]);printf("\n");a=x[0];for(i=0;i<n;i++){if(x[i]>=a){k=i;s=0;for(j=0;j<k;j++){s=s+p[j];}F[i-1]=s;a=x[k];}if(a==x[n-1]){F[n-1]=1.0;}}a=x[0];for(i=0;i<n;i++){if(a==x[0]){F1[0]=p[0]/2;}if(a<x[i]){k=i;s=0;for(j=0;j<k;j++){s=s+p[j];}F1[i]=s+p[i]/2;a=x[k];}}for(i=0;i<n;i++){s=0;k=10;q=F1[i];code[i][j]=0;for(t=0,j=0;t<10;t++){if(q!=0){a=(int)(q*2);code[i][j]=a;b=(float)a/k;s=s+b;q=q*2-a;k=k*10;j++;}}F2[i]=s;}for(i=0;i<n;i++){q=log(1/p[i])/log(2)+1;l[i]=(int)(log(1/p[i])/log(2)+1);if((q-l[i])>0){l[i]=l[i]+1;}}printf("输出l[n]:\n");for(i=0;i<n;i++)printf("%4d",l[i]);printf("\n");printf("x p(x) F(x) F1(x) F2(x) l(x) Codeword:\n");for(i=0;i<n;i++){printf("%-5d%-8.3f%-8.4f%-8.4f%-8.4f%4d ",x[i],p[i],F[i],F1[i],F2[i],l[i]);for(j=0;j<l[i];j++){printf("%d",code[i][j]);}printf("\n");}}2.香农编码源代码：#include<stdio.h>#include<math.h>#define n 6void main(){int i,j,t,x[n],L[n],code[n][n]={0};float p[n],Pa[n],l[n],q,max;printf("输入一组数组符号：x[n]\n");for(i=0;i<n;i++)scanf("%d",&x[i]);printf("\n");printf("输入符号的相应概率：p[n]\n");for(i=0;i<n;i++)scanf("%f",&p[i]);printf("\n");for(j=0;j<n-1;j++) /*排序*/{for(i=0;i<n-j;i++){if(p[i+1]>p[i]){max=p[i];p[i]=p[i+1];p[i+1]=max;t=x[i];x[i]=x[i+1];x[i+1]=t;}}}Pa[0]=0; /*累加*/ for(i=1;i<n;i++){Pa[i]=Pa[i-1]+p[i-1];}for(i=0;i<n;i++) /*码字长度*/{l[i]=log(1/p[i])/log(2);L[i]=(int)(log(1/p[i])/log(2));if(l[i]==L[i]){L[i]=(int)(log(1/p[i])/log(2));}else{L[i]=(int)(log(1/p[i])/log(2))+1;}}for(i=0;i<n;i++) /*编码*/{q=Pa[i];for(j=0;j<L[i];j++){q=q*2;if(q>1){code[i][j]=1;q=q-1;}else{code[i][j]=0;}}}printf("x p(x) P(x) l(x)=log(1/p(x)) 码字长L(x) Codeword:\n"); for(i=0;i<n;i++){printf("%-5d%-8.3f%-8.2f%-20.4f%-8d ",x[i],p[i],Pa[i],l[i],L[i]);for(j=0;j<l[i];j++){printf("%d",code[i][j]);}printf("\n");}}1. Shannon-Fano-Elias编码的结果如下：2.香农编码结果：五、实验总结：通过Shannon-Fano-Elias编码与Shannon编码可以知道，Shannon-Fano-Elias编码与Shannon编码类似，只是香农编码首先进行排序，然后按照其公式计算其码字。

elias编码原理
Elias编码原理是一种对正整数进行编码的统一编码，由Peter Elias发明。

适用于预先无法获知最大编码整数的情况，而且小整数出现频率高，大整数出现频率低的情况。

其编码原理是对任何正整数NUM，对INT（Log2（NUM））+1进行一元编码，后缀上NUM二进制串除去最高位的子串。

例如：5的编码为001，01。

Elias编码可以分为Elias Delta Coding和Elias Gamma Coding两种。

1、Elias Delta Coding原理是对任何正整数NUM，对INT（Log2（NUM））+1进行Delta编码，后缀上NUM二进制串除去最高位的子串。

2、Elias Gamma Coding原理是对任何正整数NUM，对INT（Log2（NUM））+1进行Gamma编码，后缀上NUM二进制串除去最高位的子串。

关于Elias编码的解码思路，首先需要计算出Elias编码的开始的0的个数n，然后根据n可以确定数字的长度，再根据长度就可以通过截取字符串的方式得到原始数字。

Elias编码是一种非常优秀的压缩算法，它可以将任何正整数转化为一个二进制字符串，并且当数字较大时，转化出来的字符串仍然比较短。

此外，它还可以根据数字的大小动态地调整压缩后的长度，使得压缩后的数据既简洁又易于理解。

因此，Elias编码在实际应用中具有广泛的应用价值。

实验报告课程名称：信息论与编码姓名：系：专业：年级：学号：指导教师：职称：年月日实验三 Shannon 编码一、实验目的1、熟悉离散信源的特点；2、学习仿真离散信源的方法3、学习离散信源平均信息量的计算方法4、熟悉 Matlab 编程二、实验原理给定某个信源符号的概率分布，通过以下的步骤进行香农编码 1、信源符号按概率从大到小排列；12.......n p p p ≥≥≥2、确定满足下列不等式的整数码长i K 为()()1i i i lb p K lb p -≤<-+3、为了编成唯一可译码，计算第i 个消息的累加概率：4、将累加概率i P 变换成二进制数；5、取i P 二进制数的小数点后i K 位即为该消息符号的二进制码字。

三、实验内容1、写出计算自信息量的Matlab 程序2、写出计算离散信源平均信息量的Matlab 程序。

3、将程序在计算机上仿真实现，验证程序的正确性并完成习题。

四、实验环境Microsoft Windows 7 Matlab 6.5五、编码程序计算如下信源进行香农编码，并计算编码效率：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.06543210a a a a a a a P X MATLAB 程序：(1) a=[0.2 0.18 0.19 0.15 0.17 0.1 0.01]; k=length(a);y=0; for i=1:k-111()i i k k P p a -==∑for n=i+1:kif (a(i)<a(n))t=a(i);a(i)=a(n);a(n)=t;endendends=zeros(k,1);b=zeros(k,1);for m=1:ks(m)=y;y=y+a(m);b(m)=ceil(-log2(a(m)));z=zeros(b(m),1);x=s(m);p=b2d10(x);for r=1:b(m)z(r)=p(r);enddisp('Êä³ö½á¹ûΪ£º')disp('³öʸÅÂÊ'),disp(a(m))disp('ÇóºÍ½á¹û'),disp(s(m))disp('±àÂëλÊý'),disp(b(m))disp('×îÖÕ±àÂë'),disp(z')end(2) function y=b2d10(x)for i=1:8temp=x.*2;if(temp<1)y(i)=0;x=temp;elsex=temp-1;y(i)=1;endend(3) p=[0.2 0.19 0.18 0.17 0.15 0.1 0.01]; sum=0;sum1=0;for i=1:7a(i)=-log2(p(i));K(i)=ceil(a(i));R(i)=p(i)*K(i);sum=sum+R(i);c(i)=a(i)*p(i);sum1=sum1+c(i);endK1=sum;H=sum1;Y=H/K1;disp('ƽ¾ùÐÅÏ¢Á¿'),disp(H)disp('ƽ¾ùÂ볤'),disp(K1)disp('±àÂëЧÂÊ'),disp(Y)六、实验结果输出结果为：出事概率0.2000，求和结果0，编码位数3，最终编码000出事概率0.1900，求和结果0.2000，编码位数3，最终编码001出事概率0.1800，求和结果0.3900，编码位数3，最终编码011出事概率0.1700，求和结果0.5700，编码位数3，最终编码100出事概率0.1500，求和结果0.7400，编码位数3，最终编码101出事概率0.1000，求和结果0.8900，编码位数4，最终编码1110出事概率0.0100，求和结果0.9900，编码位数7，最终编码1111110编码效率：平均信息量2.6087平均码长3.1400编码效率0.8308七、实验总结通过本次的实验，掌握了Shannon编码的实验原理以及编码过程。

信息论基础Shannon-Fano-Elias编码与Shannon编码一、实验目的1. 进一步熟悉Shannon-Fano-Elias编码算法2. 进一步熟悉Shannon编码算法3. 学习编码程序的调试二、实验内容1.编程实现Shannon-Fano-Elias编码算法2.编程实现Shannon编码算法三、实验环境Microsoft visual c++6.0和个人计算机四、实验结果1.编程实现Shannon-Fano-Elias编码算法#include"iostream.h"#include<iomanip.h>#include"vector"#include"algorithm"#include"math.h"using namespace std;struct bitree{//定义结构用于存储编码结果的二叉树结构,在译码时用到char ch; //用于存储码符号char mz; //用于存储码字bitree * lchild;bitree * rchild;};struct data{//用于存储相关的信源符号以及其概率double p;char ch;vector<char> code;int ml;};bool sortspecial(data dt1,data dt2){//用于排序时用return dt1.p>dt2.p;}void print2(vector<char>vd){//用于打印译码结果for(int i=0;i<vd.size();i++)cout<<vd[i]<<" ";cout<<endl;}void read(vector <data> &vd){//用于读入相关的信源符号以及概率int n;while(true){cout<<"请输入信源符号数:";cin>>n;cout<<"请输入相应的信源符号及其概率:"<<endl;data dt;int i=0;while(i<n){cin>>dt.ch;cin>>dt.p;dt.ml=0;vd.push_back(dt);i++;}double sum=0;vector<data>::iterator pit;/* for(pit=vd.begin();pit!=vd.end();pit++){sum+=pit->p;}if(sum!=1){cout<<"你输入的概率不符合要求,请重新输入."<<endl;sum=0;continue;}*/sort(vd.begin(),vd.end(),sortspecial);break;}}void append(char ch1,char ch2,bitree *&bt){//用于再构造码字二叉树时向其中添加结点bitree * bit=new bitree;bit->ch=ch1;bit->mz=ch2;bit->lchild=NULL;bit->rchild=NULL;if(ch1=='0')bt->rchild=bit;else bt->lchild=bit;}void Creatmz1(vector<data>& vd,int begin1,int end1 ,double pn ,bitree *&bt) {//进行编码,用递归的方法进行编码int begin=begin1,end=end1;if(begin==end) return;else if(begin+1==end){return;}else if(begin+2==end){vd[begin].code.push_back('0');vd[begin].ml++;append('0',vd[begin].ch,bt);vd[end-1].code.push_back('1');vd[end-1].ml++;append('1',vd[end-1].ch,bt);return;}else{double sum0=0,sum1=0,sum2=0;do{sum1+=vd[begin].p;sum2=sum1+vd[begin+1].p;begin++;}while(fabs(sum1/pn-0.5)>fabs(sum2/pn-0.5));//用于找到上下两组码的分点使得其概率和近于相同for(int i=begin1;i<begin;i++){vd[i].code.push_back('0');vd[i].ml++;}if(begin1+1 == begin){append('0',vd[begin1].ch,bt);}else append('0','0',bt);for(int j=begin;j<=end1-1;j++){vd[j].code.push_back('1');vd[j].ml++;}if(begin+1 == end1){append('1',vd[begin].ch,bt);}else append('1','0',bt);Creatmz1(vd,begin1 ,begin,sum1,bt->rchild );//对分点前的进行编码Creatmz1(vd,begin ,end1,pn-sum1,bt->lchild);//对分点后的进行编码*/ }}void print1(vector<data> vd){//用于打印编码结果cout<<"xi"<<setw(8)<<"P(xi)"<<setw(8)<<"码长"<<setw(8)<<"码字"<<setw(8)<<endl;for(int i=0;i<vd.size();i++){cout<<vd[i].ch<<setw(8)<<vd[i].p<<setw(8)<<vd[i].ml<<setw(8);for(int j=0;j<vd[i].code.size();j++)cout<<vd[i].code[j];cout<<setw(8)<<endl;}}void clear(bitree * & bt){//对二叉树的动态存储空间进行释放if(bt!=NULL&&bt->lchild!=NULL)clear(bt->lchild);if(bt!=NULL&&bt->rchild!=NULL)clear(bt->rchild);delete bt;}bool des_code(vector <char> & vr,vector <char> vt,bitree *bt){//用二叉编码树进行解码if(bt==NULL){cout<<"码树不存在!!!"<<endl;return false;}int pit=0;bitree * mbt=bt;while ((mbt->lchild!=NULL||mbt->rchild!=NULL)||pit<vt.size()){if(mbt->lchild==NULL&&mbt->rchild==NULL&&mbt->mz!='0'){vr.push_back(mbt->mz);mbt=bt;}if(mbt->lchild!=NULL&& vt[pit]=='1'){mbt=mbt->lchild;pit++;}else if(mbt->rchild!=NULL&& vt[pit]=='0'){mbt=mbt->rchild;pit++;}else if(mbt->lchild!=NULL&&mbt->rchild!=NULL) break;}if(mbt->lchild!=NULL&&mbt->rchild!=NULL){cout<<"你输入的是一个错误的码序列,请较正后再输入."<<endl;return false;}else {vr.push_back(mbt->mz);return true;}}void read1(vector<char>& vd){//用于读入要解码的序列cout<<"请输要译码的序列(以'#'结束):"<<endl;char dt;int i=0;cin>>dt;while(dt!='#'){vd.push_back(dt);cin>>dt;}}void print_H_L_R(vector<data>vd){//用于计算并打印信息熵,平均码长,效率double H=0,L=0,R=0;for(int i=0;i<vd.size();i++){H+=vd[i].p*(log10(1/vd[i].p)/log10(2));L+=vd[i].p*(double)vd[i].ml;}R=H/L;cout<<"此码的信息熵(H)是:"<<H<<endl;cout<<"此码的平均码长(L)为:"<<L<<endl;cout<<"此码的效率(U)为:"<<R<<endl;}int main(){bitree * bt=new bitree;bt->ch = '#';bt->mz = '*';bt->lchild=NULL;bt->rchild=NULL;vector <data> vd;vector <char> vr;vector <char> vt;cout<<"************下面将对Fano编,译码的过程进行演示*************"<<endl;cout<<"__________________________________________________________"<<endl;cout<<endl;cout<<"************下面显示编码的过程及相关参数和结果************"<<endl;read(vd);if(vd.size()==1){vd[0].code.push_back('0');vd[0].ml++;append('0',vd[0].ch,bt);}cout<<endl;Creatmz1(vd,0,vd.size(),1,bt);cout<<"************** 编码结果**************"<<endl;print1(vd);print_H_L_R(vd);cout<<endl;cout<<"************ 下面将进行译码过程操作的演示************"<<endl;cout<<endl;read1(vt);if(des_code(vr,vt,bt))print2(vr);clear(bt);return 1;}2.编程实现Shannon编码算法#include<stdio.h>#include<string.h>#include<math.h>void main(){ FILE *fp1,*fp2;int i,j,q,n,c[100][100]={0},l[100]={0};float f[100]={0}, p[100]={0},x[100]={0};char ch1,ch2;fp1=fopen("in2.txt","r");fp2=fopen("out2.txt","w");for(q=0;q<2;q++){fscanf(fp1,"%d",&n);printf("%d\n",n);for(i=0;i<n;i++){fscanf(fp1,"%c%f",&ch1,&p[i]);printf("%f ",p[i]);}printf("\n");f[0]=0;for(i=1;i<n;i++){f[i]=f[i-1]+p[i-1];}for(i=0;i<n;i++){x[i]=1/p[i];l[i]=ceil((log(x[i])/log(2))) ;}for(i=0;i<n;i++)for(j=0;j<l[i];j++){c[i][j]=(int)(f[i]*2);f[i]=f[i]*2-c[i][j];}for(i=0;i<n;i++){ for(j=0;j<l[i];j++){printf("%d",c[i][j]);fprintf(fp2,"%d",c[i][j]);}printf("\n");fprintf(fp2,"\n");}fscanf(fp1,"%c",&ch2);}}五、实验总结1．遇到的问题、分析并的出方案（列出遇到的问题和解决办法，列出没有解决的问题）：Shannon-Fano-Elias编码算法和Shannon编码算法的程序不会编，在参考了大量文献后得出以上程序，调试过程很复杂，得出的最终结果不确定是正确的。

数字通信中的信源编码和信道编码摘要：如今社会已经步入信息时代，在各种信息技术中,信息的传输及通信起着支撑作用.而对于信息的传输，数字通信已经成为重要的手段。

本论文根据当今现代通信技术的发展，对信源编码和信道编码进行了概述性的介绍。

关键词：数字通信；通信系统;信源编码；信道编码Abstract：Now it is an information society。

In the all of information technologies，transmission and communication of information take an important effect。

For the transmission of information，Digital communication has been an important means。

In this thesis we will present an overview of source coding and channel coding depending on the development of today’s communica tion technologies.Key Words：digital communication; communication system; source coding; channel coding1.前言通常所谓的“编码”包括信源编码和信道编码。

编码是数字通信的必要手段。

使用数字信号进行传输有许多优点, 如不易受噪声干扰，容易进行各种复杂处理，便于存贮，易集成化等。

编码的目的就是为了优化通信系统.一般通信系统的性能指标主要是有效性和可靠性.所谓优化，就是使这些指标达到最佳。

除了经济性外，这些指标正是信息论研究的对象.按照不同的编码目的，编码可主要分为信源编码和信道编码。

在本文中对此做一个简单的介绍.2.数字通信系统通信的任务是由一整套技术设备和传输媒介所构成的总体—-通信系统来完成的.电子通信根据信道上传输信号的种类可分为模拟通信和数字通信.最简单的数字通信系统模型由信源、信道和信宿三个基本部分组成.实际的数字通信系统模型要比简单的数字通信系统模型复杂得多。

2009年5月第14卷第3期 西　安　邮　电　学　院　学　报JOURNAL OF XI ’AN UN IV ERSIT Y OF POST AND TEL ECOMMUN ICA TIONS May 2009Vol 114No 13收稿日期:2009-03-02作者简介:谢　勰(1981-),女,安徽安庆人,西安邮电学院信息与控制系助教。

关于Shannon 编码的若干注记谢　勰(西安邮电学院信息与控制系,陕西西安　710121)摘要:通过反例指出若干对Shannon 编码中关于舍入的误解,并利用区间二叉树给出Shannon 编码的简单证明。

提出了Shannon 编码成立的弱条件,它能保证Shannon 编码仍是前缀码。

关键词:Shannon 编码;区间二叉树;前缀码中图分类号:TN911.21 文献标识码:A 文章编号:1007-3264(2009)03-0058-03引言信息论起源于Shannon [1],Shannon 全面且深入地介绍了经典信息论的概念、定理和应用,其中最重要的是熵概念。

由熵的定义可得到合适的码长,并进而构造出性能较好的前缀码,即Shannon 编码[1]。

不过,Shannon 编码要求概率值按递减次序排列,还要对累积分布函数进行舍入。

鉴于其限制条件和具体操作步骤不够直观,无法显露出Shannon 编码为前缀码的本质原因,因此有必要对Shannon 编码给出直观的证明,还需要给出更为本质的限制条件。

1　若干对Shannon 编码的误解由于[1]仅对Shannon 编码作了相当简短的介绍与证明,容易引起误解。

虽然[2]是一本信息论领域的权威著作,但它对Shannon 编码的描述也存在一定的含糊性。

而[3]给出的方法更是完全错误的。

其根源在于[1-3]均未对舍入做出严格的表述,为此必须给出关于二进制小数舍入(R ound )的准确定义。

为方便起见,不妨记1/2l 的二进制小数形式为(0.1)l 。

shannon第三编码定理-回复什么是Shannon第三编码定理？Shannon第三编码定理是由美国数学家克劳德·E·香农于1948年提出的一项重要定理，也被称为数据压缩定理或信息论中的定理。

该定理阐述了在具有随机性的数据中，编码后的平均编码长度与数据的熵之间的关系。

香农第三编码定理的公式可以表示为：H(X) ≤L(X) < H(X) + 1其中，H(X)代表数据的熵，L(X)代表编码后数据的平均编码长度。

为什么需要数据压缩？数据压缩是信息技术中非常重要的一部分。

在我们日常的生活、工作和学习中，我们的电脑、手机等设备都需要存储和传输大量的数据。

然而，存储和传输大量的数据所需的时间、空间和成本都非常高昂。

因此，对数据进行压缩可以帮助我们节省存储空间、提高数据传输速度，并降低相关的成本。

此外，数据压缩在网络传输和存储过程中也起到了重要的作用。

尤其在互联网时代，我们需要轻松快捷地共享和传输各种类型的数据。

因此，数据压缩技术成为必不可少的工具。

如何理解Shannon第三编码定理？Shannon第三编码定理揭示了数据压缩的基本原理。

从定理中可以看出，任何具有随机性的数据都可以通过编码来减少存储空间和传输成本。

定理中的L(X)表示编码后数据的平均编码长度，而H(X)表示数据的熵，也就是数据中所包含的信息的量。

定理表明，编码后的平均编码长度L(X)必然大于等于数据的熵H(X)，但是小于熵加一。

也就是说，通过合理的编码方法，我们可以将数据的平均编码长度控制在非常接近熵的范围内，从而实现高效的压缩效果。

举例来说，假设我们有一个具有随机性的二进制数据，其中0和1的出现频率大致相等。

根据Shannon第三编码定理，我们可以将每个0和每个1分别编码为不等长的比特串，使得整个数据的平均编码长度尽可能接近熵。

这样就可以实现对原始数据的高效压缩。

Shannon第三编码定理的应用Shannon第三编码定理的应用非常广泛。

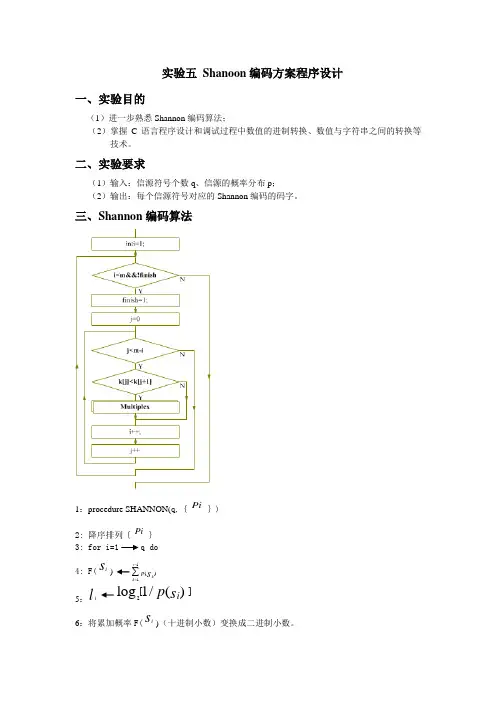
实验五 Shanoon 编码方案程序设计一、实验目的（1）进一步熟悉Shannon 编码算法；（2）掌握C 语言程序设计和调试过程中数值的进制转换、数值与字符串之间的转换等技术。

二、实验要求（1）输入：信源符号个数q 、信源的概率分布p ；（2）输出：每个信源符号对应的Shannon 编码的码字。

三、Shannon 编码算法1：procedure SHANNON(q,｛Pi ｝)2: 降序排列｛Pi ｝ 3: for i=1 q do 4: F(i s ) 5：i l 2[]log 1/()i p s 6：将累加概率F(i s )（十进制小数）变换成二进制小数。

11()i kk p s -=∑l个二进制数字作为第i个消息的码字。

7：取小数点后i8：end for9：end procedure四、实验代码# include<stdio.h># include<math.h># include<stdlib.h>//# include<unistd.h>//# include<values.h># include<string.h># define DELTA 1e-6//误差范围void sort(float*,int);//排序int main(){register int i,j;int n; //字符个数int temp;float *p_i; //转移概率float *P_i; //累加概率int *l_i; //码长char **C; /*Code set*///两个指针？float sum,p;//sum用来测试数据正确行，p存中间数据//while(1);fscanf(stdin,"%d",&n);//读入np_i=(float *)calloc(n,sizeof(float));P_i=(float *)calloc(n,sizeof(float));l_i=(int *)calloc(n,sizeof(int)); //分配存储空间for(i=0;i<n;i++)fscanf(stdin,"%f",&p_i[i]);//读入信道转移概率//判断输入数据是否合法sum=0.0;for(i=0;i<n;i++)sum+=p_i[i];if(fabs(sum-1.0)>DELTA)//判断输入概率和是否为1fprintf(stderr,"Invalid input data \n");fprintf(stdout,"Startin g…\n\n");sort (p_i,n);//调用排序函数排序for(i=0;i<n;i++){p=(-(log(p_i[i])))/log(2.0);l_i[i]=(int)ceil(p);//计算码长 ,cell为向上取整函数}C=(char **)calloc(n,sizeof(char *));//为C*分配存储空间for(i=0;i<n;i++){C[i]=(char *)calloc(l_i[i]+1,sizeof(char));//为C分配存储空间 C[i][0]='\0';//字符串的初始化}//计算累加概率P_i[0]=0.0;for(i=1;i<n;i++)P_i[i]=P_i[i-1]+p_i[i-1];//全加//编码for(i=0;i<n;i++){for(j=0;j<l_i[i];j++){P_i[i]=P_i[i]*2;temp=(int)(P_i[i]);P_i[i]=P_i[i]-temp;//十进制小数转二进制if(temp==0)C[i]=strcat(C[i],"0");elseC[i]=strcat(C[i],"1");//编码续接} }//输出结果fprintf(stdout,"The output coding is :\n"); for(i=0;i<n;i++)fprintf(stdout,"%s",C[i]);fprintf(stdout,"\n\n");while(1);//释放内存for(i=n-1;i>=0;i--){ free(C[i]);free(C);free(p_i);free(P_i);free(l_i);while(1);}exit(0);}//排序函数void sort(float *k,int m){int i=1;int j=1;int finish=0;//结束标记位float temp;while(i<m&&!finish){finish=1;for(j=0;j<m-i;j++){//冒泡排序if(k[j]<k[j+1]){//降序排列temp=k[j];k[j]=k[j+1];k[j+1]=k[j];finish=0;}i++;}}四、实验结果。

信息论实验报告姓名：王健学号：100610325Fano编码一、方法介绍Fano编码的目的是产生具有最小冗余的码词（code word）。

其基本思想是产生编码长度可变的码词。

码词长度可变指的是，被编码的一些消息的符号可以用比较短的码词来表示。

估计码词长度的准则是符号出现的概率。

符号出现的概率越大，其码词的长度越短。

Fano编码是从概率匹配角度出发，对于离散的无记忆信源，构造的一个变长的无失真编码。

符号从最大可能到最少可能排序，将排列好的心愿符号分化为两大组，使两组的概率和近于相同，并各赋予一个二元码符号“0”和“1”。

只要有符号剩余，以同样的过程重复这些集合以此确定这些代码的连续编码数字。

依次下去，直至每一组的只剩下一个信源符号为止。

当一组已经降低到一个符号，显然，这意味着符号的代码是完整的，不会形成任何其他符号的代码前缀。

二、方法原理范诺编码算法步骤：（1）按照符号出现的概率减少的顺序将待编码的符号排成序列。

（2）将符号分成两组，使这两组符号概率和相等或几乎相等。

（3）将第一组赋值为0，第二组赋值为1。

（4）对每一组，重复步骤2的操作。

三、优缺点1、缺点当信源符号较多，并有一些符号概率很接近时，分两组的组合方法会有很多，还有赋码元的任意性，因此Fano编码出的码字是不唯一的。

这种编码方法不能使短码得到充分的利用。

Fano编码虽属于概率匹配范畴，但并为严格遵守匹配规则，即不是按照“概率大码长小，概率小码长大”来决定码长，有时会出现概率小码长反而小的情况。

可能某种分大组的结果，会出现后面小组“概率和”相差较远，因而使平均码长增加。

只有对特殊概率分布的信源才是最优编码，所以Fano编码不是最佳的编码方法。

2、优点Fano码的编码方法实际上是构造哈夫曼树的一种方法，所以Fano编码是即时码。

Fano编码是变长编码，这种编码方法往往在编码码长不是很长的情况下就可以编译出编码效率很高而且无失真编码。

Fano码也考虑了统计特性，使经常出现的信源能对应码长短的码字。

实验二Shannon编码一、实验目的及要求a)实验目的1.通过本实验实现信源编码——Shannon编码2.编写M文件实现，掌握Shannon编码方法b)实验要求1.了解Matlab中M文件的编辑、调试过程2.编写程序实现Shannon编码算法二、实验步骤及运行结果记录a)实验步骤1.输入Shannon编码程序2.运行程序，按照提示输入相应信息，并记录输入信息，及运行结果。

3.思考：在程序中加入排序子程序，使其在输入信源概率时，不要求输入顺序。

b)实验结果y =0.2000 0 2.3219 3.00000.1900 0.2000 2.3959 3.00000.1800 0.3900 2.4739 3.00000.1700 0.5700 2.5564 3.00000.1500 0.7400 2.7370 3.00000.1000 0.8900 3.3219 4.00000.0100 0.9900 6.6439 7.0000code =000；code = 001；code = 011；code =100；code = 101；code =1110；code =1111110三、实验流程图（附一）四、程序清单，并注释每条语句（附二）五、实验小结香农编码是码符号概率大的用短码表示，概率小的是用长码表示，程序中对概率排序，最后求得的码字就依次与排序后的符号概率对应。

此程序缺点是，第一个码字都是以0开始，因为对累加概率求二进制后，小数点后的数都是0，取几位由码长确定，而香农编码是不唯一的，如果手动编码就不存在这样的问题。

后面求得的编码没有下标就需要注意是与上面排序后的信源符号对应。

附一附二N=input('请输入信源符号个数:')%输入信源符号个数p=zeros(1,N);%生成1*4的零矩阵for i=1:Np(1,i)=input('请输入各信源符号出现的概率:')%输入各个信源符号的概率endp=fliplr(sort(p));%将概率从大到小进行排序if abs(sum(p)-1)>10e-10error('输入概率不符合概率分布')%检验所输入的概率是否正确endy=zeros(N,4);%生成N*4零矩阵for i=1:Ny(i,1)=p(1,i);%将各个符号出现的概率放入y矩阵的第一列中y(1,2)=0;if i>1y(i,2)=y(i-1,2)+y(i-1,1); %第二列其余的元素用此式求得,即为累加概率endy(i,3)=log2(1./p(i))%求各个信源符号的信息熵放入y矩阵的第三列中y(i,4)=ceil(y(i,3))%求码长endA=y(:,2);%取出y中的第二列元素B=y(:,4);%取出y中的第四列元素for i=1:Ncode=shannoncode(A(i),B(i))%生成码字endfunction [C]=shannoncode(A,B)%对累加概率求二进制的函数C=zeros(1,B);%生成零矩阵用于存储生成的二进制数，对二进制的每一位进行操作temp=A;%temp赋初值for i=1:B%累加概率转化为二进制，循环求二进制的每一位，A控制生成二进制的位数 temp=temp*2;if temp>1temp=temp-1;C(1,i)=1;elseC(1,i)=0;endendend。

仙农—范诺编码方法的C语言实现
钟明全;王长林
【期刊名称】《四川通信技术》
【年(卷),期】2000(030)004
【摘要】按照概率匹配的方法，即概率大的编码短的原则，可以在给定信息条件下，减少平均编码长度，提高编码效率，使每个码元所载荷的平均信息量为最大。

【总页数】4页(P42-45)
【作者】钟明全;王长林
【作者单位】西南交通大学;西南交通大学
【正文语种】中文
【中图分类】TN911.21
【相关文献】
1.香农编码与香农-弗诺编码方法的研究及C#实现 [J], 张燕红;刘瑜;孟海翠;刘晓娣
2.关于范爱农生平的一件新史料——汪梅峰《吊范爱农诔文》的发现 [J], 汪国泰
3.“愿抛碧血换共和”:辛亥革命元老范鸿仙 [J], 宫博广
4.范爱农其人和《哀范君三章》——《鲁迅诗直寻》之一 [J], 锡金
5.范鸿仙:愿将碧血换共和 [J], 倪洪
因版权原因，仅展示原文概要，查看原文内容请购买。

shannon第三编码定理-回复什么是Shannon第三编码定理？Shannon第三编码定理是信息论中的一个重要结果，它给出了对于一个离散无记忆信源，任意一段长度为n的消息的编码长度的一个下界。

这个下界由信源的熵函数以及消息的条件熵函数决定，它表达了最优编码的紧致性，即在最佳的编码方案下，消息的编码长度尽可能地接近信息的熵。

Shannon第三编码定理的表述如下：对于一个离散无记忆信源X，它的熵为H(X)，给定一个长度为n的消息，在最佳编码方案下，平均编码长度L(X^n)满足以下不等式：L(X^n) ≥ n * H(X) + O(log(n))其中，O(log(n))是一个增长速度远低于线性的函数。

为了理解Shannon第三编码定理，我们需要先了解几个基本概念：1. 信源（Source）：信源是指产生消息的物理或逻辑系统。

在信息论中，信源被假定为离散无记忆的，即它产生的消息是离散的并且相互独立的。

2. 消息（Message）：消息是信源产生的离散符号序列。

在信息论中，我们通常用字母X来表示信源产生的消息。

3. 熵（Entropy）：熵是信源的不确定性度量，它衡量了信源输出的不确定性。

对于一个离散无记忆信源X，它的熵H(X)可以通过以下公式计算：H(X) = -∑P(x)log2P(x)其中，P(x)是信源输出为x的概率。

有了这些基本概念的了解，我们现在可以回到Shannon第三编码定理。

假设我们有一个长度为n的消息，我们想要找到一个最佳的编码方案，使得编码长度尽可能地短。

根据信息论的基本原理，我们知道熵是编码长度的下界，即L(X^n) ≥ n * H(X)。

这意味着，如果我们使用每个消息的平均编码长度大于n * H(X)，那么我们肯定可以找到一个更紧凑的编码方案。

但是，这个下界并不是很有用，因为它本质上是线性的，即随着消息长度的增加，平均编码长度也会线性增加。

这在实际应用中并不可行，因为消息往往是变长的。

shannon第三编码定理-回复中括号内的内容是"shannon第三编码定理"。

下面是一篇关于Shannon 第三编码定理的1500-2000字的文章。

Shannon 第三编码定理是信息论中一个重要的定理，它揭示了信息传输的极限。

香农第三编码定理同时具有实际应用性和理论深度，为我们理解信息传输的效率和可靠性提供了重要的指导。

首先，我们需要了解一下信息论的基本概念。

信息论是研究信息量、信息传输和信息储存的一门学科。

它的核心概念是“信息熵”，它度量了信息系统的不确定性。

信息熵越大，信息系统的不确定性就越高，反之亦然。

然后，我们来介绍一下Shannon 第三编码定理。

这个定理是由克劳德·香农在1948年提出的，它给出了一种理论上的极限，即信息传输的最高速率。

具体而言，Shannon 第三编码定理指出，对于一个离散无记忆信源产生的信号流，它的最高传输速率取决于信道的带宽和信噪比之积。

通俗地讲，如果带宽越大或者信噪比越高，那么最高传输速率就越高。

这个定理为我们设计和优化信息传输系统提供了重要的指导。

接下来，让我们更详细地解释Shannon 第三编码定理的原理。

首先，我们需要明确信道的带宽和信噪比的概念。

信道的带宽是指信道所能传输的最高频率的范围。

信噪比是指信号的功率与噪声的功率之比。

在传输过程中，信号会受到噪声的干扰，信噪比越高，信号的清晰度就越高，传输质量就越好。

在这个基础上，Shannon第三编码定理的关键在于信息传输速率的计算。

信息传输速率的计算公式为：C = B * log2(1+S/N)其中，C表示信息传输速率，B表示信道的带宽，S/N表示信噪比。

从上面的公式可以看出，当信噪比越大时，信息传输速率也会随之增加。

这是因为信噪比的增加意味着信号受到噪声的干扰越小，传输质量越好，信息传输速率也就越高。

而带宽的增加也会提高信息传输速率。

这个定理的意义在于它告诉我们，为了提高信息传输速率，我们可以从两个方面入手。