下载文档原格式
斯坦纳树解法-概述说明以及解释1.引言1.1 概述概述部分是文章的开篇部分，用于介绍主题和问题背景。
下面是一个示例：概述斯坦纳树（Steiner Tree）是图论中的一个经典问题，旨在找到一个具有最小总权重的联通子图，以连接给定一组节点。
斯坦纳树问题在实际生活中有着广泛的应用，例如通信网络设计、电力系统规划和生物信息学等领域。
本文将详细介绍斯坦纳树的概念、应用领域以及解法的基本原理。
首先，我们将给出斯坦纳树的定义和问题描述，以便读者对该问题有一个清晰的认识。
然后，我们将探讨斯坦纳树在不同领域中的应用，以展示它在实际问题中的重要性。
接下来，我们将介绍一些经典的斯坦纳树解法，包括近似算法和精确算法，并详细讨论它们的基本原理和优缺点。
通过本文的阅读，读者将能够了解斯坦纳树问题的背景和意义，掌握不同领域中的应用案例，并对斯坦纳树解法的基本原理有一定的了解。
此外，我们还将对斯坦纳树解法的优点和局限性进行讨论，并展望未来在这一领域的发展方向。
接下来，在第二节中，我们将开始具体介绍斯坦纳树的概念和应用领域。
1.2 文章结构【文章结构】本文主要分为引言、正文和结论三个部分。
下面将对每个部分进行详细介绍。
1. 引言引言部分主要包括概述、文章结构和目的三个方面的内容。
在概述部分，将简要介绍斯坦纳树解法的背景和重要性。
2. 正文正文部分是文章的核心部分，主要包括斯坦纳树的概念、应用领域和解法的基本原理三个方面的内容。
2.1 斯坦纳树的概念在本小节中，将详细解释什么是斯坦纳树，斯坦纳树的定义和特点。
2.2 斯坦纳树的应用领域本小节将介绍斯坦纳树的应用领域，包括网络通信、电力系统、交通规划等方面的应用案例。
2.3 斯坦纳树解法的基本原理在本小节中，将详细介绍斯坦纳树解法的基本原理和算法，包括构建斯坦纳树的思路和具体步骤。
同时，可以提及一些经典的斯坦纳树解法算法和优化方法。
3. 结论结论部分对斯坦纳树解法的优点和局限性进行总结，并对未来的发展方向进行展望。
克鲁斯卡尔算法求最小生成树的最短路径克鲁斯卡尔算法的核心思想是从图的边集中选取边来构建最小生成树，首先将图中的所有边按照权重进行排序。
然后依次取最小权重的边，如果这条边的加入不会形成环路，则将它加入最小生成树的边集中。
重复这个过程，直到最小生成树中的边数等于顶点数减一，或者所有的边都已经考虑过。
假设有一个包含n个顶点的带权无向图G=(V,E)，其中，V表示顶点的集合，E表示边的集合。
假设我们要求解G的最小生成树。
1.初始化边集E'为空集，集合S={v}，v是图中任意一个顶点。
2.对所有的边进行排序，按照边的权重从小到大排列。
3.从排序后的边集中依次选取边e，如果边e的两个顶点都不在集合S中，则将边e加入集合S，并加入边集E'中。
4.重复步骤3，直到E'中的边数等于n-1在克鲁斯卡尔算法中，需要使用并查集来判断选定的边e是否会形成环路。
并查集是一种数据结构，用于维护元素的等价关系。
它有两个主要操作，即查找和合并。
使用并查集的步骤如下：1.初始化并查集，使得每个元素都是一个单独的集合。
2.对每一条边e=(u,v)，如果u和v在同一个集合中，则说明加入这条边会形成环路；否则，将这两个集合合并。
3.重复步骤2，直到所有的边都考虑过。
接下来，我们通过一个具体的例子来说明克鲁斯卡尔算法的具体过程。
假设有以下的带权无向图G=(V,E)，其中，V={A,B,C,D,E,F,G}，E为边的集合，每条边的权重如下：AE:5AB:7AG:8BF:7BC:9CD:5CG:9DE:15DF:6EG:11EF:8FG:9按照权重对边进行排序：CD:5AE:5DF:6AB:7BF:7EF:8AG:8CG:9BC:9FG:9DE:15EG:11从最小的边开始选取，首先选取CD:5，加入到最小生成树的边集中。
最小生成树的边集：{"CD:5"}接下来选取AE:5，加入到最小生成树的边集中。
最小生成树克鲁斯卡尔算法
最小生成树克鲁斯卡尔算法是一种基于贪心思想的图论算法，主
要用于解决图的最小生成树问题。
该算法精简高效，在实际应用中广
泛使用。
最小生成树问题是指，在一个带权无向图中，选取一些边，使得
它们组成一棵树，且这棵树的所有边的权值之和最小。
这个问题可以
用克鲁斯卡尔算法来解决。
克鲁斯卡尔算法的思想是，首先将所有边按照权值从小到大排序，依次将每条边加入到已选的边集合中，如果加入该边后形成了环路，
则不选择该边。
最终生成的边集合就是该图的最小生成树。
这个算法的时间复杂度为O(ElogE)，其中E为边数。
虽然速度不
如其他复杂度更快的算法，但克鲁斯卡尔算法的代码简洁易懂，并且
适用于边数较小的图，正因为如此，在实际应用中它的使用非常广泛。
在大型计算机网络中，最小生成树算法常用于广域网的拓扑设计
问题。
在城市交通规划中，也可以应用最小生成树算法，来设计更加
合理的交通路线。
需要注意的是，最小生成树仅仅是起到了将所有节点连接起来的
作用，它并不保证任意两个节点之间都有最短路径。
如果需要求解两
点间的最短路径问题，需要使用单源最短路径算法，如Dijkstra算法
和Bellman-Ford算法等。
总之，最小生成树克鲁斯卡尔算法在实际应用中扮演着重要的角色，尤其在计算机网络和城市规划领域的应用非常广泛。
学习并掌握这个算法，对于解决实际问题具有重要的指导意义。
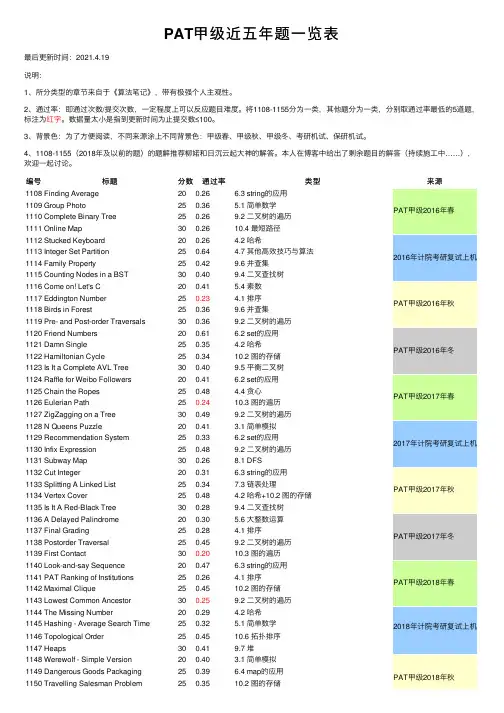
PAT 甲级近五年题⼀览表最后更新时间：2021.4.19说明：1、所分类型的章节来⾃于《算法笔记》，带有极强个⼈主观性。
2、通过率：即通过次数/提交次数，⼀定程度上可以反应题⽬难度。
将1108-1155分为⼀类，其他题分为⼀类，分别取通过率最低的5道题，标注为红字。
数据量太⼩是指到更新时间为⽌提交数≤100。
3、背景⾊：为了⽅便阅读，不同来源涂上不同背景⾊：甲级春、甲级秋、甲级冬、考研机试、保研机试。
4、1108-1155（2018年及以前的题）的题解推荐柳婼和⽇沉云起⼤神的解答。
本⼈在博客中给出了剩余题⽬的解答（持续施⼯中……），欢迎⼀起讨论。
编号标题分数通过率类型来源1108Finding Average 200.26 6.3 string 的应⽤PAT 甲级2016年春1109Group Photo250.36 5.1 简单数学1110Complete Binary Tree 250.269.2 ⼆叉树的遍历1111Online Map 300.2610.4 最短路径1112Stucked Keyboard 200.26 4.2 哈希2016年计院考研复试上机1113Integer Set Partition 250.64 4.7 其他⾼效技巧与算法1114Family Property250.429.6 并查集1115Counting Nodes in a BST 300.409.4 ⼆叉查找树1116Come on! Let's C 200.41 5.4 素数PAT 甲级2016年秋1117Eddington Number 250.23 4.1 排序1118Birds in Forest250.369.6 并查集1119Pre- and Post-order Traversals 300.369.2 ⼆叉树的遍历1120Friend Numbers 200.61 6.2 set 的应⽤PAT 甲级2016年冬1121Damn Single 250.35 4.2 哈希1122Hamiltonian Cycle 250.3410.2 图的存储1123Is It a Complete AVL Tree 300.409.5 平衡⼆叉树1124Raffle for Weibo Followers 200.41 6.2 set 的应⽤PAT 甲级2017年春1125Chain the Ropes 250.48 4.4 贪⼼1126Eulerian Path 250.2410.3 图的遍历1127ZigZagging on a Tree 300.499.2 ⼆叉树的遍历1128N Queens Puzzle 200.41 3.1 简单模拟2017年计院考研复试上机1129Recommendation System 250.33 6.2 set 的应⽤1130Infix Expression 250.489.2 ⼆叉树的遍历1131Subway Map 300.268.1 DFS 1132Cut Integer200.31 6.3 string 的应⽤PAT 甲级2017年秋1133Splitting A Linked List 250.347.3 链表处理1134Vertex Cover 250.48 4.2 哈希+10.2 图的存储1135Is It A Red-Black Tree 300.289.4 ⼆叉查找树1136A Delayed Palindrome 200.30 5.6 ⼤整数运算PAT 甲级2017年冬1137Final Grading 250.28 4.1 排序1138Postorder Traversal 250.459.2 ⼆叉树的遍历1139First Contact300.2010.3 图的遍历1140Look-and-say Sequence 200.47 6.3 string 的应⽤PAT 甲级2018年春1141PAT Ranking of Institutions 250.26 4.1 排序1142Maximal Clique250.4510.2 图的存储1143Lowest Common Ancestor 300.259.2 ⼆叉树的遍历1144The Missing Number200.29 4.2 哈希2018年计院考研复试上机1145Hashing - Average Search Time 250.32 5.1 简单数学1146Topological Order 250.4510.6 拓扑排序1147Heaps300.419.7 堆1148Werewolf - Simple Version 200.40 3.1 简单模拟PAT 甲级2018年秋1149Dangerous Goods Packaging 250.39 6.4 map 的应⽤1150Travelling Salesman Problem250.3510.2 图的存储1151LCA in a Binary Tree 300.279.2 ⼆叉树的遍历1152Google Recruitment200.25 5.4 素数PAT 甲级2018年冬1153Decode Registration Card of PAT 250.21 4.1 排序1154Vertex Coloring 250.3710.2 图的存储1155Heap Paths 300.479.7 堆7-1Sexy Primes 200.20 5.4 素数7-2Anniversary 250.30 6.2 set 的应⽤7-3Telefraud Detection 250.149.6 并查集7-4Structure of a Binary Tree 300.209.2 ⼆叉树的遍历7-1Forever200.15 5.2 最⼤公约数与最⼩公倍数+5.4 素数+8.1 DFS 7-2Merging Linked Lists 250.317.3 链表处理7-3Postfix Expression 250.379.2 ⼆叉树的遍历7-4Dijkstra Sequence 300.4010.4 最短路径7-1Good in C 200.12 3.3 图形输出7-2Block Reversing 250.297.3 链表处理7-3Summit 250.4210.2 图的存储7-4Cartesian Tree 300.539.2 ⼆叉树的遍历7-1Conway's Conjecture 200.14 5.4 素数2019年计院考研复试上机7-2Play with Linked List 250.227.3 链表处理7-3Unsuccessful Searches 250.29 5.1 简单数学7-4Ambulance Dispatch 300.0810.4 最短路径7-1Happy Numbers 200.30 4.2 哈希7-2Zigzag Sequence 250.40 5.1 简单数学7-3Is It An AVL Tree 250.419.5 平衡⼆叉树7-4Index of Popularity 300.1910.2 图的存储7-1Prime Day 200.47 5.4 素数7-2The Judger 250.15 4.2 哈希7-3Safari Park250.41 3.1 简单模拟7-4Replacement Selection 300.1813.3 快乐模拟7-1Panda and PP Milk 200.16 4.7 其他⾼效技巧与算法7-2How Many Ways to Buy a Piece of Land 250.448.1 DFS 7-3Left-View of Binary Tree 250.559.2 ⼆叉树的遍历7-4Professional Ability Test 300.1810.4 最短路径+10.6 拓扑排序7-1The Closest Fibonacci Number 200.37 5.1 简单数学7-2Subsequence in Substring 250.24 3.6 字符串处理7-3File Path250.387.1 栈的应⽤7-4Chemical Equation300.188.1 DFS 7-1Standard Form of Polynomial 200.44 5.1 简单数学7-2Distance of Triples 250.07 4.5 ⼆分7-3Partial School Ranking 250.259.6 并查集7-4Shopping With Coupons 300.05 4.4 贪⼼7-1Arithmetic Progression of Primes 200.16 5.4 素数7-2Lab Access Scheduling 250.44 4.4 贪⼼7-3Structure of Max-Heap 250.329.7 堆7-4Recycling of Shared Bicycles 300.3910.4 最短路径7-1Square Friends20数据量太⼩5.1 简单数学7-2One Way In, Two Ways Out 25数据量太⼩4.6 two pointers 7-3Preorder Traversal 25数据量太⼩9.2 ⼆叉树的遍历7-4Load Balancing30数据量太⼩8.1 DFS。
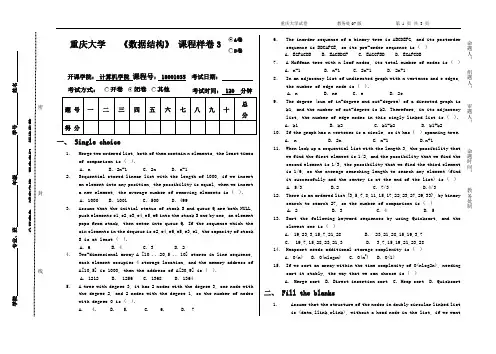
重庆大学 《数据结构》 课程样卷 3开课学院： 计算机学院 课程号： 18001035 考试日期：考试方式：考试时间： 120 分钟一、 Single choice1． Merge two ordered list, both of them contain n elements, the least timesof comparison is ( ).A. nB. 2n-1C. 2nD. n-12． Sequential stored linear list with the length of 1000, if we insertan element into any position, the possibility is equal, when we insert a new element, the average number of removing elements is ( ). A. 1000 B. 1001 C. 500 D. 4993． Assume that the initial status of stack S and queue Q are both NULL,push elements e1,e2,e3,e4,e5,e6 into the stack S one by one, an element pops from stack, then enter into queue Q. If the sequence which the six elements in the dequeue is e2,e4,e6,e5,e3,e1, the capacity of stack S is at least ( ).A. 6B. 4C. 3D. 24． Two-dimensional array A [10 .. 20,5 .. 10] stores in line sequence,each element occupies 4 storage location, and the memory address of A[10,5] is 1000, then the address of A[20,9] is ( ). A. 1212 B. 1256 C. 1368 D. 13645． A tree with degree 3, it has 2 nodes with the degree 3, one node withthe degree 2, and 2 nodes with the degree 1, so the number of nodes with degree 0 is ( ).A. 4.B. 5.C. 6.D. 76． The inorder sequence of a binary tree is ABCDEFG, and its postordersequence is BDCAFGE, so its pre-order sequence is ( ) A. EGFACDB B. EACBDGF C. EAGCFBD D. EGAFCDB7． A Huffman tree with n leaf nodes, its total number of nodes is ( )A. n-1B. n+1C. 2n-1D. 2n+18． In an adjacency list of undirected graph with n vertexes and e edges,the number of edge node is ( ).A. nB. neC. eD. 2e9． The degree (sum of in-degree and out-degree) of a directed graph isk1, and the number of out-degree is k2. Therefore, in its adjacency list, the number of edge nodes in this singly linked list is ( ). A. k1 B. k2 C. k1-k2 D. k1+k210． If the graph has n vertexes is a circle, so it has ( ) spanning tree.A. nB. 2nC. n-1D.n+111． When look up a sequential list with the length 3, the possibility thatwe find the first element is 1/2, and the possibility that we find the second element is 1/3, the possibility that we find the third element is 1/6, so the average searching length to search any element (find it successfully and the sentry is at the end of the list) is ( ) A. 5/3 B.2 C. 7/3 D.4/312． There is an ordered list {3,5,7,8,11,15,17,22,23,27,29,33}, by binarysearch to search 27, so the number of comparison is ( ) A. 2 B. 3 C. 4 D. 513． Sort the following keyword sequences by using Quicksort, and theslowest one is ( )A. 19,23,3,15,7,21,28B. 23,21,28,15,19,3,7C. 19,7,15,28,23,21,3D. 3,7,15,19,21,23,28 14． Heapsort needs additional storage complexity is ( )A. O(n)B. O(nlog 2n)C. O(n 2) D. O(1)15． If we sort an array within the time complexity of O(nlog2n), needingsort it stably, the way that we can choose is ( )A. Merge sortB. Direct insertion sortC. Heap sortD. Quicksort二、 Fill the blanks1.Assume that the structure of the nodes in doubly circular linked list is (data,llink,rlink), without a head node in the list, if we want命题人：组题人：审题人：命题时间： 教务处制学院 专业、班 年级 学号 姓名公平竞争、诚实守信、严肃考纪、拒绝作弊封线密to insert the node which pointer s points after the node pointer ppoints, then execute as the following statements:; ; ___ _; ;2.Both stack and queue are _______linear structure.3.The four leaf nodes with the weight 9,2,5,7 form a Huffman tree, itsweighted path length is ________.4.In order to ensure that an undirected graph with six vertexes isconnected, need at least ______ edges.5.An n-vertex directed graph, if the sum of all vertices’ out-degreeis s, then the sum of all vertices’ degree is__ ___.6.The Depth-First traversal of a graph is similar to the binarytree_______ traversal; the Breadth-first graph traversal algorithmis similar to the binary tree ______traversal.7. A connected graph with n vertexes and e edges has ____ edges of itsspanning tree.8.The time complexity of binary searching is _____; if there are 100elements, the maximum number of comparisons by binary searching is____.9.Sort n elements by merge sort, the requiring auxiliary space is _____.10.Sort a linear list with 8 elements by Quicksort, at the best, thecomparison time is ______.三、 Application1. Begin from the vertex A, seek the minimum spanning tree by using Primalgorithms2. The following is AOE network:(1) How much time does it take to complete the whole project?(2) Find out all of the critical path.(9 points)3. Assume that a set of keywords is {1，12，5，8，3，10，7，13，97},tryto complete the following questions:(9 points)(1) Choose the keywords in sequence to build a binary sort tree Bt;(2) Draw the structure of the tree after deleting node “12”from thebinary tree Bt.4. The keyword sequence is {503,87,512,61,908,170,897,275,653,462}, usingradix sorting method to sort them in ascending order, try to write every trip results of sort. （9 points）四、 Algorithm1.The following algorithm execute on a singly linked list without headnode, try to analyze and write its function.(5 points)void function(LinkNode *head){LinkNode *p,*q,*r;p=head;q=p->next;while(q!=NULL){r=q->next;q->next=p;p=q;q=r;}head->next=NULL;head=p;}2.Design an algorithm to divide a singly linked list ‘A’ with a headpointer ‘a’ into two singly linked list ‘A’ and ‘B’, whose head pointers are ‘a’and ‘b’, respectively. On the condition that linked list A has all elements of odd serial number in the previous linked listA and linked listB has all elements of even serial number in the previouslinked list A, in addition, the relative order of the original linked list are maintained.(7 points)3. The type of binary tree is defined as follows:typedef struct BiTNode {char data;struct BiTNode *lchild,*rchild;}BiTNode, *BiTree;Please design an algorithm to count how many leaf nodes the binary tree have. （8 points）。
openjudge答案【篇一：整理的-----acm题目及答案】a + b problem (4)1001 sum problem (5)1002 a + b problem ii (6)1005 number sequence (8)1008 elevator (9)1009 fatmouse trade (11)1021 fibonacci again (13)1089 a+b for input-output practice (i) (14)1090 a+b for input-output practice (ii) (15)1091 a+b for input-output practice (iii) (16)1092 a+b for input-output practice (iv) (17)1093 a+b for input-output practice (v) (18)1094 a+b for input-output practice (vi) (20)1095 a+b for input-output practice (vii) (21)1096 a+b for input-output practice (viii) (22)1176 免费馅饼 (23)1204 糖果大战 (25)1213 how many tables (26)2000 ascii码排序 (32)2001 计算两点间的距离 (34)2002 计算球体积 (35)2003 求绝对值 (36)2004 成绩转换 (37)2005 第几天？ (38)2006 求奇数的乘积 (40)2007 平方和与立方和 (41)2008 数值统计 (42)2009 求数列的和 (43)2010 水仙花数 (44)2011 多项式求和 (46)2012 素数判定 (47)2014 青年歌手大奖赛_评委会打分 (49)2015 偶数求和 (50)2016 数据的交换输出 (52)2017 字符串统计 (54)2019 数列有序! (55)2020 绝对值排序 (56)2021 发工资咯：） (58)2033 人见人爱a+b (59)2037 今年暑假不ac (61)2039 三角形 (63)2040 亲和数 (64)2045 不容易系列之(3)—— lele的rpg难题 (65)2049 不容易系列之(4)——考新郎 (66)2056 rectangles (68)2073 无限的路 (69)2084 数塔 (71)2201 熊猫阿波的故事 (72)2212 dfs (73)2304 electrical outlets (74)2309 icpc score totalizer software (75)2317 nasty hacks (77)2401 baskets of gold coins (78)2500 做一个正气的杭电人 (79)2501 tiling_easy version (80)2502 月之数 (81)2503 a/b + c/d (82)2504 又见gcd (83)2519 新生晚会 (84)2520 我是菜鸟，我怕谁 (85)2521 反素数 (86)2522 a simple problem (88)2523 sort again (89)2524 矩形a + b (90)2535 vote (91)2537 8球胜负 (93)2539 点球大战 (95)2547 无剑无我 (98)2548 两军交锋 .............................................................. 99 2549 壮志难酬 ............................................................. 100 2550 百步穿杨 ............................................................. 101 2551 竹青遍野 ............................................................. 103 2552 三足鼎立 ............................................................. 104 2553 n皇后问题 ............................................................ 105 2554 n对数的排列问题 ...................................................... 106 2555 人人都能参加第30届校田径运动会了 .................................... 107 2560buildings ............................................................ 110 2561 第二小整数 ........................................................... 112 2562 奇偶位互换 ........................................................... 113 2563 统计问题 ............................................................. 114 2564 词组缩写 ............................................................. 115 2565 放大的x .............................................................. 117 2566 统计硬币 ............................................................. 118 2567 寻梦 ................................................................. 119 2568 前进 ................................................................. 121 2569 彼岸 (123)2700 parity ............................................................... 124 2577 how to type . (126)北京大学：1035 spell checker ........................................................ 129 1061 青蛙的约会 ........................................................... 133 1142 smith numbers ........................................................ 136 1200 crazy search ......................................................... 139 1811 primetest ........................................................... 141 2262 goldbachs conjecture ................................................ 146 2407relatives ............................................................ 150 2447rsa .................................................................. 152 2503babelfish ............................................................ 156 2513 colored sticks . (159)acm算法：kurxx最小生成树 (163)prim ....................................................................... 164 堆实现最短路 ............................................................... 166 最短路dij普通版 (167)floyd (168)bell_man ................................................................... 168 拓扑排序 ................................................................... 169 dfs强连通分支 .............................................................. 170 最大匹配 ................................................................... 172 还有两个最大匹配模板 ....................................................... 173 最大权匹配,km算法 .......................................................... 175 两种欧拉路 (177)无向图： ............................................................... 177 有向图： (178)【最大流】edmonds karp (178)dinic (179)【最小费用最大流】edmonds karp对偶算法 (181)acm题目：【题目】排球队员站位问题 (182)【题目】把自然数Ｎ分解为若干个自然数之和。
Introducing Regina,the3-manifold topology softwareBenjamin A.BurtonAuthor’s self-archived versionAvailable from .au/~bab/papers/AbstractAn overview is presented of Regina,a freely available software package for3-manifold topologists.In addition to working with3-manifold triangulations,Regina includes support for normal surfaces and angle structures.The features of the software are described in detail, followed by examples of research projects in which Regina has been used.1IntroductionExperimental work in the study of3-manifold topology has been a historically challenging task.Topological calculations for even simple3-manifold triangulations are often remarkably difficult to perform by hand.Furthermore,triangulations and3-manifolds are difficult to represent and manipulate using standard programming languages.Because of this,relatively little software has been available until recently to assist with these calculations.One prominent exception is SnapPea[Weeks91],under development for over a decade, which provides excellent support for the study of hyperbolic3-manifolds.More recently a number of other tools have become available,many of which are listed at the computational topology website /.Regina is a software package that unites a number of standard3-manifold topology algo-rithms and procedures within a friendly user interface,as well as adding previously unavailable features to the current body of experimental tools.Under development since1999,its growth has to a large extent been guided by its use in a variety of research projects,some of which are noted in Section3.Algorithms that are implemented include triangulation simplification, normal surface enumeration,angle structure analysis and the calculation of algebraic and combinatorial invariants.This software is released under the GNU General Public License and is publicly avail-able from /.Both the user interface and the underlying programmer’s interface are thoroughly documented.Regina continues to grow and currently enjoys a new release every few months.Special thanks must go to David Letscher who assisted with the early phases of development.Thanks also to Marc Culler,Nathan Dunfield,William Jaco,Richard Rannard,J.Hyam Rubinstein and JeffWeeks for many fruitful discussions.In Section2we present a detailed description of the capabilities of Regina.Section3closes with some examples of research projects that have made use of this software.2FeaturesSince its inception,Regina has been carefully designed for rigour and extensibility.The soft-ware is written primarily in the C++programming language and runs under GNU/Linux and related operating systems.A list of the more noteworthy features of Regina is presented below.2.1TriangulationsThe primary objects with which a user interacts when running Regina are3-manifold tri-angulations.As such,a large part of the software is devoted to the creation,analysis and1manipulation of triangulations.2.1.1CreationThe following methods are supported for creating triangulations.•Manual construction of triangulations by entering individual tetrahedron face identifica-tions by hand;•Automatic generation of standard triangulations such as layered solid tori and layered lens spaces[Jaco and Rubinstein03a,Jaco and Rubinstein06];•Automatic construction of Seifertfibred spaces over the2-sphere with up to three ex-ceptionalfibres;•Reconstruction of triangulations from dehydration strings[Callahan et al.99];•Importing triangulations saved from SnapPea[Weeks91].2.1.2AnalysisProperties of a triangulation that the software can compute include the following.•Detailed combinatorial information about the skeleton and boundary components,in-cluding vertex links and the shapes formed by the various triangulation faces;•A variety of homology and homotopy groups;•The quantum invariants of Turaev and Viro[Turaev and Viro92];•3-sphere recognition,as well as a complete connected sum decomposition for closed ori-entable triangulations[Jaco and Rubinstein03a];•Triangulation attributes relating to the existence of particular types of normal surface, such as0-efficiency[Jaco and Rubinstein03a]and the existence of splitting surfaces(de-scribed in Section2.3.3).Pairs of triangulations can be tested for direct isomorphism,or for whether one trian-gulation is isomorphic to a subcomplex of another.In addition the software contains a variety of recognition routines for detecting particular well-formed structures within a tri-angulation.These routines recognise smaller building blocks that often appear within larger triangulations,such as layered solid tori[Jaco and Rubinstein03a,Jaco and Rubinstein06] and thin I-bundles[Burton07].Furthermore,they can detect complete triangulations be-longing to a number of infinite families described in[Burton03],[Martelli and Petronio01] and[Matveev98].As a result Regina can frequently recognise the underlying3-manifolds for well-structured triangulations that it has not previously encountered.2.1.3ManipulationFor the manipulation of a triangulation,the following procedures are available.•Elementary moves(transformations local to a small number of tetrahedra),such as Pach-ner moves and other transformations described in[Burton07],many of which were sug-gested by Letscher;•Automated simplification in which the software attempts to use a combination of these elementary moves to reduce the number of tetrahedra as far as possible,though there is no guarantee that the smallest possible number of tetrahedra will be achieved;•Conversion to a0-efficient triangulation where possible for closed orientable3-manifolds [Jaco and Rubinstein03a];•Barycentric subdivision and the truncation of ideal vertices(vertices whose links are neither2-spheres nor discs);•Conversion of a non-orientable triangulation to an orientable double cover;•Crushing normal surfaces within a triangulation to a point,as described in Section2.3.2.22.2Census CreationRegina can form censuses of all3-manifold triangulations satisfying various sets of constraints.The census algorithm is described in[Burton07]and contains significant optimisations forcensuses of closed minimal P2-irreducible triangulations.In particular the face pairing graphresults of[Burton04]are incorporated into the algorithm,as are the more standard resultsrelating to low degree edges[Burton04,Callahan et al.99,Matveev98].Census creation can require significant amounts of computing time(months or years in some cases).As a result,support is provided for splitting this process into pieces and distributingthese pieces amongst several machines.In addition to forming new censuses,Regina ships with a number of prepackaged cen-suses including closed3-manifolds[Burton03,Burton07],cusped hyperbolic3-manifolds[Callahan et al.99]and knot and link complements(tabulated by Joe Christy).A censuslookup facility for arbitrary triangulations is provided.2.3Normal SurfacesThe theory of normal surfaces is a powerful tool for the study of3-manifolds and for thedevelopment of algorithms for their analysis.Normal surfaces were introduced by Kneser[Kneser29]and further developed by Haken[Haken61,Haken62]who used them to constructan algorithm for recognising the unknot.Haken furthermore began the construction of analgorithm for solving the homeomorphism problem for a certain large class of3-manifolds.Difficulties with the methods of Haken were resolved by Jaco and Oertel and by Hemion[Jaco and Oertel84,Hemion92],leading to afinite time algorithm for determining whethertwo closed irreducible3-manifolds are homeomorphic in the case in which one of these3-manifolds contains an embedded two-sided incompressible surface.Normal surfaces feature in a number of3-manifold decomposition,homeomorphism and recognition algorithms[Jaco et al.02,Jaco and Tollefson95,Rubinstein95,Rubinstein97]as well as in algorithms for the simplification of3-manifold triangulations[Jaco and Rubin-stein03a,Jaco and Rubinstein03b].For a more extensive review of normal surface theory,the reader is referred to[Hemion92].2.3.1CreationProviding a computational tool for the study of normal surfaces was in fact the originalmotivation behind this software.As such,Regina is capable of enumerating all vertex normalsurfaces or almost normal surfaces1within a triangulation,an operation required by mosthigh-level topological algorithms that utilise normal surface theory.Regina can perform this vertex enumeration in a variety of coordinate systems.For an n-tetrahedron triangulation this includes the7n standard triangle and quadrilateral coordi-nates,as well as the smaller set of3n quadrilateral-only coordinates introduced by Tollefsonfor algorithmic efficiency[Tollefson98].The enumeration can be restricted to embedded nor-mal surfaces or can be expanded to include immersed and singular surfaces.Furthermore,elementary support is present for spun normal surfaces,which are non-compact surfaces withinfinitely many discs found in ideal triangulations[Tillmann02].2.3.2AnalysisFor the analysis of normal surfaces,Regina offers the following facilities.•Viewing normal surfaces in a variety of coordinate systems,including the standard andquadrilateral-only coordinates discussed above as well as the edge weight coordinatesintroduced by Casson;•Calculating basic properties of normal surfaces such as Euler characteristic,orientabilityand one-sidedness;•Recognising standard surfaces within a triangulation such as splitting surfaces(see Sec-tion2.3.3below)and vertex and edge links;1Almost normal surfaces are closely related to normal surfaces and are used by Rubinstein in his3-sphere recognition algorithm[Rubinstein95,Rubinstein97].3•Filtering large lists of normal surfaces by various properties such as Euler characteristic, orientability and boundary.In addition the program can crush a normal surface to a point within a triangulation. Crushing is a powerful tool for the analysis of the role played by a surface within a3-manifold, and is used in Jaco and Rubinstein’s0-efficiency algorithm[Jaco and Rubinstein03a].2.3.3Splitting SurfacesSplitting surfaces represent a particular class of normal surfaces whose presence can offer insight into the triangulations containing them.A splitting surface contains precisely one quadrilateral disc within each tetrahedron and no other normal or almost normal discs.These surfaces have a number of interesting combinatorial and topological properties,described in detail in[Burton03].As mentioned earlier,Regina can detect whether splitting surfaces occur within a triangu-lation.It also provides support for splitting surface signatures,which are compact text-based representations from which splitting surfaces and their enclosing3-manifold triangulations can be reconstructed.In addition to performing such reconstructions,the software can form censuses of all possible splitting surface signatures of a given size.2.4Angle StructuresAngle structures,studied originally by Casson and then developed by Lackenby and Rivin [Lackenby00a,Lackenby00b,Rivin94,Rivin03],represent a purely algebraic generalisation of hyperbolic structures.An angle structure on an ideal triangulation is formed by assigning an interior dihedral angle to each edge of every tetrahedron in such a way that a variety of linear equations and inequalities are satisfied.The formation of angle structures is remarkably similar to the formation of normal surfaces, in which a series of triangle and quadrilateral coordinates are assigned to every tetrahedron with a set of linear equations and inequalities similarly imposed upon them.Thus it has been relatively straightforward to extend the normal surface enumeration code used by Regina in such a way that the software can also enumerate vertex angle structures.Included in the requirements of an angle structure is the condition that each dihedral angle θsatisfies0≤θ≤π.In addition to the enumeration of vertex angle structures,Regina can identify whether a triangulation supports any strict angle structures(for which each dihedral angleθsatisfies0<θ<π)or any taut angle structures(for which each dihedral angle is precisely0orπ).2.5ScriptingRegina offers the ability to write and run arbitrary scripts in the Python scripting language. These scripts are essentially high-level programs with immediate access to the mathematical core of Regina,and are ideal for performing repetitive tasks over large sets of data.Such tasks might include performing a sequence of tests upon all triangulations in a census,or testing a prototype for a new algorithm.Regina datafiles can contain embedded scripts,and different files can share code through the use of external libraries of routines.2.6Interfaces and DocumentationThe usual method of running Regina provides a full graphical interface that a user can easily understand and use.Alternatively,for those requiring immediate access to the mathematical core of the software,an interactive command-line interface is offered from which users can con-trol the program using the Python scripting language described above.A variety of specialised utility programs are also available.Significant effort has been spent on documentation for the software.A full reference manual is available for end users to assist them in working with Regina.This reference manual can be read online at /docs/.For users writing Python scripts or for programmers seeking to modify or extend the software,the routines offered by the underlying mathematical core are also fully documented.42.7Data FilesThe datafiles used for saving triangulations and other information adhere to a well-organised hierarchical structure.This structure not only allows multiple triangulations,normal surface lists and other topological structures to be stored together in an organised fashion but it also supports the storing of miscellaneous data such as text notes and Python scripts.Thefile format is well documented in the reference manual and uses compressed XML2,allowing for the simple transfer of native Regina data to and from other programs.3ApplicationsWe close with some examples of research projects in which Regina has been used with success.•In[Burton07]a census is presented of all closed non-orientable minimal P2-irreducible triangulations formed from≤putational support from Regina was required not only for the formation of the census but also for the detailed combinatorial analysis of the resulting triangulations.A similar census of orientable triangulations appears in[Burton03],again relying upon Regina for much computational support.•Various constraints upon the structures of minimal triangulations are proven in[Bur-ton04].For this research Regina was used to obtain and process data that originally motivated the results,as well as to measure the subsequent improvements to the census algorithm.•Research into the existence of taut angle structures on ideal triangulations is described in[Burton et al.03].Here Regina was used to process large bodies of census data to locate and subsequently analyse triangulations that do not support taut structures.•For the studies of0-efficiency and1-efficiency described in[Jaco and Rubinstein03a] and[Jaco and Rubinstein03b],Regina has assisted with the construction and analysis of pathological triangulations.AcknowledgementsThe author would like to acknowledge the support of the American Institute of Mathematics, the Australian Research Council and the Grayce B.Kerr Chair at Oklahoma State University. References[Burton03]Benjamin A.Burton.Minimal Triangulations and Normal Surfaces.PhD thesis, University of Melbourne,2003.Available from /.[Burton04]Benjamin A.Burton.“Face pairing graphs and3-manifold enumeration.”J.Knot Theory Ramifications,13(8):1057–1101,2004.[Burton07]Benjamin A.Burton.“Structures of small closed non-orientable3-manifold tri-angulations.”J.Knot Theory Ramifications,16(5):545–574,2007.[Burton et al.03]Benjamin A.Burton,Ensil Kang,and J.Hyam Rubinstein.“Triangulations of3-manifolds III:Taut structures in low-census manifolds.”In preparation,2003.[Callahan et al.99]Patrick J.Callahan,Martin V.Hildebrand,and Jeffrey R.Weeks.“A census of cusped hyperbolic3-manifolds.”p.,68(225):321–332,1999.[Haken61]Wolfgang Haken.“Theorie der Normalfl¨a chen.”Acta Math.,105:245–375,1961.[Haken62]Wolfgang Haken.“¨Uber das Hom¨o omorphieproblem der3-Mannigfaltigkeiten.I.”Math.Z.,80:89–120,1962.[Hemion92]Geoffrey Hemion.The Classification of Knots and3-Dimensional Spaces.Oxford Science Publications.Oxford University Press,Oxford,1992.2XML is the Extensible Markup Language,an open and widely-supported text-based data format.5[Jaco et al.02]William Jaco,David Letscher,and J.Hyam Rubinstein.“Algorithms for es-sential surfaces in3-manifolds.”In Topology and Geometry:Commemorating SISTAG, number314in Contemporary Mathematics,pages107–124.Amer.Math.Soc.,Provi-dence,RI,2002.[Jaco and Oertel84]William Jaco and Ulrich Oertel.“An algorithm to decide if a3-manifold is a Haken manifold.”Topology,23(2):195–209,1984.[Jaco and Rubinstein03a]William Jaco and J.Hyam Rubinstein.“0-efficient triangulations of3-manifolds.”J.Differential Geom.,65(1):61–168,2003.[Jaco and Rubinstein03b]William Jaco and J.Hyam Rubinstein.“1-efficient triangulations of3-manifolds.”In preparation,2003.[Jaco and Rubinstein06]William Jaco and J.Hyam Rubinstein.“Layered-triangulations of 3-manifolds.”Preprint,arXiv:math/0603601,March2006.[Jaco and Tollefson95]William Jaco and Jeffrey L.Tollefson.“Algorithms for the complete decomposition of a closed3-manifold.”Illinois J.Math.,39(3):358–406,1995. [Kneser29]Hellmuth Kneser.“Geschlossene Fl¨a chen in dreidimensionalen Mannigfaltigkei-ten.”Jahresbericht der Deut.Math.Verein.,38:248–260,1929.[Lackenby00a]Marc Lackenby.“Taut ideal triangulations of3-manifolds.”Geom.Topol.,4: 369–395(electronic),2000.[Lackenby00b]Marc Lackenby.“Word hyperbolic Dehn surgery.”Invent.Math.,140(2): 243–282,2000.[Martelli and Petronio01]Bruno Martelli and Carlo Petronio.“Three-manifolds having com-plexity at most9.”Experiment.Math.,10(2):207–236,2001.[Matveev98]Sergei V.Matveev.“Tables of3-manifolds up to complexity 6.”Max-Planck-Institut f¨u r Mathematik Preprint Series,(67),1998.Available from http://www.mpim-bonn.mpg.de/html/preprints/preprints.html.[Rivin94]Igor Rivin.“Euclidean structures on simplicial surfaces and hyperbolic volume.”Ann.of Math.(2),139(3):553–580,1994.[Rivin03]Igor Rivin.“Combinatorial optimization in geometry.”Adv.in Appl.Math.,31(1): 242–271,2003.[Rubinstein95]J.Hyam Rubinstein.“An algorithm to recognize the3-sphere.”In Proceedings of the International Congress of Mathematicians(Z¨u rich,1994),volume1,pages601–611.Birkh¨a user,Basel,1995.[Rubinstein97]J.Hyam Rubinstein.“Polyhedral minimal surfaces,Heegaard splittings and decision problems for3-dimensional manifolds.”In Geometric Topology(Athens,GA, 1993),volume2of AMS/IP Stud.Adv.Math.,pages1–20.Amer.Math.Soc.,Providence, RI,1997.[Tillmann02]Stephan Tillmann.On character varieties:surfaces associated to mutation& deformation of hyperbolic3-manifolds.PhD thesis,University of Melbourne,2002. [Tollefson98]Jeffrey L.Tollefson.“Normal surface Q-theory.”Pacific J.Math.,183(2):359–374,1998.[Turaev and Viro92]Vladimir G.Turaev and Oleg Y.Viro.“State sum invariants of3-manifolds and quantum6j-symbols.”Topology,31(4):865–902,1992.[Weeks91]Jeffrey R.Weeks.SnapPea.Hyperbolic3-manifold software,1991–2000.Available from /weeks/index/SnapPea.html.Benjamin A.Burton,Department of Mathematics and Statistics,The University of Melbourne, 3010VIC,Australia(**************)6。
1.图论Graph Theory1.1.定义与术语Definition and Glossary1.1.1.图与网络Graph and Network1.1.2.图的术语Glossary of Graph1.1.3.路径与回路Path and Cycle1.1.4.连通性Connectivity1.1.5.图论中特殊的集合Sets in graph1.1.6.匹配Matching1.1.7.树Tree1.1.8.组合优化Combinatorial optimization1.2.图的表示Expressions of graph1.2.1.邻接矩阵Adjacency matrix1.2.2.关联矩阵Incidence matrix1.2.3.邻接表Adjacency list1.2.4.弧表Arc list1.2.5.星形表示Star1.3.图的遍历Traveling in graph1.3.1.深度优先搜索Depth first search (DFS)1.3.1.1.概念1.3.1.2.求无向连通图中的桥Finding bridges in undirected graph1.3.2.广度优先搜索Breadth first search (BFS)1.4.拓扑排序Topological sort1.5.路径与回路Paths and circuits1.5.1.欧拉路径或回路Eulerian path1.5.1.1.无向图1.5.1.2.有向图1.5.1.3.混合图1.5.1.4.无权图Unweighted1.5.1.5.有权图Weighed —中国邮路问题The Chinese post problem1.5.2.Hamiltonian Cycle 哈氏路径与回路1.5.2.1.无权图Unweighted1.5.2.2.有权图Weighed —旅行商问题The travelling salesman problem1.6.网络优化Network optimization1.6.1.最小生成树Minimum spanning trees1.6.1.1.基本算法Basic algorithms1.6.1.1.1.Prim1.6.1.1.2.Kruskal1.6.1.1.3.Sollin（Boruvka）1.6.1.2.扩展模型Extended models1.6.1.2.1.度限制生成树Minimum degree-bounded spanning trees1.6.1.2.2.k小生成树The k minimum spanning tree problem(k-MST)1.6.2.最短路Shortest paths1.6.2.1.单源最短路Single-source shortest paths1.6.2.1.1.基本算法Basic algorithms1.6.2.1.1.1. ..................................................................................................... D ijkstra1.6.2.1.1.2. .......................................................................................... B ellman-Ford1.6.2.1.1.2.1.....................................Shortest path faster algorithm(SPFA)1.6.2.1.2.应用Applications1.6.2.1.2.1. ........................... 差分约束系统System of difference constraints1.6.2.1.2.2. .......................... 有向无环图上的最短路Shortest paths in DAG1.6.2.2.所有顶点对间最短路All-pairs shortest paths1.6.2.2.1.基本算法Basic algorithms1.6.2.2.1.1. ....................................................................................... F loyd-Warshall1.6.2.2.1.2. .................................................................................................... Johnson 1.6.3.网络流Flow network1.6.3.1.最大流Maximum flow1.6.3.1.1.基本算法Basic algorithms1.6.3.1.1.1. ........................................................................ Ford-Fulkerson method1.6.3.1.1.1.1.......................................................... E dmonds-Karp algorithm1.6.3.1.1.1.1.1. ................................................... M inimum length path1.6.3.1.1.1.1.2. ........................................... Maximum capability path1.6.3.1.1.2. ............................................... 预流推进算法Preflow push method1.6.3.1.1.2.1.................................................................................. P ush-relabel1.6.3.1.1.2.2........................................................................... Relabel-to-front1.6.3.1.1.3. .......................................................................................... Dinic method1.6.3.1.2.扩展模型Extended models1.6.3.1.2.1. ............................................................................... 有上下界的流问题1.6.3.2.最小费用流Minimum cost flow1.6.3.2.1.找最小费用路Finding minimum cost path1.6.3.2.2.找负权圈Finding negative circle1.6.3.2.3.网络单纯形Network simplex algorithm1.6.4.匹配Matching1.6.4.1.二分图Bipartite Graph1.6.4.1.1.无权图-匈牙利算法Unweighted - Hopcroft and Karp algorithm1.6.4.1.2.带权图-KM算法Weighted –Kuhn-Munkres(KM) algorithm1.6.4.2.一般图General Graph1.6.4.2.1.无权图-带花树算法Unweighted - Blossom (Edmonds)1.图论Graph Theory1.1. 定义与术语Definition and Glossary1.1.1.图与网络Graph and Network二元组(),V E称为图(graph)。
CS 668 - Spring ‘06Student Research Presentations(RB 122)Date/Time Presenter TitleMonday, April 10 4:00 pm Fabien Poulard Utility of random generated graphs tooptimize peer-to-peer networksMonday, April 10 4:30 pm Todd Chaffins Performance Comparison of VertexColoring Algorithms on CPUs and GPUsWednesday, April 12 4:00 pm James Haberly Graph-theoretic image processingtechniquesWednesday, April 124:30 pmMahbub Majumder Graceful labeling of treesMonday, April 17 4:00 pm Hsiaoying Su Path-finding - An application of graphtheory in computer gamesMonday, April 17 4:30 pm Mandeep SinghAtwalTree Vertex Splitting Problem -Applications to Distribution NetworksWednesday, April 19 4:00 pm Bryan Ritz Analysis of Techniques Used in DrawingGraphs with Subgraphs (with Case Study) See the following pages for abstracts.Monday, April 104:00 pmUtility of random generated graphs to optimize peer-to-peer networksFabien PoulardThe first peer-to-peer networks emerged with the Gnutella protocol in the early 2000, thanks to a team of developers at Nullsoft. When tested in a lab, the protocol was able to manage some hundreds nodes; but when released, it was quickly used by thousands of users, creating as much nodes and revealing the weaknesses of its conception. Since then the peer-to-peer has evolved and some others protocols have appeared, fixing partially the weaknesses of Gnutella. However, those protocols do not really implement a real peer-to-peer network, but a kind of topologically hybrid network sharing characteristics of the decentralized topology and some characteristics from other topologies (most likely hierarchy and centralized).As at the origins the peer-to-peer was developed to share music files (Nullsoft develops a widely used mp3 player product) “illegally”, there was no more research to extend the capabilities and exploit the peer-to-peer networks. However, nowadays, peer-to-peer is considered as a possible topology for a lot of networks, and especially for the mobile device applications. So, improving the algorithms at the origin of Gnutella becomes industrially interesting.Much progress has been achieved in the last few years, especially due to graph theory. The main issues to resolve are about preserving the connectivity of the graph when adding or removing a peer and in making the graph evolve towards an expander graph to optimize the exchanges between clients. However, the huge constraint is to make that happen with a minimum number of transactions considering that each manipulation of the network implies latencies and loss of packets that will have to be resent. Another issue is the fault tolerance, as each node can fail due to the extreme heterogeneity of the network, it must always be possible to find another path from one node to another.The different techniques I will try to cover during the presentation are based on the random transformation of regular graphs and the de Bruijn graphs. We will see how they can be applied to the original Gnutella to improve its efficiency without losing its decentralized characteristics.References• Peer-to-peer Networks based on Random Transformations of Connected Regular Undirected Graphs, P. Mahlmann, C. Schindelhauer, ACM July 2005• Graph-Theoretic Analysis of Structured Peer-to-Peer Systems : Routing Distances and Fault Resilience, D. Loguinov, J. Casas, X. Wang, IEEE/ACM Transactions on Networking • Distributed Construction of Random Expander Networks, C. Law, K. Siu, IEEE INFOCOM• The diameter of random massive graphs, L. Lu, Proceedings of the twelfth annual ACMSIAM symposium on Discrete algorithms• Generating Random Regular Graphs, J.H. Kim, V.H. Vu, Proceedings of the thirty-fifth annual ACM symposium on Theory of computing• On the Fundamental Tradeoffs Between Routing Table Size and Network Diameter in Peer-to-peer Networks, J. Xu, IEEE INFOCOMMonday, April 104:30 pmPerformance Comparison of Vertex Coloring Algorithms on CPUs and GPUsTodd ChaffinsCurrent high-end graphics processing units (GPUs) have evolved from dump co-processors with fixed functionality into highly capable stream processors. [Purcell, et al. 2002] In the ever-growing games industry there is a demand to be able to create more realistic graphics and effects. The current trend is to create these realistic graphics and effects through the use of graphics code known as shaders [Harris, et al. 2003]. Shaders are small pieces of code which determine how graphics are rendered on the screen. These shaders and their adoption in games require the graphics card manufacturers to create faster and more programmable GPUs. This pressure will continue and as such the speed and programmability of GPUs are set to continue to increase as time goes on. [Christen 2005]This increase in processing power and the parallel nature of GPUs has led to the adoption of the GPU for general purpose computations outside of the realm of graphics. While the GPU has made vaster architectural changes over recent years CPUs have also made advances. Aside from the common increases associated with CPUs (clock speed and cache), CPUs have moved to be more parallel with a dual-core architecture. With parallel vertex-coloring algorithms [Kale, et al. 1995] the question is raised as to which approach will yield the fastest results when performing vertex-coloring: CPU based, GPU based, or a hybrid CPU/GPU approach. This research seeks to implement, instrument, and measure the performance of these approaches in a quantitative manner and evaluate the economy of these approaches.References:[Purcell, et al. 2002] Purcell, T.J., Buck, I., Mark, W.R. and Hanrahan, P. Ray Tracing on Programmable Graphics Hardware. In Proceedings of SIGGRAPH 2002, ACM / ACM Press. 2002.[Christen 2005] Christen M.: Ray Tracing on GPU. Diploma thesis, University of Applied Sciences Basel, Switzerland, 2005.[Kale, et al. 1995] L. V. Kale, B. H. Richards, and T. D. Allen. Efficient parallel graph coloring with prioritization. In Lecture Notes in Computer Science, volume 1068, pages 190{208. Springer-Verlag, August 1995.[Harris, et al. 2003] Mark Harris, Greg James, Physically-Based Simulation on Graphics Hardware, GameDevelopers Conference, 2003.Wednesday, April 124:00 pmGraph-theoretic image processing techniquesJames HaberlyThe aim of my proposed topic would be to present an exposition on Graph Theoretic approaches and algorithms as they’re being researched for use in image processing and machine vision. Some example problems in the area of image processing and machine vision are; computational complexity, object recognition, object measurement, image segmentation, edge detection, noise detection and filtering, line, arc and other feature detection, image coding and compression.The project will be focused on presenting how graph theoretic algorithms with examples such as the Prim and Kruskal algorithms for minimum spanning trees, Dijkstra’s and Dial's shortest path and graph theoretic Euclidean distance mapping techniques are being examined for problem solving in the image processing and machine vision fields.I do not want to yet limit the scope of this proposal by proposing an exposition on any one paper or problem since I’m just beginning the research phase of the project. A couple specific areas that may become the main focus of the project are:1. Improvements in computational speed using graph-theoretic image processing techniques [1].2. Object recognition using a graph theoretical approach [2].The image processing and machine vision industry is a fast growing and exciting field. I’m looking forward to researching the topic further.References:[1] “Faster Graph-Theoretic Image Processing via Small-World and Quadtree Topologies” Leo Grady and Eric L. Schwartz Dept. of Imaging & Visualization, Siemens Corp. Res. Inc., Princeton, NJ, USA; This paper appears in: Computer Vision and Pattern Recognition, 2004. CVPR 2004. Proceedings of the 2004 IEEE Computer Society Conference on Publication Date: 27 June-2 July 2004Volume: 2, On page(s): II-360- II-365 Vol.2[2] "Color Invariant Object Recognition using Entropic Graphs" Jan C. van Gemert, Gertjan J. Burghouts, Frank J. Seinstra, Jan-Mark Geusebroek Intelligent Systems Lab Amsterdam, Informatics Institute, University of Amsterdam, Kruislaan 403, 1098 SJ Amsterdam, The Netherlands.[3] “Graph-Theoretical Methods in Computer Vision” Ali Shokoufandeh1 and Sven Dickinson2 G.B. Khosrovshahi et al. (Eds.): Theoretical Aspects of Computer Science, LNCS 2292, pp. 148–174, 2002.Wednesday, April 124:30 pmGraceful labeling of TreesMahbub MajumderA tree T with n vertices is said to be gracefully labeled if its vertices are labeled with the integers [1..n] such that the edges, when labeled with the difference between their endpoint vertex labels, are uniquely labeled with the integers [1..n-1]. If T can be gracefully labeled, it is called a “graceful tree”.The concept of graceful labeling of trees and graphs was introduced by Rosa (1967). The term “graceful labeling” was invented by Golomb (Golomb 1972). The Graceful Tree Conjecture states that all trees are graceful. There have been over 670 papers to date on various graph labeling methods and issues (Gallian 2005). So far, no proof of the truth or falsity of the conjecture has been found. Even though the conjecture is open, some partial results have been proved (Gallian 2005).My motivation in pursuing this project came from its nature and the study many people have put into it. My aim with this project work is to1.Find out current works and results.2.Study and understand the condition of gracefulness3.If possible, add some ideas in graceful LabelingReferences:Gallian J. A., A Dynamic Survey of Graph Labeling (2005), Electronic Journal of Combinatorics.Golomb S.W. How to number a graph. In R.C. Read, editor, Graph Theory and Computing, pages 23-37. Academic Press, 1972.Rosa A., On certain valuations of the vertices of a graph, Theory of Graphs (Internat. Symposium, Rome, July 1966), Gordon and Breach, N.Y. and Dunod Paris (1967) 349-355.Monday, April 174:00 pmPath-finding - An application of graph theory in computer gamesHsiaoying SuGraph theory is widely used in solving and presenting computer games. One of the most common applications is path-finding. Path-finding algorithms grant agents in the virtual world the ability to consciously find their own way around the land. They can also be used in real life to find driving directions, such as the service offered by many popular web sites. The project is going to focus on the game implementation.Path-finding algorithms are usually, but not only, used in computer games catalogued as role playing games (RPGs). Programmers build a virtual world for the games. The characters, or called autonomous agents, have certain level of artificial intelligence. The simplest way to present their intelligence is to find their own paths moving around the world without hitting a tree or going through a wall. The successful implementation of path-finding is important to the artificial intelligence performance of a game.According to the numbers of sources and destinations, path-finding algorithms can be roughly divided into three categories: single source, single pair, and all pairs. In single source algorithms, the path from one node to all the others is required. However, single pair algorithms take a specific source and destination. Only one path is required in response. The all pairs algorithm returns the shortest paths from every node to all other nodes.This project plans to explore different path-finding algorithms and their complexity. Furthermore, coding these algorithms in JEdit and practically experiment their efficiency. In single source algorithms, Dijkstra’s Algorithm and Bellman-Ford-Moore, which deals with negative arc-lengths graph, would be discussed. Then, the most popular algorithm A* (A star) would be presented to implement single-pair shortest path finding. To find out all-pairs shortest paths, the algorithms described above could be used in a naïve but inefficient way. The project then would seek out whether there exist more efficient algorithms to solve the problem.Path-finding related topics have been discussed on more application than research. However, there are still some interesting studies going on. One of a recent research is about solving incoherent behavior of multiple units in a cluttered environment. Another one is to discuss an open problem of emulating the rich complexity of real pedestrians in urban environment. The two papers are listed below as references.References•Kamphuis A., Overmars M. H.: Motion planning: Finding Paths for Coherent Groups using Clearance. In Eurographics/ACM SIGGRAPH Symposium on Computer Animation (2004).•Shao W., Terzopoulos D.: Artificial intelligence for animation: Autonomous pedestrians. In Eurographics/ACM SIGGRAPH Symposium on Computer Animation (2005).Monday, April 174:30 pmTree Vertex Splitting Problem - Applications to Distribution NetworksMandeep Singh AtwalIn an Ethernet network, the number of connections (taps) and their intervening distances are limiting factors [BN90]. Repeaters are used to regenerate the signal every 500 meters or so [BN90]. If these repeaters were not used, “standing waves” (additive reflections) would distort the signal and cause errors [BN90]. Because collision detection depends partly on timing, only five 500-meter segments and four repeaters can be placed in series before the propagation delay becomes longer than the maximum allowed time period for detecting a collision [BN90].Directed acyclic graphs (dags) or directed trees can be used to model such interconnection networks. Each edge of such a tree is labeled with a real number called its weight. Trees with edge weights are called weighted trees. Nodes or vertices in the tree correspond to receiving stations and edges correspond to transmission lines [HSR98]. Each edge weight corresponds to the delay in traversing that edge [HSR98]. However, as stated above, the network may not be able to tolerate losses in signal strength beyond a certain level.In places where the loss exceeds the tolerance level, repeaters have to be placed. Given a network and a loss tolerance level Tree Vertex Splitting Problem is to determine an optimal placement of repeaters.RESEARCH OBJECTIVESThe proposed research aims at the study of Tree Vertex Splitting Problem (TVSP). Designing the algorithms for TVSP and analyzing in terms of the computing time and space requirements. The most efficient algorithm can then possibly be implemented inC++/Java.However, it is not an objective to implement the algorithm for the proposed study. REFERENCES[BN90] Barry Nance, Network Programming in C, QUE Corporation 1990,ISBN: 0-88022-569-6, page # 23.[HSR98] Ellis Horowitz, Sartaj Sahni, Sanguthevar Rajasekaran, Fundamentals of Computer Algorithms, Galgotia Publications’ Pvt. Ltd. 1998,ISBN: 81-7515-257-5, page # 203.[PRS98] Doowon Paik, Sudhakar Reddy, Sartaj Sahni, Vertex Splitting In Dags And Application To Partial Scan Designs And Lossy Circuits, International Journal of Foundations of Computer Science, 1998.[ME93] Matthias Mayer, Fikret Ercal, Genetic Algorithms for Vertex Splitting in DAGs, Proceedings of the 5th International Conference on Genetic Algorithms, 1993, ISBN: 1-55860-299-2[SR96] Stephanie Forrest, Genetic Algorithms, ACM Computing Surveys, Vol. 28, No. 1, March 1996.Wednesday, April 194:00 pmAnalysis of Techniques Used in Drawing Graphs with Subgraphs(with Case Study)Bryan RitzIn the paper “Drawing Graphs Within Graphs” [5] by Paul Holleis, Thomas Zimmermann, and Daniel Gmach, the authors present methods for helping to reduce complexity of large and complicated graphs and subgraphs. The methods of finding an optimal layout of subgraphs and a summary graph, of the use of connection sets, and of the use of motifs are all combined into an approach for emphasizing subgraphs within graphs. This paper will attempt to evaluate the worthiness of these methods through examination of sources used in the paper and by applying the methods to a case study in the form of a complex graph (displayed using JEdit).References:1. F. J. Brandenburg. Graph clustering 1: Cycles of cliques. In Proceedings of the Graph Drawing 1997, volume 1353 of Lecture Notes in Computer Science, Berlin, Germany, 1997. Springer.2. G. Di Battista, P. Eades, R. Tamassia, and I. G. Tollis. Graph Drawing: Algorithms for the Visualization of Graphs. Prentice-Hall, Englewood Cliffs, N.J., 1999.3. T. M. J. Fruchterman and E. M. Reingold. Graph drawing by force-directed placement. Software-Practice and Experience, 21(11):1129-1164, 1991.4. T. Kamada and S. Kawai. An algorithm for drawing general undirected graphs. Information Processing Letters, 31(1):7-15, 1989.5. P. Holleis, T. Zimmermann, D. Gmach. Drawing Graphs Within Graphs. Journal of Graph Algorithms and Applications, 9(1):7-18, 2005.Case Study will use TouchGraph as applied to .1) Go to /TGGoogleBrowser.html2) Enter “” without the quotes in the text field and hit enter.。
